冀教版九年级数学上册知识点
- 格式:docx
- 大小:148.66 KB
- 文档页数:6

冀教版九年级数学知识点学习这件事不在乎有没有人教你,最重要的是在于你自己有没有觉悟和恒心。
任何科目学习方法其实都是一样的,不断的记忆与练习,使知识刻在脑海里。
下面是小编给大家整理的一些九年级数学的知识点,希望对大家有所帮助。
九年级数学知识点空间与图形图形的认识:1、点,线,面点,线,面:①图形是由点,线,面构成的。
②面与面相交得线,线与线相交得点。
③点动成线,线动成面,面动成体。
展开与折叠:①在棱柱中,任何相邻的两个面的交线叫做棱,侧棱是相邻两个侧面的交线,棱柱的所有侧棱长相等,棱柱的上下底面的形状相同,侧面的形状都是长方体。
②N棱柱就是底面图形有N条边的棱柱。
截一个几何体:用一个平面去截一个图形,截出的面叫做截面。
视图:主视图,左视图,俯视图。
多边形:他们是由一些不在同一条直线上的线段依次首尾相连组成的封闭图形。
弧,扇形:①由一条弧和经过这条弧的端点的两条半径所组成的图形叫扇形。
②圆可以分割成若干个扇形。
角线:①线段有两个端点。
②将线段向一个方向无限延长就形成了射线。
射线只有一个端点。
③将线段的两端无限延长就形成了直线。
直线没有端点。
④经过两点有且只有一条直线。
比较长短:①两点之间的所有连线中,线段最短。
②两点之间线段的长度,叫做这两点之间的距离。
角的度量与表示:①角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点。
②一度的1/60是一分,一分的1/60是一秒。
角的比较:①角也可以看成是由一条射线绕着他的端点旋转而成的。
②一条射线绕着他的端点旋转,当终边和始边成一条直线时,所成的角叫做平角。
始边继续旋转,当他又和始边重合时,所成的角叫做周角。
③从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线。
平行:①同一平面内,不相交的两条直线叫做平行线。
②经过直线外一点,有且只有一条直线与这条直线平行。
③如果两条直线都与第3条直线平行,那么这两条直线互相平行。

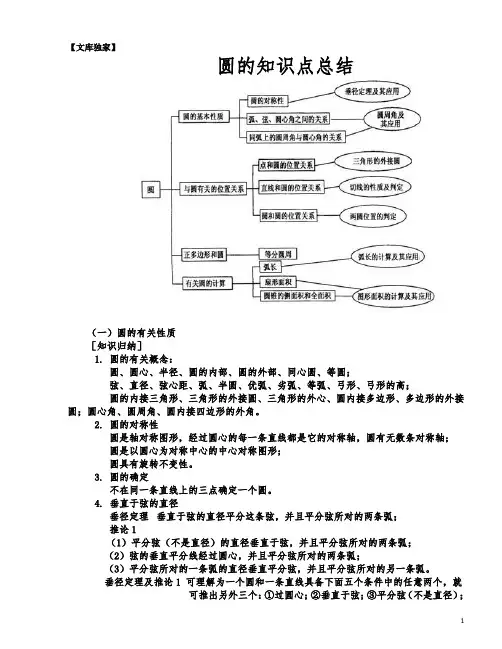
【文库独家】圆的知识点总结(一)圆的有关性质[知识归纳]1. 圆的有关概念:圆、圆心、半径、圆的内部、圆的外部、同心圆、等圆;弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、弓形的高;圆的内接三角形、三角形的外接圆、三角形的外心、圆内接多边形、多边形的外接圆;圆心角、圆周角、圆内接四边形的外角。
2. 圆的对称性圆是轴对称图形,经过圆心的每一条直线都是它的对称轴,圆有无数条对称轴;圆是以圆心为对称中心的中心对称图形;圆具有旋转不变性。
3. 圆的确定不在同一条直线上的三点确定一个圆。
4. 垂直于弦的直径垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧;推论1(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
垂径定理及推论1 可理解为一个圆和一条直线具备下面五个条件中的任意两个,就可推出另外三个:①过圆心;②垂直于弦;③平分弦(不是直径);④平分弦所对的优弧;⑤平分弦所对的劣弧。
推论2圆的两条平行弦所夹的弧相等。
5. 圆心角、弧、弦、弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;所对的弦的弦心距相等。
推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
此定理和推论可以理解成:在同圆或等圆中,满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等;②两个圆心角所对的弧相等;③两个圆心角或两条弧所对的弦相等;④两条弦的弦心距相等。
圆心角的度数等于它所对的弧的度数。
6. 圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半;推论1同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧也相等;推论2半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径;推论3如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。




冀教版九年级上册数学考点在人类历史发展和社会生活中,数学发挥着不可替换的作用,同时也是学习和研究现代科学技术必不可少的基本工具。
不同的数学家和哲学家对数学的确切范畴和定义有一系列的看法。
今天作者在这给大家整理了一些冀教版九年级上册数学考点,我们一起来看看吧!冀教版九年级上册数学考点☆内容提要☆一、平面直角坐标系1.各象限内点的坐标的特点2.坐标轴上点的坐标的特点3.关于坐标轴、原点对称的点的坐标的特点4.坐标平面内点与有序实数对的对应关系二、函数1.表示方法:⑴解析法;⑵列表法;⑶图象法。
2.肯定自变量取值范畴的原则:⑴使代数式成心义;⑵使实际问题有意义。
3.画函数图象:⑴列表;⑵描点;⑶连线。
三、几种特别函数(定义→图象→性质)1. 正比例函数⑴定义:y=kx(k≠0) 或y/x=k。
⑵图象:直线(过原点)⑶性质:①k 0,…②k 0,…2. 一次函数⑴定义:y=kx+b(k≠0)⑵图象:直线过点(0,b)—与y轴的交点和(-b/k,0)—与x轴的交点。
⑶性质:①k 0,…②k 0,…⑷图象的四种情形:3. 二次函数⑴定义:特别地,都是二次函数。
⑵图象:抛物线(用描点法画出:先肯定顶点、对称轴、开口方向,再对称地描点)。
用配方法变为,则顶点为(h,k);对称轴为直线x=h;a 0时,开口向上;a 0时,开口向下。
⑶性质:a 0时,在对称轴左侧…,右侧…;a 0时,在对称轴左侧…,右侧…。
4.反比例函数⑴定义:或xy=k(k≠0)。
⑵图象:双曲线(两支)—用描点法画出。
⑶性质:①k 0时,图象位于…,y随x…;②k 0时,图象位于…,y随x…;③两支曲线无穷接近于坐标轴但永久不能到达坐标轴。
四、重要解题方法1. 用待定系数法求解析式(列方程[组]求解)。
对求二次函数的解析式,要公道选用一样式或顶点式,并应充分运用抛物线关于对称轴对称的特点,寻觅新的点的坐标。
以下图:2.利用图象一次(正比例)函数、反比例函数、二次函数中的k、b;a、b、c的符号。


新冀教版九年级上册数学全册期末复习必背知识点归纳1. 有理数的四则运算- 加法:有理数相加时保留同号后合并绝对值,异号先转化为同号再合并绝对值。
- 减法:有理数相减转化为加法,注意减去一个数等于加上这个数的相反数。
- 乘法:有理数相乘符号同正负规律,绝对值相乘。
- 除法:有理数相除符号同正负规律,绝对值相除。
2. 代数式与多项式- 代数式:由数字、字母及运算符号组成的式子。
- 多项式:由多个代数项经过加法或减法运算得到的代数式。
3. 分式与整式- 分式:由分子和分母分别用代数式表示的符号。
- 整式:没有分式的代数式。
4. 图形的坐标表示- 直角坐标系:一个平面上以两条互相垂直的直线为基准线,确定平面上的点位置。
- 坐标:平面上的点在直角坐标系中的位置。
5. 一次函数- 函数:根据一些输入值通过某种规则得到输出值的关系。
- 一次函数:函数的自变量的最高次数为1的函数。
6. 二次根式- 平方根:数的平方根是指一个数的平方等于这个数。
- 二次根式:含有平方根的式子。
7. 平面图形与空间图形- 平面图形:在平面上画出的图形。
- 空间图形:在空间中用线段、射线、直线画的图形。
8. 数据的收集整理与概述- 数据收集:通过观察或实验,获得或记录相关事物数量或特征的过程。
- 数据整理:对收集到的数据进行筛选、处理和归纳,并用合适的图表形式展示。
- 数据概述:根据数据的统计特征和分布规律描述、分析和总结数据。
9. 事件与概率- 事件:对随机试验可能结果的划分。
- 概率:事件发生的可能性。
10. 统计抽样与统计推断- 统计抽样:从总体中抽取样本进行统计。
- 统计推断:通过对样本的统计数据作出关于总体的推断。
以上是《新冀教版九年级上册数学全册》期末复习必背知识点的详细归纳,希望能对你的复习有所帮助。

冀教版九年级数学上册知识点23章数据分析23.1 平均数和加权平均数平均数是指n个数的和与n的比值,也称为算术平均数,记作x。
我们一般用x = (x1 + x2 +。
+ xn)/n来计算平均数。
若已知n个数x1.x2.xn和一组正数w1.w2.wn,则这n个数的加权平均数为(x1w1 + x2w2 +。
+ xnwn)/(w1 + w2 +。
+ wn),其中w1.w2.wn分别为这n个数的权重。
23.2 中位数和众数中位数是指将n个数据按大小顺序排列后,如果n为奇数,则处于中间位置的数据为中位数;如果n为偶数,则处于中间位置的两个数据的平均数为中位数。
众数是指一组数据中出现次数最多的数据。
一组数据的众数可能不止一个,也可能没有众数。
23.3 方差方差是指n个数据与平均数之差的平方的平均数,用s^2表示。
具体地,设n个数据的平均数为x,各个数据与平均数之差的平方分别为(x1-x)^2.(x2-x)^2.(xn-x)^2,则这组数据的方差为s^2 = [(x1-x)^2 + (x2-x)^2 +。
+ (xn-x)^2]/n。
方差的大小反映了数据波动(或离散程度)的大小,当数据分布比较分散时,方差较大;当数据分布比较集中时,方差较小。
23.4 用样本估计总体由于抽样的任意性,相同样本容量的不同样本的平均数一般也不同。
当样本容量较小时,差异可能还较大。
但是当样本容量增大时,样本的平均数的波动变小,逐渐趋于稳定,且与总体的平均数比较接近。
因此,在实际中经常用样本的平均数估计总体的平均数。
同样的道理,我们也用样本的方差估计总体的方差。
24章一元二次方程24.1 一元二次方程一元二次方程是指只含有一个未知数,且未知数的最高次数为2的整式方程。
一元二次方程的一般形式为ax^2 + bx + c = 0,其中a≠0.其中,ax^2是二次项,a是二次项系数,bx是一次项,b是一次项系数,c是常数项。
一元二次方程的解也称为这个方程的根。

初三数学知识点冀教版初三数学知识点归纳三角形的垂心的性质:1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
2.三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
例如在△ABC中3.垂心O关于三边的对称点,均在△ABC的外接圆圆上。
4.△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形。
5.H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
6.△ABC,△ABO,△BCO,△ACO的外接圆是等圆。
7.在非直角三角形中,过O的直线交AB、AC所在直线分别于P、Q,则AB/AP?tanB+AC/AQtanC=tanA+tanB+tanC8.三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
9.设O,H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA.10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
11.锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短。
12.西姆松(Simson)定理(西姆松线):从一点向三角形的三边所引垂线的垂足共线的重要条件是该点落在三角形的外接圆上。
13.设H为非直角三角形的垂心,且D、E、F分别为H在BC,CA,AB上的射影,H1,H2,H3分别为△AEF,△BDF,△CDE的垂心,则△DEF≌△H1H2H3.14.三角形垂心H的垂足三角形的三边,分别平行于原三角形外接圆在各顶点的切线。
九年级上册数学复习知识点考点1:确定事件和随机事件考核要求:(1)理解必然事件、不可能事件、随机事件的概念,知道确定事件与必然事件、不可能事件的关系;(2)能区分简单生活事件中的必然事件、不可能事件、随机事件。
考点2:事件发生的可能性大小,事件的概率考核要求:(1)知道各种事件发生的可能性大小不同,能判断一些随机事件发生的可能事件的大小并排出大小顺序;(2)知道概率的含义和表示符号,了解必然事件、不可能事件的概率和随机事件概率的取值范围;(3)理解随机事件发生的频率之间的区别和联系,会根据大数次试验所得频率估计事件的概率。
23章 数据分析23.1平均数和加权平均数1、一般地,我们把n 个数n x x x ,...,,21的和与n 的比,叫做这n 个数的算术平均数,简称平均数,记作-x ,读作“x 拔”,即)....(11n x x nx ++=-2、已知n 个数n x x x ,...,,21,若n w w w ,...,,21为一组正数,则把nnn w w w w x w x w x ......212211+++++叫做n 个数n x x x ,...,,21的加权平均数,n w w w ,...,,21分别叫做这n 个数的权重,简称权。
23.2中位数和众数1、一般地,将n 个数据按大小顺序排列,如果n 为奇数,那么把处于中间位置的数据叫做这组数据的中位数;如果n 为偶数,那么把处于中间位置的两个数据的平均数叫做这组数据的中位数。
2、一般地,把一组数据中出现次数最多的那个数据叫做众数。
一组数据的众数可能不止一个,也可能没有众数。
23.3方差 设n个数据n x x x ,...,,21的平均数为-x ,各个数据与平均数偏差的平方分别是22221)(,...,)(,)(------x x x x x x n 。
偏差平方的平均数叫做这组数据的方差,用2s 表示,即⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-++-+-=---222212)(...)()(1x x x x x x n s n当数据分布比较分散时,方差较大;当数据分布比较集中时,方差较小。
因此,方差的大小反映了数据波动(或离散程度)的大小。
23.4用样本估计总体由于抽样的任意性,即使是相同的样本容量,不同样本的平均数一般也不同;当样本容量较小时,差异可能还较大。
但是当样本容量增大时,样本的平均数的波动变小,逐渐趋于稳定,且与总体的平均数比较接近。
因此,在实际中经常用样本的平均数估计总体的平均数。
同样的道理,我们也用样本的方差估计总体的方差。
24章 一元二次方程 24.1一元二次方程1、只含有一个未知数,并且未知数的最高次数为2的整式方程,叫做一元二次方程。
一元二次方程的一般形式为).0(02≠=++a c bx ax 其中,2ax是二次项,a 是二次项系数,bx 是一次项,b 是一次项系数,c 是常数项。
一元二次方程的解也叫做这个方程的根。
24.2解一元二次方程1、配方法:通过配方,把一元二次方程变形为一边为含未知数的一次式的平方,另一边为常数,当常数为非负数时,利用开平方,将一元二次方程转化为两个一元一次方程,从而求出原方程的根。
配方时,先将常数项移至等号右边,然后将二次项系数化为1,再在方程两边同时加上一次项系数一半的平方。
2、对于一元二次方程02=++c bx ax : 当042>-ac b 时,方程有两个不相等的实数根; 当042=-ac b 时,方程有两个相等的实数根; 当042<-ac b 时,方程没有实数根。
我们把ac b 42-叫做一元二次方程02=++c bx ax 的根的判别式。
3、当042≥-ac b 时,一元二次方程02=++c bx ax 的两实数根可以用aac b b x 242-±-=求出。
这个式子叫做一元二次方程的求根公式。
利用求根公式解一元二次方程的方法叫做公式法。
4、因式分解法:把一元二次方程的一边化为0,另一边分解成两个一次因式的乘积,进而转化为两个一元一次方程,从而求出原方程的根。
24.3 一元二次方程根与系数关系如果一元二次方程02=++c bx ax 的两根分别为21,x x ,那么ac x x a b x x =•-=+2121,。
24.4一元二次方程的应用 25章 图形的相似 25.1比例线段1、如果选用同一度量单位,量得线段a 和b 的长度分别为m 和n ,我们就把m 和n 的比叫做线段a 和b 的比,记作n m b a ::=,或nmb a =。
2、在四条线段dc b a ,,,中,如果a 与b 的比等于c 与d 的比,即dcb a =,我们就把这四条线段叫做成比例线段,简称比例线段。
此时也称这四条线段成比例。
3、比例的基本性质如果dcb a =,那么bc ad =。
如果bc ad =,那么d cb a =(0,≠d b )特别地,如果cb b a =,即ac b =2,就把b 叫做a,c 的比例中项。
如果k n m d c b a ====...,那么k nd b m c a =++++++......4、黄金分割在线段AB 上有一点C ,如果点C 把AB 分成的两条线段AC 和BC 满足ACBCAB AC =,那么称线段AB 被点C 黄金分割,点C 称为线段AB 的黄金分割点,ABAC称为黄金比。
黄金比618.0215≈-=AB AC 每条线段上的黄金分割点都有两个。
25.2 平行线分线段成比例 (1) 基本事实两条直线被一组平行线所截,截得的对应线段成比例。
对应线段是指两条直线被一组平行线所截得的线段(AB 与DE 、BC 与EF 、AC 与DF),对应线段成比例是指同一直线上的两条线段的比,等于另一条直线上与它们对应的线段的比。
DFEFAC BC DF DE AC AB EF DE BC AB ===,, (2)推论1平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
ACCEAB BD EC AE DB AD AC AE AB AD ===,, (3) 推论2平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例。
在△ABC 中,DE ∥BC ,BCDEAC AE AB AD == 25.3相似三角形(1)对应角相等、对应边成比例的两个三角形叫做相似三角形,相似三角形对应边的比叫做它们的相似比。
如果两个三角形相似,那么它们的对应角相等,对应边成比例。
(2)利用平行线分线段成比例判定两个三角形相似平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截得的三角形与原三角形相似。
25.4 相似三角形的判定 相似三角形的判定定理(1) 两角对应相等的两个三角形相似。
(2) 两边对应成比例且夹角相等的两个三角形相似。
(3) 三条边对应成比例的两个三角形相似。
(4) 直角边和斜边对应成比例的两个直角三角形相似。
25.5 相似三角形的性质 相似三角形的性质定理(1)相似三角形对应高的比、对应中线的比、对应角平分线的比,都等于相似比。
(2)相似三角形周长的比等于相似比。
(3)相似三角形面积的比等于相似比的平方。
l 3l 2l 1F E D C B AAB C DEEDC BAEDCBA25.7 相似多边形和图形的位似(1)形状相同的图形称为相似图形。
一般地,如果两个多边形的对应角相等、对应边成比例,那么这两个多边形就叫做相似多边形。
相似多边形对应边的比叫做它们的相似比。
(2)两个图形不仅相似,而且经过每对对应顶点的直线相交于一点,对应边互相平行(或重合),我们把这样的两个图形称为位似图形,对应顶点所在直线的交点称为位似中心,这时的相似比又称位似比。
(3)位似图形的画法①确定位似中心(位似中心可以在图形外部、图形内部或图形的边上);②选取图形的关键点(一般是顶点)并分别连接各关键点与位似中心,并延长成射线; ③根据位似比在射线上取点,得到各关键点的对应点; ④顺次连接各对应点,得到相应的位似图形。
26章 解直角三角形 26.1 锐角三角函数1、如图,在Rt △ABC 中,∠C=90°∠A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即batan =∠∠=的邻边的对边A A A∠A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即casin =∠=斜边的对边A A∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即cbcos =∠=斜边的邻边A A2、一些特殊角的三角函数值3、在直角三角形中,锐角α的对边与斜边的比、邻边与斜边的比以及对边与邻边的比,都是唯一确定的;当锐角α变化时,相应的比值也会发生相应的变化。
我们把锐角α的正弦、余弦和正切统称为α的三角函数。
为方便起见,今后将()()()222tan ,cos ,sin ααα分别记作ααα222tan ,cos ,sin 。
30° 45° 60° sinα12 22 32 cosα32 2212 tanα 331 326.3解直角三角形1、在直角三角形中,除直角外,还有三条边和两个锐角共五个元素。
由这五个元素中的已知元素求出其余未知元素的过程,叫做解直角三角形。
2、在Rt △ABC 中,∠C=90° 三边之间的关系是222c b a =+; 两锐角之间的关系是 90=∠+∠B A ; 边角之间的关系是c asin =∠=斜边的对边A Ac bcos =∠=斜边的邻边A A b atan =∠∠=的邻边的对边A A A在边角之间的关系中,将∠A 换成∠B ,同时将a,b 交换,即可得到∠B 与边之间的关系式。
根据以上关系,如果知道五个元素中的两个元素(至少有一个是边),就可以求出其他三个元素。
26.4解直角三角形的应用我们通常把坡面的垂直高度h 和水平宽度l 的比lh叫做坡面的坡度(或坡比),坡面与水平面的夹角α叫做坡角。
显然,lh =αtan 27章 反比例函数 27.1 反比例函数一般地,如果变量y 和变量x 之间的函数关系可以表示成)0(≠=k k xky 为常数,且的形式,那么称y 为x 的反比例函数,k 称为比例系数,自变量x 的取值范围是不等于0的实数。
27.2 反比例函数的图像和性质 反比例函数)0(≠=k k xky 为常数,且的图像由分别位于两个象限内的两条曲线组成,这样的曲线叫做双曲线。
对于反比例函数xky =,当k>0时,它的图像位于第一、三象限,在每个象限内,y 的值随x 的值增大而减小;当k<0时,它的图像位于第二、四象限,在每个象限内,y 的值随x 的值增大而增大。
27.3反比例函数的应用28章 圆28.1圆的概念及性质(1)平面上,到定点的距离等于定长的所有点组成的图形,叫做圆,这个定点叫做圆心,这条定长叫做圆的半径。
(2)圆是轴对称图形,过圆心的每一条直线都是它的对称轴。
圆也是中心对称图形,圆心是它的对称中心。
(3)圆上任意两点间的线段叫做这个圆的一条弦。
过圆心的弦叫做这个圆的直径。
(4)圆上任意两点间的部分叫做圆弧,简称弧。
圆的直径将这个圆分成能够完全重合的两条弧,这样的一条弧叫做半圆。
(5)大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧。
(6)能够完全重合的两个圆叫做等圆。
能够完全重合的两条弧叫做等弧。