对数公式及对数函数的总结.pdf

对数函数计算公式对数函数是数学中的一种重要函数，广泛应用于科学、工程和金融等领域。

它的计算公式主要包括自然对数函数的计算公式和常用对数函数的计算公式。

1.自然对数函数：自然对数函数以常数e（自然对数的底数）为底，表示为ln(x)或者log_e(x)。

自然对数函数的计算公式如下：ln(x) = ∫(1/x) dx其中，∫(1/x) dx表示对函数1/x进行积分。

一般来说，计算出一些数的自然对数可以利用公式ln(x) = ∫(1/t) dt，将t从1积分到x 即可。

例如，计算ln(2)可以采用以下步骤：ln(2) = ∫(1/t) dt= [ln(t)]1皿2= ln(2) - ln(1)= ln(2)2.常用对数函数：常用对数函数以10为底，表示为log(x)。

常用对数函数的计算公式如下：log(x) = log10(x) = log(x)/log(10)其中，log(x)表示以10为底的对数，log(10)表示10的对数。

常用对数函数的计算可以通过计算ln(x)和ln(10)的比值得到。

例如，计算log(100)可以采用以下步骤：log(100) = ln(100) / ln(10)= 2 / log(10)=2此外，对数函数还有一些常用的性质和定理，也可以用于计算中。

例如，对数函数的换底公式：log_b(x) = log_a(x) / log_a(b)其中，log_b(x)表示以b为底的对数，log_a(x)表示以a为底的对数，log_a(b)表示以a为底，b为底的对数的比值。

对数函数在实际应用中有着广泛的应用。

它可以用于求解指数方程、计算复利、解决概率问题等。

比如在金融领域，对数函数可以用来计算复利利率，计算股票价格的涨幅等。

在科学研究中，对数函数可以用于分析曲线的趋势、解决指数增长问题等。

总之，对数函数是数学中一种重要的函数，它有着广泛的应用和计算公式。

通过掌握对数函数的计算公式，我们可以更好地理解和应用对数函数，解决实际问题。

对数函数知识点总结对数函数是指可以用对数形式表示的函数，它的定义域为正实数集合，值域为实数集合。

对数函数具有一些特殊的性质和运算规则，在数学中得到广泛应用。

本文将对对数函数的定义、性质、运算规则以及常见的应用进行总结。

一、对数函数的定义与性质：1. 对数的定义：对于任意的正实数a和b (a ≠ 1)，对数函数 y = loga(b) 表示满足 a^y = b 的唯一实数y。

2.对数函数的定义域为正实数集合，值域为实数集合。

3. 常见的对数函数是以自然常数e为底的自然对数函数 y = ln(x)和以常数10为底的常用对数函数 y = log10(x)。

4. 对数函数与指数函数是互逆变换关系，即 loga(a^x) =a^(loga(x)) = x。

5. 对数函数的图像特点：以对数函数 y = loga(x) 为例，当 a > 1 时，函数图像过点(1,0)，在区间(0,+∞)上是单调递增的，当x趋于0时，y趋于负无穷；当 a < 1 时，函数图像过点(1,0)，在区间(0,+∞)上是单调递减的，当x趋于0时，y趋于正无穷。

6. 对数函数具有对称性，即 loga(a/x) = -loga(x)。

二、对数函数的运算规则：1. 对数的乘法规则：loga(mn) = loga(m) + loga(n)。

2. 对数的除法规则：loga(m/n) = loga(m) - loga(n)。

3. 对数的幂次规则：loga(m^p) = p * loga(m)。

4. 对数的换底公式：loga(b) = logc(b) / logc(a)，其中c为任意的正实数（c ≠ 1）。

5. 对数函数的反函数：对于对数函数 y = loga(x)，其反函数为指数函数 x = a^y。

三、对数函数的应用：1.解指数方程和指数不等式：对于形如a^x=b或a^x<b的方程或不等式，可以通过取对数将其转化为对数方程或对数不等式进行求解。

关于对数函数的所有公式
1、指数函数的定义：
对数函数时在实数集中定义的一类函数，它的定义是：对任意的正实数x，存在一个实数y使得 e^y = x，则称y为x的对数，记作y =
log_e x 或者y = ln x.
2、对数函数的性质：
（1）对数函数是单调递增函数
（2）ln x > 0时，函数图像开口向上
（3）单调递减函数的图像等于反函数的图像
（4）当x > 0时，y = ln x在实数轴上的图像与x = e^y在实数轴上的图像是互逆的
（5）若x, y > 0，则 x > y <=> ln x > ln y
3、对数函数的基本函数关系：
（1）ln（xy）= ln x+ln y
（2）ln（x/y）= ln x−ln y
（3）ln（x^a）= a * ln x
（4）ln（e^x）= x
（5）ln 1 = 0
（6）ln e = 1
4、延伸函数的定义和性质：
（1）任意正实数x，存在一个实数y使得 b^y = x，则称y为x的以b为底的对数，记作 y=log_bx
（2）任意正实数x，存在一个实数y使得 e^(cy) = x，则称y为x 的以c为指数的对数，记作 y=clog_ex
（3）任意正实数x，存在一个实数y使得 b^(cy) = x，则称y为x 的以b*c为底的对数，记作 y=log_b(cx)
（4）对数函数的基本的关系也适用于延伸函数的定义
5、对数函数的函数变换：
（1）y=f(x)，其中f(x)为一次函数：
y=a*ln x+b
（2）y=f(x)。

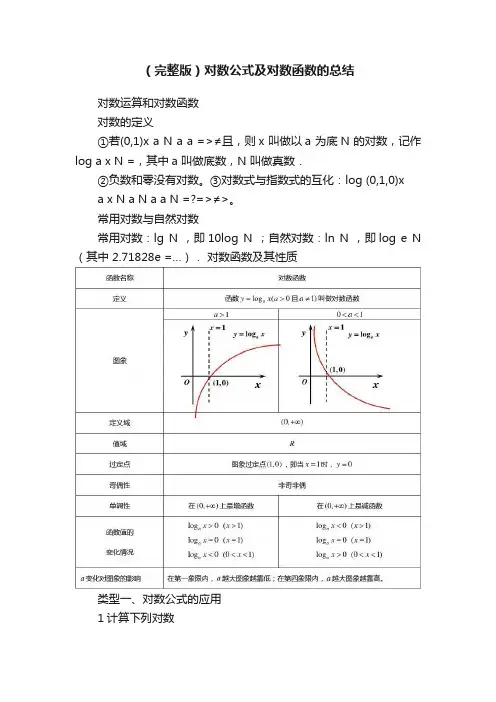
（完整版）对数公式及对数函数的总结对数运算和对数函数对数的定义①若(0,1)x a N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．②负数和零没有对数。

③对数式与指数式的互化：log (0,1,0)xa x N a N a a N =?=>≠>。

常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中2.71828e =…）．对数函数及其性质类型一、对数公式的应用1计算下列对数=-3log 6log 22 =?31log 12log 2222=+2lg 5lg =61000lg=+64log 128log 22 =?)24(log 432 =++)2log 2)(log 3log 3(log 9384=++3log 23log 2242 =?16log 27log 32 =+-2log 90log 5log 333=++c b a 842log log log =+++200199lg 43lg 32lgΛ =++32log 8log 8log 842 =+25.0log 10log 255 =-64log 325log 225 =)))65536(log (log (log log 22222 解对数的值：18lg 7lg 37lg214lg -+- 0 =-+-1)21(2lg 225lg-1 13341log 2log 8??-? ???的值0 提示：对数公式的运算如果0,1,0,0a a M N >≠>>，那么（1）加法：log log log ()a a a M N MN += （2）减法：log log log a a aMM N N-= （3）数乘：log log ()na a n M M n R =∈ （4）log aN a N = （5）log log (0,)b n a a nM M b n R b=≠∈（6）换底公式：log log (0,1)log b a b NN b b a=>≠且（7）1log log =?a b b a （8）a b b a log 1log =类型二、求下列函数的定义域问题 1函数)13lg(13)(2++-=x xx x f 的定义域是)1,31(-2设()x x x f -+=22lg，则??+??? ??x f x f 22的定义域为 ()()4,11,4Y --3函数()f x = ]1,0()0,1(Y - ）提示：（1）分式函数，分母不为0，如0,1≠=x xy 。

对数公式及对数函数的总结对数是数学中的一个重要概念。

如果一个数N可以表示为a的x次方（a>0且a≠1），那么x就是以a为底N的对数，记作x=logaN。

其中a称为底数，N称为真数。

负数和零没有对数。

对数式与指数式可以互相转化：x=logaN等价于ax=N （a>0，a≠1，N>0）。

常用的对数有lgN（即以10为底N的对数）和lnN（即以自然常数e为底N的对数）。

自然常数e≈2..对数函数是指函数y=logax（a>1或0<a<1）的图像。

它的定义域为正实数集，值域为实数集。

对数函数的图像经过点（1,0），在（0，+∞）上是增函数，在（0，1）上是减函数。

当x=1时，y=0.对数函数既非奇函数也非偶函数。

对数公式在数学中有广泛的应用。

例如，可以用对数公式计算各种对数值，如log26-log23=2，log212+log25=log=3，等等。

还可以用对数公式来解对数的值，如lg14-2lg7+lg7/lg18-2lg2-(-1)=log0.5，以及2(lg2+lg5)+log3(4/27)的值等。

在第一象限内，a越大图像越靠下，在第四象限内，a越大图像越靠上。

总之，对数及其函数在数学中有着广泛的应用，是不可或缺的数学工具。

4、已知a>b>c，那么a>b>c。

3、设a=log3π，b=log23，c=log32，则a>b>c。

2、如果a>b>logc1，那么B选项___c。

5、如果a>1，且a-x-logaxy。

1、已知函数f(x)=logx，如果f(ab)=1，则f(a)+f(b)=2.6、设函数f(x)={x-1，x<2；2logx-1，x≥2}，那么f(f(2))=2log2-1.7、设函数f(x)满足：当x≥4时，f(x)=1/x；当x<4时，f(x)=f(x+1)，那么f(2+log23)=1/7.参数问题部分无需改写。

对数函数的运算公式对数函数是高中数学中最常见的函数之一，它在各种数学问题中都有广泛的应用。

本文将为大家介绍对数函数的运算公式，包括基本的对数公式、对数运算法则、对数换底公式等等。

一、基本的对数公式在我们熟知的自然对数 $\ln x$ 中，$e$ 是一个非常特殊的数，它的近似值约为 $2.718$。

在对数函数中，$10$ 也是一个特殊的数，因为我们使用的数码系统就是 $10$ 进制的。

下面是一些基本的对数公式：1. $\ln 1 = 0$，因为 $e^0 = 1$。

2. $\ln e = 1$，因为 $e^1 = e$。

3. $\ln a^x = x\ln a$，因为 $a^x = e^{x\ln a}$。

二、对数运算法则在讲解对数运算法则之前，我们先明确一下以下符号的含义：1. $a$，$b$，$x$，$y$ 是正实数。

2. $n$ 是正整数。

3. $k$ 是任意实数。

下面是一些对数运算法则：1. $\log_a(xy) = \log_a x + \log_a y$。

2. $\log_a \left(\frac{x}{y}\right) = \log_a x - \log_a y$。

3. $\log_a x^n = n \log_a x$。

4. $\log_a x^k = \frac{k}{\ln a} \log_a x$。

5. $\log_a a = 1$。

6. $\log_a 1 = 0$。

7. $\log_a a^x = x$。

8. $\log_a x^{\log_b a} = \frac{\log_a x}{\log_a b}$。

三、对数换底公式在学习对数函数时，我们经常需要将一个对数用另一个底数的对数表示出来。

这就是对数换底公式。

下面是对数换底公式的表述：$$\log_a x = \frac{\log_b x}{\log_b a}$$其中 $a$ 和 $b$ 表示不同的底数。

对数换底公式可以理解为转化一个数字在另一种记数法下的表达式。

(完整版)对数函数公式汇总引言对数函数是数学中常见的一类函数，具有广泛的应用。

本文将对常见的对数函数公式进行汇总和解释，旨在帮助读者更好地理解和应用这些公式。

一、自然对数函数自然对数函数（Natural logarithm n）是以底数为常数e（自然常数）的对数函数。

其公式如下：$$ y = \ln(x) $$其中，x为自变量，y为函数值。

二、常用对数函数$$ y = \log_{10}(x) $$其中，x为自变量，y为函数值。

三、换底公式换底公式（Change of Base Formula）用于将对数函数转换到不同的底数上。

对于任意正数a、b和x，换底公式如下：$$ \log_a(x) = \frac{\log_b(x)}{\log_b(a)} $$四、对数函数的性质- 对数函数的定义域为(0, +∞)，值域为(-∞, +∞)。

- 自然对数函数和常用对数函数是单调递增函数，即函数随着自变量的增加而增加。

- 对数函数的图像是一条曲线，其形状取决于底数。

五、对数函数的应用对数函数广泛应用于科学、工程、经济等领域。

主要的应用包括：1. 数据比较：对数函数可以用于比较数据的大小，特别是在数据跨度较大的情况下，比较各个数据点的对数值可以更加直观地观察数据的差异。

2. 指数增长：对数函数常用于模拟指数增长的现象，如人口增长、病毒传播等。

3. 解方程：对数函数常用于解决含对数的方程，通过变换可以简化计算过程，提高解题效率。

结论本文对自然对数函数、常用对数函数及其应用进行了总结和解释。

通过深入理解对数函数的基本公式和性质，读者可以更好地应用对数函数解决实际问题，提高数学建模的能力。

对数函数知识点总结(共12页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--对数函数（一）对数1．对数的概念：一般地，如果N a x=)1,0(≠>a a ，那么数x 叫做以．a 为底．．N 的对数，记作：N x a log =（a — 底数，N — 真数，N a log — 对数式）说明：○1 注意底数的限制0>a ，且1≠a ；○2 x N N a a x=⇔=log ；○3 注意对数的书写格式． 两个重要对数：○1 常用对数：以10为底的对数N lg ； ○2 自然对数：以无理数 71828.2=e 为底的对数的对数N ln ．（二）对数的运算性质如果0>a ，且1≠a ，0>M ，0>N ，那么：○1 M a (log ·=)N M a log ＋N a log ； ○2 =N Ma log M a log －N a log ； ○3 na M log n =M a log )(R n ∈． 注意：换底公式abb c c a log log log =（0>a ，且1≠a ；0>c ，且1≠c ；0>b ）．利用换底公式推导下面的结论（1）b mnb a n a mlog log =；（2）a b b a log 1log =．（二）对数函数1、对数函数的概念：函数0(log >=a x y a ，且)1≠a 叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）．注意：○1 对数函数的定义与指数函数类似，都是形式定义，注意辨别。

如：x y 2log 2=，5log 5x y = 都不是对数函数，而只能称其为对数型函数．○2 对数函数对底数的限制：0(>a ，且)1≠a ．对数函数·例题解析例1．求下列函数的定义域：（1）2log x y a =； （2）)4(log x y a -=； （3）)9(log 2x y a -=．解：（1）由2x >0得0≠x ，∴函数2log x y a =的定义域是{}0x x ≠；（2）由04>-x 得4<x ，∴函数)4(log x y a -=的定义域是{}4x x <；（3）由9-02>-x 得-33<<x ，∴函数)9(log 2x y a -=的定义域是{}33x x -<<．例2．求函数251-⎪⎭⎫ ⎝⎛=xy 和函数22112+⎪⎭⎫⎝⎛=+x y )0(<x 的反函数。

对数公式与对数函数的总结对数公式是数学中常用的一类公式，对数函数则是对数公式的应用。

下面是对数公式与对数函数的总结：一、对数公式的定义和性质：1. 定义：设a>0且a≠1，b是任意正数，则称满足a^x=b的方程x=log_a(b)为以a为底的对数方程，其中x称为以a为底b的对数，记作x=log_a(b)。

其中，底数a决定对数的性质，真数b是要求的值。

2.特性：- 若a^x=b，则x=log_a(b)；- 对于任意a、b，log_a(1)=0，log_a(a)=1，log_1(a)是无定义的；- a^log_a(b)=b，log_a(a^x)=x，log_a(b^x)=xlog_a(b)；- 对于任意x，log_a(a^x)=x，a^log_a(x)=x；- 对于任意a、b、c，log_a(bc)=log_a(b)+log_a(c)，log_a(b/c)=log_a(b)-log_a(c)，log_a(b^c)=clog_a(b)；- 对于任意a，b>0且c>0且c≠1，若log_a(b)=log_c(b)，则a=c；- 对于任意a，b、c>0，若log_a(c)=d且log_b(c)=e，则d=log_a(b)e；- 设a>1，则对数函数y=log_a(x)是单调递增函数，且图像关于y=ax对称；- 设0<a<1，则对数函数y=log_a(x)是单调递减函数，且图像关于y=ax对称。

二、常见的对数公式及其应用：1. 换底公式：设x>0，a>0且a≠1，b>0且b≠1，则有log_a(b)=log_c(b)/log_c(a)，其中c为任意正数。

应用：用换底公式，可以将任意底数的对数转换为以10或以e为底的对数，方便计算。

2. 对数的乘法法则：对于任意a>0且a≠1、b>0且b≠1，以及任意正整数n，有log_a(b^n)=nlog_a(b)。

(完整版)对数函数公式汇总1. 自然对数函数的定义自然对数函数（Natural logarithm function）是指以常数e为底的对数函数，通常用ln(x)来表示。

自然对数函数的定义域是正实数集，即x>0。

常用的性质包括：- ln(1) = 0- ln(e) = 1- ln(xy) = ln(x) + ln(y)- ln(x/y) = ln(x) - ln(y)- ln(x^a) = a * ln(x)，其中a为任意实数2. 常用对数函数的定义- log(1) = 0- log(10) = 1- log(xy) = log(x) + log(y)- log(x/y) = log(x) - log(y)- log(x^a) = a * log(x)，其中a为任意实数3. 一般对数函数的定义一般对数函数（General logarithm function）是以任意正实数a 为底的对数函数，通常用log_a(x)表示。

一般对数函数的性质与自然对数函数和常用对数函数类似。

4. 对数函数的图像对数函数的图像与指数函数的图像呈现出一种对称关系，具体表现为：- 自然对数函数 y = ln(x) 的图像以y轴为渐近线，随着x的增大而增大，但增速逐渐减慢。

- 常用对数函数 y = log(x) 的图像以y = 0、x = 1为渐近线，随着x的增大而增大，但增速逐渐减慢。

- 一般对数函数 y = log_a(x) 的图像与自然对数函数和常用对数函数具有类似的特性。

5. 对数函数的应用对数函数在数学、物理、经济等领域中有广泛的应用，其中一些典型的应用包括：- 对数函数可以用来求解指数方程，即 x^a = b 的形式，可以通过取对数转化成一般形式求解。

- 对数函数可以用来描述物质的分解、增长和衰变过程，例如放射性衰变、经济增长等。

1 / 2指数函数和对数函数y a a a x =>≠01且定义域为R ，底数是常数，指数是自变量。

a 必须a a >≠01且。

如果a N a a =>≠()01且，那么数b 就叫做以a 为底的对数，记作b N a =log （a 是底数，N 是真数，log a N 是对数式。

）由于N a b =>0故log a N 中N 必须大于0。

当N 为零的负数时对数不存在 求35x=中的x ，化为对数式x =log 35即成。

对数恒等式：由a N b N ba ==()log ()12a N a N log =对数的性质：①负数和零没有对数； ②1的对数是零；③底数的对数等于1。

对数的运算法则：()()log log log a a a MN M NM N R =+∈+，()log log log aa a M NM N M N R =-∈+，()()log loga na N n N N R =∈+ ()log log a n a N nN N R =∈+13、对数函数：定义：指数函数y a a a x=>≠()01且的反函数y x a =log x ∈+∞(,)0叫做对数函数。

1、对三个对数函数y x y x ==log log 212，，y x =lg 的图象的认识。

：4、对数换底公式：log log log log (.)log b a a n e g N N bL N N e N L N N ====其中…称为的自然对数称为常数对数27182810 由换底公式可得：L N N e NN n ===lg lg lg ..lg 043432303由换底公式推出一些常用的结论：（1）log log log log a b a b b ab a ==11或· （2）log log a m a n b m n b =（3）log log a n a n b b = （4）log amn a m n=-----精心整理，希望对您有所帮助!。

12 对数与对数函数知识梳理1．对数2.对数函数的图象与性质3.反函数指数函数y ＝a x (a >0且a ≠1)与对数函数y ＝log a x (a >0且a ≠1)互为反函数，它们的图象关于直线y ＝x 对称． 要点整合1．化简对数式可用下列两个基本公式(1)倒数公式：log a b ·log b a ＝1(a >0，b >0，a ≠1，b ≠1)． (2)换底公式：log a N ＝log b Nlog b a(a >0，b >0，N >0，且a ≠1，b ≠1)．2．利用指数函数与对数函数单调性比较大小或解不等式与求最值问题时，注重“同底法”．题型一. 对数式的化简与求值例1.(1)设函数f (x )＝⎩⎨⎧1＋log 2（2－x ），x <1，2x －1，x ≥1，则f (－2)＋f (log 212)＝( )A ．3B ．6C ．9D ．12(2)化简12lg 3249－43lg 8＋lg 245＝__________．解析： (1)因为－2<1，所以f (－2)＝1＋log 2(2＋2)＝1＋log 24＝1＋2＝3.因为log 212>1，所以f (log 212)＝2log 212－1＝122＝6.所以f (－2)＋f (log 212)＝3＋6＝9.故选C. (2)12lg 3249－43lg 8＋lg 245＝12×(5lg 2－2lg 7)－43×32lg 2＋12(lg 5＋2lg 7) ＝52lg 2－lg 7－2lg 2＋12lg 5＋lg 7 ＝12lg 2＋12lg 5＝12lg(2×5)＝12. [答案] (1)C (2)12(1)在对数运算中，要熟练掌握对数式的定义，灵活使用对数的运算性质、换底公式和对数恒等式对式子进行恒等变形，多个对数式要尽量化成同底数的形式．(2)对数式的求值与化简常用的结论(a >0且a ≠1) ①log a 1＝0.②log a a ＝1.③a log a N ＝N (N >0)． ④log a b ·log b a ＝1(b >0且b ≠1)．变式1．若2a ＝5b ＝m ，且1a ＋1b ＝12，则m 的值为( )A ．10B ．10C ．1010D ．100解析：选D.由题意得a ＝log 2m ，b ＝log 5m .∴1log 2m ＋1log 5m ＝12.即log m 2＋log m 5＝12. ∴log m 10＝12.∴m 12＝10，即m ＝100，故选D.变式2．若x log 23＝1，则3x ＋3－x ＝( )A ．53B ．52C ．32D ．23解析：选B.∵x log 23＝1， ∴log 23x ＝1，∴3x ＝2，3－x ＝12，∴3x ＋3－x ＝2＋12＝52.故选B.变式3．已知函数f (x )是定义在R 上的奇函数，当x ＞0时，f (x )＝2＋f ⎝⎛⎭⎫12log 2x ，则f (－2)＝__________．解析：由f ⎝⎛⎭⎫12＝2＋f ⎝⎛⎭⎫12×log 212＝2－f ⎝⎛⎭⎫12，得f ⎝⎛⎭⎫12＝1，所以当x ＞0时，f (x )＝2＋log 2x ，所以f (2)＝2＋log 22＝3，又f (x )是奇函数， 所以f (－2)＝－f (2)＝－3. 答案：－3题型二. 对数函数的图象及应用例2. (1)在同一直角坐标系中，函数f (x )＝x a (x >0)，g (x )＝log a x 的图象可能是( )(2)已知函数f (x )＝|log 2x |，0<m <n ，且f (m )＝f (n )，若函数f (x )在区间[m 2，n ]上的最大值为2，则m 2＝__________．解析： (1)两图象均不可能过点(0，1)，A 错；B 选项中，f (x )＝x a 中a 满足a >1，而g (x )＝log a x 中a 满足0<a <1，矛盾，B 错；类似B 选项的判断方法知C 错；D 正确．故选D.(2)作出函数f (x )＝|log 2x |的图象如图．由题意可得0<m <1<n ，∴0<m 2<m ，结合图象可知函数f (x )在[m 2，n ]上的最大值为f (m 2)，则有－log 2m 2＝2，m 2＝2－2＝14.[答案] (1)D (2)141．判断基本函数图象的方法(1)理清函数名称和其基本图象的对应． (2)利用特殊点或单调性进行取舍． 2．翻折图象(图形)的两个主要变换 (1)y ＝f (x )―――――――――――→将x 轴下方图象翻折到x 轴上方保留原x 轴上方的图象y ＝|f (x )|；(2)y ＝f (x )――――――――――→保留y 轴右侧的图象并作其关于y 轴对称的图象y ＝f (|x |)．变式1．若函数y ＝log a x (a >0，且a ≠1)的图象如图所示，则下列函数图象正确的是( )解析：选B.由题意y ＝log a x (a >0，且a ≠1)的图象过(3，1)点，可解得a ＝3.选项A 中，y ＝3－x＝⎝⎛⎭⎫13x，显然图象错误；选项B 中，y ＝x 3，由幂函数图象可知正确；选项C 中，y ＝(－x )3＝－x 3，显然与所画图象不符；选项D 中，y ＝log 3(－x )的图象与y ＝log 3x 的图象关于y 轴对称，显然不符．故选B.变式2．已知函数f (x )＝⎩⎨⎧log 2x ，x ＞0，3x ，x ≤0，且函数h (x )＝f (x )＋x －a 有且只有一个零点，则实数a 的取值范围是( )A ．[1，＋∞)B ．(1，＋∞)C ．(－∞，1)D ．(－∞，1]解析：选B.如图所示，在同一坐标系中分别作出y ＝f (x )与y ＝－x ＋a 的图象，其中a 表示直线在y 轴上的截距．由图可知，当a ＞1时，直线y ＝－x ＋a 与曲线y ＝f (x )只有一个交点，即函数h (x )只有一个零点．题型三. 对数函数的性质及应用例3. (1)若a >b >0，0<c <1，则( ) A ．log a c <log b c B ．log c a <log c b C ．a c <b cD ．c a >c b(2)已知函数f (x )＝log a 3＋x3－x(a ＞0，且a ≠1)．①判断f (x )的奇偶性，并说明理由；②当0＜a ＜1时，求函数f (x )的单调区间． [解] (1)选B.法一：(通性通法)因为0<c <1，所以y ＝log c x 在(0，＋∞)单调递减，又0<b <a ，所以log c a <log c b ，故选B.法二：(特值法)取a ＝4，b ＝2，c ＝12，则log 412＝－12>log 212，排除A ；412＝2>212，排除C ；⎝⎛⎭⎫124<⎝⎛⎭⎫122，排除D.故选B.(2)f (x )＝log a 3＋x3－x(a ＞0，a ≠1，－3＜x ＜3)．①因为f (－x )＋f (x )＝log a 3－x 3＋x ＋log a 3＋x3－x＝log a 1＝0，所以f (－x )＝－f (x )，又定义域(－3，3)关于原点对称．所以f (x )是奇函数．②令t ＝3＋x 3－x ＝－1－6x －3，则该函数在(－3，3)上是增函数，当0＜a ＜1时，函数y ＝log a t 是减函数，所以f (x )＝log a3＋x3－x(0＜a ＜1)在(－3，3)上是减函数， 即函数f (x )的单调递减区间是(－3，3)． 例4. 设a ＝log 36，b ＝log 510，c ＝log 714，则( )A ．c>b>aB ．b>c>aC ．a>c>bD ．a>b>c 答案 D变式. 若log a (a 2＋1)<log a 2a<0，则a 的取值范围是( ) A ．(0,1)B ．(0，12)C ．(12，1) D ．(0,1)∪(1，＋∞)答案 C解析 由题意得a>0，故必有a 2＋1>2a ， 又log a (a 2＋1)<log a 2a<0，所以0<a<1， 同时2a>1，∴a>12.综上，a ∈(12，1)．例5. 已知函数f(x)＝log a (3－ax)．(1)当x ∈[0,2]时，函数f(x)恒有意义，求实数a 的取值范围；(2)是否存在这样的实数a ，使得函数f(x)在区间[1,2]上为减函数，并且最大值为1？如果存在，试求出a 的值；如果不存在，请说明理由．解 (1)∵a>0且a ≠1，设t(x)＝3－ax ， 则t(x)＝3－ax 为减函数，x ∈[0,2]时，t(x)的最小值为3－2a ， 当x ∈[0,2]时，f(x)恒有意义， 即x ∈[0,2]时，3－ax>0恒成立． ∴3－2a>0.∴a<32.又a>0且a ≠1，∴a ∈(0,1)∪⎝⎛⎭⎫1，32.【感悟提升】在解决与对数函数相关的比较大小或解不等式问题时，要优先考虑利用对数函数的单调性来求解．在利用单调性时，一定要明确底数a的取值对函数增减性的影响，及真数必须为正的限制条件．变式1.(1)设a＝log32，b＝log52，c＝log23，则()A．a>c>b B．b>c>aC．c>b>a D．c>a>b(2)若f(x)＝lg(x2－2ax＋1＋a)在区间(－∞，1]上递减，则a的取值范围为()A．[1,2) B．[1,2]C．[1，＋∞) D．[2，＋∞)(3)设函数212log,0()log(),0,x xf x x x>⎧⎪=⎨-<⎪⎩若f(a)>f(－a)，则实数a的取值范围是()A．(－1,0)∪(0,1) B．(－∞，－1)∪(1，＋∞) C．(－1,0)∪(1，＋∞) D．(－∞，－1)∪(0,1)答案(1)D(2)A(3)C解析(1)∵3<2<3,1<2<5，3>2，∴log33<log32<log33，log51<log52<log55，log23>log22，∴12<a<1,0<b<12，c>1，∴c>a>b.1．比较大小问题是高考的常考题型，应熟练掌握比较大小的基本方法：(1)作差(商)法；(2)函数单调性法；(3)中间值法(特别是以0和1为中间值)．利用对数函数单调性比较大小的基本方法是“同底法”，即把不同底的对数式化为同底的对数式，然后根据单调性来解决．2．利用对数函数的性质，求与对数函数有关的函数的值域和单调性问题时，必须弄清三方面的问题：一是定义域，所有问题都必须在定义域内讨论；二是底数与1的大小关系；三是函数的构成形式，即它是由哪些基本初等函数通过初等运算构成或复合而成的．A．a>b>c B．b>c>aC．c>b>a D．b>a>c变式2．已知函数f (x )＝log a 1－mxx －1是奇函数(a >0，a ≠1)．(1)求m 的值；(2)判断f (x )在区间(1，＋∞)上的单调性． 解：(1)∵f (x )是奇函数，∴f (－x )＝－f (x )在其定义域内恒成立，即log a 1＋mx －x －1＝－log a 1－mx x －1，∴1－m 2x 2＝1－x 2恒成立，∴m ＝－1或m ＝1(舍去)，即m ＝－1.(2)由(1)得f (x )＝log a x ＋1x －1(a >0，a ≠1)，令u (x )＝x ＋1x －1＝1＋2x －1，则u (x )在(1，＋∞)上为减函数．∴当a >1时，f (x )在(1，＋∞)上是减函数； 当0<a <1时，f (x )在(1，＋∞)上是增函数．。

最全对数公式整理1.对数定义：对于任意的正实数x和正实数a(a≠1)，定义a为底的对数函数y=log_a(x)表示满足a^y=x的实数y。

其中a为底，x为真数，y为对数。

2.换底公式：对于任意的正实数x和正实数a,b(a,b≠1)，有以下换底公式：log_a(x) = log_b(x) / log_b(a)3.对数幂法则：对于任意的正实数a(a≠1)，x和y，有以下对数幂法则：log_a(x^n) = n * log_a(x)log_a(x * y) = log_a(x) + log_a(y)log_a(x / y) = log_a(x) - log_a(y)4.对数乘法公式：对于任意的正实数a和b(a,b≠1)，有以下对数乘法公式：log_a(b * c) = log_a(b) + log_a(c)5.对数除法公式：对于任意的正实数a和b(a,b≠1)，有以下对数除法公式：log_a(b / c) = log_a(b) - log_a(c)6.对数根公式：对于任意的正实数a和b(a,b≠1)，有以下对数根公式：log_a(b^(1/n)) = (1/n) * log_a(b)7.自然对数公式：ln(x⋅x) = ln(x) + ln(x)ln(x/x) = ln(x) − ln(x)ln(x^n) = n * ln(x)8.常用对数公式：常用对数是以10为底的对数，通常用log表示，有以下常用对数公式：log(x⋅x) = log(x) + log(x)log(x/x) = log(x) − log(x)log(x^n) = n * log(x)9.对数的性质：(1)xxx_x(1)=0，x≠1(2)xxx_x(x)=1，x≠1(3)x^(xxx_x(x))=x，x≠1，x>0(4)xxx_x(x⋅x)=xxx_x(x)+xxx_x(x)，x≠1，x>0，x>0(5)xxx_x(x/x)=xxx_x(x)−xxx_x(x)，x≠1，x>0，x>0(6)xxx_x(x^x)=x*xxx_x(x)，x≠1，x>0总结：对数公式是数学中非常重要的一类公式，通过运用这些公式可以简化对数运算，从而方便求解各种数学问题。