长方体和正方体的展开图 练习题

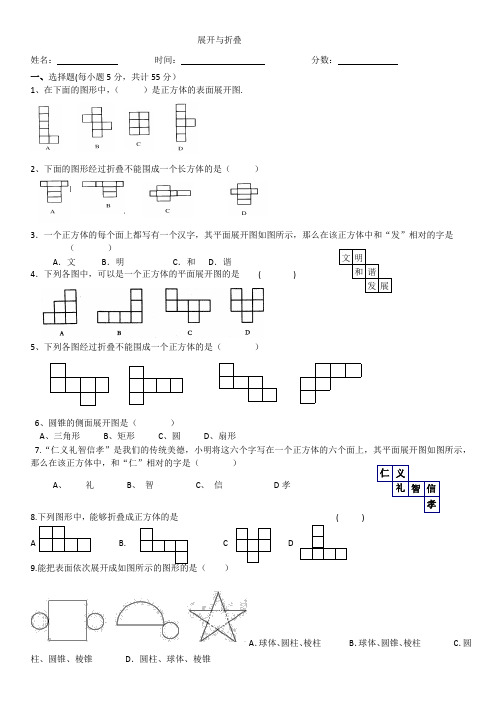
展开与折叠姓名：时间：分数：一、选择题(每小题5分，共计55分）1、在下面的图形中，（）是正方体的表面展开图.2、下面的图形经过折叠不能围成一个长方体的是（）3．一个正方体的每个面上都写有一个汉字，其平面展开图如图所示，那么在该正方体中和“发”相对的字是（）A．文B．明C．和D．谐4．下列各图中，可以是一个正方体的平面展开图的是( )5、下列各图经过折叠不能围成一个正方体的是（）6、圆锥的侧面展开图是（）A、三角形B、矩形C、圆D、扇形7.“仁义礼智信孝”是我们的传统美德，小明将这六个字写在一个正方体的六个面上，其平面展开图如图所示，那么在该正方体中，和“仁”相对的字是（）A、礼B、智C、信D孝8.下列图形中，能够折叠成正方体的是( )A B. C D9.能把表面依次展开成如图所示的图形的是（）A．球体、圆柱、棱柱B．球体、圆锥、棱柱C．圆柱、圆锥、棱锥D．圆柱、球体、棱锥文明和谐发展信智礼义仁孝10.下列平面图形，不能沿虚线折叠成立体图形的是（）A．B．C．D．11.一个几何体的展开图如图所示，这个几何体是（）A.三棱柱B．三棱锥C．四棱柱D．四棱锥二、填空题（每空3分，共计36分）1、人们通常根据底面多边形的＿将棱柱分为三棱柱、四棱柱、五棱柱……因此，长方体和正方体都是_____棱柱2、如果一个棱往是由12个面围成的，那么这个棱柱是棱柱.3、一个六棱柱模型，它的上、下底面的形状、大小都相同，底面边长都是5cm，侧棱长4cm，则它的所有侧面的面积之和为______.4、哪种立体图形的表面能展开成下面的图形（）（）（）（）（）（）5、一个直棱柱共有n个面，那么它共有______条棱，______个顶点6.如图是正方体的展开图，则原正方体相对两个面上的数字之和的最小值的是____．如图是某多面体的展开图，请根据要求回答下列问题：（1）如果A在多面体的底部，谁在上面（2）如果F在前面，谁在后面（3）如果C在右面，谁在左面。

第一单元长方体和正方体【例1】有一个无盖的正方体纸盒，下底标有字母“M”，沿图中粗线将其剪开展成平面图形会是（）。

解析：根据正方体的表面展开图共有11种情况，本题中“M”是底面，如果沿图中粗线将其剪开展成平面图形，四个小正方形会连在一起，并且标有“M”底面应和最边上的一个小正方形连在一起，可由此进行选择。

解答：B【例2】一种无盖的长方体玻璃鱼缸，它的长和宽都是40厘米，高是20厘米，做2个这样的鱼缸，至少要多少平方厘米的玻璃？解析：根据题意可知，如果把两个鱼缸‘口口’对接，就可变成一个棱长是40厘米的正方体（如下图），这样一来只要求出它的表面积即可知道做这两个鱼缸一共需要多少玻璃。

解答：40×40×6=9600（平方厘米）答：至少需要9600平方厘米玻璃。

【例3】如下图，有一块长40厘米、宽20厘米的长方形铁皮，在铁皮的四个角上分别剪去一个边长是5厘米的小正方形，做一个深5厘米的长方体无盖铁盒。

这个铁盒的容积是多少立方厘米？解析：根据题意可知，这样做成的长方体铁盒的长是用长方形铁皮的长减去两个小正方形的边长，即40－5×2=30（厘米），宽是用长方形铁皮的宽减去两个小正方形的边长，即20－5×2=10（厘米），高就是小正方形的边长5厘米，因此，此时焊接成的长方体铁盒的容积是30×10×5=1500（立方厘米）。

解答：40－5×2=30（厘米）20－5×2=10（厘米）30×10×5=1500（立方厘米）答：这个铁盒的容积是1500立方厘米。

【例4】一个长方体，如果高增加2厘米，就变成一个正方体，这时表面积比原来增加56平方厘米，原来长方体的体积是多少立方厘米？解析：根据题意，可以作出下图。

表面积比原来的长方体增加了56平方厘米，从图中可看出，高增加了2厘米，使长方体变成了正方体，而增加的面积只是四周4个面的面积，跟顶面和底面无关，所以只要将56÷4=14（平方厘米）就可以求出增加的四个面中的其中一个面的面积。

期末知识大串讲苏教版数学六年级上册期末章节考点复习讲义第一单元《长方体和正方体》知识点01：长方体和正方体的认识1.长方体的特征长方体是由6个长方形（也可能有2个相对的面是正方形）围成的立体图形，有6个面、12条棱和8个顶点，相对的面完全相同、相对的棱长度相等。

2. 长方体的长、宽、高的含义长方体相交于同一顶点的三条棱的长度，分别叫作它的长、宽、高。

知识点02：：长方体和正方体的展开图1.沿着正方体（或长方体）的棱将其剪开，可以把正方体（或长方体）展开成一个平面图形，这个平面图形就是正方体（或长方体）的展开图。

2.正方体（或长方体）的展开图的特点：在展开图中，正方体的6个面完全相同（长方体相对的面完全相同），相对的面完全隔开。

3. 一个表面涂色的正方体，把每条棱平均分成相等的若干份，然后切成同样大的小正方体。

（1）3面涂色的小正方体有8个。

（2）如果用n表示把正方体的棱平均分成的份数（n为大于或等于2的自然数），用a、b分别表示2面涂色和1面涂色的小正方体的个数，那么a=(n-2)×12，b=(n-2)2×6。

知识点32：长方体、正方体的表面积计算1.意义长方体（或正方体）6个面的总面积。

2.计算方法（1）长方体的表面积=长×宽×2+长×高×2+宽×高×2=（长×宽+长×高+宽×高）×2。

（2）正方体的表面积=棱长×棱长×6。

知识点42：体积与体积单位1.体积的意义：物体所占空间的大小叫作物体的体积。

2.容积的意义：容器所能容纳物体的体积叫作容器的容积。

常用的体积单位有立方厘米、立方分米和立方米，可以分别写成cm³、dm³和m³。

计量液体的体积，通常用升或毫升作单位。

1立方分米 = 1升，1立方厘米 = 1毫升知识点五：长方体和正方体的体积1.长方体的体积=长×宽×高，字母公式为V=a bh。

第二课时长方体与正方体的展开图教学内容：P12例3、“试一试”“练一练”、练习三第6—7题教学目标：1、使学生通过观察实物、动手操作等活动认识长方体、正方体的展开图，进一步加深对长方体和正方体特征的认识。

能在展开图中找到长方体、正方体相对的面，能判断一些平面图形折叠后能否围成长方体、正方体。

2、使学生在活动中初步感受平面图形与立体图形的相互转换，通过建立图形的表象的过程，进一步积累空间与图形的学习经验，增强空间观念。

3、让学生进一步感受图形学习的乐趣，增强合作意识。

教学重点：认识长方体、正方体展开图。

教学难点：学习判断展开图能否围成长方体、正方体的方法。

教学资源：教师、学生每人准备正方体、长方体纸盒各一个、剪刀学生按小组分别准备教科书14页思考题中所需的若干张硬纸（每种6张）教学过程：一、复习导入1、说说长方体和正方体的特征。

2、师：这节课，我们要继续研究有关长方体和正方体的知识。

请你闭上眼睛想一想，长方体或正方体的六个面铺开，在同一平面上，会是什么样子？这就是这节课我们要研究的内容：认识长方体、正方体的展开图。

（板书）二、自主探究1、教师提出要求：展开正方体要注意每个面都要完整地保留，而且六个面要连成一片。

教师演示：像例3那样，并按照例题所示的步骤进行操作，得到正方体的展开图。

2、把展开图再复原成立体图，再进一步展开、复原，让学生从展开图中找到3组相对的面标出来，观察六个面的位置，你有什么发现？小组交流，汇报：相对的两个面中间隔着一个面。

3、让学生独立一剪，并在小组里交流自己得到的展开图，在交流中认识不同的正方体展开图，并思考展开图中的各个面与原来各个面的关系。

展示不同的展开图，观察归类：。

对于小学几何而言，立体图形的表面积和体积计算，既可以很好地考查学生的空间想象能力，又可以具体考查学生在公式应用中处理相关数据的能力，所以，很多重要考试都很重视对立体图形的考查．如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．cba HGFEDCBA①在六个面中，两个对面是全等的，即三组对面两两全等． (叠放在一起能够完全重合的两个图形称为全等图形．) ②长方体的表面积和体积的计算公式是： 长方体的表面积：2()S ab bc ca =++长方体； 长方体的体积：V abc =长方体．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形． 如果它的棱长为a ，那么：26S a =正方体，3V a =正方体．长方体与正方体的体积立体图形示例 体积公式 相关要素长方体V abh = V Sh =三要素：a 、b 、h 二要素：S 、h正方体3V a =V Sh =一要素：a 二要素：S 、h不规则形体的体积常用方法： ①化虚为实法 ②切片转化法 ③先补后去法 ④实际操作法 ⑤画图建模法【例 1】 一个长方体的棱长之和是28厘米，而长方体的长宽高的长度各不相同，并且都是整厘米数，则长方体的体积等于 立方厘米。

例题精讲长方体与正方体（二）【例2】将几个大小相同的正方体木块放成一堆，从正面看到的视图是图（a），从左向右看到的视图是图（b），从上向下看到的视图是图（c），则这堆木块最多共有___________块。

【例3】一根长方体木料，体积是0.078立方米．已知这根木料长1.3米．宽为3分米，高该是多少分米?孙健同学把高错算为3分米．这样，这根木料的体积要比0.078立方米多多少?【例4】如图，两个同样的铁环连在一起长28厘米，每个铁环长16厘米。

8个这样的铁环依此连在一起长厘米。

【例5】某工人用薄木板钉成一个长方体的邮件包装箱，并用尼龙编织条(如图所示)在三个方向上的加固．所用尼龙编织条分别为365厘米，405厘米，485厘米．若每个尼龙加固时接头重叠都是5厘米．问这个长方体包装箱的体积是多少立方米?高长【例6】某工人用木板钉成一个长方体邮件包装箱，并用三根长度分别为235厘米、445厘米、515厘米的尼龙带进行加固（如下图），若每根尼龙带加固时截头重叠都是5厘米，那么这个长方体包装箱的体积是立方米。

2021-2021学年苏教版六年级数学上册《长方体和正方体的展开图》同步练习一．选择题（共8小题）1．下面图形沿虚线折叠后能围成长方体的有（）A．①B．①②C．①②③D．①②③④2．长方体的6个面展开后，（）A．都是长方形B．至少有2个面是长方形C．至少有4个面是长方形D．都是正方形3．下面的图形经过折叠不能围成一个长方体的是（）。

A．B．C．D．4．下面的图形中，能按虚线折成正方体的是（）A．B．C．5．在下面的图形中，（）不是正方体的表面展开图．A．B．C．D．6．如图是一个无盖的正方体纸盒纸盒侧面有一个★，下面展开图可以围成该正方体的是（）A．B．C．D．7．下面是一个长方体的四个面，另两个面的面积和是（）平方厘米。

A．25B．35C．40D．708．如图，将右边的纸片折起来可以做成一个正方体。

这个正方体2号面的对面是（）号面。

A．3B．5C．6二．填空题（共10小题）9．选择下面可以组成一个长方体．（填编号）10．一张长方形纸长40厘米，宽8厘米，把它对折再对折．打开后，围成一个高8厘米的长方体的侧面．如果要给这个长方体配一个底面，底面积是平方厘米．11．沿虚线折可以将，围成长方体，底面积是，体积是（单位：cm）12．正方体6个面上分别写着1、2、3、4、5、6．与2相对的面上的数字是，与6相对的面上的数字是．13．将下边的展开图围成正方体后，1号面的对面是面。

如果这个正方体的棱长是4厘米，它的体积是立方厘米。

14．如图，把这个平面展开图折叠成立方体，与“E”相对的字母是．15．如图是一个正方体纸盒的展开图，当折叠成正方体纸盒时，D点与点重合。

16．下面图形中能折成正方体的是。

17．右面是一个无盖的长方体纸盒的展开图．与④号面相对的面是号面，纸盒的底面是号面．18．请在下面的展开图中找出相对的面．在长方体的展开图中，1和相对，3和相对，6和相对．三．判断题（共5小题）19．长方体的6个面展开后，至少有4个面是长方形．（判断对错）2021左面A、B、C三个盒子展开后分别是右面的D、E、F．（判断对错）21．将如图的展开图围成正方体后，与“1”相对的是“3”。

长方体正方体展开图练习
1、如右图。

这是一个( )体，有( ）条棱，有( ）个面，有（）个顶点,棱长一共是（）,表面积是（ )。

2、这时一个（）体。

它的上、下底面的形状是（），长和宽分别是（）和（），它的左右形状是( ），边长是（）.
3、
4、右图是一个正方体的展开图。

5、下图是一个长方体的展开图，找出相对的两个面，并说一说它们是长方体的哪几个面？（单位：m）
相对的面是（）号和（)号,（）号和（）号以及( ）号和（）号。

其中( )号和（）号是长方体的上、下面，( ）号和（）号是长方体的前，后面，（)号和（）号是长方体的左、右面。

6、把相对应的字母填在括号里。

7、工人师傅做一个正方体框架，用去36米角钢。

这个框架的边长是多少？如果要在这个框架上钉上木板,多少木板才够？
8、哪个展开图形能围成正方体？请在对应的括号里打勾.。

长方体与正方体必须掌握的九种题型练习及解析一、长方体与正方体必须掌握的几种题型1 --高的变化引起表面积的变化1、一个长方体，如果高增加2厘米就成了正方体，而且表面积要增加56平方厘米，原来这个长方体的体积是多少立方厘米?2、一个长方体，如果高减少2厘米就成了正方体，而且表面积要减少56平方厘米，原来这个长方体的体积是多少立方厘米?3、一个长方体，长a分米，宽b分米，高h分米，如果高减少3分米，这个长方体表面积比原来减少（）平方分米?体积比原来减少（）立方分米二、长方体与正方体必须掌握的几种题型2 --段的变化1、一个长方体长2米，截面是边长3厘米的正方形，将这个长方体木料锯成五段后，表面积一共增加了多少平方厘米2、将一个长3米的长方体木料平均截成3段，表面积一共增加了0.36平方分米，这根木料的体积是多少立方分米3、一段长2m的长方体木料，将它截成5段后，表面积增加了40平方分米，这根木料的体积是多少立方分米？4、把一根长3米的长方体木料据成3段后，表面积增加18平方分米这根木料原来的体积是多少立方米1、一个正方体的表面积是48平方厘米，将它平均分成两个小长方体，每个小长方体的表面积是多少2、一个正方体的表面积是96平方厘米，将它平均分成两个小长方体，每个小长方体的体积是多少立方厘米3、一个正方体的体积是125立方厘米，它的表面积是多少平方厘米4、一个正方体切成两个小长方体后,表面积增加18平方厘米。

两个小长方体表面积的和是多少？四、长方体与正方体必须掌握的几种题型4 --拼的变化1、用8个棱长都是2厘米的正方体拼成一个长方体，拼成的长方体的表面积最多是多少平方厘米最少是多少平方厘米？2、用12个棱长都是2厘米的正方体拼成一个长方体，一共有多少种拼法，每种拼法拼成的长方体的表面分别是多少？3、用四个棱长都是3厘米的正方体拼成一个长方体，拼成的长方体的表面积可能是多少4、用6个棱长是1厘米的正方体,拼成一个表面积是最小的长方体，这个长方体的表面积是多少？倍数1、一个正方体棱长扩大2倍，表面积扩大（）倍，体积扩大（）倍，表面积增加（）倍，体积增加（）倍。

2023-2024学年六年级上册数学第一单元长方体和正方体练习一、图形计算1．求表面积：2．计算下面图形的表面积和体积。

3．计算如图立体图形的表面积和体积。

（单位：cm）二、选择题4．一个正方体，至少再添上（）个同样大的正方体才能拼成一个大正方体。

A．3B．7C．85．有个长方体，长、宽、高分别是7厘米、5厘米、6厘米，分别将其表面涂上红色，然后将它们分割成棱长为1厘米的小正方体，一面涂色的有（）块。

A．48B．47C．946．一个长9分米、宽8分米、高5分米的长方体纸盒，最多能放入（）个棱长2分米的木块。

（不考虑纸盒厚度）（）。

A．40B．45C．30D．327．一个长方体的底面是周长为20厘米的正方形，它的侧面展开图也正好是一个正方形，这个长方体的体积是（）立方厘米。

A．400B．200C．125D．5008．如图是一个正方体的表面展开图，若在正方体的各面填上数，使得对面两数之和为8，A 处所填的数是（）。

A．4B．7C．6D．无法确定9．一个长方体正好可以切成两个正方体，表面积增加了8平方厘米，这个长方体的体表面积是（）。

A．24平方厘米B．40平方厘米C．48平方厘米D．80平方厘米10．长方体的底面积不变，高扩大4倍，体积扩大（）倍。

A．8B．16C．64D．411．下边图中，比较它们的表面积，我认为（）。

A．甲表面积大B．乙表面积大C．表面积一样大D．无法比较三、填空题12．900立方厘米＝()升 4.5立方米＝()立方分米6立方米80立方分米＝()立方米＝()立方分米13．一盒牛奶的包装盒上写着“净含量是300ml”，小婷实际测量了外包装盒长是6厘米，宽是4厘米，高是12厘米，根据以上数据，你认为包装盒标注的净含量真实吗？()（填“真实”或“虚假”）理由：___________。

14．如图是由同样大小的小方块堆积起来的，已知每个小方块的棱长是1厘米，它的体积是()立方厘米，表面积是()平方厘米。