SPSS数据正态性检验解析

19. 正态性检验实际中，经常需要检验数据是否服从正态分布。

一、Kolmogorov-Smirnov(K - S) 单样本检验这是一种分布拟合优度检验，即将一个变量的累积分布函数与特定分布进行比较。

有数据文件：对“数学成绩”“英语成绩”做正态性检验。

1.【分析】——【非参数检验】——【单样本】，打开“单样本非参数检验”窗口，【目标】界面勾选“自动比较观察数据和假设数据”2.【字段】界面，勾选“使用定制字段分配”，将要检验的变量“数学成绩”“英语成绩”选入【检验字段】框，3. 【设置】界面，选择“自定义检验”，勾选“检验观察分布和假设分布（Kolmogorov-Smimov检验）”点【选项】，打开“Kolmogorov-Smimov检验选项”子窗口，选择“正态分布”，勾选“使用样本数据”，点【确定】回到原窗口，点【运行】得到结果说明：样本量大于50用Kolmogorov-Smirnov检验，样本量小于50用Shapiro-Wilk检验；原假设H0：服从正态分布；H1：不服从正态分布。

P值<0.05, 拒绝原假设H0；P值>0.05, 接受原假设H0, 即服从正态分布；本例中，“数学成绩”、“英语成绩”的P值都>0.05, 故服从正态分布。

双击上面结果可以看到更详细的检验结果：注：类似的操作也可以检验数据是否服从“二项、均匀、指数、泊松”等分布。

二、用“旧对话框”进行上述检验1.【分析】——【非参数检验】——【旧对话框】——【1-样本K-S】，打开“单样本Kolmogorov-Smirnov检验”窗口，将要检验的变量选入【检验变量列表】框，【检验分布】勾选“常规”，2.点【精确】，打开“精确检验”窗口，勾选“精确”，“仅渐进法”——只计算检验统计量的渐近分布的近似概率值，而不计算确切概率，适用用样本量较大，P值远离α=0.05，节省计算时间，否则可能结果偏差较大；“Monte Carlo”——利用模拟抽样方法求得P值的近似无偏估计，适合大样本数据，节省计算时间；“精确”——计算精确的概率值（P值）。

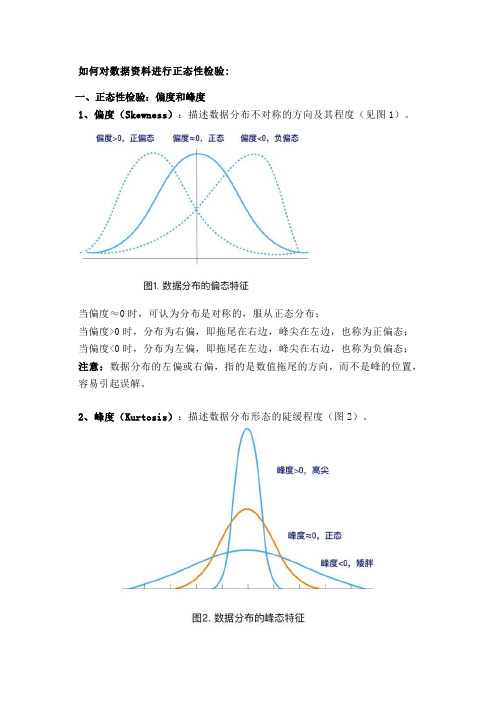
如何对数据资料进行正态性检验:一、正态性检验：偏度和峰度1、偏度（Skewness）：描述数据分布不对称的方向及其程度（见图1）。

当偏度≈0时，可认为分布是对称的，服从正态分布；当偏度>0时，分布为右偏，即拖尾在右边，峰尖在左边，也称为正偏态；当偏度<0时，分布为左偏，即拖尾在左边，峰尖在右边，也称为负偏态；注意：数据分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置，容易引起误解。

2、峰度（Kurtosis）：描述数据分布形态的陡缓程度（图2）。

当峰度≈0时，可认为分布的峰态合适，服从正态分布（不胖不瘦）；当峰度>0时，分布的峰态陡峭（高尖）；当峰度<0时，分布的峰态平缓（矮胖）；利用偏度和峰度进行正态性检验时，可以同时计算其相应的Z评分（Z-score），即：偏度Z-score=偏度值/标准误，峰度Z-score=峰度值/标准误。

在α=0.05的检验水平下，若Z-score在±1.96之间，则可认为资料服从正态分布。

了解偏度和峰度这两个统计量的含义很重要，在对数据进行正态转换时，需要将其作为参考，选择合适的转换方法。

3、SPSS操作方法以分析某人群BMI的分布特征为例。

(1) 方法一选择Analyze → Descriptive Statistics → Frequencies将BMI选入Variable(s)框中→点击Statistics →在Distribution框中勾选Skewness和Kurtosis(2) 方法二选择Analyze → Descriptive Statistics → Descriptives将BMI选入Variable(s)框中→点击Options →在Distribution框中勾选Skewness和Kurtosis4、结果解读在结果输出的Descriptives部分，对变量BMI进行了基本的统计描述，同时给出了其分布的偏度值0.194（标准误0.181），Z-score = 0.194/0.181 = 1.072，峰度值0.373（标准误0.360），Z-score = 0.373/0.360 = 1.036。

如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

以上两种方法以Q-Q图为佳，效率较高。

3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图判断方法：观测离群值和中位数。

5、茎叶图类似与直方图，但实质不同。

二、计算法1、偏度系数（Skewness）和峰度系数（Kurtosis）计算公式：g1表示偏度，g2表示峰度，通过计算g1和g2及其标准误σg1及σg2然后作U检验。

两种检验同时得出U<U0.05=1.96，即p>0.05的结论时，才可以认为该组资料服从正态分布。

由公式可见，部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。

2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验（D检验）和Shapiro- Wilk（W检验）。

SAS中规定：当样本含量n≤2000时，结果以Shapiro – Wilk（W检验）为准，当样本含量n >2000时，结果以Kolmogorov – Smirnov（D检验）为准。

SPSS中则这样规定：（1）如果指定的是非整数权重，则在加权样本大小位于3和50之间时，计算Shapiro-Wilk统计量。

对于无权重或整数权重，在加权样本大小位于3和5000之间时，计算该统计量。

由此可见，部分SPSS教材里面关于“Shapiro – Wilk适用于样本量3-50之间的数据”的说法是在是理解片面，误人子弟。

（2）单样本Kolmogorov-Smirnov检验可用于检验变量（例如income）是否为正态分布。

如何使⽤SPSS对数据进⾏正态性检验在我们阅读⽂献时，我们经常会看到类似这样的句⼦：当数据服从正态分布时，我们要使⽤这种统计⽅法进⾏检验，当数据不服从正态分布时，我们要使⽤那种⽅法进⾏检验。

你⼀定会有疑问，这是为什么呢？判断数据是否服从正态分布在这⼀过程中到底起到什么作⽤呢？其实很多时候，在我们获得数据之后都需要从单⼀样本中获得样本的信息，并通过统计分析的⽅法来估计总体的参数信息。

在进⾏统计分析之前，我们需要识别样本的分布特征。

如果你不了解样本的分布特征就会⾯临选择错误的统计检验的风险。

许多统计⽅法在使⽤时都会假定数据是服从正态分布的，⽐如单/双样本-T检验。

那么，我们拿到⼀些数据之前，就要验证⼀下这些数据是否是服从正态分布的。

下⾯，⼩编就来给⼤家简单讲⼀讲如何使⽤SPSS对数据进⾏正态性检验。

先给⼤家看⽂献中的⼀个例⼦：从某单位职⼯2018年体检中获得24名职⼯的⾎清总胆固醇( mmol/L)的测量结果如下：通过计算得到24名职⼯的⾎清总胆固醇的均数为=3.88，标准差为S=0.73。

通过编制频数表，画出直⽅图，如下：从图中可以看出，在均数附近的频数较⼤（⼈数较多），并以此为中⼼左右基本对称，在处理资料时，我们就把它当做数学上的正态分布（图中曲线圆滑）。

那么如何⽤SPSS验证数据是否服从正态分布呢？检验数据是否服从正态分布的⽅法有很多，这⾥先给⼤家介绍⼏种简单的⽅法。

1.正态曲线图点击“分析”，“描述性统计”中的“频率”。

将数据选⼊变量，点击图表-直⽅图-在直⽅图中显⽰正态曲线。

获得以下结果：由图可看出，图中的点⼤致都在⼀条直线上，所以数据满⾜正态分布。

检验数据是否服从正态分布的⽅法有很多，这⾥只是介绍了⼏种很简单的检验⽅法。

在对数据进⾏统计分析时，⾸先要了解清楚数据的分布特征才能选择正确的⽅法，做到万⽆⼀失。

参考链接：[1] 安胜利.统计学系列讲座第2讲正态分布与参考值范围估计[J].护理学报,2006(03):93-94.[2] 施⽉仙,赵岳,侯亚红,⾼敏,王丽君,尚少梅.⾎液透析患者并发⾼磷⾎症的⾮疾病性因素研究[J].中华护理杂志,2018,53(10):1186-1191.声明。

SPSS数据正态性检验解析正态性检验是数据分析中的一个关键步骤，它通常用于检查一个数据集是否符合正态分布。

如果数据集符合正态分布，则可以使用更广泛的统计方法。

SPSS软件是一个广泛使用的统计分析工具，它提供了一系列的正态性检验方法，用于帮助用户评估他们的数据是否符合正态分布。

本文将介绍如何使用SPSS进行正态性检验。

正态性检验数据的正态性是指数据集在正态分布上的贴合程度。

在正态分布中，数据的均值、中位数和众数相等，数据分散程度由标准差来度量。

正态分布在自然界中非常普遍，例如，身高、体重和智力得分通常符合正态分布。

正态性检验是用于检查一个数据集是否符合正态分布的一种方法。

如果数据集的分布不是正态分布，则在分析数据时需要采取更多的措施。

一些因素导致数据不符合正态分布，例如较小的样本量、抽样偏差、异常值等。

正态性检验的目的是确定一个分布是否足够接近正态分布，以使得正态性假设在数据分析中得到保证。

正态性假设是很重要的，在大多数情况下，如果数据是接近正态分布，则可以使用更广泛的统计方法。

如果数据不符合正态分布，则需要使用非参数方法。

SPSS中的正态性检验SPSS提供了一系列正态性检验方法，用于分析数据集的正态性。

以下将分别介绍这些方法：1.直方图与正态概率图检验直方图可以通过展示数据集的频率分布来检查正态性。

用户可以通过观察直方图形状是否类似于正态分布来评估正态性。

此外，正态概率图也可以用来评估正态性。

正态概率图绘制了每个观测值在正态分布上的位置，并将这些观测值与理论正态分布进行比较。

2.基于统计值的正态性检验SPSS中的一些统计测试可以用于定量检测正态性。

例如，Shapiro-Wilk检验是一种基于统计值的正态性检验方法。

这种测试计算数据的W值，如果W值不显著，则数据符合正态分布。

其他常用的基于统计值的正态性检验方法包括Kolmogorov-Smirnov检验和Anderson-Darling检验。

3.用Q-Q图检验正态性Q-Q图是评估一个数据集是否为正态分布的一种图形方法。

一、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

以上两种方法以Q-Q图为佳，效率较高。

3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图判断方法：观测离群值和中位数。

5、茎叶图类似与直方图，但实质不同。

二、计算法1、偏度系数（Skewness）和峰度系数（Kurtosis）计算公式：g1表示偏度，g2表示峰度，通过计算g1和g2及其标准误σg1及σg2然后作U 检验。

两种检验同时得出U<U0.05=1.96，即p>0.05的结论时，才可以认为该组资料服从正态分布。

由公式可见，部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。

2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验（D检验）和Shapiro- Wilk（W 检验）。

SAS中规定：当样本含量n≤2000时，结果以Shapiro – Wilk（W检验）为准，当样本含量n >2000时，结果以Kolmogorov – Smirnov（D检验）为准。

SPSS中则这样规定：（1）如果指定的是非整数权重，则在加权样本大小位于3和50之间时，计算Shapiro-Wilk统计量。

对于无权重或整数权重，在加权样本大小位于3和5000之间时，计算该统计量。

由此可见，部分SPSS教材里面关于“Shapiro – Wilk适用于样本量3-50之间的数据”的说法是在是理解片面，误人子弟。

（2）单样本Kolmogorov-Smirnov检验可用于检验变量（例如income）是否为正态分布。

正态分布检验一、正态检验的必要性[1]当对样本是否服从正态分布存在疑虑时，应先进行正态检验；如果有充分的理论依据或根据以往积累的信息可以确认总体服从正态分布时，不必进行正态检验。

当然，在正态分布存疑的情况下，也就不能采用基于正态分布前提的参数检验方法，而应采用非参数检验。

二、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

以上两种方法以Q-Q图为佳，效率较高。

3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图判断方法：观测离群值和中位数。

5、茎叶图类似与直方图，但实质不同。

三、计算法1、峰度（Kurtosis）和偏度（Skewness）（1）概念解释峰度是描述总体中所有取值分布形态陡缓程度的统计量。

这个统计量需要与正态分布相比较，峰度为0表示该总体数据分布与正态分布的陡缓程度相同；峰度大于0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；峰度小于0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。

峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。

峰度的具体计算公式为：注：SD就是标准差σ。

峰度原始定义不减3，在SPSS中为分析方便减3后与0作比较。

偏度与峰度类似，它也是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性。

这个统计量同样需要与正态分布相比较，偏度为0表示其数据分布形态与正态分布的偏斜程度相同；偏度大于0表示其数据分布形态与正态分布相比为正偏或右偏，即有一条长尾巴拖在右边，数据右端有较多的极端值；偏度小于0表示其数据分布形态与正态分布相比为负偏或左偏，即有一条长尾拖在左边，数据左端有较多的极端值。

如何在spss中进行正态分布检验1(转)标签：一、图示法1、P-P图以样本的累计频率作为横坐标，以安装正态分布计算的相应累计概率作为纵坐标，把样本值表现为直角坐标系中的散点。

如果资料服从整体分布，则样本点应围绕第一象限的对角线分布。

2、Q-Q图以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，把样本表现为指教坐标系的散点。

如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。

以上两种方法以Q-Q图为佳，效率较高。

3、直方图判断方法：是否以钟形分布，同时可以选择输出正态性曲线。

4、箱式图判断方法：观测离群值和中位数。

5、茎叶图类似与直方图，但实质不同。

二、计算法1、偏度系数（Skewness）和峰度系数（Kurtosis）计算公式：g1表示偏度，g2表示峰度，通过计算g1和g2及其标准误σg1及σg2然后作U检验。

两种检验同时得出U<=，即p>的结论时，才可以认为该组资料服从正态分布。

由公式可见，部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。

2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验（D检验）和Shapiro- Wilk（W检验）。

SAS中规定：当样本含量n≤2000时，结果以Shapiro –Wilk（W检验）为准，当样本含量n >2000时，结果以Kolmogorov –Smirnov（D检验）为准。

SPSS中则这样规定：（1）如果指定的是非整数权重，则在加权样本大小位于3和50之间时，计算Shapiro-Wilk统计量。

对于无权重或整数权重，在加权样本大小位于3 和5000 之间时，计算该统计量。

由此可见，部分SPSS教材里面关于“Shapiro –Wilk适用于样本量3-50之间的数据”的说法是在是理解片面，误人子弟。

（2）单样本Kolmogorov-Smirnov 检验可用于检验变量（例如income）是否为正态分布。

正态性检验和正态转换的⽅法以及在SPSS中的实现正态性检验的⽅法以及在SPSS中的实现本⽂将汇总正态检验常⽤的⽅法以及各种⽅法的适⽤条件和在SPSS中的实现，此外，还将提及将⾮正态分布转化为正态分布的⽅法，以及选择转化⽅法的依据。

⼀、正态检验⽅法1.1观察分布，预先判断先做直⽅图看看是否⼤概符合正态分布，Graph-->legacy dialogs-->histogram-->选⼊变量--》OK.如果距离正态分布的样⼦太远了，就不要做以下⼯作了。

1.2计算偏度(Skewness)和峰度(Kurtosis) ，当它们接近0时，为正态这是⼀种⽐较直观的⽅法，⽤于初步判断。

1)在SPSS中通⽤菜单栏Analyze—Reports—Case Summaries分析过程Statistics的选择项中计算偏度(Skewness)和峰度(Kurtosis) ;2)通过Analyze—Reports—Report Summaies in Row s分析过程Report 的Summary 的选择项计算偏度、峰度；或者通过Reprts—Report Summaries in Columns 分析过程的Summary 选择项计算偏度和峰度;3)通过Analyze—Descriptive Statistics—Frequencies分析过程的Statistics的选择项Distribution中计算偏度、峰度;4)通过Analyze—Descriptive Statist ics—Descr iptives分析过程的Opt ions的选择项Distribution中计算偏度、峰度;5)通过Analyze—Compare means—means 分析过程的Options 的选择项Statistics 中选择统计量Skewness (偏度)、Kurto sis (峰度)来对数据资料进⾏正态性检验。

附偏度和峰度统计意义:偏度主要是研究分布形状是否对称:约等于0 则可以认为分布是对称的；>0 则可以认为右偏态，此时在均值右边的数据更为分散；<0 则可以认为左偏态，此时在均值左边的数据更为分散。

spss 数据正态分布检验一、Z检验二、相关系数检验三、独立样本T检验四、相依样本T检验五、χ²独立性检验一、Z检验第一步：录入数据。

1．命名“变量视图”；2．“数据视图”中输入数据；第二步：进行分析。

第三步：设置变量；第四步：得到结果：二、相关系数检验在一项研究中，一个学生想检查生活意义和心理健康是否相关。

同意参与这项研究的30个学生测量了生活意义和心理健康。

生活意义的得分范围是10-70分（更高的得分表示更强的生活意义），心理健康的得分范围是5-35分（更高的得分表示更健康的心理状态）。

在研究中基本的兴趣问题也可以用研究问题的方式表示，例如例题：生活意义和心理健康相关吗？相关系数数据的例子Participant Meaning in Life Well-being Participant Meaning in Life Well-being1 35 192 65 273 14 194 35 355 65 346 33 347 54 358 20 289 25 1210 58 2111 30 1812 37 2513 51 1914 50 2515 30 2916 70 31 17 25 1218 55 2019 61 3120 53 2521 60 3222 35 1223 35 2824 50 2025 39 2426 68 3427 56 2828 19 1229 56 3530 60 35说明：变量participant包含在数据中，但不用输入SPSS。

在spss中输入数据及分析步骤1：生成变量1．打开spss。

2．点击“变量视图”标签。

在spss中将生成两个变量，一个是生活意义，另一个是心理健康。

变量分别被命名为meaning和wellbeing。

3．在“变量视图”窗口前两行分别输入变量名称meaning和wellbeing。

步骤2：输入数据1．点击“数据视图”，变量meaning和wellbeing出现在数据视图前两列。