测量学测量误差的基本知识

B 观测者的误差
C 测量误差
D 外界条件的变化
难度系数 c
若观测量的真值为X，观测值为li(i=1,2,…,n)，其算术 平均值为L，则描述观测值的（真）误差的正确表达式是 （A ）
A 观测值的（真）误差为 i= li -X; B 观测值的（真）误差为 i = X-L; C 观测值的（真）误差为 i = L-X; D 观测值的（真）误差为 i= li -X;
难度系数 A
L1、L2、L3为一组等精度观测值，其误差分别为-7mm, -2mm, +7mm，则它们的精度为（ A ）
A L1、L2、L3的精度相同； B L1最高、L3最低； C L3最高、L1最低； D L2最高、L1与L3相同 。
难度系数 B
丈量了D1、D2两段距离，其观测值及中误差分别为： D1=105.53m±0.05m，D2=54.60m±0.05m，这说明 ( A B ).
A D1和D2的中误差相同， B D1的相对精度高于D2的相对精度 C D1和D2的中误差不相同 D D1的相对精度低于D2的相对精度 E D1的相对精度与D2的相对精度相同。
难度系数 B
难度系数 B
精度指标
衡量精度的指标有：（ A C D ）
A 中误差
B 对中误差
C 相对误差
D 容许误差
E 偶然误差
难度系数 C
若水平角测量的中误差为6，则其极限误差可以取 值为（ C E ）
A 3
B 6
C 12
D 15
E 18
难度系数 C
观测值L1、L2为同一组等精度观测值，其含义是（ C D E ） A L1、L2的真误差相等 B L1、L2的改正数相等 C L1、L2的中误差相等 D L1、L2的观测条件基本相同 E L1、L2服从同一种误差分布

果对函数f（Δ ）求二阶导数等于零，可得曲线拐点的横坐标为：Δ 拐 ＝ ±σ 。由于曲线f（Δ ）横轴和直线Δ ＝－σ ，Δ ＝＋σ 之间的曲边梯形面
之差称为真误差，用Δ 表示。设三角形内角和的观测值为li，真值为X，则
三角形的真误差可由下式求得
用式（5.1）算得358个三角形内角和的真误差，现将358个真误差按3″为一 区间，并按绝对值大小进行排列，按误差的正负号分别统计出在各区间的误
差个数k，并将k除以总个数n（本例n＝358）误差来看，其误差的出现在数
值大小和符号上没有规律性，但观察大量的偶然误差就会发现其存在着一定 的统计规律性，并且误差的个数越多这种规律性就越明显。下面以一个测量
实例来分析偶然误差的特性。
某测区在相同的观测条件下观测了358个三角形的内角，由于观测值存在误 差，故三角形内角之和不等于理论值180°（也称真值）。观测值与理论值
值（有界性）；
②绝对值较小的误差出现的概率大，绝对值大的误差出现的概率小（单峰性）； ③绝对值相等的正、负误差出现的概率大致相等（对称性）；
④当观测次数无限增加时，偶然误差算术平均值的极限为零（补偿性）。即
式中，“［］”为总和号，即
为了更直观地表达偶然误差的分布情况，还可以用图示形式描述误差分布， 图5.1就是按表5.1的数据绘制的。其中以横坐标表示误差正负与大小，纵坐
1)仪器及工具由于测量仪器制造和仪器校正不完善，都会使测量结果产生测
量误差。 2)观测者由于观测者的技术水平和感觉器官鉴别能力的限制，使得在安置仪
器、瞄准目标及读数等方面都会产生误差。
3)外界条件观测过程所处的外界条件，如温度、湿度、风力、阳光照射等因 素会给观测结果造成影响，而且这些因素随时发生变化，必然会给观测值带

第6章
测量误差及数据处理的基本知识
第6章
测量误差及数据处理的基本知识
6．1 概述
6．1．1 测量与观测值
通过一定的仪器和方法在一定的环境下游操作人员 对某量进行量测，称为观测，获得的数据称为观测值。 6．1．2 观测与观测值的分类
1．同精度观测和不同精度观测
构成测量工作的要素包括观测者、测量仪器和外界条 件，通常将这些测量工作的要素统称为观测条件。
在实际测量工作中，以三倍中误差作为偶然误差的 容许值，称为容许误差。
6．4．4 相对误差
相对误差是中误差与观测值之比．是个无量纲数，在测 量上通常将其分子化为1，即用K＝1/N的形式来表示。 如：1/1000，1/5000等。 显然．相对中误差愈小(分母越大)．说明观测结果的精 度愈高，反之愈低。 相对中误差的分子也可以是闭合差或容许误差，这时分别称 为相对闭合差及相对容许误差。
该曲线称为高斯偶然误差分布曲线。 在概率论中，称为正态分布曲线。 在一定的观测条件下，对应着一个 确定的误差分布。 曲线的纵坐标y=概率/间距，它是 偶然误差⊿的函数，记为f(⊿)。
f(⊿ i)d⊿是偶然误差出现在微小区间(⊿ i + d⊿/2, ⊿ i +-d⊿/2) 内的概率，记为
p(⊿ i)= f(⊿ i)d⊿
6．1．3 测量误差及其来源
1．测量误差的定义 测量中的被观测量，客观上都存在着一个真实 值．简称真值。 对该量进行观测得到观测值。观测值与真值之差， 称为真误差．即
真误差＝观测值-真值
2．测量误差的反映
“必要观测”：为确定某一个被观测量或几何形体 所需要的最少的观测。
“多余观测”：在确定某一个被观测量或几何形体 所进行的观测过程中超过必要观测的观测。

加权算术平均值 相应观测值的权
三、最可靠值（最或是值）的精度评定 单位权中误差
权为1的观测值 中误差
m0
pvv
n 1
vi=li-x
测回数
最可靠值的中误差
Mx
加权平均值 的中误差
m0 p
pvv p n 1
举例
在水准测量中，已知从三个已知高程点A、B、C 出发，测得E点的三个高程观测值及各水准路线
偶然误差 – 在一定的观测条件下，单个误差的出现没有一定的规律性， 其数值大小和符号都不固定，大量的误差有统计规律的误差 – 偶然误差决定了观测结果的精密度； – 研究测量误差主要是针对偶然误差而言
二、研究目的
（1） 求取最可靠值（最或是值） （2） 衡量精度（结果的可靠性） 三、研究误差的出发点或原则： （1）根据不同的测量目的，允许在测量结果中含有一定程度 的测量误差 （2）目标并不是简单地使测量误差越小越好，而是要设法将 误差限制在与测量目的相适应的范围内 （3）分析测量误差，制定出衡量观测成果质量的标准，并求 得未知量的最合理最可靠的结果
等精度直接观测值的最可靠值
观测值
一、求最可靠值（最或是值）
最可靠值 证明
l1 l2 ln l x n n
观测次数
∵
△1=l1－X △2=l2－X
0 lin
n l X n
Hale Waihona Puke n ……… … △n=ln－X
l nX
n n n
§6.2
举例 ： b a c
偶然误差特性
一、偶然误差的四个特性
△i=ai+bi+ci-180°
（i=1,2, ··· ··· ··358）

河海大学测绘科学与工程系
偶然误差的四个特性
1.有界性：
在一定的条件下，偶然误差的绝对值不会超过一定的限度；
2.集中性：
绝对值小的误差比绝对值大的误差出现的机会多；
3.对称性：
绝对值相等的正负误差出现的机会相等；
4.抵偿性：
偶然误差的算术平均值趋近于零，即：
lim 1 2 n lim 0
来源：这主要是由于粗心大意或各种干扰引起。如瞄错目标、读错大数，操作错 误、测量环境的异常变化、仪器故障等。 特点：无规律，单个误差具有离群的特征，粗差值大大超过系统误差或偶然误差。
如何处理粗差？ Ⅰ 加强观测者的责任心，培养细致的业务作风 Ⅱ 闭合差检验，剔除孤值 Ⅲ 近代平差中的抗差估计、粗差探测方法等
当观测值真值已知时的中误差计算
--理论上可用标准差来计算
方差：中误差的平方
D
2
lim n
n
lim n
2 n
标准差：
D lim n
n
lim n
2 n
实际测量中，观测个数 n 是有限的，由有限个观测值的偶然误差 求得的标准差的近似值（估值）为中误差，用 m 表示。
m 1 2 2 2 ... n2 2
4.抵偿性：
偶然误差的算术平均值趋近于零，即：
lim 1 2 n lim 0
n
n
n n
频率直方图
误差概率分布曲线
直方图
k n
d△
(频率/组距)
k/n(频率)
－△
+△
-1.6 -1.2 -0.8 -0.4 0 0.4 0.8 1.2 1.6 -1.4 -1.0 -0.6 -0.2 0.2 0.6 1.0 1.4

②仪器构造本身也有一定误差。
例如：
水准仪的视准轴与水准轴不平行，则测量结果中含有i 角 误差或交叉误差。
水准尺的分划不均匀，必然产生水准尺的分划误差。
3
2、人的原因
观测者感官鉴别能力有一定的局限性。观测者的习惯 因素、工作态度、技术熟练程度等也会给观测者成果带来 不同程度的影响。
3、外界条件
例如：外界环境如温度、湿度、风力、大气折光等因素 的变化，均使观测结果产生误差。 例如：温度变化使钢尺产生伸缩阳光曝晒使水准气泡偏 移，大气折光使望远镜的瞄准产生偏差，风力过大使仪器安置 不稳定等。 人、仪器和外界环境通常称为观测条件； 观测条件相同的各次观测称为等精度观测； 观测条件不相同的各次观测称为不等精度观测。
⑤ 随着 n 的增大，m 将趋近于σ 。
17
必须指出： 同精度观测值对应着同一个误差分布，即对应着同一个标 准差，而标准差的估计值即为中误差。 同精度观测值具有相同的中误差。 例3: 设对某个三角形用两种不同的精度分别对它进行了10次 观测，求得每次观测所得的三角形内角和的真误差为
第一组： +3″, -2″, -4″,+2″,0″,-4″,+3″, +2″, -3″, -1″； 第二组： 0″, -1″, -7″,+2″,+1″,+1″,- 8″, 0″, +3″, -1″.
2
n
lim
n

n
13
•
从5-3式可以看出正态分布具有前述的偶然误差特性。即:
1.f(△)是偶函数。即绝对值相等的正误差与负误差求得 的f(△)相等，所以曲线对称于纵轴。这就是偶然误差的第三 特性。 • 2.△愈小，f(△)愈大。当△=0时，f(△)有最大值; 反之， △愈大，f(△)愈小。当n→±∞时，f(△) →0,这就是偶然误 差的第一和第二特性。 • 3.如果求f(△)二阶导数并令其等于零，可以求得曲线拐 点横坐标： △拐=± • 如果求f(△)在区间± 的积分，则误差出现在区间内 的相对次数是某个定值 ，所以当 愈小时，曲线将愈陡峭， 即误差分布比较密集；当 愈大时，曲线将愈平缓，即误差 分布比较分散。由此可见，参数 的值表征了误差扩散的特 征。

倾斜角度α＝15°00„00“，其中误差m
求相应水平距离和中误差。
D s cos＝48.296 m
D D dD ds d s
f f f dZ dx1 dx2 ...... dxn x1 x2 xn
函数的真误差和独立观测值的真误差之 间的关系式。
f f f Z x1 x2 ...... xn x1 x2 xn
f fi xi
Z f1x1 f 2 x2 ...... f n xn
特点：符号、大小相同或按一定规律变化；
重复观测难以发现。 尽可能消除或限制到最小程度。
处理方法：
1、检校仪器；
2、加改正数； 3、 采用适当的观测方法，使系统误差相互抵消 或减弱。
2、偶然误差：
定义：在相同的观测条件下进行一系列观测， 如果误差出现的符号和数值大小都表现出偶 然性，即从单个误差来看，该误差的大小及 符号没有规律，但从大量误差的总体来看， 具有一定的统计规律，这类误差称为偶然误 差或随机误差。
2
2
2
求任意函数中误差的方法和步骤：
1、列出独立观测值的函数式：
z f ( x1 , x2 ,... xn )
2、写出真误差关系式，对函数进行全微分：
f f f dz dx1 dx2 ... dxn x1 x2 xn
3、写出中误差的关系式：
f f f 2 2 m xn 2 mx1 mx2 ... mz x x x 1 2 n
2 2 2 2
几种简单函数的中误差计算式
1、倍函数：
z kx
z x1 x2
mz kmx
mz mx 1 mx 2

lim
n→ ∞
∆1 + ∆ 2 +L ∆ n n
= lim
[∆ ]
n
n→ ∞
=0
本章此处及以后“ 表示取括号中下标变量的代数和， 本章此处及以后“[ ]”表示取括号中下标变量的代数和， 表示取括号中下标变量的代数和 即∑∆i=[∆]
பைடு நூலகம்
§6.1 观测误差来源及其分类 6.1.3 观测误差的分类及其处理方法
土木工程测量
第六章 测量误差的基本知识
1
§6.1 观测误差来源及其分类 6.1.1 观测及观测误差
对未知量进行测量的过程，称为观测。 对未知量进行测量的过程，称为观测。 观测 测量所获得的数值称为观测值。 测量所获得的数值称为观测值。 观测值 进行多次测量时， 进行多次测量时，观测值之间往往存在差异。这种差异实 观测值与其真实值(简称为真值) 质上表现为观测值与其真实值(简称为真值)之间的差异，这种 差异称为测量误差 观测误差。 差异称为测量误差 或 观测误差。 代表观测值， 代表真值， 用Li代表观测值，X代表真值，则有 Δi=Li-X (6-1) 式中Δ 就是观测误差， 真误差，简称误差 误差。 式中Δi就是观测误差，通常称为 真误差，简称误差。 一般情况下，只要是观测值必然含有误差。 一般情况下，只要是观测值必然含有误差。
§6.1 观测误差来源及其分类 6.1.3 观测误差的分类及其处理方法
根据性质不同， 根据性质不同，观测误差可分为系统误差和偶然误差 符号和大小保持不变或按一定规律变化。 1、系统误差——符号和大小保持不变或按一定规律变化。 系统误差 符号和大小保持不变或按一定规律变化 系统误差具有积累性，对测量结果影响很大。 系统误差具有积累性，对测量结果影响很大。 尽量设法消除和减小系统误差，方法有： 尽量设法消除和减小系统误差，方法有： 在观测方法和观测程度上采用必要的措施， ①在观测方法和观测程度上采用必要的措施，限制或削弱系 统误差的影响。 统误差的影响。 ②找出产生系统误差的原因和规律，对观测值进行系统误差 找出产生系统误差的原因和规律， 的改正。 的改正。 ③将系统误差限制在允许范围内。 将系统误差限制在允许范围内。 经纬仪照准部管水准器轴不垂直于仪器竖轴的误差对水 不垂直于仪器竖轴 如，经纬仪照准部管水准器轴不垂直于仪器竖轴的误差对水 平角的影响，将其影响减小到允许范围内。 平角的影响，将其影响减小到允许范围内。

第五章测量误差基本知识一、名词解释1．中误差[南京师范大学2011年]答：中误差是衡量观测精度的一种数字标准，又称“标准差”或“均方根差”，是指在相同观测条件下的一组真误差平方中数的平方根。

2．误差传播定律[东北大学2015年]答：误差传播定律是指反映观测值的中误差与观测值函数的中误差之间关系的定律，它根据函数的形式把函数的中误差以一定的数学式表达出来。

3．偶然误差答：偶然误差是指在相同的观测条件下，对某一量进行一系列的观测，误差出现的符号和数值大小都不相同，从表面上看没有任何规律性的误差。

4．系统误差答：系统误差是指在相同的观测条件下，对某一量进行一系列的观测，出现的符号和数值上相同，或按一定的规律变化的误差。

二、填空题1．精度的3个标准是，，。

【答案】中误差；相对误差；极限误差2．中误差作为极限误差。

【答案】2倍【解析】根据极限误差的定义，常把2倍中误差作为极限误差。

3．已知X=L1+L2，Y=（L1+L2）/2，Z=X·Y。

L1、L2中误差均为m，则X、Y、Z的中误差分别为，，。

【答案】m2；22m；22m4．某平面三角形中，观测了α、β两个内角，其测角中误差均为±6″，则此三角形第三个内角γ的中误差为。

【答案】±8.5″5．现有DJ6的经纬仪，用测回法观测一个角，要使测角中误差达到±6”，求至少要观测测回。

【答案】32【解析】该题考点是第五章误差理论，要理解6的含义，6指一测回方向观测的中误差，根据协方差传播率可求得测回数。

三、判断题1．广义算术平均值的权，不等于观测值权之和。

（）【答案】错误【解析】不等精度观测值的加权平均值计算公式可以写成线性函数的形式：，根据线性函数的误差传播公式，得：，按式，以（m为单位权中误差），得：。

按式，加权平均值的权即为观测值的权之和：。

2．当每公里水准测量的精度相同时，水准路线观测高差的权与路线长度成正比。

（）【答案】错误【解析】“权”的原来意义为秤锤，用做“权衡轻重”之意。

第五章 测量误差的基本知识
5.1 测量误差概述 5.2 衡量精度的标准 5.3 误差传播定律 5.4 算术平均值及其中误差 5.5 加权平均值及其中误差
5.1 测量误差概述
测量实践中可以发现， 测量实践中可以发现，测量结果 不可避免的存在误差 比如： 存在误差， 不可避免的存在误差，比如： 1.对同一量的多次观测值不相同； 对同一量的多次观测值不相同； 对同一量的多次观测值不相同 2.观测值与理论值存在差异。 观测值与理论值存在差异。 观测值与理论值存在差异
5.3 误差传播定律
阐述观测值中误差与观测值函数的中误 差之间关系的定律，称为误差传播定律 误差传播定律。 差之间关系的定律，称为误差传播定律。 一、观测值的函数 1.和差函数 2.倍函数 3.线性函数 4.－般函数
Z = x1 + x 2 + L + x n
Z = mx
Z = k1 x1 + k 2 x 2 + L + k n x n
mZ = ± (
∂f 2 2 ∂f ∂f 2 2 ) m1 + ( ) 2 m2 + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ +( ) 2 mn ∂x1 ∂x2 ∂xn
5.4 算术平均值及观测值的中误差
一、求最或是值
设在相同的观测条件下对未知量观测了n次 设在相同的观测条件下对未知量观测了 次 ， 观测值为l 中误差为m 观测值为 1、l2……ln，中误差为 1、m2、…mn，则 其算术平均值（最或然值、似真值） 其算术平均值（最或然值、似真值）L 为：
二、研究测量误差的目的和意义
分析测量误差产生的原因及其性质。 分析测量误差产生的原因及其性质。 确定未知量的最可靠值及其精度。 确定未知量的最可靠值及其精度。 正确评价观测成果的精度。 正确评价观测成果的精度。

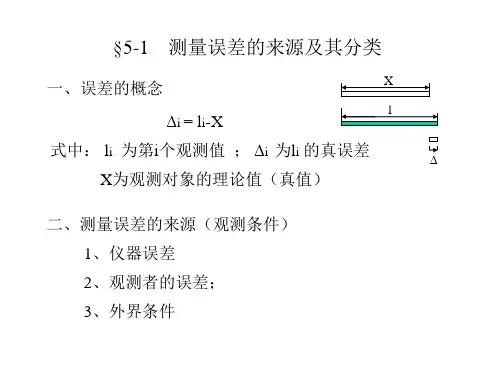
第五章 测量误差及测量平差§5.1 测量误差概述一、测量误差的概念某量的各测量值相互之间或观测值与理论值之间的往往存在着某些差异，说明观测中存在误差。

观测值与真值之差称为测量误差，也叫真误差。

X l i i -=∆ （i =1、2、……、n ） X 为真值。

二、研究测量误差的目的分析测量误差的产生原因、性质和积累规律；正确地处理测量成果，求出最可靠值；评定测量结果的精度；为选择合理的测量方法提供理论依据。

三、测量误差产生的原因1.测量仪器因素2.观测者的因素3.外界条件的因素测量观测条件——测量仪器、观测人员和外界条件这三方面的因素综合起来称为测量观测条件。

等精度观测——测量观测条件相同的各次观测称为等精度观测。

非等精度观测——测量观测条件不相同的各次观测称为非等精度观测。

四、测量误差的分类1.系统误差在相同的观测条件下对某量作一系列观测，如果误差的大小、符号表现出系统性，或按一定的规律变化，或保持不变，这种误差称为系统误差。

其特点：具有累积性，但可以采用适当的观测方法或加改正数来消除或减弱其影响。

2.偶然误差在相同的观测条件下对某量作一系列观测，如果误差的大小和符号不定，表面上没有规律性，但实际上服从于一定的统计规律性，这种误差称为偶然误差。

偶然误差单个的出现上没有规律性，不能采用适当的观测方法或加改正数来消除或减弱其影响。

因此，观测结果中偶然误差占据了主要地位，是偶然误差影响了观测结果的精确性。

五、减少测量误差的措施对系统误差，通常采用适当的观测方法或加改正数来消除或减弱其影响。

对偶然误差，通常采用多余观测来减少误差，提高观测成果的质量。

§5.2 偶然误差的特性一、精度的含义1.准确度准确度是指在对某一个量的多次观测中，观测值对该量真值的偏离程度。

2.精密度精密度是指在对某一个量的多次观测中，各观测值之间的离散程度。

3.精度精度也就是精确度，是评价观测成果优劣的准确度与精密度的总称，表示测量结果中系统误差与偶然误差的综合影响的程度。

[] n

0
12
三、算术平均值
算术平均值： x L1 L2 Ln [Li ]
n
n
为什么取算术平均值：
i x Li
Li x i
x [Li ] x [i ]
n
n
当n ： [] 0
n
xx
13
如何解决随机误差产生的矛盾
•18世纪末，在测量学、天文学等实践中提出了如 何消除由于观测误差引起的观测量之间的矛盾的问 题 •1794年，年仅17岁的高斯（C.F.Gauss）提出了解 决这个问题的方法——最小二乘法 •19世纪初，高斯用自己提出的方法解决了当时的 一个天文学难题.
4.5%
P(3m 3m) 99.7%
0.3%
取极限误差(容许误差)： 或：
容 3m 容 2m
21
(3)相对误差
1 相对误差：绝对误差的绝对值与观测值之比 N 绝对误差：真误差、中误差、容许误差
意义： 观测 1000m 观测 800m
中误差 中误差
m 2cm m 2cm
•偶然误差(random errors)
如果误差在大小和符号上都表现出偶然性，即从单个 误差看，该误差的大小和符号没有规律
•粗差(gross error)
错误 7
4、误差的消除
系统误差的解决？ 1、进行计算改正； 2、分析它对观测的影响规律，采取各种方法来 消除系统误差，或者减小它对观测成果的影响。 偶然误差的解决？ 进行多余观测，通过测量平差、数据处理理论， 确定被认为是最可靠的结果。 粗差的解决？ 尽量避免，检核
3
-1
总数
80
82
162

所谓精度，就是指误差分布的密集或离散的程度，为了衡量 观测值的精度高低，可以用误差分布表、绘制直方图或画出误 差分布曲线的方法进行比较。 衡量精度的标准有以下几种：
中误差 允许误差（极限误差） 相对误差
m 21 22 2n
n
n
例 ：对某一距离进行五次丈量，其真误差分别为－6mm 、－5mm、－2mm、+1mm、+6mm，求观测值中误差。 根据上式可知
2. 观测值的和或差函数
函数 Z=x±y 的中误差：
mz2 mx2 my2
或mz
mx2

m
2 y
例2 在三角ABC中，观测了∠A和∠B，其中误差 分别为 mA 6" ， mB 8" ，求∠C的中误差？
解： ∵C=180－(A+B) ∴
mc mA2 mB2 62 82 10
2

3

4

5
);
m x2

m 5
3、结论：

Pi mi2 ; (i = 1,2, ……n)
式中:P为权，是任意常数。
水准测量与距离丈量中，各路线的权与该路线的测站数
或距离的公里数成反比。
即
1 pi Ni
或
1 pi Si
同精度观测值的算术平均值的权与观测次数成正比。 即
Pi=Ni
设对某量进行n次观测，其观测值中误差及权分别为： 观测值 l1 , l2 …… ln 中误差 m1, m2 …… mn 权 p1 ,p2 …… pn
则加权平均值为:
x加 p1l1 p2l2 pnln [ pl]
p1 p2 pn

[z 2 ] [x 2 ] 2[xy] [y 2 ] n n n n
mz
2
mx
2
2 2 2 mz mx my
?
0
my2
2 2 mz mx my
（二）倍乘函数 已知：mx, 求：mz=?
z kx
[ z z ] mz n z k x
平方
f 2 mxn xn
2
再按照线性函 数进行计算
f 2 f 2 m mx1 mx2 x1 x2
小结
中误差关系式：
my 2 f12 m12 f 22 m2 2 ... f n2 mn 2

2
2 3
f ( x) 0.9545
x =Δ
-24″ -18 -12 -6 0 +6 +12 +18 +24″
f ( x) 0.9973
3
dΔ
极限误差取值
允 2m
或： 允 3m
§5.3 误差传播定律及其应用
设有函数式： y f ( x1 , x2 ...)
i [ ] i=1 即 Lim —— = Lim —— =0 n n n n
n
§5.2 评定精度的标准 一、方差和标准差（中误差）
正态曲线公式： 2 1 Y = f() =—— e 22 2
2
方差： D()
2 n 2 i 1
2 f ()d
F 2 F 2 mZ m1 m2 x1 x2
2
2
F 2 mn xn
2
l
1 n ln

东北大学测量学习题与答案测量误差的基本知识选择题1. 在等精度观测的条件下，正方形一条边a 的观测中误差为m ，则正方形的周长（Ｓ=4a ）中的误差为（ ）Ａ.m ； Ｂ.2m ； Ｃ.4m1. 丈量某长方形的长为α=20±m 004.0，宽为b=15±m 003.0，它们的丈量精度（）Ａ相同； Ｂ.不同； Ｃ.不能进行比较2. 衡量一组观测值的精度的指标是（ ）Ａ.中误差； Ｂ.允许误差； Ｃ.算术平均值中误差3. 在距离丈量中，衡量其丈量精度的标准是（ ） Ａ.相对误差； Ｂ.中误差； Ｃ .往返误差4. 下列误差中（ ）为偶然误差Ａ.照准误差和估读误差； Ｂ.横轴误差和指标差； Ｃ.水准管轴不平行与视准轴的误差5. 若一个测站高差的中误差为站m ，单程为ｎ个测站的支水准路线往返测高差平均值的中误差为（ ）Ａ.nm 站； Ｂ.m n 站2/ Ｃ. m n 站6. 在相同的观条件下，对某一目标进行ｎ个测站的支水准路线往返测高差平均值的中误差为（ ）Ａ.[]n m /∆∆=； Ｂ.[]）（1/-=n m υυ； Ｃ. []）（1/-=n n m υυ7. 对三角形进行５次等精度观测，其真误差（闭合差）为：+4″；-3″；+1″；-2″；+6″，则该组观测值的精度（ ）Ａ.不相等； Ｂ.相等； Ｃ.最高为+1″8. 经纬仪对中误差属（ ）Ａ.偶然误差； Ｂ.系统误差； Ｃ.中误差9. 尺长误差和温度误差属（ ）Ａ.偶然误差； Ｂ.系统误差； Ｃ.中误差10.一条直线分两段丈量，它们的中误差分别为1m 和2m ，该直线丈量的中误差为（ ）Ａ.2221m m +； Ｂ. 2221m m ⋅； Ｃ. ()2221m m +11.一条附和水准路线共设ｎ站，若每站水准测量中误差为ｍ，则该路线水准测量中误差为（ ）Ａ.ｍｎ⨯； Ｂ.ｎｍ/； Ｃ.ｎｍ⨯12.某基线丈量若干次计算得到平均长为540m ，平均值之中误差为±0.05m ，则该基线的相对误差为（ ）Ａ.0.0000925； Ｂ.1/11000； Ｃ.1/1000013.下面是三个小组丈量距离的结果，只有（ ）组测量的相对误差不低于1/5000的要求Ａ.100m ±0.025m ； Ｂ.200m ±0.040m ； Ｃ.150m ±0.035m14.对某量进行ｎ次观测，若观测值的中误差为ｍ，则该量的算术平均值的中误差为（ ）Ａ. ｍｎ⨯； Ｂ.m/n ； Ｃ.m/n15.某直线段ＡＢ的坐标方位角为230º，其两端间坐标增量的正负号为（ ）Ａ. y x ∆+∆-, Ｂ. y x ∆-∆+, Ｃ. y x ∆-∆-,16.小三角锁近似平差主要考虑（ ）Ａ.测角误差； Ｂ.基线误差； Ｃ.起始边方位角的误差17.在全圆测回法的观测中，同一盘位起始方向的两次读数之差叫（ ）Ａ.归零差； Ｂ.测回差； Ｃ.C 2互差18.四等水准测量中,黑面高差减红面高差±0.1m 应不超过（ ） Ａ.２ｍｍ Ｂ.３ｍｍ； Ｃ.５ｍｍ19.用导线全长相对闭合差来衡量导线测量精度的公式是( ) Ａ.D M K = Ｂ.()D D K ∆=/1； Ｃ.()∑=D f D K /1 20.导线的坐标增量闭合差调整后，应使纵、横坐标增量改正数之和等于（ ）Ａ.纵、横坐标增值量闭合差，其符号相同； Ｂ.导线全长闭合差，其符号相同；Ｃ.纵、横坐标增量闭合差，其符号相反 判断题在测量工作中，误差和错误都是不可避免的。

系统误差的来源与消除方法
总结词
系统误差的来源主要包括测量设备误差、环境因素误差和测量方法误差。消除系统误差的方法包括校准设备、改 进测量方法和采用适当的修正公式。
详细描述
系统误差的来源多种多样，其中最常见的是测量设备误差，如仪器的刻度不准确、零点漂移等。此外，环境因素 如温度、湿度和气压的变化也可能导致系统误差。为了消除这些误差，可以采用定期校准设备、选择适当的测量 方法和采用修正公式等方法。
相对测量法
通过比较被测量与标准量之间 的差异来得到被测量的值，并 评估误差。
组合测量法
将被测量与其他已知量进行组 合，通过测量组合量来得到被
测量的值，并评估误差。
测量结果的表示与处理
测量结果的表示
测量结果应包括被测量的值、单位、 测量不确定度以及置信区间等。
异常值的处理
在数据处理过程中，如果发现异常值， 应进行识别、判断和处理，以确保测 量结果的准确性和可靠性。
测量学第五章 测量误差 基本知识
contents
目录
• 测量误差概述 • 系统误差 • 随机误差 • 粗大误差 • 测量误差的估计与处理
测量误差概述
01
测量误差的定义
测量误差
在测量过程中，由于受到测量仪器、 环境条件、操作者技能等因素的影响 ，使得测量结果与被测量的真实值之 间存在一定的差异。
不确定度的评定方法
不确定度的传递
不确定度的评定方法包括A类评定和B类评 定，其中A类评定基于统计分析，B类评定 基于经验和信息。
在多个量之间存在函数关系时，需要将各 个量的不确定度传递到最终的测量结果中 ，以确保最终结果的准确性和可靠性。
THANKS.
数据修约
根据测量不确定度对数据进行修约， 以确保数据的完整性和一致性。

已知：mx1, mx2, --- mxn 求：my=?
my [ y y ] n
y=?
dy y
§5.4
误差传播定律及其应用
概念
误差传播定律：阐述观测值的中误差与观测值
函数中误差的关系的定律。
倍数函数
函数形式
和差函数
线性函数
一般函数
（一）和差函数
例如：用水准测量测定两点间的高差h=(a-b)，a 为后视读数，b为前视读数，称h为观测值a和b的 函数。 又例如距离 S 分 n 段丈量，各段长度分别为 S1 、 S2 、 … ， Sn ，则 S=S1+S2+….Sn ，称距离 S 是各分 段长度S1，S2、…，Sn的函数 这些数学式都是直接观测值之和或差，因此称为 和差函数。
2
2
2
2
设每个自变量都观测了 多次，i 1,2,3....n
y i
i 1
n
2
n
f1
n
2
(x1 ) i
i 1
n
2
n
1 2
f2
2
(x 2 ) i
i 1
n
2
n
...
n 当n ， lim 2 f 1 f 2
2 f1 f 2
解：第一组观测值的中误差：
0 2 2 2 12 (3) 2 4 2 32 (2) 2 (1) 2 2 2 (4) 2 m1 2.5 10
第二组观测值的中误差：
(1) 2 2 2 (6) 2 0 2 (1) 2 7 2 12 0 2 (3) 2 (1) 2 m2 3.2 10
S′