《工程电磁场基础及应用》教学课件第3章
- 格式：ppt
- 大小：2.69 MB
- 文档页数：44
下载文档原格式
合集下载
工程电磁场PPT
工程电磁场PPT
PPT文档演模板
2020/11/12
工程电磁场PPT
PPT文档演模板
工程电磁场PPT
教育部电子信息与电气学科教学指导委员会 基础课教学指导分委员会
《电磁场》课程教学基本要求
PPT文档演模板
工程电磁场PPT
PPT文档演模板
工程电磁场PPT
电磁学三大实验定律： 库仑定律， 安培定律， 法拉第定律。
Reaction Field
提升力
Magnetic Force
PPT文档演模板
Levitation Force (mN): Theory 45.72 Lorentz 42.04 Maxwell Str 44.60 Virt Work 44.73
工程电磁场PPT
2-D Magnetostatics (2-D静磁场)
电场强度E (V/m) － 8000 8000 200/f 200/f 67 67 67/f1/2 14 9.85f1/2 28
磁场强度H (A/m)
7000 7000/f2 900/f 0.9/f
1.13 1.13 0.17/f 0.17/f1/2 0.036 0.026f1/2 0.073
磁感应强度B (μT) 9000 9000/f2 1100/f 1.1/f 1.4 1.4 0.21/f
雷达
工程电磁场PPT
PPT文档演模板
电磁波暗室（无反射）
工程电磁场PPT
PPT文档演模板
工程电磁场PPT
PPT文档演模板
工程电磁场PPT
PPT文档演模板
电场脉冲模拟器
工程电磁场PPT
PPT文档演模板
开阔地试验
工程电磁场PPT
磁悬浮分析
PPT文档演模板
2020/11/12
工程电磁场PPT
PPT文档演模板
工程电磁场PPT
教育部电子信息与电气学科教学指导委员会 基础课教学指导分委员会
《电磁场》课程教学基本要求
PPT文档演模板
工程电磁场PPT
PPT文档演模板
工程电磁场PPT
电磁学三大实验定律： 库仑定律， 安培定律， 法拉第定律。
Reaction Field
提升力
Magnetic Force
PPT文档演模板
Levitation Force (mN): Theory 45.72 Lorentz 42.04 Maxwell Str 44.60 Virt Work 44.73
工程电磁场PPT
2-D Magnetostatics (2-D静磁场)
电场强度E (V/m) － 8000 8000 200/f 200/f 67 67 67/f1/2 14 9.85f1/2 28
磁场强度H (A/m)
7000 7000/f2 900/f 0.9/f
1.13 1.13 0.17/f 0.17/f1/2 0.036 0.026f1/2 0.073
磁感应强度B (μT) 9000 9000/f2 1100/f 1.1/f 1.4 1.4 0.21/f
雷达
工程电磁场PPT
PPT文档演模板
电磁波暗室（无反射）
工程电磁场PPT
PPT文档演模板
工程电磁场PPT
PPT文档演模板
工程电磁场PPT
PPT文档演模板
电场脉冲模拟器
工程电磁场PPT
PPT文档演模板
开阔地试验
工程电磁场PPT
磁悬浮分析
《电磁场》课件—第三章 静电场5(静电能量和力)
=
U2
2Sε 0
ε
0S
2
d
= U 2ε0S
2d 2
方向？
[例3] 两同轴圆柱导体中间介质ε=ε0，R1=5cm，R2=6cm，U=1000V，忽 略边缘效应，求内圆柱所受的力。(习题3.30)
x
[解] 1）求静电能
R2
R1
A) 求法一、因为：
E=
λ 2πε 0 ρ
U
∫ U = R2 Edρ R1
45ε
∫ We
=
1 2
ϕρdV
V'
带电体
∫ = 1 ⋅ 2
a 0
ρa2 3ε 0
+
ρa 2 6ε
−
ρr 2 6ε
ρ
4πr2dr
=
2πρ 2a5
1
9ε 0
+
1
45ε
作业
3.26 3.27 3.32 • 讨论题
见通知
菩提本无树，明镜亦非台——虚功
B) 求法二、
f
= − ∂We ∂g
qk
=
−
∂ ∂x
Q2 2C
=
−
Q2 2
∂ ∂x
ε
x 0S
=
−
Q2 2ε 0 S
= − U 2ε0S 2x2
x=d
C) 求法三、利用库仑定律
采用无限大带电平面的计算公式：
E" = σ 2ε 0
E = σ ,U = Q d ε0 ε0S
f
= QE" = Q Q
2Sε 0
∞ E' (∏)dr = Q
R2
4πε 0 R2
R2
工程电磁场理论与应用讲义-3
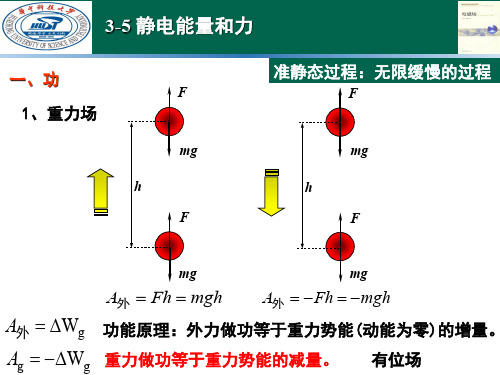
第3章 电磁场分析的数学模型3.1 电磁场控制方程的表述电磁场数值分析的具体任务，就是要求解一个与特定问题相联系的偏微分方程定解问题。
根据数学物理方程的理论，所谓定解问题指的是在某一确定区域内成立的微分方程加上定解条件。
对于静态电磁场问题，或者可化为复数计算的正弦稳态电磁场问题，定解条件就是微分方程中的未知函数在该区域边界上所满足的条件，亦即边界条件；对于时变电磁场问题，则定解条件除了边界条件以外，还包括整个区域未知函数在初始时刻的值，亦即初始条件。
针对这一定解问题的求解，发展了如上节所述的各种解算方法。
因此，为了得到正确的解答，第一步工作就是要写出定解问题的表达式，也就是建立特定电磁场问题的恰当的数学模型。
定解问题中的偏微分方程通常称为控制方程。
选择哪种物理量作为控制方程中的未知函数，建立什么形式的微分方程，将影响问题求解的难易程度。
本节将从麦克斯韦方程组出发，介绍各种情况下电磁场控制方程的表述方式。
3.1.1 麦克斯韦方程组[54] 100多年前，麦克斯韦对前人在实验中得出的电磁场的基本定律进行了数学上的总结和提升，引入了位移电流的概念，创立了后来以其命名的方程组，完善了电磁场理论。
其著作《Treatise on Electricity and Magnetism 》成书于1873年。
从理论框架上看，麦克斯韦方程组加上洛仑兹力的计算公式，合起来构成了静止及运动媒质中电动力学的基础，概括了发电机、电动机和其它电磁装置的工作原理，也概括了电磁波的发射、传播和接收的原理。
科学技术发展的实践证明，描述电磁场宏观性质的麦克斯韦方程组正确反映了电磁场中各物理量之间的相互关系，是电磁场的基本方程。
在大学普通物理和电类专业的电工原理课程中，都对麦克斯韦方程组作了基本的介绍。
本节主要从电磁场数值计算的需要出发来加以说明。
麦克斯韦方程组的微分形式可以表述为：t∂∂+=⨯∇D J H (3-1) t∂∂-=⨯∇B E (3-2) 0=⋅∇B (3-3)ρ=⋅∇D (3-4)式中，H 、B 、D 、E 、J 、ρ 分别为磁场强度（A/m ）、磁感应强度（或称磁通密度，T ）、电位移（或称电通密度，C/m 2）、电场强度（V/m ）、电流密度（A/ m 2）和电荷密度（C/ m 3）。
工程电磁场第三章PPT资料35页
3 .1电流与电流密度 1.电流与电流密度 电荷有规则的运动形成电流； 导电媒质中的电流称为传导电流； 不导电空间电荷运动形成的电流称为运流电流； 不随时间变化的电流是恒定电流，维持恒定电流的电场称为恒定电场。
密度为ρ的体电荷以速度v运动形成体电流密度J
穿过面积S的电流就是电流密度J在该面积上的通量
由电场强度的分界面条件
电位移矢量的分界面条件
导体与理想介质分界面
结论2 导体与理想介质分界面上必有面电荷。
E 1 t E 2 t J1/t 10
结论3 电场切向分量不为零，导体非等位体，导体表面非等位面
若 1 （理想导体），导体内部电场为零，电
流分布在导体表面，导体不损耗能量。 导体周围介质中的电场：
2.电动势 图3-2-1所示为一个典型的导电回路。
为了衡量电源将其他能量转换为电能的能力， 我们把单位正电荷从电源负极运动到 正极，局外力所做的功定义为电源的电动势， 用e表示，且
在电源中，除局外电场外，也存在库仑电场，故总的电场强度为 在电源以外的其他区域，只存在库仑电场，故总的电场强度
如果积分路径经过电源，则电场强度的闭合线积分等于电源的电动势
定电场的辅助方程。
3. 2恒定电场的基本方程 1. 局外场
要维持导电媒质中的恒定电流。就必须有恒定的电场强度。 在一个闭合回路中库仑电场的电场强度E闭合线积分为零。要维持恒定电流，电荷 在沿闭合回路运动时，还必须受到局外力的作用。
提供局外力的装置就是电源。在电源中，其他形式的能量(如化学能、机械能和光 能等)转换为电能。在整个闭合回路中，电能又转换为别的形式的能量。
（1）从良导体一侧看，进入的电流线近似与分界面垂直。 （2）在不良导体中放入良导体电极，从不良导体一侧看，可以认为电流 线垂直进入或流出电极表面，电极表面可作为等位面处理。
密度为ρ的体电荷以速度v运动形成体电流密度J
穿过面积S的电流就是电流密度J在该面积上的通量
由电场强度的分界面条件
电位移矢量的分界面条件
导体与理想介质分界面
结论2 导体与理想介质分界面上必有面电荷。
E 1 t E 2 t J1/t 10
结论3 电场切向分量不为零，导体非等位体，导体表面非等位面
若 1 （理想导体），导体内部电场为零，电
流分布在导体表面，导体不损耗能量。 导体周围介质中的电场：
2.电动势 图3-2-1所示为一个典型的导电回路。
为了衡量电源将其他能量转换为电能的能力， 我们把单位正电荷从电源负极运动到 正极，局外力所做的功定义为电源的电动势， 用e表示，且
在电源中，除局外电场外，也存在库仑电场，故总的电场强度为 在电源以外的其他区域，只存在库仑电场，故总的电场强度
如果积分路径经过电源，则电场强度的闭合线积分等于电源的电动势
定电场的辅助方程。
3. 2恒定电场的基本方程 1. 局外场
要维持导电媒质中的恒定电流。就必须有恒定的电场强度。 在一个闭合回路中库仑电场的电场强度E闭合线积分为零。要维持恒定电流，电荷 在沿闭合回路运动时，还必须受到局外力的作用。
提供局外力的装置就是电源。在电源中，其他形式的能量(如化学能、机械能和光 能等)转换为电能。在整个闭合回路中，电能又转换为别的形式的能量。
（1）从良导体一侧看，进入的电流线近似与分界面垂直。 （2）在不良导体中放入良导体电极，从不良导体一侧看，可以认为电流 线垂直进入或流出电极表面，电极表面可作为等位面处理。
《工程电磁场》课件
● 本课程学习将遵循数学建模、分析的主线索展开，因此，除微积分基 础知识外，矢量分析与场论、数理方程(偏微分方程)与特殊函数等数学知识 和工具都应成为定性乃至定量分析电磁场问题所必备的知识基础。
2. 掌握常用分析、计算的方法
● 通过例题、习题等环节不断提高逻辑思维、分析与解题能力，这也是 理论联系实际、通过实践能动地理解和深化概念的过程。
三、学习方法
电磁场理论体系完整、简练，内涵丰富、概念性强，且较抽象。同时， 应用数学知识与工具较多，涉及知识面宽，故更需要注意科学的学习方法
1. 深入理解，建立正确的物理概念，并熟练运用必须的数学 知识和工具
● 实践证明，正确理解物理概念是学习中困难的主要方面，故需抓住此 主要矛盾，通过深入钻研，使之得以缓解。
度)J(r,t),其量值为
J lim i di
S Sn 0
n
dSn
其方向习惯上定义为正电荷运动的方向。
(单位: A/m2)
(1.2)
§1.3 矢量分析教学中的若干讨论点
1. 点函数在不同坐标系下的数学描述
例1.1 设标量点函数(r)在直角坐标系下的表示式为(x，y，z)＝ x2＋y2－z，试写出该点函数在圆柱坐标系下的表示式，并以给定点的函
想化实际带电系统的电荷分布形态为如下四种形式：
（1）点电荷 q(r,t)：
（2）电荷体密度 (r,t)q：r C
（3）电荷面密度
r(r,tlVi)m：0 qVr
dq r
dV
C/m3
（4）电荷线密度
r(r,tl)Sim ：0 qSr
§1.1 电磁场的物理模型及其分析
根据电磁现象和过程分析的物理模型构造的本质，可建立如下电磁 场分析与电路分析的物理模型之间的对比关系。
2. 掌握常用分析、计算的方法
● 通过例题、习题等环节不断提高逻辑思维、分析与解题能力，这也是 理论联系实际、通过实践能动地理解和深化概念的过程。
三、学习方法
电磁场理论体系完整、简练，内涵丰富、概念性强，且较抽象。同时， 应用数学知识与工具较多，涉及知识面宽，故更需要注意科学的学习方法
1. 深入理解，建立正确的物理概念，并熟练运用必须的数学 知识和工具
● 实践证明，正确理解物理概念是学习中困难的主要方面，故需抓住此 主要矛盾，通过深入钻研，使之得以缓解。
度)J(r,t),其量值为
J lim i di
S Sn 0
n
dSn
其方向习惯上定义为正电荷运动的方向。
(单位: A/m2)
(1.2)
§1.3 矢量分析教学中的若干讨论点
1. 点函数在不同坐标系下的数学描述
例1.1 设标量点函数(r)在直角坐标系下的表示式为(x，y，z)＝ x2＋y2－z，试写出该点函数在圆柱坐标系下的表示式，并以给定点的函
想化实际带电系统的电荷分布形态为如下四种形式：
（1）点电荷 q(r,t)：
（2）电荷体密度 (r,t)q：r C
（3）电荷面密度
r(r,tlVi)m：0 qVr
dq r
dV
C/m3
（4）电荷线密度
r(r,tl)Sim ：0 qSr
§1.1 电磁场的物理模型及其分析
根据电磁现象和过程分析的物理模型构造的本质，可建立如下电磁 场分析与电路分析的物理模型之间的对比关系。
《工程电磁场》课件
《工程电磁场》ppt课件
目录
contents
绪论电磁场的基本理论工程电磁场的数值分析方法工程电磁场的实验研究工程电磁场的应用案例
01
绪论
总结词
工程电磁场的定义、重要性及与其他学科的关系
详细描述
工程电磁场是一门研究电磁场理论及其应用的学科，它在现代工程技术和科学领域中具有非常重要的地位。工程电磁场与物理学、数学、电子学、通信工程等多个学科有着密切的联系，是这些学科的重要基础之一。
详细描述
矩量法是一种用于分析电磁场中电流分布的数值分析方法。它将连续的电流分布离散化为有限个矩量，每个矩量可以用简单的函数来表示。然后通过求解这些矩量的线性方程组，得到原电流分布的近似解。矩量法在电磁场数值分析中具有广泛的应用，尤其适用于分析复杂结构的电磁散射和辐射问题。
04
工程电磁场的实验研究
在电力工业中，电磁场被广泛应用于发电、输电、配电和电机控制等领域。发电机和变压器利用电磁场将机械能转换为电能，输电线路利用电磁场传输电能，电动机利用电磁场将电能转换为机械能。
提高电力系统的稳定性和效率
通过研究和应用电磁场理论，电力工程师可以优化电力系统的设计和运行，提高电力传输的稳定性和效率，减少能源损失，降低环境污染。
详细描述
有限元法是一种广泛应用于工程电磁场数值分析的方法。它将复杂的电磁场问题分解为多个简单的子问题，通过离散化处理，将连续的求解域转化为有限个小的互连子域，每个子域可以用简单的近似函数来表示。然后通过求解这些子域的方程组，得到原问题的近似解。
一种将连续的求解域离散化为有限个离散点，并利用差分近似表示原偏微分方程的方法。
总结词
详细描述
总结词
详细描述
总结词
详细描述
目录
contents
绪论电磁场的基本理论工程电磁场的数值分析方法工程电磁场的实验研究工程电磁场的应用案例
01
绪论
总结词
工程电磁场的定义、重要性及与其他学科的关系
详细描述
工程电磁场是一门研究电磁场理论及其应用的学科，它在现代工程技术和科学领域中具有非常重要的地位。工程电磁场与物理学、数学、电子学、通信工程等多个学科有着密切的联系，是这些学科的重要基础之一。
详细描述
矩量法是一种用于分析电磁场中电流分布的数值分析方法。它将连续的电流分布离散化为有限个矩量，每个矩量可以用简单的函数来表示。然后通过求解这些矩量的线性方程组，得到原电流分布的近似解。矩量法在电磁场数值分析中具有广泛的应用，尤其适用于分析复杂结构的电磁散射和辐射问题。
04
工程电磁场的实验研究
在电力工业中，电磁场被广泛应用于发电、输电、配电和电机控制等领域。发电机和变压器利用电磁场将机械能转换为电能，输电线路利用电磁场传输电能，电动机利用电磁场将电能转换为机械能。
提高电力系统的稳定性和效率
通过研究和应用电磁场理论，电力工程师可以优化电力系统的设计和运行，提高电力传输的稳定性和效率，减少能源损失，降低环境污染。
详细描述
有限元法是一种广泛应用于工程电磁场数值分析的方法。它将复杂的电磁场问题分解为多个简单的子问题，通过离散化处理，将连续的求解域转化为有限个小的互连子域，每个子域可以用简单的近似函数来表示。然后通过求解这些子域的方程组，得到原问题的近似解。
一种将连续的求解域离散化为有限个离散点，并利用差分近似表示原偏微分方程的方法。
总结词
详细描述
总结词
详细描述
总结词
详细描述
电磁场与电磁波第3章ppt_图文
q
4 0
1 rP
1 rQ
O
选参考点位于无穷远处，即令rQ ，得 P
rP q
4 0rP
P
由此得到点电荷电位的一般表达式 q 4 0r
对于位于r的点电荷，电位表达式为
q
q
40 r r 40R
无限长线电荷：设线电荷l在原点，参考点Q，场点 (电位
微分形式：
D
E 0
本构关系：D E
边界条件
en E1 E2 0
en
D1
D2
S
或
E1t E2t
D1n
D2 n
S
对于理想介质，有
en E1 E2
0 或
en D1 D2 0
x a 处，φ2 (a) = 0
x b处，φ1(b) =φ2 (b),
2 ( x)
x
1(x)
x
xb
S0 0
所以 D1 = 0
C2a + D2 = 0
C1b + D1 = C2 b + D2
C2
-
C1
=
-ρS0 ε0
由此解得
C1
=
-ρS0 (b ε0a
证明 对于单个点电荷产生的场
把试探电荷q0从P移到Q 设电荷q0 受到的电场力为F， 在该力作用下的位移为dl，
则电场力做功为 dW F dl qE dl
WPQ
Q
F dl
P
Q
Q
F cos θdl Fdr
工程电磁场基础1-PPT课件
参考书目
1《 工程电磁场》 王泽忠, 全玉生, 卢斌先编著，清 华大学出版社 2《工程电磁场基础》孙敏主编，科学出版社
超星数字图书馆，网址：202.118.72.18 sslibrary/ (80万册图书试用) 方正Apabi数字图书馆，网址：202.118.72.3
第一章 矢量分析与场论基础
矢量运算的有关公式 场的基本概念 标量场的等值面方程和矢量场的矢量线方程 源点和场点的基本概念及其相互关系 梯度的定义
定义了场量的空间点称为场点。在直角坐标系中，场点 Ｍ 可以由它的三个坐标ｘ， ｙ，ｚ确定。因此，一个标量场和一个矢量场可分别用坐标的标量函数和矢量函数表 示，即
其中，矢量函数Ａ（Ｍ）的坐标表示式可写成上式。式中，函数Ａｘ，Ａｙ，Ａｚ分别 为矢量函数Ａ 在直角坐标系中三个坐标轴上的投影，为三个标量函数；ｅｘ，ｅｙ， ｅｚ分别为ｘ，ｙ，ｚ轴正方向的单位矢量。
α ，β ，γ 分别为矢量Ａ 与三个坐标轴正方向之间的夹角，称为方向角。ｃｏｓα ， ｃｏｓβ ，ｃｏｓγ 称为方向余弦。根据矢量与其分量 之间 的 关 系，矢 量 函数 Ａ （Ｍ）可写成
如果场中的物理量不仅与点 的空间位置有关，而且随时 间变化，则称这种场为时变 场；反之，若场中的物理量 仅与空间位置有关而不随时 间变化，则称这种场为恒定 场。
（６）矢量的混合积
２．矢量函数的微分公式
３．矢量函数的积分公式
式中，Ｂx(t)，By(t)，Bz(t)分别是 Ax(t),Ay(t),Az(t)的原函数；Ｃｘ，Ｃｙ，Ｃｚ 是任意常数
1.2 场的基本概念和可视化 1 场的概念 在自然界中，许多问题是定义在确定空间区域上的，在该 区域上每一点都有确定的量与之对应，我们称在该区域上定 义了一个场。 如电荷在其周围空间激发的电场，电流在周围空间激发的 磁场等。如果这个量是标量我们称该场为标量场；如果这个 量是矢量，则称该场为矢量场。如果场与时间无关，称为静 态场，反之为时变场。从数学上看，场是定义在空间区域上 的函数。如果空间中的每一点都对应着某个物理量的一个确 定的值，我们就说在这空间里确定了该物理量的场。
工程电磁场 第3章
b E dl
b
（3-3）
电位参考点选取的一般原则是：① 电位的 表达式要有意义，如在点电荷产生的电场中不 能选取点电荷所在处为电位参考点，以及在均 匀电场中不能选取无穷远处作为电位参考点 （否则空间中多数位置处的电位为无穷大而失 去实际意义）等；② 同一问题只能选取一个 电位参考点。一般地，若电荷分布在有限区域 内，则可选取无穷远处为电位参考点；若电荷 不是分布在有限区域内，则应根据实际情况将 参考点选在有限区域内。
2
2 1 2
1
2
d R cos 2
2 d d R R 2R cos 2 2
d R cos 2
d R R R cos R 2 2
介质可分为无极性介质和有极性介质。不 论是无极性介质还是有极性介质，在外电场作 用下，每一个分子的束缚电荷都形成电偶极子， 从而介质处于被极化状态，介质内含有大量的 电偶极子，对外呈现带电现象。这样，介质中 的场强变为场源电荷（自由电荷）与介质中束 缚电荷产生的场强的叠加，从而改变原来的场 分布，其总的效应是使介质中的场强被削弱。
类似于自由空间中自由体电荷分布产生的电 位， 极化介质外任一点的电位应为介质内所有束缚 电荷在该点产生的宏观电位， 尽管两者产生电位的 性质不同。 为了计算这个宏观电位， 引入一个新的物理量 —极化强度 P ：
1 P lim V 0 V
p
i 1
n
i
C
m2
（3-23）
这样，将式（3-21）中的 p 用 PdV 代之，即 得极化介质内体积元 dV 内的电偶极矩在介质外 任一点 p 处产生的电位微元为
（3-25）
式中 V 为极化介质的体积， an 为包围体积 V 的封闭面 S 上的面积微元矢量 dS 的外法向单位 矢量。将式（3-25）和式（3-7b）相比较可知， 体积分中的 ( P) 相当于一种体电荷密度； 面积 分中的 (P an ) 相当于一种面电荷密度。为此，前 者称为束缚体电荷密度，记为 p ；后者称为束缚 面电荷密度，记为 ps ，即
工程电磁场chap3
第三章
2. 真空中的安培环路定律
恒定磁场
B 的旋度 B0J
等式两边取面积分
用斯托克斯定理
Bdl l
0I
S(B)dS0SJdS
n
Bdl l
0
Ik
k1
真空中的安培环路定律
思考 当电流与安培环路呈右手螺旋关系时，电流取正 值，否则取负；
环路上的 B 仅与环路交链的电流有关吗？
边值问题
解析法
有限差分法 有限元法 分离变量法 镜像法
电感的计算 磁场能量及力 磁路及其计算
返回 上页 下页
第三章
恒定磁场
本章要求
深刻理解磁感应强度、磁通、磁化、磁场强度 的概念。
掌握恒定磁场的基本方程和分界面衔接条件。 了解磁位及其边值问题。
熟练掌握磁场、电感、能量与力的各种计算方 法。了解磁路及其计算方法。
d B x 2 0 K π d xc o s2 0 K π d x y 2 π (0 x K 2 d y x 2 y )
根据对称性 ,By = 0
B x
0Ky dx 2π (x2y2)
20K0
x arctygex
B
Idl
sin
2
4π(R2 x2 )
图3.1.3 圆形载流回路
根据圆环电流对 P 点的对称性，
dB xdB sin dB y0
siθ nR/r
返回 上页 下页
第三章
dBx
0Idl
sin
2
4π(R2 x2)
sin
恒定磁场
BBxex
4π(R 20Ix2)sinldlex
无外磁场作用时，介质对
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
折射定律
tan 1 1 tan 2 2
电流线的折射
返回 上页 下页
第3章
恒定电场
用不同导电媒质分界面上电场强度和传导电流密度的 衔接条件分析导电媒质中的情况 。
恒定电场的两种情况： 1、导电媒质中的恒定电场 （保守场）
2、通有恒定电流的导体周围电介质或空气中的 恒定电场。
返回 上页 下页
第3章
恒定电场
拓宽复习第一章相关内容为3.2.2应用 三种电流：
传导电流——电荷在导电媒质中的定向运动。
运动电流——带电粒子在真空中的定向运动。 位移电流——随时间变化的电场产生的假想电流。
证明：
对于均匀截面的导体有
R l
S
J 与 E 之关系
返回 上页 下页
第3章
恒定电场
对各向同性导电媒质中任选一段长度为元电流管,
管的横截面在此长度上可认为是均匀的
dl
di = J dS
J
dU E dl
dS
元电流管
U IR
E dl = J dS dl
dS
dl的方向就是 dS 的法线方向，故有
定义：单位时间内通过某一横截面的电量。
I dq A dt
返回 上页 下页
第3章
电流密度
恒定电场
1. 电流面密度 J
体电荷 以速度 v 作匀速运动形成的电流。
电流密度 J v A m2
电流
I SJ dS
电流面密度矢量
电流的计算
返回 上页 下页
第3章
恒定电场
2. 电流线密度 K
面电荷 在曲面上以速度 v 运动形成的电流。
由此可得功率密度
恒定电场
p dP dA dt J E dV dV
—焦耳定律微分形式
P V J EdV UI I 2R
—焦耳定律积分形式
返回 上页 下页
第3章
恒定电场
3.2.3 恒定电场基本方程及分界面上的衔接条件
基本方程
1. J 的散度
电荷守恒原理 J dS q dV
J E
返回 上页 下页
第3章
恒定电场
焦尔定律的微分形式
自由电荷在导电媒质中移动时，必然会与其它质点 发生碰撞。若要在导体内维持恒定电流，必须持续 地对电荷提供能量，这些能量最终都转化为热能。
导体每单位体积内有N个自由电子，平均加速度
为 v ，则
J = N -ev
导体中存在电场强度 E，则每一电子所受的力为
电流线密度 K v A m
电流
I l (K en ) dl
en 是垂直于 dl，且通过 dl 与曲面相切的单位矢量。
电流线密度及其通量
返回 上页 下页
第3章
工程应用
恒定电场
媒质磁化后的表面磁化电流；
同轴电缆的外导体视为电流线密度分布；
高频时，因集肤效应，电流趋于导体表面分布。 3. 元电流的概念
* 他认为这和运转中的摩擦现象一样，都是动力损失的根源。
* 1841年《电的金属导体产生的热和电解时电池组中的热》---- 著名的焦 耳定律，又称 I 2R 定律。
* 建立了能量转化的普遍概念，在1843年----13组实验数据----结果：“能 使1磅的水温度升温华氏一度的热量等于（可转化为）把838磅重物提升1 英尺的机械功。”这是焦耳得到的与现代热功当量值最接近的数值。
返回 上页 下页
第3章
3.2 恒定电场的基本方程
恒定电场
3.2.1电源与恒定电场
• 电源是一种能将其它形式的能量，如：热能、机械能和化 学能等转换成电能的装置，它能把电源内导体分子或原子
中的正负电荷分开，电场的分布将不随力称为局外力，把作用于
单位正电荷上的局外力设想为一等效场强，称为局外场强，
返回 下页
第3章
恒定电场
通有直流电流的导电媒质中同时存在着电流场和 恒定电场。恒定电场是动态平衡下的电荷产生的，它 与静电场有相似之处。
本章要求: 理解各种电流密度的概念，通过欧姆定律和焦耳定 律深刻理解场量之间的关系。
掌握导电媒质中的恒定电场基本方程和分界面衔 接条件。
熟练掌握静电比拟法和电导的计算。
用 表E示e ，方向由电源负极指向正极。
• 用局外场强来描述电源的特性，电源电动势与局外场强的
关系为
e l Ee dl
+
-
Ee
通过含源导电煤质的电流密度为 ：
E
J E + Ee
J
电源示意图
返回 上页 下页
第3章
恒定电场
在电源以外区域中，则只存在库仑电场。库 仑场强不是由静止电荷产生，而是由处于动态平 衡下的恒定电荷（即电荷的分布不随时间改变） 产生。
元电流是元电荷以速度 v 运动形成的电流
媒质的磁化电流
νdV (体电流元) JdV
dq νdS (面电流元） KdS
νdl (线电流元） Idl
返回 上页 下页
第3章
3.2.2 欧姆定律和焦耳定律的微分形式
恒定电场
在线性媒质中
J E 欧姆定律 微分形式。
U RI 欧姆定律 积分形式。
J 与 E 共存，且方向一致。
第3章
恒定电场
第 3 章 恒定电场
3.1 从电气研究的热潮到焦耳定律的建立
焦耳是英国著名实验物理学家。
* 16岁起与其兄弟一起到著名化学家道尔顿那里学习；
* 时值电气研究的热潮，他就投入到研究起磁电机来。
* 从1838年到1842年的几年中，焦耳一共写了九篇论文。
* 他注意到电机和电路中的发热现象，开始进行电流的热效应的研究。
F = -eE
返回 上页 下页
第3章
恒定电场
在 dt 时间内，电场力对每一电子所做的功为
dAe F dl = -eE vdt
移动元体积 dV内的所有电子，需要做功
dA NdV dAe N -ev EdVdt
将J = N -ev 代入可得
dA J EdVdt
返回 上页 下页
第3章
S
t
V t
在恒定电场中
q 0 t
亦称电流连续性方程
J dS 0 散度定理 JdV 0
S
V
故 J 0
恒定电场是一个无源场，电流线是连续的。
返回 上页 下页
第3章
2. E 的旋度 所取积分路径不经过电源，则
恒定电场
E dl 0 斯托克斯定理 ( E) dS 0
l
S
得 E 0 恒定电场是无旋场。
3. 恒定电场（电源外）的基本方程
积分形式 微分形式
SJ dS 0
J 0
l E dl 0
E 0
构成方程 J E
结论： 恒定电场是无源无旋场。 返回 上页 下页
第3章
分界面的衔接条件
由 l E dl 0 SJ dS 0
恒定电场
E1t E2t
得
J1n J2n
说明分界面上 E 切向分量连 续，J 的法向分量连续。