2 求导法则与求导基本公式
- 格式:ppt
- 大小:452.50 KB
- 文档页数:26


§2 求导法则上一节我们讲述了导数的相关知识,要求大家:深刻理解导数概念,能准确表达其定义;明确其物理、几何意义,会求曲线上一点的切线方程;能够从定义出发求某些函数的导数;知道导数与导函数的区别和联系;明确导数与单侧导数,可导与连续的关系.特别要注意,要学会从导数定义出发求某些导数的导数.例如,我们上节课已计算出左边所列的导函数,并且我们知道,计算函数在一点的导数或某区间上的导函数归结为极限的计算.因此,从理论上来讲,给了一个函数(不管它是简单函数,还是复杂函数),总可用定义求其导数(只要极限存在).但从我们计算左边几个函数的经验知道,用定义计算函数的导数是比较繁琐的.试想对基本初等函数的导数计算(用定义求导)都如此繁琐,对一般的初等函数更是不可想象.因此,我们不能满足于只用导数定义求导数,而应去寻找一些求导数的一般方法,以便能较方便地求出初等函数的导数.在给出较一般的方法之前,先看以下函数如何求导数:x x x f cos sin )(1+=x x g 2sin )(1= x x x f cos sin )(2⋅=)sin()(2ax x g = xxx f a log cos )(3=x x g arcsin )(3= x c x f sin )(4=xx g arccos )(4=一、导数的四则运算问题1 设,求.x x x f cos sin )(±=)('x f 分析 利用导数的定义及极限的四则运算知,.)'(cos )'(sin sin cos )('x x x x x f ±== 即)'(cos )'(sin )'cos (sin x x x x ±=±一般地,有如下和的导法则:定理1(和的导数) 设)(x f ,)(x g 在x 点可导,则 )()(])()([x g x f x g x f '±'='± (求导是线性运算)证明 令 )()()(x g x f x y +=。



求函数的导数公式函数的导数公式是描述函数在某一点处斜率的一种数学工具,对于一般的函数f(x),它的导数可以用下面的公式来表示:1.导数的定义公式f'(x) = lim(h->0) [f(x + h) - f(x)]/h在这个公式中,f(x + h)表示以点(x + h, f(x + h))为端点的割线斜率,f(x)是函数f(x)在点x处的函数值,h表示x + h与x之差,即点(x + h, f(x + h))与点(x, f(x))之间的距离。
这个公式是导数定义的最基本形式,通常用于求解复杂函数的导数。
2.基本求导公式f'(x) = k,k为常数[f(x)g(x)]' = f'(x)g(x) + f(x)g'(x)[f(g(x))]’ = f'(g(x))g'(x)f’(x)/g(x) = [f'(x)g(x) - f(x)g'(x)]/[g(x)]^2[f(x)]^n = nf'(x)[f(x)]^(n-1),n为正整数这里列举了一些常用的求导公式。
对于任何由基本函数组成的函数,都可以使用这些公式求其导数。
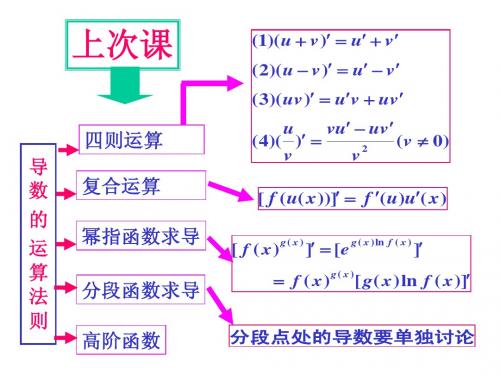
3.导数的运算法则导数具有很好的运算性质,常用的运算法则有:(1)线性性质:f(x) ±g(x)的导数为f'(x) ±g'(x),kf(x)的导数为kf'(x),k为常数。
(2)乘积法则:[f(x)g(x)]' = f'(x)g(x) + f(x)g'(x)。
(3)商数法则:[f(x)/g(x)]' = [f'(x)g(x) - f(x)g'(x)]/[g(x)]^2。
(4)复合函数的求导法则:如果y = f(g(x)),那么y' = f'(g(x))g'(x)。
以上是函数导数的一些基本公式和运算法则。
§ 2求导法则上一节我们讲述了导数的相关知识 ,要求大家:深刻理解导数概念 ,能准确表达其定义;明确其物理、几何意义,会求曲线上一点的切线方程 ;能够从定义出发求某些函数的导数;知道导数与导函数的区别和联系 ;明确导数与单侧导数,可导与连续的关系•特别要注意,要学 会从导数定义出发求某些导数的导数•例如,我们上节课已计算出左边所列的导函数,并且我们知道,计算函数在一点的导数或某区间上的导函数归结为极限的计算 •因此,从理论上来讲给了一个函数(不管它是简单函数,还是复杂函数),总可用定义求其导数 (只要极限存在)但从我们计算左边几个函数的经验知道 ,用定义计算函数的导数是比较繁琐的•试想对基本初等函数的导数计算(用定义求导)都如此繁琐,对一般的初等函数更是不可想象•因此,我们不能满足于只用导数定义求导数,而应去寻找一些求导数的一般方法 ,以便能较方便地求出初等函数的导数 •在给出较一般的方法之前,先看以下函数如何求导数:f 1(x) si nx cosxg 1(x) si n 2x f 2(x) sin x cosx g 2(x) sin (ax) cosxg 3(x) arcsinx log a x、导数的四则运算即(sin x cosx)' (sin x)' (cosx)'一般地,有如下和的导法则:定理i (和的导数) 设f(x),g(x)在x 点可导,则[f(x) g(x)] f (x) g (x)(求导是线性运算) 证明令 y(x) f (x) g(x)y [f(x x) g(x x)] [f(x) g(x)] xx f(xX ) f(x) g(x x) g(x)xxf (x)g (x) 当 x 0 时。
_xxx问题 2 设 f (x) sinx a ,则 f'(x) (sinx)'(a )' cosx a ln a 对吗? 分析 一般地,有如下乘积的求导法则:f 3(x) f 4(x)csin x g 4(x) arccosx问题1设f(x) sin x cosx ,求 f '(x).分析利用导数的定义及极限的四则运算知f' (x) cosx sin x(sin x)' (cosx)'.定理2 (积的导数)设f (x), g(x )在x 点可导,则 f (x) g(x) f(x) g(x)(它导它不导,它不导它导,然后加起来) 令 y(x) f(x[f(x) g(x)] 证明f(x) g(x) x) g(x x) f(x) g(x)X(分子 f(x) g(x f(x x) f(x) / g(xX) f(x) g(x X))x) f(x)g(X X) g(X)xxf (X) g(x) f (X) g(x)当 x0时。
常用的基本求导法则与导数公式在微积分中,求导是一项重要的基本操作。
通过求导,我们可以计算一个函数在给定点的斜率,求得函数的极值和拐点,以及解决各种实际问题。
本文将介绍一些常用的基本求导法则与导数公式,帮助大家更好地理解求导的过程与应用。
一、导数的定义导数描述的是一个函数在某点附近的变化率。
对于函数y = f(x),其在点x处的导数表示为f'(x)或dy/dx。
导数的定义为:f'(x) = lim┬(h→0)〖(f(x+h)-f(x))/h〗二、常用的基本求导法则1. 常数法则若C为常数,则d(C)/dx = 0。
2. 幂函数法则对于函数y = x^n,其中n为任意实数,使用幂函数法则可以得到其导数:d(x^n)/dx = nx^(n-1)3. 四则运算法则对于两个可导函数f(x)和g(x),使用四则运算法则可以得到它们的和、差、积和商的导数:若h(x) = f(x) ± g(x),则h'(x) = f'(x) ± g'(x)若h(x) = f(x) * g(x),则h'(x) = f'(x) * g(x) + f(x) * g'(x)若h(x) = f(x) / g(x),则h'(x) = (f'(x) * g(x) - f(x) * g'(x)) / g^2(x),其中g(x)≠04. 反函数法则若y = f(x)的反函数为x = g(y),且g(y)在y点可导,则有:d(g(y))/dy = 1 / f'(x)5. 复合函数法则若y = f(u)和u = g(x)是可导函数,则复合函数y = f(g(x))的导数为:(d(f(u))/du) * (d(g(x))/dx)6. 指数函数法则对于函数y = a^x,其中a为常数且a>0,使用指数函数法则可以得到其导数:d(a^x)/dx = ln(a) * a^x三、导数公式1. 常见函数的导数公式- 常数函数导数为0- 幂函数导数为nx^(n-1)- 指数函数导数为a^x * ln(a)- 对数函数ln(x)的导数为1/x- 正弦函数sin(x)的导数为cos(x)- 余弦函数cos(x)的导数为-sin(x)- 正切函数tan(x)的导数为sec^2(x)2. 反函数的导数公式若y = f(x)的反函数为x = g(y),且f'(x)和g'(y)均存在且不为0,则有以下关系:f'(x) = 1 / g'(y)3. 链式法则对于复合函数y = f(u)和u = g(x),使用链式法则可以得到复合函数的导数:dy/dx = (df/du) * (du/dx)四、应用示例1. 求函数f(x) = 3x^2 - 2x + 1在x = 2处的导数。