《初等几何研究》作业

《初等几何研究》作业一、填空题1、对直线a上任意两点A、B，把B以及a上与B在A同侧的点的集合称作，并记作。

2、在绝对几何中，外角定理的内容是：。

3、第四组公理由条公理组成，它们的名称分别是。

4、欧氏平行公理是：。

5、罗氏几何公理系统与欧氏几何公理系统的共同之处是，不同之处是。

6、几何证明的基本方法，从推理形式上分为法与归纳法；从思维方向上分为法与分析法；从命题结构上分为证法与间接证法，其中间接证法包括法与法。

7、过反演中心的圆，其反演图形是（过或不过）反演中心的。

8、锐角三角形的所有内接三角形中，周长最短的是三角形。

9、锡瓦定理：设⊿ABC的三边（所在直线）BC、CA、AB上分别有点X、Y、Z，则AX、BY、CZ三线共点（包括平行）的充要条件是。

10、解作图问题的常用方法有：、、、等。

11、数学公理系统的三个基本问题是性、性和性.12、对于共面的直线a和a外两点A、B，若a与(AB)相交，则称A、B在a的，否则称A、B在a的 .13、命题：“过直线外一点，至少有一条直线与已知直线共面但不相交”是定理的推论.14、证明直线和圆的连续性时，主要依据了原理.15、罗氏平行公理是： .16、在罗氏几何中，共面的两条直线有种关系，它们分别是17、几何证明的通用方法一般有法、法、法、法、法、法等.18、等边三角形外接圆周上任一点到三顶点的连线段中，最长线段与另两条线段之和具有的关系.19、尺规可作图的充要条件是 .20．由公理可以证明，线段的合同关系具有性、性、性和性.21．如果线段与角对应，那么线段的中点与角的对应.22．命题：“线段小于任意一条连接其两个端点的折线”是定理的推论.23．绝对几何包括有组公理，它们分别是 .24．写出一条与欧氏平行公理等价的命题： .25．在罗氏几何中，两条直线为分散线的充要条件是 .26、．常用的几何变换有等27．托勒密定理：四边形ABCD是圆内接四边形，则 .28．请写出两条作图公法： .29．在希尔伯特给出的欧几里得公理系统中，三角形的定义是：。

《初等几何研究》作业一、填空题1、对直线a 上任意两点A 、B ，把B 以及a 上与B 在A 同侧的点的集合称作 射线（或半直线），； ，并记作 AB 。

2、在绝对几何中，外角定理的内容是： 三角形的外角大于任一不相邻的内角 。

3、第四组公理由 两 条公理组成，它们的名称分别是 度量公理（或阿基米德公理）和康托儿公理 。

4、欧氏平行公理是：对任意直线a 及其外一点A ，在a 和A 决定的平面上，至多有一条过A 与a 不相交的直线 。

5、罗氏几何公理系统与欧氏几何公理系统的共同之处是 前4组公理（或绝对几何） ，不同之处是 平行公理 。

6、几何证明的基本方法，从推理形式上分为 演绎 法与归纳法；从思维方向上分为 综合 法与分析法；从命题结构上分为 直接 证法与间接证法，其中间接证法包括 反证 法与 同一 法。

7、过反演中心的圆，其反演图形是 不过 （过或不过）反演中心的 直线 。

8、锐角三角形的所有内接三角形中，周长最短的是 垂足三角形。

9、锡瓦定理：设⊿ABC 的三边（所在直线）BC 、CA 、AB 上分别有点X 、Y 、Z ，则AX 、BY 、CZ 三线共点（包括平行）的充要条件是1=⋅⋅ZBAZYA CY XC BX 。

10、解作图问题的常用方法有： 交轨法 、三角奠基法、 代数法 、 变换法 等。

11、数学公理系统的三个基本问题是 相容性、 独立性和 完备 性.33．①答案不惟一.34．①（0，+∞），②，（0，π/2），③连续，④单调递减. 35．①平移，②旋转，③轴对称.36． ①1=⋅⋅ZB AZYA CY XC BX （或－1）37．①写出已知与求作，②分析，③作法，④证明，⑤讨论.12、对于共面的直线a和a外两点A、B，若a与(AB)相交，则称A、B在a的异侧，否则称A、B在a的同侧.13、命题：“过直线外一点，至少有一条直线与已知直线共面但不相交”是外角定理的推论.14、证明直线和圆的连续性时，主要依据了戴德金分割原理.15、罗氏平行公理是：对任意直线a及其外一点A，在a和A决定的平面上，至多有一条过A与a不相交的直线.，16、在罗氏几何中，共面的两条直线有3种关系，它们分别是平行，相交，分散.17、几何证明的通用方法一般有化归法、类比法、构造法、数形结合法、变换法、模型法等.18、等边三角形外接圆周上任一点到三顶点的连线段中，最长线段与另两条线段之和具有相等的关系.19、尺规可作图的充要条件是所求的量可用已知量的有理式或只含平方根的无理式表出.20．由公理可以证明，线段的合同关系具有反身性、对称性、传递性和可加性.21．如果线段与角对应，那么线段的中点与角的角平分线对应.22．命题：“线段小于任意一条连接其两个端点的折线”是外角定理的推论.23．绝对几何包括有四组公理，它们分别是结合公理、顺序公理、合同公理、连续公理. 24．写出一条与欧氏平行公理等价的命题：.25．在罗氏几何中，两条直线为分散线的充要条件是.26、．常用的几何变换有合同变换、相似变换、射影变换、反演变换等27．托勒密定理：四边形ABCD是圆内接四边形，则1=⋅⋅ZBAZYACYXCBX（或－1）.28．请写出两条作图公法：过两点可作一条直线（或其部分）。

《初等几何研究》综合测试题（二）适用专业：数学教育专业 考试时间：120分钟一、选择题（本题共8小题，每小题3分，共24分）1.如图，∠1=∠2，∠3=∠4，EC=AD ，证明AB D ≌EBC 时，应用的方法是_______。

A. AAS ；B.SAS ；C.SSS ；D.定义。

2.已知：三角形的两边长为2和7，第三边的数值是奇数，那么 这个三角形的周长是__________。

A.14；B.15；C.16；D.17.3.判定四边形是正方形的条件是________-。

A.对角线相等；B.对角线相等且互相垂直；C.对角线互相垂直平分； D ．对角线相等且互相垂直平分。

4.有一个多边形的内角和是外角和的122倍，则边数是__________。

A.14；B.7；C.21；D.10.5.在正三角形、等腰梯形、矩形和圆这四种图形中是轴对称图形，又是中心对称图形的有__________。

A.1种；B.2种；C.3种；D.4种。

6.圆的弦长等于它的半径，那么这条弦所对的圆周角的度数是__________。

A.30°；B.60°；C.150°；D.30°或150°.7.在平移过程中，对应线段A.互相平行且相等；B.互相垂直且相等；C.互相平行（或在同一条直线上）且相等；D.以上都不对。

8.下列关于平移的说法中正确的是___________。

A.以原图形中的一点为端点，且经过它的对应点的射线的方向是平移的方向；B.平移后的两个图形中两个顶点连成的线段长是平移的距离；C.原图形中两个顶点连成的线段长是平移的距离；D.以对应点中的一点为端点的射线是平移的方向。

二、判断题（本题共5小题，每小题2分，共10分）1.互补两角有一条公共边，则这两个角的平分线所组成的角一定是直角。

（ ）2.有一边对应相等的两个等腰直角三角形全等。

（ ）3.任意两个等腰三角形都相似。

（ ）4.同角的余角都相等。

初等几何研究习题解集
习题一（12页）
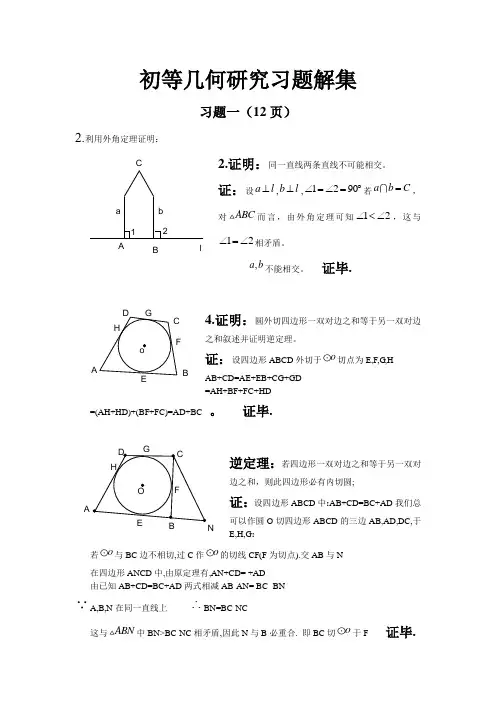
2.利用外角定理证明：
2.证明：同一直线两条直线不可能相交。

证：设a l ⊥,b l ⊥,1290∠=∠=︒若a b C =，对ABC 而言，由外角定理可知12∠<∠，这与12∠=∠相矛盾。

,a b 不能相交。

证毕.
4.证明：圆外切四边形一双对边之和等于另一双对边之和叙述并证明逆定理。

证：设四边形ABCD 外切于o 切点为E,F,G,H
AB+CD=AE+EB+CG+GD
=AH+BF+FC+HD =(AH+HD)+(BF+FC)=AD+BC。

证毕.
逆定理：若四边形一双对边之和等于另一双对边之和，则此四边形必有内切圆; 证：设四边形ABCD 中:AB+CD=BC+AD 我们总可以作圆O 切四边形ABCD 的三边AB,AD,DC,于
E,H,G :
若o 与BC 边不相切,过C 作o 的切线CF(F 为切点).交AB 与N 在四边形ANCD 中,由原定理有,AN+CD= +AD 由已知AB+CD=BC+AD 两式相减AB-AN= BC- BN A,B,N 在同一直线上 ∴BN=BC-NC
这与ABN 中BN>BC-NC 相矛盾,因此N 与B 必重合. 即BC 切o 于F 证毕. 21
l B A C b a
B A
N
A
习题二（18页）
1.证明：两院相交点不能在连心线同一侧;
证:若o与I的交点AB在连心线的同一侧,由于两圆关于轴I对称,那么点A关于I对称点N也是I与o德交点,这样相交圆有三个交点,其交点不能在连心线的同一
侧. 证毕.。

汕头职业技术学院初等几何研究习题课数学教育（师范类）1. I是△ABC的内心，AI、BI、CI的延长线分别交△ABC的外接圆于D、E、F求证：EF⊥AD。

D AB C EFI 五、关于平行与垂直2. A、B、C、D在圆周上相继的四点，P、Q、R、S分别是弧AB、BC、、CD、DA的中点，求证：PR⊥QS。

ACBP QDRS3. 凸四边形ABCD的每条对角线皆平分它的面积，求证：ABCD是平行四边形。

A BDC4. 已知：△BCX 和△DAY 是□ABCD 外的等边三角形，E 、F 、G 、H 是YA 、AB 、XC 、CD 的中点。

求证：EFGH 是平行四边形。

ABXD C YE F GH5. 在△ABC的各边上向外作正方形BCDE、CAFG、ABHI，其中心依次为O1、O2、O3求证：AO1⊥O2O3。

AO1O2BCO36. 在正方形ABCD 内任取一点E ，连接AE 、BE ，在△ABE 外以AE 、BE 为边作正方形AEMN 和EBFG ，连NC 、AF 。

求证：NC∥AF 。

A BCD E MNFG7. 以□ABCD的对角线AC为一边的两侧各作一个正三角形ACP、ACQ。

求证：BPDQ是□。

ABPDCQ8. 已知：凸五边形的四条边平行于所对的对角线。

求证：第五边也平行于所对的对角线。

CA B DE9.在△ABC中，∠B≠90°，BC边的垂直平分线交AB于D，△ABC的外接圆在A、C两点之切线交于E.求证：DE∥BC.AD EB C10.P 是正方形ABCD 的边CD 上的一点,过D 作AP 的垂线分别交AP 、BC 于Q 、R ，O 是正方形的中心.求证:OP ⊥OR.ABCDOPR12. 给定正方形ABCD ，P 、Q 分别人为AB 、BC 上的点，满足BP=BQ ，自B 作BH ⊥PC 于H ，求证:∠DHQ=900.ABCDO PHQ13. 在△ABC中，AB=AC，O为外心，D为AB的中点，E是△ACD的重心。

初等几何研究试题一、选择题 （5分⨯4=20分）1. 如图,CD EF AB ||||,已知20=AB ,,80=CD 100=BC 那么，EF 的值是____. A. 10, B.12, C.16, D.20第1题图 第2题图 2. 如图,在ABC ∆中,P 是AC 上的点,取BP 的中点Q ,连结CQ 并延长与AB 交于D ,则ABP S ∆与ACD S ∆的关系是_____.A. ABP ACD S S ∆∆<B. ABP ACD S S ∆∆=C. ABP ACD S S ∆∆>D. 不能确定.3. 如图，在ABC ∆中，BE 、CF 分别是AC 、AB 边上的高，o A 45=∠，那么，FBCE AEF S S :=______.A 1:1B 2:1C 3:1D 4:1第3题图 第4题图4. 如图，ABCD 是面积为1的正方形，PCB ∆是正三角形，PBD ∆的面积为_____.A.213- B. 8132- C. 43D. 413-二、填空题 （5分⨯4=20分）1．如图,已知正方形ABCD 的边长为1,E 为AD 的中点，P 为CE 的中点，F 为BP 的中点，则BFD S =_____.第1题图 第2题图 2．如图,AB 是圆O 直径，4=AB ，弦3=BC ，ABC ∠的平分线交半圆于D ,BC AD ,的延长线交于E ,DCE ABCD S S :=______.3．已知圆O 是ABC ∆的外接圆，半径为r ,CO BO AO ,,分别交对边于F E D ,,, 则：CF BE AD 111++=______.(用r 表示)4．ABC ∆的三条高分别为c b a h h h ,,,又ABC ∆内任一点P 到三边距离分别为c b a p p p ,,，则=++c c b b a a h p h p h p ______.三、证明题(12分⨯5=60分)1. 在ABC ∆中，过点A 作直线BC l ||，B ∠的平分线交AC 于D ,交直线l 于E ,C ∠的平分线交AB 于F ,交直线l 于G ,且FG DE =,求证: ABC ∆是等腰三角形.2．M是以AB为直径的上不同于BA、的任一点，C是直径AB上的定点，过M作CM 垂直的直线交过处BD、,求证：A、的切线于E（1）ED,成等比数列；BM,EC（2）BEAD⋅是定值.3．三条中线把ABC∆分成6个三角形，若这6个三角开的内切圆中有4个相等，求ABC∆是正三角形.4．从等腰ABC ∆的底边AC 上的中点M 作BC 边的垂线MH ，点P 为线段MH 的中点，求证：BP AH ⊥.5．已知： ABC ∆内接于圆O ，N M L ,,分别是弧AB CA BC ,,的中点，连结LM NM ,分别交BC AB ,于E D ,；I 是ABC ∆的内心，求证： (1)BC DE ||;(2)IE DI DE +=.。

《初等几何研究》考试A 卷一、单项选择题（本题共5个小题,每小题2分，共10分） 1.条件:||p x x =,条件2:q x x ≥-,则p 是q 的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.命题“若 ab=0,则a=0或b=0”的逆否命题是( )A. 若a=0或b=0,则ab=0B.若0ab ≠,则0a ≠或0b ≠C.若 0a ≠或0b ≠,则0ab ≠D. 若 0a ≠且0b ≠,则0ab ≠3.在空间中,以下命题中真命题的个数为( )(1)垂直于同一条直线的两直线平行;(2)到定点距离等于定长的点的轨迹是圆;(3)有三个角是直角的四边形是矩形;(4)自一点向一条已知直线引垂线有且仅有一条。

A.0个 B.1个 C.2个 D.3个4.A B C ∆的顶点与一点O 所连的直线依次交对边所在直线于点X,Y,Z,则( ) A.1X BYCZ AX C YA Z B = B. 1B XC YA ZX C YA Z B =-C.1X BYCZ AX C YA Z B =- 或1B XC YA ZX C YA Z B = D.以上都不对5.两个正数之和为常数,则其乘积当两变数相等时为( )A.最小B.最大C.最小或最大D.不能达到最小或最大二、填空题（本题共10个小题,每小题2分，共20分）1、 称为绝对几何命题。

2、三角形任一顶点到垂心的距离 外心到对边的距离。

3、三角形中，大边上的角平分线较4、直角三角形中，斜边与其上的高之和 两条直线边之和。

5、三角形外接圆周上任一点在三边（所在直线）上的射影6、“凡直角皆相等”的否命题为 。

7、不能经有限次数使用直尺和圆规完成作图的问题称为 。

8、设直线12//a a ,则关于12,a a 的两个轴反射的乘积是一个 。

9、在作图题中,可以先作成图形的一个三角形从而奠定了全部图形的基础,这种作图法称为 。

10、设三角形两角的平分线相等,则此三角形必为 。

《初等几何研究》综合测试题（三）适用专业：数学教育专业 考试时间：120分钟一、选择题（本题共8小题，每小题3分，共24分）1.两个三角形有两边和一角对应相等，则两个三角形__________。

A.一定全等；B.一定不全等；C.可能全等，可能不全等；D.以上都不是。

2.在在正三角形、等腰梯形、矩形和圆这四种图形中是轴对称图形，又是中心对称图形的有__________。

A.1种；B.2种；C.3种；D.4种。

3.如图，在等腰梯形ABCD 中，AD//BC ，AC 与BD 相交于点O ， 则图中面积相等的三角形共有___________。

A.1对；B.2对；C.3对；D.4对。

4. 在正三角形、等腰梯形、矩形和圆这四种图形中是轴对称图形，又是中心对称图形的有__________。

A.1种；B.2种；C.3种；D.4种。

5.如图，在 ABC 中，DE//BC ，如果AE:EC=3:2, 那么DE:BC 等于________。

A ．3:5； B ．3:2; C ．2:3；D ．2:5。

6.⊙O 中，AB 、CD 是两条平行弦，位于圆心的两侧，AB=40cm ，CD=48cm ，AB 、CD 的距离为22cm ，则⊙O 的半径是__________。

A.15cm ；B.20cm ；C.25cm ；D.30cm 。

7.在平移过程中，对应线段A.互相平行且相等；B.互相垂直且相等；C.互相平行（或在同一条直线上）且相等；D.以上都不对。

8.下列关于平移的说法中正确的是___________。

A.原图形中两个顶点连成的线段长是平移的距离；B.平移后的两个图形中两个顶点连成的线段长是平移的距离；C.以对应点中的一点为端点的射线是平移的方向。

D.以原图形中的一点为端点，且经过它的对应点的射线的方向是平移的方向；二、 判断题（本题共5小题，每小题2分，共10分）1.角的大小与边的长短有关。

（ ）2.一个钝角减去一个直角，其差必为一个锐角。

第 1 页 （共 2 页）4一、填空题（本大题共 8 题，每空 2 分，共 20分）1、当结论的反面只有一款时，否定了这一款便完成证明，这种较单纯的反证法叫做； 2、设CM 是ABC ∆的中线，则当12CM AB >时，C ∠是 角； ３、两个平行平面的距离等于12cm ，一条直线和它们相交成60，则这条直线夹在两平面间的线段长为 ；4、一些作图题中，往往可先作成图形的一个三角形，其余部分可由此三角形陆续作出，这种作图方法称为 ，此三角形称为 ；5、在ABC ∆中，若AB AC >，CD BE 、分别是C ∠和B ∠的平分线，则CD 与BE 的大小关系是 ；6、已知ABC ∆的三边分别为3cm ，5cm ，6cm ，则ABC ∆的内切圆半径r= ；7、到两定点A 、B 的距离之比为定比k 的点的轨迹是 和 ；8、设圆内接正五、六、十边形的边长分别为5a 、6a 、10a ，则它们之间的关系为 。

二、计算题（本大题共 2 题，每题8 分，共 16 分）1、在直二面角的棱上有两点A 、B ，AC 和BD 各在这个二面角的一个面内，并且都垂直于棱AB ，设8,6,24AB cm AC cm BD cm ===，求CD 的长。

2、设正方形ABCD 内接于O ，P 为DC 上一点，2PA PC ==，求P B P D ⋅的值。

三、证明题（本大题共 4 题，每小题10 分，共40 分）1、四边形ABCD 中，设AB CD =，M ，N 分别是AD 、BC的中点，证明直线MN 与AB 、CD 所成的交角相等。

2、证明：梯形两腰的中点，两对角线的中点，四点共线。

C第 2 页 （共 2 页）3、设BE 、CF 是ABC ∆的高，在射线BE 上截取BP AC =，在射线CF 上截取CQ AB =，证明AP 与AQ 相等且垂直。

4、在圆内接四边形ABCD 中，BC CD =，求证：22AB AD BC =AC ⋅+四、轨迹（本大题共 1 题， 12 分）1、设定圆中互相垂直的两弦的平方和是常数，则此两弦所在直线交点的轨迹是一圆。

初等几何研究第二版朱德祥朱维宗答案期中考试题1. P18 T5四边形有一双对角互补，则必为圆内接四边形2. P26 T3 两圆O与O’相交于点P，M是OO’的中点，过P任做直线交两圆与A及A’，Q是AA’的中点。

证明MP=MQ。

3. P27 T10 在中，证明BC边的中垂线和角A的平分线相交在外接圆周上;他们的,ABC交点距B、C两点，距内切圆心，距角A的旁切圆心都等远 4. P30 例4 蝴蝶定理5. 证明勾股定理(毕达哥拉斯)6. P39 T11 证明欧拉线7. P41 例3 三角形中，大边上的平分角线较小P18 T5四边形有一双对角互补，则必为圆内接四边形首先证?A+?C=180如图所示，连接DO, BO. 设优角BOD为θ?圆周角等于所对的圆心角的一半??C=1/2?BOD,同理，?A=1/2θ??A+?C=1/2*360=180，即两角互补。

同理可证?ABC+?ADC=180.所以对角互补。

T6 证明:等腰三角形底边延长线上任意一点到两腰的距离之差等于一腰上的高。

S,S,S ,ABP,ACP,ABC111AB*PF--AC*PE=AC*CH AB=AC 222PF--PE=CH圆内接偶数边凸多边形相间诸角之和等于其余各角之和 Tp5226、从圆上一点到其内接四边形一双对边的距离之积，等于从该点到两条对角线的距离之积设圆内接四边形ABCD，P是其外接圆上任一点，过P分别作对角线AC,BD;边,BC,,DA的垂线，垂足依次为E,F;G,H,。

根据简单几何定理:三角形两边之积等于第三边上的高与外接圆直径之积R中 PA*PC=R*PE (1) ,PAC,PDB,PD*PB=R*PF (2),PAD PA*PD=R*PG (3)PB*PC=R*PH (4) ,PBC(1)*(2)=(3)*(4)=所以得证P27 T9 在三角形ABC中，分别以AB和AC为一边向外做等边三角形ABD和ACE，求证CD=BEAE=AC,AB=AD, ？，DAB,，EAC ？，DAC,，EAB ？,AEB,,ACD ？CD,BEP31 4.四边形ABCD中，设AD=BC。

《初等几何研究》综合测试题（十四）适用专业：数学教育专业 考试时间：120分钟一、选择题（本题共8小题，每小题3分，共24分）1.等腰三角形的两条边的长为___________。

A.B. ；C.D.或 2.等腰三角形底边长为5cm ，一腰上的中线把其周长分为两部分之差为3cm ，则腰长为__________。

A.2cm ；B.8cm ；C.2cm 或8cm ；D.以上结论都不对。

3.下列四组图形中，是相似形的一组是_________。

A.各有一个角是30°的两个等腰三角形；B.底角为40°的两个等腰三角形；C.各有一个角是120°的两个等腰三角形；D.邻边之比都等于2的两个平行四边形。

4.三条线段长度分别是3，4，6，则以此三条线段为边___________。

A.能构成锐角三角形；B.能构成钝角三角形；C.能构成直角三角形；D.不能构成三角形。

5.扇形的面积为S ，弧长为l ，则扇形中心角的度数为________。

A.2180()l S π ；B. 2180()S l π ；C. 290()l Sπ；D. 290()S l π 。

6.下列命题中能用来判断一条线段是半径的命题是__________。

A.过圆心且垂直于切线的直线必经过切点；B.过切点且垂直于切线的直线必经过圆心；C.圆的切线垂直于过切点的半径；D.过半径的外端且垂直于这条半径的直线是圆的切线。

7下列图形中，轴对称图形有__________。

①角 ② 三角形 ③ 圆 ④线段 ⑤正方形 ⑥扇形 ⑦平行四边形 ⑧等腰梯形 A.3个；B.4个；C.5个；D.6个。

8.如图，有A 、B 、C 三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在_________。

A.在AC 、BC 两边高线的交点处； B.在AC 、BC 两边中线的交点处；C.在AC 、BC 两边垂直平分线的交点处；D.在∠A 、∠B 两内角平分线的交点处。

初等几何研究试题答案（II ）二、关于和、差、倍、分线段（角）1、 等腰ABC 中，0100,A B ∠=∠的平分线交AC 于D ，证明：BD+AD=BC 。

D 'BCA4321证：在BC 上取点D ,,使BD ,=BD,连结DD ,0100A ∠=且BD 平分∠ABC00120,40C ∴∠=∠=又BD=BD ,,0380∴∠=,23C ∠+∠=∠0240∴∠=即2C ∠=∠ ,,CD DD ∴=又03180A ∠+∠=∴点A 、D 、D ，、B 四点共圆且14∠=∠∴DD,=ADBC=BD,+CD ,=BD+AD已知，ABCD 是矩形，BC=3AB,P 、Q 位于BC 上，且BP=PQ=QC, 求证：∠DBC +∠DPC=∠DQC解：作矩形BCEF 与矩形ABCD 相等，在EF 上选取点O 使得FO=2EO.连结BO 、DO 。

由图可知，由BO=DO ，且有△BF O ≌△OED,∵∠FBO+∠BOF=90º ∠BOF=∠DOE ∴∠BOF+∠DOE=90º ∴∠BOD=90º △BOD 为等腰直角三角形 有∠DBO=45º ∴∠DBP+∠QBO=45º ∵∠DPC=∠QBO ∴∠DBP+∠DPC=45º ∵△DQC 为等腰直角三角形∴有∠DQC=45º 因此，有∠DBP+∠DPC=∠DQCP QAB CF EO P D3、圆内接四边形ABCD 的对角线AC 、BD 交于X ，由X 向AB 、BC 、CD 和DA 作垂线,垂足分别为A ´、B ´、C ´和D ´. 求证：A ´B ´+C ´D ´=B ´C ´+D ´A ´证明：（方法一）∵X 、A ´、A 、D ´四点共圆(对角和180°) ∴∠XA ´D ´=∠XAD ´又∵∠XAD ´=∠XBC(圆周角）同理∠XA ´B ´=∠XBC,即∠XA ´D ´=∠XA ´B ´ 同理可得∠XB ´A ´=∠XB ´C ´,∠XC ´B ´=∠XC ´D ´, ∠XD ´C ´=∠XD ´A ´∴X 是四边形A ´B ´C ´D ´的内心。

《初等几何研究》作业参考答案一．填空题1．①射线（或半直线），②。

2. ①两，②度量公理（或阿基米德公理）和康托儿公理。

3．①前4组公理（或绝对几何），②平行公理。

4．①平移，②旋转，③轴对称. 5．1=⋅⋅ZBAZYA CY XC BX 。

6．①交轨法，②三角奠基法，③代数法，④变换法。

7．①反身性、②对称性、③传递性、④可加性. 8．外角. 9．答案不惟一.10．①演绎，②综合，③直接，④反证，⑤同一； 11．1=⋅⋅ZBAZYA CY XC BX .（答－1也对） 12． ①过两点可作一条直线（或其部分），②已知圆心和半径可作一圆(或其部分). 13．①不共线的三点A 、B 、C 及(AB)、(BC)、(CA)构成的点的集合。

14．连续. 15．答案不惟一. 16．①不过，②圆.17．1=⋅⋅ZB AZYA CY XC BX （或－1）.18．①写出已知与求作，②分析，③作法，④证明，⑤讨论. 19．①相容，②独立，③完备.20．合同变换、相似变换、射影变换、反演变换等21．对任意直线a 及其外一点A ，在a 和A 决定的平面上，至少有两条过A 与a 不相交的直线. 22．①代数，②解析，③三角，④面积，⑤复数，⑥向量. 23．相等。

24．所求的量可用已知量的有理式或只含平方根的无理式表出． 二．问答题1．对于公理系统∑，若有一组具体事物M ，其性质是已知的，在规定∑中每一个基本概念指M 中某一具体事物后，可验证∑中每个公理在M 中都成立，则称M 为公理系统∑的一个模型；2．①若AB ≡B A ''，则d(AB)=d(B A '')；②当C BA ˆ时，有d(AB)+d(BC)=d(AC).3．命题“三角形的内角和不大于两个直角” 与欧氏平行公理不等价。

4．结合，介于，合同；结合——即有公共点，介于——即在…之间，合同——相等或完全相等. 5．长度、角度、相等、全等、运动、移置、叠合、重合等.6．由第五公设引出了该公理独立性的问题，对该问题的研究导致了非欧几何等结果的产生. 7．通常用“在……上”、“属于”、“通过”等语句来表述。

第 1 页 （共 2 页）1一、填空题（本大题共6题，每空3分，共24分）1、已知G 为ABC ∆的重心，并且,,AB c AC b BC a ===，则AG = .2、若xy 和xz 平行于同一直线，则x y z 、、三点的位置关系是 .3、若将ABC ∆绕点A 按逆时针旋转90︒，B 点变到E 点，C 点变到F 点，成为AEF ∆，则BC EF 、的大小关系为 ，BC 与EF 的夹角为 .4、已知AB 是O 的直径，AX 是切线，50AXB ∠=︒，BX 交O 于点C ，则B OC ∠＝ .5、在ABC ∆中，90,15,1ACB ABC BC ∠=︒∠=︒=，则AC 的长为 .6、设正方形ABCD 内接于O ，P 为AD 弧上一点，PA =，4PC =，则PB = ，PD = .二、计算题（本大题共2题，每小题8分，共16分）1、一点到平面上两点的连线长是51和30，这两线在平面上的射影比为5:2，求这点到平面的距离.2、如图，在ABC ∆中，M 是BC 边的中点，12,16,AB AC E F ==、分别在AC AB 、上，直线EF 和AM 相交于点G ，若2AE AF =，求:EG GF 的值.三、证明题（本大题共5题，第1、２小题每题8分，第3、4小题每题10分,第5小题12分,共48分）1、已知正方形ABCD 中，45,EBF E F ∠=︒、分别在AD 和CD 上，求证：EF AE FC =+.（8分）2、从平行四边形ABCD 的对角线BD 上一点P 作两组对边的垂线，交AB BC CD DA 、、、于E F G H 、、、，证明：//EF GH .（8分）FD页 （共 2 页）3、证明:三角形中大边上的中线较小.（10分）4、已知ABC ∆内接于O D ，是BC 延长线上一点，DA 切O 于点A ADB ∠，的平分线分别交AB AC 、于E F 、，求证：（1）AE AF =；（2）2AE BE CF =⋅.（10分）5、在正ABC ∆的AB AC 、上各有一动点D E 、，且BD AE =，求证：BE CD 、的交点P 的轨迹是以BC 为弦，内接角为120︒的一段圆弧∑.（12分）四、作图题（本大题共1题，12分）１、已知ABC ∆，过BC 边上一定点P 作一直线，把三角形分成两个等积形.DB CP。

初等几何研究习题答案初等几何研究习题答案几何学是数学的一个重要分支，它研究的是形状、大小、相对位置以及它们之间的关系。

初等几何是几何学的基础，是我们学习数学的第一步。

在初等几何的学习过程中，习题是不可或缺的一部分。

通过解答习题，我们可以巩固所学的知识，提高解决问题的能力。

在这篇文章中，我将为大家提供一些初等几何习题的答案，并探讨一些解题思路。

1. 题目：已知直角三角形ABC，其中∠C=90°，AC=5cm，BC=12cm。

求AB的长度。

解答：根据勾股定理，直角三角形的两个直角边的平方和等于斜边的平方。

设AB=x cm，则根据勾股定理得到方程：5^2 + x^2 = 12^2。

解这个方程可以得到x的值，进而求得AB的长度。

2. 题目：已知平行四边形ABCD，其中AB=5cm，BC=8cm，∠A=60°。

求对角线AC的长度。

解答：平行四边形的对角线相等，所以AC=BD。

根据余弦定理，可以得到方程：AC^2 = AB^2 + BC^2 - 2 * AB * BC * cos∠A。

将已知的数值代入方程，解得AC的长度。

3. 题目：已知等腰梯形ABCD，其中AB∥CD，AB=7cm，CD=12cm，AD=BC=5cm。

求高的长度。

解答：等腰梯形的高是两个底边之间的垂直距离。

根据勾股定理，可以得到方程：AD^2 = AB^2 - h^2。

将已知的数值代入方程，解得高的长度。

4. 题目：已知正方形ABCD，其中AB=8cm。

点E是BC边上的一个点，且BE=3cm。

连接AE，求∠AEB的度数。

解答：正方形的对角线相等，所以AC=BD。

根据正方形的性质，可以得知∠AEB = ∠AED + ∠DEB。

由于AE=AD，所以∠AED=∠ADE。

根据三角形的内角和定理，可以得到∠AED+∠ADE+∠DEB=180°。

将已知的数值代入方程，解得∠AEB的度数。

通过以上几道习题的解答，我们可以看到初等几何的解题思路大致有两种：一种是利用几何定理和公式进行计算，另一种是利用图形的性质和特点进行推理。

《初等几何研究》综合测试题（九）适用专业：数学教育专业 考试时间：120分钟一、选择题（本题共8小题，每小题3分，共24分）1.下列命题中正确的是__________。

A.两个全等的三角形是关于某直线对称的轴对称图形；B.两个全等的等腰三角形是关于某直线对称的轴对称图形；C.关于某直线对称的两个三角形是全等形；D.关于某直线对称的两个三角形不一定是全等形。

2.如果一个多边形的内角和等于外角和得4倍，那么这个多边形是________。

A.四边形；B.六边形；C.八边形；D.十边形。

3.如图，平行四边形ABCD 中，DB=DC ，∠C=70°，AE ⊥BD 于E,则∠DAE 为________。

A.20°；B.25°；C.30°；D.35°。

4.如果 AB C 和 A ′B ′C ′面积相等，且AB: A ′B ′=9:25， 那么AB 与A ′B ′边上的高的比是________。

A.9:25；B.25:9；C.3:5；D.5：3。

5. AB C 的三边长分别为6，8，10，并且以A ，B ，C ，三点为圆心， 作两两相外切的圆，那么这三个圆的半径分别为__________。

A.3，4，5；B.2，4，6；C.6，8，10；D.4，6，8.6.两个同心圆的半径分别是3cm ，6cm ，大圆的一条弦AB=10cm ，小圆和AB 的位置关系是______。

A.相离；B.相切；C.相交；D.不能确定。

7.如图， AB C 和 ADE 均为正三角形，则图中可看作是旋转关系的三角形是________。

A ． ABC 和 ADE ；B. AB C 和 ABD ；C. AB D 和 ACE;D. A CE 和 ADE 8.如图，CD 是Rt AB C 斜边AB 上的高，将 B CD 沿CD 折叠，B 点恰好落在AB 的中点E 处，则∠A 等于_________。

《初等几何研究》综合测试题（一）适用专业：数学教育专业 考试时间：120分钟一、 选择题（本题共8小题，每小题3分，共24分）1.在 ABC 中，AB=AC ，高BF 、CE 交于高AD 上一点O ，图中全等三角形的对数是_____。

A.4；B.5；C.6；D.7.2.已知：如图， ABC 中，∠BAC=90°,AD ⊥BC 于D, 若AB=2，BC=3，则DC 的长度是________。

A.83； B.23； C.43； D.53。

3.下面4个图形中，不是轴对称图形的是_________。

A.有两个内角相等的三角形；B.有一个内角是45°的直角三角形；C.有一个内角是30°的直角三角形；D.有一个内角是30°，一个内角是120°的三角形。

4.下列条件中，不能判别四边形是平行四边形的是_________。

A.一组对边平行，另一组对边相等；B.两组对边分别平行；C.对角线互相平分；D.一组对边平行且相等。

5.若一个四边形既是轴对称图形，又是中心对称图形，则这个四边形是_________。

A.直角梯形；B.等腰梯形；C.平行四边形；D.矩形。

6.下列语句正确的是________。

A.圆可以看作是到圆心的距离等于半径的点的集合。

B.圆的内部可以看作是到定点的距离小于定长的点的集合。

C.圆的一部分叫做弧。

D.能够互相重合的弧叫做等弧。

7.在平移过程中，对应线段A.互相平行且相等；B.互相垂直且相等；C.互相平行（或在同一条直线上）且相等；D.以上都不对。

8.下列关于平移的说法中正确的是___________。

A.以原图形中的一点为端点，且经过它的对应点的射线的方向是平移的方向；B.平移后的两个图形中两个顶点连成的线段长是平移的距离；C.原图形中两个顶点连成的线段长是平移的距离；D.以对应点中的一点为端点的射线是平移的方向。

二、 判断题：（本题共5小题，每小题2分，共10分）1.如图1，直线a ，b ，c 在同一平面内，a//b ，a 与c 相交于P ，则b 与c 也一定相交。