【配套K12】八年级数学上册第一章全等三角形练习十四无答案新版苏科版

苏科版八年级数学上册《第一章全等三角形》单元测试含答案(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（苏科版八年级数学上册《第一章全等三角形》单元测试含答案(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为苏科版八年级数学上册《第一章全等三角形》单元测试含答案(word版可编辑修改)的全部内容。

第一章全等三角形单元测试一、单选题(共10题；共30分）1.如图,已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）A、∠A=∠CB、AD=CBC、BE='DF'D、AD∥BC2。

如图，D在AB上，E在AC上,且∠B=∠C，那么补充下列条件后,不能判定△ABE≌△ACD的是（）A、AD=AEB、BE=CDC、∠AEB=∠ADCD、AB=AC3.如图所示，△ABD≌△CDB,下面四个结论中，不正确的是（）A.△ABD和△CDB的面积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBD D。

AD∥BC,且AD=BC4。

如图，在下列条件中,不能证明△ABD≌△ACD的是（)A。

BD=DC，AB=AC B.∠ADB=∠ADC，BD=DCC.∠B=∠C,∠BAD=∠CADD.∠B=∠C，BD=DC5.已知图中的两个三角形全等，则∠1等于( ）A。

72° B。

60° C.50° D.58°6.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时,得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积=12AC•BD,其中正确的结论有（）A.0个B.1个C.2个 D。

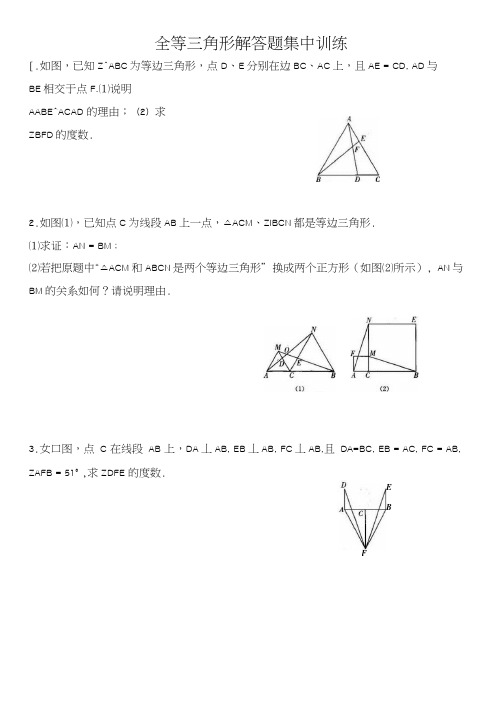
全等三角形解答题集中训练[.如图，已知Z^ABC为等边三角形，点D、E分别在边BC、AC上，且AE = CD, AD与BE相交于点F.⑴说明AABE^ACAD 的理由；（2）求ZBFD的度数.2.如图⑴，已知点C为线段AB上一点，△ACM、ZiBCN都是等边三角形.⑴求证：AN = BM；⑵若把原题中“△ACM和ABCN是两个等边三角形”换成两个正方形（如图⑵所示）, AN与BM的关系如何？请说明理由.3.女口图，点 C 在线段AB 上，DA丄AB, EB丄AB, FC丄AB,且DA=BC, EB = AC, FC = AB,ZAFB = 51° ,求ZDFE 的度数.EBF4.如图，在ZXABC中，D是BC的中点，DE±DF，试判断BE + CF与EF的大小关系，并证明你的结论.A5.如图，四边形ABCD中，CD//AB, E是AD中点，CE交BA延长线于点F.⑴试说明：CD = AF；⑵若BC=BF,试说明：BE丄CF.6•—张长方形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆成如图所示的形式，使点B、F、C、D在同一条直线上.⑴求证：AB丄ED；⑵若PB = BC，请找出图中与此条件有关的一对全等三角形，并给予证明.7.已知在 RtAABC 中，AC=BC, ZC = 90° , D 为边 AB 的中点，ZEDF = 90° , ZEDF 绕点D 旋转，它的两边分别交AC 、CB （或它们的延长线）于点E 、F.当ZEDF 绕点D 旋转到DE 丄AC 于点E 时（如图⑴），易证S ADEF +S ACEF = |S A ABC当ZEDF 绕点D 旋转到DE 和AC 不垂直时，在图⑵和图⑶这两种情况下，上述结论是 否成立?若成立，请给予说明；若不成立，S&EF 、S^EF 、Spc 又有怎样的数量关系？请写 出你的猜想，不需说明.8•数学作业本发下来了，徐波想：“我应该又是满分吧”，翻开作业本，一个大红的错号 映入眼帘，徐波不解了，“我哪里做错了呢”？下面是题目和徐波的解法，亲爱的同学, 你知道他哪儿错了吗？你能帮他进行正确的说明吗？女口图，ZBAC 是钝角，AB = AC, D, E 分别在AB, AC 上，且CD = BE.试说明ZADC=A A ABE ^A ACD , A ZADC=ZAEB.ZAEB.徐波的解法：在AACD 和ZiABE 中,AB = AC （已知）BE = CD （已知） ZBAE = ZCAD （公共角）9•如图，已知直线h//h,线段AB在直线/i±, BC垂直于厶交b于点C,且AB^BC, P是线段BC 上异于两端点的一点，过点P的直线分别交％、厶于点Q、E (点A、E位于点B的两侧)，满足BPTE,连接AP、CE.(1)求证：△ABP竺△CBE；(2)连结AZ)、BD,与AP相交于点F.如图2.①当匹=2时，求证：APLBD-,BP②当竺w 5>1)时，设的面积为Si, APCE的面积为S2,求込的值.BP S2:L0.如图，在四边形ABCD中，AB=BC, BF是ZABC的平分线，AF〃DC,连接ACCF.求证：CA 是ZDCF的平分线.FB口•两个大小不同的等腰直角三角形三角板按图1所示的位置放置，图2是由它抽象出的几何图形，AB = AC, AE = AD, ZBAC= ZEAD = 90° , B, C, E在同一条直线上，连接DC.（丄）请找出图2中与AABE全等的三角形，并给予证明（说明：结论中不得含有未标识的字母）；（2）证明：DC丄BE.12.如图AABC的边BC在直线/上，AC丄BC,且AC=BC； AEFP的边FP也在直线/, 边EF与边AC重合，且EF = FP.⑴在图1中，请你通过观察、测量，猜想并写出AB与AP所满足的数量关系和位置关系；⑵将AEFP沿直线/向左平移到图三的位置时，EP交AC于点Q,连接AP, BQ,猜想并写出BQ 与AP所满足的数量关系和位置关系，请证明你的猜想；⑶将AEFP沿直线x向左平移到图3的位置时，EP的延长线交AC的延长线于点Q, 连接AP, BQ,你认为⑵中所猜想的BQ与AP的数量关系和位置关系还成立吗？若成立，请给出证明；若不成立，请说明理由.an和ZDGE的度数.14.如图所示，已知AE丄AB, AF丄AC, AE=AB, AF=AC. 求证：(1) EC=BF；(2) EC±BF.15.在△ ABC 中，ZACB = 90° , AC=BC,直线MN 经过点C,且AD丄MN, BE±MN, 垂足分别为点D, E.求证：DE = AD + BE.17•如图，在ZXABC中，ZACB = 90° , AC=BC, AE是边BC ±的中线，过点C作CF丄AE,垂足为点F,过点B作BD±BC交CF的延长线于点D.⑴求证：AE = CD；(2)若AC=12cm,求BD 的长.18.如图，已知CE丄AB, BD丄AC,垂足分别为点E, D, BD与CE交于点0,且A0平分ZBAC.(1)图中有多少对全等三角形？请一一列举出来(不必说明理由).⑵小明说：欲证BE = CD,可先证明厶A0F空△A0D,得到AE = AD,再证明△ ADB^A AEC.得到AB = AC,然后利用等式的性质得到BE = CD,请问他的说法正确吗？如果正确，请按照他的说法写出推导过程；如果不正确，请说明理由.⑶要得到BE = CD,你还有其他思路吗？若有，请写出推理过程. A17•八年级⑴班同学到野外上数学活动课，为测量池塘两点A, B的距离，设计了如下的方案：(I)如图①，先在平地上取一个可直接到达A, B的点C,连接AC, BC,并分别延长AC至点D, BC 至点E,使DC = AC, EC=BC,最后测出DE的长即为AB的距离；(II)如图②，先过B点作AB的垂线BF,再在BF上取C, D两点使BC = CD,接着过D 点作BD的垂线DE,交AC的延长线于点E,则测出DE的长即为AB的距离.阅读后回答下列问题：⑴方案(I)是否可行？_______ ;(填“可行”或“不可行”)⑵方案(II)是否可行？请说明理由；⑶如果将方案(II)中作BF丄AB, ED丄BF改成满足ZABD= ZBDE#90° ,其他条件不变，方案(II)是否可行？(直接回答即可，不必说明理由)18•在数学课本中我们研究过这样一道题目：⑴如图①，ZACB = 90° , AC=BC, BE±MN, AD丄MN,垂足分别为E, D.图中哪条线段与AD相等？⑵试问在图①这种情况下线段DE, AD, BE具有怎样的等量关系？请写出来，不需要说明理由；⑶当直线CE绕点C旋转到图②中直线MN的位置时，试问DE, AD, BE具有怎样的等量关系？请写出这个等量关系，并说明理由.①19.已知点P是RtAABC斜边AB上一动点（不与点A, B重合）分别过点A, B向直线CP作垂线，垂足分别为点E, F, Q为斜边AB的中点.⑴如图当点P与点Q重合时，AE与BF的位置关系是_____________ , QE与QF的数量关系是______ ;（2）如图2,当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；⑶如图3,当点P在线段BA（或AB）的延长线上时，此时⑵中的结论是否成立？请画出图形并给予证明.20.如图，在ZV\BC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F,连接CF.求证:(1)AF=CD；(2)ZAFC=ZCDA.21.如图，在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE, AC, AE=AC.求证：(1)A ABE^A CDA；(2)AD//EC.22.如图，点/W, N分别是正五边形ABCDE的边BC, CD上的点，且BM=CN, AM交BN 于点P.(1)求证：ZVIB/W空△BC/V；⑵求ZAPN的度数.23•已知：如图，在AABC中，DE、DF是AABC的中位线，连接EF、AD,其交点为0.求证：(1)A CDE^ADBF；(2)OA^OD.24..如图1,在/XABC中，ZBAC为直角，点Q为射线BC上一点，连接AD,以AD为一边且在AQ的右侧作正方形4DEF.如图（1）,则知Q = Z ___________ ⑵若AB^AC,①当点Q 在线段BC上时（与点B不重合），如图2,问CF、BD有怎样的关系?并说明理由.②当点D在线段BC的延长线上时，如图3,①中的结论是否仍然成立,直接写出结论.（10 分）图325•如图，已知正方形ABCD中，边长为10cm,点E在AB边上，BE=6cm.(1)如果点P在线段BC上以4cm/秒的速度由B点向C点运动，同时，点0在线段CD 上以acm/^的速度由C点向Z)点运动，设运动的时间为/秒，①CP的长为_______ c m (用含/的代数式表示)；②若以E、B、P为顶点的三角形和以P、C、0为顶点的三角形全等，求a的值.(2)若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿正方形ABCD四边运动•则点P与点0会不会相遇？若不相遇，请说明理由•若相遇，求出经过多长时间点P与点0第一次在正方形ABCD的何处相遇？。

苏科版八年级数学上册第1章全等三角形同步解答专项练习题1．如图，∠A＝∠BCD，CA＝CD，点E在BC上，且EC＝AB．求证：DE∥AB．2．如图，在△ABC中，∠C＝90°，DE⊥AB于点E，AE＝AC，∠B＝50°，求∠DAC的大小．3．如图，已知△ABC≌△AEF中，∠EAB＝26°，∠F＝54°．（1）△ABC可以经过图形的变换得到△AEF，请你描述这个变换；（2）求∠AMB的度数．4．如图，在Rt△ABC和Rt△EFD中，∠ABC＝∠EFD＝90°，AC＝ED，AC⊥ED，垂足为M，连接EA．（1）△ABC与△EFD全等吗？为什么？（2）若∠AEF＝∠DEF，判断∠AEC与∠ACE的数量关系，并说明理由．5．如图，已知AB＝AC，∠1＝∠2＝∠3，BE＝EF，证明BC＝FC．6．如图1，∠DAB＝90°，CD⊥AD于点D，点E是线段AD上的一点，若DE＝AB，DC ＝AE．（1）判断CE与BE的关系是．（2）如图2，若点E在线段DA的延长线上，过点D在AD的另一侧作CD⊥AD，并保持CD＝AE，DE＝AB，连接CB，CE，BE，试说明（1）中结论是否成立，并说明理由．7．如图，点F、G分别在正五边形ABCDE的边BC、CD上，连结AF、BG相交于H，△ABF≌△BCG．（1）求∠ABC的度数；（2）求∠AHG的度数．8．如图，AD、BC相交于点O，AD＝BC，∠C＝∠D＝90°．（1）求证：△ACB≌△BDA；（2）若∠ABC＝31°，求∠CAO的度数．9．如图，在四边形△ABCD中，AB＝AC，BE平分∠CBA，连接AE，若AD＝AE ，∠DAE＝∠CAB．（1）求证：△ADC≌△AEB；（2）若∠CAB＝36°，求证：CD∥AB．10．已知：如图，AC＝BD，AD＝BC，AD，BC相交于点O，过点O作OE⊥AB，垂足为E．求证：（1）△ABC≌△BAD．（2）AE＝BE．11．如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．（1）请判断FC与AD的数量关系，并说明理由；（2）若AB＝6，AD＝2，求BC的长度．12．如图，已知∠MON，点A，B在边ON上，OA＝3，AB＝5，点C是射线OM上一个动点（不与点O重合），过点B作BD⊥AC，交直线AC于点D，延长BD至点E，使得DE ＝BD，连接BC，EC，AE，OE．（1）说明△ACE≌△ACB的理由；（2）直接写出OE的取值范围．13．在Rt△ABC中，∠BAC＝90°，E，F分别是AB，AC上的点．且EF∥BC，作EG平分∠AEF交AC于点G，在EF上取点D，使ED＝EA，连接DG并延长，交BA的延长线于点P，连接PF．（1）试说明：PD⊥EF；（2）若ED＝DF，求∠B的大小．14．如图，在△ADC中，DB是高，点E是DB上一点，AB＝DB，EB＝CB，M，N分别是AE，CD上的点，且AM＝DN．（1）试说明：△ABE≌△DBC；（2）探索BM和BN的位置关系和数量关系，并说明理由．15．如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，且AF＝DC，连接CF．（1）求证：BD＝DC．（2）如果AB＝AC，试猜测四边形ADCF的形状，并证明你的结论．16．已知：如图，BD、CE是△ABC的高，BD、CE交于点F，BD＝CD，CE平分∠ACB．（1）如图1，试说明BE＝CF．（2）如图2，若点M在边BC上（不与点B重合），MN⊥AB于点N，交BD于点G，请直接写出BN与MG的数量关系，并画出能够说明该结论成立的辅助线，不必书写过程．17．综合与探究如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，CE的延长线交BD 于点F．（1）求证：△ACE≌△ABD．（2）若∠BAC＝∠DAE＝50°，请直接写出∠BFC的度数．（3）过点A作AH⊥BD于点H，求证：EF+DH＝HF．18．在△ABC中，AB＝AC，点D是直线BC上一点，连接AD，以AD为边向右作△ADE，使得AD＝AE，∠DAE＝∠BAC，连接CE．（1）如图1，当点D在BC边上时，①若∠BAC＝40°时，则∠DCE＝°；②若∠BAC＝80°时，则∠DCE＝°；③观察以上结果，猜想∠BAC与∠DCE的数量关系，并说明理由．（2）当点D在BC的延长线上时，请判断∠BAC与∠DCE的数量关系，并说明理由．19．如图，△ABC中，CD⊥AB，垂足为D．BE⊥AC，垂足为G，AB＝CF，BE＝AC．（1）求证：AE＝AF；（2）求∠EAF的度数．20．如图，AB＝AC，AD＝AE，∠BAC＝∠DAE．（1）求证：△ABD≌△ACE；（2）若∠1＝25°，∠2＝30°，求∠3的度数．参考答案1．证明：在△ABC和△CED中，，∴△ABC≌△CED（SAS），∴∠B＝∠DEC，∴DE∥AB．2．解：∵DE⊥AB，∠C＝90°，∴∠ACD＝∠AED＝90°，在Rt△ACD和Rt△AED中，，∴Rt△ACD≌Rt△AED（HL），∴∠DAC＝∠DAE，∵∠C＝90°，∠B＝50°，∴∠BAC＝40°，∴∠DAC＝20°．3．解：（1）∵△ABC≌△AEF，∠EAB＝26°，∴△ABC绕点A顺时针旋转26°得到△AEF．（2）∵△ABC≌△AEF，∠F＝54°，∴∠C＝∠F＝54°，∠EAF＝∠BAC，∴∠FAC＝∠EAB＝26°，∴∠AMB＝∠C+∠FAC＝54°+26°＝80°．4．解：（1）△ABC≌△EFD，理由如下：∵∠ABC＝90°，∠EFD＝90°，AC⊥ED，∴∠EFD＝∠ABC＝∠AMD，∠BAC+∠ACB＝90°＝∠BAC+∠EDF，∴∠ACB＝∠EDF，在△ABC和△EFD中，，∴△ABC≌△EFD（AAS）；（2）∠ACE＝∠AEC，理由如下：在△AEF和△DEF中，，∴△AEF≌△DEF（ASA），∴EA＝ED，又∵AC＝DE，∴EA＝CA，∴∠ACE＝∠AEC．5．证明：∵AB＝AC，∠1＝∠2，∴AD⊥BC，∴∠ADC＝90°，∵∠2＝∠3，∠ACD＝∠BCE，∴∠BEC＝∠ADC＝90°，∴∠FEC＝90°，∴∠BEC＝∠FEC，在△BEC和△FEC中，，∴△BEC≌△FEC（SAS），∴BC＝FC．6．解：（1）CE＝BE且CE⊥BE，理由如下：∵CD⊥AD，∴∠CDE＝90°，∵∠DAB＝90°，∴∠CDE＝∠EAB，在△CDE和△EAB中，，∴△CDE≌△EAB（SAS），∴CE＝BE，∠CED＝∠EBA，∵∠EBA+∠BEA＝90°，∴∠CED+∠BEA＝90°，∴∠CEB＝90°，∴CE⊥BE，∴CE＝BE且CE⊥BE．（2）（1）中结论成立，理由如下：∵CD⊥AD，∴∠CDE＝90°，∵∠DAB＝90°，∴∠CDE＝∠EAB，在△CDE和△EAB中，，∴△CDE≌△EAB（SAS），∴CE＝BE，∠CED＝∠EBA，∵∠EBA+∠BEA＝90°，∴∠CED+∠BEA＝90°，∴∠CEB＝90°，∴CE⊥BE，∴CE＝BE且CE⊥BE．7．解：（1）∵正五边形的内角和为：（5﹣2）×180°＝540°，∴∠ABC＝×540°＝108°；（2）∵△ABF≌△BCG，∴∠BAF＝∠CBG，∵∠BAF+∠ABH＝∠AHG，∴∠CBH+∠ABH＝∠AHG＝∠ABC＝×540°＝108°，∴∠AHG＝108°．8．（1）证明：∵∠D＝∠C＝90°，∴△ABC和△BAD都是直角三角形，在Rt△ABC和Rt△BAD中，，∴Rt△ABC≌Rt△BAD（HL）；（2）解：∵Rt△ABC≌Rt△BAD，∴∠ABC＝∠BAD＝31°，∵∠C＝90°，∴∠BAC＝59°，∴∠CAO＝∠CAB﹣∠BAD＝28°．9．（1）证明：∵∠DAE＝∠CAB，∴∠DAE﹣∠CAE＝∠CAB﹣∠CAE．∴∠DAC＝∠EAB．在△DAC和△EAB中∵∴△DAC≌△EAB（SAS）（2）证明：∵AB＝AC，∠CAB＝36°，10．证明（1）在ABC和△BAD中，，∴△ABC≌△BAD（SSS）；（2）∵△ABC≌△BAD，∴∠CBA＝∠DAB，∴OA＝OB，∵OE⊥AB，∴AE＝BE．11．解：（1）FC＝AD，理由如下：∵AD∥BC（已知），∴∠ADC＝∠ECF（两直线平行，内错角相等），∵E是CD的中点（已知），∴DE＝EC（中点的定义）．在△ADE与△FCE中，，∴△ADE≌△FCE（ASA），∴FC＝AD（全等三角形的性质）．（2）∵△ADE≌△FCE，∴AE＝EF，AD＝CF（全等三角形的对应边相等），∵BE⊥AE，∴BE是线段AF的垂直平分线，∴AB＝BF＝BC+CF，∴AB＝BC+AD，∵AB＝6，AD＝2，∴BC＝4．12．解：（1）解法一：∵BD⊥AC，DE＝BD，∴AC是BE的垂直平分线．∴AE＝AB，CE＝CB，在△ACE和和ACB中，，∴△ACE≌△ACB（SSS）．解法二：∵BD⊥AC，∴∠CDE＝∠CDB＝90°．∵DE＝BD，CD＝CD，∴△CDE≌△CDB（SAS）．∴∠ECD＝∠BCD，CE＝CB．又∵AC＝AC，∴△ACE≌△ACB（SAS）．（2）由（1）知，AE＝AB，在△OAE中，由三角形的三边关系可知，AE﹣OA≤OE＜AE+OA，即2≤OE＜8．13．解：（1）∵EG平分∠AEF，∴∠AEG＝∠DEG，在△AEG和△DEG中，，∴△AEG≌△DEG（SAS），∴∠GAE＝∠GDE＝90°，∴PD⊥EF；（2）∵ED＝DF，PD⊥EF，∴EG＝GF，∴∠GFE＝∠GEF，∴∠AEG＝∠GEF＝∠GFE，∵∠AEG+∠GEF+∠GFE＝90°，∴∠AEG＝∠GEF＝∠GFE＝30°，∴∠AEF＝60°，∵EF∥BC，∴∠AEF＝∠B＝60°．14．（1）证明：∵DB是高，∴∠ABE＝∠DBC＝90°．在△ABE和△DBC中，，∴△ABE≌△DBC（SAS）；（2）解：BM＝BN，BM⊥BN，理由如下：∵△ABE≌△DBC，∴∠BAM＝∠BDN，在△ABM和△DBN中，，∴△ABM≌△DBN（SAS），∴BM＝BN，∠ABM＝∠DBN，∴∠DBN+∠DBM＝∠ABM+∠DBM＝∠ABD＝90°，∴MB⊥BN．15．（1）证明：∵E是AD的中点，∴AE＝DE．∵AF∥BC，∴∠FAE＝∠BDE，∠AFE＝∠DBE．在△AFE和△DBE中，，∴△AFE≌△DBE（AAS）．∴AF＝BD．∵AF＝DC，∴BD＝DC．（2）解：四边形ADCF是矩形；证明：∵AF＝DC，AF∥DC，∴四边形ADCF是平行四边形．∵AB＝AC，BD＝DC，∴AD⊥BC，即∠ADC＝90°．∴平行四边形ADCF是矩形．16．解：（1）∵BD⊥AC，CE⊥AB，∴∠ADB＝∠BDC＝∠AEC＝90°，∴∠A+∠ABD＝90°，∠A+∠ACE＝90°，∴∠ABD＝∠ACE，在△ABD和△FCD中，，∴△ABD≌△FCD（ASA），∴AB＝CF，∵CE平分∠ACB，∴∠ACE＝∠BCE＝22.5°，在△ACE和△BCE中，，∴△ACE≌△BCE（ASA），∴AE＝BE，∴BE＝AB＝CF；（2）BN＝MG，理由如下：如图，过点M作MH∥AC，交AB于H，交BD于P，∵BD＝CD，BD⊥CD，∴∠DBC＝∠DCB＝45°，∵MH∥AC，∴∠PMB＝∠DCB＝∠PBM＝45°，∠BPM＝∠BDC＝90°，∴BP＝PM，∵∠BHP+∠HBP＝90°，∠BHP+∠HMN＝90°，∴∠HBP＝∠HMN，在△BHP和△MGP中，，∴△BPH≌△MPG（ASA），∴GM＝BH，∵MN⊥AB，CE⊥AB，∴MN∥CE，∴∠BMN＝∠BCE＝∠ACB＝22.5°，∴∠BMN＝∠HMN＝22.5°，在△BMN和△HMN中，，∴△BMN≌△HMN（ASA）∴BN＝NH，∴BN＝BH＝MG．17．（1）证明：∵∠BAC＝∠DAE．∴∠CAE＝∠BAD．在△ACE和△ABD中，，∴△ACE≌△ABD（SAS）；（2）解：∵△ACE≌△ABD，∴∠AEC＝∠ADB，∴∠AEF+∠AEC＝∠AEF+∠ADB＝180°．∴∠DAE+∠DFE＝180°，∵∠BFC+∠DFE＝180°，∴∠BFC＝∠DAE＝∠BAC＝50°；（3）证明：如图，连接AF，过点A作AJ⊥CF于点J．∵△ACE≌△ABD，＝S△ABD，CE＝BD，∴S△ACE∵AJ⊥CE，AH⊥BD．∴，∴AJ＝AH．在Rt△AFJ和Rt△AFH中，，∴Rt△AFJ≌Rt△AFH（HL），∴FJ＝FH．在Rt△AJE和Rt△AHD中，，∴Rt△AJE≌Rt△AHD（HL），∴EJ＝DH，∴EF+DH＝EF+EJ＝FJ＝FH．18．解：（1）①当∠BAC＝40°时，∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴∠B＝∠ACE，∴∠BAC+∠DCE＝∠BAC+∠BCA+∠ABC＝180°；∴∠DCE＝180°﹣40°＝140°，故答案为：140；②当∠BAC＝80°时，∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴∠B＝∠ACE，∴∠BAC+∠DCE＝∠BAC+∠BCA+∠ABC＝180°；∴∠DCE＝180°﹣80°＝100°，故答案为：100；③∠BAC+∠DCE＝180°．理由如下：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴∠B＝∠ACE，∴∠BAC+∠DCE＝∠BAC+∠BCA+∠ABC＝180°；（2）当点D在BC的延长线上，∠BAC＝∠DCE，如图所示：∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，在△ABD和△ACE中，∴△ABD≌△ACE（SAS），∴∠B＝∠2，∵∠BAC+∠B+∠3＝180°，∠DCE+∠2+∠3＝180°，∴∠BAC＝∠DCE．19．（1）证明：∵CD⊥AB，BE⊥AC，∴∠CAD+∠ACD＝∠CAD+∠EBA＝90°，∴∠ACD＝∠EBA，在△AEB和△FAC中，，∴△AEB≌△FAC（SAS），∴AE＝FA；（2）解：∵△AEB≌△FAC，∴∠E＝∠CAF，∵∠E+∠EAG＝90°，∴∠CAF+∠EAG＝90°，即∠EAF＝90°．20．（1）证明：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠1＝∠EAC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：∵△ABD≌△ACE，∴∠ABD＝∠2＝30°，∵∠1＝25°，∴∠3＝∠1+∠ABD＝25°+30°＝55°．。

苏科版数学八年级上册第一章全等三角形单元综合练习一、选择题1、下列说法正确的是（）A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等2、在△ABC 中，AC ＝6，中线AD ＝5，则边AB 的取值范围是（）A.1＜AB ＜11B.4＜AB ＜13C.4＜AB ＜16D.11＜AB ＜163、在△ABC 和△DEF 中，给出下列四组条件：①AB =DE ，BC =EF ，∠C =∠F ；②∠A =∠D ，∠B =∠E ，∠C =∠F ；③∠B =∠E ，BC =EF ，∠C =∠F ；④AB =DE ，∠B =∠E ，BC =EF ；其中能判定△ABC ≌△DEF 的有（）A.1组B.2组C.3组D.4组4、根据下列已知条件，能够画出唯一△ABC 的是（）A.AB=5，BC=6，∠A=70°B.AB=5，BC=6，AC=13C.∠A=50°，∠B=80°，AB=8D.∠A=40°，∠B=50°，∠C=90°5、如图，把长短确定的两根木棍AB 、AC 的一端固定在A 处，和第三根木棍BM 摆出△ABC ，木棍AB 固定，木棍AC 绕A 转动，得到△ABD ，这个实验说明（）A.△ABC 与△ABD 不全等B.有两边分别相等的两个三角形不一定全等C.两边和它们的夹角分别相等的两个三角形全等D.有两边和其中一边的对角分别相等的两个三角形不一定全等6、如图，AB ⊥CD ，且AB ＝CD ．E 、F 是AD 上两点，CE ⊥AD ，BF ⊥AD ．若CE ＝a ，BF＝b ，EF ＝c ，则AD 的长为（）A.a ＋cB.b ＋cC.a ＋b －cD.a －b ＋c 7、如图，在方格纸中，以AB 为一边作△ABP ，使之与△ABC 全等，从P 1，P 2，P 3，P 4四个点中找出符合条件的点P ，则点P 有（）A.1个B.2个C.3个D.4个8、如图，已知长方形ABCD 中，8cm AD =，6cm AB =，点E 为AD 的中点，若点P 在线段AB 上以2cm/s 的速度由点A 向点B 运动．同时，点Q 在线段BC 上由点C 向点B 运动，若AEP △与BPQ V 全等，则点Q 的运动速度是（）A.6或83B.2或6C.2或23D.2或83二、填空题9、如图，在∠AOB 的两边上，分别取OM ＝ON ，再分别过点M 、N 作OA 、OB 的垂线，交点为P ，画射线OP ，则OP 平分∠AOB 的依据是_____．（填SAS 或AAS 或HL ）10、如图，在△ABC 中，∠B ＝∠C ，BF ＝CD ，BD ＝CE ，∠FDE ＝65°，则∠A ＝____．11、如图，是一个33 的正方形网格，则∠1+∠2+∠3+∠4=________．12、如图，△ABC 中，点D 在边BC 上，DE ⊥AB 于E ，DH ⊥AC 于H ，且满足DE=DH ，F 为AE 的中点，G 为直线AC 上一动点，满足DG ＝DF ，若AE=4cm ，则AG=_____cm ．13、如图，△ABC 和△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ，且点B ，D ，E 在同一条直线上，若∠CAE ＋∠ACE ＋∠ADE ＝130°，则∠ADE 的度数为________°．14、如图，已知锐角∠AOB，在射线OA上取点C、E，分别以点O为圆心，OC、OE长为半径作弧，交射线OB于点D、F；连接CF、DE交于点P．下列结论：①CE＝DF；②PE ＝PF；③△ODE≌△COF；④点P在∠AOB的平分线上．其中正确的结论是_______．（填上正确的序号）15、如图，四边形ABCD中，AB＝AD，AC＝5，∠DAB＝∠DCB＝90°，则四边形ABCD 的面积为_____．16、如图，已知△ABC，AB＝AC＝10cm，∠B＝∠C，BC＝8cm，点D为AB的中点．如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段AC上由C点向A点运动．若点Q的运动速度为v cm/s，则当△BPD与△CQP全等时，v的值为_______cm/s．三、解答题17、如图，B、C、E三点在同一条直线上，AC∥DE，AC=CE，∠ACD=∠B．（1）求证：BC=DE（2）若∠A=40°，求∠BCD的度数．18、如图，在四边形ABCD中，AB∥CD，∠1＝∠2，AD＝EC．（1）求证：△ABD≌△EDC；（2）若AB＝2，BE＝3，求CD的长．19、如图，AC、BD相交于点O，AB=AD，BC=CD．求证：AC⊥BD．20、在△AEB和△DEC中，AC、BD相交于点P，AE、BD相交于点O，AE＝BE，DE＝CE，∠AEB＝∠DEC．（1）求证：AC=BD；（2）求证：∠APB＝∠AEB．21、如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD．（1）证明：Rt△BCE≌Rt△DCF；（2）若AB=21，AD=9，求AE的长．22、数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：根据以下情境，解决下列问题：作法：①在OA 和OB 上分别截取OD 、OE ，使OD OE =．②分别以D 、E 为圆心，以大于12DE 的长为半径作弧，两弧在AOB ∠内交于点C ．③作射线OC ．则OC 就是AOB ∠的平分线．（1）李老师用尺规作角平分线时，用到的三角形全等的判定方法是______．小聪只带了直角三角板，他发现利用三角板也可以作角平分线，方法如下：步骤：①利用三角板上的刻度，在OA 和OB 上分别截取OM 、ON ，使OM ON =．②分别过M 、N 作OM 、ON 的垂线，交于点P ．③作射线OP ．则OP 为AOB ∠的平分线．（2）小聪的作法正确吗？请说明理由．23、如图，在△ABC 中，∠B=60°，△ABC 的角平分线AD 、CE 相交于点O ，（1）求∠AOC 的度数；（2）求证：OE=OD ；（3）．猜测AE ，CD ，AC 三者的数量关系，并证明.24、（1）如图1，AD 是△ABC 的中线，延长AD 至点E ，使ED =AD ，连接CE ．①证明△ABD ≌△ECD ；②若AB ＝5，AC ＝3，设AD ＝x ，可得x 的取值范围是_______；（2）如图2，在△ABC 中，D 是BC 边上的中点，DE ⊥DF ，DE 交AB 于点E ，DF 交AC于点F ，连接EF ，求证：BE ＋CF ＞EF ．25、（1）观察理解：如图1，∠ACB ＝90°，AC ＝BC ，直线l 过点C ，点A ，B 在直线l 同侧，BD ⊥l ，AE ⊥l ，垂足分别为D ，E ，求证：△AEC ≌△CDB ．（2）理解应用：如图2，过△ABC 边AB 、AC 分别向外作正方形ABDE 和正方形ACFG ，AH 是BC 边上的高，延长HA 交EG 于点I ．利用（1）中的结论证明：I 是EG 的中点．（3）类比探究：①将图1中△AEC 绕着点C 旋转180°得到图3，则线段ED 、EA 和BD 的关系_______；②如图4，直角梯形ABCD 中，AD BC ∥，AB ⊥BC ，AD ＝2，BC ＝3，将腰DC 绕D 点逆时针旋转90°至DE ，△AED 的面积为．26、（1）【初步探索】如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是_______________；（2）【灵活运用】如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由；（3）【拓展延伸】知在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB 的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请直接写出∠EAF与∠DAB的数量关系．一、选择题1、下列说法正确的是（）A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等【答案】C【详解】解：A、形状相同的两个三角形全等，说法错误，应该是形状相同且大小也相同的两个三角形全等；B、面积相等的两个三角形全等，说法错误；C、完全重合的两个三角形全等，说法正确；D、所有的等边三角形全等，说法错误；故选：C．2、在△ABC中，AC＝6，中线AD＝5，则边AB的取值范围是（）A.1＜AB＜11B.4＜AB＜13C.4＜AB＜16D.11＜AB ＜16【答案】C【详解】如图，延长AD至E，使DE＝AD，∵AD是△ABC的中线，∴BD＝CD，在△ABD和△ECD中，BD＝CD，∠ADB＝∠EDC，AD＝DE，∴△ABD≌△ECD（SAS），∴AB＝CE，∵AD＝5，∴AE＝5＋5＝10，∵10＋6＝16，10−6＝4，∴4＜CE＜16，即4＜AB＜16．故选：C．3、在△ABC和△DEF中，给出下列四组条件：①AB=DE，BC=EF，∠C=∠F；②∠A=∠D，∠B=∠E，∠C=∠F；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，∠B=∠E，BC=EF；其中能判定△ABC≌△DEF的有（）A.1组B.2组C.3组D.4组【答案】B【详解】解：①AB=DE，BC=EF，∠C=∠F，不能根据SSA判定△ABC≌△DEF；②∠A=∠D，∠B=∠E，∠C=∠F，不能根据AAA判定△ABC≌△DEF；③∠B=∠E，BC=EF，∠C=∠F，可根据ASA判定△ABC≌△DEF；④AB=DE，∠B=∠E，BC=EF，可根据SAS判定△ABC≌△DEF；故能判定△ABC≌△DEF的有③④两组，故选：B．4、根据下列已知条件，能够画出唯一△ABC的是（）A.AB=5，BC=6，∠A=70°B.AB=5，BC=6，AC=13C.∠A=50°，∠B=80°，AB=8D.∠A=40°，∠B=50°，∠C=90°【答案】C【详解】A.∠A不是AB、BC的夹角，画出的△ABC不唯一；B.5+6＜13，不能构成三角形；C .AB 为∠A 、∠B 的夹边，能画出唯一的△ABC ；D .△ABC 的边长不一定，不能画出唯一的△ABC .故选C .5、如图，把长短确定的两根木棍AB 、AC 的一端固定在A 处，和第三根木棍BM 摆出△ABC ，木棍AB 固定，木棍AC 绕A 转动，得到△ABD ，这个实验说明（）A.△ABC 与△ABD 不全等B.有两边分别相等的两个三角形不一定全等C.两边和它们的夹角分别相等的两个三角形全等D.有两边和其中一边的对角分别相等的两个三角形不一定全等【答案】D【解析】【分析】根据全等三角形的判定方法即可判断；【详解】由题意可知：AB ＝AB ，AC ＝AD ，∠ABC ＝∠ABD ，满足有两边和其中一边的对角分别相等，但是△ABC 与△ABD 不全等，故选：D ．6、如图，AB ⊥CD ，且AB ＝CD ．E 、F 是AD 上两点，CE ⊥AD ，BF ⊥AD ．若CE ＝a ，BF＝b ，EF ＝c ，则AD 的长为（）A.a ＋cB.b ＋cC.a ＋b －cD.a －b ＋c【答案】C【详解】解：∵AB CD ⊥，CE AD ⊥，BF AD ⊥，∴90AFB CED ∠=∠=︒，90A D ∠+∠=︒，90C D ∠+∠=︒，∴A C ∠=∠．∵AB CD =，A C ∠=∠，90CED AFB ∠=∠=︒，∴ABF ≌AAS CDE △（），∴AF CE a ==，BF DE b ==．∵EF c =，∴AD AF DF a b c a b c =+=+-=+-（）．故选：C ．7、如图，在方格纸中，以AB 为一边作△ABP ，使之与△ABC 全等，从P 1，P 2，P 3，P 4四个点中找出符合条件的点P ，则点P 有（）A.1个B.2个C.3个D.4个【答案】C【解析】【详解】要使△ABP 与△ABC 全等，必须使点P 到AB 的距离等于点C 到AB 的距离，即3个单位长度，所以点P 的位置可以是P 1，P 2，P 4三个，故选C ．8、如图，已知长方形ABCD 中，8cm AD =，6cm AB =，点E 为AD 的中点，若点P 在线段AB 上以2cm/s 的速度由点A 向点B 运动．同时，点Q 在线段BC 上由点C 向点B 运动，若AEP △与BPQ V 全等，则点Q 的运动速度是（）A.6或83B.2或6C.2或23D.2或83【答案】A【详解】解：∵ABCD 是长方形，∴∠A =∠B =90°，∵点E 为AD 的中点，AD =8cm ，∴AE =4cm ，设点Q 的运动速度为x cm/s ，①经过y 秒后，△AEP ≌△BQP ，则AP =BP ，AE =BQ ，26248y y xy -⎧⎨-⎩＝＝，解得，3283x y ⎧=⎪⎪⎨⎪=⎪⎩，即点Q 的运动速度83cm/s 时能使两三角形全等．②经过y 秒后，△AEP ≌△BPQ ，则AP =BQ ，AE =BP ，28462y xy y -⎧⎨-⎩＝＝，解得：61x y ⎧⎨⎩＝＝，即点Q 的运动速度6cm/s 时能使两三角形全等．综上所述，点Q 的运动速度83或6cm/s 时能使两三角形全等．故选：A ．二、填空题9、如图，在∠AOB 的两边上，分别取OM ＝ON ，再分别过点M 、N 作OA 、OB 的垂线，交点为P ，画射线OP ，则OP 平分∠AOB 的依据是_____．（填SAS 或AAS 或HL）【答案】HL【详解】解：由题意知OM ＝ON ，∠OMP ＝∠ONP ＝90°，OP ＝OP ，∴在Rt OMP 和Rt ONP 中，OP OP OM ON =⎧⎨=⎩，∴Rt OMP ≌Rt ONP （HL ），∴∠AOP＝∠BOP，∴OP是∠AOB的平分线．故答案为：HL．10、如图，在△ABC中，∠B＝∠C，BF＝CD，BD＝CE，∠FDE＝65°，则∠A＝____．【答案】50°【详解】在△BDF和△CED中，BF CD B C BD CE=⎧⎪∠=∠⎨⎪=⎩，∴△BDF≌△CED（SAS），∴∠BFD=∠CDE，∵∠FDE+∠EDC=∠B+∠BFD，∴∠B=∠FDE=65°，∴∠A=180°-∠B-∠C=180°-65°-65°=50°，故答案为：50°．11、如图，是一个33⨯的正方形网格，则∠1+∠2+∠3+∠4=________．【答案】180°.【详解】解：∵∠1和∠4所在的三角形全等，∴∠1+∠4=90°，∵∠2和∠3所在的三角形全等，∴∠2+∠3=90°，∴∠1+∠2+∠3十∠4=180°．故答案为：180．12、如图，△ABC中，点D在边BC上，DE⊥AB于E，DH⊥AC于H，且满足DE=DH，F为AE的中点，G为直线AC上一动点，满足DG＝DF，若AE=4cm，则AG=_____cm ．【答案】2或6.【详解】∵DE⊥AB，DH⊥AC，∴∠AED=∠AHE=90°.在△ADE和△ADH中，∵AD=AD,DE=DH,∴△ADE≌△ADH(HL),∴AH=AE=4cm.∵F为AE的中点，∴AF=EF=2cm.在△FDE和△GDH中，∵DF=DG,DE=DH,∴△FDE≌△GDH(HL),∴GH=EF=2cm.当点G在线段AH上时，AG=AH-GH=4-2=2cm;当点G在线段HC上时，AG=AH+GH=4+2=6cm;故AG的长为2或6.13、如图，△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，且点B，D，E在同一条直线上，若∠CAE＋∠ACE＋∠ADE＝130°，则∠ADE的度数为________°．【答案】65【详解】解：∵∠BAC=∠DAE，∴∠BAC−∠DAC=∠DAE−∠DAC，∴∠BAD=∠CAE，∵AB=AC，AD=AE，∴在△BAD和△CAE中，AB ACBAD CAEAD AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△CAE（SAS），∴∠ABD=∠ACE，∵∠CAE+∠ACE+∠ADE=130°，∴∠ABD+∠BAD+∠ADE=130°，∵∠ADE=∠ABD+∠BAD，∴2∠ADE=130°，∴∠ADE=65°．故答案为：65．14、如图，已知锐角∠AOB，在射线OA上取点C、E，分别以点O为圆心，OC、OE长为半径作弧，交射线OB于点D、F；连接CF、DE交于点P．下列结论：①CE＝DF；②PE ＝PF；③△ODE≌△COF；④点P在∠AOB的平分线上．其中正确的结论是_______．（填上正确的序号）【答案】①②③④【详解】解：由作法得OE=OF，OC=OD，∴OE-OC=OF-OD，即CE=DF，所以①的结论正确；在△ODE和△OCF中，OE OF O O OD OC=⎧⎪∠=∠⎨⎪=⎩，∴△ODE≌△OCF（SAS），所以③的结论正确；∴∠OED=∠OFC，在△PCE和△PDF中，CPE DPF PEC PFDCE DF∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△PCE≌△PDF（AAS），∴PE=PF，所以②的结论正确；∴PC=PD，连接OP，如图，在△OCP和△OPD中，OC OD OP OP PC PD=⎧⎪=⎨⎪=⎩，∴△OCP≌△OPD（SSS），∴∠COP=∠DOP，所以④的结论正确；综上，①②③④均正确，故答案为：①②③④．15、如图，四边形ABCD 中，AB ＝AD ，AC ＝5，∠DAB ＝∠DCB ＝90°，则四边形ABCD 的面积为_____．【详解】如图，过A 作AE ⊥AC ，交CB 的延长线于E ，∵∠DAB=∠DCB=90°，∴∠D+∠ABC=180°=∠ABE+∠ABC ，∴∠D=∠ABE ，又∵∠DAB=∠CAE=90°，∴∠CAD=∠EAB ，又∵AD=AB ，∴△ACD ≌△AEB （ASA ），∴AC=AE ，即△ACE 是等腰直角三角形，∴四边形ABCD 的面积与△ACE 的面积相等，∵S △ACE =12×5×5=12.5，∴四边形ABCD 的面积为12.5，故答案为12.5．16、如图，已知△ABC ，AB ＝AC ＝10cm ，∠B ＝∠C ，BC ＝8cm ，点D 为AB 的中点．如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段AC 上由C 点向A 点运动．若点Q 的运动速度为v cm/s ，则当△BPD 与△CQP 全等时，v 的值为_______cm/s ．【答案】3或154【详解】①设运动了t 秒，BP CQ =，BPD CQP ≅△△，∵点D 是AB 的中点，∴152BD AB ==∵BD PC =，∴83BP =-，∴B 点向C 点运动了33t =，1t =秒∵BPD CQP ≅△△，∴BP CQ =，∴31v =⨯，∴3cm /sv =②设运动了t 秒，当BD CQ =时，BDP QCP≅V V ∵5BD =，142PB PC BC ===，∴34t =，解得43t =秒∵BD CQ =，∴453v =⨯，∴15cm /s 4v =故答案为：3或154．三、解答题17、如图，B 、C 、E 三点在同一条直线上，AC ∥DE ，AC=CE ，∠ACD=∠B ．（1）求证：BC=DE（2）若∠A=40°，求∠BCD的度数．【详解】（1）∵AC ∥DE ，∴∠ACB=∠DEC ，∠ACD=∠D ，∵∠ACD=∠B ．∴∠D=∠B ，在△ABC 和△DEC 中，===ACB E B D AC CE ∠∠⎧⎪∠∠⎨⎪⎩，∴△ABC ≌△CDE （AAS ），∴BC=DE ；（2）∵△ABC ≌△CDE ，∴∠A=∠DCE=40°，∴∠BCD=180°–40°=140°．18、如图，在四边形ABCD 中，AB ∥CD ，∠1＝∠2，AD ＝EC ．（1）求证：△ABD ≌△EDC ；（2）若AB ＝2，BE ＝3，求CD的长．【答案】（1）见解析；（2）CD ＝5．【详解】（1）证明：∵AB ∥CD ，∴∠ABD ＝∠EDC ．在△ABD 和△EDC 中，12ABD EDC AD EC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△EDC （AAS ），（2）∵△ABD ≌△EDC ，∴AB ＝DE ＝2，BD ＝CD ，∴CD ＝BD ＝DE +BE ＝2+3＝5．19、如图，AC 、BD 相交于点O ，AB=AD ，BC=CD ．求证：AC ⊥BD ．【详解】∵在△ABC 和△ADC 中AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩，∴△ABC ≌△ADC （SSS ）∴∠BAC ＝∠DAC∵在△ABO 和△ADO 中AB AD BAO DAC AO AO =⎧⎪∠=∠⎨⎪=⎩，∴△ABO ≌△ADO （SAS ），∴∠AOB ＝∠AOD又∵∠AOB ＋∠AOD ＝180°，∴∠AOB ＝90°，∴AC ⊥BD20、在△AEB 和△DEC 中，AC 、BD 相交于点P ，AE 、BD 相交于点O ，AE ＝BE ，DE ＝CE ，∠AEB ＝∠DEC ．（1）求证：AC=BD ；（2）求证：∠APB ＝∠AEB．【解析】【1】证明：∵∠AEB =∠DEC ，∴∠AEB +∠AED =∠DEC +∠AED ，∴∠BED =∠AEC ，在△BED 与△AEC 中，AE BE AEC BED DE CE =⎧⎪∠=∠⎨⎪=⎩∴△BED ≌△AEC （SAS ），∴AC =BD ．【2】证明∵△BED ≌△AEC ，∴∠EBD =∠EAC ，∵∠EBD +∠BOE +∠AEB =∠AOP +∠APB +∠EAC =180°，又∵∠BOE =∠AOP ，∴∠AEB =∠APB ．21、如图，已知AC 平分∠BAD ，CE ⊥AB 于E ，CF ⊥AD 于F ，且BC =CD ．（1）证明：Rt △BCE ≌Rt △DCF ；（2）若AB =21，AD =9，求AE 的长．【详解】（1）∵AC 平分∠BAD ，CE ⊥AB 于E ，CF ⊥AD 于F ，∴CF=CE ，∠DFC=∠BEC=90°，在Rt △BCE 和Rt △DCF 中，CE CF BC CD =⎧⎨=⎩，∴Rt △BCE ≌Rt △DCF （HL ）；（2）∵AC 平分∠BAD ，CE ⊥AB 于E ，CF ⊥AD 于F ，∴CF=CE ，∠CFA=∠CEA=90°，在Rt △AFC 和Rt △AEC 中，CF CE AC AC=⎧⎨=⎩，∴Rt △AFC ≌Rt △AEC （HL ），∴AF=AE ，由（1）知Rt △BCE ≌Rt △DCF ，则BE=DF ，∵AB=21，AD=9，∴AB=AE+EB=AF+EB=AD+DF+DF =AD+2DF=9+2DF=21，解得，DF=6，∴AE=AF=AD+DF=9+6=15，即AE 的长是15．22、数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：根据以下情境，解决下列问题：作法：①在OA 和OB 上分别截取OD 、OE ，使OD OE =．②分别以D 、E 为圆心，以大于12DE 的长为半径作弧，两弧在AOB ∠内交于点C ．③作射线OC ．则OC 就是AOB ∠的平分线．（1）李老师用尺规作角平分线时，用到的三角形全等的判定方法是______．小聪只带了直角三角板，他发现利用三角板也可以作角平分线，方法如下：步骤：①利用三角板上的刻度，在OA 和OB 上分别截取OM 、ON ，使OM ON =．②分别过M 、N 作OM 、ON 的垂线，交于点P ．③作射线OP ．则OP 为AOB ∠的平分线．（2）小聪的作法正确吗？请说明理由．【详解】解：（1）李老师用尺规作角平分线时，用到的三角形全等的判定方法SSS ．故答案为SSS ；（2）解：小聪的作法正确．理由：∵PM OM ⊥，PN ON ⊥；∴90OMP ONP ∠=∠=︒，在Rt OMP △和Rt ONP △中，∵OP OP =，OM ON =，∴()Rt OMP Rt ONP HL △△≌∴MOP NOP ∠=∠，∴OP 平分AOB ∠．23、如图，在△ABC 中，∠B=60°，△ABC 的角平分线AD 、CE 相交于点O ，（1）求∠AOC 的度数；（2）求证：OE=OD ；（3）．猜测AE ，CD ，AC 三者的数量关系，并证明.【详解】（1）在△ABC 中，∠B ＝60°，∴∠BAC ＋∠BCA ＝180°−∠B ＝180°−60°＝120°．∵AD 平分∠BAC ，CE 平分∠ACB ，∴∠OAC ＝∠OAB ＝12∠BAC ，∠OCD ＝∠OCA ＝12∠ACB ，在△OAC 中，∠AOC ＝180°−（∠OAC ＋∠OCA ）＝180°−12（∠BAC ＋∠ACB ）＝180°−12×120°＝120°；（2）∵∠AOC ＝120°，∴∠AOE ＝∠DOC ＝180°−∠AOC ＝180°−120°＝60°，在AC 上截取AF ＝AE ，连接OF，如图，在△AOE 和△AOF 中，{AE AFOAE OAF OA OA∠∠＝＝＝∴△AOE ≌△AOF （SAS ），∴OE=OF ，∴∠AOE＝∠AOF ，∴∠AOF ＝60°，∴∠COF ＝∠AOC−∠AOF ＝120°−60°＝60°，又∠COD ＝60°，∴∠COD ＝∠COF ，在△COD 和△COF 中，{COD COFOC OC OCD OCF∠∠∠∠＝＝＝，∴△COD ≌△COF （ASA ），∴OD ＝OF ，∴OE=OD ；（3）∵△AOE ≌△AOF ，△COD ≌△COF ，∴AE ＝AF ，CF ＝CD ，又∵AF ＝AE ，∴AC ＝AF ＋CF ＝AE ＋CD ，即AE ＋CD ＝AC.24、（1）如图1，AD 是△ABC 的中线，延长AD 至点E ，使ED =AD ，连接CE ．①证明△ABD ≌△ECD ；②若AB ＝5，AC ＝3，设AD ＝x ，可得x 的取值范围是_______；（2）如图2，在△ABC 中，D 是BC 边上的中点，DE ⊥DF ，DE 交AB 于点E ，DF 交AC于点F ，连接EF ，求证：BE ＋CF ＞EF ．【详解】（1）①∵AD 是△ABC 的中线，∴CD ＝BD ，在△ABD 与△ECD 中，AD ED ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△ECD （SAS ）②1＜x ＜4，理由如下：∵△ABD ≌△ECD ，AB ＝5，∴AB ＝EC =5，∵ED =AD ，AD ＝x ，∴AE=2x ．由△ACE 三边关系得：EC AC AE EC AC -<<+，又∵AC ＝3，∴53253x -<<+，解得：1＜x ＜4．故答案是：1＜x ＜4．（2）延长FD 到G ，使得DG ＝DF ，连接BG 、EG ．∵D 是BC 边上的中点，∴CD ＝DB ．在△CDF 与△BDG 中，DF DG CDF BDG CD BD ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△CDF ≌△BDG （SAS ）．∴CF ＝BG ，∵DE ⊥DF ，∴EDF EDG ∠=∠．在△EDF 与△EDG 中，DF DG EDF EDG ED ED ⎧⎪∠=∠⎨⎪⎩＝＝，∴△EDF ≌△EDG ．∴EF ＝EG ．在△BEG 中，BE +BG ＞EG ，即BE +CF ＞EF．25、（1）观察理解：如图1，∠ACB ＝90°，AC ＝BC ，直线l 过点C ，点A ，B 在直线l 同侧，BD ⊥l ，AE ⊥l ，垂足分别为D ，E ，求证：△AEC ≌△CDB ．（2）理解应用：如图2，过△ABC 边AB 、AC 分别向外作正方形ABDE 和正方形ACFG ，AH 是BC 边上的高，延长HA 交EG 于点I ．利用（1）中的结论证明：I 是EG 的中点．（3）类比探究：①将图1中△AEC 绕着点C 旋转180°得到图3，则线段ED 、EA 和BD 的关系_______；②如图4，直角梯形ABCD 中，AD BC ∥，AB ⊥BC ，AD ＝2，BC ＝3，将腰DC 绕D 点逆时针旋转90°至DE ，△AED 的面积为．【详解】（1）证明：∵BD ⊥l ，AE ⊥l ，∴∠AEC ＝∠BDC ＝90°，又∵∠ACB ＝90°∴∠A +∠ACE ＝∠ACE +∠BCD ＝90°，∴∠A ＝∠BCD ，在△AEC 和△CDB 中，AEC CDB A BCD AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEC ≌△CDB （AAS ）；（2）证明：分别过点E 、G 向HI 作垂线，垂足分别为M 、N ，由（1）得：△EMA ≌△AHB ，△ANG ≌△CHA ，∴EM ＝AH ，GN =AH ，∴EM =GN ，在△EMI 和△GNI 中，90EIM GIN EMI GNI EM GN ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△EMI ≌△GNI （AAS ）；∴EI =IG ，即I是EG的中点；（3）解：①由（1）得：△AEC ≌△CDB ，∴CE =BD ，AE =CD ，∵ED =CD -CE ，∴ED =EA －BD ；故答案为：ED =EA －BD②如图，过点C 作CP ⊥AD 交AD 延长线于点P ，过点E 作EQ ⊥AD 交AD 延长线于点Q ，根据题意得：∠CDE =90°，CD =DE ，由（1）得：△CDP ≌△DEQ ，∴DP =EQ ，直角梯形ABCD 中，AD BC ∥，AB ⊥BC ，∴AB ⊥AD ，∴AB ∥CP ，∴BC ⊥CP ，∵BC =3，∴AP =BC =3，∵AD =2，∴DP =AP -AD =1，∴EQ =1，∴△ADE 的面积为1121122AD EN �创=．故答案为：126、（1）【初步探索】如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是_______________；（2）【灵活运用】如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由；（3）【拓展延伸】知在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB 的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请直接写出∠EAF与∠DAB的数量关系．【答案】（1）∠BAE+∠FAD=∠EAF；（2）仍成立，理由见解析；（3）∠EAF=180°-12∠DAB【详解】解：（1）∠BAE+∠FAD=∠EAF．理由：如图1，延长FD到点G，使DG=BE，连接AG，∵∠B=∠ADF=90°，∠ADG=∠ADF=90°，∴∠B=∠ADG=90°，又∵AB=AD，∴△ABE≌△ADG（SAS），∴∠BAE=∠DAG，AE=AG，∵EF=BE+FD=DG+FD=GF，AF=AF，∴△AEF≌△AGF（SSS），∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF；故答案为：∠BAE+∠FAD=∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG=BE，连接AG，∵∠B+∠ADF=180°，∠ADG+∠ADF=180°，∴∠B=∠ADG，又∵AB=AD，∴△ABE≌△ADG（SAS），∴∠BAE=∠DAG，AE=AG，∵EF=BE+FD=DG+FD=GF，AF=AF，∴△AEF≌△AGF（SSS），∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF；（3）∠EAF=180°-12∠DAB．证明：如图3，在DC延长线上取一点G，使得DG=BE，连接AG，∵∠ABC+∠ADC=180°，∠ABC+∠ABE=180°，∴∠ADC=∠ABE，又∵AB=AD，∴△ADG≌△ABE（SAS），∴AG=AE，∠DAG=∠BAE，∵EF=BE+FD=DG+FD=GF，AF=AF，∴△AEF≌△AGF（SSS），∴∠FAE=∠FAG，∵∠FAE+∠FAG+∠GAE=360°，∴2∠FAE+（∠GAB+∠BAE）=360°，∴2∠FAE+（∠GAB+∠DAG）=360°，即2∠FAE+∠DAB=360°，∴∠EAF=180°-12∠DAB．。

苏科版八年级上册数学第一章全等三角形含答案一、单选题(共15题，共计45分)1、下列命题中，假命题是( )A.一组邻边相等的平行四边形是菱形；B.一组邻边相等的矩形是正方形；C.一组对边相等且有一个角是直角的四边形是矩形；D.一组对边平行且另一组对边不平行的四边形是梯形.2、如图，△ABC≌△FED，则下列结论错误的是（）A.EC=BDB.EF∥ABC.DF=BDD.AC∥FD3、根据下列已知条件，能够画出唯一△ABC 的是（）A.AB=6，BC=5，∠A=50°B.AB=5，BC=6，AC=13C.∠A=50°，∠B=80°，AB=8D.∠A=40°，∠B=50°，∠C=90°4、以下命题中正确的是（）A.三角形的外角大于它的内角B.两个全等三角形一定关于某条直线轴对称C.有两边和一角对应相等的两个三角形全等D.有一个角是60°的等腰三角形是等边三角形5、如图，小华剪了两条宽为的纸条，交叉叠放在一起，且它们较小的交角为，则它们重叠部分的面积为（）A.1B.2C.D.6、如图，已知，则∠α等于（）A.72°B.60°C.58°D.50°7、如图，都是等边三角形，且B，C，D在一条直线上，连结，点M，N分别是线段BE，AD上的两点，且，则的形状是（）A.等腰三角形B.直角三角形C.等边三角形D.不等边三角形8、如图，在等腰中，，，点在边上，且，点在线段上，满足，若，则是多少？（）A.9B.12C.15D.189、如图，在中，，分别以的边向外作正方形，连接EC、BF，过B作于M，交AC于N，下列结论：≌；；；，其中正确的是（）A. B. C. D.10、已知：如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足.下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=AE=EC；④BA+BC=2BF.其中正确的是（）A.①②④B.①②③C.②③④D.①②③④11、如图，在平面直角坐标系中，菱形的顶点A，D在反比例函数的图象上，对角线平行x轴，点O在上，且，连接，，若，则k的值为（）A.25B.C.45D.12、如图，已知∠1=∠2， AC=AE，下列条件无法确定△ABC≌△ADE的（） .A.∠C=∠EB.BC=DEC.AB=ADD.∠B=∠D13、在△ABC中和△DEF中，已知BC=EF，∠C=∠F，增加下列条件后还不能判定△ABC≌△DEF的是（）A.AC=DFB.∠B=∠EC.∠A=∠DD.AB=DE14、如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（）A.∠M=∠NB.AM=CNC.AB=CDD.AM∥CN15、下列各图中，a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）A.甲和乙B.只有乙C.甲和丙D.乙和丙二、填空题(共10题，共计30分)16、如图，已知∠3=∠4，要说明△ABC≌△DCB，（1）若以“SAS”为依据，则需添加一个条件是________（2）若以“AAS”为依据，则需添加一个条件是________（3）若以“ASA”为依据，则需添加一个条件是________17、中，，，则中线的取值范围是________.18、如图，若AB＝AD，∠BAC＝∠DAC，则△ABC≌△ADC，全等的依据是________；19、如图，△ABC≌△ADE，且点E在BC上，若∠DAB＝30°，则∠CED＝________.20、如图，把等腰直角三角板放平面直角坐标系内，已知直角顶点的坐标为，另一个顶点的坐标为，则点的坐标为________.21、如图，△ABC为正三角形，BD是角平分线，点F在线段BD上移动，直线CF与AB交于点E，连结AF，当AE=AF时，∠BCE=________°.22、如图，BC∥EF，AC∥DF，添加一个条件________，使得△ABC≌△DEF．23、如图，点B、F、C、E在一条直线上，已知BF=CE，AC∥DF，请你添加一个适当的条件________，使得△ABC≌△DEF．24、如图，若△OAD≌△OBC，且∠O=65°，∠C=20°，则∠OAD=________度．25、如图，已知BC=EC，∠BCE=∠ACD，要使△ABC≌△DEC，则应添加的一个条件为________.（答案不唯一，只需填一个）三、解答题(共5题，共计25分)26、如图，已知AB=AD，且AC平分∠BAD，求证：BC=DC27、如图，四边形ABCD是矩形，点E是AD的中点，点F是BC的中点．求证：△ABF≌△CDE．28、已知：如图，，，求证：点C是线段AB的中点.29、如图，且，求证：.30、如图，AB=AC，AD=AE，。

苏科版八年级上册数学第一章全等三角形1.1全等图形一、选择题1.全等的两个图形面积（）A.不相等B.相等C.不一定相等D.不能确定2.下列图形中，不能分成两个全等图形的是（）A B C D3.下列说法：①用一张像底冲洗出来的2张1寸相片是全等形；②所有的正三角形是全等形；③全等形的周长相等；④面积相等的图形一定是全等形．其中正确的是( )A．①②③B．①③④C．①③D．③4.如图所示，A，B，C，D，E，F几个区域中，其中全等图形的对数为（）A．1 B．2 C．3 D．45.下面是5个全等的正六边形 A、B、C、D、E ，请你仔细观察 A、B、C、D 四个图案，其中与 E 图案完全相同的是( ) .6.如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出( )A．2个B．4个C．6个D．8个7.如图，下面4个正方形的边长都相等，其中阴影部分的面积相等的图形有( )A．0个B．2个C．3个D．4个8.如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上，将△ABC沿着DE折叠压平，A与A'重合，若∠A＝75°，则∠1＋∠2等于( )．A．150°B．210°C．105°D．75°二、填空题9.是全等图形。

10.请写出全等图形的性质（一条即可）11.已知三角形ABC和三角形DEF全等，期中AB和DE是一组对应边长，如果DE的长度是5cm，则AB的长度是cm。

12.已知下图的两个三角形全等，∠A=50°，∠B=65°，则∠C’= °13.在如图所示的4×4正方形网格中，∠1+∠4+∠7= °14.如图的图案是由全等的图形拼成的，其中．AD=2.5cm，BC=3.5 cm，则AF= cm．15.如图，将标号为A，B，C，D的正方形沿图中的虚线剪开后，得到标号为N，P，Q，M的四个图形，•试按照“哪个正方形剪开后与哪个图形”的对应关系填空：•A•与对应；B与对应；C与对应；D与对应．16.如图，等边△ABC的边长为1 cm，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A'处，且点A'在△ABC外部，则阴影部分图形的周长为__________cm．三、解答题17.用直线将下列图形中的全等图形连起来．18.如图，是一块“L”形状的木板，请你用线段把它分成四个全等的部分，并且每一部分的形状仍要保持“L”形．19.如图，某地板砖厂要制作一批正六边形地板砖，为适应市场需求，要求在地板砖上设计的图案能够把正六边形六等分，请你帮他设计等分图案．（•至少设计两种）20.如图中有12棵树，请你把这个正方形划分为四块，要求每块的形状、大小都相同，并且每块中恰好有3棵树．21.如图，将Rt△ABC(其中∠B＝34°，∠C＝90°)绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，旋转角最小是多少度？22.玩具店有A、B、C三种型号的拼板（如图），其中A型板每块3元，B型板每块4元，C 型板每块5元．小明现在想拼一个与右图6×6的正方形全等的图案，且只选一种型号的材料．那么小明选哪种材料最省钱，要用多少元？参考答案：1.B2.A3.C4.C5.C6.B7.C8.A9.能够互相重合的平面图形10.面积相等或周长相等（答案不唯一）11.512.6513.13514.2415.M、N、、Q、P.16.317.．①与⑨，③与⑧，④与⑩，⑤与⑦18.如答图所示．19.20.21.124°22.选A型材料，要36元．。

苏科版八年级数学上册 第一章 全等三角形 综合训练一.选择题1.下列各组中的两个图形属于全等图形的是（ ）A ．B ．C ．D ．2.下列说法正确的是( )A. 两个面积相等的三角形是全等图形B. 两个长方形是全等图形C. 两个周长相等的圆是全等图形D. 两个正方形是全等图形3.下列各图中a 、b 、c 为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC 全等的是（ ）A ．甲和乙B ．乙和丙C ．甲和丙D ．只有丙4.已知△ABC ≌△DEF ，AB =2，AC =4，若△DEF 的周长为偶数，则EF 的取值为 （ ）A ．3B ．4C ．5D ．3或4或55.如图，已知的面积为12，平分，且于点，连结ABC A AD BAC ∠AD BD ⊥D ，则的面积是（ ）CD ADC A A ．10 B ．8 C ．6 D ．46.如图，在△ABC 中，D ，E 分别是边AC ，BC 上的点，若△ADB ≌△EDB ≌△EDC ，则∠C 的度数为 （ ）A ．90°B ．100°C ．105°D ．120°7.如图，，若，，则的度数ABC ADE ∆≅∆40B ∠=︒30E ∠=︒DAE ∠为（ ）A ．B ．C ．D ．70︒110︒120︒130︒8.若，且，，则的度数为ABC DEF ≌△△50A ∠=︒60B ∠=︒F ∠（ ）A ．50°B ．60°C ．70°D ．80°9.如图，要测量池塘两岸相对的两点A ，B 的距离，可以在池塘外取AB 的垂线BF 上的两点C ，D ，使BC ＝CD ，再画出BF 的垂线DE ，使E 与A ，C 在一条直线上，可得△ABC ≌△EDC ，这时测得DE 的长就是AB 的长．判定△ABC ≌△EDC 最直接的依据是（ ）A ．HLB ．SASC ．ASAD ．SSS10.在△ABC 中和△DEF 中，已知BC=EF ，∠C=∠F，增加下列条件后还不能判定△ABC≌△DEF 的是（ ）A ．AC=DFB ．∠B=∠EC ．∠A=∠D D ．AB=DE11.如图，已知∠ABC =∠DCB ，下列所给条件不能证明△ABC ≌△DCB 的是（ ）A ．∠A =∠DB ．AB =DC C ．∠ACB =∠DBCD ．AC =BD12.已知，如图，△ABC 中，AD 是角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别E ，F ．下列说法：① DE =DF ；② AE =AF ；③ AD 平分∠EDF ；④ AD ⊥BC ；⑤图中共有3对全等三角形．其中正确的有( )A ．2个B ．3个C ．4个D ．5个二.填空题13.一个三角形的三边为2、4、，另一个三角形的三边为、2、5，若这两个三角形全x y 等，则______．x y +=14.下图是由全等的图形组成的，其中AB ＝3cm ，CD ＝2AB ，则AF ＝ ．15.如图，ΔABC ≌ΔDEC ，点B ，C ，D 在同一条直线上，且CE =2，CD =4，则BD 的长__________．16.如图，已知方格纸中是4个相同的小正方形，则的度数为______.12∠+∠17.如图，在方格纸中，以AB 为一边作△ABP ，使之与△ABC 全等，从P 1，P 2，P 3，P 4四个点中找出符合条件的点P ，则点P 有________个.18.如图，，，要使，应添加的条件是_________．（只需AC AD =12∠=∠ABC AED ≌△△写出一个条件即可）三.解答题19.如图，已知点 B、F、C、E 在一条直线上，BF = CE，AC = DF，且AC∥DF．求证：∠B =∠E.A A20.如图，在ABC和ADE中，AB＝AC，AD＝AE，∠BAD＝∠CAE．求证∠ABD＝∠ACE．21.如图，AD是△ABC的中线，分别过点B.C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F.求证：BE＝CF.22.如图，△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点P从A点出发沿A-C-B路径向终点运动，终点为B点；点Q从B点出发沿B-C-A路径向终点运动，终点为A点．点P和Q 分别以每秒1cm和3cm的运动速度同时开始运动，两点都要到相应的终点时才能停止运动．在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．问：点P运动多少时间时，△PEC与△QFC全等？请说明理由．。

第4题图第5题 第一章 全等三角形 单元练习一、选择题（在每小题所给出的四个选项中恰有一项是符合题目要求的）1．下列条件中，不能判定△ABC ≌△A ′B ′C ′的是 （ ）A ．AB =A ′B ′，∠A =∠A ′，AC =A ′C ′B ．AB =A ′B ′，∠A =∠A ′，∠B =∠B ′C ．AB =A ′B ′，∠A =∠A ′，∠C =∠C ′D ．∠A =∠A ′，∠B =∠B ′，∠C =∠C ′2．如图，小敏做了一个角平分仪ABCD ，其中AB =AD ，BC =DC ，将仪器上的点A 与∠PRQ 的顶点R 重合，调整AB 和AD ，使它们分别落在角的两边上，过点A ，C 画一条射线AE ，AE 就是∠PRQ 的平分线。

此角平分仪的画图原理是：根据仪器结构，可得△ABC ≌△ADC ，这样就有∠QAE =∠P AE 。

则说明这两个三角形全等的依据是（ ）A ． SASB ． ASAC ． AASD ． SSS3．如图，△ABC 和△DEF 中，AB =DE 、∠B =∠DEF ，添加下列哪一个条件无法证明△ABC ≌△DEF （ ）A ．AC ∥DFB ．∠A =∠DC ．AC =DFD ．∠ACB =∠F4．如图，在△ABC 中，AQ =PQ ，PR =PS ，PR ⊥AB 于点R ，PS ⊥AC 于点S ，则三个结论：①AS =AR ；②QP ∥AR ；③△BPR ≌△QPS 中 （ ）A ．全部正确B ．仅①和②正确C ．仅①正确D ．仅①和③正确5．如图是一个风筝设计图，其主体部分（四边形ABCD ）关于BD 所在的直线对称，AC 与BD 相交于点O ，且AB ≠AD ，则下列判断不正确的是 （ ）A ．△ABD ≌△CBDB ．△ABC 是等边三角形 C ．△AOB ≌△COBD ．△AOD ≌△COD6．下列命题中,不正确的是 ( )A ．各有一个角为95°，且底边相等的两个等腰三角形全等；B ．各有一个角为40°，且底边相等的两个等腰三角形全等；C ．各有一个角为40°，且其所对的直角边相等的两个直角三角形全等；D ．各有一个角为40°，且有斜边相等的两个直角三角形全等．二、填空题（不需写出解答过程，请把答案直接填写在相应位的置．．．．．上） 7．如图，在Rt △ABC 中，∠C =90°，AC =10，BC =5，PQ =AB ，点P 和点Q 分别在AC 和AC 的垂线ADB ACD E上移动，则当AP =时，才能使△ABC 和△APQ 全等．2第8题图 第9题图8．如图，DE ⊥AB 于E ，DF ⊥AC 于F ，若BD =CD ，BE =CF ，则下列结论：①DE =DF ；②AD 平分∠BAC ；③AE =AD ；④AB +AC =2AE 中正确的是 ．9．如图，a ∥b ，点A 在直线a 上，点C 在直线b 上，∠BAC =90°，AB =AC ，∠1=30°，则∠2的度数为 ．10．如图，△ABC 中，P 、Q 分别是BC 、AC 上的点，作PR ⊥AB ，PS ⊥AC ，垂足分别是R 、S ， 若AQ ＝PQ ，PR ＝PS ，下面四个结论：①AS ＝AR②QP ∥AR ③△BRP ≌△QSP ，④AP 垂直平分RS ．其中正确结论的序号是 （请将所有正确结论的序号都填上）．三、解答题（请在答题的指定区域内作答，解答时应写出必要的文字说明、证明 过程或演算步骤）11．（2015•无锡）已知：如图，AB ∥CD ，E 是AB 的中点，CE =DE ．求证：（1）∠AEC =∠BED ； （2）AC =B D ．12．如图，ABC ∆为等边三角形，D 为边BA 延长线上一点，连接CD ，以CD 为一边作等边三角形CDE ∆，连接AE ．（1）求证：CBD ∆≌CAE ∆．（2）判断AE 与BC 的位置关系，并说明理由．13如图，△ABC 是等边三角形，AE =CD ，BQ ⊥AD 于Q ，BE 交AD 于P ． 第7题图D（1）求证：△ABE ≌△CAD ；（2）求∠PBQ 的度数．14．如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点。

苏科版八年级上册数学第一章全等三角形含答案一、单选题(共15题，共计45分)1、如图的中，，且为上一点.今打算在上找一点，在上找一点，使得与全等，以下是甲、乙两人的作法：（甲）连接，作的中垂线分别交、于点、点，则、两点即为所求（乙）过作与平行的直线交于点，过作与平行的直线交于点，则、两点即为所求对于甲、乙两人的作法，下列判断何者正确？（）A.两人皆正确B.两人皆错误C.甲正确，乙错误D.甲错误，乙正确2、下列四组条件中，可以判定与全等的是（）A. B.C.D.3、下列条件不能判定两个直角三角形全等的是（）A.两条直角边对应相等B.斜边和一锐角对应相等C.斜边和一直角边对应相等D.两个锐角对应相等4、如图，∠CAB=∠DAB下列条件中不能使△ABC≌△ABD的是（）A.∠C=∠DB.∠ABC=∠ABDC.AC=ADD.BC=BD5、如图，已知∠1=2，AC=AD，从下列条件：①AB=AE②BC=ED③∠C=∠D④∠B=∠E中添加一个条件，能使△ABC≌△AED的有（）A.1个B.2个C.3个D.4个6、如图，在△ABC和△DBE中，AB=BC，DB=EB，∠ABC=∠DBE=50°.若∠BDC=25°，AD=4，DE= ，则CD的长为（）A. B. C. D.27、如图，在△ABC和△DEC中，已知BC=EC，∠B=∠E，还需添加一个条件才能使△ABC≌△DEC，不能添加的一个条件是（）A.∠BCE=∠ACDB.AC=DCC.∠A=∠DD.AB=DE8、下列叙述中错误的是（）A.能够完全重合的图形称为全等图形B.全等图形的形状和大小都相同C.所有正方形都是全等图形D.形状和大小都相同的两个图形是全等图形9、如图，△ABC≌△CDA，AB=5，BC=7，AC=6，则AD边的长为（）A.5B.6C.7D.不确定10、如图，△ABC≌△DEF，∠A=50°，∠C=30°，则∠E的度数为（）A.30°B.50°C.60°D.100°11、如图，某同学把一块三角形的玻璃打破成了三块，现要到玻璃店去配一块大小、形状完全相同的玻璃，那么他可以（）A.带①去B.带②去C.带③去D.带①和②去12、如图，E，B，F，C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（）A. B. C. D.13、如图，已知B、E、C、F在同一条直线上，BE=CF，AB∥DE，则下列条件中，不能判断△ABC≌△DEF的是（）A.AB=DEB.∠A=∠DC.AC∥DFD.AC=DF14、如图，四边形ABCD是平行四边形，点E在边BC上，如果点F是边AD上的点，那么△CDF与△ABE不一定全等的条件是（）A.DF=BEB.AF=CEC.CF=AED.CF∥AE15、如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为（）A.4B.6C.16D.55二、填空题(共10题，共计30分)16、如图，在△ABC中，AB＝AC，∠BAC＝120°，点D为AB边上一点（不与点B重合），连接CD，将线段CD绕点D逆时针旋转90°，点C的对应点为E，连接BE.若AB＝6，则△BDE面积的最大值为________.17、如图，△ABC≌△DEC，∠A＝70°，∠ACB＝60°，则∠E的度数为________18、如图，点E，F分别为正方形ABCD的边BC，CD上一点，AC，BD交于点O，且∠EAF=45°，AE，AF分别交对角线BD于点M，N，则有以下结论：①∠AEB=∠AEF=∠ANM；②EF=BE+DF；③△AOM∽△ADF；④S△AEF=2S△AMN，以上结论中，正确的是________ .（请把正确结论的序号都填上）19、如图，已知AC=BD，∠1=∠2，那么△ABC≌________ ，其判定根据是________。

新苏科版八年级数学上册《全等三角形》练习【基础训练】1．如图，△ ABC ≌△ FED ，且 BC － ED ，那么∠ A ＝_______ ，AD ＝ _______．2．如图，若△ABC ≌△ A 1B 1C1，且∠ A ＝110°，∠ B＝ 40°，则∠ C1＝ _______．3．如图，△ ABC ≌△ AED ，∠ C＝40°，∠ EAC ＝ 30°，∠ B＝ 30°，则∠ D＝ _______．4．如图，△ABC 是直角三角形， BC 是斜边，将△ ADC 绕点 A 顺时针旋转后，能与△ AD'B 重合，假如 AD ＝ 3，那∠ AD' 的长度为 _______．5．已知图中的两个三角形全等，则么 a 的度数是 ()．A ． 72°B． 60°C． 58°D． 50°6．如图，在Rt△ ABC 中，∠ ACB ＝ 90°，∠ A＝ 50°，将其折叠，使点 A 落在边 CB 上的 A' 处，折痕为CD ，则∠ A'DB 等于 ()．A ． 40°B． 30°C． 20°D． 10°7．如图，点 A 、D 、C、 F 在同向来线上，△ ABC ≌△ DEF， AC 和 DF 是对应边，∠ A 与∠EDC 是对应角，∠ A ＝ 80°，∠ ACB ＝ 50°，求∠ F、∠ E 的度数．【提优拔尖】8．如图，已知△ABF ≌△ DCE ，BE 、 FC 在同向来线上，BE＝ 2 cm，求 CF 的长．9．如图，已知△ABE ≌△ ADC ，∠ 1＝ 36°，∠ DAE ＝ 76°，∠ B＝ 25°．求∠ DAC 、∠C的度数．10．如图，已知△ ABC ≌△ DEF ，点 A 、 F、 C、D 在同向来线上，∠ ABC ＝ 135°，∠ A ＝20°．求∠ DFE 和∠ E 的度数．11．如图，若△ ABC ≌△ ADE ，试说明∠ BAD 与∠ CAE 的大小关系．12．如图， AB 和 CD 订交于点 O，△ ACO ≌△ BDO ，试说明AC ∥BD ．13．如图，△ ABC 绕极点 A 顺时针旋转，若∠B＝ 30°，∠ C＝ 40°，求：(1)顺时针旋转多少度，旋转后的△ AB'C 的极点 B' 与原△ ABC 的极点 C 和 A 在同向来线上；(2)再持续旋转多少度，点C'与点 A、点 C 在同向来线上．（原△ ABC 是指开始地点）14．如图，△ A'B'C 是由△ ABC 沿射线 AC 方向平移 2 cm 获得，若AC ＝3 cm ，则 A'C ＝_______cm ．15．如图，在矩形 ABCD 中，AB ＝ 10，BC ＝ 5，点 E、F 分别在 AB 、CD 上，将矩形 ABCD沿 EF 折叠，使点 A 、D 分别落在矩形 ABCD 外面的点 A 1、 D 1处，则暗影部分图形的周长为()．A ．15B．20C．25D．3016．如图，将△AOB 绕点 O 按逆时针方向旋转45°后获得△ A'OB' ，若∠ AOB ＝ 15°，则∠ AOB' 的度数是 ()．A ．25°B． 30°C． 35°D． 40°参照答案1．∠ F FC 2． 30°3． 40° 4． 3 5．D 6．D7． 50° .8． 2 cm9． 43°10． 25° .11．∠ BAD= ∠ CAE12．略13． (1)110 °． (2)70 ° .14． 1 15． D16． B。