当前位置：文档之家 › 高等数学中的两个重要极限

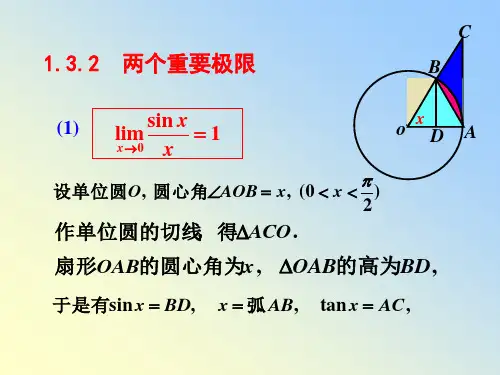
高等数学中的两个重要极限

  • 格式：ppt
  • 大小：1.52 MB
  • 文档页数：64

下载文档原格式

  / 64

合集下载

两个重要极限

两个重要极限

高等数学 两个重要极限 (Two important limits)
advanced mathematics
sin x 1. lim =1 x0 x
1 0.75 0.5 0.25
f ( x)
5
s i nx x
10 15
-15
-10
-5
o
-0.25 -0.5
高等数学 两个重要极限 (Two important limits)
例10
解
求极限
2x 3 x lim( ) . x 2 x 1
2x 3 x 2 l i m( ) l i m(1 )x x 2 x 1 x 2x 1
2 x 1 2 x 2 2 x 1
2 lim(1 ) x 2x 1
2 lim(1 ) x 2x 1
2 x 1 1 2 2
e
2x x 2 x 1 lim
e.
2 (1 ) 2x 1 lim 1 x 2 2 (1 ) 2x 1
2 x 1 2
e.
高等数学
advanced mathematics
3 1 另解: 2x 3 x 2x )x l i m( ) l i m( x 2 x 1 x 1 1 2x 3 x 3 x l i m(1 ) (1 ) x 2x 2 x lim x 1 x 1 x l i m(1 ) (1 ) x 2x 2x


4x 1 5 x
解
4 2 (2)求 lim(1 ) x 3x 3x 3x 4 2 4 4 2 e2 lim(1 ) lim(1 ) x x 3x 3x
e .3 x

高等数学中两个重要极限

高等数学中两个重要极限
x
X -10 -100
(1 1 ) x 2.868 2.732 x
-1000 -10000
2.720 2.7183
-100000 …
2.71828
li( m 11)xe x x
li(m 11)xe (1 )
x x
令t 1,
lim (1
1
)
x
lim(1
1
t)t
e
x x
x
t 0
1
lim(1 t)t e (1 )
1 x 1 ,
sinx coxs
CD
即coxs sinx1. x
sin x lim 1.
x x0＋
Ox BA
例 1 求 lim tan x x 0 x
解
limtanxlim (sinx1)
x 0 x x 0 cosx x
sinx 1 lim( )
x0 x cosx
limsinxlim 1 x0 x x0 cosx
0.001 …. 0.9999998
X －1 －0.5
sin x
0.84147 0.95885
x
－0.1 0.99833
－0.01 0.99998
－0.001 …. 0.9999998
lim six n1 x 0 x
证明 limsinx1. x x0＋
证
即sinxxtanx
各 式 同 除 以 s i n x ( 因 为 s i n x 0 ) ,得
t0
1
推 广 为 某 过 程 中 的 无 穷 小 量 ,lim (1) e 某过程
使 用lim (11)xe 须 注 意 : x x
(1)类 型 :

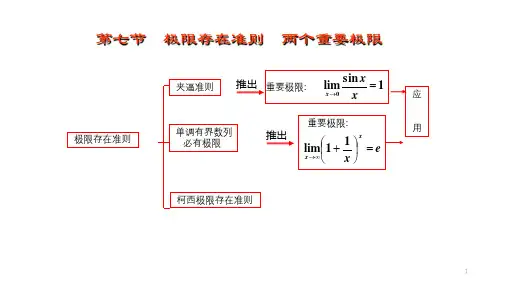
高等数学 第1章 第七节 极限存在准则 两个重要极限

高等数学 第1章 第七节 极限存在准则 两个重要极限

则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,（舍去）
lim n
xn
3.
14
3.两个重要极限的应用
例6： 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解： lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知：
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明：
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x

极限的两个重要极限公式

极限的两个重要极限公式

极限的两个重要极限公式极限是高等数学中的重要概念，具有广泛的应用。

在研究函数的性质、求导、积分等方面，极限都起着重要的作用。

本文将介绍两个重要的极限公式，它们分别是复合函数的极限公式和级数的比较判别法。

一、复合函数的极限公式复合函数是由两个或多个函数组合而成的函数，例如f(g(x))。

当我们需要计算复合函数的极限时，可以使用复合函数的极限公式，它的表述如下：设函数f(x)在x0处连续，g(x)在x0处极限存在且等于a，则有：lim f(g(x)) = f(a)x→x0这个公式的意义是，当自变量x趋近于x0时，函数g(x)的值趋近于a，因此f(g(x))的值也趋近于f(a)。

这个公式的证明可以使用ε-δ定义，但在这里我们不再赘述。

这个公式的应用非常广泛，特别是在微积分中，它可以用于求导和积分。

例如，当我们需要求f(g(x))的导数时，可以先求出g(x)的导数，然后将它代入f(x)中，再乘以g'(x)，即可得到f(g(x))的导数。

同样地，当我们需要对f(g(x))求积分时，可以将它转化为f(u)du的形式，其中u=g(x)，du=g'(x)dx，然后再对f(u)进行积分。

二、级数的比较判别法级数是由无穷多个数相加得到的数列，例如1+1/2+1/3+1/4+...。

在研究级数的性质时，我们经常需要判断它是否收敛。

如果一个级数收敛，那么它的和就是一个有限的数；如果一个级数发散，那么它的和就是无穷大或无穷小。

级数的比较判别法是判断级数收敛性的一种方法，它的表述如下：设有两个级数an和bn，如果存在一个正整数N，使得当n>N 时，有an≤bn，则有：若级数bn收敛，则级数an也收敛。

若级数an发散，则级数bn也发散。

这个公式的意义是，如果级数an的每一项都小于等于级数bn 的对应项，那么an的收敛性和bn的收敛性是相同的。

如果bn收敛，那么an也收敛；如果an发散，那么bn也发散。

这个公式的证明也比较简单，可以使用比较原理和收敛级数的性质进行推导。

高等数学1.6极限存在准则、两个重要极限

高等数学1.6极限存在准则、两个重要极限

二、两个重要极限
例4
1 cos x 求 lim . 2 x0 x
2 x x 2 sin 2sin 2 1 lim 2 解 原式 lim 2 x 0 2 x x 0 x 2 2 2
0 0
sin x lim 1 x 0 x
lim cos x 1,
x 0
x x0 x x0
lim f ( u ) A， 则 lim f [ g ( x )] A lim f ( u )
u a
证明
lim(1 x ) e
x 0
1 x
x x0 1 x
u a
1 1 令 x , lim(1 )t ＝ lim(1 x ) t t t x0
x x0 ( x ) x x0 ( x )
f ( x) lim h( x ) A, 那末 xlim x
( x)
0
存在, 且等于 A 上述两准则称为两边夹准则.
例1 求 lim( n 解：
1 n 1
2

1 n 2
2

1 n n
2
).
n n n
2
n
x 1 sin x 1, cos x 1 sin x cos x x
A
下面证 lim cos x 1,
x0
2 x x x 2 2 1 cos x 2 sin 2( ) , 2 2 2
0 cos x 1 x2 lim 0, lim(1 cos x ) 0, x0 x0 2 sin x lim cos x 1, lim1 1, lim x 0 x0 x0 x
(2)
1 x lim (1 ) e x x

高教社2024高等数学第五版教学课件-1.3 两个重要极限

高教社2024高等数学第五版教学课件-1.3 两个重要极限
则若有函数()在0 的某邻域内恒有
() ≤ () ≤ ()，
那么当 → 0 时，有 ≤ () ≤ ()，
即
故
≤ () ≤ ，
() = .
→0
= 1.
(−)
证：因为
−
−
−

=
=
，

所以我们只需讨论 → 0+ 的情形，

→∞
→∞ 2 + 1
1+
= 1 +
→∞
方法二
2 + 3

→∞ 2 + 1
=
2
2+1
2
2+1
3
1+
2
=
1
→∞
1+
2
+1

→∞

→∞
1+
1+
3
2
1
2
2 3
3 ×2
1
2×2
2+1
2
2+1
2
⋅ 1+
2
2+1
∙ 1 +
→∞
1
2
2
2+1
1
2
= ⋅ 1 = .
+1
∙ 1+
∙ 1+
3
2
1
2
=
3
2
×1
1
2
×1
=


→0
例3 计算
解
≠ 0， ≠ 0）






→0

=

高等数学 第六节 极限存在准则 两个重要极限


1 + 2 +⋯+ n < I n 2 2 2 n +n n +n n +n < 1 + 2 +⋯+ n , n2 + 1 n2 + 1 n2 + 1
+ 即 1 + 22 ⋯ + n < In < 1 + 2 + ⋯ + n , n +n n2 + 1
n(n + 1) n(n + 1) < In < , 2 2 2(n + 1) 2(n + n)
n
或 lim(1+ x)
x→0
1 x
=e .
e = 2.7182818284 59045⋯ (无理数 ⋯ )
sin x =1 . 2) . lim x→0 x
弦长 AB = 2 sin x , 弧长 AB = 2 x , 切线长 CD = 2 tan x .
F
A C
x
B
E
D
7
sin x < x < tan x . ( x > 0)
∀ε > 0 , ∃ N1 , 当 n > N1 时, A − ε < yn < A + ε ;
∃ N 2 , 当 n > N 2 时, A − ε < zn < A + ε , 从而 , 当 n > max{ N1 , N 2 } 时 ,
A − ε < yn ≤ xn ≤ z n < A + ε
n→∞
13
uk + uk uk −1 − uk −1 − uk −1uk uk uk−1 = − (1 + uk ) (1 + uk −1 ) 1+ uk 1+ uk−1 uk − uk −1 = > 0 ⇒ uk +1 > uk , { un } 单调增加 . (1 + uk ) (1 + uk −1 )

同济大学高等数学§1.3.2 两个重要极限


n n
n n n n
lim (1 1 )n n n 1
由夹逼准则
lim (1
n
1 )n1 lim (1
n1
n
n
1
)1 1
e,
lim (1 x
im (1 1 )x e 令 t x, x x
lim (1
x
1 )x x
lim (1 1)t t t
x
x2
x2
1
又 lim (1 xe x ) x , lim (1 1 )5n .
x0
n 2n
3
例5 求 lim(3 2x)x1
x1
3
1
解：原式 lim[1 2(1 x)]x1 lim[(1 2) 2 ]6 e 6
x1
0
sin 1
例6
求lim
x
x ln(1 x) ln x
sin 1
x
2n
故 lim y lim 2n
lim ( 2n sin x ) sin x 。
n
n
x sin 2n
n
x sin 2n
x
x
②当 x 0 时， y 1 ， lim y lim 11 。
n n
∴ lim cos x cos x n 2 22
cos x 2n
sin x
x
,
x0
1, x 0
。
4）
lim (1
t
1 )t t 1
lim (1
t
1 )t 1(1 1 )
t 1
t 1
e.
lim (1 1 )x e x x
令t 1, x
lim(1
1

高等数学 第二章 极限与连续 2.6 两个重要极限

sin kx kx k lim sin kx kx
k 1 k .
解： 原式 k lim x 0
kx 0
例4
求
2 sin x
2 2 x 2
解： 原式 lim 例5 求
x 0
sin lim x 2 x 0 2
1
x 2

2

1 2
1
2
解： 令 t
例11
求 x
lim (
x 2
x
2
2
x 1
)
x
x x x x 解： lim ( 2 ) lim lim x x x x 1 x 1 x 1 x 1 x 1
x
x
x
x
1 1 lim 1 1 x x 1 x 1
x,
OAB 的高为 BD ,
于是有
sin x BD ,
tan x AC ,
C
二、两个重要极限
B
(1)
lim
sin x x
x 0
1
0 0
型
x
o
D
A
△AOB 的面积＜圆扇形AOB的面积＜△AOD的面积
即
1 2
sin x

1 2
tan x
(0 x

2

2
sin x x tan x ,
单调减少
定理2.12
准则Ⅱ
单调有界数列必有极限.
几何解释:
m
x1
x 2 x 3x n x n 1
A
M
x
C

高等数学_极限存在准则


(1 n1 1) n 1
n
1 n1 1
e (P53~54)
lim (1 1 ) n 1 lim [(1 1 ) n 1 1） e （ n ] n n
n
x
lim (1 1 ) x e x
目录 上页 下页 返回 结束
当
时, 令 x (t 1) , 则
O
目录
x0
上页 下页
x
返回 结束
定理1. lim f ( x) A
x x0 ( x )
xn x0 , f ( xn ) 有定义
有 lim f ( xn ) A .
n
且
( xn )
说明: 此定理常用于判断函数极限不存在 .
法1 找一个数列
n
xn x0 ,
n
π n
R
sin π n
cos π n
说明: 计算中注意利用
目录 上页 下页 返回 结束
2. 证: 当 x 0 时, 设 n x n 1, 则
1 )n (1 n 1

1 ) x (1 1 ) n 1 (1 x n
n n
lim (1 n1 1) n lim
sin t t
1
目录
上页
下页
返回
结束
例4. 求
解: 原式 = lim
x 2 sin 2 2
x0
x
2
1 lim 2 x0
x sin 2
x 2
1 12 2
2
例5. 已知圆内接正 n 边形面积为
An n R 2 sin π cos π n n
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
1 x lim (1 ) ? x x
1000 10000 100000 …
2.717 2.718
-1000 -10000
2.71827
-100000 …
X
x
-10
-100
1 2.868 2.732 (1 ) x
2.720 2.7183
2.71828
1 x lim (1 ) e x x
sin t 所以 , 原式 5lim 5 1 5 t 0 t
注：在运算熟练后可不必代换，直接计算：
sin 5 x sin 5 x lim 5lim 5 1 5 x 0 x 0 5x x
推广： 设 为某过程中的无穷小量 ,
某过程
lim
sin

1
练习1. 求下列极限:
x 0 u0
u0
2 x

2 u
1 u 2
lim[(1 u) ]
[lim(1 u) ]
u0 1 u 2
e 2
方法二 掌握熟练后可不设新变量
lim 1 x lim[(1 x ) ]2
x 0 x 0 1 x 2 2 x
1 x
[lim(1 x )
O x B
C D A
sin x lim 1. ＋ x 0 x
tan x 例 1 求 lim x0 x tan x sin x 1 解 lim lim( ) x 0 x 0 cos x x x sin x 1 lim( ) x 0 x cos x sin x 1 lim lim x 0 x 0 cos x x
当 x 时 1 0 且 | sin x | 1 x
sin x 故 lim 0 x x
sin x lim 1 x 0 x
练习3：下列等式正确的是（
B
）
sin x A. lim 1; x x
1 C. lim x sin 1; x 0 x
1 B. lim x sin 1; x x 1 sin x 1 ． D. lim x x
sin 3x （） 1 lim x 0 x
sin 3x 3sin 3x sin 3 x 解：lim lim 3lim 3 1 3 x 0 x 0 x 0 x 3x 3x
sin 5 x （2） lim x 0 3x
sin 5 x sin 5 x 5 5 5 解：lim lim( )( ) 1 x 0 x 0 3x 5x 3 3 3
(2) lim[ f (x ) g (x )] limf (x ) limg (x )
f (x ) limf (x ) . (3) 若 limg(x ) 0，lim g (x ) limg (x )
(4) lim[cf ( x)] c lim f ( x )
(5) lim[ f ( x )]k [lim f ( x )]k
x A. lim 1 x 0 x
1 C. lim x sin 1 x 0 x
x B. lim 1 x 0 x
sin x D. lim 1 x x
x 1 当（ 练习6. 已知 f ( x ) tan x
A ）时，
f ( x) 为无穷小量.
A. x 0
C. x
B. x 1
D. x
sin x ，当 练习7. 已知 f ( x) 1 x f ( x) 为无穷小量．
练习8. 练习9.
x 0
时，
x sin x 1 lim ______ x x
x sin x lim ______ 0 x 0 x
第二个重要极限
X 10 100 1 (1 ) 2.594 2.705 x
x 0
]
e
2
例3
解
x 1 3x lim( ) x x x 1 3x 1 3x lim( ) lim(1 ) x x x x
1 x lim （ 1 ) x x
3
e

练习1. 计算 l i m (1 2 x ) .
x 0
1 x lim (1 ) e x x
1 令t , x
(1 )
1 1 x t)t e lim(1 ) lim(1 t 0 x x
lim(1 t ) e
t 0
1 t
(1 )
1
推广 为某过程中的无穷小量 , lim (1 ) e
1 x2 1
x 2 1 1 l i m 1 e 2 . x x
例2
1 x . 计算 lim
x 0
2 x
解
方法一 所以
令 u = -x， 因为 x 0 时 u 0，
1 x l i m(1 u) lim
x 2
因为
x 2 1 2
x x 1 1 1 1 1 ， 且 lim 1 e ， x x x x
所以，有
lim 1 x x
x 1 2
lim 1 x x 1
1 lim 1 x _________ x
x 2
2 e
1 1 x 7、 lim(1 ) _________ . e x x
思考题
2 x 计算 lim x 3 x
解 因为
x2
2 x 3 x ( 1) 1 1 . 3 x 3 x x3
练习4：下列等式不正确的是（ D ） sin x x 1; B lim 1; A lim x 0 x 0 x sinx 1 1 x sin 1; D lim x sin 1 C lim x x 0 x x

练习5. 下列极限计算正确的是（ B ）
sin x 极限 lim x 0 x
1 x 极限 lim (1 ) x x
预备知识
1.有关三角函数的知识
sin x tan x cos x
sin 0 0
cos0=1
| sin x | 1
| cos x | 1
2.有关对数函数的知识
ln x log e x
以e为底的指数函数y=ex的反函数 y = logex， 叫做自然对数，在工程技术中经常被运用，常简 记为 y = ln x. 数 e 是一个无理数，它的前八位数是： e = 2.718 281 8
sin( x 1) 1 1 1 lim lim 1 x 1 x 1 x 1 x 1 11 2
例4 解
1 求 lim x sin x x
1 sin 1 x 1 lim x sin lim x x x 1 x
思考题
sin x 1 lim lim sin x x x x x
2 lim (1 ) e .
0 某过程
1
练 习 题
sin x sin x 1、 lim lim x 0 x x 0 x
sin 2 x sin 2 x sin 2 x 3x 2 lim 2、 lim lim x 0 sin 3 x x 0 2 x sin 3 x 3 x 0 sin 3 x
x u 5
两个重要极限的证明
两个重要极限的证明
sin x 例 证明 lim 1. x 0 x 证 AOB 面积 < 扇形AOB 面积 < AOC 面积, 即
R2 R2 R2 sin x x tan x , 2 2 2
R2 各式同除以正值 sin x , 得 2 x 1 1 , sin x cos x
sin x 即 cos x 1. x
B C R x
sin x 使用 lim 1 时须注意 : x 0 x
(1)类型：
(2)推广形式:
0 型 0
某过程
lim
sin

1
）
（
某过程
lim 0
x (3)等价形式： lim 1 x 0 sin x
sin( x 1) 例 3 求 lim 2 x 1 x 1
sin( x 1) sin( x 1) sin( x 1) 1 lim lim[ ] 解 lim 2 x 1 x 1 ( x 1)( x 1) x 1 x 1 x 1 x 1
1 x
解
lim (1 2 x ) l i m (1 2 x )
x 0 x 0
1 x
1 2 2x
e .
2
x x ) . 练习2. 求 lim ( x 1 x
x x 1 解 lim ( ) lim 1 x x 1 x x (1 ) x 1 1 x lim (1 ) x x
0.99998
0.9999998
sin x lim 1 x 0 x
证明
sin x lim 1. ＋ x 0 x
证
即 sin x x tan x
各式同除以sin x (因为sin x 0), 得 x 1 1 , sin x cos x
sin x 即 cos x 1. x
某过程
1 x 使用 lim(1 ) e x x
(1)类型:
须注意 :
1
1 型
某过程

(2)推广形式: lim (1 ) e
（
某过程
lim 0
1 t
）
(3)等价形式：lim(1 t ) e
t 0
例1 解
1 计算 l i m 1 . x x