应用时间序列分析 第5章

第五章时间序列分析一、单项选择题1.构成时间数列的两个基本要素是( C )（2012年1月）A.主词和宾词B.变量和次数C.现象所属的时间及其统计指标数值D.时间和次数2．某地区历年出生人口数是一个( B )（2011年10月）A．时期数列 B.时点数列C.分配数列D.平均数数列3.某商场销售洗衣机，2008年共销售6000台，年底库存50台，这两个指标是( C ) （2010年10）A.时期指标B.时点指标C.前者是时期指标，后者是时点指标D.前者是时点指标，后者是时期指标4.累计增长量( A ) （2010年10）A.等于逐期增长量之和B.等于逐期增长量之积C.等于逐期增长量之差D.与逐期增长量没有关系5.某企业银行存款余额4月初为80万元，5月初为150万元，6月初为210万元，7月初为160万元，则该企业第二季度的平均存款余额为（ C ）（2009年10）万元万元万元万元6.下列指标中属于时点指标的是( A ) （2009年10）A.商品库存量B.商品销售量C.平均每人销售额D.商品销售额7.时间数列中，各项指标数值可以相加的是( A ) （2009年10）A.时期数列B.相对数时间数列C.平均数时间数列D.时点数列8.时期数列中各项指标数值（ A ）（2009年1月）A.可以相加B.不可以相加C.绝大部分可以相加D.绝大部分不可以相加10.某校学生人数2005年比2004年增长了8%，2006年比2005年增长了15%，2007年比2006年增长了18%，则2004-2007年学生人数共增长了（ D ）（2008年10月）％+15％+18％％×15％×18％C.（108％+115％+118％）-1 ％×115％×118％-1二、多项选择题1.将不同时期的发展水平加以平均而得到的平均数称为( ABD )（2012年1月）A.序时平均数B.动态平均数C.静态平均数D.平均发展水平E.一般平均数2．定基发展速度和环比发展速度的关系是( BD )（2011年10月）A．相邻两个环比发展速度之商等于相应的定基发展速度B.环比发展速度的连乘积等于定基发展速度C.定基发展速度的连乘积等于环比发展速度D.相邻两个定基发展速度之商等于相应的环比发展速度E.以上都对3.常用的测定与分析长期趋势的方法有( ABC ) （2011年1月）A.时距扩大法B.移动平均法C.最小平方法D.几何平均法E.首末折半法4.时点数列的特点有( BCD ) （2010年10）A.数列中各个指标数值可以相加B.数列中各个指标数值不具有可加性C.指标数值是通过一次登记取得的D.指标数值的大小与时期长短没有直接的联系E.指标数值是通过连续不断的登记取得的5.增长1%的绝对值等于（ AC ）（2010年1）A.增加一个百分点所增加的绝对量B.增加一个百分点所增加的相对量C.前期水平除以100D.后期水平乘以1%E.环比增长量除以100再除以环比发展速度6.计算平均发展速度常用的方法有（ AC ）（2009年10）A.几何平均法(水平法)B.调和平均法C.方程式法(累计法)D.简单算术平均法E.加权算术平均法7.增长速度（ ADE ）（2009年1月）A.等于增长量与基期水平之比B.逐期增长量与报告期水平之比C.累计增长量与前一期水平之比D.等于发展速度-1E.包括环比增长速度和定基增长速度8.序时平均数是（ CE ）（2008年10月）A.反映总体各单位标志值的一般水平B.根据同一时期标志总量和单位总量计算C.说明某一现象的数值在不同时间上的一般水平D.由变量数列计算E.由动态数列计算三、判断题1.职工人数、产量、产值、商品库存额、工资总额指标都属于时点指标。

5月 282
6月 260
7月 270
平均库存额 （万元）
（1）将表格填写完整 （2）计算第一季度平均库存额和上半年年平均库存额
第五章A
• 2、简述时间序列的水平分析指标 • 答：发展水平、平均发展水平、增长量、 平均增长量 • 3、发展水平：又称发展量，是时间序列中 的各个指标数值，它反映现象在各个时期 (或时点)发展所达到的规模或水平，是计算 动态分析指标的基础
• 4、简述相对数时间数列计算序时平均数的 方法 • （1）分子序列和分母序列都为时期序列 • （2）分子分母都为时点序列 • （3）分子分母一个时期序列一个时点序列
1月 1日
工人数 1800
2月 1日
1850
3月 1日
1870
4月 1日
1872
职工数
2300
2350
2370
2372
一直该企业第一季度工业总产值为833.4万元
（1）该企业一季度工人占职工人数的比重
（2）一季度工人劳动生产率
月份
月初库存额 （万元）
1 280 272

时间序列分析方法第05章最大似然估计最大似然估计(Maximum Likelihood Estimation, MLE)是一种常用的统计学方法，用于估计时间序列模型的参数。

在时间序列分析中，最大似然估计可以用于估计自回归(AR)、移动平均(MA)、自回归滑动平均(ARMA)等模型的参数。

最大似然估计的基本思想是寻找最能解释已观测到的数据的模型参数。

具体来说，最大似然估计根据已观测到的数据样本，通过优化模型参数使得该样本的出现概率最大化。

换句话说，最大似然估计通过寻找最可能产生观测到的数据样本的模型参数值，来估计真实的未知参数值。

最大似然估计的主要步骤如下：1.选择合适的时间序列模型。

根据数据的特征和背景知识，确定适合的时间序列模型。

常见的时间序列模型包括AR、MA、ARMA、ARIMA等。

2.建立模型的似然函数。

似然函数是一个关于模型参数的函数，表示了在给定参数值的情况下，观测到数据样本的概率。

3.对似然函数取对数，得到对数似然函数。

似然函数通常非常复杂，可能难以直接处理。

取对数可以简化计算，并不改变估计值的最优性质。

4.求解对数似然函数的最大值。

通过优化算法(如牛顿法、梯度下降法)求解对数似然函数的最大值，得到最大似然估计值。

5.检验估计结果。

最大似然估计得到的估计值通常具有一些统计性质，可以进行假设检验、置信区间估计等。

最大似然估计方法在时间序列分析中具有广泛的应用，可以用于估计参数、进行模型选择和模型比较等。

然而，最大似然估计方法也有一些限制和假设，它假设数据是独立同分布的，且服从一些特定的概率分布。

对于一些时间序列数据，可能不满足这些假设，或者需要使用其他方法进行估计。

总之，最大似然估计是一种重要的时间序列分析方法，可以用于估计自回归、移动平均等模型的参数。

它通过优化模型参数，使得模型生成观测到的数据样本的概率最大化。

最大似然估计方法在实际应用中具有广泛的应用，并可以通过检验统计性质来评估估计结果的准确性和有效性。

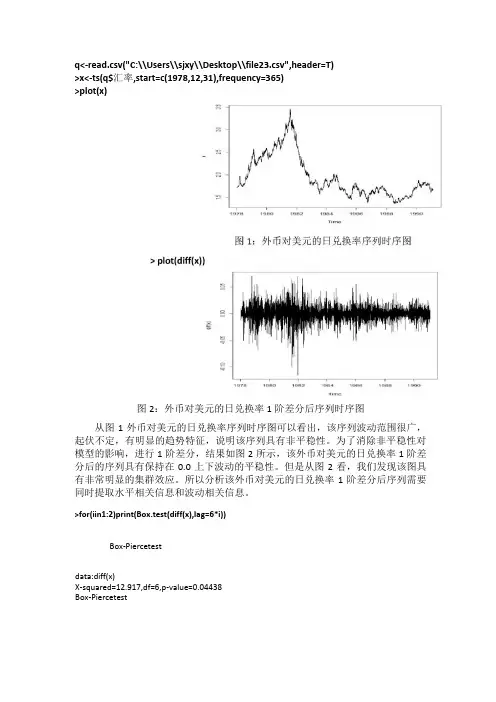
q<-read.csv("C:\\Users\\sjxy\\Desktop\\file23.csv",header=T)>x<-ts(q$汇率,start=c(1978,12,31),frequency=365)>plot(x)图2：外币对美元的日兑换率1阶差分后序列时序图从图1外币对美元的日兑换率序列时序图可以看出，该序列波动范围很广，起伏不定，有明显的趋势特征，说明该序列具有非平稳性。

为了消除非平稳性对模型的影响，进行1阶差分，结果如图2所示，该外币对美元的日兑换率1阶差分后的序列具有保持在0.0上下波动的平稳性。

但是从图2看，我们发现该图具有非常明显的集群效应。

所以分析该外币对美元的日兑换率1阶差分后序列需要同时提取水平相关信息和波动相关信息。

>for(iin1:2)print(Box.test(diff(x),lag=6*i))Box-Piercetestdata:diff(x)X-squared=12.917,df=6,p-value=0.04438Box-Piercetestdata:diff(x)X-squared=29.712,df=12,p-value=0.003085>acf(diff(x))图3：外币对美元的日兑换率1阶差分后序列自相关图>pacf(diff(x))Serie-sdifT<|x誉-Iaooaozo04o oa□oaa1oLag图4：外币对美元的日兑换率1阶差分后序列偏自相关图延迟6阶和12阶后，P值分别为p-value=0.04438、p-value=0.003085,且都小于置信水平0.05，说明该外币对美元的日兑换率1阶差分后的序列不是纯随机序列。

水平信息的提取主要是对差分后自相关与偏自相关的考察。

外币对美元的日兑换率1阶差分后序列自相关图如图3所示,该图在延迟1阶之后几乎所有值都落在2倍标准差区域内波动,具有突然衰减且衰减的速度非常快,根据衰减的速度判断,以及具有短期相关性,判断该自相关具有截尾性。

2、相对数时间数列 它是把一系列同类相对数指标按 时间先后顺序 排列而成的数列。
3、平均数时间数列 它是把一系列同类平均数指标按时间向后顺序 排列而成的数列 。
绝对数时间数列的分类
绝对数时间数列按数列反映时间状态的不同； 又可分为时期数列和时点数列。 时期数列
当数列中的指标为时期指标，反映现象在各段时期 内发展过程的总量时，即为时期数列。
—— 27.8 84.2 173.4
—— 27.8 56.4 89.2
—— 106.7 120.4 142.0
—— 106.7 112.8 118.0
四、增长速度
概念：由增长量与基期水平之比。 作用：说明报告期水平较基期水平增长的相对程度。 种类：增长速度也分为定基增长速度和环比增长速度。 定基增长速度的一般通式为；
a1-a0, a2-a1, a3-a2，……，an-1-an-2 ，an-an-1。
两种增长量之间关系： 各逐期增长量之和，等于相应时期的
累计增长量：
(a i a i 1) a n a 0
两相邻时期累计增长量之差，等于相 应时期的逐期增长量：
(a i a 0 ) (a i 1 a 0 ) a i a i 1
作用：说明现象报告期水平较基期水平的相对增 长结果。
种类：由基期水平选择的不同可把增长量分为累 计增长量和逐期增长量。
累计增长量是指报告期水平与固定基期水平之差。 一般通式为：
a1-a0, a2-a0, a3-a0，……，an-1-a0 ，an-a0。 逐期增长量是指报告期水平与前一期水平之差。
一般通式为：
（7） ——
（8）
举例
年份
发展水 增长量（万 平（万 元） 元） 累计 逐期

50
乘积季节模型
使用场合
序列的季节效应、长期趋势效应和随机波动之间有着复 杂地相互关联性，简单的季节模型不能充分地提取其中 的相关关系
构造原理
短期相关性用低阶ARMA(p,q)模型提取
季节相关性用以周期步长S为单位的ARMA(P,Q)模型提取
假设短期相关和季节效应之间具有乘积关系，模型结构
3
差分运算的实质
差分方法是一种非常简便、有效的确定 性信息提取方法
Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息
差分运算的实质是使用自回归的方式提 取确定性信息
d
d xt (1 B)d xt (1)i Cdi xti i0
5/10/2019
模型中有部分系数省缺了，那么该模型 称为疏系数模型。
5/10/2019
课件
34
疏系数模型类型
如果只是自相关部分有省缺系数，那么该疏系 数模型可以简记为ARIMA(( p1,, pm ), d, q)
p1,, pm 为非零自相关系数的阶数
如果只是移动平滑部分有省缺系数，那么该疏 系数模型可以简记为 ARIMA( p, d, (q1,, qn ))
26
建模
定阶
ARIMA(0,1,1)
参数估计
(1 B)xt 4.99661 (1 0.70766 B) t
Var(t ) 56.48763
模型检验
模型显著 参数显著
5/10/2019
课件
27
ARIMA模型预测
原则
最小均方误差预测原理
Green函数递推公式
一阶差分

4. 不规则变动（I）
是一种无规律可循的偶然性的变 动，包括严格的随机变动和不规 则的突发性影响很大的变动两种 类型。比如股票的价格波动。
前三种都是可以解释的变 动，只有不规则变动是无法解 释的。
传统的时间序列分析的主 要内容就是将这些成分从时间 序列中分离出来，然后将它们 之间的关系用一定的数学关系 式予以表达，并进行分析。
1. 长期趋势（T）
现象在较长时期内受某种根 本性因素作用而形成的总的 变动趋势。比如GDP总量长 期看来具有上升趋势。
2. 季节变动（S）
现象在一年内随着季节的变化 而重复出现的有规律的周期性 变动。比如通常商业上有“销 售淡季”和“销售旺季”。
3. 周期性（C）
现象以若干年为周期所呈现出的围 绕长期趋势的一种波浪形态的有规 律的变动。比如我们常说的经济周 期，5年或者10年一个循环。
• 时期序列的主要特点有： ① 时期序列中各个观察值可以相加，相加后的观察 值表示现象在更长时期内发展过程的总量。 ② 时期序列中每个指标数值的大小与时期的长短有 直接联系，即具有时间长度。 ③ 时期序列中的指标数值一般采用连续登记办法获 得。
2．时点序列
• 当时间序列中所包含的总量指标都是反映社会经 济现象在某一瞬间上所达到的水平时，这种总量 指标时间序列即为时点序列。在时点序列中，相 邻两个时点指标之间的距离为“间隔”。
相对指标时间序列中各个指标数值都是相对数，其计算基础不同，不能直接相加。在编制相对指 标时间序列时，要注意百分号的表示及其在表中的位置和作用。
（三）平均指标时间序列
将同一平均指标的数值按其发生的时间先后顺序排列而成的数列叫做平均指数时间序列。它反映 社会经济现象一般水平的变化过程和发展趋势。
平均指标时间序列中每个指标数值都是平均数，不能相加，相加起来没有经济意义

a a

n 118729 129034 132616 132410 124000 5
127357.8
②时点序列
若是连续时点序列： 计算方法与时期序列一样； 若是间断时点序列： 则必须先假设两个条件，分别是 假设上期期末水平等于本期期初水平； 假设现象在间隔期内数量变化是均匀的。 间隔期相等的时点序列 采用一般首尾折半法计算。 例如：数列 a i , i 0,1,2, n 有 n 1 个数据，计算 期内的平均水平 a n a n 1 a 0 a1 a1 a 2
（3）联系
环比发展速度的乘积等于相应的定基发展速度，
n n i 0 i 1 i 1
相邻两期的定基发展速度之商等于后期的环比发展速度
i i 1 i 0 0 i 1
（二）增减速度
1、定义：增长量与基期水平之比 2、反映内容：现象的增长程度 3、公式：增长速度
0.55
二、时间序列的速度分析指标
（一）发展速度 （二）增长速度 （三）平均发展水平
（四）平均增长速度
（一）发展速度
1、定义：现象两个不同发展水平的比值 2、反映内容：反映社会经济现象发展变化快慢相对程度 3、公式：v 报告期水平 100%
基期水平
（1）定基发展速度
是时间数列中报告期期发展水平与固定基期发展水平对比所 得到的相对数，说明某种社会经济现象在较长时期内总的发 展方向和速度，故亦称为总速度。 （2）环比发展速度 是时间数列中报告期发展水平与前期发展水平之比，说明某 种社会经济现象的逐期发展方向和速度。
c

a
b
均为时期或时点数列，一个时期数列一个时点数列，注意平均的时间长度 ，比如计算季度的月平均数，时点数据需要四个月的数据，而时期数据则 只需要三个月的数据。

第一章习题答案略第二章习题答案2.1答案：（1）不平稳，有典型线性趋势（2）1-6阶自相关系数如下（3）典型的具有单调趋势的时间序列样本自相关图2.2答案：（1）不平稳（2）延迟1-24阶自相关系数（3）自相关图呈现典型的长期趋势与周期并存的特征2.3答案：（1）1-24阶自相关系数（2）平稳序列（3）非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。

由于延迟1-12阶Q统计量的P值均显著大于0.05，所以该序列为纯随机序列。

2.5答案（1）绘制时序图与自相关图（2）序列时序图显示出典型的周期特征，该序列非平稳（3）该序列为非白噪声序列2.6答案（1）如果是进行平稳性图识别，该序列自相关图呈现一定的趋势序列特征，可以视为非平稳非白噪声序列。

如果通过adf检验进行序列平稳性识别，该序列带漂移项的0阶滞后P值小于0.05，可以视为平稳非白噪声序列（2）差分后序列为平稳非白噪声序列2.7答案（1）时序图和自相关图显示该序列有趋势特征，所以图识别为非平稳序列。

（2）单位根检验显示带漂移项0阶延迟的P值小于0.05，所以基于adf检验可以认为该序列平稳（3）如果使用adf检验结果，认为该序列平稳，则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳，那么一阶差分后序列为平稳非白噪声序列2.8答案（1）时序图和自相关图都显示典型的趋势序列特征（2）单位根检验显示该序列可以认为是平稳序列（带漂移项一阶滞后P值小于0.05）（3）一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--（） 221112() 1.96110.7t Var x φ===--（） 22213=0.70.49ρφ==（）12122221110.490.7=0110.71ρρρφρρ-==-（4） 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有：,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=（）1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=（） 1112223340.70.15=0φρφφφ====-（）3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩（） （）模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩（） 3.5证明:该序列的特征方程为：320c c λλλ--+=，解该特征方程得三个特征根：11λ=，2λ=3λ=无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。

第05章多元时间序列分析⽅法142第五章多元时间序列分析⽅法[学习⽬标]了解协整理论及协整检验⽅法；掌握协整的两种检验⽅法：E-G 两步法与Johansen ⽅法； ? 熟悉向量⾃回归模型VAR 的应⽤； ? 掌握误差修正模型ECM 的含义及检验⽅法； ? 掌握Granger 因果关系检验⽅法。

第⼀节协整检验前⾯介绍的ARMA 模型要求时间序列是平稳的，然⽽实际经济运⾏中的⼤多数时间序列都是⾮平稳的，通常采取差分⽅法消除时间序列中的⾮平稳趋势，使得序列平稳后建⽴模型，这就是第四章所介绍的ARIMA 模型。

但是，变换后的时间序列限制了所要讨论问题的范围，并且有时变换后的序列由于不具有直接的经济意义，从⽽使得转换为平稳后的序列所建⽴的时间序列模型的解释能⼒⼤⼤降低。

1987年，Engle 和Granger 提出的协整理论及其⽅法，为⾮平稳时间序列的建模提供了另⼀种重要途径。

①⽬前，协整问题研究已经成为20世纪80年代末到90年代以来经济计量学建模理论的⼀个重⼤突破，在分析变量之间的长期均衡关系中得到⼴泛应⽤。

⼀、协整概念与定义在经济运⾏中，虽然⼀组（两个或两个以上）时间序列变量(例如⼈民币汇率与外汇储备、货币供应量和股票指数)都是随机游⾛，但它们的某个线性组合却可能是平稳的，在这种情况下，我们称这两个变量是平稳的，既存在协整关系。

其基本思想是，如果两个(或两个以上)的时间序列变量是⾮平稳的，但它们的某种线性组合却表现出乎稳性，则这些变量之间存在长期稳定关系，即协整关系。

根据以上叙述，我们将给出协整这⼀重要概念。

⼀般⽽⾔，协整(cointegration)是指两个或两个以上同阶单整的⾮平稳时间序列的组合是平稳时间序列，则这些变量之间的关系的就是协整的。

为何会有协整问题存在呢？这是因为许多⾦融、经济时间序列数据都是不平稳的，但它们可能受到某些共同因素的影响，从⽽在时间上表现出共同趋势，即变量之间存在⼀定稳定关系，他们的变化受到这种关系的制约，因此它们的某种线性组合可能是平稳的，即存在协整关系。

第五章时间序列分析习题第五章时间序列分析习题⼀、填空题1．时间序列有两个组成要素：⼀是，⼆是。

2．在⼀个时间序列中，最早出现的数值称为，最晚出现的数值称为。

3．时间序列可以分为时间序列、时间序列和时间序列三种。

其中是最基本的序列。

4．绝对数时间序列可以分为和两种，其中，序列中不同时间的数值相加有实际意义的是序列，不同时间的数值相加没有实际意义的是序列。

5．已知某油⽥1995年的原油总产量为200万吨，2000年的原油总产量是459万吨，则“九五”计划期间该油⽥原油总产量年平均增长速度的算式为。

6．发展速度由于采⽤的基期不同，分为和两种，它们之间的关系可以表达为。

7．设i=1，2，3，…，n，a i为第i个时期经济⽔平，则a i/a0是发展速度，a i/a i-1是发展速度。

8．计算平均发展速度的常⽤⽅法有⽅程式法和.9．某产品产量1995年⽐1990年增长了105%，2000年⽐1990年增长了306．8％，则该产品2000年⽐1995增长速度的算式是。

10．如果移动时间长度适当，采⽤移动平均法能有效地消除循环变动和。

11．时间序列的波动可分解为长期趋势变动、、循环变动和不规则变动。

12．⽤最⼩⼆乘法测定长期趋势，采⽤的标准⽅程组是。

⼆、单项选择题1．时间序列与变量数列( )A都是根据时间顺序排列的B都是根据变量值⼤⼩排列的C前者是根据时间顺序排列的，后者是根据变量值⼤⼩排列的D前者是根据变量值⼤⼩排列的，后者是根据时间顺序排列的2．时间序列中，数值⼤⼩与时间长短有直接关系的是( )A平均数时间序列B时期序列C时点序列D相对数时间序列3．发展速度属于( )A⽐例相对数B⽐较相对数C动态相对数D强度相对数4．计算发展速度的分母是( )A报告期⽔平B基期⽔平C实际⽔平D计划⽔平5．某车间⽉初⼯⼈⼈数资料如下：A 296⼈B 292⼈C 295 ⼈D 300⼈6．某地区某年9⽉末的⼈⼝数为150万⼈，10⽉末的⼈⼝数为150．2万⼈，该地区10⽉的⼈⼝平均数为( )A150万⼈ B150．2万⼈ C150．1万⼈ D ⽆法确定 7．由⼀个9项的时间序列可以计算的环⽐发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 8．采⽤⼏何平均法计算平均发展速度的依据是( )A 各年环⽐发展速度之积等于总速度B 各年环⽐发展速度之和等于总速度C 各年环⽐增长速度之积等于总速度D 各年环⽐增长速度之和等于总速度9．某企业的科技投,3,2000年⽐1995年增长了58．6％，则该企业1996—2000年间科技投⼊的平均发展速度为( ) A5%6.58 B5%6.158 C6%6.58 D6%6.15810．根据牧区每个⽉初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采⽤的公式是( )A 简单平均法B ⼏何平均法C 加权序时平均法D ⾸末折半法 11．在测定长期趋势的⽅法中，可以形成数学模型的是( )A 时距扩⼤法B 移动平均法C 最⼩平⽅法D 季节指数法三、多项选择题1．对于时间序列，下列说法正确的有( )A 序列是按数值⼤⼩顺序排列的B 序列是按时间顺序排列的C 序列中的数值都有可加性D 序列是进⾏动态分析的基础E 编制时应注意数值间的可⽐性 2．时点序列的特点有( )A 数值⼤⼩与间隔长短有关B 数值⼤⼩与间隔长短⽆关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的3．下列说法正确的有( )A 平均增长速度⼤于平均发展速度B 平均增长速度⼩于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( )A 增长速度=%100?基期⽔平增长量 B 增长速度=%100?报告期⽔平增长量C 增长速度= 发展速度—100％D 增长速度=%100?-基期⽔平基期⽔平报告期⽔平E 增长速度= %100?基期⽔平报告期⽔平5．采⽤⼏何平均法计算平均发展速度的公式有( ) A 1 231201-?=n n a a a a a a a a nx B 0a a nx n =C 1a a nx n = D R n x = E nx x ∑=A 第⼆年的环⽐增长速度⼆定基增长速度=10％B 第三年的累计增长量⼆逐期增长量=200万元C 第四年的定基发展速度为135％D 第五年增长1％绝对值为14万元E 第五年增长1％绝对值为13．5万元7．下列关系正确的有( )A 环⽐发展速度的连乘积等于相应的定基发展速度B 定基发展速度的连乘积等于相应的环⽐发展速度C 环⽐增长速度的连乘积等于相应的定基增长速度D 环⽐发展速度的连乘积等于相应的定基增长速度E 平均增长速度=平均发展速度-1 8．测定长期趋势的⽅法主要有( )A 时距扩⼤法B ⽅程法C 最⼩平⽅法D 移动平均法E ⼏何平均法 9．关于季节变动的测定，下列说法正确的是( ) A ⽬的在于掌握事物变动的季节周期性 B 常⽤的⽅法是按⽉(季)平均法C 需要计算季节⽐率D 按⽉计算的季节⽐率之和应等于400％E 季节⽐率越⼤，说明事物的变动越处于淡季 10．时间序列的可⽐性原则主要指( )A 时间长度要⼀致B 经济内容要⼀致C 计算⽅法要⼀致D 总体范围要⼀致E 计算价格和单位要⼀致四、判断题1．时间序列中的发展⽔平都是统计绝对数。

2.随机项的估计
Rˆt xt Tˆt Sˆt ,t 1,2,,24.
1
-125
119
-64 61.9
14.7
-223.3 209.5 52.1 -136.8
-34.6 60
146.5 4.8
-121.1
87.6 -14.7
-38.3
4.8 -12.8 48 24.6
-30.5 -34.4
方法二：回归直线法
1790-1980年间每10年的美国人口总数
例4
1985至2000年广州月平均气温
例5
北京地区洪涝灾害数据
例5 虚线是成灾面积
图
一、时间序列的定义
时间序列:按时间次序排列的随机变量序列
X1, X 2,
(1.1)
n 个观测样本:随机序列的 n个有序观测值
x1, x2 ,, xn
(1.2)
《应用时间序列分析》
何书元 编著 北京大学出版社
广泛的应用领域：
金融经济 气象水文 信号处理 机械振动
………… 目的：描述、解释、预测、控制 本书主要介绍时间序列的基本知识、常用的建模和预测 方法
Wolfer记录的300年的太阳黑子数
光大证券2009.09.18-
《应用时间序列分析》
目录
第一章 时间序列 第二章 自回归模型 第三章 滑动平均模型与自回归滑动平均模型 第四章 均值和自协方差函数的估计 第五章 时间序列的预报 第六章 ARMA模型的参数估计
3. 随机项估计即为 {Xt Tˆt Sˆt}
方法一：分段趋势法
一、分段趋势图(年平均)
趋势项估计为
Tˆ1 Tˆ2 Tˆ3 Tˆ4 5873.0 Tˆ5 Tˆ6 Tˆ7 Tˆ8 5875.0 Tˆ9 Tˆ10 Tˆ11 Tˆ12 5853.0 Tˆ13 Tˆ14 Tˆ15 Tˆ16 6073.7 Tˆ17 Tˆ18 Tˆ19 Tˆ20 6262.6 Tˆ21 Tˆ22 Tˆ23 Tˆ24 6384.5

22
Yt s
Yt
Yt s
( Xt ,Yts )
( Xt ,Yts )
X t s
Xt
Xts
图5-3 互相关函数示意图
(xt , yts ) xy (s) （5.6） (xt , yts ) xy (s) （5.7）
23
对互相关函数非对称性的理解
互相关关系的非对称性是指（Xt，Yt-s) 和（Xt，Yt+s)通常不等的性质 。比如假设Xt是 某种商品的广告费， 对于该种商品的销售额Yt 来说是广告费是一个领先的变量， 它对Yt-s （s>0）的影响可能很小 ，甚至为零，Xt但是 对于Yt+s的影响会比较大，因为当前的广告费会 对未来的销售额产生影响。至于相关性会到达什 么程度，或者什么方向，要根据实际问题而言。
32
如前所述，如果输入的时间序列是白噪声， 则可以得到如（5.11）和(5.12)式那样简单的脉 冲响应函数与互相关函数的关系式，为了达到这 个目的，我们对Xt和Yt做预白化处理， 即建立模 型过滤Xt和Yt。使输入的是 Xt和Yt，而输出的是 两个白噪声序列t和t。
关于传递函数的预白化过程通过统计软件可 以得到。
j 1vj1 2vj1 rvjr
这恰好是一个r阶的差分方程，可见当j>b+s时 的脉冲响应函数是该方程的解，所以当jb+s+1时， 脉冲响应函数呈指数衰减。 ，r个初始响应函数为
bsr1, bsr2 ,, vbs
结合这3点，我们可以得到三个参数r、s和b的值。
13
三、常见的传递函数的形式
设 Ytk 0 Xtk 1Xtk1 tk
将两边同时乘以Xt，则
Ytk Xt 0 Xtk Xt 1Xtk1Xt

第一题data yx_51;input x@@;difx=dif(x);t=l+_n_-l;cards;304 303 307 299296 293 301 293 301 295 284 286 286 287 284 282 278 281 278 277 279 278 270 268 272 273 279 279 280 275 271277 278 279 283 284 282 283 279 280 280 279 278 283 278 270 275 273 273 272 275 273273 277 274 274 272 280 282 292 295 295 294 290 291 288 288 290 293 288 289 Z91 293 293 290 288 287 Z89 292 288 288 285 282286 286 287 284 283 286 282 287 286 287 292292 294 291 2882899procgplot;plot x*t=ldifx*t=2;symbo1lc=red v=circle i=join;symbo12c=ye11ow v=st ar i=join;run;procarima;identifyvar=x(1);estima tep=l;run;结果如下时序图：-阶差分后时序图:di fi10-10・2010 20 30 40 50 60 70 60 90 100 110SAS系统2014年05月06日星期二下午10时47分58秒1The ARI MA ProcedureName of Variable = xPeriod(s) of DifferencingMean of forking SeriesStandard DeviationNumber of Observations Observation(s) eliminated by differenci1 -0.14151 3.6145371061Autocorrelat ionsStd Error0 1 13.064881-2.020214 1.00000 -.154832 0.251847 0.019283 -0.803468 -.063154 -1.166473 -.089285 -0.407940 -.03122 • *6 1.366363 0.10463 榊：7 2.461031 0.188378 -0.727748 -.05570 :務9 0.622454 0.04764 « :10 -1.716200 -.13136 •出林11 0.824106 0.06308 * :12 0.136572 0.0104513 0.636280 0.04097 ♦.14 -1.830163 -.1400815 2.002506 0.15327 曲16 -1.865607 -.1428017 -0.535607 ■•04100・ *18 0.849572 0.06503 *19 0.473360 0.03623 ♦20 0.560746 0.04292 * ,21 -2.602490 ••1992022-0.104103 -.0079723-0.666324 -.05100 • *24 -0.537108 -.04111 ・«Lag Covariance Correlation •1 9 8 7 6 5 4 3 2 10 12 3 4 5 6 7 8 9 1marks two stand&rd errors 0.037129 0.099424 0.039458 0.099912 0.100662 0.100753 0.101773 0.105010 0.105289 0.105492 0.107024 0.107374 0.107384 0.107531 0.109239 0.111249 0.112965 0.113106 0.113458 0.113567 0.113720 0.116965 0.116970 0.117180Inverse AutocorrelationsThe ARINA Procedure1 2 0.12567 -0.059293 0.024024 0.17471 *>K«.5 0.03817来■6 ・0.17242 • ； •冷肾；? -0.219D68 0.08852 佛岀•9 -0.01671 10 -0.0015711 -0.09685 ■榊12 0.0151813 0.09241 删.14 0.06628* • 15 -0.18306 H4nh*16 0.07964 1? 0.08334 180.01169Lftg Correlftt ionSAS 糸统19 -0.05799 • #■20 0.01034 ■21 0.1762&22 0.08267 桝.23 ・0.01342 •24 0.06638* .Correlat ion 2 -19 83 4 5 6 7 8 9 11-0.15463 2 -0.004753 -0.06853 • *4 -0.113595 -0.06560 • *6 0.087427 0.215518 -0.004829 0.04333 « •10 ・0.07757 •11 0.07S3& 12 0.04034 13 -0.00237 14 -0.1993415 0.12464榊：16 -0.03053 :**17 -0.06859 .*18 -0.01418 19 0.06543 « ・ 20 0.06544 «・21 -0.18418 22 -0.12096 23 0.04340 24-0.08493Lag Correlat ion 2ai4^05H06tl 星期二 I 、午 10旳47甘58抄 2Inverse Autocorrelat ions-19876 Partial Autocorrelat ionsAutocorrelation Check for White Noise To Lac 6 12 IS 24Ch 卜 Square 5.44 12.72 21.69 28.05DF 6 12 18 24Pr > ChiSq 0.4830 0.3896 0.2462 0.2579A 1 ______ _____ | _ ■ •-0.155 0.0190.188 -0.0560.041 -0.140 0.0360.043 Hutuuur rciat imi3-0.031 0.063 -0.041 -0.0510.105 0.010 0.065 -0.041-0.069 0.0480.153 -0.199-0.088-0.131-0.143-0.008Conditional Least SquaresEstimationStandardApproxParatneterEstimate Error t :Value Pr > Itl LagMU-0.14201 0.30359 -0.47 0.6409 0AR1,1-0.154780.09692-1.600.11331The ARIMA ProcedureConstant Est imate Var ianee Est iinate Sid Error EstimateAIC SBCNumber of Residuals AIC and SBC do not includeCor re I at ions of Pa.rameterEstimatesEst imated MeanPeriod(s) of D i f ferenc iAutoregressive Factors Factor 1：1 + 0.15478 B^(1)通过原始数据的时圧图可以明显看出，此圧列非平稳，因而对丿子列进行一阶 差分。

基本公式
ai 若时间数列ci bi
a 则: c b
⑴ a、b均为时期数列时
a a N a cb c b b N b b
a 1 ca
利润计划完成程度（﹪）
ai 计划利润（万元） bi 实际利润（万元） ci
月
份
一 200
二 300
三 400
250
125
解：①第二季度各月的劳动生产率：
12.6 10000 元 人 c1 6300 四月份： 2000 2000 2 14.6 10000 c2 6952 .4元 人 五月份： 2000 2200 2 16.3 10000 c3 7409 .1元 人 六月份： 2200 2200 2
[分析] 属于时间间隔不等的间断时点数列,采用加权 算术平均法计算。
500 560 560 580 580 600 3 4 5 2 2 2 a 3 45 568(人)
练习：1、2006年各季度工业总产值如下，求该市平均每季度工业总产值。
季度 工业总产值 （万元）
一 32600
上半年平均固定资产额为：
60 70 60 61 64 64 70 2 64(万元) b 2 7 -1
序时平均数计算示例
[例5-4]根据表计5-5算2001年的平均职工人数。
表5-5 某企业2001年职工人数资料 单位:人
时 间 职工人数 1月1日 500 4月1日 560 7 月 31 日 580 12 月 31 日 600
第二节 时间数列的水平指标
一、发展水平
（一）概念：时间序列中各项具体的指标数值。 字母表示: a0,a1, a2 ,an-1, …,an 相关概念：

第二章习题答案2.1（1）非平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（1）自相关系数为：0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.0940.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.0660.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118（2）平稳序列（3）白噪声序列2.4，序列不LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363。

显著性水平=0.05能视为纯随机序列。

2.5（1）时序图与样本自相关图如下（2）非平稳 （3）非纯随机 2.6（1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)） （2）差分序列平稳，非纯随机第三章习题答案3.1 解：1()0.7()()t t t E x E x E ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-）B 7.01(t t t B B B x εε)7.07.01()7.01(221 +++=-=-229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ022=φ3.2 解：对于AR （2）模型：⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得：⎩⎨⎧==15/115/721φφ3.3 解：根据该AR(2)模型的形式，易得：0)(=t x E原模型可变为：t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==1.98232σ⎪⎩⎪⎨⎧=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ⎪⎩⎪⎨⎧=-====015.06957.033222111φφφρφ3.4 解：原模型可变形为：t t x cB B ε=--)1(2由其平稳域判别条件知：当1||2<φ，112<+φφ且112<-φφ时，模型平稳。

114333 124810 115823 123626 2 2 Y 9 1 119758.56 （万人）
相对数序列的序时平均数
（计算方法）
1. 先分别求出构成相对数或平均数的分子ai 和分母 bi 的平均数
2. 再进行对比，即得相对数或平均数序列的 序时平均数 3. 基本公式为
(i=1,2,…,n)
3. 各逐期增长量之和等于最末期的累积增长量
平均增长量
（概念要点）
• • 1. 观察期内各逐期增长量的平均数 2. 描述现象在观察期内平均增长的数 量
•
3. 计算公式为逐期增长量之和 平均增长量 逐期增长量个数 累积增长量 观察值个数 1
时间序列的速度分析
发展速度
=（ （ 1 25%） （ 1 25%） 1 20%） 1 87.5% 1999年定基增长速度 = 1+87.5% 1 15% 1 115.6% 2000年环比增长速度 = 1+132.5% 1 115.6% 1 7.8%
2、时点序列 如果统计指标是时点指标，则这种时间序列称为时 点序列。时点序列的特点： （1）不可加性，即时点序列中各时点上的同一空间 的数值不具有可加性。 （2）指标数值的大小与时间间隔的长短无直接关系， 即不具有时间长度。 （3）指标值一般采用间断登记的办法获得。
时间序列的分类
时间序列
绝对数序列
解：第三产业国内生产总值的平均数
103442.3 a 20688.46 （亿元） n 5 全部国内生产总值的平均数
i 1
a
n
i
327447.3 b 65489.46 （亿元） n 5 第三产业国内生产总值所占平均比重