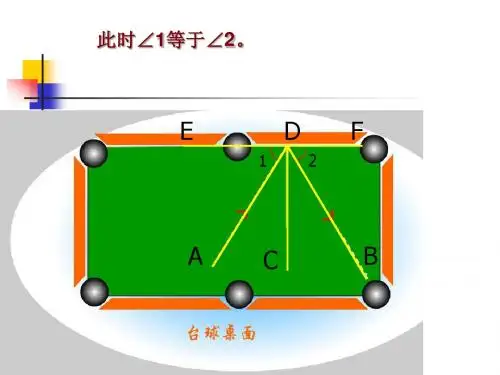
台球桌面上的角

平行线、相交线、角经典例题讲解与练习平行线与相交线（1）一、知识概述（一）从台球桌面上的角，引出有关角的概念1、两角互余、互补的概念及性质（1）定义：如果两个角的和是180°，那么这两个角互为补角.（如图）简称互补.如果两个角的和是90°，那么这两个角互为余角.（如图）简称互余.说明：①互余、互补是指两个角的关系.②互补或互余的两个角，只与它们的和有关，而与其位置无关.③用数学语言表述为：若∠α＋∠β=180°，则∠α与∠β互补；反之，若∠α与∠β互补，则∠α＋∠β=180°.若∠α＋∠β =90°，则∠α与∠β互余；反之若∠α与∠β互余，则∠α＋∠β=90°. （2）性质：①同角或等角的补角相等.②同角或等角的余角相等.2、对顶角的概念（1）如果一个角的两边分别是另一个角的两边的反向延长线，这样的两个角叫做对顶角.如图中的∠1和∠3，∠2和∠4是对顶角.由对顶角的位置特点也可将其描述为：①两条直线相交成四个角，其中不相邻的两个角叫做对顶角.②一个角的两边分别是另一个角的两边的反向延长线，这两个角叫做对顶角.说明：只有两条直线相交时，才能产生对顶角，对顶角是成对出现的.③对顶角的本质特征是：两个角有公共顶点，其两边互为反向延长线.（2）对顶角的性质：对顶角相等.（二）探索直线平行的条件1、两条直线相交构成四个有公共顶点的角.一条直线与两条直线相交得八个角，简称“三线八角”，则不共顶点的角的位置关系有同位角、内错角、同旁内角.如图所示，直线 AB、CD被直线EF所截，形成了8个角.（1）同位角：两个角都在两条直线的同侧，并且在第三条直线（截线）的同旁，这样的一对角叫做同位角.如∠1和∠5，∠3和∠7，∠4和∠8，∠2和∠6.（2）内错角：两个角都在两条直线之间，并且在第三条直线（截线）的两旁，这样的一对角叫做内错角.例如∠3和∠5，∠4和∠6.（3）同旁内角：两个角都在两条直线之间，并且在第三条直线（截线）的同旁，这样的一对角叫做同旁内角.例如∠4和∠5，∠3和∠6.2、两条直线平行的条件：两条直线被第三条直线所截，如果（1）同位角相等，两直线平行. （2）内错角相等，两直线平行. （3）同旁内角互补，两直线平行.二、重难点知识剖析1、互为补角和互为邻补角的关系. 互为补角是两个角的和为 180°，与它们的位置无关. 而互为邻补角既与它们的和为 180°有关，又与位置有关，不要混淆.2、灵活运用互余、互补等知识点以及对顶角的性质列方程求解，即学会用代数法解几何题的方法.3、证明两直线平行时，必须弄清所用条件中的同位角、内错角、同旁内角是哪两条直线被哪一条直线所截而成的，因为推出的结论是除截线外的另两条直线平行.平行线与相交线（2）一、知识概述1、平行线的特征特征一：两条平行线被第三条直线所截，同位角相等，简单说成“两直线平行，同位角相等”，使用方法如图：∵ a∥b，∴∠1=∠2（两直线平行，同位角相等）特征二：两直线平行，内错角相等 .使用方法：∵ a∥b，∴∠2=∠3（两直线平行，内错角相等）特征三：两直线平行，同旁内角互补 .使用方法：∵ a∥b，∴∠2＋∠4=180°（两直线平行，同旁内角互补）2、直线平行的条件与平行线的特征的区分表。

2.1台球桌面上的角《21 台球桌面上的角》台球，作为一项备受欢迎的室内运动，其桌面看似简单，实则蕴含着丰富的几何奥秘。

其中，角的存在和变化尤为关键。

当我们站在台球桌前，准备击球的那一刻，目光所及之处尽是各种角度。

球与球之间的位置关系，球与桌边的碰撞轨迹，无一不是由角来决定的。

首先，让我们来了解一下台球桌面上最基本的角——直角。

台球桌的四个角通常都是直角，这为我们提供了一个稳定的边界和参考。

当球滚向桌边，与直角边碰撞时，其反弹的方向遵循着一定的规律。

这种规律是基于物理学中的反射原理，即入射角等于反射角。

比如说，一个球以一定的角度撞击桌边，如果入射角是 30 度，那么它反弹的角度也会是 30 度。

这一规律在我们击球时的策略制定中起着至关重要的作用。

如果我们想要将目标球打进特定的口袋，就需要准确地计算出击球的角度，以及球与桌边碰撞后的反弹角度。

除了直角，还有许多其他类型的角在台球桌上发挥着作用。

比如，两个球之间形成的夹角。

当我们想要通过击打一个球来撞击另一个球时，这两个球之间的夹角就决定了击球的力度和方向。

如果夹角较小，我们可能需要更精准的控制力度，以免击球后无法达到预期的效果；而如果夹角较大，那么击球的容错率相对会高一些。

再来说说球在桌面上滚动时形成的动态角。

当球沿着直线滚动，然后因为碰撞改变方向，这就形成了一个角度的变化。

这种变化对于我们判断球的后续轨迹至关重要。

有时候，一个小小的角度偏差可能会导致球完全偏离目标口袋，让我们错失得分的机会。

在实际的台球比赛或娱乐中，我们经常会遇到需要通过巧妙地利用角度来实现复杂击球的情况。

比如“斯诺克”比赛中，选手们常常会通过将母球藏在其他球后面，使得对手难以直接击打目标球。

这时，球与球之间形成的多个角度关系就需要选手们进行精确的计算和判断。

此外，不同的击球点也会影响球的旋转和角度变化。

如果我们击打母球的上部，球会向前旋转，与桌边碰撞后的角度变化相对较小；而如果击打母球的下部，球会向后旋转，与桌边碰撞后的角度变化则会较大。

2·1 台球桌面上的角1．互为余角定义：互为余角.即：如果两个角的和是直角，那么称这两个角互为余角(complementary angle),也就是说其中一个角是另一个角的余角.注意：(强调)(1)互为余角是对两个角而言的.(2)互为余角仅仅表明了两个角的数量关系，而没有限制角的位置关系.2.互为补角定义互为补角.即：如果两个角的和是平角，那么称这两个角互为补角(supplementary angle).同角或等角的余角相等，同角或等角的补角相等.3.对顶角定义像这样，直线AB与直线CD相交于点O，∠1与∠2有公共顶点，它们的两边互为反向延长线，这样的两个角叫对顶角.对顶角：如果两个角有公共顶点，它们的两边互为反向延长线，那么这样的两个角叫做对顶角.对顶角相等.对顶角的本质特征是：两个角有公共顶点，两个角的两边互为反向延长线.要在图形中准确地找出对顶角，需两看：(1)看是不是两条直线相交所得的角;(2)看是不是有公共顶点而没有公共边(或不相邻)的两个角.另外，从对顶角的定义还可知：对顶角总是成对出现的，它们是互为对顶角；一个角的对顶角只有一个.两条直线相交于一点，有2对对顶角，三条直线相交于一点，有6对对顶角，n 条直线相交于一点，共有n (n －1)对对顶角.1. 如果∠α的余角是∠β，那么∠β的补角是（ ）A. 180°－∠αB. 90°－∠αC. 90°＋∠αD. ∠α－180°【解析】∵∠α的余角是∠β∴∠β的补角为：∴选择C2. 已知，如图，直线AB 、CD 相交于点O ，OB 平分∠DOE ，若∠DOE ＝60°，则∠AOC 的度数是__________【解析】3. 如图，点O 是直线AB 上一点，∠AOE ＝∠FOD ＝90°，OB 平分∠COD（1）找出图中与∠DOE 互余的角；（2）找出图中与∠DOE 互补的角. ∴∠β=-∠α90 1801809090 -∠β=--∠α=+∠α() C EA BD O∠=∠DOE OB DOE 60，平分∴∠=∠=⨯=BOD DOE 12126030 又对顶角相等 ∠=∠AOC DOB()∴∠=AOC 30【解析】（1）∵∠AOE ＝∠FOD ＝90°∴∠EOF 与∠BOD 都是∠DOE 的余角又∵OB 平分∠COD∴∠BOC ＝∠BOD∴与∠DOE 互余的角有：∠EOF ，∠BOD ，∠BOC（2）∵∠AOE ＝∠FOD ＝90°∴∠AOF ＝∠EOD （同角的余角相等）又∵∠AOF ＋∠FOB ＝180°∴∠FOB 是∠AOF 的一个补角又∵∠FOB ＝∠EOF ＋∠EOB ＝∠BOC ＋∠EOB ＝∠EOC∴∠DOE 的补角有：∠FOB ，∠EOC4.下图中有对顶角吗？若有，请指出，若没有，请说明理由.【解析】图(1)、(2)、(3)中没有对顶角，因为这三个图形中的∠1、∠2不是两条直线相交所形成的.图(4)中有对顶角，分别是∠1与∠3；∠2与∠4 EFDA BOC ∴∠+∠=∠+∠=DOE EOF DOE BOD 9090 ，∴∠+∠=∠+∠=FOE AOF FOE EOD 9090 ，5. 如图：（1）若∠3＝∠4，则________//________，理由是_________（2）若∠1＝100°，∠2＝80°，则______//_________，理由是_________（3）若∠3＝∠5，则_______//________，理由是______________【解析】（1）若∠3＝∠4，则AB//CD ，理由是同位角相等两直线平行；（2）若∠1＝100°，∠2＝80°，则AB//CD ，理由是同旁内角互补，两直线平行；（3）若∠3＝∠5，则AB//CD ，理由是内错角相等，两直线平行.E GA 4 B15C DF H 3 2。

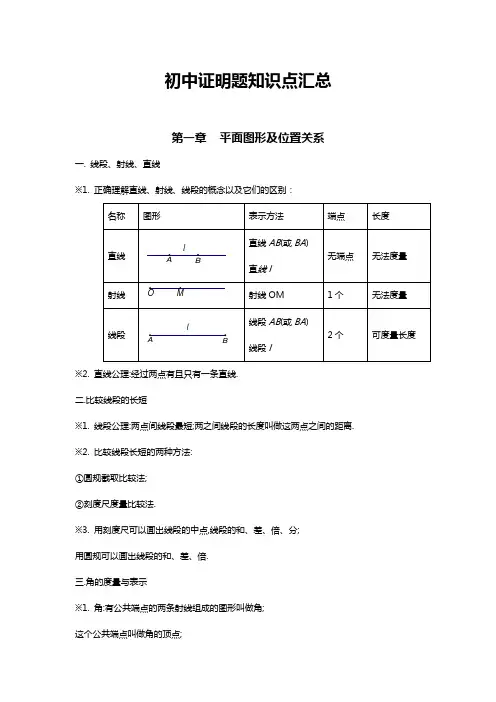
初中证明题知识点汇总第一章平面图形及位置关系一. 线段、射线、直线※1. 正确理解直线、射线、线段的概念以及它们的区别：※2. 直线公理:经过两点有且只有一条直线.二.比较线段的长短※1. 线段公理:两点间线段最短;两之间线段的长度叫做这两点之间的距离. ※2. 比较线段长短的两种方法:①圆规截取比较法;②刻度尺度量比较法.※3. 用刻度尺可以画出线段的中点,线段的和、差、倍、分;用圆规可以画出线段的和、差、倍.三.角的度量与表示※1. 角:有公共端点的两条射线组成的图形叫做角;这个公共端点叫做角的顶点;这两条射线叫做角的边.※2. 角的表示法：角的符号为“∠”①用三个字母表示，如图1所示∠AOB②用一个字母表示，如图2所示∠b③用一个数字表示，如图3所示∠1④用希腊字母表示，如图4所示∠β※经过两点有且只有一条直线。

※两点之间的所有连线中，线段最短。

※两点之间线段的长度，叫做这两点之间的距离．．．．．．．．。

1º=60’ 1’=60” ※角也可以看成是由一条射线绕着它的端点旋转而成的。

如图5所示：※一条射线绕它的端点旋转，当终边和始边成一条直线时，所成的角叫做平角．．。

如图6所示：※终边继续旋转，当它又和始边重合时，所成的角叫做周角．．。

如图7所示：※从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的．．平分线．．．。

※经过直线外一点，有且只有一条直线与这条直线平行。

※如果两条直线都与第三条直线平行，那么这两条直线互相平行。

A O B 图 1 b 图2 终边始边图5 平角 图6周角 图7 1 图3 β 图4※互相垂直的两条直线的交点叫做垂足．．。

※平面内，过一点有且只有一条直线与已知直线垂直。

※如图8所示，过点C 作直线AB 的垂线，垂足为O 点，线段CO 的长度叫做点．C ．到直线．．．AB ．．的距离．．．。

第二章 平行线与相交线一．台球桌面上的角※1．互为余角和互为补角的有关概念与性质如果两个角的和为90°（或直角），那么这两个角互为余角；如果两个角的和为180°（或平角），那么这两个角互为补角；注意：这两个概念都是对于两个角而言的，而且两个概念强调的是两个角的数量关系，与两个角的相互位置没有关系。

2.1 台球桌面上的角一、填空题:（每题3分，共21分）1.∠α＝50°24′，那么∠α的余角等于____________。

2.已知∠α、∠β互为补角，且∠α=∠β，则∠α＝___________。

3.若∠1和∠2互余，∠2 和∠3 互补，∠1＝63°，则∠3 ＝________.4.如图1，直线AB 和CD 相交于点O ，∠DOE 是直角，若∠1＝30°，则∠2＝________,∠3＝________。

∠4＝__________。

4321ODCB Acba 5432121F EDCBA(1) (2) (3) （4）5.①若∠A ＋∠B ＝90°，∠B ＋∠C ＝90°，则∠A______∠C ，理由是_________________; ②若∠1＋∠3＝180°,∠2＋∠4＝180°,且∠1＝∠2，则∠4_____ ∠3，理由是_______________________。

6.∠1与∠2互余，∠1＝50°＋2°，∠2＝4x °－2°，则∠1＝______,∠2=______.7.如图2，直线a 、b 、c 两两相交，∠1＝60°，∠2=23∠4，则∠3=_____,∠5=_______。

二、选择题:（每题4分，共36分） 8.下列说法中正确的是（ ）A.任何一个角都有余角B.一个角的余角一定是锐角C.一个角的余角可能是锐角，也可能是钝角D. 以上答案都不对 9.下列说法中正确的是( )A.有公共顶点的角是对顶角B.相等的角是对顶角C.对顶角必相等D.不是对顶角的角不相等 10.三条线相交于一点，所成的小于平角的对顶角有( ) A.3对 B.3 对 C.3对 D.3对11. 若一个角的补角是这个角的余角的3倍，则这个角是（ ） A.30° B.45° C.60° D.75° 12.如图3，∠1＞∠2，那么∠2与12（∠1－∠2）之间的关系是（ ）A.互余B.互补C.和为45°D.22.5°13.一个角的余角和这个角的补角互补，则这个角是（ ） A.45° B.90° C.135° D.不能确定14.下列说法正确的是( )A.一个角的补角一定大于这个角;B.任何一个角都有补角C.若∠1＋∠2＋∠3＝90°，则∠1、∠2、∠3互余D.一个角如有余角，则这个角的补角与它的余角的差为90°15.若互补的两个角有一条公共边，则这两个角的平分线所形成的角( ) A.一定是直角 B.一定是锐角 C.一定是钝角 D.是直角或者是锐角 16.如图4，ACB 是直线，AB ⊥CD ，EC ⊥FC ，图中共有（ ）对角互余 A.2 B.3 C.4 D.以上都不对三、解答题：（共43分）17.如图，直线AB 、CD 相交于O ，已知∠AOC ＝75°，OE 把∠B OD 分成两部分，且∠BOE ：∠EOD ＝2∶3，求∠AOE 。

2.1台球桌面上的角21 台球桌面上的角台球，作为一项广受欢迎的休闲运动，其桌面看似简单，实则蕴含着丰富的几何知识，尤其是那些看似不起眼的角。

当我们站在台球桌前，准备击球的那一刻，可能并不会立刻想到角度对于击球结果的重要性。

但只要稍加留意，就会发现，每一次击球的方向、力度以及球的滚动轨迹，都与桌面上的角息息相关。

首先，让我们来了解一下什么是台球桌面上的角。

从直观上看，台球桌的四个角是最为明显的直角。

而在击球过程中，我们更关注的是球与球之间、球与桌边形成的各种角度。

比如，当母球撞击目标球时，两者之间的夹角决定了目标球的运动方向。

在台球运动中，准确判断和利用角度是取得好成绩的关键。

一个常见的情况是，当我们想要将目标球击入某个袋口时，需要根据母球、目标球和袋口之间的角度关系来决定击球的位置和力度。

如果角度过小或过大，都可能导致击球失误。

比如说，在击打直线球时，角度相对简单，只要准确控制击球的力度，就有较大的概率将球打进。

但当遇到有角度的球时，情况就变得复杂起来。

假设目标球距离袋口有一定的角度偏差，我们就需要计算出母球应该撞击目标球的位置，以使得目标球能够沿着预期的方向滚动并进入袋口。

为了更好地理解台球桌面上的角，我们不妨做一个简单的实验。

在桌面上放置一个母球和一个目标球，然后尝试从不同的角度击打母球，观察目标球的运动轨迹。

通过多次尝试，我们会发现，当母球撞击目标球的位置不同时，目标球的运动方向和速度都会发生变化。

除了击球的角度，球与桌边碰撞时的角度也同样重要。

当球撞击桌边时，会遵循反射定律，即入射角等于反射角。

这意味着，如果我们能够准确地预测球撞击桌边后的反射角度，就可以更好地控制球的走向，为下一次击球做好准备。

在实际的比赛或娱乐中，高手们总是能够凭借着对角度的敏锐感知和精确计算，打出令人惊叹的好球。

他们可以通过巧妙地利用角度，让球在桌面上辗转腾挪，最终准确无误地进入目标袋口。

对于初学者来说，要掌握好台球桌面上的角并非易事。

七年级《生活中的数据》测试卷一、知识点：1、百万分之一：对较小数据的感受，用科学计数法表示绝对值较小数及单位的换算。

如：1微米= 米，1纳米= 米,4纳米= 微米= 毫米= 厘米= 米200千米的百万分之一是米.用科学计数法表示：0.00000368=2、近似数和有效数字：一般地，通过测量的结果都是近似的。

对于一个近似数从边第个不是的数字起，到的数位止，所有的数字都叫做这个数的有效数字.如：0.03296精确到万分位是，有个有效数字，它们是3、世界新生儿图：会从给出的信息图中得到有用信息；会画生动形象的统计图。

二、巩固练习：（一）填空选择题：1、下列数据中，是精确值的有（）个（1）在9·11恐怖事件中，估计有5000人死亡；（2）某细胞的直径为百万分之一米；（3）中国的国土面积约为960万km2（4）我家有3口人（5）一（1）班有53人（A）1 （B）2 （C）3 （D）42、下列各组数据中，（）是精确的。

（A）小明的身高是183.5米（B）小明家买了100斤大米（C）小明买笔花了4.8元（D）小明的体重是70千克3、某学生测量长度用的刻度尺的最小单位是厘米现测量一物品的结果为6.7cm ,那么位是精确值，位是估计值。

4、1纳米相当于一根头发丝直径的六万分之一，那么一根头发丝的半径为米（用科学计数法表示）5、一只蚂蚁的重量约为0.0002㎏，用科学计数法记为用科学计数法表示的数3.02×10－8，其原数为6、小东买了12.65kg苹果，精确到0.1kg，则所买苹果约为kg7、数0.8050精确到位，有个有效数字，是8、数4.8×105精确到位，有个有效数字，是9、数5.31万精确到 位，有 个有效数字，是10、一箱雪梨的质量为20.95㎏，按下面的要求分别取值：（1）精确到10㎏是 ㎏，有 个有效数字，它们是 （2）精确到1㎏是 ㎏，有 个有效数字，它们是 （3）精确到0.1㎏是 ㎏，有 个有效数字，它们是 11、2002年我国普通高校招生2756300人，若精确到万位是 人 有 个有效数字，它们是 米，12、九届人大一次会议上，李鹏同志所作的政府工作报告中指出：1997年我国粮食总产量达到492500000t ，按要求填空：（1）精确到百万位是 （用科学计数法表示）， 有 个有效数字，它们是（2）精确到亿位是 （用科学计数法表示）， 有 个有效数字，它们是13、数0.000125保留两个有效数字记为 14、北冰洋的面积是1475.0万平方千米，精确到（ ）位，有（ ）个有效数字（A ）十分位，四 （B ）十分位，五 （C ）千位，四 （D ）千位，五 15、下表是中国奥运会奖牌回眸统计表及历届奖牌总数折线图（1） 完成上表（2） 把第23届奖牌总数在统计图上标出，并完成此折线统计图70（二）解答题1、举例说明哪些是近似数，哪些是准确数，哪些是有效数字？2、、如图，（1）写出图中阴影部分的面积；（2）当a=3，b=2时，计算阴影部分的面积（ =3.1415，保留3个有效数字，单位：cm）3、随机抽取城市30天的空气质量状况统计图如下：其中：w≤50时，空气质量为优；50＜w≤100时，空气质量为良；100＜w≤150时，空气质量为轻微污染。