电路原理(邱关源)习题参考答案第二章 电阻电路的等效变换练习测试
- 格式:doc
- 大小:206.50 KB
- 文档页数:12

电路习题解答第一章 电路模型和电路定律【题1】:由U A B =5V 可得:I AC .=-25A :U D B =0:U S .=125V 。
【题2】:D 。
【题3】:300;-100。
【题4】:D 。
【题5】:()a i i i =-12;()b u u u =-12;()c ()u u i i R =--S S S ;()d ()i i R u u =--S SS 1。
【题6】:3;-5;-8。
【题7】:D 。
【题8】:P US1=50 W ;P U S 26=- W ;P U S 3=0;P I S 115=- W ;P I S 2 W =-14;P I S 315=- W 。
【题9】:C 。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
【题14】:3123I +⨯=;I =13A 。
【题15】:I 43=A ;I 23=-A ;I 31=-A ;I 54=-A 。
【题16】:I =-7A ;U =-35V ;X 元件吸收的功率为P U I =-=-245W 。
【题17】:由图可得U E B =4V ;流过2 Ω电阻的电流I E B =2A ;由回路ADEBCA 列KVL 得 U I A C =-23;又由节点D 列KCL 得I I C D =-4;由回路CDEC 列KVL 解得;I =3;代入上 式,得U A C =-7V 。
【题18】:P P I I 12122222==;故I I 1222=;I I 12=; ⑴ KCL :43211-=I I ;I 185=A ;U I I S =-⨯=218511V 或16.V ;或I I 12=-。
⑵ KCL :43211-=-I I ;I 18=-A ;U S =-24V 。
第二章电阻电路的等效变换【题1】:[解答]I=-+9473A=0.5A;U Ia b.=+=9485V;IU162125=-=a b.A;P=⨯6125.W=7.5W;吸收功率7.5W。


《电路》邱关源 第五版课后题答案第一章 电路模型和电路定律【题1】:由U A B =5V 可得:I AC .=-25A :U D B =0:U S .=125V 。
【题2】:D 。
【题3】:300;-100。
【题4】:D 。
【题5】:()a i i i =-12;()b u u u =-12;()c ()u u i i R =--S S S ;()d ()i i R u u =--S SS 1。
【题6】:3;-5;-8。
【题7】:D 。
【题8】:P US1=50 W ;P U S 26=- W ;P U S 3=0;P I S 115=- W ;P I S 2 W =-14;P I S 315=- W 。
【题9】:C 。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
【题14】:3123I +⨯=;I =13A 。
【题15】:I 43=A ;I 23=-A ;I 31=-A ;I 54=-A 。
【题16】:I =-7A ;U =-35V ;X 元件吸收的功率为P U I =-=-245W 。
【题17】:由图可得U E B =4V ;流过2 Ω电阻的电流I E B =2A ;由回路ADEBCA 列KVL 得 U I A C =-23;又由节点D 列KCL 得I I C D =-4;由回路CDEC 列KVL 解得;I =3;代入上 式,得U A C =-7V 。
【题18】:P P I I 12122222==;故I I 1222=;I I 12=; ⑴ KCL :43211-=I I ;I 185=A ;U I I S =-⨯=218511V 或16.V ;或I I 12=-。
⑵ KCL :43211-=-I I ;I 18=-A ;U S =-24V 。
第二章 电阻电路的等效变换【题1】:[解答]I =-+9473A =0.5 A ;U I a b .=+=9485V ; I U 162125=-=a b .A ;P =⨯6125. W =7.5 W;吸收功率7.5W 。

第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻842R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA R R u i s 1082100212=+=+=V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。
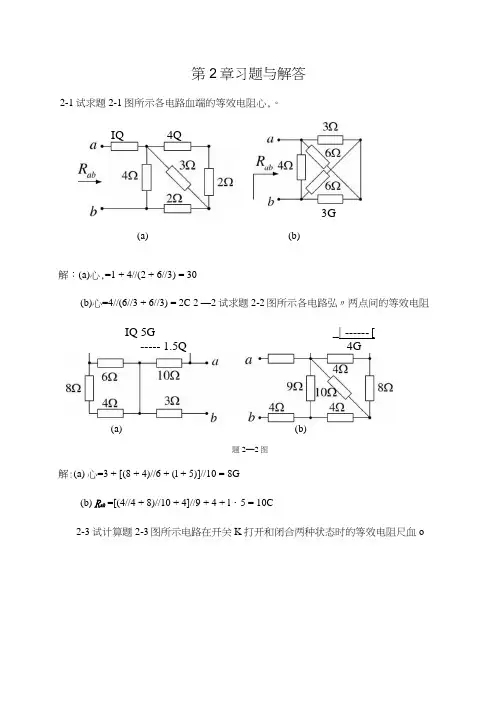
第2章习题与解答2-1试求题2-1图所示各电路血端的等效电阻心,。
解:(a)心,=1 + 4//(2 + 6//3) = 30(b)心=4//(6//3 + 6//3) = 2C 2 —2试求题2-2图所示各电路弘〃两点间的等效电阻IQ 5G_| ------ [ ----- 1.5Q 4G(a)(b)题2—2图解:(a) 心=3 + [(8 + 4)//6 + (l + 5)]//10 = 8G(b) R ah =[(4//4 + 8)//10 + 4]//9 + 4 + l ・5 = 10C2-3试计算题2-3图所示电路在开关K 打开和闭合两种状态时的等效电阻尺血oIQ 4Q3G(b)(a)题2—3图 解:(a)开关打开时心=(8 + 4)//4 = 3。
开关闭合时^,=4/74 = 20(b)开关打开时 R ah =(6 + 12)/7(6+12) = 90开关闭合时心=6//12 + 6//12 = 8。
2—4试求题2—4图(a)所示电路的电流/及题2—4图(b)所示电路的电压U 。
解:(a)从左往右流过1G 电阻的电流为I] =21/(1 + 6//12 + 3//6)二21/(l+4 + 2) = 3A 从上往下流过3 O 电阻的电流为I.= —x3 = 2A3 + 6 从上往下流过120电阻的电流为I p =—^-x3 = lA12 + 6 所以1 =【3叫2 = 1 A⑹从下往上流过6V 电压源的电流为"击莎1Q + O1V3Q 6Q(a)12Q6Q题2—4图从上往下流过两条并联支路的电流分别为2A所以U = 2x2-lx2=2V2 — 5试求题2 — 5图所示各电路ab端的等效电阻R ah,其中/?] = = 1。
2Q题2-5图解:(a)如图,对原电路做厶-丫变换后,得一平衡电桥所以心,=(*+*)//(1 + 1)= *°(b)将图中的两个Y形变成△形,如图所示2.5Q5Q 白804Q 4QT50T T2Q即得所以陰=L269G2 —6计算题2 —6图所示电路中弘b两点间的等效电阻。


第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻84R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA u i s 10100212===V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。

第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻842R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA R R u i s 1082100212=+=+=V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。

邱关源《电路》第五版参考答案答案第一章电路模型和电路定律【题1】:由U A B =5V 可得:I AC .=-25A :U D B =0:U S .=125V 。
【题2】:D 。
【题3】:300;-100。
【题4】:D 。
【题5】:()a i i i =-12;()b u u u =-12;()c ()u u i i R =--S S S ;()d ()i i R u u =--S SS 1。
【题6】:3;-5;-8。
【题7】:D 。
【题8】:P US1=50 W ;P U S 26=- W ;P U S 3=0;P I S 115=- W ;P I S 2 W =-14;P I S 315=- W 。
【题9】:C 。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
【题14】:3123I +?=;I =13A 。
【题15】:I 43=A ;I 23=-A ;I 31=-A ;I 54=-A 。
【题16】:I =-7A ;U =-35V ;X 元件吸收的功率为P U I =-=-245W 。
【题17】:由图可得U E B =4V ;流过2 Ω电阻的电流I E B =2A ;由回路ADEBCA 列KVL 得U I A C =-23;又由节点D 列KCL 得I I C D =-4;由回路CDEC 列KVL 解得;I =3;代入上式,得U A C =-7V 。
【题18】:P P I I 12122222==;故I I 1222=;I I 12=;⑴KCL :43211-=I I ;I 185=A ;U I I S =-?=218511V 或16.V ;或I I 12=-。
⑵KCL :43211-=-I I ;I 18=-A ;U S =-24V 。
第二章电阻电路的等效变换【题1】:[解答]I =-+9473A =0.5 A ;U I a b .=+=9485V ; I U 162125=-=a b .A ;P =?6125. W =7.5 W;吸收功率7.5W 。


西安交通大学 面朝大海目 录附录一:电路试卷 ........................................................ 38 附录二:习题集部分答案 (58)第一章 电路模型和电路定律一、是非题 (注:请在每小题后[ ]内用"√"表示对,用"×"表示错).1. 电路理论分析的对象是电路模型而不是实际电路。
[ ] .2. 欧姆定律可表示成 u R i =?, 也可表示成u R i =-?,这与采用的参考方向有关。
[ ].3. 在节点处各支路电流的方向不能均设为流向节点,否则将只有流入节点的电流而无流出节点的电流。
[ ] .4. 在电压近似不变的供电系统中,负载增加相当于负载电阻减少。
[ ] .5.理想电压源的端电压是由它本身确定的,与外电路无关,因此流过它的电流则是一定的,也与外电路无关。
[ ] .6. 电压源在电路中一定是发出功率的。
[ ] .7. 理想电流源中的电流是由它本身确定的,与外电路无关。
因此它的端电压则是一定的,也与外电路无关。
[ ] .8. 理想电流源的端电压为零。
[ ] .9. 若某元件的伏安关系为u =2i+4,则该元件为线性元件。
[ ] .10. 一个二端元件的伏安关系完全是由它本身所确定的,与它所接的外电路毫无关系。
[ ] .11.元件短路时的电压为零,其中电流不一定为零。
元件开路时电流为零,其端电压不一定为零。
[ ] .12. 判别一个元件是负载还是电源,是根据该元件上的电压实际极性和电流的实际方向是否一致(电流从正极流向负极)。
当电压实际极性和电流的实际方向一致时,该元件是负载,在吸收功率;当电压实际极性和电流的实际方向相反时,该元件是电源(含负电阻),在发出功率 [ ].13.在计算电路的功率时,根据电压、电流的参考方向可选用相应的公式计算功率。
若选用的公式不同,其结果有时为吸收功率,有时为产生功率。
电路答案——本资料由张纪光编辑整理(C2-241 内部专用)第一章电路模型和电路定律【题 1】:由UAB 5 V可得: I AC 2.5A: U DB0 : U S12.5V。
【题 2】: D。
【题 3】: 300; -100 。
【题 4】: D。
【题5】:a i i1i 2;b u u1u2;c u u S i i S R S;d i i S 1R Su u S。
【题 6】: 3;-5 ; -8。
【题 7】: D。
【题 8】:P US150 W ;P US26W;P US30 ; P IS115 W ; P IS214W ;P IS315W。
【题 9】: C。
【题 10】:3; -3 。
【题 11】:-5 ; -13 。
【题 12】:4(吸收); 25。
【题 13】:0.4 。
【题 14】:31I 2 3; I 1A 。
3【题 15】:I43A; I23A; I31A; I5 4 A。
【题 16】:I7A;U35 V;X元件吸收的功率为 P UI245W。
【题 17】:由图可得U EB 4 V;流过 2电阻的电流 I EB 2 A;由回路ADEBCA列KVL得U AC 2 3I ;又由节点D列KCL得 I CD 4I ;由回路CDEC列KVL解得;I 3 ;代入上式,得 U AC7 V。
【题 18】:P122 I12;故 I 22; I 1I 2;P2I 221I 2⑴ KCL:4I 13I 1;I 18;U S 2I1 1 I 18V或16.V;或I I。
2 5 A512⑵ KCL:4I 13I1;I18A;U S。
224 V第二章电阻电路的等效变换【题 1】:[解答 ]94A = 0.5 A ;U ab9I 4 8.5 V;I73U ab66 125. W = 7.5 W ;吸收I 12 1.25 A;P功率 7.5W。
【题 2】:[解答 ]【题 3】:[解答]C 。
【题 4】: [ 解答 ]等效电路如图所示,I 005. A。
电路原理(邱关源)习题答案第二章-电阻电路的等效变换练习汇总第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻842R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA R R u i s 1082100212=+=+=V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。
第2章电阻电路的等效变换2.1 复习笔记一、电路等效变换基本概念等效电路:图2-1-1中N1和N2是两个内部结构和参数均不相同的一端口电路,若它端口上的u-i(伏安特性)相同,则称N1和N2对端口u-i关系而言是互为等效电路。
图2-1-1 等效电路的定义等效变换:根据分析、计算电路的需要,将网络的某一部分进行某种变换后,用一个与其不同的电路替代,且替代前后网络的其他部分电压、电流保持不变,这种方法称为电路的等效变换。
注意:①核心是“对外等效”。
②一个电路的等效电路可有许多个,实际中一般是求出最简的等效电路。
二、电阻的等效变换1.电阻的串联和并联(1)电阻的串联如图2-1-2所示,电阻串联时,等效电阻:R eq=R1+R2+…+R k+…+R n。
分压公式图2-1-2 电阻串联的等效(2)电阻的并联如图2-1-3所示,电阻并联时,等效电阻或G eq=G1+G2+…+G k+…+G n分流公式图2-1-3 电阻并联的等效2.△联结与Y联结的等效变换(1)Y联结如图2-1-4(a)所示为电阻的Y形联结,等效电阻的计算公式为Y形电阻=(△形相邻电阻的乘积)/(△形电阻的和)可得△联结→Y联结特别地,当R12=R23=R31=R△,R1=R2=R3=R△/3。
(2)△联结如图2-1-4(b)所示为电阻的△联结,等效电阻的计算公式为△形电阻=(Y形电阻两两乘积之和)/(Y形不相邻电阻)可得Y联结→△联结特别地,当R1=R2=R3=R Y时,R12=R23=R31=3R Y。
图2-1-4 电阻的△联结与Y联结3.平衡电桥电路电桥结构如图2-1-5所示,当R1R3=R2R4时,电桥平衡,此时,c点电位与f点电位相等,电阻R上电流为零,因此,电位相等的点可以短接,电流为零的支路可以断开,等效为图2-1-5(c)的形式。
注:平衡电桥的特点常用于计算电阻电路。
图2-1-5 电桥电路三、含源支路的的等效变换1.理想电源的串、并联理想电源的串并联等效电路如表2-1-1所示。
第二章电阻电路的等效变换
“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果
2-12)33(R R ∞=23,i i 。
解:(1)
2R 和3R 为并联,其等效电阻842R k ==Ω, 则总电流
mA R R u i s 3504210011=+=+= 分流有mA i i i 333.86502132====
(2)当∞=3R ,有03=i
(3)03=R ,有0,022==u i
2-2电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:
(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?
解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如33R R i R +32R R i R R s
+(2但1R 显然s i u s i 图(a 压is u 压源s u 4s 路中s u 中的电流。
2-3电路如图所示。
(1)求s o
u u ;(2)当(//212121R R R R R R R L +=>>时,s o u u 可近似为212
R R R +,此时引起的相对误差为
当L R 为)//(21R R 的100倍、10倍时,分别计算此相对误差。
解:(1)
L L R R R R R +⨯=22R R u i s +=1R R R u Ri u s
o +==1
所以s o u u =(2)设当100=K 10=K 时2-4==21G G 解:有
(b)图
中1G 和2G 所在支路的电阻
所以[][]Ω=+=+=322//2//34R R R R ab
(c)图可以改画为图(c1)所示,这是一个电桥电路,由于4321,R R R R ==处于电桥平衡,故开关闭合与打开时的等效电阻相等。
(d)图中节点1,1'同电位(电桥平衡),所以11'-间跨接电阻2R 可以拿去(也可以用短路线替代),故Ω=++=++=5.01//)11//()11(//)//()(12121R R R R R R ab
(e)图是一个对称的电路。
解法一:由于结点1与1',2与2'等电位,结点3,3,3'''等电位,可以分别把
(e2)则=R ab 所示,故12i i =得
i i 12=所以Ω===323R i u R ab ab
(f)图中(1,1,2)ΩΩΩ和(2,2,1)ΩΩΩ构成两个Y 形连接,分别将两个Y 形转化成等值的△形连接,如图(f1)和(f2)所示。
等值△形的电阻分别为
并接两个∆形,最后得图(f3)所示的等效电路,所以
(g)图是一个对称电路。
解法一:由对称性可知,节点1,1,1'''等电位,节点2,2,2'''等电位,连接等电位点,得图(g1)所示电路。
则
解法二:根据电路的结构特点,得各支路电流的分布如图(g2)所示。
由此得端口电压 所以Ω===667.165R i u R ab ab
(1(2(3
(4支路电流,通过一些网孔回路方程和结点方程确定支路电流分布系数,然后求出断口电压和电流的比值,得出等效电阻。
2-5在图(a)电路中,Ω=Ω=Ω===2,6,12,6,2432121R R R V u V u s s 。
图(b)为经电源变换后的等效电路。
(1)求等效电路的s i 和R ;
(2)根据等效电路求3R 中电流和消耗功率;
精心整理 (3)分别在图(a),(b)中求出2,1R R 及R 消耗的功率;
(4)试问21,s s u u 发出的功率是否等于s i 发出的功率?21,R R 消耗的功率是否等于R 消耗的功率?为什么?
解:(1)利用电源的等效变换,图(a)中电阻与电压源的串联可以用电阻与电流源的并联来等效。
等效后的电路如题解2-5图所示,其中 对题解2-5图电路进一步简化得图(b)所示电路,故
(2所以3R (3则21,R R (b)图中(4)(b)图中显然s i P ≠由(3的功率之和。
这充分说明,电路的“等效”概念仅仅指对外电路等效,对内部电路(变换的电路)则不等效。
2-6对图示电桥电路,应用∆-Y 等效变换求:(1)对角线电压U ;(2)电压ab U 。
解法一:把(10,10,5)ΩΩΩ构成的∆形等效变换为Y 形,如题解图(a)所示,其中各电阻值为:
由于两条并接支路的电阻相等,因此得电流
应用KVL 得电压V U 55.245.26=⨯-⨯=
又因入端电阻Ω=++++=30242)26//()44(ab R
所以V R U ab ab 1503055=⨯=⨯=
所示,把图(b)由图(c),5)Ω构成的Y 2-7(1)试证明当L R R R ==12时,L ab
R R =,且有5.0=in o u u ; (2)试证明当22121232L L R R R R R -=时,L ab R R =,并求此时电压比in o
u u 。
解:(1)当L R R R ==12时电路为一平衡电桥,可等效为题解图(a)所示电路,所以 即5.0=in o u u
(2)把由1R 构成的Y 形电路等效变换为∆形电路,原电路等效为题解图(b)。
其中
13R R =,因为22121122121122121222296332332//L L L L L L R R R R R R R R R R R R R R R R R R R R R -=+-⨯-=+=='
所以
2-8
Ω=,202R =,174A i s 中电压ab u 。
解。
其中
所以u ab =解其中
等效电流源为
等效电阻为
所以V R i u s ab 55.22-=⨯-=⨯=
注:应用电源等效互换分析电路问题时要注意,等效变换是将理想电压源与电阻的串联模型与理想电流源与电阻的并联模型互换,其互换关系为:在量值上满足s s u Ri =或s
s u i R =,在方向上有s i 的参考方向由s u 的负极指向正
极。
这种等效是对模型输出端子上的电流和电压等效。
需要明确理想电压源与理想电流源之间不能互换。
2-9利用电源的等效变换,求图示电路的电流i 。
解:利用电源的等效变换,原电路可以等效为题解图(a),(b)和(c),所以电流
2-10o
u u 把i R u 33=即103=s o u u 即33o
u i =又因24
13o
s u i -= 即2413o
s o u u u -=
所以s o u u 3.0=
注:本
题说明,当受控电压源与电阻串联或受控电流源与电阻并联时,均可仿效
2-11即i R +1122-12解图(a)故得a ,b 端的输入电阻
解(b):在(b)图的a ,b 端子间加电压源u ,如题解图(b)所示,由KVL 和KCL 可得电压[]12111211)1()(i R R i i R i R u β++=β++=
所以a ,b 端的输入电阻)1(211β++==R R i u R ab
注:不含独立源的一端口电路的输入电阻(或输出电阻)定义为端口电压和端口电流的比值,即in u
R i =。
在求输入电阻时,(1)对仅含电阻的
二端电路,常用简便的电阻串联、并联和Y -∆变换等方法来求;(2)对含有受控源的二端电阻电路,则必须按定义来求,即在端子间加电压源u (如本题的求解),亦可加电流源i ,来求得端口电压和电流的比值。
2-13
解图(a)有因1i =即
R +β+1(1解所示。
根据由KCL 3联立求解以上式子,可得u R u i R u μ+-=)(31
即
i R u R R 1311(=+μ- 故输入电阻133131
1
)1(1R R R R R R R i u R in +μ-=+μ-==
2-14图示电路中全部电阻均为Ω1,求输入电阻in R 。
解:a ,
b
在图(d)的端口加电压源u ,则有 即电路的输入电阻Ω==4.0i u R in。