角接触球轴承的静态接触分析

角接触球轴承姿态角工程分析西安交通大学(陕西西安　710049)　丁长安　沈　钺　朱　钧洛阳工学院(河南洛阳　471039)　周福章 襄阳汽车轴承股份有限公司(湖北襄樊　441022)　张　雷 【ABSTRACT】The solution of rolling element posture angle of angular contact ball bearing is always difficult question.In general,it can be calculated by Jones's race way contr ol theor y or solved by Gupta and Harris's dynamics theories.In practice,the researchers find that the racewa y control theor y is more avail for high speed and useless for medium and low speed.Because they are much complex and some dy-namic factors are difficult to be determined,the two dynamics theories ar e rarely adopted in practical ap-plication yet.The ne w postur e angle calculation method is established based on transient equilibrium principle in the paper.This method is avail for high,medium and low speed,and the calculation result is relatively rational.The brief and exact analysis method is provided for solution of angular contact ball bearing in general speed c ondition. 在角接触球轴承运动分析中,滚动体的速度分析占据重要位置,涉及滚动体角速度的有自转角速度、公转角速度、滚动角速度和自旋角速度,这些角速度随套圈的转速、滚动体与套圈之间的接触角以及滚动体姿态角的变化而变化。

混合陶瓷角接触球轴承静力分析喻炜（天津大学机械工程学院，天津300072）摘要：通过细化接触区局部网格建立兼顾精度和效率的混合陶瓷角接触球轴承局部有限元模型，分析该轴承受轴向载荷时的应力场，分析不同轴向载荷下该轴承的接触角、轴向趋近量、接触载荷和最大接触应力并与理论值对比。

结果显示接触角、轴向趋近量、接触载荷和最大接触应力的有限元分析（FEA）结果与理论计算结果吻合。

关键字：混合陶瓷球轴承；有限元法；静力分析；ABAQUS0 引言在高速工况下（DN值大于1M），陶瓷球轴承性能优于钢轴承，因为陶瓷密度只有钢的41%，陶瓷球所受离心力为钢球的41%。

由于陶瓷和钢材料性能上的差异，经典分析理论[1]不适用于陶瓷球轴承。

预测复杂工况下（如考虑摩擦、离心力、热效应）陶瓷球轴承的疲劳寿命需要知道轴承接触区表面下的应力场，一种可行思路是将稳态温度场、稳定运转工况下的球与套圈的接触载荷和接触角、摩擦等效加载于陶瓷球轴承静力分析有限元模型，这就需要以对简单载荷下陶瓷球轴承进行精确的静力分析为基础。

本文主要目标是建立兼顾精度和计算效率的混合陶瓷角接触球轴承三维有限元模型，为后续引入摩擦、热、离心效果的混合陶瓷球轴承有限元分析奠定基础。

用该模型分析轴向载荷对混合陶瓷角接触球轴承的接触载荷、接触应力、接触角和轴向弹性趋近量的影响，并将FEA结果与理论结果对比。

1 三维局部有限元模型1.1模型简化与假设为方便与Harris理论[1]比较，以混合陶瓷角接触球轴承7218B/HQ1为算例，所做简化与假设如下：(1)滚动轴承塑性变形小，假设材料为线弹性。

(2)不考虑倒角、圆角等对静力接触分析影响不大的几何特征。

(3)考虑只受轴向载荷，则每个球所受载荷相等，因此可取包含一个球的局部轴承模型进行分析。

(4)在静力分析中，保持架作用不大，因此，忽略保持架。

(5)静力分析中摩擦力对结果影响不大，不考虑摩擦。

轴承几何尺寸如表1所示，局部轴承模型如图1所示。

薄壁角接触球轴承接触应力分析与优化设计摘要薄壁角接触球轴承是广泛应用于工业机器人的关节轴承，它有着运转精度高，承载能力强，摩擦力矩低，薄壁，轻质等诸多特点。

机器人的地运转精度，平稳性，使用寿命，以及可靠性往往会受到轴承性能的影响。

为了我国能在工业机器人产业的道路上实现完全的自主，不再只依赖于进口国外的机器人精密零部件。

我们有必要对薄壁角接触球轴承进行应力分布情况以及该轴承使用的具体工况下的接触特性进行分析，并建立优化轴承寿命的数学模型。

为以后工业机器人用薄壁角接触球轴承的设计开发提供参考。

接触负荷对轴承的性能影响至关重要，尤其是承受载荷最大的滚动体更是直接影响到了轴承的承载和疲劳寿命。

因此轴承载荷分布在所有轴承设计和分析中都是不可或缺的。

在滚动轴承中需要受受载荷的滚动体个数一般都是两个或者以上，负荷分布属于静不定问题。

一般情况负荷分布都是根据变形协调条件求出每个接触位置的接触变形与轴承内外圈相对位移之间的关系。

依据Hertz接触理论建立接触弹性变形与接触负荷的数学模型。

最后写出关于位移变形间的力学平衡方程，通过解方程组来实现轴承各点负荷精确计算。

本文在计算轴承负荷分布时借助Excel软件对计算过程进行了编程，简化了计算过程，并且适用于所有刚性支撑的角接触球轴承负荷分布的计算。

本文根据以往的设计经验选取了一系列薄壁角接触球轴承设计主参数，并利用Excel结合轴承额定寿命计算公式编写了轴承寿命计算程序。

通过正交实验助设计正交试验并通过上述程序对每一水平下轴承寿命进行精确计算，并通过极差和方差分析确定最优设计参数至此完成对轴承寿命的优化设计本文建立了ZR76/82C机器人用薄壁角接触球轴的静态有限元模型。

由于该轴承应用于机器人主轴并且考虑到机器人主轴是空心轴这个特点对柔性约束下套圈变形情况借助ANSYS仿真软件进行了仿真分析，并与刚性约束下的情况做了对比分析并得出结论。

关键词：薄壁角接触球轴承，赫兹理论，负荷分布，仿真分析，寿命Contact Characteristic Analysis and Optimization Design of Thin-walled Angular Contact Ball BearingsABSTRACTThin-wall angular contact ball bearings are widely used in industrial robots. They have high running accuracy, strong bearing capacity, low frictional torque, thin-walled, lightweight and many other features. The ground motion accuracy, stability, service life, and reliability of the robot are often affected by bearing performance. In order to achieve full autonomy in the industrial robot industry in China and it is no longer only dependent on imported robotic precision parts. It is necessary to analyze the stress distribution of the thin-walled angular contact ball bearing and the contact characteristics under the specific working conditions of the bearing, and establish a mathematical model to optimize the bearing life. Provides reference for the design and development of thin-walled angular contact ball bearings for industrial robots.The impact of the contact load on the performance of the bearing is crucial. In particular, the rolling elements with the highest load are directly affecting the bearing load and fatigue life. Therefore, the bearing load distribution is indispensable in all bearing design and analysis. The number of rolling elements that need to be subjected to load in rolling bearings is generally two or more. The load distribution is static and indefinite. In general, the load distribution is based on the deformation coordination conditions to find the relationship between the contact deformation of each contact position and the relative displacement of the inner and outer rings of the bearing. Mathematical model of contact elastic deformation and contact load based on Hertz contact theory. Finally, the mechanical equilibrium equations between displacement and deformation are written, and the exact calculation of bearing load at various points can be achieved by solving equations. This paper uses Excel software to calculate the calculation process when calculating bearing load distribution, which simplifies thecalculation process and is applicable to the calculation of load distribution of angular contact ball bearings for all rigid supports.Based on the previous design experience,this paper selects a series of main parameters of thin-walled angular contact ball bearings,and uses Excel to calculate the bearing life calculation program based on the bearing rated life calculation formula. Orthogonal experiment was used to design orthogonal test and the above program was used to accurately calculate the bearing life of each level, and the optimal design parameters were determined through range and variance analysis to complete the optimal design of bearing life.In this paper, the static finite element model of thin-walled angular contact ball axle for ZR76/82C robot is established. Because the bearing is applied to the main shaft of the robot and considering that the main shaft of the robot is a hollow shaft, this paper analyzes the deformation of the ferrule under the flexible restraint using ANSYS simulation software, and compares and analyzes the situation under the rigid restraint and draws conclusions.KEY WORDS：Thin-walled Angular Contact Ball Bearings，Hertz theory，Load distribution，Simulation analysis，Life符号说明Cr ─径向基本额定动载荷，N ；Fr ─轴承径向载荷=轴承实际载荷的径向分量，N ；Fa ─轴承轴向载荷=轴承实际载荷的轴向分量，N ；Pr ─径向当量动载荷，N ；X ─径向当量动载荷系数；Y ─轴向当量动载荷系数；Z ─单列轴承的滚动体个数；b m ─当代常用高质量淬硬轴承钢和良好加工方法的额定系数，该值随轴承类型和设计不同而异；α─轴承公称接触角，度；Dw ─钢球直径，mm ；f c ─与轴承零件几何形状、制造精度及材料有关的系数；i ─轴承中滚动体的列数；d m ─滚动体节圆直径Q jq ─轴承中内圈或者外圈与第q 个滚动体之间的接触负荷；δjq ─轴承中内圈或者外圈与第q 个滚动体之间的接触变形量；K jq ─轴承内外圈与第q 个滚动体之间的负荷与变形常量，这个值与轴承几何特征及采用的材料有关；n ─指数，在于点接触轴承中n=3/2，对线接触轴承如滚子轴承：n=10/9； Q q ─在内外圈于滚动体的接触角相等时滚道与第q 个滚动体之间的接触负荷； δq ─当轴承内外接触角相等时第q 个滚动体与内外圈弹性变形的总值； Kn ─轴承内圈、外圈与滚动体之间的总的变形与负荷常量；─接触点的主曲率，mm -1；─弹性体接触变形系数；q ─轴承滚动体的序列号，定义在径向力作用下，受力最大的编号0。

角接触球轴承热特性分析及试验摘要：滚动轴承是机械行业中最普通、应用最广的零部件，在机械设备中起着至关重要的作用。

工程实际中，滚动轴承由于发热而引起的失效严重影响设备的正常工作。

因此，对轴承的温度场研究至关重要。

本文对角接触球轴承热特性及试验进行了重点阐述。

关键词：角接触球轴承；温度场；热位移一、角接触球轴承简介角接触球轴承(Angular Contact Ball Bearings)可同时承受径向、轴向负荷，能在较高的转速下工作。

接触角越大，轴向承载能力越高。

高精度和高速轴承通常取15?度接触角。

在轴向力作用下，接触角会增大。

单列角接触球轴承只能承受一个方向的轴向载荷，在承受径向载荷时，会引起附加轴向力，必须施向相应的反向载荷，因此，该种轴承一般都成对使用。

双列角接触球轴承能承受较大的以径向载荷为主的径向、轴向双向联合载荷和力矩载荷，它能限制轴或外壳双向轴向位移，接触角为30度。

成对安装角接触球轴承能承受以径向载荷为主的径向、轴向双向联合载荷，也可承受纯径向载荷。

串联配置只能承受单一方向的轴向载荷，其他两种配置则可承受任一方向的轴向载荷。

这种类型的轴承一般由生产厂商选配组合成对提交用户，安装后有预压过盈，套圈和钢球处于轴向预加载荷状态，因而提高了整组轴承作为单个支承刚度和旋转精度。

此外，角接触球轴承在负荷作用下，会自然形成接触角，可同时承受径向负荷和单向轴向负荷，承受负荷能力随接触角的大小而改变，接触角越大，承受轴向负荷能力也大，接触角分为15°、30°、40°。

另外，增加了钢球粒数，以获得更好的轴承强度，同时将内圈或外圈的一个挡边加工成斜坡形式，分离式不要锁量，非分离式就要设计一定锁量，以确保不散套，这种轴承常用在高速运转场所。

为了平衡轴向力，经常采用配对安装，故又有面对面、背对背及同方向三种形式，随着科技进步和轴承工作条件的不同，角接触球轴承具有多种结构形式。

二、轴承组件温度场仿真以轴承组件为研究对象，用solidworks取其四分之一进行建模，采用solid70单元进行网格划分，采用8节点单元，且每个单元只有一个温度自由度，进行三维稳态、瞬态热分析。

第40卷第6期2019年12月Vol.40No.6Dec.2019大连大学学报JOURNAL OF DALIAN UNIVERSITY基于ROMAX的深沟球轴承的静态仿真接触分析孙震震，李玉光：王淑芬，杨铎，李富强（大连大学机械工程学院，辽宁大连116622）摘要：在经典的深沟球轴承接触分析中，大都把钢珠、套圈、轴、轴承座视为是刚性曲，其变形是局部的；或者利用有限元分析软件进行有限元分析时把钢珠、套圈有限元化，忽略轴、轴承座对轴承的影响。

这两种情况都降低了深沟球轴承接触分析的准确性。

针对这种问题，将仿真软件ROMAX运用到深沟球轴承的静态接触分析中。

以KOYO6910深沟球轴承为例，采用ROMAX软件建模，并对所建的模型进行刚性分析和柔性分析，结果表明：ROMAX软件所建模型的刚性接触分析结果与经典理论计算结果具有一致性；柔性分析结果显示钢珠所受载荷更加均匀，套圈变形的起伏更小。

同时在该柔性模型的基础上分析了工作间隙对深沟球轴承接触载荷、接触变形的影响，为后续的轴承功耗损失研究提供参考。

关键词：深沟球轴承；ROMAX；柔性分析中图分类号：TH133.33文献标识码：A文章编号：1008-2395（2019）06-0021-06收稿日期：2019-10-31基金项目：国家自然科学基金（51405053）；航空动力装备振动及控制教育部重点、实验室开放课题基金（VCAME201805）…作者简介：孙震震（1990-）,男，硕士研究生，研究方向：机械设计及理论。

通讯作者：李玉光（1963-）,男，教授，研究方向：机械设计及理论。

0引言滚动轴承因为结构简单、摩擦因数小、制造成本低等优点而被大量应用于机械传动系统方面，其中，具代表性的是深沟球轴承深沟球轴承主要承受径向载荷，但一般的深沟球轴承都具有一定的内部间隙，施加轴向载荷时，深沟球轴承具有一定的角接触轴承的性能。

深沟球轴承不管承受径向载荷还是轴向载荷，都会有部分或全部的滚动体与内外圈轨道之间会产生不同的载荷及分布、接触应力、接触变形。

角接触球轴承的静态接触分析陈署泉,肖曙红,杨士铁(广东工业大学　机电工程学院,广州　510006)摘要:介绍了基于经典Hertz弹性接触理论的解析计算方法和有限元仿真分析法。

实例计算结果表明,在轴承工况相同的条件下,两种分析方法得到的接触特性参数的一致性较好,但各有特点。

解析计算法编程复杂、解算难度大,只能算出接触区的主参数,而有限元法边界设置十分复杂、技术性强,可仿真轴承接触区的工作状态,且表达形象、直观。

关键词:角接触球轴承;接触特性;Hertz弹性接触理论;有限元分析中图分类号:T H133.33 文献标志码:A 文章编号:1000-3762(2009)11-0004-04Ana lysis on Con t act Perfor mance of Angul ar Con t act Ba ll Bear i n gsCHEN Shu-quan,X I A O Shu-hong,Y ANG Shi-tie(Faculty of Mechanical&Electr onic Engineering,Guangdong University of Technol ogy,Guangzhou510006,China)Abstract:This paper intr oduces the analytic method based on the classical Hertz elasticity contact theory and finite ele2 ment analysis method.The results of the calculated examp le indicate that the contact characteristic para meters are very coincident under the sa me work conditi on.Both methods have their own features.Analytic method is comp licated in p r ogramm ing,and can only work-out the key parameters.I n FE M,the setup of finite element boundary conditi ons is very comp lex,which needs good technique.But FE M can si m ulate the work state visually and obvi ously in the contact area of the bearing.Key words:angular contact ball bearing;contact characteristic;Hertz elasticity contact theory;finite ele ment analysis 机床主轴用角接触球轴承,具有良好的速度性能和支承刚性,可以同时实现轴向和径向无间隙精密旋转[1]。

第36卷第12期中　国　科　学　技　术　大　学　学　报V ol.36,No.12 2006年12月JOURNAL OF U NI VERSITY OF SCIENC E AND TEC HNOLOGY OF C HINA Dec.2006文章编号:0253-2778(2006)12-1314-07过盈配合量和预紧力对高速角接触球轴承刚度的影响*王硕桂,夏源明(中国科学技术大学力学与机械工程系,安徽合肥230027)摘要:以滚动轴承拟静力学分析和滚道控制理论为基础,给出了计及轴承安装时的过盈配合量、预紧力等因素的影响,以及计算高速角接触球轴承中钢球与内、外圈的接触刚度和轴承整体的径向刚度、轴向刚度和角刚度的完整方法和相应的程序.对B7004轴承的分析表明:配合过盈量增加,钢球与内、外圈的接触刚度以及轴承的径向刚度增大,而轴承的轴向刚度和角刚度减小;预紧力增加,钢球接触刚度、轴承刚度随之增加;预紧力较小,特别当旋转速度较高时,应仔细选择合适的预紧力,否则轴承刚度会出现不稳定的波动.关键词:过盈配合;预紧力;接触刚度;轴承刚度中图分类号:TH133.33 文献标识码:AEffect of the interference fit and axial preload in the stiffnessof the high-speed angular contact ball bearingWANG Shuo-gui,XIA Yuan-ming(Dep t.o f Modern Mechan ics,Un iver sity of Science an d Technolog y o f Ch ina,He fei230027,Ch ina)A bstract:Based o n the pseudo statics analysis and racew ay co ntro l theo ry of the bearing,the com prehensive metho d and its corresponding pro gram w ere given for calculating co ntact rigidities betw een balls and racew ay s and radial,axial,angle rigidities o f the bearing by analysing the effect o f the interference fit and axial prelo ad,etc.The results from taking B7004bearing as an example show that the contact rigidities between balls and racew ays,radial rigidity of the bearing increase and axial,angle rigidities decrease as the interference fit increases;the co ntact rigidities and bearing rigidities increase with the increase of axial preload;w hen the axial preload is smaller,especially when the rotation speed is higher,the axial preload should be carefully selected,or the bearing rigidities will exhibit unstable fluctuatio ns.Key words:interference fit;ax ial prelo ad;contact rigidity;bearing rigidity0　引言在机械运转中,为了使套圈严格定位,高速滚动球轴承与轴以及轴承座孔需要采用过盈配合,使配合面不产生间隙,由此产生了设计手册中的过盈配合量数据和一些近似公式.文献[1～3]为了进一步考虑过盈配合对轴承结构参数的影响,把滚动轴承内圈和外圈与其相关件紧配合的问题看作轴对称的平面问题,讨论了内圈伸张量和外圈收缩量对滚动轴承工作游隙的影响.为了使旋转轴在轴向和径向正确定位,提高轴的旋转精度等,滚动轴承多需要加一定的预紧力,预紧力的大小一般应根据使用经验*收稿日期:2004-04-14;修回日期:2005-12-27基金项目:中国科学技术大学基础研究基金(KY1102)资助.作者简介:王硕桂(通讯作者),男,1967年生,博士/副教授.研究方向:轴承转子系统动力学.E-m ail:w s g@u 和通过试验决定[4].为了取得更好的预紧效果,文献[5～7]还对滚动轴承预紧的类型,预紧力的计算及预紧量的确定进行了深入的分析,给出了一些近似计算公式.实质上,轴承采用过盈配合安装及加预紧力后,不仅对轴承的定位、旋转精度及轴承的游隙有影响,对滚动轴承的接触角、轴承刚度、轴承内的载荷分布以及摩擦等都有影响.Jones提出了比较完整的滚动轴承拟静力学分析和滚道控制理论[8～10],在这一理论中首先提出了滚动轴承刚度矩阵的概念,并计及离心力及陀螺力矩对刚度的影响,能比较正确反映滚动轴承的刚度.文献[11]以滚道控制理论为基础,考虑轴承在外载荷作用下的拟静力学特性,计算了角接触球轴承的刚度并与实验结果比较,发现吻合较好.文献[12,13]利用钢球接触刚度的串并联关系计算了滚动轴承的刚度.但在这些工作中均未考虑滚动轴承的过盈配合和预紧力对轴承刚度的影响.由于滚动轴承的刚度性能是滚动轴承的重要使用性能,对被支承主轴转子的动力学性能有非常重要的影响[14～16],因此,尤其在高速的情况下,更需要较精确的滚动轴承刚度参数.本文以滚动轴承拟静力学分析和滚道控制理论为基础,计及安装时的过盈配合量、预紧力和轴的旋转速度等因素,给出高速角接触球轴承中钢球与内、外圈的接触刚度和轴承整体的径向刚度、轴向刚度和角刚度的完整计算方法,并且分析轴承安装时的过盈配合量、预紧力和轴的旋转速度对这些刚度的影响规律,为轴承转子动力学分析提供了基础.1　基本理论1.1　滚动轴承过盈配合安装后的位移及接触角的变化 高速滚动球轴承与轴以及轴承座孔的紧配合可看作厚壁筒问题.滚动轴承内圈与实心轴处于过盈配合时,内圈将膨胀,内圈沟底直径将增大;外圈与轴承座孔以过盈配合安装时,外圈将收缩,外圈沟底直径将减小.根据弹性力学可以得到内圈沟底直径增大量δF和外圈沟底直径减小量δE(取绝对值)的计算公式[3]:δF=dΔf1/D F,(1)其中,d为轴承内径,Δf1为轴与轴承内圈直径方向的过盈量,D F为内圈沟底直径.轴承外径为D,且当轴承座的壁厚较厚时有δE=2d EDΔf21-d ED21+d ED21-d ED2-μb+E bE h(1+μh),(2)其中,Δf2为轴承外圈与轴承座孔直径方向的过盈量,d E为外圈沟底直径,E b,E h,μb,μh分别为轴承和轴承座的弹性模量和泊松比.向心推力球轴承的原始接触角与轴承的径向游隙、滚道沟曲率半径系数和刚球直径的关系为[18]cosα0=1-u r2(f e+f i-1)D b,(3)其中,α0为原始接触角,f i,f e分别为轴承内、外圈沟道曲率半径系数,u r为径向游隙,D b为钢球直径.当轴承以过盈配合安装后,考虑过盈配合安装位移对间隙的影响,如果定义此时的接触角为配合接触角α′,根据式(1)～(3),则有cosα′=1-u r-(δF+δE)2(f e+f i-1)D b.(4) 轴承与轴、轴承座安装好后,需要加一定的预紧力,在预紧力作用下,接触变形将使内外圈产生轴向位移,这时的接触角α与预紧前接触角α′之间的关系为[18]F a0Kn1.5Z(G D b)1.5=sinαco sα′cosα-11.5,(5)其中,F a0为轴向预紧力,G=f i+f e-1,Z为钢球数.1.2　赫兹接触刚度及轴承刚度参数由赫兹接触理论,两接触物体的接触载荷和弹性趋近量之间的关系为[17,18]:δ=F9∑ρ2π2e2E2L1/3Q2/3,(6)其中,2E=1-μ21E1+1-μ22E2;δ为两接触物体的弹性趋近量,F为第一类椭圆积分,L为第二类椭圆积分,∑ρ为两接触物体接触点在主平面内的曲率和,e为椭圆率参数(接触椭圆长半轴与短半轴之比),Q为两接触物体的接触载荷,E为两接触物体等效弹性模量,E1,E2,μ1,μ2分别为两接触物体的弹性模量和泊松比.文献[17]借助最小二乘法用线性回归得到了1315第12期过盈配合量和预紧力对高速角接触球轴承刚度的影响e ,F ,L 的下列简化方程:e =1.0339(R y /R x )0.636,(7)F =1.5277+0.60231n (R y /R x ),(8)L =1.0003+0.5968(R x /R y ).(9)其中,R x =1/(ρ11+ρ21),R y =1/(ρ12+ρ22);ρ11,ρ21,ρ12,ρ22分别为两接触物体的曲率.必须指出,R x ,R y 与接触角α相关.对式(6)关于Q 求导,可以得到赫兹接触刚度:K =1.5πeE3F2/32L F∑ρ1/3Q 1/3.(10) 如果已知球与沟道的接触角和接触载荷,利用式(10)可以求得每个球与内、外圈沟道的接触刚度:K ij =1.5πe ij E 3F ij 2/32L ij F ij ∑ρ1/3Q 1/3i ,K ej =1.5πe ej E 3F ej 2/32L ej F ej ∑ρ1/3Q 1/3e .(11) 式(11)即为计及轴承安装过盈配合量、预紧力影响的钢球接触刚度的表达式,显然,该式可直接推广到稳定旋转状态,只是相关的参数应采用动态参数,式中的下标i ,e ,j 分别表示内、外圈和第j 个钢球.由图1可知,第j 个钢球与内、外圈沟道接触刚度的径向分量和轴向分量为[12,13]K rij =K ij co s 2αij ,K a ij =K ij sin 2αij ,(12)K rej =K ej cos 2αej ,K a ej =K ej sin 2αej .(13)其中,K r i j ,K rej 分别表示第j 个钢球与内、外圈的接触刚度的径向分量;K aij ,K aej 分别表示第j 个钢球图1　钢球与内、外圈接触刚度Fig.1　Co ntact rig iditie s between balls and raceway s与内、外圈的接触刚度的轴向分量;αij ,αej 分别为第j 个钢球处于旋转状态时与内圈、外圈之间的动态接触角.利用轴承中所有Z 个球的接触刚度串并联关系,可得到轴承的径向刚度K r ,轴向刚度K a 和角刚度K θ为K r =∑Zj =1K rij K r ej Krij +K rej co s 22πZ(j -1),(14)K a =∑Zj =1K a ij K a ej K aij +K aej,(15)K θ=D 2m 4∑Zj =1K aij K aejK a ij +K a ej cos 22πZ (j -1).(16) 式(14)～(16)即为计及轴承安装过盈配合量、预紧力影响的轴承刚度的表达式,D m 为轴承中心圆直径,但为了求出球与沟道的动态接触角和接触载荷,须用以下拟静力学分析和滚道控制理论.1.3　拟静力学分析和滚道控制理论1.3.1　变形几何相容方程对于角接触球轴承,根据轴承的受载情况建立坐标系,如图2所示.另外,还建立钢球的坐标系图2　轴承受载示意图Fig.2　Schematic of the bea ring load(图3).在图3中,固定外圈沟曲率中心为坐标原点,根据变形几何关系,确定第j 个钢球中心位置的变化有以下关系式[18]:x 2aj +x 2rj -[(f e -0.5)D b +δej ]2=0,　(17)(A aj -x aj )2+(A rj -x rj )2-　[(f i -0.5)D b +δij ]2=0.(18)其中,x aj ,x rj ,A ai ,A rj 分别为外滚道曲率中心与第j个钢球球心最终位置和内滚道曲率中心的水平、垂直距离;f i ,f e 分别为轴承内外圈沟道曲率半径系数;δij ,δej 分别为第j 个钢球与内外滚道的接触弹性趋近量.1316中国科学技术大学学报第36卷图3　球中心和沟道曲率中心的相对位置Fig.3　Relativ e po sitio n of the balland race curv ature ce nter1.3.2　钢球拟静力学分析滚动轴承转速较高时,一般均属于外滚道控制,对于第j 个钢球而言,在稳定工况下,钢球的离心力F cj ,钢球自转引起的陀螺力矩M gj ,以及内外滚道对钢球的法向力Q ij ,Q ej 组成平衡力系,平衡方程式为Q ij sin αij -Q ej sin αej +2M gj D b cos αej =0,(19)Q ij co s αij -Q ej co s αej -2M gjD bsin αej +F cj =0.(20)其中,Q ij ,Q ej 分别为第j 个钢球与内圈、外圈之间的法向接触载荷.1.3.3　轴承拟静力学平衡在惯性坐标系中,轴承内圈的载荷与轴承内圈反作用与轴上载荷应该保持静力学平衡的关系.所以有方程:F a -∑Zj =1Q ijsin αij =0,(21)F r -∑Z j =1Qijcos αij =0,(22)M y -∑Zj =1Qijsin (αij )R i =0.(23)其中,F a ,F r ,M y 为轴承承受的轴向负荷、径向负荷和力矩负荷,Z 为钢球数.2　轴承刚度的数值计算方法和程序要求出滚动轴承在稳定运转状态时的刚度参数,必须求解方程(17)～(20)及方程(21)～(23)组成的非线性方程组,对于这样的非线性方程组,显然不可能给出解析解,只能用数值解法.本文给出如流程图4所示的数值解法,图中轴承位移值的修正和球心坐标值的修正均采用牛顿-拉费逊方法.图4　轴承刚度计算流程图Fig.4　Co mputa tion flo wchart o f the bearing stiffness3　计算结果及分析本文对高速角接触球轴承B7004进行了计算,轴承的原始参数列在表1中,轴承材料为钢,轴承座材料为铸铁,所有计算结果列在图5～13中.表1　高速角接触球轴承B7004的原始参数Tab.1　T he initial pa rameters of the hig h -speedang ular contact ball bearing (B7004)轴承内径d /mm20轴承外径D /m m 42球直径D b /mm 5.5中心圆直径D m /mm 31内圈沟半径r i /m m 2.970外圈沟半径r e /mm 3.135原始接触角/(°)15球数Z13图5、图6为预紧力F a 0=30N ,n =15000r /min 时钢球(j =1)接触刚度随过盈量的变化,图7、图8、图9分别表示预紧力F a 0=30N ,n =15000r /min 时轴承径向刚度、角刚度、轴向刚度随过盈量1317第12期过盈配合量和预紧力对高速角接触球轴承刚度的影响图5　钢球与内圈接触刚度随过盈量的变化(j=1) Fig.5　Change o f the co ntact rigidity between ball and inner ring w ith the shrink range(j=1)图6　钢球与外圈接触刚度随过盈量的变化(j=1) Fig.6　Change o f the co ntact rig idity betw een ball and o ute r ring with the shrink rang e(j=1)图7　轴承径向刚度随过盈量的变化Fig.7　Change of the bearing radial rig idityw ith the shrinkrange图8　轴承角刚度随过盈量的变化Fig.8　Chang e of the bearing ang ular rig iditywith the shrink r ange图9　轴承轴向刚度随过盈量的变化Fig.9　Change of the bearing axial stiff nesswith the shrink rang e的变化.从图5～图9可以看出:高速下钢球与内、外圈的接触刚度以及轴承的径向刚度随过盈量的增加而增大;轴承的轴向刚度和角刚度随过盈量的增加而减小.这是由于过盈量增加,轴承间隙减小,接触角减小,一方面导致钢球与滚道沟道的接触刚度增加,从而轴承径向刚度增加;另一方面接触角的减小,导致轴承轴向刚度、角刚度减小.图10为预紧力F a0=30N,n=40000r/min时轴承轴向刚度随过盈量的变化,图11为预紧力F a0=60N,n=40000r/min时轴承轴向刚度随过盈量的变化.从图9～11可以看出:当预紧力F a0=30N,轴的转速从15000r/min增加到40000r/min时,轴承的轴向刚度出现不规则的波动;当F a0增加到60N时,波动消失.所以,高速旋转轴承需要一定的预紧力,否则轴承在运转的过程中会出现不稳定性.对于本文计算用的轴承,制造厂推荐在轻载情况下预紧力为60～100N,这与本文计算结果是一致的.1318中国科学技术大学学报第36卷图10　轴承轴向刚度随过盈量的变化Fig.10　Change o f the bearing axial stiffnesswith the shrink range图11　轴承轴向刚度随过盈量的变化Fig.11　Change o f the bearing axial stiffnesswith the shrink range图12　钢球接触刚度随转速的变化(j =1)Fig.12　Chang e of the bea ring co ntact stiffnesswith the r otate speed (j =1)图12为预紧力F a 0=100N ,轴与轴承内圈及轴承外圈与轴承座孔的过盈量均为0.004mm 时,钢球接触刚度随转速的变化.从中可以看出:旋转速度提高,球的离心力增加,球与外圈沟道的接触角变小,接触载荷增加,导致球与外圈沟道法向接触刚度增加;同时球与内圈沟道的接触角变大,球与内圈沟道法向接触刚度减小.图13为转速n =40000r /min ,轴与轴承内圈及轴承外圈与轴承座孔的过盈量均为0.004mm 时,轴承径向刚度和轴向刚度随预紧力的变化.从中可以看出:预紧力增加,轴承径向刚度和轴向刚度随之增加.这是由于预紧力增加,不仅提高了球与内外圈沟道的接触角,而且提高了球与内外圈沟道的接触载荷,从而提高钢球接触刚度、轴承的径向刚度、轴向刚度.图13　轴承径向刚度、轴向刚度随预紧力的变化Fig.13　Change of the radial and ax ial stiffnessw ith the pretig htening fo rce4　结论本文给出了对于高速角接触球轴承计及轴承内外圈过盈配合量和轴向预紧力影响时,计算钢球与内、外圈的接触刚度和轴承整体的径向刚度、轴向刚度和角刚度的完整方法,编写了相应的程序.该方法和程序对其他类型的球轴承也适用.用该方法和程序分析研究了过盈量、轴向预紧力等因素对B7004轴承诸刚度的影响,这些影响可归纳为以下规律:配合过盈量的增加,钢球与内、外圈的接触刚度以及轴承的径向刚度增大,而轴承的轴向刚度和角刚度减小;预紧力增加,钢球与内、外圈的接触刚度以及轴承径向刚度、轴向刚度和角刚度随之增加;特别当预紧力较小且轴的旋转速度较高时,轴承刚度会出现波动.实际应用中,通常加一定的预紧力以提高滚动轴承的刚度,进而提高轴的旋转精度,减小振动等,这与计算结果是一致的.同时从计算结果还可以看出:过盈量、轴向预紧力等因素对角接触球轴承径向刚度、轴向刚度和角刚度的影响,是由于这些因素变化时,角接触球轴承接触角变化,导致钢球与滚道沟道的接触刚度变化,进而对外表现为轴承径向刚度、轴向刚度和角刚度的变化.1319第12期过盈配合量和预紧力对高速角接触球轴承刚度的影响参考文献(References)[1]王树梅,孙林,童燕.滚动轴承工作游隙的计算方法[J].轴承,1984,(2):1-8.[2]方希铮.高速精密轴承的一种设计方法[J].轴承,1984,(4):1-10.[3]冈本纯三.球轴承的设计计算[M].北京:机械工业出版社,2003.[4]刘泽九,贺士荃.滚动轴承的额定负荷与寿命[M].北京:机械工业出版社,1982.[5]姜韶峰,刘正士,杨孟祥.角接触球轴承的预紧技术[J].轴承,2003,(3):1-4.[6]贾群义.角接触球轴承预紧量的计算及选择[J].轴承,1996,(1):5-7.[7]侯广军.角接触球轴承预加载荷值的计算、实施与测量[J].磨床与磨削,2000,(1):49-51.[8]Jones A B.T he mathematical theory of rolling elementsbearings[M]//M echanical Design and Systems Handbo ok.N ew York:M cGraw-Hill,1966,13:1-76. [9]Jo nes A B,M cG ro n J M.Ro tor-bearing dy namicstechnology desig n g uide.P art2:Ball bea rings[R].O H:Wright Patter so n A ir Fo rce A ero P ropulsio n Lab,A F AP L-T R-78-6:1-62.[10]Jones A B.A general theory fo r ela stically constrainedball and radial rolle r bea ring s[J].T rans.A SM E,J.Ba sic Eng.,1960,82:309-320.[11]陈宗农,董荣歌.角接触球轴承静态刚度计算[J].轴承,1993,(3):2-7.[12]H arris T A.Ro lling Bearing Analy sis[M].3rd ed..N ew Yo rk:John W iley and So ns,I nc.,1990.[13]邱明,蒋兴奇,杜迎辉,等.高速精密角接触球轴承刚度计算[J].轴承,2001,(11):5-8.[14]Kim S M,Lee K J,Lee S K.Effect o f bearing suppor tstructure on the hig h-speed spindle bearing compliance[J].Internatio nal Jour nal of M achine T ools a ndM anufacture,2002,42(3):365-373.[15]M ekid S.High precisio n linear slide.P art I:De sig nand constructio n[J].Inter national Journal of M achineT o ols and M anufacture,2000,40(7):1039-1050. [16]Ganesan R.Dynamic response and stability of a ro to r-support sy stem with non-sy mmetric bearing clearances[J].M echanism and M achine Theo ry,1996,31(6):781-798. [17]哈姆罗克B J,道森D.滚动轴承润滑[M].北京:机械工业出版社,1988.[18]万长森.滚动轴承的分析方法[M].北京:机械工业出版社,1987.(上接第1284页)[8]Lux T,M a rchesi M.Scaling and criticality in asto cha stic multi-agent mode l o f a financial market[J].Na ture,1999,397(6719):498-500.[9]Co nt R.Empirical pro per ties o f a sset returns:stylizedfacts and statistica l issues[J].Q uantitativ e Finance,2001,1(2):223-236.[10]Z ho u T,Zhou P L,W ang B H,et al.M odeling sto ckmarket ba sed on genetic cellular automata[J].Int.J.M od.P hy s.B,2004,18:2697-2702.[11]Lévy H,Lévy M,Solo mon S.M icro sco pic Simulatio nof Fina ncial M arkets[M].N ew Yo rk:Academic P ress,2000.[12]Z HO U Pei-ling,Y AN G Chun-x ia,Z HO U T ao.Analy zing the chao tic behavior of an a rtificial sto ck ma rket[J].Journal of U niver sity o f Science and T echnolog y of China,2004,34(4):442-443.周佩玲,杨春霞,周涛.虚拟股市建模与混沌分析[J].中国科学技术大学学报,2004,34(4):442-443.[13]Yang C X,Zhou T,Zhou P L,et al.Study o nev olvement co mplexity in an artificial sto ck market[J].Chin.Phys.Lett.,2005,22:1014-1017.[14]Scafetta N,Grig olini P.Scaling de tection in timese ries:Diffusio n entr opy analy sis[J].Phys.Rev.E,2002,66:036130.[15]Y ang H J,Z hao F C,Qi L Y,et al.Tempo ral seriesanaly sis appro ach to spectra of complex netw or ks[J].P hy s.Rev.E,2004,69:066104.[16]Y ang H J,Z hao F C,Zhang W,et al.Diffusio n entro pyapproach to com plexity for a Hodg kin–Hux leyneuron[J].Physica A:Statistical and T heo reticalP hy sics,2005,347:704-710.[17]Peng C K,Buldy rev S V,H avlin S,et al.M o saico rga nizatio n of D NA nucleotides[J].P hy s.Rev.E,1994,49:1685-1689.[18]H urst H E,Black R P,Simaika Y M.L ongter msto rage:A n e xperimental study[M].L ondo n: Constable,1965.[19]Feders J.F ractals[M].New Yo rk:PlenumP ublisher s,1988.[20]Ig naccolo M,A lleg rini P,G rig olini P,e t al.Scaling innon-statio nary time se ries.(Ⅰ)[J].Phy sica A: Statistica l and Theo retical Physics,2004,336:595-622.[21]Dow Jones I ndustrial A verag e Inde x[EB/O L].http:///hq s=%5EDJI.[22]Ig naccolo M,A lleg rini P,G rig olini P,e t al.Scaling innon-statio nary time series(Ⅱ):T een birthphenomenon[J].Physica A:Statistical M echanics a ndits A pplicatio ns,2004,336:623-637.1320中国科学技术大学学报第36卷。

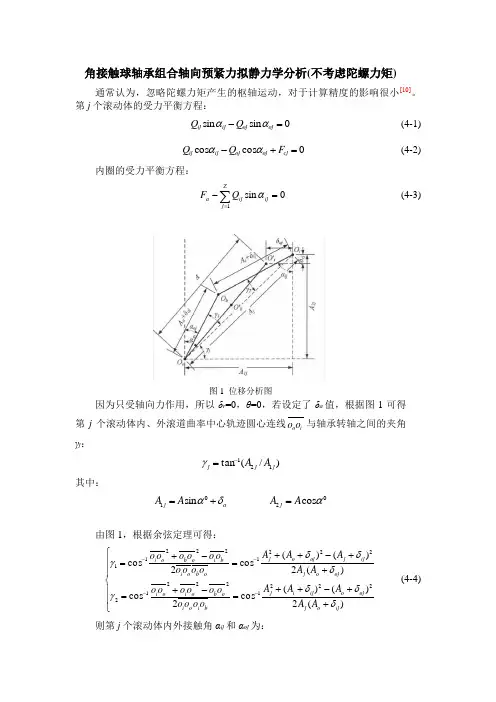
角接触球轴承组合轴向预紧力拟静力学分析(不考虑陀螺力矩)通常认为，忽略陀螺力矩产生的枢轴运动，对于计算精度的影响很小[10]。

第j 个滚动体的受力平衡方程：0sin sin =-oj oj ij ij Q Q αα (4-1) 0cos cos =+-cj oj oj ij ij F Q Q αα (4-2)内圈的受力平衡方程：∑==-Zj ij ij a Q F 10sin α (4-3)图1 位移分析图因为只受轴向力作用，所以δr =0，θ=0，若设定了δa 值，根据图1可得第j 个滚动体内、外滚道曲率中心轨迹圆心连线i o o o 与轴承转轴之间的夹角γj ：)/(tan 121j j j A A -=γ其中：a j A A δα+=01sin 02cos αA A j =由图1，根据余弦定理可得：⎪⎪⎩⎪⎪⎨⎧++-++=-+=++-++=-+=----)(2)()(cos 2cos )(2)()(cos 2cos222122212222122211ij o j oj o ij i j bi o i o b o i o i oj o j ij j oj o j o b o i bi o b o i A A A A A o o o o o o o o o o A A A A A o o o o o o o o o o δδδγδδδγ (4-4) 则第j 个滚动体内外接触角αij 和αoj 为：⎪⎩⎪⎨⎧--=+-=122/2/γγπαγγπαj oj j ij (4-5) 由赫兹接触理论可得：⎪⎩⎪⎨⎧==5.15.1ojoj oj ijij ij K Q K Q δδ (4-6) 若设定了δa 的值，在每一个角位置处，结合式(4-4)-(4-6)，可对式(4-1)和(4-2)进行求解得到αij 、αoj 及δij 、δoj 。

δa 的迭代方法选两种(1)渐变(2)采用公式(4-3)重新计算δa 。