第5章凸轮典型例题
- 格式:pdf
- 大小:201.55 KB
- 文档页数:10

凸轮机构习题及答案凸轮机构习题及答案凸轮机构是机械工程中常见的一种机构,广泛应用于各种机械设备中。
它通过凸轮的运动来驱动其他机构实现特定的功能。
在学习凸轮机构的过程中,习题是一个很好的辅助工具,可以帮助我们更好地理解和掌握凸轮机构的原理和应用。
下面,我们将介绍一些凸轮机构的习题及其答案,希望对大家有所帮助。
习题一:一个凸轮的基圆半径为30mm,凸轮半径为40mm,凸轮的转角为60°,求凸轮的凸度。
解答:凸度是指凸轮上凸起部分的最大高度。
根据凸度的定义,我们可以得到凸度与凸轮的基圆半径、凸轮半径和凸轮的转角之间的关系式:凸度 = 凸轮半径 - 基圆半径代入已知条件,可得:凸度 = 40mm - 30mm = 10mm所以,凸轮的凸度为10mm。
习题二:一个凸轮的基圆半径为25mm,凸轮半径为40mm,凸轮的转角为90°,求凸轮的凸度。
解答:同样地,我们可以利用凸度的定义来求解这个问题。
代入已知条件,可得:凸度 = 40mm - 25mm = 15mm所以,凸轮的凸度为15mm。
习题三:一个凸轮的基圆半径为20mm,凸轮半径为50mm,凸轮的转角为120°,求凸轮的凸度。
解答:按照前面的方法,我们可以得到:凸度 = 50mm - 20mm = 30mm所以,凸轮的凸度为30mm。
通过以上几个习题,我们可以看到凸度与凸轮的基圆半径、凸轮半径和凸轮的转角之间的关系。
凸度越大,凸轮上的凸起部分越高,相应地,凸轮的运动也会更加剧烈。
除了凸度,凸轮机构还有其他一些重要的参数,比如凸轮的轴心偏距、凸轮的转速等。
在实际应用中,我们需要综合考虑这些参数,以确保凸轮机构的正常运行。
此外,凸轮机构还有一些常见的应用,比如在汽车发动机中,凸轮机构用于控制气门的开闭;在纺织机械中,凸轮机构用于控制织机的工作节奏等等。
凸轮机构的应用非常广泛,对机械工程师来说是一项重要的技术。
综上所述,凸轮机构是机械工程中一种常见的机构,通过凸轮的运动来驱动其他机构实现特定的功能。


第1章 平面机构的结构分析解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题图 题图绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
计算下列机构自由度,并说明注意事项。
计算下列机构的自由度,并确定杆组及机构的级别(图a 所示机构分别以构件2、4、8为原动件)。
题图题图第2章 平面机构的运动分析试求图示各机构在图示位置时全部瞬心。
题图在图示机构中,已知各构件尺寸为l AB =180mm , l BC =280mm , l BD =450mm , l CD =250mm , l AE =120mm , φ=30o , 构件AB 上点E 的速度为 v E =150 mm /s ,试求该位置时C 、D 两点的速度及连杆2的角速度ω2 。
在图示的摆动导杆机构中,已知l AB =30mm , l AC =100mm , l BD =50mm , l DE =40mm ,φ1=45o ,曲柄1以等角速度ω1=10 rad/s 沿逆时针方向回转。
求D 点和E 点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题图题图在图示机构中,已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30o, 角速度ω1=10 rad/s ,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题图图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
(3)在给出的速度和加速度图中,给出构件2上D 点的速度矢量2pd 和加速度矢量2''d p 。

机械原理凸轮机构习题与答案(五篇材料)第一篇:机械原理凸轮机构习题与答案解:曲柄的存在的必要条件是1)最短杆与追长杆的杆长之和应小于或等于其余两杆的长度之和;2)连架杆与机架必有最短杆1).杆件1为曲柄2).在各杆长度不变的情况下,选取c杆做为机架就可以实现双摇杆机构试以作图法设计一偏置尖底推杆盘形凸轮的轮廓曲线。
已知凸轮以等角速度顺时针回转,正偏距e=10,基园半径r0=30mm.推杆运动规律为:凸轮转角δ=0~150时,推杆00.凸轮转角δ=180~300时推杆等速上升16mm;.凸轮转角δ=150~180时推杆远休;等加速回程16mm;.凸轮转角δ=300~360时推杆近休。
解:解题步骤1)首先绘制位移S与转角δ的关系曲线S-δ曲线。
2)根据S-δ曲线、凸轮基园半径和正偏距,绘制凸轮的轮廓曲线。
000000凸轮仅用了0度,90度,150度,180度,300度几个点绘制轮廓曲线,同学们绘制时英多用些点(一般取12个点,再勾画轮廓曲线)第二篇:机械原理_凸轮机构设计机械原理课程设计——凸轮机构设计(一)目录 (1)_________________________(一)、题目及原始数据 (2)(二)、推杆运动规律及凸轮廓线方程 (3)(三)、(四)、(五)、(六)、(七)、(八)、计算程序方框图..........................5 计算源程序..............................6 程序计算结果及分析......................10 凸轮机构图..............................15 心得体会................................16 参考书. (16)(一)、题目及原始数据试用计算机辅助设计完成偏置直动滚子推杆盘形凸轮机构的设计,凸轮以1rad/s的角速度沿逆时针方向转动。
要求:(1)、推程运动规律为等加速等减速运动,回程运动规律为五次多项式运动规律;(2)、打印出原始数据;(3)、打印出理论轮廓和实际轮廓的坐标值;(4)、打印出推程和回程的最大压力角,以及出现最大压力角时凸轮的相应转角;(5)、打印出凸轮实际轮廓曲线的最小曲率半径,以及相应的凸轮转角;(6)、打印出凸轮运动的位移;(7)、打印最后所确定的凸轮的基圆半径。
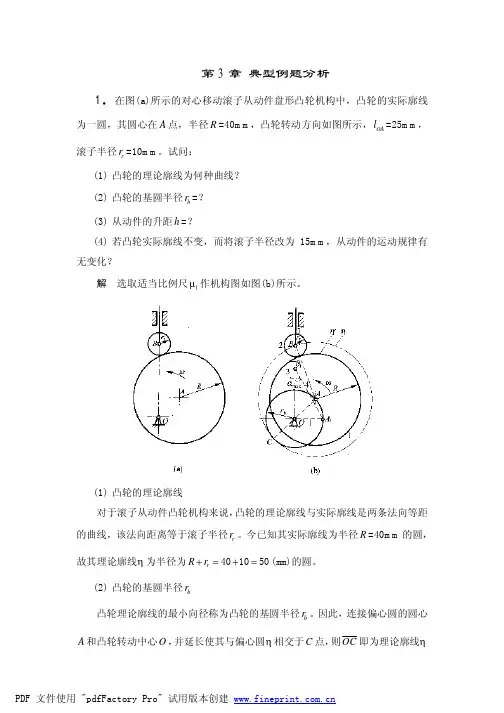
第3章 典型例题分析1.在图(a)所示的对心移动滚子从动件盘形凸轮机构中,凸轮的实际廓线为一圆,其圆心在A 点,半径R =40mm ,凸轮转动方向如图所示,OA l =25mm ,滚子半径r r =10mm 。
试问:(1) 凸轮的理论廓线为何种曲线?(2) 凸轮的基圆半径b r =?(3) 从动件的升距h =?(4) 若凸轮实际廓线不变,而将滚子半径改为15mm ,从动件的运动规律有无变化?解 选取适当比例尺l µ作机构图如图(b)所示。
(1) 凸轮的理论廓线对于滚子从动件凸轮机构来说,凸轮的理论廓线与实际廓线是两条法向等距的曲线,该法向距离等于滚子半径r r 。
今已知其实际廓线为半径R =40mm 的圆,故其理论廓线η为半径为401050r R r +=+=(mm)的圆。
(2) 凸轮的基圆半径b r凸轮理论廓线的最小向径称为凸轮的基圆半径b r 。
因此,连接偏心圆的圆心A 和凸轮转动中心O ,并延长使其与偏心圆η相交于C 点,则OC 即为理论廓线η的最小向径,它即为凸轮的基圆半径b r 。
由图(b)可知()(4010)2525b AC AO AO r l l R r l =−=+−=+−=(mm)(3) 从动件的升距h从动件上升的最大距离h 称为从动件的升距,它等于理论廓线η的最大和最小向径之差。
因此,()2540102550OA r b h l R r r =++−=++−=(mm)(4) 滚子半径改为15mm 后从动件的运动规律当凸轮的实际廓线η′保持不变,而将滚子半径r r 由10mm 增大至15mm 后,连杆长度AB l 将随之由50mm 增至55mm ,因此从动件将随之变化。
若希望从动件3的运动规律保持不变,正确的做法是让理论廓线η保持不变,作该理论廓线的法向等距离曲线,并使之距离等于15mm ,得到新的实际廓线。
2.某技术人员欲设计一台打包机,其推送包装物品的机构如图1所示。
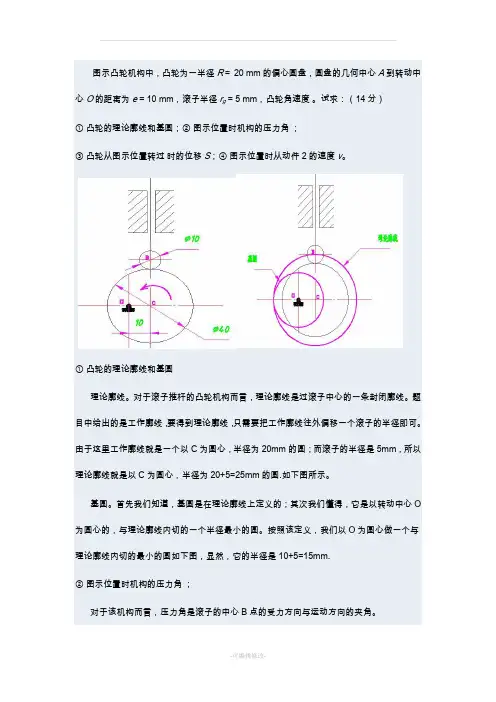
图示凸轮机构中,凸轮为一半径R=20 mm的偏心圆盘,圆盘的几何中心A到转动中心O的距离为e= 10 mm,滚子半径r g= 5 mm,凸轮角速度。
试求:(14分)①凸轮的理论廓线和基圆;②图示位置时机构的压力角;③凸轮从图示位置转过时的位移S;④图示位置时从动件2的速度v。
①凸轮的理论廓线和基圆理论廓线。
对于滚子推杆的凸轮机构而言,理论廓线是过滚子中心的一条封闭廓线。
题目中给出的是工作廓线,要得到理论廓线,只需要把工作廓线往外偏移一个滚子的半径即可。
由于这里工作廓线就是一个以C为圆心,半径为20mm的圆;而滚子的半径是5mm,所以理论廓线就是以C为圆心,半径为20+5=25mm的圆.如下图所示。
基圆。
首先我们知道,基圆是在理论廓线上定义的;其次我们懂得,它是以转动中心O 为圆心的,与理论廓线内切的一个半径最小的圆。
按照该定义,我们以O为圆心做一个与理论廓线内切的最小的圆如下图,显然,它的半径是10+5=15mm.②图示位置时机构的压力角;对于该机构而言,压力角是滚子的中心B点的受力方向与运动方向的夹角。
B点的速度方向。
由于B点是推杆与滚子的连接点,所以它也就是推杆上的B点。
由于推杆在上下平移,推杆上任何一点的轨迹都是沿着推杆的直线,所以任何一点的速度方向都是推杆直线的方向,因此推杆上的B点速度方向也在该直线上。
B点的受力方向。
推杆上的B点与理论廓线接触,在忽略摩擦的前提下,其受力方向其实就是理论力学中的光滑接触面中的反力方向。
光滑接触面的反力是公法线方向。
由于推杆的B点是尖点,无所谓法线,所以公法线方向就是理论廓线在该点的法线方向。
而理论廓线是一个圆,圆上任何一点的法线方向都是从从该点指向圆心的。
所以BC的方向就是公法线方向。
显然,速度方向与力的方向重合,所以压力角是0度。
这是我们最希望的压力角。
压力角越小,则凸轮机构的传力性能越好。
③凸轮从图示位置转过时的位移S;对于这种问题,总是用反转法通过作图测量出来的。

第5章凸轮机构1.从动件的运动规律:等速,等加速等减速,余弦加速度,正弦加速度2.动力特性:刚性冲击,柔性冲击3.设计原理:反转法,比例尺,等分基圆,偏置从动件压力角与自锁条件4.基本参数:基圆半径,滚子半径,平底尺寸【思考题】5-1 凸轮机构的应用场合是什么?凸轮机构的组成是什么?通常用什么办法保证凸轮与从动件之间的接触?5-2 凸轮机构分成哪几类?凸轮机构有什么特点?5-3 为什么滚子从动件是最常用的从动件型式?5-4 凸轮机构从动件的常用运动规律有那些?各有什么特点?5-5 图解法绘制凸轮轮廓的原理是什么?为什么要采用这种原理?5-6 什么情况下要用解析法设计凸轮的轮廓?5-7 设计凸轮应注意那些问题?5-8 从现有的机器上找出两个凸轮机构应用实例,分析其类型和运动规律?A级能力训练题1.在凸轮机构的几种基本的从动件运动规律中,运动规律使凸轮机构产生刚性冲击,运动规律产生柔性冲击,运动规律则没有冲击。
2.在凸轮机构的各种常用的推杆运动规律中,只宜用于低速的情况,宜用于中速,但不宜用于高速的情况,而可在高速下应用。
3.设计滚子推杆盘形凸轮轮廓线时,若发现凸轮轮廓线有变尖现象,则在尺寸参数的改变上应采取的措施是或。
4.移动从动件盘形凸轮机构,当从动件运动规律一定时,欲同时降低升程的压力角,可采用的措施是。
若只降低升程的压力角,可采用方法。
5.凸轮的基圆半径是从到的最短距离。
6.设计直动滚子推杆盘形凸轮机构的工作廓线时,发现压力角超过了许用值,且廓线出现变尖现象,此时应采用的措施是__________________________________________。
7.与其他机构相比,凸轮机构的最大优点是。
(1)便于润滑(2)可实现客种预期的运动规律(3)从动件的行程可较大(4)制造方便,易获得较高的精度8.凸轮的基圆半径越小,则凸轮机构的压力角,而凸轮机构的尺寸。
(1)增大(2)减小(3)不变(4)增大或减小9.设计凸轮廓线对,若减小凸轮的基圆半径r b,则凸轮廓线曲率半径将。

第5章凸轮机构1.从动件的运动规律:等速,等加速等减速,余弦加速度,正弦加速度2.动力特性:刚性冲击,柔性冲击3.设计原理:反转法,比例尺,等分基圆,偏置从动件压力角与自锁条件4.基本参数:基圆半径,滚子半径,平底尺寸【思考题】5-1 凸轮机构的应用场合是什么?凸轮机构的组成是什么?通常用什么办法保证凸轮与从动件之间的接触?5-2 凸轮机构分成哪几类?凸轮机构有什么特点?5-3 为什么滚子从动件是最常用的从动件型式?5-4 凸轮机构从动件的常用运动规律有那些?各有什么特点?5-5 图解法绘制凸轮轮廓的原理是什么?为什么要采用这种原理?5-6 什么情况下要用解析法设计凸轮的轮廓?5-7 设计凸轮应注意那些问题?5-8 从现有的机器上找出两个凸轮机构应用实例,分析其类型和运动规律?A级能力训练题1.在凸轮机构的几种基本的从动件运动规律中,运动规律使凸轮机构产生刚性冲击,运动规律产生柔性冲击,运动规律则没有冲击。
2.在凸轮机构的各种常用的推杆运动规律中,只宜用于低速的情况,宜用于中速,但不宜用于高速的情况,而可在高速下应用。
3.设计滚子推杆盘形凸轮轮廓线时,若发现凸轮轮廓线有变尖现象,则在尺寸参数的改变上应采取的措施是或。
4.移动从动件盘形凸轮机构,当从动件运动规律一定时,欲同时降低升程的压力角,可采用的措施是。
若只降低升程的压力角,可采用方法。
5.凸轮的基圆半径是从到的最短距离。
6.设计直动滚子推杆盘形凸轮机构的工作廓线时,发现压力角超过了许用值,且廓线出现变尖现象,此时应采用的措施是__________________________________________。
7.与其他机构相比,凸轮机构的最大优点是。
(1)便于润滑(2)可实现客种预期的运动规律(3)从动件的行程可较大(4)制造方便,易获得较高的精度8.凸轮的基圆半径越小,则凸轮机构的压力角,而凸轮机构的尺寸。
(1)增大(2)减小(3)不变(4)增大或减小9.设计凸轮廓线对,若减小凸轮的基圆半径r b,则凸轮廓线曲率半径将。


解:曲柄的存在的必要条件是 1)最短杆与追长杆的杆长之和应小于或等于其余两杆的长度之和;2)连架杆与机架必有最短杆
1). 杆件1为曲柄
2).在各杆长度不变的情况下,选取c 杆做为机架就可以实现双摇杆机构
2 试以作图法设计一偏置尖底推杆盘形凸轮的轮廓曲线。
已知凸轮以等角速度顺时针回转,正偏距10e =,基园半径030r mm =0
.~150δ0推杆运动规律为:凸轮转角=0时,推杆等速上升16mm; 0.~180δ0凸轮转角=150时推杆远休;
.~300δ0凸轮转角=180时推杆等加速回程16mm; 0.~360δ0凸轮转角=300时推杆近休。
解:解题步骤1)首先绘制位移S 与转角δ的关系曲线S δ-曲线。
2)根据S δ-曲线、凸轮基园半径和正偏距,绘制凸轮的轮廓曲线。
凸轮仅用了0度,90度,150度,180度,300度几个点绘制轮廓曲线,同学们绘制时英多用些点(一般取12个点,再勾画轮廓曲线)。

5-1 凸轮以匀角速度ω绕O 轴转动,杆AB 的A 端搁在凸轮上。
图示瞬时AB 杆处于水平位置,OA 为铅直。
试求该瞬时AB 杆的角速度的大小及转向。
解: r e a v v v += 其中,22e r v e -=ωe v v e a ωφ==tg所以lel v a AB ωω==(逆时针)5-2. 平底顶杆凸轮机构如图所示,顶杆AB 可沿导轨上下移动,偏心圆盘绕轴O 转动,轴O 位于顶杆轴线上。
工作时顶杆的平底始终接触凸轮表面。
该凸轮半径为R ,偏心距e OC =,凸轮绕轴O 转动的角速度为ω,OC 与水平线成夹角ϕ。
求当︒=0ϕ时,顶杆的速度。
(1)运动分析轮心C 为动点,动系固结于AB ;牵连运动为上下直线平移,相对运动为与平底平行直线,绝对运动为绕O 圆周运动。
(2)速度分析,如图b 所示5-3. 曲柄CE 在图示瞬时以ω0绕轴E 转动,并带动直角曲杆ABD 在图示平面内运动。
若d 为已知,试求曲杆ABD 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e av v v +=0a 2ωl v =;0e a 2ωl v v ==01e1ωω==AO v BC O (顺时针) 5-4. 在图示平面机构中,已知:AB OO =1,cm 31===r B O OA ,摇杆D O 2在D 点与套在AE 杆上的套筒铰接。
OA 以匀角速度rad/s 20=ω转动,cm 332==l D O 。
试求:当︒=30ϕ时,D O 2的角速度和角加速度。
解:取套筒D 为动点,动系固连于AE 上,牵连运动为平动 (1)由r e a v v v += ①得D 点速度合成如图(a ) 得 ϕtg e a v v =, 而r v e 0ω= 因为 r v a 0331ω⨯=,所以 rad/s 67.02==lv aD O ω 方向如图(a)所示(2)由r e na a a a a a +=+τ ②得D 点加速度分析如图(b ) 将②式向DY 轴投影得θϕϕτsin sin cos e n a a a a a -=-错了而r a la e D O na 2022ωω==θϕsin sin r l =所以ϕθϕτcos sin sin e na a a a a -=2rad/s 05.2cos sin sin 2-=-==ϕθϕετl a a l a e n a a DO 什么东西?,方向与图(b)所示相反。
第五章凸轮机构及其设计基本要求了解凸轮机构的应用及其分类。
介绍推杆常用的运动规律及其选择。
学会用图解法设计盘形凸轮的轮廓曲线。
掌握凸轮机构基本尺寸的确定。
基本概念题与答案1.什么是基圆、基圆半径?答:以凸轮理论廓线的最小向径为半径所作的圆,叫基圆,其半径称为基圆半径。
2.什么是推程、升程(又称行程)推程运动角?答:从动件由距凸轮转动中心最低位置到最远位置的过程称作推程,推程过程中从动件的最大位移称升程(行程)。
推程过程中凸轮转过的角度称为推程运动角。
3.什么是远休止角、回程运动角、近休止角?答:远休止角:从动件在距凸轮回转中心最远的位置停留不动,这时对应的凸轮转角称为远休止角。
回程运动角:从动件以一定运动规律降回初始位置,这时凸轮转过的角度。
近休止角:从动件在距凸轮回转中心最近的位置停留不动,这时对应的凸轮转角称为近休止角。
4.什么是刚性冲击和柔性冲击?答:刚性冲击:由加速度产生的惯性力突变为无穷大,致使机构产生的强烈冲击。
柔性冲击:由加速度产生的惯性力为有限值的变化,使机构产生的冲击。
5.凸轮轮廓的形状起什么作用?由什么来决定?答:作用:实现从动件的运动规律,取决于从动件的运动规律。
6.图解法设计凸轮廓线的方法是什么?什么是反转法?答:方法:反转法,凸轮不动,从动件连同机架一起按凸轮的角速度的相反方向绕凸轮回转中心转动,而从动件仍按预定的运动规律相对机架运动,从动件尖顶的轨迹即为凸轮廓线,这种方法称为凸轮廓线的反转法设计。
7.直动从动件盘形凸轮廓线设计的已知条件是什么?设计中注意什么?答:(1)从动件的运动规律,即从动件的位移线图。
(2)基圆半径。
(3)从动件导路偏距e 和位置。
(4)凸轮等角速度转动及其转向。
注意:(1)取μs、μL、μδ比例尺、按已知条件作图。
(2)反转法。
(3)从动件位移在基圆外截取。
(4)所有位移点用光滑曲线连接成凸轮廓线。
8.滚子从动件盘形凸轮廓线设计,以哪一点作为尖顶来设计理论廓线?答:以滚子中心为尖顶来进行设计。
05凸轮机构及其设计1.凸轮机构中的压力角是和所夹的锐角。
2.凸轮机构中�使凸轮与从动件保持接触的方法有和两种。
3.在回程过程中�对凸轮机构的压力角加以限制的原因是。
4.在推程过程中�对凸轮机构的压力角加以限制的原因是。
5.在直动滚子从动件盘形凸轮机构中�凸轮的理论廓线与实际廓线间的关系是。
6.凸轮机构中�从动件根据其端部结构型式�一般有、、等三种型式。
7.设计滚子从动件盘形凸轮机构时�滚子中心的轨迹称为凸轮的廓线�与滚子相包络的凸轮廓线称为廓线。
8.盘形凸轮的基圆半径是上距凸轮转动中心的最小向径。
9.根据图示的dd 2 s��2�运动线图�可判断从动件的推程运动是_________________________________�从动件的回程运动是____________________________________________。
10.从动件作等速运动的凸轮机构中�其位移线图是线�速度线图是线。
11.当初步设计直动尖顶从动件盘形凸轮机构中发现有自锁现象时�可采用、、等办法来解决。
12.在设计滚子从动件盘形凸轮轮廓曲线中�若出现时�会发生从动件运动失真现象。
此时�可采用方法避免从动件的运动失真。
13.用图解法设计滚子从动件盘形凸轮轮廓时�在由理论轮廓曲线求实际轮廓曲线的过程中�若实际轮廓曲线出现尖点或交叉现象�则与的选择有关。
14.在设计滚子从动件盘形凸轮机构时�选择滚子半径的条件是。
15.在偏置直动从动件盘形凸轮机构中�当凸轮逆时针方向转动时�为减小机构压力角�应使从动件导路位置偏置于凸轮回转中心的侧。
16.平底从动件盘形凸轮机构中�凸轮基圆半径应由来决定。
17.凸轮的基圆半径越小�则凸轮机构的压力角越�而凸轮机构的尺寸越。
18.凸轮基圆半径的选择�需考虑到、�以及凸轮的实际廓线是否出现变尖和失真等因素。
19.当发现直动从动件盘形凸轮机构的压力角过大时�可采取��等措施加以改进�当采用滚子从动件时�如发现凸轮实际廓线造成从动件运动规律失真�则应采取�等措施加以避免。
第5章凸轮机构一、填空题1.凸轮机构中的压力角是和所夹的锐角。
2.凸轮机构中,使凸轮与从动件保持接触的方法有和两种。
3.设计滚子从动件盘形凸轮机构时,滚子中心的轨迹称为凸轮的廓线;与滚子相包络的凸轮廓线称为廓线。
4.盘形凸轮的基圆半径是上距凸轮转动中心的最小向径。
5.从动件作等速运动的凸轮机构中,其位移线图是线,速度线图是线。
6.当初步设计直动尖顶从动件盘形凸轮机构中发现有自锁现象时,可采用、、等办法来解决。
7.在设计滚子从动件盘形凸轮轮廓曲线中,若出现时,会发生从动件运动失真现象。
此时,可采用方法避免从动件的运动失真。
8.用图解法设计滚子从动件盘形凸轮轮廓时,在由理论轮廓曲线求实际轮廓曲线的过程中,若实际轮廓曲线出现尖点或交叉现象,则与的选择有关。
9.在设计滚子从动件盘形凸轮机构时,选择滚子半径的条件是。
10.平底从动件盘形凸轮机构中,凸轮基圆半径应由来决定。
11.凸轮的基圆半径越小,则凸轮机构的压力角越,而凸轮机构的尺寸越。
12.凸轮基圆半径的选择,需考虑到、,以及凸轮的实际廓线是否出现变尖和失真等因素。
13.在许用压力角相同的条件下,从动件可以得到比从动件更小的凸轮基圆半径。
或者说,当基圆半径相同时,从动件正确偏置可以凸轮机构的推程压力角。
14.直动尖顶从动件盘形凸轮机构的压力角是指;直动滚子从动件盘形凸轮机构的压力角是指。
15.凸轮的基圆半径越小,则机构越,但过于小的基圆半径会导致压力角,从而使凸轮机构的传动性能变。
16.凸轮机构从动件运动规律的选择原则为。
17.凸轮机构中的从动件速度随凸轮转角变化的线图如图所示。
在凸轮转角处存在刚性冲击,在处,存在柔性冲击。
二、判断题1.偏置直动尖顶从动件盘形凸轮机构中,其推程运动角等于凸轮对应推程廓线所对中心角;其回程运动角等于凸轮对应回程廓线所对中心角。
------------- ( )2.在直动从动件盘形凸轮机构中进行合理的偏置,是为了同时减小推程压力角和回程压力角。
习题5-1从动件的常用运动规律有哪几种?它们各有什么特点?各适用于什么场合?5-2在滚子直动从动件盘形凸轮机构中,若凸轮实际轮廓曲线保持不变,而增大或减小滚子半径,从动件运动规律是否发生变化?5-3何谓凸轮机构的压力角?当凸轮轮廓曲线设计完成后,如何检杳凸轮转角为》时机构的压力角(X?若发现压力角超过许用值,可采用什么措施减小推程压力角?5-4从动件的运动规律如下:^=90° ,八=30°,九=180°,八,=60°,行程h=20mni,推程中以等速运动规律上升;回程以等加速等减速运动规律返回原处。
试用图解法绘制从动件位移线图、速度线图和加速度线图,并分析凸轮机构运动中的冲击特性。
5-5试在下图所示三个凸轮机构中,画出凸轮的基圆以及按规定转向31转过45°时机构的压力角。
5-6用作图法设计偏置直动滚子从动件盘形凸轮机构。
已知凸轮以等角速度顺时针方向回转,凸轮回转中心偏于从动件右侧。
偏距e=10mm,基圆半径r0=40mm,滚子半径r T=10mm,从动件的行程h=20 mm,从动件的运动规律如下:^ = 150 ° , ^=30° ,八=120°,几=60°,从动件在推程以简谐运动规律上升,在回程以等加速等减速运动规律返回原处,试绘出从动件位移线图及凸轮轮廓曲线。
习题解答:5-1从动件的常用运动规律有哪几种?它们各有什么特点?各适用于什么场合?从动件常用运动规律特性比较运动规律Vmax(hco/5t)X amax(h<o/5t2)X冲击推荐应用范围等速 1.0oo刚性低速轻载等加等减速 2.0 4.0柔性中速轻载五次多项式 1.88 5.77无咼速中载余弦加速度 1.57 4.93柔性中速中载正弦加速度 2.0 6.28无高速轻载改进正弦加速度 1.76 5.53无高速重载5-5、(例题)压力角如图所示5-5、解:—3 15-6以凸轮回转中心0为圆心,以及以e为半径作偏距圆。
第3章 典型例题分析
1.在图(a)所示的对心移动滚子从动件盘形凸轮机构中,凸轮的实际廓线为一圆,其圆心在A 点,半径R =40mm ,凸轮转动方向如图所示,OA l =25mm ,滚子半径r r =10mm 。
试问:
(1) 凸轮的理论廓线为何种曲线?
(2) 凸轮的基圆半径b r =?
(3) 从动件的升距h =?
(4) 若凸轮实际廓线不变,而将滚子半径改为15mm ,从动件的运动规律有无变化?
解 选取适当比例尺l µ作机构图如图(b)所示。
(1) 凸轮的理论廓线
对于滚子从动件凸轮机构来说,凸轮的理论廓线与实际廓线是两条法向等距的曲线,该法向距离等于滚子半径r r 。
今已知其实际廓线为半径R =40mm 的圆,故其理论廓线η为半径为401050r R r +=+=(mm)的圆。
(2) 凸轮的基圆半径b r
凸轮理论廓线的最小向径称为凸轮的基圆半径b r 。
因此,连接偏心圆的圆心A 和凸轮转动中心O ,并延长使其与偏心圆η相交于C 点,则OC 即为理论廓线η
的最小向径,它即为凸轮的基圆半径b r 。
由图(b)可知
()(4010)2525b AC AO AO r l l R r l =−=+−=+−=(mm)
(3) 从动件的升距h
从动件上升的最大距离h 称为从动件的升距,它等于理论廓线η的最大和最小向径之差。
因此,
()2540102550OA r b h l R r r =++−=++−=(mm)
(4) 滚子半径改为15mm 后从动件的运动规律
当凸轮的实际廓线η′保持不变,而将滚子半径r r 由10mm 增大至15mm 后,连杆长度AB l 将随之由50mm 增至55mm ,因此从动件将随之变化。
若希望从动件3的运动规律保持不变,正确的做法是让理论廓线η保持不变,作该理论廓线的法向等距离曲线,并使之距离等于15mm ,得到新的实际廓线。
2.某技术人员欲设计一台打包机,其推送包装物品的机构如图1所示。
已知机构的位置和某些尺寸参数如表1,工作要求从动滑块的行程H =400mm ,其运动规律如表2。
根据结构及强度等条件已选定滚子半径r r =25mm ,试设计所需的凸轮工作轮廓。
图1
表1 已知条件 mm 1x 1y 0x 0y AB l AC l CD l
230 250 320 650 313 672 450
表2 滑块的运动规律 凸轮转角/()o 滑动运动方向及运动规律
0 ~ 120 由左向右,以绝对值相等的等加速、等减速规律移动H
120 ~ 150 在右端停止不动
150 ~ 210 由右向左,以绝对值相等的等加速、等减速规律移动H
210 ~ 360
在左右端停止不动 解 这是摆动滚子从动件盘形凸轮机构的设计题。
与一般的设计题不同的是:凸轮所直接推动的从动件是摆杆AC ,而已知的是远离凸轮的滑块的运动规律。
因此,在设计凸轮机构前,需要首先将已知的滑块的运动规律追溯到摆杆AC 上,即首先通过滑块的运动规律,求出摆杆AC 的运动规律,然后才设计凸轮的轮廓曲线。
该题设计步骤如下:
(1) 确定滑块对应于凸轮转角的位移
由于滑块按等加速等减速规律移动,故其位移方程为抛物线方程。
在等加速段,212
s at =,若将加速度过程的时间分为若干等份,则由方程可知,各等份时间之后的位移比例关系为1s :2s :3s …=1:4:9…根据这一比例关系,可用图2右则所示的作图法求出滑块上D 点在的等加速等减速过程中的各个位置0D ,1D ,2D ,3D ,…,8D 。
图中,01:02:03:04=1:4:9:16,87:86:85:84=1:4:9:16。
(2) 确定摆杆AC 对应于凸轮转角的运动规律
根据已知条件,作出摆杆滑块机构的运动简图。
以各个D 点为圆心,以CD l 为半径作圆(实际作图时,注意作图比例尺l µ),与点C 的圆弧轨迹相交于0C ,1C ,2C ,…,8C 等点,从而可得到滚子中心B 的各个位置0B ,1B ,2B ,…,8B ,如图2所示。
图2
(3) 将凸轮转角分度
以O 为圆心,以0OB 长为半径作凸轮的基圆。
然后以O 为圆心,以0OA 长为半径作转轴圆。
由于凸转顺时针方向转动,故应按逆时针方向反求取从动摆杆转轴A 的各个分点。
凸轮转120o 时,滑块作等加速等减速运动,其中对应有凸轮的8个等分转角,故在凸轮转角120o 范围内,在转轴圆上求取1A ,2A ,…,8A 等8个的等分点,如图所示。
它们代表反转过程中从动摆杆的转轴A 所依次占据的位置。
(4) 绘制凸轮理论廓线η和实际廓线η′
以1A ,2A ,…,8A 各点为圆心,以00A B 为半径作圆弧,与基圆分别相交于1E ,2E ,…,
8E 等点。
量取¼¼1101E F B B =,¼¼2202E F B B =,¼¼3303E F B B =,…,¼¼8808E F B B =,得1F ,2F ,…,
8F 等点,以光滑曲线连接各个F 点,即得凸轮理论廓线η。
再作一系列滚子圆的包络线,即得凸轮的实际廓线η′。
在凸轮转角为120o ~150o 的30o
区间内,滑块在右端静止不动,此时对应的凸轮廓线为以凸轮转轴O 为圆心的圆弧,如图所示。
在凸轮转角为150o ~210o 的60o 区间内,滑块又以等加速等减速规律由右向左返回到初
始点0D ,由于此时的总行程仍为H ,因此在将区间的凸轮转角8等分的情况下,各个位移与正行程时相同,所以可直接利用正行程时所求出的位移量,而不必另行作图求滑块的位置。
回程阶段等加速等减速段及静止段凸轮廓线的求法如图所示,不再赘述。
(5) 校核压力角是否超过许用值和凸轮廓线是否出现运动失真现象,并采取相应措施。
设计完成后应检查压力角是否超过许用值和凸轮廓线是否出现运动失真现象,若出现这两种情况,则应改变O 点的位置重新设计。
3.在如图所示的三个凸轮机构中,已知R =40mm ,a =20mm ,e =15mm ,r r =20mm 。
试用反转法求从动件的位移曲线)(ϕs s −,并比较之。
(要求选用同一比例尺,画在同一坐标系中,均以从动件最低位置为起始点)。
4. 试用作图法求出如图所示凸轮机构中当凸轮从图示位置转过o 45后机构的压力角,并在图上标注出来。
5. 在如图所示的凸轮机构中,从动件的起始上升点均为C 点。
(1) 试在图上标注出从C 点接触到D 点接触时,凸轮转过的角度ϕ及从动件走过的位移;
(2) 标出在D 点接触时凸轮机构的压力角α。
6. 图(a),(b),(c),(d)所示是按图1所示的从动件运动规律绘制的4个凸轮的廓线,其长度比例尺l s µµ=。
试分别指出它们各错在什么地方?
7.已知凸轮机构的实际廓线,试分析确定:
1)为使推程的压力角较小凸轮的转向;
2)凸轮的基圆半径;
3)凸轮机构的偏距;
4)凸轮的理论廓线;
5)从动件的行程;
6)从动件在最高位置时的压力角;
7)推程运动角;
8)从动件有无远休止角。
解:
5)从动件的行程IB h
7)推程运动角 8)从动件有无远休止角。
(其他见图示)
δ
8.在图示机构中已知凸轮以
2
ω的角速度顺时针方向转动,试找出图示机构中的全部瞬心,指明哪些是绝对瞬心,哪些是相对瞬心。
并用瞬心法求出从动件3的速度(用图及表达式表示)。
先求P
23v v l
P P P 32321223 ==ω
9.图示为一偏置直动滚子从动件盘形凸轮机构。
试在图上:
(1)画出并标明基圆与偏距圆;
(2)作出并标明凸轮按ω方向转过60°后,从动件与凸轮廓线接触处的压力角α;
(3)作出并标明滚子从图示位置反转到B处与凸轮接触时,对应的凸轮转角ϕ。
10.在图示直动平底从动件盘形凸轮机构中,请指出:
1)图示位置时凸轮机构的压力角α
2)图示位置从动件的位移
3)图示位置时凸轮的转角
4)图示位置时从动件与凸轮的瞬心
5)凸轮机构的基圆
1)图示位置时凸轮机构的压力角α0
2)图示位置从动件的位移B1B3
3)图示位置时凸轮的转角
4)图示位置时从动件与凸轮的瞬心P0
5)凸轮机构的基圆
11.试在图示凸轮机构中,
(1)画出理论轮廓曲线、基圆与偏距圆;
(2)标出从动件与凸轮从接触点C到接触点D时,该凸轮转过的转角ϕ;(3)标出从动件与凸轮在D点接触的压力角α;
(4)标出在D点接触时的从动件的位移s。
δ
12.在图示对心直动滚子从动件盘形凸轮机构中,凸轮的实际廓线为一圆,圆心在O
=25mm,滚子半径r r 点。
半径R=40mm,凸轮绕回转中心A以逆时针方向旋转,L
OA
=10 mm,试求:
(1)凸轮的基圆r0;
(2)从动件的行程;
(3)在图上画出C点压力角α
和D点接触时的位移h D、压力角αD。
c
13.图示摆动从动件盘形凸轮机构中,已知机构尺寸和凸轮转向。
当凸轮转过°
90时,从动件摆动多大角度?并标出该位置凸轮机构的压力角。