9、第九章刚体的平面运动

刚体的简单运动：平移、定轴转动第九章刚体的平面运动刚体的复杂运动：刚体的平面运动平面运动平移+转动绕不断运动的轴的转动本章内容：刚体平面运动的分解；平面运动刚体的角速度、角加速度；刚体上各点的速度、加速度。

行星齿轮机构（动画）行星轮平面运动：在运动中，刚体上的任意一点与某一固定 平面始终保持相等的距离。

曲柄连杆机构用一个平行于固定平面的平面截割连杆； 连杆 截面S ：一个平面图形平面图形上各点的运动可以代表刚体内所有点的运动。

过平面图形上任一点作垂直于图形的直线；直线作平移刚体作平面运动 刚体的平面运动可简化为平面图形在它的自身平面内运动。

— 平面图形的运动方程 x y oo' Mϕ线段上任一点O '的位置 ⎪⎩⎪⎨⎧==='')()()(321t f t f y t f x o o ϕ平面图形在其平面上位置的确定平面图形的运动方程由两部分组成：平面图形按O'点的运动方程的平移；线段与固定坐标轴x 轴的夹角 ϕ平面图形绕O'点转角为的转动。

ϕ例如车轮的运动．例如车轮的运动．车轮的平面运动可以看成是车轮随同车厢的平动和相对车厢的转动的合成．车轮对于静系的平面运动（绝对运动）车厢（动系Ax' y') 相对静系的平动（牵连运动）车轮相对车厢（动系Ax' y'）的转动（相对运动）我们称动系上的原点Ａ为基点，于是 车轮的平面运动随基点A 的平动 绕基点A'的转动刚体的平面运动可以分解为随基点的平动和绕基点的转动．再例如: 平面图形Ｓ在∆ｔ时间内从位置I 运动到位置II ✶以A 为基点: 随基点A 平动到A'B''后, 绕基点转角到A'B' ✷以B 为基点: 随基点B 平动到A''B'后, 绕基点转 角到A'B' 图中看出：AB // A'B'' // A''B' ，于是有 21ϕϕ∆=∆1ϕ∆2ϕ∆2121212010, ; , lim lim εεωωωω∆ϕ∆∆ϕ∆∆∆====→→dt d dt d tt t t §9-1 刚体平面运动的概述和运动分解所以，平面运动随基点平动的运动规律与基点的选择有关，而绕基点转动的规律与基点选取无关．(即在同一瞬间，图形绕任一基点转动的ε ,ω都是相同的）基点的选取是任意的。

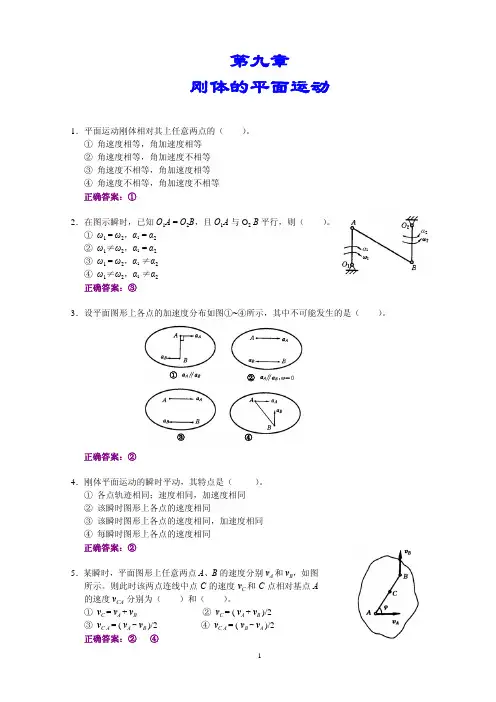
第九章刚体的平面运动1．平面运动刚体相对其上任意两点的（ ）。

① 角速度相等，角加速度相等② 角速度相等，角加速度不相等③ 角速度不相等，角加速度相等④ 角速度不相等，角加速度不相等正确答案：①2．在图示瞬时，已知O 1A = O 2B ，且O 1A 与O 2 B 平行，则（ ）。

① ω1 = ω2，α1 = α2② ω1≠ω2，α1 = α2③ ω1 = ω2，α1 ≠α2④ ω1≠ω2，α1 ≠α2正确答案：③3．设平面图形上各点的加速度分布如图①~④所示，其中不可能发生的是（ ）。

正确答案：②4．刚体平面运动的瞬时平动，其特点是（ ）。

① 各点轨迹相同；速度相同，加速度相同② 该瞬时图形上各点的速度相同③ 该瞬时图形上各点的速度相同，加速度相同④ 每瞬时图形上各点的速度相同正确答案：②5．某瞬时，平面图形上任意两点A 、B 的速度分别v A 和v B ，如图所示。

则此时该两点连线中点C 的速度v C 和C 点相对基点A的速度v CA 分别为（ ）和（ ）。

① v C = v A + v B ② v C = ( v A + v B )/2③ v C A = ( v A - v B )/2 ④ v C A = ( v B - v A )/2正确答案：② ④α1α2 ①②③④6．平面图形上任意两点A 、B 的加速度a A 、a B 与连线AB 垂直，且a A ≠ a B ，则该瞬时，平面图形的角速度ω和角加速度α应为（ ）。

① ω≠0，α ≠0② ω≠0，α = 0③ ω = 0，α ≠0④ ω = 0，α = 0正确答案：③7．平面机构在图示位置时，AB 杆水平，OA 杆鉛直。

若B 点的速度v B ≠0，加速度τB a = 0，则此瞬时OA 杆的角速度ω和角加速度α为（ ）。

① ω = 0，α ≠0② ω≠0，α = 0③ ω = 0，α = 0④ ω≠0，α ≠0正确答案：②8．在图示三种运动情况下，平面运动刚体的速度瞬心：（a ）为（ ）；（b ）为（ ）；（c ）为（ ）。

⌒ ⌒第九章 刚体的平面运动9-1 椭圆规尺AB 由曲柄OC 带动，曲柄以角速度0ω绕O 轴匀速转动，如图所示。

如OC=BC=AC=r ，并取C 为基点，求椭圆规尺AB 的平面运动方程。

解：取C 为基点。

将规尺的平面运动分解为随基点的平动和绕基点的转动。

因为 ,r AC CB OC === 所以 CBO COB ∠=∠ 设此角为ϕ，则t 0ωϕ=故规尺AB 的平面运动方程为 t r x C 0c o s ω=，t r y C 0sin ω=，t 0ωϕ= 9-3 半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动，如图所示。

如曲柄OA 以等角加速度α绕O 轴转动，当运动开始时，角速度00=ω，转角00=ϕ。

求动齿轮以中心A 为基点的平面运动方程。

解：动齿轮的平面运动可分解为以A 为基点的平动和绕A 点的转动。

在图示坐标系中，A 点的坐标为：ϕcos )(r R x A += （1） ϕsin )(r R y A +=（2）因为 α是常数，当0=t 时，000==ϕω 所以 22t αϕ=设小轮上开始时啮合点为M ，则AM 起始位置为水平。

设任一时刻AM 绕A 的转角为A ϕ，由图可见，NAM A ∠=ϕ，且θϕϕ+=A因动齿轮作纯滚动，有CM CM =0，即θϕr R = 所以ϕθrR =故得 ϕϕrrR A +=（3）以221t αϕ=代入（1）、（2）、（3）式中， 得动齿轮的平面运动方程为 22cos )(t r R x A α+=22sin )(t r R y A α+=2)(21at rr R A +=ϕ9-5 如图所示，在筛动机构中，筛子的摆动是由曲柄杆机构所带动。

已知曲柄OA 的转速min /40r n OA =，m 3.0=OA 。

当筛子BC 运动到与点O 在同一水平线上时，︒=∠90BAO 。

求此瞬时筛子BC 的速度。

解：由图示机构知BC 作平移，图示位置时，B v 与CBO 夹角为30°，与AB 夹角为60°。

第九章刚体的平面运动刚体的平面运动是工程机械中较为常见的一种刚体运动，它可以看作为平移与转动的合成，也可以看作为绕不断运动的轴的转动。

在运动中，刚体上的任意一点与某一固定平面始终保持相等的距离。

平面运动刚体上的各点都在平行于某一固定平面的平面内运动。

注意与平移区别()Oϕ'--基点，转角，Oxy--定系用一个平面图形代表作平面运动的刚体；用平面内的任意线段的位置来确定平面图形的位置；用线段上任意点0′的坐标和一个夹角来确定该线段的位置。

平面图形的运动方程对于任意的平面运动，可在平面图形上任取一点O′，称为基点。

在这一点假想地安上一个平移参考系O’x’y’，平面图形运动时，动坐标轴方向始终保持不变，可令其分别平行于定坐标轴Ox和Oy，平面的平面运动可看成为随同基点的平移和绕基点转动这两部分运动的合成。

平移坐标系-'''y x O平移-----牵连运动转动-----相对运动四、重要结论：平面运动可取任意基点而分解为平移和转动。

其中平移的速度和加速度与基点的选择有关，而平面图形绕基点转动的角速度和角加速度与基点的选择无关.任何平面图形的运动可分解为两个运动(1)牵连运动，即随同基点O′的平移；(2)相对运动，即绕基点O′的转动。

平面图形内任一点M的运动也是两个运动的合成，因此可用速度合成定理来求它的速度，这种方法称为基点法。

注意：此处动点、动系、基点在同一个刚体上。

但属于刚体上的不同点。

点M 的牵连速度v v点M的相对速度v vω'M O v v v v 'ωv v AB v v ω结论：平面图形内任一点的速度等于基点的速度与该点随图形绕基点转动速度的矢量和。

平面图形内任意两点A 和B 的速度确定基点A ，一般应使V A 为已知条件。

O’M 上速度分布图角速度与相对速度有关AABAABBAvlABvωϕ=v v v应使V B位于平行四边形的对角线上V BA=AB·ω，此处ω是尺AB的角速度3、角速度分析例9-2图所示平面机构中，AB=BD=DE=l=300mm。