tarjan算法的原理

c++中tarjan算法求割点
摘要：
一、C++中Tarjan算法求割点简介
1.Tarjan算法的原理
2.C++中实现Tarjan算法求割点的步骤
二、C++中Tarjan算法求割点的具体实现
1.定义相关数据结构
2.初始化并处理未访问过的顶点
3.寻找割点
三、C++中Tarjan算法求割点的代码实例
1.代码展示
2.运行结果及解析
正文：
一、C++中Tarjan算法求割点简介
Tarjan算法是一种用于求解强连通分量（Strongly Connected Component，简称SCC）的算法。

它通过递归的方式，寻找一个有向图中的割点（Cut Point），即在一个强连通分量中，删除这个顶点后，原图不再保持强连通。

在C++中实现Tarjan算法求割点的过程中，需要先对给定的图进行预处理，然后遍历图中的顶点，最终找到所有的割点。

二、C++中Tarjan算法求割点的具体实现
1.定义相关数据结构
在C++中实现Tarjan算法求割点，首先需要定义一些相关的数据结构。

这里我们定义一个邻接表表示图，用一个数组vis表示顶点访问情况，用一个数组dfn表示顶点的发现时间，用一个数组low表示顶点的低度。

2.初始化并处理未访问过的顶点
遍历图中的顶点，对于未访问过的顶点，我们将其作为当前割点，并将其加入集合S中。

然后遍历与当前顶点相连的所有顶点，将它们加入集合S中，并更新它们的低度。

3.寻找割点
在遍历完所有顶点后，我们再次遍历图中的顶点，对于每个顶点，如果它的低度为1，那么它就是一个割点。

（转）全⽹最!详!细!tarjan算法讲解全⽹最详细tarjan算法讲解，我不敢说别的。

反正其他tarjan算法讲解，我看了半天才看懂。

我写的这个，读完⼀遍，发现原来tarjan这么简单！tarjan算法，⼀个关于图的联通性的神奇算法。

基于DFS（迪法师）算法，深度优先搜索⼀张有向图。

！注意！是有向图。

根据树，堆栈，打标记等种种神（che）奇（dan）⽅法来完成剖析⼀个图的⼯作。

⽽图的联通性，就是任督⼆脉通不通。

的问题。

了解tarjan算法之前你需要知道：强连通，强连通图，强连通分量，解答树（解答树只是⼀种形式。

了解即可）不知道怎么办神奇海螺～：嘟噜噜～！强连通(strongly connected)：在⼀个有向图G⾥，设两个点 a b 发现，由a有⼀条路可以⾛到b，由b⼜有⼀条路可以⾛到a，我们就叫这两个顶点（a，b）强连通。

强连通图：如果在⼀个有向图G中，每两个点都强连通，我们就叫这个图，强连通图。

强连通分量strongly connected components)：在⼀个有向图G中，有⼀个⼦图，这个⼦图每2个点都满⾜强连通，我们就叫这个⼦图叫做强连通分量［分量：：把⼀个向量分解成⼏个⽅向的向量的和，那些⽅向上的向量就叫做该向量（未分解前的向量）的分量］举个简单的栗⼦：⽐如说这个图，在这个图中呢，点1与点2互相都有路径到达对⽅，所以它们强连通.⽽在这个有向图中，点1 2 3组成的这个⼦图，是整个有向图中的强连通分量。

解答树：就是⼀个可以来表达出递归枚举的⽅式的树（图），其实也可以说是递归图。

反正都是⼀个作⽤，⼀个展⽰从“什么都没有做”开始到“所有结求出来”逐步完成的过程。

“过程！”神奇海螺结束tarjan算法，之所以⽤DFS就是因为它将每⼀个强连通分量作为搜索树上的⼀个⼦树。

⽽这个图，就是⼀个完整的搜索树。

为了使这颗搜索树在遇到强连通分量的节点的时候能顺利进⾏。

每个点都有两个参数。

1，DFN［］作为这个点搜索的次序编号（时间戳），简单来说就是第⼏个被搜索到的。

转载-Tarjan算法（求SCC） 说到以Tarjan命名的算法，我们经常提到的有3个，其中就包括本⽂所介绍的求强连通分量的Tarjan算法。

⽽提出此算法的普林斯顿⼤学的Robert E Tarjan教授也是1986年的图灵奖获得者（具体原因请看本博“历届图灵奖得主”⼀⽂）。

⾸先明确⼏个概念。

1. 强连通图。

在⼀个强连通图中，任意两个点都通过⼀定路径互相连通。

⽐如图⼀是⼀个强连通图，⽽图⼆不是。

因为没有⼀条路使得点4到达点1、2或3。

2. 强连通分量。

在⼀个⾮强连通图中极⼤的强连通⼦图就是该图的强连通分量。

⽐如图三中⼦图{1,2,3,5}是⼀个强连通分量，⼦图{4}是⼀个强连通分量。

其实，tarjan算法的基础是DFS。

我们准备两个数组Low和Dfn。

Low数组是⼀个标记数组，记录该点所在的强连通⼦图所在搜索⼦树的根节点的Dfn值（很绕嘴，往下看你就会明⽩），Dfn数组记录搜索到该点的时间，也就是第⼏个搜索这个点的。

根据以下⼏条规则，经过搜索遍历该图（⽆需回溯）和对栈的操作，我们就可以得到该有向图的强连通分量。

1. 数组的初始化：当⾸次搜索到点p时，Dfn与Low数组的值都为到该点的时间。

2. 堆栈：每搜索到⼀个点，将它压⼊栈顶。

3. 当点p有与点p’相连时，如果此时（时间为dfn[p]时）p’不在栈中，p的low值为两点的low值中较⼩的⼀个。

4. 当点p有与点p’相连时，如果此时（时间为dfn[p]时）p’在栈中，p的low值为p的low值和p’的dfn值中较⼩的⼀个。

5. 每当搜索到⼀个点经过以上操作后（也就是⼦树已经全部遍历）的low值等于dfn值，则将它以及在它之上的元素弹出栈。

这些出栈的元素组成⼀个强连通分量。

6. 继续搜索（或许会更换搜索的起点，因为整个有向图可能分为两个不连通的部分），直到所有点被遍历。

由于每个顶点只访问过⼀次，每条边也只访问过⼀次，我们就可以在O（n+m）的时间内求出有向图的强连通分量。

Tarjan算法Tarjan算法Tarjan求强连通分量概念：如果两个顶点互相可达，则它们是强连通的。

如果⼀幅有向图中任意两个顶点都是强连通的，则这幅有向图也是强连通的。

强连通分量就是图中具有连通性的⼀个最⼤⼦集，⼀般可以⽤来缩点，即相互到达的⼀堆点可以将他们有⽤的信息统⼀到⼀个点上去。

求解强连通分量的⽅法⼀般会使⽤Tarjan算法。

⾸先我们需要学会dfs树,定义⼏种边：树边，连接dfs树中的⽗节点和⼦节点的边。

横叉边，连接dfs树中的不在⼀个⼦树中的两个节点的边。

前向边，连接dfs树中的⼀个节点连向他的⼦树中深度差⼤于等于2，也就是不直接相连的两点的边。

后向边，连接dfs树中的⼀个节点连向他的祖先的边，⼜叫返祖边。

求解：dfn[i]表⽰i节点的时间戳，low[i]表⽰i节点的所属的强连通分量i的时间戳的最⼩值，也可以说是i或i的⼦树能够追溯到的最早的栈中节点的时间戳。

发现如果在dfs树中出现了后向边说明后向边连接的两点之间的环⼀定是强连通的，但不⼀定是最⼤⼦集。

我们有个性质：如果low[i]⽐dfn[i]⼩，说明他有⼀条连向祖宗的后向边，所以要保留在栈中。

如果当前low[i]等于dfn[i]说明他搜索的栈中没有可以连向他祖宗的边，当前栈中的点⼀定就是low[栈中的点]等于dfn[i]的点，也可以有能连向i的反向边。

有如果树边没有被找到过，则有low[u]=min(low[u],low[v]);也就是⽤v的所能连向的点的最⼩时间戳来更新u。

如果此点已经⼊栈，说明此时这是⼀条回边，因此不能⽤low[v]更新，⽽应该：low[u]=min(low[u],dfn[v]);因为，low[v]可能属于另⼀个编号更⼩的强连通分量⾥，⽽u可以连接到v但v不⼀定与u相连，所以可能u、v并不属于同⼀个强连通分量。

但是第⼀种情况如果low[v]⽐low[u]⼩的话，v⼀定有包括u的强连通分量，Tarjan求割点和桥概念：在⽆向连通图中，双连通分量分为点双和边双，点双为⼀个连通分量删去任意⼀个点都保持连通，边双为删去任意⼀条边都保持连通。

强连通算法--Tarjan个⼈理解+详解⾸先我们引⼊定义：1、有向图G中，以顶点v为起点的弧的数⽬称为v的出度，记做deg+（v）；以顶点v为终点的弧的数⽬称为v的⼊度，记做deg-（v）。

2、如果在有向图G中，有⼀条<u，v>有向道路，则v称为u可达的，或者说，从u可达v。

3、如果有向图G的任意两个顶点都互相可达，则称图 G是强连通图，如果有向图G存在两顶点u和v使得u不能到v，或者v不能到u，则称图G 是强⾮连通图。

4、如果有向图G不是强连通图，他的⼦图G2是强连通图，点v属于G2，任意包含v的强连通⼦图也是G2的⼦图，则乘G2是有向图G的极⼤强连通⼦图，也称强连通分量。

5、什么是强连通？强连通其实就是指图中有两点u，v。

使得能够找到有向路径从u到v并且也能够找到有向路径从v到u，则称u，v是强连通的。

然后我们理解定义：既然我们现在已经了解了什么是强连通，和什么是强连通分量，可能⼤家对于定义还是理解的不透彻，我们不妨引⼊⼀个图加强⼤家对强连通分量和强连通的理解：标注棕⾊线条框框的三个部分就分别是⼀个强连通分量，也就是说，这个图中的强连通分量有3个。

其中我们分析最左边三个点的这部分：其中1能够到达0,0也能够通过经过2的路径到达1.1和0就是强连通的。

其中1能够通过0到达2,2也能够到达1，那么1和2就是强连通的。

.........同理，我们能够看得出来这⼀部分确实是强连通分量，也就是说，强连通分量⾥边的任意两个点，都是互相可达的。

那么如何求强连通分量的个数呢？另外强连通算法能够实现什么⼀些基本操作呢？我们继续详解、接着我们开始接触算法，讨论如何⽤Tarjan算法求强连通分量个数：Tarjan算法，是⼀个基于Dfs的算法（如果⼤家还不知道什么是Dfs，⾃⾏百度学习），假设我们要先从0号节点开始Dfs，我们发现⼀次Dfs 我萌就能遍历整个图（树），⽽且我们发现，在Dfs的过程中，我们深搜到了其他强连通分量中，那么俺们Dfs之后如何判断他喵的哪个和那些节点属于⼀个强连通分量呢？我们⾸先引⼊两个数组：①dfn【】②low【】第⼀个数组dfn我们⽤来标记当前节点在深搜过程中是第⼏个遍历到的点。

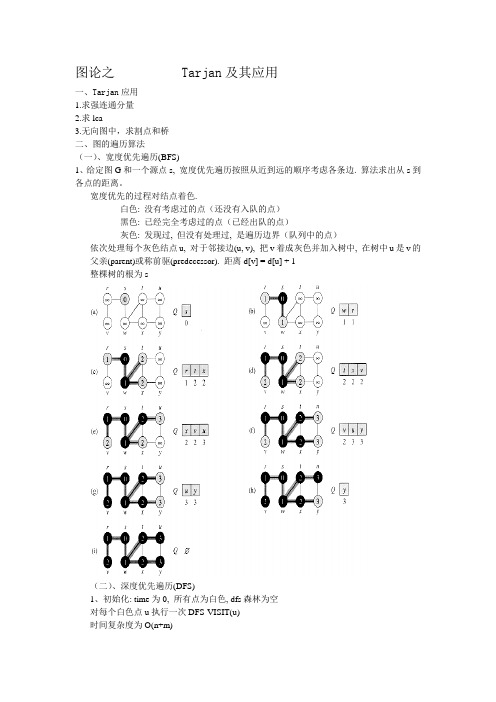
图论之 Tarjan及其应用一、Tarjan应用1.求强连通分量2.求lca3.无向图中，求割点和桥二、图的遍历算法（一）、宽度优先遍历(BFS)1、给定图G和一个源点s, 宽度优先遍历按照从近到远的顺序考虑各条边. 算法求出从s到各点的距离。

宽度优先的过程对结点着色.白色: 没有考虑过的点（还没有入队的点）黑色: 已经完全考虑过的点（已经出队的点）灰色: 发现过, 但没有处理过, 是遍历边界（队列中的点）依次处理每个灰色结点u, 对于邻接边(u, v), 把v着成灰色并加入树中, 在树中u是v的父亲(parent)或称前驱(predecessor). 距离d[v] = d[u] + 1整棵树的根为s（二）、深度优先遍历(DFS)1、初始化: time为0, 所有点为白色, dfs森林为空对每个白色点u执行一次DFS-VISIT(u)时间复杂度为O(n+m)2、伪代码三、DFS树的性质1、括号结构性质对于任意结点对(u, v), 考虑区间[d[u], f[u]]和[d[v], f[v]], 以下三个性质恰有一个成立: 完全分离u的区间完全包含在v的区间内, 则在dfs树上u是v的后代v的区间完全包含在u的区间内, 则在dfs树上v是u的后代2、定理(嵌套区间定理):在DFS森林中v是u的后代当且仅当d[u]<d[v]<f[v]<f[u], 即区间包含关系. 由区间性质立即得到。

四、边的分类1、一条边(u, v)可以按如下规则分类树边(Tree Edges, T): v通过边(u, v)发现后向边(Back Edges, B): u是v的后代前向边(Forward Edges, F): v是u的后代交叉边(Cross Edges, C): 其他边，可以连接同一个DFS树中没有后代关系的两个结点, 也可以连接不同DFS树中的结点。

判断后代关系可以借助定理12、算法当(u, v)第一次被遍历, 考虑v的颜色白色, (u,v)为T边灰色, (u,v)为B边(只有它的祖先是灰色)黑色: (u,v)为F边或C边. 此时需要进一步判断d[u]<d[v]: F边(v是u的后代, 因此为F边)d[u]>d[v]: C边(v早就被发现了, 为另一DFS树中)时间复杂度: O(n+m)定理: 无向图只有T边和B边(易证)3、实现细节if (d[v] == -1) dfs(v); //树边, 递归遍历else if (f[v] == -1) show(“B”); //后向边else if (d[v] > d[u]) show(“F”); // 前向边else show(“C”); // 交叉边注：d(入栈时间戳）和f 数组（出栈时间戳）的初值均为-1, 方便了判断四、强连通图1、在有向图G 中，如果两点互相可达，则称这两个点强连通，如果G 中任意两点互相可达，则称G 是强连通图。

Tarjan算法Taijan算法是求有向图强连通分量的算法。

Tarjan 算法主要是在 DFS 的过程中维护了⼀些信息：dfn、low 和⼀个栈。

1. 栈⾥存放当前已经访问过但是没有被归类到任⼀强连通分量的结点。

2. dfn[u] 表⽰ DFS 第⼀次搜索到 u 的次序。

3. Low(u) 记录该点所在的强连通⼦图所在⼦树的根节点的 Dfn 值。

基本思路： 在深度搜索中会搜索到已访问的节点，产⽣环，即连通分量的⼀部分，环与环的并集仍是连通分量。

由于深度搜索总是会回溯，所以将强连通图中最早搜索到的节点认为是根节点，它的dfn 和 low都是最⼩的。

之后会深度搜索⼦树的所有节点，确定所有与回边相关的环，在出现环时，环上的节点的值就会统⼀为环上最⼩的值。

直到回溯到根节点 dfn = low 的标志，输出连通分量，其他节点low相同，但dfn要⽐根节点⼤。

⾄于（ u， v ）访问到新的节点，在初始化下 v 的 low 值是递增的，但是 v 在进⼊深度搜索后，它返回的值会变化。

当 v 出现在环中被处理了， v 的 low 值会变⼩。

此时 u 也⼀定在环中， v 的low 值变⼩，是由于有⼀条回边连接到的 u 的⽗辈的节点，⽗辈的节点 - 顶点 - u - v - ⽗辈的节点构成了⼀个环。

伪码解析：Tarjan(u){DFN[u]=Low[u]=++Index // 为节点u递增地设定次序编号和Low初值Stack.push(u) // 存放已经访问过但没有被归类到任⼀强连通分量的结点for each (u, v) in E //深度搜索if ( v is not visted ) { Tarjan( v )　Low [ u ] = min( Low[ u ] , Low[ v ] ); // 初始化下 low[ v ] ⽐较⼤，若 low [ v ]变⼩， v 在环中，u 也在环中，且两个环相连通。

}else if (v in S) // 如果节点v还在栈内，出现回边，出现环Low [ u ] = min( Low[ u ], DFN[ v ] )if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根v = S.pop // 将v退栈，print vuntil (u== v)}。

Tarjan算法详解刚学的⼀个新算法，终于有时间来整理⼀下了。

想必都对著名的 ‘太监’ 算法早有⽿闻了吧。

Tarjan Tarjan 算法是⼀种求解有向图强连通分量的算法，它能做到线性时间的复杂度。

实现是基于DFS爆搜，深度优先搜索⼀张有向图。

！注意！是有向图。

然后根据树，堆栈，打标记等种种神奇扯淡⽅法来完成拆解⼀个图的⼯作。

如果要理解Tarjan，我们⾸先要了解⼀下，什么叫做强连通。

强连通 ⾸先，我们将可以相互通达的两个点，称这两个点是强连通的。

⾃然，对于⼀张图，它的每两个点都强连通，那么这张图就是⼀张强连通图。

⽽⼀张有向图中的极⼤强连通⼦图就被命名为强连通分量。

那么，举个栗⼦吃吧。

（盗图⼩丸⼦光荣上线，come from 百度） 对于上⾯的那张有向图来说，{1,2,3,4}，{5}，{6}分别相互连通，是这张图的三个强连通分量。

算法思想简解 Tarjan是在dfs的基础上将每⼀个强连通分量当做搜索树种的⼀个⼦树的遍历⽅法。

那么我们就可以在搜索的时候，将当前的树中没有访问过的节点加⼊堆栈，然后在回溯的时候判断栈顶到其中的节点是否是⼀个强连通分量。

故⽽我们在遍历的时候，定义如下变量来记录我们的遍历过程。

1.dfn[i]=时间戳（节点i被搜索的次序） 2.low[i]=i或i的⼦树所能寻找到的栈中的节点序号。

所以，当dfn[i]==low[i]时，i或i的⼦树可以构成⼀个强连通分量。

算法图解（盗图愉悦） 在这张图中我们从节点1开始遍历，依次将1， 3，5加⼊堆栈。

当搜索到节点6时，发现没有可以向前⾛的路，开始回溯。

回溯的时候会发现low[5]=dfn[5],low[6]=dfn[6]，那么{5}，{6}分别是两个强连通分量。

直到回溯⾄节点3，拓展出节点4. 结果⾃然就是拓展到了节点1，发现1在栈中，于是就⽤1来更新low[4]=low[3]=1; 然后回溯节点1，将点2加⼊堆栈中。

tarjan算法简洁模板-回复什么是Tarjan算法？Tarjan算法是一种基于深度优先搜索（DFS）的图算法，用于寻找有向图中的强连通分量（Strongly Connected Component, SCC）。

它由美国计算机科学家Robert Tarjan在1972年提出，并被广泛应用于图论和网络分析等领域。

为什么需要寻找强连通分量？强连通分量是一种图中具有特殊性质的子图，其中的任意两个顶点都可以通过有向边相互到达。

在网络分析和图论中，强连通分量代表了一组高度相互关联的节点，具有重要的意义。

例如，在社交网络中，强连通分量可能表示具有密切联系的朋友圈；在软件工程中，强连通分量可以帮助识别出相互依赖的模块。

Tarjan算法的思想是什么？Tarjan算法的基本思想是通过DFS遍历图，对每个节点进行编号和标记，并根据节点的低点值（Low Point）进行划分，以构建强连通分量。

具体步骤如下：1. 初始化变量：创建一个空栈，用于存储访问过的节点；初始化节点编号为0，用一个数组记录每个节点的索引号；初始化节点的低点值为节点编号，用一个数组记录每个节点的低点值；初始化一个布尔型数组，用于标记节点是否在栈中。

2. 对每个未访问的节点u，调用DFS函数进行递归遍历。

3. 在DFS函数中，首先给节点u赋予一个唯一的索引号，并将节点u入栈，并将节点u的索引号和低点值设置为当前节点计数器。

然后遍历u的所有邻接节点v，如果v未被访问，则递归调用DFS函数。

4. 在递归调用的过程中，更新节点u的低点值为u和v的最小值，并将已经访问过的节点v标记为在栈中。

5. 当递归调用结束后，如果节点u的索引号等于低点值，说明节点u开始构成了一个强连通分量。

从栈顶依次弹出节点，直到节点u。

被弹出的节点就是强连通分量的一部分，将这些节点存储起来。

6. 重复以上步骤，直到所有节点都被访问过。

如何实现Tarjan算法？以下是一种简洁的Python实现Tarjan算法的模板：pythondef tarjan(graph):index = {} # 用于记录每个节点的索引号low = {} # 用于记录每个节点的低点值stack = [] # 用于存储访问过的节点visited = {} # 用于标记节点是否在栈中result = [] # 存储所有的强连通分量# 初始化变量def dfs(node):index[node] = len(index)low[node] = len(low)stack.append(node)visited[node] = Truefor neighbor in graph[node]:if neighbor not in index:dfs(neighbor)low[node] = min(low[node], low[neighbor]) elif neighbor in visited:low[node] = min(low[node], index[neighbor])if index[node] == low[node]:component = []while stack[-1] != node:component.append(stack.pop())visited.pop(component[-1])component.append(stack.pop())visited.pop(component[-1])result.append(component)for node in graph:if node not in index:dfs(node)return result总结：Tarjan算法是一种基于深度优先搜索的图算法，用于查找有向图中的强连通分量。

[算法]Tarjan算法求割点(声明：以下图⽚来源于⽹络)Tarjan算法求出割点个数⾸先来了解什么是连通图在图论中，连通图基于连通的概念。

在⼀个⽆向图 G 中，若从顶点i到顶点j有路径相连（当然从j到i也⼀定有路径），则称i和j是连通的。

如果 G 是有向图，那么连接i和j的路径中所有的边都必须同向。

如果图中任意两点都是连通的，那么图被称作连通图。

如果此图是有向图，则称为强连通图（注意：需要双向都有路径）。

图的连通性是图的基本性质。

——摘⾃度娘通俗易懂，不在解释。

举个例⼦吧：如上图，各个节点皆可以到达任意节点，所以该图为连通图。

再来了解什么是割点在⼀个⽆向图中，如果有⼀个顶点集合，删除这个顶点集合以及这个集合中所有顶点相关联的边以后，图的连通分量增多，就称这个点集为割点集合。

如果某个割点集合只含有⼀个顶点X（也即{X}是⼀个割点集合），那么X称为⼀个割点。

——摘⾃度娘了解完定义之后，不难通过定义来求出图的割点——暴⼒DFS。

即是：从1到n遍历每⼀个点，每次遍历到这个点时，只需要删除该点，判断删除后是否会增加联通量即可。

这种⽅法时间复杂度最坏为O(n×(n+m))，只要数据⼤⼀点就会被卡爆，这⾥不详细叙述。

使⽤Tarjan算法求割点可以参考依然定义：dfn（时间戳），low（该集合中最早遍历到的点的时间戳）观察上图，可以发现割点求法可以分成两种情况讨论。

1. 若该点为根节点，若有该节点拥有两个及以上互不相连的⼦树，则删除该点会得到这些⼦树。

所以该点为割点。

（now == root && child >= 2）2. 若该点不为根节点，若不存在可以在DFS中可以遇到已访问节点的连边时（通俗的说，就是不可以找到回去的路），则该点为割点。

（now != root && low[next] >= dfn[now]）low的值可以证明发现：low的初始值为该节点的时间戳。