【2013版中考12年】江苏省苏州市2002-2013年中考数学试题分类解析 专题05 数量和位置变化

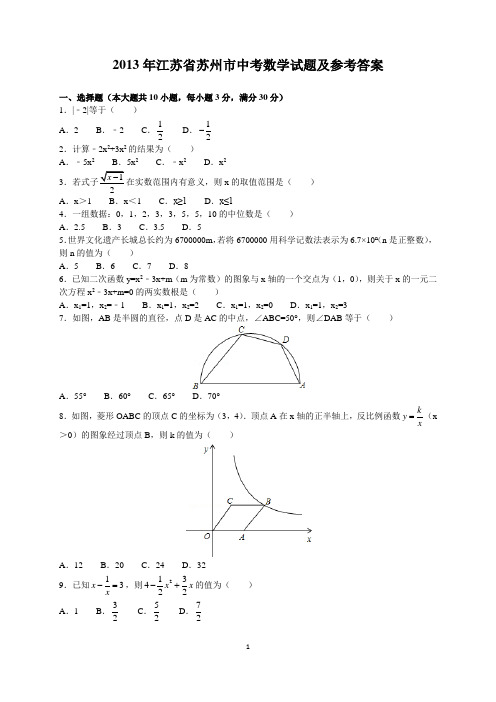
2013年江苏省苏州市中考数学试题及参考答案一、选择题（本大题共10小题，每小题3分，满分30分）1．|﹣2|等于（）A．2 B．﹣2 C．12D．12-2．计算﹣2x2+3x2的结果为（）A．﹣5x2B．5x2C．﹣x2D．x23x的取值范围是（）A．x＞1 B．x＜1 C．x≥1D．x≤14．一组数据：0，1，2，3，3，5，5，10的中位数是（）A．2.5 B．3 C．3.5 D．55．世界文化遗产长城总长约为6700000m，若将6700000用科学记数法表示为6.7×10n（n是正整数），则n的值为（）A．5 B．6 C．7 D．86．已知二次函数y=x2﹣3x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x2﹣3x+m=0的两实数根是（）A．x1=1，x2=﹣1 B．x1=1，x2=2 C．x1=1，x2=0 D．x1=1，x2=37．如图，AB是半圆的直径，点D是AC的中点，∠ABC=50°，则∠DAB等于（）A．55°B．60°C．65°D．70°8．如图，菱形OABC的顶点C的坐标为（3，4）．顶点A在x轴的正半轴上，反比例函数kyx=（x＞0）的图象经过顶点B，则k的值为（）A．12 B．20 C．24 D．329．已知13xx-=，则213422x x-+的值为（）A．1 B．32C．52D．7210．如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上．顶点B的坐标为（3，点C的坐标为（12，0），点P为斜边OB上的一个动点，则PA+PC的最小值为（）A B C D．二、填空题（本大题共8个小题，每小题3分，共24分）11．计算：a4÷a2=．12．分解因式：a2+2a+1=．13．方程15121x x=-+的解为．14．任意抛掷一枚质地均匀的正方体骰子1次，骰子的六个面上分别刻有1到6的点数，掷得面朝上的点数大于4的概率为．15．按照如图所示的操作步骤，若输入x的值为2，则输出的值为．16．如图，AB切⊙O于点B，OA=2，∠OAB=30°，弦BC∥OA，劣弧BC的弧长为．（结果保留π）17．如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，顶点A、C分别在x，y轴的正半轴上．点Q在对角线OB上，且QO=OC，连接CQ并延长CQ交边AB于点P．则点P的坐标为．18．如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD内部．将AF延长交边BC于点G．若1CGGB k=，则ADAB=用含k的代数式表示）．三、解答题（本大题共11小题，共76分） 19．（5分）计算：())311-++20．（5分）解不等式组：()21213x x x -⎧⎪⎨-+⎪⎩≥＜．21．（5分）先化简，再求值：23111x x x x -⎛⎫÷+- ⎪--⎝⎭，其中2x =． 22．（6分）苏州某旅行社组织甲乙两个旅游团分别到西安、北京旅行，已知这两旅游团共有55人，甲旅游团的人数比乙旅游团的人数的2倍少5人．问甲、乙两个旅游团个有多少人？ 23．（6分）某企业500名员工参加安全生产知识测试，成绩记为A ，B ，C ，D ，E 共5个等级，为了解本次测试的成绩（等级）情况，现从中随机抽取部分员工的成绩（等级），统计整理并制作了如下的统计图：（1）求这次抽样调查的样本容量，并补全图①；（2）如果测试成绩（等级）为A ，B ，C 级的定位优秀，请估计该企业参加本次安全生产知识测试成绩（等级）达到优秀的员工的总人数．24．（7分）如图，在方格纸中，△ABC 的三个顶点及D ，E ，F ，G ，H 五个点分别位于小正方形的顶点上．（1）现以D ，E ，F ，G ，H 中的三个点为顶点画三角形，在所画的三角形中与△ABC 不全等但面积相等的三角形是 （只需要填一个三角形）（2）先从D ，E 两个点中任意取一个点，再从F ，G ，H 三个点中任意取两个不同的点，以所取得这三个点为顶点画三角形，求所画三角形与△ABC 面积相等的概率（用画树状图或列表格求解）．25．（7分）如图，在一笔直的海岸线l上有AB两个观测站，A在B的正东方向，AB=2（单位：km）．有一艘小船在点P处，从A测得小船在北偏西60°的方向，从B测得小船在北偏东45°的方向．（1）求点P到海岸线l的距离；（2）小船从点P处沿射线AP的方向航行一段时间后，到点C处，此时，从B测得小船在北偏西15°的方向．求点C与点B之间的距离．（上述两小题的结果都保留根号）26．（8分）如图，点P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长交边AD于点F，交CD的延长线于点G．（1）求证：△APB≌△APD；（2）已知DF：FA=1：2，设线段DP的长为x，线段PF的长为y．①求y与x的函数关系式；②当x=6时，求线段FG的长．27．（8分）如图，在Rt△ABC中，∠ACB=90°，点D是AB边上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．（1）求证：BD=BF；（2）若CF=1，cosB=35，求⊙O的半径．28．（9分）如图，点O为矩形ABCD的对称中心，AB=10cm，BC=12cm，点E、F、G分别从A、B、C三点同时出发，沿矩形的边按逆时针方向匀速运动，点E的运动速度为1cm/s，点F的运动速度为3cm/s，点G的运动速度为1.5cm/s，当点F到达点C（即点F与点C重合）时，三个点随之停止运动．在运动过程中，△EBF关于直线EF的对称图形是△EB′F．设点E、F、G运动的时间为t （单位：s）．（1）当t=s时，四边形EBFB′为正方形；（2）若以点E、B、F为顶点的三角形与以点F，C，G为顶点的三角形相似，求t的值；（3）是否存在实数t，使得点B′与点O重合？若存在，求出t的值；若不存在，请说明理由．29．（10分）如图，已知抛物线y=12x2+bx+c（b，c是常数，且c＜0）与x轴分别交于点A、B（点A位于点B的左侧），与y轴的负半轴交于点C，点A的坐标为（﹣1，0）．（1）b=，点B的横坐标为（上述结果均用含c的代数式表示）；（2）连接BC，过点A作直线AE∥BC，与抛物线y=12x2+bx+c交于点E，点D是x轴上的一点，其坐标为（2，0）．当C，D，E三点在同一直线上时，求抛物线的解析式；（3）在（2）条件下，点P是x轴下方的抛物线上的一个动点，连接PB，PC，设所得△PBC的面积为S．①求S的取值范围；②若△PBC的面积S为整数，则这样的△PBC共有个．参考答案与解析一、选择题（本大题共10小题，每小题3分，满分30分）1．|﹣2|等于（）A．2 B．﹣2 C．12D．12-【知识考点】绝对值．【思路分析】根据绝对值的性质可直接求出答案．【解答过程】解：根据绝对值的性质可知：|﹣2|=2．故选A．【总结归纳】此题考查了绝对值的性质，要求掌握绝对值的性质及其定义，并能熟练运用到实际运算当中．绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．2．计算﹣2x2+3x2的结果为（）A．﹣5x2B．5x2C．﹣x2D．x2【知识考点】合并同类项．【思路分析】根据合并同类项的法则，即系数相加作为系数，字母和字母的指数不变即可求解．【解答过程】解：原式=（﹣2+3）x2=x2，故选D．【总结归纳】本题主要考查合并同类项得法则．即系数相加作为系数，字母和字母的指数不变．3x的取值范围是（）A．x＞1 B．x＜1 C．x≥1D．x≤1【知识考点】二次根式有意义的条件．【思路分析】根据二次根式有意义的条件可得x﹣1≥0，再解不等式即可．【解答过程】解：由题意得：x﹣1≥0，解得：x≥1，故选：C．【总结归纳】此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．4．一组数据：0，1，2，3，3，5，5，10的中位数是（）A．2.5 B．3 C．3.5 D．5【知识考点】中位数．【思路分析】根据中位数的定义先把这组数据从小到大排列，再求出最中间两个数的平均数即可．【解答过程】解：将这组数据从小到大排列为：0，1，2，3，3，5，5，10，最中间两个数的平均数是：（3+3）÷2=3，则中位数是3；故选B．【总结归纳】此题考查了中位数，掌握中位数的概念是解题的关键，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）．5．世界文化遗产长城总长约为6700000m，若将6700000用科学记数法表示为6.7×10n（n是正整数），则n的值为（）A．5 B．6 C．7 D．8【知识考点】科学记数法—表示较大的数．【思路分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答过程】解：将6700000用科学记数法表示为6.7×106，故n=6．故选B．。

江苏省苏州市201３年中考数学试卷一、选择题(本大共10小题,每小题３分，满分３0分）1.（3分)（20１３•苏州）|﹣2|等于（)A. 2B．﹣2 C. D.考点: 绝对值．分析:根据绝对值的性质可直接求出答案.解答：解:根据绝对值的性质可知:｜﹣2｜＝2.故选A.点评：此题考查了绝对值的性质,要求掌握绝对值的性质及其定义,并能熟练运用到实际运算当中.绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．２．(3分)(2０13•苏州)计算﹣2x2+3x２的结果为()A. ﹣5ｘ2Ｂ. 5ｘ2C．﹣x2D．x2考点: 合并同类项.分析:根据合并同类项的法则，即系数相加作为系数,字母和字母的指数不变即可求解．解答:解：原式＝(﹣２+3)ｘ2=x２，故选D．点评：本题主要考查合并同类项得法则.即系数相加作为系数，字母和字母的指数不变.3.(3分）（2０13•苏州)若式子在实数范围内有意义,则ｘ的取值范围是( ）Ａ．x＞1 B. x<１ C. x≥1 Ｄ．x≤1考点：二次根式有意义的条件．分析:根据二次根式有意义的条件可得x﹣１≥0，再解不等式即可．解答：解：由题意得:x﹣1≥0,解得:x≥1,故选:C．点评:此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数.４．(3分）(２0１3•苏州）一组数据：0，1，2，3,3，5，5,10的中位数是（)A．2.5 B．３C．３.5 D. 5考点: 中位数．分析:根据中位数的定义先把这组数据从小到大排列，再求出最中间两个数的平均数即可．解答：解：将这组数据从小到大排列为:0,1,2,３，3,５,5,10,最中间两个数的平均数是:（3＋3）÷2＝3,则中位数是3;故选B．点评：此题考查了中位数，掌握中位数的概念是解题的关键,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数).５．（3分)（2013•苏州）世界文化遗产长城总长约为6７00000m，若将６700000用科学记数法表示为６．７×10ｎ（ｎ是正整数）,则ｎ的值为( ）A．5Ｂ. ６C．7Ｄ. 8考点：科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10ｎ的形式，其中1≤|a|<10，n为整数．确定ｎ的值时,要看把原数变成a 时，小数点移动了多少位，ｎ的绝对值与小数点移动的位数相同.当原数绝对值>1时，n是正数;当原数的绝对值＜１时,n是负数.解答：解:将６7000０0用科学记数法表示为６.7×106,故n＝6.故选B.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式，其中１≤|ａ|＜１０,n为整数，表示时关键要正确确定a的值以及n的值.6．（3分)(２０13•苏州)已知二次函数y=x2﹣3ｘ＋m(m为常数）的图象与ｘ轴的一个交点为(１,0),则关于x的一元二次方程ｘ２﹣3x+m＝0的两实数根是（）A. ｘ1=1，x2=﹣１B. x１=1，x2=2 Ｃ．ｘ1=1,ｘ2=0 Ｄ．x1=1,x2=3考点：抛物线与x轴的交点．分析:关于x的一元二次方程x2﹣３x+ｍ=0的两实数根就是二次函数ｙ＝x２﹣3x+m(m为常数）的图象与ｘ轴的两个交点的横坐标．解答：解：∵二次函数的解析式是ｙ=ｘ2﹣3x+m(m为常数），∴该抛物线的对称轴是:ｘ=.又∵二次函数y＝x2﹣3x＋m（m为常数)的图象与ｘ轴的一个交点为（１,0）,∴根据抛物线的对称性质知，该抛物线与x轴的另一个交点的坐标是（2，0),∴关于x的一元二次方程ｘ2﹣３x＋m＝０的两实数根分别是:ｘ1=1,x２=2．故选Ｂ.点评:本题考查了抛物线与x轴的交点．解答该题时，也可以利用代入法求得m的值，然后来求关于ｘ的一元二次方程x2﹣3x＋m=0的两实数根．7．（3分）(２0１３•苏州）如图，AB是半圆的直径，点D是AC的中点，∠ABC＝50°，则∠DAB等于()A．5５° B. 60°Ｃ．65°Ｄ. 70°考点: 圆周角定理;圆心角、弧、弦的关系.专题：计算题．分析：连结BD,由于点D是AＣ弧的中点，即弧CD=弧AD，根据圆周角定理得∠ＡＢD=∠CBD，则∠ABD=２5°,再根据直径所对的圆周角为直角得到∠ＡDB=９0°,然后利用三角形内角和定理可计算出∠ＤAB的度数.解答：解：连结BＤ,如图，∵点D是AC弧的中点，即弧CD=弧AD,。

2013年苏州市初中毕业暨升学考试试卷数学本试卷由选择题、填空题和解答题三大题组成．共29小题，满分130分．考试时间120分钟．注意事项：1．答题前，考生务必将自己的姓名、考点名称、考场号、座位号用0.5毫米黑色墨水签字笔填写在答题卡的相应位置上，并认真核对条形码上的准考号、姓名是否与本人的相符；2．答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案；答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题；3．考生答题必须答在答题卡上，保持卡面清洁，不要折叠，不要弄破，答在试卷和草稿纸上一律无效．一、选择题：本大题共有10小题，每小题3分，共30分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将选择题的答案用2B铅笔涂在答题卡相应的位置上．1．2-等于A．2 B．－2 C．±2 D．±2．计算－2x2＋3x2的结果为A．－5x2B．5x2C．－x2D．x23在实数范围内有意义，则x的取值范围是A．x>1 B．x<1 C．x≥1 D．x≤14．一组数据：0，1，2，3，3，5，5，10的中位数是A．2.5 B．3 C．3.5 D．55．世界文化遗产长城总长约为6700000m，若将6700000用科学记数法表示为6.7×10n（n是正整数），则n的值为A．5 B．6 C．7 D．86．已知二次函数y＝x2－3x＋m（m为常数）的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程x2－3x＋m＝0的两实数根是A．x1＝1，x2＝－1 B．x1＝1，x2＝2C．x1＝1，x2＝0 D．x1＝1，x2＝37．如图，AB是半圆的直径，点D是AC的中点，∠ABC＝50°，则∠DAB等于A．55°B．60°C．65°D．70°8．如图，菱形OABC的顶点C的坐标为(3，4)，顶点A在x轴的正半轴上．反比例函数y＝ (x>0)的图象经过顶点B，则k的值为A．12 B．20 C．24 D．329．已知x－＝3，则4－x2＋x的值为A．1 B．C．D．10．如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，3），点C的坐标为（，0），点P为斜边OB上的一动点，则PA＋PC的最小值为A．13B．31C．3192+D．27二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相对应的位置上．11．计算：a4÷a2＝▲．12．因式分解：a2＋2a＋1＝▲．13．方程15121x x=-+的解为▲．14．任意抛掷一枚质地均匀的正方体骰子1次，骰子的六个面上分别刻有1到6的点数，掷得面朝上的点数大于4的概率为▲．15．按照下图所示的操作步骤，若输入x的值为2，则输出的值为▲．16．如图，AB 切⊙O 于点B ，OA ＝2，∠OAB ＝30°，弦BC ∥OA ，劣弧»BC 的弧长为 ▲ ． （结果保留π）17．如图，在平面直角坐标系中，四边形OABC 是边长为2的正方形，顶点A ，C 分别在x ，y 轴的正半轴上．点Q 在对角线OB 上，且OQ ＝OC ，连接CQ 并延长CQ 交边AB 于点P ，则点P 的坐标为( ▲ ， ▲ )．18．如图，在矩形ABCD 中，点E 是边CD 的中点，将△ADE 沿AE 折叠后得到△AFE ，且点F 在矩形ABCD 内部．将AF 延长交边BC 于点G ．若1CG GB k =，则AD AB = ▲ （用含k 的代数式表示）．三、解答题：本大题共11小题，共76分，把解答过程写在答题卡相应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明．作图时用2B 铅笔或黑色墨水签字笔．19．（本题满分5分）计算：()()031319-+++．20．（本题满分5分） 解不等式组：()21213x x x -≥⎧⎪⎨-<+⎪⎩21．（本题满分5分）先化简，再求值：23111x x x x -⎛⎫÷+- ⎪--⎝⎭，其中x ＝3－2．22．（本题满分6分）苏州某旅行社组织甲、乙两个旅游团分别到西安、北京旅游．已知这两个旅游团共有55人，甲旅游团的人数比乙旅游团的人数的2倍少5人．问甲、乙两个旅游团各有多少人？23．（本题满分6分）某企业500名员工参加安全生产知识测试，成绩记为A，B，C，D，E共5个等级，为了解本次测试的成绩（等级）情况，现从中随机抽取部分员工的成绩（等级），统计整理并制作了如下的统计图：(1)求这次抽样调查的样本容量，并补全图①；(2)如果测试成绩（等级）为A，B，C级的定为优秀，请估计该企业参加本次安全生产知识测试成绩（等级）达到优秀的员工的总人数．（图②）24．（本题满分7分）如图，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点分别位于小正方形的顶点上．(1)现以D，E，F，G，H中的三个点为顶点画三角形，在所画的三角形中与△ABC不全等．．．但面积相等的三角形是▲（只需要填一个三角形）；(2)先从D，E两个点中任意取一个点，再从F，G，H三个点中任意取两个不同的点，以所取的这三个点为顶点画三角形，求所画三角形与△ABC面积相等的概率（用画树状图或列表格求解）．25．（本题满分7分）如图，在一笔直的海岸线l上有A，B两个观测站，A在B的正东方向，AB＝2（单位：km）．有一艘小船在点P处，从A测得小船在北偏西60°的方向，从B测得小船在北偏东45°的方向．(1)求点P到海岸线l的距离；(2)小船从点P处沿射线AP的方向航行一段时间后，到达点C处．此时，从B测得小船在北偏西15°的方向．求点C与点B之间的距离．（上述2小题的结果都保留根号）26．（本题满分8分）如图，点P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长BP交边AD于点F，交CD的延长线于点G．(1)求证：△APB≌△APD；(2)已知DF：FA＝1：2，设线段DP的长为x，线段PF的长为y．①求y与x的函数关系式；②当x＝6时，求线段FG的长．27．（本题满分8分）如图，在Rt△ABC中，∠ACB＝90°，点D是边AB上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．(1)求证：BD＝BF；(2)若CF＝1，cosB＝，求⊙O的半径．28．（本题满分9分）如图，点O为矩形ABCD的对称中心，AB＝10cm，BC＝12cm．点E，F，G分别从A，B，C三点同时出发，沿矩形的边按逆时针方向匀速运动，点E的运动速度为1cm/s，点F的运动速度为3cm／s，点G的运动速度为1.5cm／s．当点F到达点C（即点F与点C重合）时，三个点随之停止运动．在运动过程中，△EBF关于直线EF的对称图形是△EB'F，设点E，F，G运动的时间为t（单位：s）．(1)当t＝▲ s时，四边形EBFB'为正方形；(2)若以点E，B，F为顶点的三角形与以点F，C，G为顶点的三角形相似，求t的值；(3)是否存在实数t，使得点B'与点O重合？若存在，求出t的值；若不存在，请说明理由．29．（本题满分10分）如图，已知抛物线y＝x2＋bx＋c（b，c是常数，且c<0）与x轴分别交于点A，B（点A位于点B的左侧），与y轴的负半轴交于点C，点A的坐标为(－1，0)．(1)b＝▲，点B的横坐标为▲（上述结果均用含c的代数式表示）；(2)连接BC，过点A作直线AE∥BC，与抛物线y＝x2＋bx＋c交于点E．点D是x轴上一点，其坐标为(2，0)，当C，D，E三点在同一直线上时，求抛物线的解析式；(3)在(2)的条件下，点P是x轴下方的抛物线上的一动点，连接PB，PC，设所得△PBC的面积为S．①求S的取值范围；②若△PBC的面积S为整数，则这样的△PBC共有▲个．2013年苏州市初中毕业暨升学考试试卷数学试题参考答案一、选择题1．A 2．D 3．C 4．B 5．B6．B 7．C 8．D 9．D 10．B二、填空题11．a 2 12．(a ＋1)2 13．x ＝2 14．15．20 16．3π 17．(2，4－22) 18．1k + 三、解答题19．原式＝3．20．3≤x<521．原式＝12x +． 3 22．甲、乙两个旅游团分别有35人、20人．23．(1)样本容量为50．补图正确；(2)估计该企业参加本次安全生产知识测试成绩（等级）达到优秀的员工的总人数为370人．24．(1)△DFG 或△DHF ；(2)画树状图：所画三角形与△ABC 面积相等的概率为25．(1)点P 到海岸线的距离为31) km ．(2)点C 与点B 2km ．26．(1)证明略(2)①y ＝x②FG 的长度为527．(1) 证明略(2)28．(1)2.5(2)t ＝145或－14＋ (3)不存在29．(1)＋c ，－2c ；(2)y ＝x 2－x －2．(3)①0<S<5 ②11．考试高分秘诀是什么？试试这四个方法，特别是中考和高考生谁都想在考试中取得优异的成绩，但要想取得优异的成绩，除了要掌握好相关的知识定理和方法技巧之外，更要学会一些考试技巧。

【2013版中考12年】江苏省苏州市2002-2013年中考数学试题分类解析专题07 统计与概率一、选择题1.（江苏省苏州市2005年3分）初二（1）班有48名学生，春游前，班长把全班学生对春60，游地的意向绘制成了扇形统计图，其中，“想去苏州乐园的学生数”的扇形圆心角是则下列说法正确的是【】A．想去苏州乐园的学生占全班学生的60% B．想去苏州乐园的学生有12人1 C．想去苏州乐园的学生肯定最多 D．想去苏州乐园的学生占全班学生的62.（江苏省苏州市2005年3分）下图的转盘被划分成六个相同大小的扇形，并分别标上1，2，3，4，5，6这六个数字，指针停在每个扇形的可能性相等。

四位同学各自发表了下述见解：甲：如果指针前三次都停在了3号扇形，下次就一定不会停在3号扇形；乙：只要指针连续转六次，一定会有一次停在6号扇形；丙：指针停在奇数号扇形的概率与停在偶数号扇形的概率相等；丁：运气好的时候，只要在转动前默默想好让指针停在6号扇形，指针停在6号扇形的可能性就会加大。

其中，你认为正确的见解有【】A．1个 B．2个 C．3个 D．4个【答案】A。

【考点】几何概率。

【分析】随机事件发生的可能性大小在0至1之间，可能性大的也不是肯定会发生，可能性小的也不是肯3.（江苏省苏州市2006年3分）某校测量了初三(1)班学生的身高(精确到1cm)，按10cm 为一段进行分组，得到如下频数分布直方图，则下列说法正确的是【】A.该班人数最多的身高段的学生数为7人B.该班身高低于160.5cm的学生数为15人C.该班身高最高段的学生数为20人D.该班身高最高段的学生数为7人4.（江苏省苏州市2006年3分）下列说法正确的是【】A．一颗质地均匀的骰子已连续抛掷了2000次，其中，抛掷出5点的次数最少，则第2001次一定抛掷出5点B.某种彩票中奖的概率是1%，因此买100张该种彩票一定会中奖C．天气预报说明天下雨的概率是50％．所以明天将有一半时间在下雨D.抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等【答案】D。

【2013版中考12年】江苏省苏州市2002-2013年中考数学试题分类解析 专题05 数量和位置变化一、选择题1.（江苏省苏州市2002年3分）点P （－2，3）关于原点的对称点的坐标是【 】A. （－2，3）B. （2，－3）C. （2，3）D.（－2，－3）2.（江苏省苏州市2002年3分）如图，已知△ABC 中，BC=8，BC 上的高，D 为BC 上一点， EF∥BC，交AB 于点E ，交AC 于点F （EF 不过A 、B ），设E 到BC 的距离为，则△DEF 的面积关于的函数的图象大致为【 】3.（江苏省苏州市2006年3分）下列函数中，自变量x 的取值范围是x>2的函数是【 】 A. y x 2=- B. y 2x 1=- C. y x 2=- D. y 2x 1=-4.（江苏省苏州市2008年3分）函数1y=x 2+中，自变量x 的取值范围是【 】 A ．x ≠0 B．x ≠l C．x ≠－2 D ．x ≠－15.（江苏省苏州市2010年3分）函数11y x =-的自变量x 的取值范围是【 】 A ．0x ≠ B ．1x ≠ C ．1x ≥ D ．1x ≤6. （2012江苏苏州3分）已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B 1在y 轴上，点C 1、E 1、E 2、C 2、E 3、E 4、C 3在x 轴上．若正方形A 1B 1C 1D 1的边长为1，∠B 1C 1O=60°， B 1C 1∥B 2C 2∥B 3C 3，则点A 3到x 轴的距离是【 】7.（2013年江苏苏州3分）如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（33C的坐标为（12，0），点P为斜边OB上的一动点，则PA＋PC的最小值为【】二、填空题1. （江苏省苏州市2002年2分）函数中自变量的取值范围是 ▲ _【答案】2x ≥。

【考点】函数自变量的取值范围，二次根式有意义的条件。

【2013版中考12年】江苏省苏州市2002-2013年中考数学试题分类解析专题11 圆一、选择题1.（江苏省苏州市2002年3分）如图，⊙O的弦AB=8cm，弦CD平分AB于点E。

若CE=2 cm，则ED长为【】A. 8cmB. 6cmC. 4cmD. 2cm2.（江苏省苏州市2002年3分）如图，四边形ABCD内接于⊙O，若∠BOD=1600，则∠BCD=【】A. B. C. D.故选B。

3.（江苏省苏州市2002年3分）如图，⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D。

DF⊥AC，垂足为F，DE⊥BC，垂足为E。

给出下列4个结论：①CE=CF，②∠ACB=∠EDF ，③DE是⊙O的切线，④AD=BD。

其中一定成立的是【】A. ①②③B. ②③④C. ①③④D. ①②④【答案】D。

④如图，连接AD，BD。

根据圆内接四边形的外角等于内对角得∠DCE=∠DAB，又∵∠DCE=∠DCF，∠DCA=∠DBA，∴∠DAB=∠DBA＜900。

∴AD=BD。

综上所述，①②④正确。

故选D。

4.（江苏省苏州市2003年3分）如图，四边形ABCD内接于⊙O，若它的一个外角∠DCE=700，则∠BOD=【】A. 350B. 700C. 1100D. 14005.（江苏省苏州市2004年3分）如图，AB是⊙的直径，弦CD垂直平分OB，则∠BDC=【】Ａ。

15° Ｂ。

20° Ｃ。

30° Ｄ。

45°【答案】【考点】圆周角定理，线段垂直平分线的性质，等边三角形的判定和性质。

【分析】连接OC，BC，∵弦CD垂直平分OB，∴根据线段垂直平分线上的点到线段两端距离相等的性质，得OC=BC。

又∵OC=OB，∴△OCB是等边三角形。

∴∠COB=60°。

∴根据同弧所对圆周角是圆心角一半的圆周角定理，得∠D=30°。

故选C。

6.（江苏省苏州市2008年3分）如图．AB为⊙O的直径，AC交⊙O于E点，BC交⊙O于D点，CD=BD，∠C=70°．现给出以下四个结论：；④CE·AB=2BD2．①∠A=45°；②AC=AB：③AE BE其中正确结论的序号是【】A．①② B．②③ C．②④ D．③④7. （2012江苏苏州3分）一组数据2，4，5，5，6的众数是【】A. 2B. 4C. 5D. 6【答案】C。

【2013版中考12年】江苏省苏州市2002-2013年中考数学试题分类解析 专题06 函数的图像与性质一、选择题1.（江苏省苏州市2003年3分） 已知a 1<-，点()()()123a 1y a y a 1y -+，，，，，都在函数2y=x 的图像上，则【 】A. 123y y y <<B. 132y y y <<C. 321y y y <<D. 213y y y <<2.（江苏省苏州市2004年3分）已知正比例函数y=(3k —1)x ，若y 随x 的增大而增大，则的取值范围是【 】A k ＜0B k ＞ 0C k ＜31 D k ＞313.（江苏省苏州市2005年3分）将直线x y 2=向上平移两个单位，所得的直线是【 】A ．22+=x yB ．22-=x yC ．)2(2-=x yD ．)2(2+=x y 【答案】A 。

【考点】一次函数图象与平移变换。

【分析】直线平移时k 的值不变，只有b 发生变化，因此，原直线的k=2，b=0，向上平移两个单位得到了新直线，新直线的k=2，b=0+2=2。

∴新直线的解析式为22y x =+。

故选A 。

4.（江苏省苏州市2010年3分）如图，已知A 、B 两点的坐标分别为(2，0)、(0，2)，C的圆心坐标为(－1，0)，半径为1．若D 是C 上的一个动点，线段DA 与y 轴交于点E ，则ABE ∆面积的最小值是【 】A ．2B ．1C ．22-D ．22-5.（江苏省苏州市2011年3分）如图，已知A 点坐标为（5，0），直线(0)y x b b =+>与y 轴交于点B ，连接AB ，∠a =75°，则b 的值为【 】A ．3B 53C ．4D 536. （2012江苏苏州3分）若点（m ，n ）在函数y=2x+1的图象上，则2m-n 的值是【 】 A.2 B.-2 C.1 D. -17.（2013年江苏苏州3分）已知二次函数2y x 3x m =-+（m 为常数）的图象与x 轴的一个交点为(1，0)，则关于x 的一元二次方程2x 3x m 0-+=的两实数根是【 】 A ．x 1＝1，x 2＝－1 B ．x 1＝1，x 2＝2 C ．x 1＝1，x 2＝0D ．x 1＝1，x 2＝38.（2013年江苏苏州3分）如图，菱形OABC 的顶点C 的坐标为（3，4），顶点A 在x 轴的正半轴上．反比例函数y kx=(x>0)的图象经过顶点B ，则k 的值为【 】A．12 B．20 C．24 D．32二、填空题1.（江苏省苏州市2002年2分）抛物线的顶点坐标是▲2. （江苏省苏州市2002年2分）设有反比例函数，、为其图象上的两点，若时，，则的取值范围是▲3. （江苏省苏州市2003年2分）已知点（1，－2）在反比例函数ky=x的图像上，则k=▲ 。

江苏省南京市2002-2013年中考数学试题分类解析 专题11 圆一、选择题1.（江苏省南京市2002年2分）如图，正六边形ABCDEF 的边长是a,分别以C 、F 为圆心，a 为半径画弧，则图中阴影部分的面积是【 】A 、21r 6π B 、21r 3π C 、22r 3π D 、24r 3π2. （江苏省南京市2003年2分）如图，AB 是⊙O 的直径，P 是AB 延长线上的一点，PC 切⊙O 于点C ，PC ＝3，PB ＝1，则⊙O 的半径等于【 】．（A ）25 （B ）3 （C ）4 （D ） 29∵PC，PA 分别是圆的切线与割线，∴PC 2=PB•PA。

∵PC=3，PB=1，∴PA=9，AB=8。

∴半径为4．故选C 。

3. （江苏省南京市2003年2分）正方形ABCD 的边长是2cm ，以直线AB 为轴旋转一周，所得到的圆柱的侧面积为【 】．（A ）16π2cm （B ）8π2cm （C ）4π2cm （D ）42cm4. （江苏省南京市2004年2分）如图，A ，B 是⊙O 上的两点，AC 是⊙O 的切线，∠B=70°，则∠BAC 等于【 】A 、70°B 、35° C、20° D 、10°5. （江苏省南京市2006年2分）如图，点A 、B 、C 在⊙O 上，AO∥BC，∠OAC=20°，则∠AOB的度数是【 】A.1O °B.20°C.40°D.70°【答案】C 。

【考点】圆周角定理，平行线的性质。

【分析】∵∠OAC=20°，AO∥BC，∴∠ACB =∠OAC=20°。

∴∠AOB=2∠ACB =40°。

故选C 。

6. （江苏省南京市2008年2分）如图，⊙O是等边三角形ABC的外接圆，⊙O的半径为2，则等边三角形ABC的边长为【】7. （江苏省南京市2008年2分）如图，已知⊙O的半径为1，AB与⊙O相切于点A，OB与的值等于【】⊙O交于点C，OD⊥OA，垂足为D，则cos AOB二、填空题1. （江苏省南京市2002年2分）如图，AB是⊙O的直径，弦CD⊥AB，垂足为G，F是CG 的中点，延长AF交⊙O于E，CF＝2，AF＝3，则EF的长是▲ .2. （江苏省南京市2003年2分）如图，⊙O的两条弦AB、CD相交于点P，PD＝2PB，PC＝2cm，则 PA＝▲ cm．3. （江苏省南京市2004年2分）如图，割线PAB与⊙O交于点A、B，割线PCD与⊙O交于点C 、D ，PA=PC ，PB=3cm ，则PD= ▲ cm ．4. （江苏省南京市2007年3分）如图，⊙O 是△ABC 的外接圆，∠C=30°，AB=2cm ，则⊙O 的半径为▲ cm ．5. （江苏省南京市2008年3分）已知1O 和2O 的半径分别为3cm 和5cm ，且它们内切，则圆心距12O O 等于 ▲ cm ．6. （江苏省南京市2008年3分）如图，有一圆形展厅，在其圆形边缘上的点A处安装了一台监视器，它的监控角度是65．为了监控整个展厅，最少需在圆形边缘上共．安装．．这样的监视器▲ 台．7. （江苏省2009年3分）如图，AB是⊙O的直径，弦CD∥AB．若∠ABD=65°，则∠ADC=▲ ．8. （江苏省2009年3分）已知正六边形的边长为1cm，分别以它的三个不相邻的顶点为圆心，1cm长为半径画弧（如图），则所得到的三条弧的长度之和为▲ cm（结果保留π）．弧长6011CmB1803ππ⋅⋅==。