2014友好三中高三数学周测试九

2014哈三中校三模】黑龙江省哈三中2014届高三第三次高考模拟考试数学文Word版含答案XXX2013-2014年高三下学期第三次高考模拟考试数学试卷（文史类）考试说明：本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟。

1.答题前，请填写姓名和准考证号码。

选择题使用2B铅笔填涂，非选择题使用0.5毫米黑色字迹的签字笔书写，字体工整，字迹清楚。

2.请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效。

3.保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀。

第I卷选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

）1.已知全集U=R，集合A={x|x-2x-3>0}，B={x|2<x<4}，那么集合(C∪A)∩B=A) {x-1≤x≤4} (B) {x^2<x≤3} (C) {x^2≤x<3} (D) {x-1<x<4}2.复数1+i+i+⋯+i等于A) i (B) -i (C) 2i (D) -2i3.已知a=2.3^(210)，b=log2 3，c=log2 4，则A) a>b>c (B) a>c>b (C) b>c>a (D) c>b>a4.已知直线m,n和平面α，则XXX的一个必要条件是A) m//α，n//α (B) m⊥α，n⊥α (C) m//α，n⊂α (D) m,n与α成等角5.已知x与y之间的一组数据。

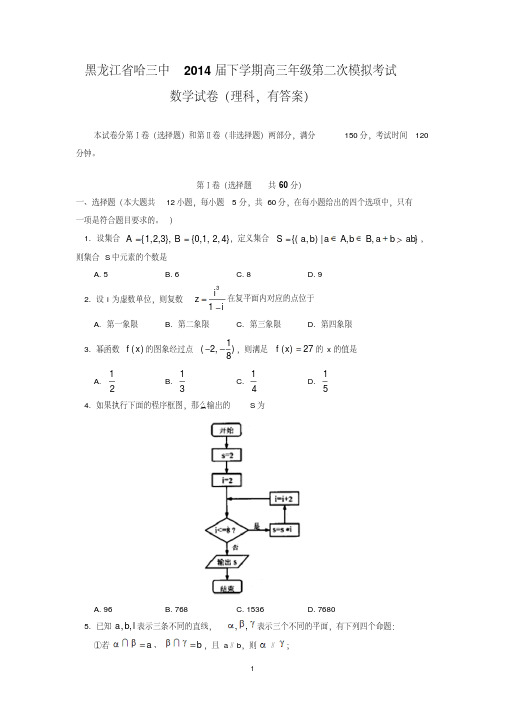
x 1 2 3y 3 5.5 7已求得关于y与x的线性回归方程为ŷ=2.1x+0.85，则m 的值为A) 1 (B) 0.85 (C) 0.7 (D) 0.56.在数列{an}中，已知a1+a2+⋯+an=2n-1，则a1^2+a2^2+⋯+an^2=A) n^2 (B) n(4n-1) (C) 4n-1 (D) 3n^27.执行如图所示的程序框图，若输出S=15，则框图中①处可以填入A) n>4 (B) n>8 (C) n>16 (D) n<16开始S=0,n=1S=S+nn=2n否①是输出S结束8.已知z=2x+y，其中实数x,y满足x+y≤2，且z的最大值是最小值的4倍，则a的值是A) 2/11 (B) 1/11 (C) 4 (D) 11/49.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>b)$的右焦点为$F$，过$F$的直线$l$交双曲线的渐近线于$A,B$两点，且与其中一条渐近线垂直，若$AF=4FB$，则该双曲线的离心率是$\frac{5}{4}$。

2014年黑龙江省某校高考数学三模试卷（文科）一、选择题（每小题5分，共60分）1. 设复数z =(1−i)2（i 是虚数单位），则z ¯的虚部是（ ） A 2i B −2i C 2 D −22. 已知cosα=−13，α是第三象限角，则tanα=( )A 2√2B −2√2C √24 D −√243. 已知条件p:a <0，条件q:a 2>a ，则￢p 是￢q 的（ ）A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件 4. 已知等比数列{a n }的前n 项和为S n ，且满足S6S 3=9，则公比q =( )A 12B ±12C 2D ±25. 已知双曲线C:x 2a 2−y 2b 2=1(a >0, b >0)离心率为3，直线y =2与双曲线C 的两个交点间的距离为√6，则双曲线C 的方程是（ ） A 2x 2−y 2=1 B x 2−y 28=1 Cx 25−y 210=1 D4x 25−y 210=16. 王明早晨在6:30∼7:00之间离开家去上学，送奶员在早上6:45∼7:15之把牛奶送到王明家，则王明离开家之前能取到牛奶的概率为（ ） A 18B 14C 78D 587. 如图是“二分法”解方程的流程图．在①∼④处应填写的内容分别是（ ）A f(a)f(m)<0；a =m ；是；否B f(b)f(m)<0；b =m ；是；否 C f(b)f(m)<0；m =b ；是；否 D f(b)f(m)<0；b =m ；否；是8. 设x ，y ∈R ，a >0，且|x|+|y|≤a ，2x +y +1最大值小于2，则实数a 的取值范围为（ ）A (0, 1)B (0, 12) C [12, 1) D (0, 1]9. 已知△ABC 中，BC =2，∠A =π3，则|AB →+AC →|的最大值（ ） A√213 B 2√213C 2√3D 4√3 10.Rt △ABC 中CA =CB =√2，M 为AB 的中点，将△ABC 沿CM 折叠，使A ，B 之间的距离为1，则三棱锥M −ABC 外接球的表面积为( ) A16π3B 4πC 3πD 7π311. 已知A ，B 是抛物线y 2=4x 上异于顶点O 的两个点，直线OA 与直线OB 的斜率之积为定值−4，△AOF ，△BOF 的面积为S 1，S 2，则S 12+S 22的最小值为（ ） A 8 B 6 C 4 D 212. 函数f(x)={2x 3+3x 2，x ≤0axex，x >0在[−2, 2]上的最大值为1，则实数a 的取值范围是（ ） A [0, +∞) B [0, e] C (−∞, 0] D (−∞, e]二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中横线上） 13. 过点P(3, 4)作抛物线x 2=2y 的两条切线，切点分别为A 、B ，则直线AB 的斜率为________．14. 某几何体的三视图如图所示(x =1)，则该几何体的体积为________．15. 利用回归分析的方法研究两个具有线性相关关系的变量时，下列说法正确的是：________①相关系数r 满足|r|≤1，而且|r|越接近1，变量间的相关程度越大，|r|越接近0，变量间的相关程度越小；②可以用R 2来刻画回归效果，对于已获取的样本数据，R 2越小，模型的拟合效果越好； ③如果残差点比较均匀地落在含有x 轴的水平的带状区域内，那么选用的模型比较合适；这样的带状区域越窄，回归方程的预报精度越高；④不能期望回归方程得到的预报值就是预报变量的精确值． 16. 数列{a n }的通项为a n =(−1)n (2n −1)⋅cosnπ2+1前n 项和为S n ，则S 60=________．三、解答题（本大题共70分.解答应写出文字说明、证明过程或演算步骤） 17. 已知向量n →=(√3sin x4, −1)，n →=(cos x4, cos 2x4)，记f(x)=m →⋅n →，（1）求f(x)的值域和单调递增区间；（2）在△ABC中，角A、B、C的对边分别是a、b、c，且满足(2a−c)cosB=bcosC，若f(A)=−12，a=2，求△ABC的面积．18. 如图，四边形ABCD是边长为2的正方形，DE⊥平面ABCD，AF // DE，DE=2AF，BE与平面ABCD所成角的正切值为√22．（1）求证：直线AC // 平面EFB；（2）求直线AC与平面ABE所成角的正弦值．19. 某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩，统计后获得成绩数据的茎叶图（以十位数字为茎，个位数字为叶），如图所示：（1）分别计算两组数据的平均数，并比较哪个班级的客观题平均成绩更好；（2）从这两组数据中分别抽取一个数据，求其中至少有一个是满分的概率；（3）规定：客观题成绩不低于55分为“优秀客观卷”，从甲班的十个数据中任意抽取两个，求两个都是“优秀客观卷”的概率．20. 已知中心在原点O，焦点在x轴上的椭圆C方程为x2a2+y2b2=1，椭圆上的点到焦点距离最大值为3，离心率e=12．（1）求椭圆C的方程；（2）A，B为椭圆上的点，△AOB面积为√3，求证：|OA|2+|OB|2为定值．21. 已知f(x)=axe kx−1，g(x)=lnx+kx．（1）求g(x)的单调区间；（2）当k=1时，f(x)≥g(x)恒成立，求a的取值范围．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题记分，做题时请写清题号.【选修4-1：几何证明选讲】22. 如图，假设两圆O1和O2交于A、B，⊙O1的弦BC交⊙O2于E，⊙O2的弦BD交⊙O1于F，证明：（1）若∠DBA =∠CBA ，则DF =CE ； （2）若DF =CE ，则∠DBA =∠CBA ．【选修4-4：坐标系与参数方程】23. 已知直线l 的参数方程为{x =−1+ty =2+t （t 为参数），在直角坐标系xOy 中以O 为极点，x 轴正半轴为极轴建立坐标系．圆C 的极坐标方程分别为ρ2=4√2ρsin(θ−π4)−6 （1）求直线l 与圆C 的直角坐标方程；（2）设A(−1, 2)，P ，Q 为直线l 与圆C 的两个交点，求|PA|+|AQ|．【选修4-5：不等式选讲】 24. 设函数f(x)=|x −a|．（1）当a =2时，解不等式f(x)≥4−|x −1|；（2）若f(x)≤1的解集为{x|0≤x ≤2}，1m +12n =a(m >0, n >0)．求证：m +2n ≥4．2014年黑龙江省某校高考数学三模试卷（文科）答案1. C2. A3. B4. C5. B6. A7. B8. B9. C 10. D 11. D 12. D 13. 3 14. 1615. ①③④ 16. 12017. 解：（1）由题意可得f(x)=m →⋅n →=√3sin x4cos x4−cos 2x4=√32sin x 2−1+cos x22=sin(x2−π6)−12， 故函数的值域为[−32, 12]．令 2kπ−π2≤x 2−π6≤2kπ+π2，k ∈z ，求得 4kπ−2π3≤x ≤4kπ+4π3，k ∈z ，故函数的单调递增区间为[4kπ−2π3, 4kπ+4π3]，k ∈z ．（2）在△ABC 中，∵ (2a −c)cosB =bcosC ，由正弦定理可得 2sinAcosB −sinCcosB =sinBcosC ，即 2sinAcosB =sinA ，∴ cosB =12，B =π3．∵ f(A)=sin(A 2−π6)−12=−12，∴ sin(A 2−π6)=0，∴ A 2−π6=0，∴ A =π3，∴ C =π−A −B =π3，∴ A =B =C ，∴ △ABC 为等边三角形，再根据a =2，可得△ABC 的面积S =12×2×2sin π3=√3． 18. （1）证明：设AC ，BD 交于O ，取EB 中点M ，连结FM ，MO ， 在△BDE 中，OM = // 12DE ，FA = // 12DE ，∴ OM = // FA ，∴ 四边形FAOM 是平行四边形，∴ FG // AO ，又AO 不包含平面EFB ，FG ⊂平面EFB ， ∴ 直线AC // 平面EFB ．（2）解：∵ ED ⊥平面ABCD ， ∴ BD 是BE 在面ABCD 上的射影，∴ ∠EBD 是直线BE 与平面BCD 所成的角，tan∠EBD =EDBD =ED 2√2=√22，解得ED =2，以D 为原点，DA 为x 轴，DC 为y 轴，DE 为z 轴，建立空间直角坐标系，由题意知A(2, 0, 0)，C(0, 2, 0)， B(2, 2, 0)，E(0, 0, 2)，∴ AC →=(−2,2,0)，AB →=(0,2,0)，AE →=(−2,0,2)， 设平面ABE 的法向量n →=(x,y,z)，则{n →⋅AE →=−2x +2z =0˙，取x =1，得n →=(1,0,1)， 设直线AC 与平面ABE 所成角为θ， sinθ=|cos <AC →，n →>|=√8×√2=12． ∴ 直线AC 与平面ABE 所成角的正弦值为12．19. 解：（1）甲、乙两组数据的平均数分别为51.5，49，甲班的客观题平均成绩更好．（2）设从甲班数据中取1个数据，至少有1个满分为事件A ， 从乙班数据中取1个数据，至少有1个满分为事件B ， 则P(A)=210=15，P(B)=110，则从这两组数据中分别抽取一个数据，至少有一个是满分的概率是P(AB)=15⋅110=150．（3）设从甲班数据中任取2个数据，两个都是优秀客观卷为事件C甲班10个数据中任意抽取两个有9+8+7+6+5+4+3+2+1=45种情况 甲班10个数据中任意抽取两个都是优秀客观卷有5+4+3+2+1=15种情况 则P(C)=1545=13． 20. 解：（1）由题意可得{a +c =3c a=12，解得{a =2c =1， ∴ b 2=3，∴ 椭圆C 的方程为x 24+y 23=1．（2）设A(x 1, y 1)，B(x 2, y 2)，①当直线AB 斜率不存在时，S △AOB =√3=|x 1y 1|⇒x 12y 12=3⇒y 123=1x 12，代入x 124+y 123=1，得x 12=2，则y 12=32，∴ |OA|2+|OB|2=x 12+y 12+x 22+y 22=2(x 12+y 12)=7； ②当直线AB 斜率存在时，设直线AB:y =kx +m ，与x 24+y 23=1联立得，(4k 2+3)x 2+8kmx +4m 2−12=0，△=48(4k 2−m 2+3)>0，由韦达定理得，{x 1+x 2=−8km4k 2+3x 1x 2=4m 2−124k 2+3， 原点O 到直线AB 的距离d =√1+k 2，|AB|=√1+k 2|x 1−x 2|=√1+k 2√(x 1+x 2)2−4x 1x 2=√1+k 2⋅√(−8km 4k 2+3)2−4⋅4m 2−124k 2+3=4k 2+3˙，则S △AOB =√3=12√1+k 2|x 1−x 2|√1+k2，代入整理得14=(4k 2+3)−m 2(4k 2+3)2⋅m 2，化简得2m 2=3+4k 2，∴ |OA|2+|OB|2=x 12+y 12+x 22+y 22=x 12+(3−34x 12)+x 22+(3−34x 22)=14(x 12+x 22)+6=14[(x 1+x 2)2−2x 1x 2]+6=14[(−8km 4k 2+3)2−2⋅4m 2−124k 2+3]+6 =2⋅4k 2m 2−3m 2+12k 2+9(4k 2+3)2+6=2⋅(4k 2−3)m 2+12k 2+9(4k 2+3)2+6=2⋅(4k 2−3)⋅4k 2+32+12k 2+9(4k 2+3)2+6=7．综上，|OA|2+|OB|2=7（定值）． 21. 解：（1）∵ g(x)=lnx +kx ， ∴ g′(x)=1x +k…当k ≥0时，g ′(x)>0在(0, +∞)恒成立，则 (0, +∞)是g(x)的增区间 … 当k <0时，由g′(x)>0⇒1x >−k ⇒0<x <−1k ， 则 (0,−1k )是g(x)的单调递增区间； 由g′(x)<0⇒1x<−k ⇒x >−1k，则(−1k，+∞)是g(x)的单调递减区间 …（2）若f(x)≥g(x)恒成立，即axe x −1≥lnx +x ，则a ≥lnx+x+1xe x恒成立 …设ℎ(x)=lnx+x+1xe x，ℎ′(x)=(1+x)e x −(xe x +e x )(lnx+x+1)(xe x )2=(1+x)e x (−lnx−x)(xe x )2…令ℎ′(x)>0，则−lnx −x >0，令u(x)=−lnx −x ，则u′(x)=−1x −1<0，即u(x)=−lnx −x 在(0, +∞)为减函数，且u(1)=−1<0，u(1e)=1−1e>0，故∃t ∈(0, 1)使u(t)=−lnt −t =0，…8分∴ 当x ∈(0, t)时，u(x)>0，即ℎ′(x)>0，ℎ(x)在(0, t)上递增， 当x ∈(t, +∞)时，u(x)<0，即ℎ′(x)<0，ℎ(x)在(t, +∞)上递减， ∴ 当x =t 时，ℎ(x)取最大值ℎ(t)=lnt+t+1te t=1te t =1t⋅1t=1，…10分∴ a ≥1...12分22. 证明：连接AC ，AD ，AE ，AF ，则∵ ADEB 是圆内接四边形， ∴ ∠AEC =∠D ， 同理∠C =∠AFD ，从而∠DAF =∠CAF(1)∵ ∠DBA =∠CBA ， ∴ AD =AE ，AF =AC ， ∴ △ADF ≅△AEC ， ∴ DF =CE ；（2）∵ DF =CE ， ∴ △ADF ≅△AEC ， ∴ AD =AE ，∴ ∠DBA =∠CBA ．23. 解：（1）直线l 的参数方程为{x =−1+ty =2+t （t 为参数），消去t 可得x −y +3=0；圆C 的极坐标方程分别为ρ2=4√2ρsin(θ−π4)−6=4ρsinθ−4ρcosθ−6，∴ x 2+y 2=4y −4x −6，即(x +2)2+(y −2)2=2； （2）易知A 在直线l 上，|PA|+|AQ|=|PQ| 圆心C 到直线l 的距离d =√2=√2，圆C 半径R =√2，∴ (12|PQ|)2+d 2=R 2，解得|PQ|=√6…24. （1）解：当a =2时，不等式f(x)≥4−|x −1|即为|x −2|≥4−|x −1|， ①当x ≤1时，原不等式化为2−x ≥4+(x −1)， 得x ≤−12， 故x ≤−12；②当1<x <2时，原不等式化为2−x ≥4−(x −1)， 得2≥5，故1<x <2不是原不等式的解； ③当x ≥2时，原不等式化为x −2≥4−(x −1)， 得x ≥72， 故x ≥72．综合①②③知，原不等式的解集为(−∞,−12]∪[72,+∞)． （2）证明：由f(x)≤1得|x −a|≤1， 从而−1+a ≤x ≤1+a ．∵ f(x)≤1的解集为{x|0≤x ≤2}， ∴ {−1+a =0，1+a =2，得a =1，∴ 1m +12n =a =1． 又m >0，n >0， ∴ m +2n =(m +2n)(1m +12n)=2+(2n m +m 2n) ≥2+2√2nm ⋅m2n =4， 当且仅当2n m=m 2n，即m =2n ，等号成立． 此时，联立1m +12n =1， 得{m =2，n =1，则m +2n =4，故m +2n ≥4，得证．。

吉林省九校联合体2014年春学期高三第二次摸底考试数学试卷（理科）一、选择题（每小题5分，共60分）1. 已知{}{},3,21,≤=≤≤-==x x N x x M R U 则()=N M C U （ ） A.{}32≤≤x x B.{}32≤<x x C.{}321≤≤-≤x x x 或 D.{}321≤<-<x x x 或 2．已知复数iiz ++=12,则复数z 在复平面内对应的点在 ( ) A ．第一象限 B.第二象限 C. 第三象限 D.第四象限 3．在等差数列{}n a 中，,7,8451==+a a a 则=5a （ ） A.11 B.10 C.7 D.34．抛物线()022>=p px y 的准线经过双曲线122=-y x 的左焦点，则=p （ ）A.22B.2C.22D.24 5．将函数x x y 2cos 2sin +=的图象向左平移4π个单位，所得图象的解析式是（ ） A.x x y 2sin 2cos += B. x x y 2sin 2cos -= C.x x y 2cos 2sin -= D.x x y cos sin =6．先后两次抛掷一枚骰子，在得到点数之和不大于6的条件下，先后出现的点数中有3的概率为（ ） A.31 B.52 C.51 D.61 7．一个棱锥的三视图如图所示，则它的体积为 ( ) A ．12 B ．32C ．1D ．138．执行如图所示的程序框图，则输出的结果为( ) A.20 B.30 C.40 D.509.一个空间四边形ABCD 的四条边及对角线AC 的长均为2，二面角B AC D --的余弦值为31，则下列论断正确的是（ ） A.四边形ABCD 的四个顶点在同一球面上且此球的表面积为π3 B.四边形ABCD 的四个顶点在同一球面上且此球的表面积为π4 C.四边形ABC 的四个顶点在同一球面上且此球的表面积为π33 D.不存在这样的球使得四边形ABCD 的四个顶点在此球面上10．如图，在四面体OABC 中，,13===BC AC 则=⋅（ ） A.8 B.6 C.4 D.311．已知函数()x f y =是定义在R 上的增函数，函数()1-=x f y 的图象关于点()0,1对称。

整)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（东北三省三校2014年高三第二次联合模拟考试数学(理)试卷及答案(推荐完整)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为东北三省三校2014年高三第二次联合模拟考试数学(理)试卷及答案(推荐完整)的全部内容。

(推荐完整)编辑整理:张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方，但是我们任然希望东北三省三校2014年高三第二次联合模拟考试数学（理）试卷及答案（推荐完整）这篇文档能够给您的工作和学习带来便利。

同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力.本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为 <东北三省三校2014年高三第二次联合模拟考试数学（理)试卷及答案（推荐完整)> 这篇文档的全部内容。

东北三省三校2014年高三第二次联合模拟考试（哈师大附中、东北师大附中、辽宁实验中学)数学理试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题)两部分,共150分,考试时间120分钟。

第Ⅰ卷（选择题 共60分)一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中,只有一项是符合题目要求的。

）1。

若}7,6,5{}3,2,1{}8,7,6,5,4,3,2,1{===B A U ，，，则()()U U C A C B = A 。

｛4,8} B. {2，4,，6，8｝ C. {1,3，5，7｝ D. {1，2，3,5,6，7}2。

2014年河南省洛阳市高考数学三模试卷（文科）一、选择题：本题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 21−i +1=( )A 1−iB 1+iC 2−iD 2+i 2. 已知：p:1x 2−x−6<0，q:x 2−2x −3<0，则￢p 是￢q 的（ ）A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件 3. 某学生在高三的四次模拟考试中，其数学解答题第20题的得分情况如表：A y =−0.7x +1.75B y =−0.5x +4.75C y =0.5x +2.5D y =0.7x +1.75 4. 集合A ={2, 3}，B ={1, 2, 3}，从A ，B 中各取任意一个数，则这两个数之和等于5的概率为（ ）A 16B 13C 12D 235. 一个直六棱柱的底面是边长为4的正六边形，侧棱长为6，则它的外接球的体积为（ ） A500π3B 500π C4000π3D 4000π6. 某程序框图如图所示，该程序运行后输出的k 的值是( )A 4B 5C 6D 77. 已知等比数列{a n }的前n 项和为S n ，且a 1+a 3=52，a 2+a 4=54，则S n a n=( )A 4n−1B 4n −1C 2n−1D 2n −18. 某几何体的三视图如图所示，图中的四边形都是边长为1的正方形，两条虚线互相垂直，则该几何体的体积是（ ）A 16B 12C 56D 19. 函数f(x)=ln(x +1)−2x(x >0)的零点所在的大致区间是（ ）A (0, 1)B (1, 2)C (2, e)D (3, 4)10. 已知△ABC 为锐角三角形，则点P(sinA −cosB, cosC −sinB)必位于直角坐标系中的（ ）A 第一象限B 第二象限C 第三象限D 第四象限11. 在△ABC 中，A =120∘，|AB|=1，△ABC 的面积为√34，若以A ，B 为焦点的椭圆经过点C ，则该椭圆的离心率为（ ） A √33B√3−12 C √32D √3−112. 设f(x)是定义在R 上的奇函数，且f(2)＝0，当x >0时，有xf′(x)−f(x)>0恒成立，则不等式x 2⋅f(x)>0的解集为（ ）A (−2, 2)B (−∞, −2)∪(2, +∞)C (−2, 0)∪(2, +∞)D (−∞, −2)∪(0, 2)二、填空题：本题共4个小题，每小题5分，共20分．13. 已知变量x ，y 满足约束条件{y ≤2x +y ≥1x −y ≤1，则z =3x +y 的取值范围是________．14. 在数列{a n }中，a n =3a n−1+2，a 1=2，则通项a n =________．15. 抛物线x 2=4y 的准线l 与y 轴交于点P ，若直线l 绕点P 以每秒π12弧度的角速度按逆时针方向旋转t 秒钟后，恰与抛物线第一次相切，则t =________．16. 已知△ABC 外接圆的半径为1，圆心为O ，且2OA →+AB →+AC →=0，|OA →|=|AB →|，E ，F 为边AC 的三等分点，则BE →⋅BF →=________．三、解答题：本题共5小题，共70分，解答题应写出文字说明、证明过程和演算步骤． 17. 在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足bsinA =√3acosB ． （1）求角B 的大小； （2）求y =2sin 2A +cos(2π3−2A)取最大值时角A 的大小．18. 某种产品按质量标准分成五个等级，等级编号x 依次为1，2，3，4，5，现从一批产品中随机抽取20件，对其等级编号进行统计分析，得到频率分布表如下：（1）若所抽取的20件产品中，等级编号为4的恰有2件，等级编辑为5的恰有4件，求a ，b ，c 的值．（2）在（1）的条件下，将等级编辑为4的2件产品记为x1、x2，等级编辑为5的4件产品记为y1，y2，y3，y4，现从x1、x2，y1，y2，y3，y4，这6件产品中任取两件（假定每件产品被取出的可能性相同），写出所有可能的结果，并求这两件产品的等级编号恰好相同的概率．19. 如图，四边形ABCD是正方形，点E为边AD的中点，DC．将△ABE折起到三角形PBE的位置，且平面PBE⊥平面点F在边DC上，且DF=14BCDE．（1）证明：平面PBE⊥平面PEF；（2）求直线PF与平面BCDE所成的角的正切值．20. 已知△ABC的内切圆的三边AB，BC，CA的切点分别为D，E，F，已知B(−√2, 0)，C(√2, 0)，内切圆圆心为I(1, t)(t≠0)，设点A的轨迹为L．（1）求L的方程；（2）设直线y＝2x+m交曲线L于不同的两点M，N，当|MN|＝2√5时，求m的值．21. 已知函数f(x)＝ax+xlnx（a为常数，e为自然对数的底数），曲线y＝f(x)在点（e, f(e)）处的切线方程为y＝3x−e．（1）求f(x)的单调区间；（2）若k∈Z，且k<f(x)对任意x>1都成立，求k的最大值．x−1请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题记分，作答时，用2B铅笔在答题卷上把所选题目对应的题号涂黑．【选修4-1：几何证明选项】22. 如图，已知AB是⊙O的直径，C为⊙O上一点，以C为切点的切线交AB的延长线于点P，AM⊥CP，垂足为M，CD⊥AB，垂足为D．（1）求证：AD=AM；（2）若⊙O的直径为2，∠PCB=30∘，求PC的长．【选修4-4：坐标系与参数方程】23. 已知直线l的参数方程为{x=−√3ty=−2+t，（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cos(θ−π3)．（1）求直线l的参数方程化为普通方程，将圆C的极坐标方程化为直角坐标方程；（2）求圆C上的点到直线l距离的取值范围．【选修4-5：不等式选项】24. 已知函数f(x)=2|x+1|−|x−3|（1）求不等式f(x)≥5的解集；（2）当x∈[−2, 2]时，关于x的不等式f(x)−|2t−3|≥0有解，求实数t的取值范围．2014年河南省洛阳市高考数学三模试卷（文科）答案1. D2. B3. D4. B5. A6. A7. D8. C9. B10. D11. B12. C13. [−1, 11]14. 3n−115. 316. 5317. 解：（1）由bsinA=√3acosB及正弦定理得sinBsinA=√3sinAsinB，∵ 0<A<π，∴ sinA≠0，∴ sinB=√3cosB，即tanB=√3，∵ 0<B<π，∴ B=π3．（2）y=2sin2A+cos(2π3−2A)=1−cos2A−12cos2A+√32sin2A=√32sin2A−32cos2A+1=√3sin(2A−π3)+1，∵ B=π3，∴ 0<A<2π3，∴ −π3<2A−π3<π，∴ 当2A−π3=π2时，即A=5π12时，y有最大值√3+1．18. 解：（1）由频率分布表得a+0.3+0.35+b+c=1，即a+b+c=0.35，∵ 抽取的20件产品中，等级编号为4的恰有2件，∴ b=220=0.1，等级编号为5的恰有4件，∴ c=420=0.2，∴ a=0.35−b−c=0.05．故a=0.05，b=0.10，c=0.20．（2）从产品x1，x2，y1，y2，y3，y4中任取两件，所有可能的结果为：{x1, x2}，{x1, y1}，{x1, y2}，{x1, y3}，{x1, y4}，{x2, y1}，{x2, y2}，{x2, y3}，{x2, y4}，{y1, y2}，{y1, y3}，{y1, y4}，{y2, y3}，{y2, y4}，{y3, y4}，共15个．设A表示“从x1、x2，y1，y2，y3，y4，这6件产品中任取两件这两件产品的等级编号恰好相同”则A包含的基本事件为：{x1, x2}，{y1, y2}，{y1, y3}，{y1, y4}，{y2, y3}，{y2, y4}，{y3, y4}，共7个，故所求概率为：p=715．19. （1）证明：∵ 点E为边AD的中点，点F在边DC上，且DF=14DC，∴ ∠BEF=90∘，∴ EF⊥BE，∵ 平面PBE⊥平面BCDE，且平面PBE∩平面BCDE=BE，∴ EF⊥平面PBE，∵ EF⊂平面PEF，∴ 平面PBE⊥平面PEF．（2）解：在△PBE中作PO⊥BE，垂足为O，则∵ 平面PBE⊥平面BCDE，且平面PBE∩平面BCDE=BE，∴ PO⊥平面PBE，连接OF，则∠PFO为直线PF与平面BCDE所成的角．设AB=4，由（1）得PB=4，PE=2，BE=2√5，PO=4√55，OE=12AO=2√55，∵ OE⊥EF，∴ EF=√5，OE=2√55，∴ OF =√295， ∴ tan∠PFO =POOF =4√2929． 20. 设点A(x, y)，由题意得：|AB|−|AC|＝|BD|−|CP|＝|BE|−|CE|＝(1+√2)−(√2−1)＝2，根据双曲线定义知：点A 的轨迹是以B ，C 为焦点，实轴长为2的双曲线的右支（除去点E ）， ∴ l 的方程为x 2−y 2＝1，x >1．设M(x 1, y 1)，N(x 2, y 2)，由{x 2−y 2=1y =2x +m ，得3x 2+4mx +m 2+1＝0，∵ 直线y ＝2x +m 交x 2−y 2＝1(x >1)于不同的两点M ，N ， ∴ 方程3x 2+4mx +m 2+1＝0的两根均在(1, +∞)内，∴ {△=16m 2−3×4×(m 2+1)>0−4m2×3>13×12+4m ×1+m 2+1>0 ， ∴ m <−√3，且m ≠−2，设M(x 1, y 1)，N(x 2, y 2)，则x 1+x 2=−4m 3，x 1x 2=m 2+13，∴ |MN|=√1+22√(x 1+x 2)2−4x 1x 2 =√5⋅√4m 2−129=2√53×√m 2−3，∵ |MN|＝2√5，∴ 2√53×√m 2−3=2√5，∴ m 2＝12，∵ m <−√3，且m ≠−2，∴ m ＝−2√3．21. 求导数可得f′(x)＝a +lnx +1，∵ 函数f(x)＝ax +xlnx 的图象在点x ＝e （e 为自然对数的底数）处的切线斜率为3， ∴ f′(e)＝3，∴ a +lne +1＝3，∴ a ＝1， ∴ f(x)＝x +xlnx ，f′(x)＝lnx +2， 由f′(x)>0得x >1e 2，由f′(x)<0得0<x <1e 2．∴ f(x)的单调递减区间为(0, 1e 2)，单调递增区间为(1e 2, +∞)． 当x >1时，令g(x)=f(x)x−1=x+xlnx x−1，则g′(x)=x−2−lnx (x−1)2，设ℎ(x)＝x −2−lnx ，则ℎ′(x)＝1−1x =x−1x>0，ℎ(x)在(1, +∞)上为增函数，∵ ℎ(3)＝1−ln3<0，ℎ(4)＝2−ln4>0， ∴ ∃x 0∈(3, 4)，且ℎ(x 0)＝0，当x ∈(1, x 0)时，ℎ(x)<0，g′(x)<0，g(x)在(1, x 0)上单调递减；当x ∈(x 0, +∞)时，ℎ(x)>0，g′(x)>0，g(x)在(x 0, +∞)上单调递增． ∴ g(x)min ＝g(x 0)=x 0+x 0lnx 0x 0−1，∵ ℎ(x0)＝x0−2−lnx0＝0，∴ x0−1＝1+lnx0，g(x0)＝x0，∴ k<x0∈(3, 4)，∴ k的最大值为3．22. （1）证明：∵ AB是⊙O的直径，∴ ∠ACB=90∘，∴ ∠ACD+∠BCD=90∘，∵ CD⊥AB，∴ ∠ABC+∠BCD=90∘，∴ ∠ACD=∠ABC，∵ 以C为切点的切线交AB的延长线于点P，∴ ∠MCA=∠ABC=∠ACD，∵ ∠AMC=∠ADC=90∘，AC=AC，∴ △AMC≅△ADC，∴ AD=AM；（2）解：∵ ∠PCB=30∘，以C为切点的切线交AB的延长线于点P，∴ ∠PAC=∠PCB=30∘，在Rt△ABC中，AB=2，∠BAC=30∘，∴ BC=1，∠ABC=60∘，∴ ∠BPC=30∘，∴ ∠BPC=∠BCP，BC=BP=1，由切割线定理得PC2=PB⋅PA=PB(PB+BA)=3，∴ PC=√3．23. 解：（1）由{x=−√3ty=−2+t（t为参数）得直线l的普通方程为x+√3y+2√3=0又∵ ρ=4cos(θ−π3)=2cosθ+2√3sinθ，∴ ρ2=2ρcosθ+2√3ρsinθ，∴ x2+y2−2x−2√3y=0，即(x−1)2+(y−√3)2=4；（2）由(x−1)2+(y−√3)2=4得圆心C(1, √3)，半径r=2．∴ 圆心C到直线l的距离d=√3|√12+(√3)2=2+√3>2．直线l与圆C相离．∴ 圆C上的点到直线l的距离的取值范围是[√3，√3+4]．24. 解：（1）f(x)=2|x+1|−|x−3|={x+5,x≥33x−1,−1<x<3−x−5,x≤−1，由式f(x)≥5，可得{x+5≥5x≥3①，或{3x−1≥5−1<x<3②，或{−x−5≥5x≤−1．解①求得x≥3，解②求得2≤x<3，解③求得x≤−10．故不等式的解集为[2, +∞)∪(−∞, −10]．（2）当x∈[−2, 2]时，f(x)∈[−4, 5]，∵ 关于x的不等式f(x)−|2t−3|≥0有解，∴ 5−|2t−3|≥0，即−5≤2t−3≤5，求得−1≤t≤4，故t的范围为[−1, 4]．。

乌鲁木齐地区2014年高三年级第三次诊断性测验试卷理科数学试题参考答案及评分标准1。

选B。

【解析】∵,∴2。

选B.【解析】∵，对应的点为在第二象限3.选C.【解析】由知或，分别解之，得或.4。

选A。

【解析】∵，∴，且,又，∴，∴5。

选C。

【解析】∵,此时，为使输出的，必须有，所以6。

选B。

【解析】由题意及正弦定理得,∴,∴，又，故，∴，而，∴，即，将代入，得,∴,或，而，故7。

选B。

【解析】此几何体的直观图如图所示，∴8.选D.【解析】依题意，有,即，其中且，∴，即，,由且,得,∴，，故,选D（此时)。

9。

选D。

【解析】令,∵其图象关于对称,∴，即，∴…⑴令，∵其图象关于直线对称，∴，即,∴…⑵由⑴⑵得，，∴…⑶∴,由⑵得∴；∴A对；由⑶，得,即，∴B对；由⑴得，，又,∴,∴C对；若，则，∴，由⑶得，又,∴，即，与题意矛盾，∴D错。

10。

选C.【解析】∵，，∴的图象在处的切线方程为，它与圆相切，∴，即，∵时有,∴，∴的最大值是，此时。

11。

选C.【解析】设的外接圆的圆心为,由,,知,∴点为的中点,∴,设直线交球于和,不妨设点在线段内，∴为四面体高的最大值,∴，依题意知，,即，当且仅当点与重合时，取最大值，此时，由，得，∴，∴。

12。

选B.【解析】不妨设的两条渐近线的方程分别为和则右焦点到直线的距离，又由，得，∵，∴…①∵，∴…②，①②联立,解得在中，，而且∴，即，解得，或（舍）∴,即，∴离心率二、填空题：共4小题，每小题5分,共20分。

13。

填。

【解析】∵,令，即,∴常数项为14。

填.【解析】设点,由，得，又∵点在椭圆上，∴,∴…①，∵点在椭圆上，∴…②,由①②可得。

∴射线的斜率为．15。

填。

【解析】依题意，有，是常数。

∴，即,易知,∴,令，解得16。

填。

【解析】依题意，设直线的方程为，它与抛物线交于点,线段的中点的坐标为，则，…⑴由方程组，得到以为根的一元二次方程，则且，…⑵不妨设，依题意知，即…⑶,将⑵代入⑶,化简得，即，∴…⑷又∵，∴，故，而，得，代入⑷,化简得三、解答题17．（本小题满分12分）(Ⅰ）∵成等差数列，∴，∴，即,∴公比∴…6分(Ⅱ）由（Ⅰ）知，，∵∴…12分18．（本小题满分12分)取的中点,连接,则有∥，故平面,在正三角形中，是的中点，故,如图，以为原点，分别以所在直线为轴，轴,轴建立空间直角坐标系，则,,，（Ⅰ）∵，∴,即又∵，∴，即而,∴平面;…6分(Ⅱ)设平面的法向量为，则有，即,令，则即，由（Ⅰ）知平面的一个法向量为设二面角的平面角为，易知，∴．…12分19．（本小题满分12分)设“两位专家都同意通过"为事件，“只有一位专家同意通过”为事件，“通过复审"为事件．(Ⅰ)设“某应聘人员被录用”为事件，则∵，，∴…6分（Ⅱ）根据题意,表示“应聘的人中恰有人被录用”．∵,，，,∴的分布列为20．（本小题满分12分）（Ⅰ）分别过作准线的垂线，垂足分别是则∴，∴，∴…①中，…②,中，…③将②③代入①，得,∴∴∴,∴．…6分（Ⅱ）依题意可知，抛物线为，直线的斜率存在且，的方程为，设交点，，满足，即满足，∴，∴，且设，由,其中，得，∴，而代入，得,化为：得,，而且，∴，或，或，或．…12分21．（本小题满分12分）(Ⅰ）令，则,当时，，函数递减当时，，函数递增，故在处取得最小值即，对,有，故令，则，当时,，函数递增当时，，函数递减，故在处取得最大值即，对，有,故∴…6分(Ⅱ）令,则⑴当时,，∴当,∴，∴，∴函数为减函数，∴当时，,即时,成立⑵当时,则对，,∴,∴,∴函数为减函数,∴当时，，即时，成立⑶当时,由，知∴当时，∴，，∴当时,∴，，，∴函数的减区间为,增区间为又∵∴对，故,当时，成立⑷当时，有,∴即,与题意矛盾综合⑴⑵⑶⑷,，对，有．…12分22．（本小题满分10分）（Ⅰ）如图，由题意可知∴∽，∴,同理，,又∵，∴，∴…5分(Ⅱ)如图，由切割线定理，得，∵∥∴，又∵切圆于,∴，∴，∴∽，∴，即∴，即，∴为线段的中点．…10分23．(本小题满分10分）（Ⅰ)设曲线上任意点的坐标为(）依题意，直线的普通方程为点到的距离为∵，∴，∴即，当，即时,…5分(Ⅱ)设射线的极坐标方程为，依题意可知,动点的极坐标为，，由,得…⑴点在直线上，∴…⑵，，∴…⑶,将其代入⑴得，即由,∴，其中∴所求动点的轨迹是以为圆心，为半径的圆除原点后的部分…10分24．(本小题满分10分）(Ⅰ）∵∵∵，∴，∴，同理，，∴∴∴…5分(Ⅱ）∵，∴，由柯西不等式得即,∴故,，当且仅当时不等式取等号…10分以上各题的其他解法,限于篇幅从略，请相应评分。

一、选择题：CDDAB AACCB二、填空题：11.9 12.y =sin 44x ππ⎛⎫-⎪⎝⎭ 13. 3 14. 3,2⎡⎫+∞⎪⎢⎣⎭三、选做题：①cos =2ρθ ②(),8-∞ 四、解答题：16.解：⑴在ABC ∆中， 2222211cos 222a b c a b C ab ab +-+-=== \∠3ACB π=………4分⑵由正弦定理知2sin 233sin 3c a πθπθπ⎛⎫⋅- ⎪⎛⎫⎝⎭==- ⎪⎝⎭ ………6分 \()212cos 3f a a πθθ⎛⎫=+-⋅+ ⎪⎝⎭24sin 12cos 3333πππθθθ⎛⎫⎛⎫⎛⎫=++-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2221cos 221333ππθθ⎡⎤⎛⎫⎛⎫=-+++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦52222cos 23333ππθθ⎤⎛⎫⎛⎫=-+++ ⎪ ⎪⎥⎝⎭⎝⎭⎦545sin 2336πθ⎛⎫=-+⎪⎝⎭……10分 由于20,3πθ⎛⎫∈ ⎪⎝⎭，故仅当3πθ=时，()f θ取得最大值3. ………12分17.解：⑴3次传球，传球的方法共有33327⨯⨯=种，3次传球结束时，球恰好回到甲手中的传球方法为236A =种，故所求概率为29………5分 ⑵易知ξ的所有可能取值为0,1,2 ………6分 ()()()86641610;1;22727279P P P ξξξ++=======， ………9分 \ξ的分布列为………10分因此，8161220122727927E ξ=⨯+⨯+⨯=.………12分18. 解：设菱形对角线交于点O ，易知PO AC ⊥且3PO = 又1PB OB ==.由勾股定理知，PO BD ⊥ 又,AC BD ABCD ACBD O ?面,\PO ⊥平面ABCD (3)建立如图空间直角坐标系，()()(0,0,0,0,0,3,1,0,0O P B ()()0,,A C ，()1,0,0D -，⎪⎭⎫ ⎝⎛1,0,32M ， ⎪⎭⎫⎝⎛-1,0,32N ………5 ⑴显然，()AP =，平面MNC 的法向量(m =，由AP ∥n ，知⊥AP 平面MNC ………8分⑵设面NPC 的法向量为(),,n x y z = 由0,0n NPn CP ??取1z =，得()3,3,1n =- ………10分39cos ,m n m n m n×\==所以平面NPC 与平面MNC ………12分 19. 解：⑴由132n n n a a ++=⨯得1112220n n n n a a a ++-=-==-=，∴对一切*,2nn n N a ∈=，可知{}n a 是首项为2，公比为2的等比数列. ………5分 （通过归纳猜想，使用数学归纳法证明的，亦应给分）（2）由（1）知1212112121n n n n nn a b a ++===+--- ………6分 证一：111111212112()21(21)(21)(21)(21)2121n n n n n n n n n +++++-=<=--------11114()2121n n n b +\<+--- ………10分121111144()44212121n n n b b b n n n ++\++鬃?<+-=+-<+---……12分 证二：∵12-n ≥12-n （仅当1=n 时等号成立），故此，122-n ≤221-n ……10分从而，n b b b +++ 21≤2212112-+++++n n 2214--+=n n ＜4+n ……12分20.解：⑴设(,)P x y ，由题意知0y >1y =+，得24x y =故所求点P 的轨迹方程为24x y =（y ＞0） ………5分⑵设()11,A x y 、()22,B x y ，将25y mx m =++代入24x y =得248200x mx m ---=∴12124,820x x m x x m +==-- ………7分而以线段AB 为直径的圆的方程为()()22121212120x y x x x x x y y y y y +-++-++=，即 ()()222221212121212120416x x x y x x x x x x x x x y ⎡⎤+-++-+-+=⎣⎦， 得 ()22224441041250x y mx m m y m m +--+++++=， ………10分整理成关于m 的方程 ()()22241431050m y m x y x y y -+--++-+=由于以上关于m 的方程有无数解，故2210301050y x y x y y -=--=+-+=且且， 由以上方程构成的方程组有唯一解2,1x y ==.由此可知，以线段AB 为直径的圆必经过定点()2,1. ………13分21.解：（1）易知211'()f x x x =-，11(2)ln 2,'(2)24f f \=+= \所求的切线方程为11(ln 2)(2)24y x -+=-，即44l n 20x y -+= ……4分 （2）易知2()2ln g x ax x x =-+，21221'()22(0)ax x g x ax x x x-+=-+=> ()g x 有两个不同的极值点\2()2210p x ax x =-+=在(0,)+ 有两个不同的根1212,()x x x x <则0D >且12120,0x x x x +>> 解得102a <<……6分 ()g x 在1(0,)x 递增，12(,)x x 递减，2(,)x + 递增\()g x 的极小值22222()2ln M g x ax x x ==-+又222212210(1,)2ax x x a+-+==? 且\222222211()2ln ln (1)22M M x x x x x x x ==--+=--> 则2221'()0x M x x -=<，\2()M x 在(1,)+ 递减\23()(1)2M x M <=-，故23M <- ……9分 （3）先证明：当(,)x p q Î时，()()'()f x f p f x x p->-即证：211ln ln 1x p x x p x p x +--->- 只需证：221ln ln 10p p x p x x p++----> 事实上，设221()ln ln 1()p p u x x p p x q x x p+=+----<< 易得3(2)()'()0x x p u x x --=>，()u x \在(,)p q 内递增 ()()0u x u p \>= 即原式成立 ……12分同理可以证明当(,)x p q Î时，()()'()f x f q f x x q->-综上当(,)x p q Î时，()()()()f x f p f x f q x p x q-->--. ……14分。

2014年陕西省西安市某校高考数学九模试卷（理科）一、选择题：（本大题共10个小题，每小题5分，共50分） 1. 条件p ：(x −2)2≤1，条件q:2x−1≥1，则p 是q 的（ ）A 充要条件B 充分不必要条件C 必要不充分条件D 既不充分也不必要条件 2. 根据如图算法语句，输出s 的值为（ ）A 19B 20C 100D 2103. 一个棱锥的三视图如图所示，则它的体积为（ ）A 12B 32C 1D 134. 函数f(x)=1+log 2x 与g(x)=2−x+1在同一直角坐标系下的图象大致是（ ）ABC D5. 已知向量a →=(2, 1)，b →=(sinα−cosα, sinα+cosα)，且a → // b →，则cos2α+sin2α=( )A 75B −75C 15D −156. 某班级有男生20人，女生30人，从中抽取10人作为样本，其中一次抽样结果是：抽到了4名男生、6名女生，则下列命题正确的是（ ）A 这次抽样可能采用的是简单随机抽样B 这次抽样一定没有采用系统抽样C 这次抽样中每个女生被抽到的概率大于每个男生被抽到的概率D 这次抽样中每个女生被抽到的概率小于每个男生被抽到的概率7. 圆x 2+y 2−ax +2=0与直线l 相切于点A(3, 1)，则直线l 的方程为（ ） A 2x −y −5=0 B x −2y −1=0 C x −y −2=0 D x +y −4=08. 从区间[−5, 5]内随机取出一个数x ，从区间[−3, 3]内随机取出一个数y ，则使得|x|+|y|≤4的概率是（ ） A 13 B 12 C 35 D 8159. 已知双曲线x 2a 2−y 2b 2=1(a >0, b >0)左、右焦点分别为F 1(−c, 0)，F 2(c, 0)，若双曲线右支上存在点P 使得a sin∠PF 1F 2=csin∠PF 2F 1，则该双曲线离心率的取值范围为（ ）A (0, √2−1)B (√2−1, 1)C (1, √2+1)D (√2+1, +∞)10. 定义在(−∞, 0)∪(0, +∞)上的函数f(x)，如果对于任意给定的等比数列{a n }，{f(a n )}仍是等比数列，则称f(x)为“保等比数列函数”．现有定义在(−∞, 0)∪(0, +∞)上的如下函数：①f(x)＝x 2；②f(x)＝2x ；③f(x)=√|x|；④f(x)＝ln|x|．则其中是“保等比数列函数”的f(x)的序号为（ ）A ①②B ③④C ①③D ②④二、填空题：（本大题共4小题，每小题5分，共25分） 11. 已知x ，y 的值如表所示：如果y 与x 呈线性相关且回归直线方程为y ̂=bx +3.5，那么b =________． 12. 若z =(sinθ−35)+i(cosθ−45)是纯虚数，则tanθ的值为________．13. 在圆中有结论“如图，AB 是圆O 的直径，直线AC ，BD 是圆O 过A 、B 的切线，P 是圆O 上任意一点，CD 是过P 的切线，则有PO 2=PC ⋅PD ．”类比到椭圆：“AB 是椭圆的长轴，O 是椭圆中的中心，F 1，F 2是椭圆的焦点，直线AC ，BD 是椭圆过A 、B 的切线，P 是椭圆上任意一点，CD 是过P 的切线，则有________． 14. 若(1−2x)2014=a 0+a 1x+...+a 2014x 2014，则a 12+a 222+...+a 201422014=________．选做题（请考生在三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）．【坐标系与参数方程】15. 在极坐标系中，过圆ρ=6cosθ的圆心，且垂直于极轴的直线的极坐标方程为________．【不等式选讲】16. 不等式|x +1|+|2−x|−a 2−2a ≥0对于一切x ∈R 恒成立，则实数a 的取值范围是________．【几何证明选讲】17. 如图，若PA =PB ，∠APB =2∠ACB ，AC 与PB 交于点D ，且PB =4，PD =3，则AD ⋅DC =________．三、解答题：（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤）18. 设函数f(x)=Acosωx(A >0, ω>0)的部分图象如图所示，其中△PQR 为等腰直角三角形，∠PQR =π2，PR =1．求： （1）函数f(x)的解析式；（2）函数y =f(x)−14在x ∈[0, 10]时的所有零点之和．19. 已知数列{log 2(a n −1)}(n ∈N ∗)为等差数列，且a 1=3，a 3=9． （1）求数列{a n }的通项公式； （2）证明1a 2−a 1+1a 3−a 2+...+1a n+1−a n<1．20. 如图，设四棱锥S −ABCD 的底面为菱形，且∠ABC =60∘，AB =SC =2，SA =SB =√2．（1）求证：平面SAB ⊥平面ABCD ；（2）求平面ADS 与平面ABS 所夹角的余弦值．21. 甲、乙、丙三个同学同时报名参加某重点高校2014年自主招生，高考前自主招生的程序为审核材料和文化测试，只有审核过关后才能参加文化测试，文化测试合格者即可获得自主招生入选资格．因为甲，乙，丙三人各有优势，甲，乙，丙三人审核材料过关的概率分别为12，35，25，审核过关后，甲，乙，丙三人文化测试合格的概率分别为35，12，34．（1）求甲，乙，丙三人中只有一人获得自主招生入选资格的概率；（2）设甲，乙，丙三人中材料审核过关的人数为随机变量X ，求X 的分布列和期望． 22. 设椭圆C:x 2a2+y 2b 2=1(a >b >0)的离心率e =12，右焦点到直线x a+yb=1的距离d =√217，O 为坐标原点．(1)求椭圆C 的方程；(2)若直线l 与椭圆C 交于A ，B 两点，以AB 为直径的圆过原点O ，求O 到直线l 的距离． 23. 已知函数f(x)＝lnx +x 2．(Ⅰ)若函数g(x)＝f(x)−ax 在其定义域内为增函数，求实数a 的取值范围；(Ⅱ)在(Ⅰ)的条件下，若a >1，ℎ(x)＝e 3x −3ae x x ∈[0, ln2]，求ℎ(x)的极小值；(Ⅲ)设F(x)＝2f(x)−3x 2−kx(k ∈R)，若函数F(x)存在两个零点m ，n(0<m <n)，且2x 0＝m +n ．问：函数F(x)在点（x 0, F(x 0)）处的切线能否平行于x 轴？若能，求出该切线方程；若不能，请说明理由．2014年陕西省西安市某校高考数学九模试卷（理科）答案1. B2. C3. A4. C5. B6. A7. D8. B9. C10. C11. 0.512. −3413. PF1⋅PF2=PC⋅PD14. −115. ρcosθ=316. [−3, 1]17. 718. 解：（1）由已知PR=1，∴ T=2=2πω，∴ ω=π∵ △PQR为等腰直角三角形，∴ Q到x轴的距离即为A=12∴ f(x)=12cosπx；（2）由f(x)−14=0，得cosπx=12，故x=2k+13或x=2k+53(k∈Z)，所以当x∈[0, 10]时的所有零点之和为S=(13+53)+(73+113)+⋯+(253+293)=50．19. （1）解：设等差数列{log2(a n−1)}的公差为d．由a1=3，a3=9得2(log22+d)=log22+log28，即d=1．所以log2(a n−1)=1+(n−1)×1=n，即a n=2n+1．（2）证明：因为1a n+1−a n =12n+1−2n=12n，所以1a2−a1+1a3−a2+...+1a n+1−a n=121+122+123+...+12n=12−12n×121−12=1−12n<1，即得证．20. （1）证明：连接AC ，取AB 的中点E ，连接SE 、EC ， ∵ SA =SB =√2，∴ SE ⊥AB ，AB =2，∴ SE =1，又四棱锥S −ABCD 的底面为菱形，且∠ABC =60∘， ∴ △ABC 是等边三角形，AB =2，∴ CE =√3，又SC =2，∴ SC 2=CE 2+SE 2， ∴ SE ⊥EC ， ∵ AB ∩EC =E ， ∴ SE ⊥面ABCD ， ∵ SE ⊂平面SAB ，∴ 平面SAB ⊥平面ABCD ；（2）解：由（1）知，分别以EC ，EB ，ES 为x 轴、y 轴、z 轴的正半轴建立建立空间直角坐标系．则面ABS 的一个法向量m →=(1, 0, 0)，A(0, −1, 0)，S(0, 0, 1)，D(√3，−2，0)， ∴ AD →=(√3,−1,0)，AS →=(0,1,1)， 设面ADS 的法向量n →=(x, y, z)，则AD →⋅n →=√3x −y =0，AS →⋅n →=y +z =0， 令y =√3，则x =1,z =−√3，∴ n →=(1,√3，−√3)， 设平面ADS 与平面ABS 所夹角的大小为θ，则cosθ=11⋅√7=√77． 21. 解：（1）设甲，乙，丙三人获得自主招生入选资格的概率分别为P(A)、P(B)、P(C)， 则P(A)=12×35=310，P(B)=12×35=310，P(C)=25×34=310， 所以甲，乙，丙三人中只有一人获得自主招生入选资格的概率： P =C 31310(1−310)2=0.441 （2）X 可能取值为0，1，2，3，则P(X =0)=(1−12)(1−35)(1−25)=325，P(X =1)=12×25×35+12×35×35+12×25×25=1950， P(X =2)=12×35×25+12×25×25+12×35×35=1950， P(X =3)=12×35×25=325，∴ X 的分布列为：EX =0×325+1×1950+2×1950+3×650=32． 22. 解：(1)∵ e =12， ∴ ca=12.∵ 右焦点(c, 0)到直线x a +yb =1的距离d =√217， 则√a 2+b 2=√217. 又∵ b 2+c 2=a 2， ∴ a 2=4，b 2=3， ∴ 椭圆C 的方程是：x 24+y 23=1.(2)设直线l:y =kx +m ，A(x 1, y 1)，B(x 2, y 2)， 则{3x 2+4y 2−12=0，y =kx +m ，则(4k 2+3)x 2+8kmx +4m 2−12=0， ∴ x 1+x 2=−8km 4k 2+3，x 1x 2=4m 2−124k 2+3.又∵ 直线l 与椭圆C 交于A ，B 两点，以AB 为直径的圆过原点O ， ∴ x 1x 2+y 1y 2=0，∴ x 1x 2+(kx 1−m)(kx 2−m)=0，∴ (k 2+1)x 1x 2+km(x 1+x 2)+m 2=0， 即(k 2+1)(4m 2−12)4k 2+3+−8k 2m 24k 2+3+m 2=0， 化简得m 2k 2+1=127，即√k 2+1=2√217，∴ O 到直线l 的距离为2√217. 23. （1）g(x)＝f(x)−ax ＝lnx +x 2−ax ，g ′(x)=1x+2x −a由题意知，g′(x)≥0，对任意的x ∈(0, +∞)恒成立，即a ≤(2x +1x)min又∵ x >0，2x +1x ≥2√2，当且仅当x =√22时等号成立 ∴ (2x +1x )min =2√2，可得a ≤2√2（2）由(Ⅰ)知，1<a ≤2√2，令t ＝e x ，则t ∈[1, 2]，则ℎ(t)＝t 3−3at ，ℎ(t)=3t 2−3a =3(t +√a)(t −√a) 由ℎ′(t)＝0，得t =√a 或t =−√a （舍去），∵ 1<a ≤2√2，∴ √a ∈(1,√84]若1<t ≤√a ，则ℎ′(t)<0，ℎ(t)单调递减；若√a <t ≤2，则ℎ′(t)>0，ℎ(t)单调递增 ∴ 当t =√a 时，ℎ(t)取得极小值，极小值为ℎ(√a)=a √a −3a √a =−2a √a (Ⅲ)设F(x)在（x 0, F(x 0)）的切线平行于x 轴，其中F(x)＝2lnx −x 2−kx结合题意，有{ 21nm −m 2−km =021nn −n 2−kn =0m +n =2x 02x 0−2x 0−k =0 ①-②得21n mn −(m +n)(m −n)=k(m −n) 所以k =21nm nm−n−2x 0，由④得k =2x 0−2x 0所以ln m n =2(m−n)m+n=2(m n −1)m n+1设u =m n∈(0,1)，⑤式变为lnu −2(u−1)u+1=0(u ∈(0,1))设y =lnu −2(u−1)u+1(u ∈(0,1))，y ′=1u−2(u+1)−2(u−1)(u+1)2=(u+1)2−4u u(u+1)2=(u−1)2u(u+1)2>0所以函数y =lnu −2(u−1)u+1在(0, 1)上单调递增，因此，y <y|u ＝1＝0，即lnu −2(u−1)u+1<0，也就是ln mn <2(m n −1)m n+1此式与⑤矛盾所以F(x)在（x 0, F(x 0)）的切线不能平行于x 轴。

乌鲁木齐地区2014年高三年级第三次诊断性测验试卷理科数学试题参考答案及评分标准题号 1 2 3 4 5 6 7 8 9 10 11 12 选项BBCACBBDDCCB1.选B.【解析】∵{}0,1,2,3,4,5,6A =，{}0,3B x x x =<>∴{}4,5,6A B =2.选B.【解析】∵()()()11111122i i i z i i i i +===-+--+，对应的点为11,22⎛⎫- ⎪⎝⎭在第二象限 3.选C.【解析】由()1f x >知0211x x -≤⎧⎨->⎩或1201x x >⎧⎪⎨⎪>⎩，分别解之，得1x <-或1x >.4.选A.【解析】∵3,4παπ⎛⎫∈⎪⎝⎭，∴cos 0,sin 0αα<>，且cos sin αα>， 又()21sin cos 1sin 225ααα+=+=，∴1sin cos 5αα+=-，∴34sin ,cos 55αα==- 5.选C.【解析】∵2345111113102222232S =+++++=，此时5n =，为使输出的3132S =，必须有n p ≥，所以5p =6.选B.【解析】由题意及正弦定理得sin cos 3sin cos B A A B =，∴tan 3tan B A =， ∴0,2A B π<<，又5cos C =，故25sin C =，∴tan 2C =，而A B C π++=， ∴()tan tan 2A B C +=-=-，即tan tan 21tan tan A BA B+=--，将tan 3tan B A =代入，得24tan 213tan A A =--，∴tan 1A =，或1tan 3A =-，而0,2A B π<<，故45A =︒ 7.选B.【解析】此几何体的直观图如图所示， ∴()11401444323V =⨯+⨯⨯=8.选D.【解析】依题意，有3sin 4cos 5a a -=±，即()sin 1a ϕ-=±，其中4tan 3ϕ=且02πϕ<<，∴2a k πϕπ-=+，即2a k ππϕ=++，k ∈Z ，由4tan 3ϕ=且02πϕ<<，得42ππϕ<<，∴34k a k ππππ+<<+，k ∈Z ，故，选D （此时0k =）. 9.选D.【解析】令()(1)F x f x =+，∵其图象关于()1,0对称，∴()()2F x F x =--，即()(3)1f x f x -=-+，∴()()4f x f x -=- …⑴令()(3)G x f x =+，∵其图象关于直线1=x 对称，∴()()2G x G x +=-， 即()()53f x f x +=-，∴()()44f x f x +=- …⑵ 由⑴⑵得，()()4f x f x +=-，∴()()8f x f x += …⑶∴()()()844f x f x f x -=-=+-，由⑵得()()()()()4444f x f x f x +-=--= ∴()()f x f x -=；∴A 对；由⑶，得()()282f x f x -+=-，即()()26f x f x -=+，∴B 对； 由⑴得，()()220f x f x -++=，又()()f x f x -=， ∴()()(2)(2)220f x f x f x f x -++--=-++=，∴C 对；若()()330f x f x ++-=，则()()6f x f x +=-，∴()()12f x f x +=，由⑶得()()124f x f x +=+，又()()4f x f x +=-，∴()()f x f x =-，即()0f x =，与题意矛盾，∴D 错. 10.选C.【解析】∵()0a f b '=-，()10f b=-，∴()f x 的图象在0x =处的切线方程为 10ax by ++=，它与圆221x y +=相切，1=，即221a b +=，∵0,0a b >>时有2221222a b a b++⎛⎫≤= ⎪⎝⎭，∴a b +≤∴a b +，此时2a b ==.11.选 C.【解析】设ABC ∆的外接圆的圆心为O '，由2AB BC ==，AC =，知90ABC ∠=︒，∴点O '为AC 的中点，∴OO ABC '⊥平面，设直线OO '交球O 于1D 和2D ，不妨设点O 在线段1O D '内，∴1O D '为四面体D ABC -高的最大值， ∴1112323D ABC V AB BC h h -⎛⎫=⨯⋅= ⎪⎝⎭，依题意知，2433h ≤，即2h ≤，当且仅当点D 与1D 重合时，D ABC V -取最大值，此时2h =，由()222h R R -+=，得222h R h+=，∴32R =，∴249S R ππ==. 12.选 B.【解析】不妨设22221x y a b-=的两条渐近线,OA OB 的方程分别为0bx ay -=和0bx ay +=则右焦点(),0F c 到直线OA的距离d b ==，又由FA OA ⊥，得OA a =，∵2OA OB AB +=，∴2OB AB a =- …①∵90AOB ∠=︒，∴222OA AB OB += …②，①②联立，解得43AB a = 在Rt OAB ∆中，4tan 3AB AOB OA ∠==，而2AOB AOF ∠=∠且tan bAOF a ∠=∴22tan tan 1tan AOF AOB AOF ∠∠=-∠，即22431b a b a ⎛⎫⎪⎝⎭=⎛⎫- ⎪⎝⎭，解得12b a =，或2b a =-（舍） ∴2214b a =，即2254c a =，∴离心率2c e a ==二、填空题 :共4小题，每小题5分，共20分. 13.填112.【解析】∵()843182r rrr T C x-+=-，令8403r-=，即2r =， ∴常数项为()22382112T C =-=14.填1±.【解析】设点()()1122,,,A x y B x y ，由2OB OA =，得21212,2x x y y ==，又∵点B 在椭圆2C 上，∴22221164y x +=，∴2211144y x += …①， ∵点A 在椭圆1C 上，∴221114x y +=…②，由①②可得111yx =±.∴射线OA 的斜率为1±．15.填12.【解析】依题意，有()2log f x x a -=，a 是常数. ∴()1f a =，即2log 1a a =-，易知1a =，∴()21log f x x =+，令()0f x =，解得12x =16.填21y x =+.【解析】依题意，设直线l 的方程为y kx m =+，它与抛物线2y x =交于点()()1122,,,A x y B x y ，线段AB 的中点P 的坐标为(),x y ，则122x x x +=， 122y y y +=…⑴由方程组2y kx m y x=+⎧⎨=⎩，得到以12,x x 为根的一元二次方程 20x kx m --=，则240k m ∆=+>且12x x k +=，12x x m =-…⑵不妨设12x x <，依题意知()21243x x kx m x dx +-=⎰， 即()()22112221124233x x x x k x x x x m ⎡⎤++-++-=⎢⎥⎣⎦…⑶，将⑵代入⑶，化简得()3218x x -=，即()2214x x -=，∴()2121244x x x x +-=…⑷ 又∵221122,y x y x ==，∴2212121212422222y y x x x x y x x +++====+，故122x x y =-，而122x x x +=，得122x x x +=，代入⑷，化简得21y x =+ 三、解答题17．（本小题满分12分）（Ⅰ）∵1233,2,S S S 成等差数列，∴21343S S S =+，∴()()12112343a a a a a a +=+++，即323a a =，∴公比3q =∴113n nn a a q -== …6分 （Ⅱ）由（Ⅰ）知，33log log 3nn n b a n ===，∵()()2122212122214n n n n b b b b n n n n n -+-=--+=- ∴()()()12233445212221n n n n n T bb b b b b b b b b b b -+=-+-++-()()214124222n n n n n +=-+++=-⨯=-- …12分 18．（本小题满分12分）取AC 的中点O ，连接,OF OB ，则有1A A ∥FO ，故FO ⊥平面ABC ，在正三角形ABC 中，O 是AC 的中点，故OB AC ⊥，1,OA OC OB ===如图，以O 为原点，分别以,,OA OB OF 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系，则()()()()(0,0,0,1,0,0,,1,0,0,,O A B C E F ⎛- ⎝⎭(FB =，2AE ⎛=- ⎝⎭，()2,0,0AC =-，(AF =-（Ⅰ）∵()60,3,61,3,02FB AE ⎛⎫⋅=-⋅-= ⎪⎪⎝⎭， ∴FB AE ⊥，即FB AE ⊥又∵()()0,3,62,0,00FB AC ⋅=-⋅-=， ∴FB AC ⊥，即FB AC ⊥而AEAC A =，∴FB ⊥平面AEC ； …6分（Ⅱ）设平面AEF 的法向量为(),,a b c =n ，则有00AE AF ⎧⋅=⎪⎨⋅=⎪⎩n n ，即63060a b c a c ⎧-++=⎪⎨⎪-+=⎩，令6c =，则6,3a b == 即()6,3,6=n ，由（Ⅰ）知平面AEC 的一个法向量为FB 设二面角F AE C --的平面角为θ，易知02πθ<≤，∴5cos 15FB FB θ⋅==n n． …12分 19．（本小题满分12分）设“两位专家都同意通过”为事件A ，“只有一位专家同意通过”为事件B ， “通过复审”为事件C ．（Ⅰ）设“某应聘人员被录用”为事件D ，则D A BC =+∵()111224P A =⨯=，()11121222P B ⎛⎫=⨯⨯-= ⎪⎝⎭，()310P C =∴()()()()()25P D P A BC P A P B P C =+=+= …6分 （Ⅱ）根据题意，0,1,2,3,4X =i A 表示“应聘的4人中恰有i 人被录用”()0,1,2,3,4i =．∵()04004238155625P A C ⎛⎫⎛⎫=⨯⨯= ⎪ ⎪⎝⎭⎝⎭，()31142321655625P A C ⎛⎫=⨯⨯=⎪⎝⎭，()222242321655625P A C ⎛⎫⎛⎫=⨯⨯= ⎪ ⎪⎝⎭⎝⎭，()3334239655625P A C ⎛⎫=⨯⨯=⎪⎝⎭， ()40444231655625P A C ⎛⎫⎛⎫=⨯⨯=⎪ ⎪⎝⎭⎝⎭∴X 的分布列为∵X ～()4,0.4B ，∴ 1.6EX np == …12分 20．（本小题满分12分）（Ⅰ）分别过,A B 作准线的垂线，垂足分别是11,A B则11,AF AA BF BB ==∴11AA AF HABF BB HB==， ∴AF HA BF HB =，∴AF BFHA HB=…① AHF ∆中，sin sin AF AHFHA AFH ∠=∠…②， BHF ∆中，sin sin BF AHFHB BFH∠=∠…③ 将②③代入①，得sin sin sin sin AHF AHFAFH BFH∠∠=∠∠，∴sin sin AFH BFH ∠=∠ ∴180AFH BFH BFx ∠=︒-∠=∠∴0AF BF k k +=，∴2BF AF k k =-=-．…6分 （Ⅱ）依题意可知，抛物线为24y x =，直线l 的斜率k 存在且0k ≠，l 的方程为()1y k x =+，设交点()11,A x y ，()22,B x y ，满足()214y k x y x⎧=+⎪⎨=⎪⎩， 即12,x x 满足()2222240k x k x k +-+=，∴()2242440k k ∆=-->，∴21k <，且21212242,1k x x x x k-+==设()00,M x y ，由FA FB tFM +=，其中0t ≠， X 01234P816252166252166259662516625得()()()1122001,1,1,x y x y t x y -+-=-，∴12012021x x x ty y y t +-⎧=+⎪⎪⎨+⎪=⎪⎩，而()121242y y k x x k+=++=代入2004y x =，得222422441k k kt t ⎛⎫-- ⎪⎛⎫=+ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭，化为：222444k t k t t -+=得，22444t k t t-=-，而21k <且0k ≠， ∴2t <-，或01t <<，或12t <<，或4t >． …12分 21．（本小题满分12分）（Ⅰ）令()()()()1ln 1h x f x x x x =--=-+，则()1xh x x '=+， 当10x -<≤ 时，()0h x '≤，函数()h x 递减当0x >时，()0h x '>，函数()h x 递增，故()h x 在0x =处取得最小值()00h = 即，对1x >-，有()()00h x h ≥=，故()1f x x ≥- 令()()()1ln 111x I x f x x x x =-=-+++，则()()21xI x x '=-+， 当10x -<≤ 时，()0I x '≥，函数()I x 递增当0x >时，()0I x '<，函数()I x 递减，故()I x 在0x =处取得最大值()00I = 即，对1x >-，有()()00I x I ≤=，故()11f x x≤+ ∴()111x f x x-≤≤+ …6分 （Ⅱ）令()()()()2ln 1F x g x f x x ax x =-=++-，则()()22211ax a xF x x +-'=+⑴当0a ≤时，210a -<，∴当0x ≥，∴10x +>，2210ax a +-≤∴()0F x '≤，∴函数()[],0,1y F x x =∈为减函数，∴当01x ≤≤时，()()00F x F ≤=， 即0a ≤时，()()f x g x ≥成立⑵当104a <≤时，1212a a-≥ 则对[]0,1x ∀∈，12102ax x a--≤-≤，∴10x +>，2210ax a +-≤∴()0F x '≤，∴函数()[],0,1y F x x =∈为减函数，∴当01x ≤≤时，()()00F x F ≤=，即104a <≤时，()()f x g x ≥成立 ⑶当11ln 24a <≤-时，由11ln 22-<，知12012a a-<<∴当1202ax a-≤≤时，∴10x +>，2210ax a +-≤，∴()0F x '≤当1212a x a-<≤时，∴10x +>，2210ax a +-≥，()0F x '≥，∴函数()[],0,1y F x x =∈的减区间为120,2a a -⎡⎤⎢⎥⎣⎦，增区间为12,12a a -⎡⎤⎢⎥⎣⎦又∵()()00,1ln 210F F a ==-+≤∴对[]0,1x ∀∈，()()(){}max 0,10F x F F ≤≤ 故，当01x ≤≤时，()()f x g x ≥成立⑷当1ln 2a >-时，有ln 210a +->，∴()1ln 210F a =+-> 即()()11g f >，与题意矛盾综合⑴⑵⑶⑷，(],1ln 2a ∈-∞-，对01x ≤≤，有()()f x g x ≥． …12分 22．（本小题满分10分）（Ⅰ）如图，由题意可知,ACD AEC CAD EAC ∠=∠∠=∠∴ADC ∆∽ACE ∆，∴CD ACCE AE=， 同理，BD ABBE AE =，又∵AB AC =， ∴CD BDCE BE=，∴BE CD BD CE ⋅=⋅ …5分 （Ⅱ）如图，由切割线定理，得2FB FD FC =⋅，∵CE ∥AB ∴FAD AEC ∠=∠，又∵AB 切圆于B ，∴ACD AEC ∠=∠，∴FAD FCA ∠=∠， ∴AFD ∆∽CFA ∆，∴AF FD CF AF=，即2AF FD FC =⋅∴22FB AF =，即FB FA =，∴F 为线段AB 的中点． …10分 23．（本小题满分10分）（Ⅰ）设曲线C 上任意点M 的坐标为()cos ,sin ϕϕ（02ϕπ≤<）依题意，直线l 的普通方程为40x y +-=点M 到l的距离为d ==∵02ϕπ≤<，∴9444πππϕ≤+<，3444242πππϕ⎛⎫-≤+-≤- ⎪⎝⎭即4444πϕ⎛⎫≤+-≤ ⎪⎝⎭，当342ππϕ+=，即54πϕ=时，max 1d === …5分 （Ⅱ）设射线OP 的极坐标方程为()θαα=∈R ，依题意可知，动点Q 的极坐标为(),ρα，()()1,,,P R P αρα，由2OP OQ OR⋅=，得1P ρρ⋅=…⑴点(),P P ρα在直线l 上，∴()cos sin 4P ραα+=…⑵，cos sin 0αα+≠，∴4cos sin P ραα=+…⑶，将其代入⑴得41cos sin ραα=+，即4cos sin ραα=+由cos ,sin x y ραρα==，∴()224x y x y +=+，其中0xy ≠24．（本小题满分10分） （Ⅰ）∵()()()3332223a b ca b c ab c ++-++++()()()()3332222222a b c a b c b a c c a b =++-+-+-+∵()()332222a b a b ab aa b b b a +--=-+-()()2a b a b =-+∵,a b +∈R ，∴()()20a b a b -+≥，∴3322a b a b ab +≥+，同理，3322b c b c bc +≥+，3322c a c a ca +≥+ ∴()3332222222a b c a b ab b c bc c a ca ++≥+++++ ∴()()()()33322222220a b c a b c b a c c a b ++-+-+-+≥∴()()()2223333a b c a b c a b c ++++≤++ …5分 （Ⅱ）∵,,a b c +∈R ，∴0,0,0a b b c c a +>+>+>，由柯西不等式得()()()111a b b c c a a b b c c a ⎛⎫+++++++⎡⎤ ⎪⎣⎦+++⎝⎭29≥+=即()11129a b c a b b c c a ⎛⎫++++≥ ⎪+++⎝⎭，∴23c a b a b b c c a ⎛⎫++≥ ⎪+++⎝⎭故，32a b c b c c a a b ++≥+++，当且仅当a b c ==时不等式取等号 …10分以上各题的其他解法，限于篇幅从略，请相应评分.。