多重共线性题目的检验和处理

习题1.下表给出了中国商品进口额Y 、国内生产总值GDP 、消费者价格指数CPI 。

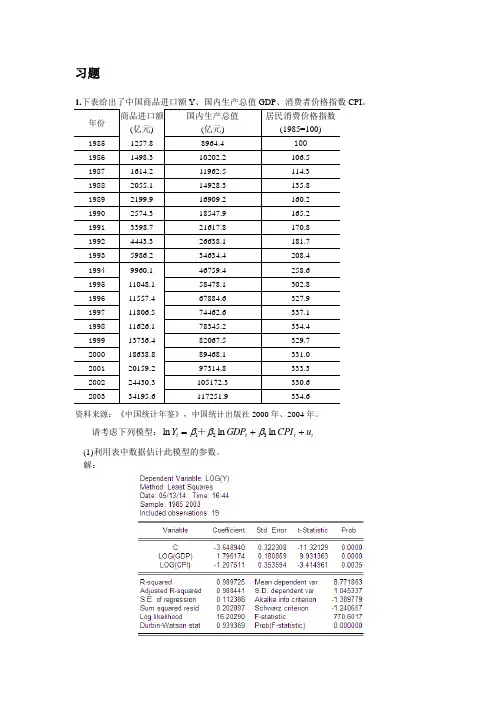
年份 商品进口额 (亿元)国内生产总值(亿元)居民消费价格指数(1985=100)1985 1257.8 8964.4 1001986 1498.3 10202.2 106.5 1987 1614.2 11962.5 114.3 1988 2055.1 14928.3 135.8 1989 2199.9 16909.2 160.2 1990 2574.3 18547.9 165.2 1991 3398.7 21617.8 170.8 1992 4443.3 26638.1 181.7 1993 5986.2 34634.4 208.4 1994 9960.1 46759.4 258.6 1995 11048.1 58478.1 302.8 1996 11557.4 67884.6 327.9 1997 11806.5 74462.6 337.1 1998 11626.1 78345.2 334.4 1999 13736.4 82067.5 329.7 2000 18638.8 89468.1 331.0 2001 20159.2 97314.8 333.3 2002 24430.3 105172.3 330.6 200334195.6117251.9334.6资料来源：《中国统计年鉴》，中国统计出版社2000年、2004年。

请考虑下列模型：i t t t u CPI GDP Y ++=ln ln ln 321βββ＋ (1)利用表中数据估计此模型的参数。

解：ln 3.6489 1.796ln 1.2075ln t t t Y GDP CPI =--＋t= （-11.32） （9.93） （-3.415）20.988770.6.0.1124R F S E ===(2)你认为数据中有多重共线性吗？多重共线性的检验 1）综合统计检验法若 在OLS 法下：R 2与F 值较大，但t 检验值较小，则可能存在多重共线性。

回归分析是统计学中常用的一种分析方法，它用于研究一个或多个自变量与一个因变量之间的关系。

然而，在进行回归分析时，经常会面临一个多重共线性的问题。

多重共线性是指在回归模型中，自变量之间存在高度相关性的情况。

当自变量之间存在多重共线性时，就会导致回归系数估计不准确，增加了回归模型的不稳定性。

这对于研究者来说是一个很大的困扰，因为他们很难判断自变量之间到底是有关系还是无关系，从而无法准确地分析自变量对因变量的影响。

多重共线性问题的存在会使得回归系数的估计值变得不稳定，回归系数的符号可能会与理论上相悖，使得回归模型的解释性大大降低。

同时，多重共线性还会增加回归系数的标准误差，导致对回归系数的假设检验结果不可信。

那么，如何解决多重共线性问题呢？首先，我们可以通过计算自变量之间的相关系数来判断是否存在多重共线性。

如果自变量之间的相关系数较高，就需要考虑采取一些措施来解决多重共线性问题。

一种解决方法是通过方差膨胀因子（VIF）来检验多重共线性。

VIF是用来判断自变量之间存在多重共线性的一个指标，通常VIF大于10就表示存在多重共线性。

其次，我们可以采取一些方法来解决多重共线性问题。

一种解决方法是通过主成分分析（PCA）来降维。

主成分分析是一种常用的降维方法，它可以将原始的自变量通过线性变换转换为一组新的主成分，从而减少自变量之间的相关性。

通过主成分分析，可以将原始的自变量转换为一组新的主成分，从而减少自变量之间的相关性，解决多重共线性问题。

另一种解决多重共线性问题的方法是通过岭回归（Ridge Regression）。

岭回归是一种常用的回归分析方法，它通过对回归系数进行惩罚，可以减少自变量之间的相关性，从而解决多重共线性问题。

通过岭回归，可以对自变量的回归系数进行缩减，从而减少多重共线性对回归系数估计的影响。

此外，我们还可以通过逐步回归法（Stepwise Regression）来解决多重共线性问题。

逐步回归法是一种常用的变量选择方法，它可以通过逐步添加或删除自变量来选择最优的回归模型。

实验四多重共线性模型的检验和处理一、实验目的：掌握多重共线性模型的检验和处理方法二、预备知识：多重共线性的检验：直观判断法（R2值、t值检验）、简单相关系数检验法、方差扩大因子法（辅助回归检验）；多重共线性的处理：先验信息法、变量变换法、逐步回归法。

三、实验内容：了解掌握使用直观判断法（R2值、t值检验）、简单相关系数检验、方差扩大因子法（辅助回归检验）对模型多重共线性进行检验；了解掌握使用先验信息法、变量变换法和逐步回归法对模型多重共线性进行处理。

四、实验步骤：（一）多重共线性的检验1、直观判断法（R2值、t值检验）根据广东数据（见附件1），先分别建立以下模型：【模型1】财政收入CS对第一产业产值GDP1、第二产业产值GDP2和第三产业产值GDP3的多元线性回归模型；【模型2】固定资产投资TZG对固定资产折旧ZJ、营业盈余YY和财政支出CZ的多元线性回归模型。

观察模型结果，初步判断模型自变量之间是否存在多重共线性问题。

2、简单相关系数检验法分别计算【模型1】和【模型2】的自变量的简单相关系数，进一步判断模型是否存在多重共线性。

3、方差扩大因子法（辅助回归检验）；分别建立【模型1】和【模型2】的辅助回归。

计算各模型各个自变量的方差扩大因子。

并将计算的结果，以表格形式列出。

确定模型是否存在严重的多重共线性。

（二）多重共线性的处理1、先验信息法、变量变换法①已知【模型1】有一先验信息：GDP3对CS的贡献是GDP1贡献的3倍。

根据该先验信息，我们可以将变量CS和GDP2作变量取对数变换，作出回归模型，判断是否消除了多重共线性。

根据该先验信息，请提出一个对模型变量变换的方法，消除模型多重共线性。

②已知【模型2】有一先验信息：在企业折旧资金和营业盈余资金主要是会计账面对区别，资金常常是混在一起用的，不区分折旧资金和营业盈余资金的使用，因此我们可以将ZJ和YY加起来作为一个大的变量使用。

使用该先验信息，作回归模型，根据模型结果，判断是否消除了多重共线性。

多重共线性的判断与修正一、多重共线性的判断1． 综合统计检验法LS Y C X1 X2 对模型进行OLS, 得到参数估计表(1) 当2,R F 很大，而回归系数的t 检验值小于临界值时，可判定该模型存在多重共线性。

(2) 当完全共线性存在时，模型的OLS 无法进行，Eviews 会提示：矩阵的逆(1()T X X -)不存在。

2. 简单相关系数检验法LS Y C X1 X2 对模型进行OLS, 得到参数估计表中的2R .点击：Quick/Group Statistics/Correlation在对话框中输入：X1 X2 , 点击OK, 即可得到简单相关系数矩阵检验：若存在 i j x x r 接近于1, 或 22,i j x x r R >，则说明,i j x x 之间存在着严重的相关性。

3. 辅助回归法(方差扩大因子法）设 121112...(1)(1)...j j k Xj X X X j X j Xk V ααααα-+=+++-+++++ (j ) LS Xj X1 X2…Xk 对(j) 进行OLS, 得到参数估计表检验：若表中 (2,1)F F k n k α>--+, 则可确定存在多重共线性。

或者(方差扩大因子法）：计算211j jVIF R =-, (2j R 为以上方程的可决系数）, 若10j VIF ≥, 则可确定存在多重共线性。

4. 逐步回归法1) 首先计算被解释变量对每个解释变量的回归方程，得到基本回归方程：LS Y C Xi OLS ，得到基本回归方程(i), i = 1,2,…,k2) 从这些基本回归方程中选出最合理的方程, 即，2R 取值最大，且t 检验显著。

比方说，0j Y Xj ββ=+3) 在这个选出的方程中增加新的解释变量, 再进行OLS 分析：LS Y C Xj Xi ( i= 1,2,…,j-1, j+1,…k)判断： 如果新加入的解释变量对2R 改进最大, 且每个系数又是t 统计显著，则保留这个新的解释变量。

计量经济学实验报告题目：关于多重共线性模型的检验和处理方法姓名：张飞飞学号：2008163050专业：工商管理指导教师：崔海燕实验时间： 2010-12-22二○一○年十二月二十五日关于多重共线性模型的检验和处理的方法一、实验目的：掌握多重共线性模型检验和处理的方法二、实验原理：判定系数检验法、逐步回归法、解释变量、相关系数检验三、实验步骤：1.创建一个新的工作文件：打开Eviews软件，点击File下的New File,创建一个新的工作文件，选择Annual,在Start Date栏中输入1983，在End date栏中输入2000，点击OK,点击保存，完成创建新的工作文件。

2.输入数据：点击Quick下的Empty Group,导入中国粮食生产函数模型的具体数据，命名被解释变量为Y,解释变量为X1、X2、X3、X4、X5，其中：Y表示粮食产量；X1表示农业化肥施用量；X2表示粮食播种面积；X3表示成灾面积；X4表示农业机械总动力；X5表示农业劳动力.点击Name保存数据，命名为Group01。

3.采用普通最小二乘法估计模型参数：点击Quick下的Estimate Equation,输入方程y c x1 x2 x3 x4 x5.点击OK,生成EQ1. 如下表所示：从结果可以看出：R-squared的值为0.982798，拟合优度比较高（一般为0.9以上），F-statistic 的值为137.1164，也比较大，说明模型上存在多重共线性，但无法看出变量之间的关系。

4.进行多重共线性检验：主要运用综合统计检验和采用解释变量之间的相关系数进行检验。

由综合统计检验法（步骤3)，可以看出存在多重共线性，继而进行解释变量之间的相关下系数检验。

点击Quick下的Groupstatistics,选择Correlations,打开Series List界面，输入X1 X2 X3 X3 X4 X5,点击OK,生成Group02,结果如下图：从结果可以看出：X1和X4之间的相关系数为0.960278，最接近1，说明X1和X4之间存在高度相关性。

什么是多重共线性如何进行多重共线性的检验多重共线性是指在统计模型中，独立变量之间存在高度相关性或者线性依赖关系，从而给模型的解释和结果带来不确定性。

在回归分析中，多重共线性可能导致系数估计不准确、标准误差过大、模型的解释变得复杂等问题。

因此，对于多重共线性的检验和处理是非常重要的。

一、多重共线性的检验多重共线性的检验可以通过以下几种方式进行：1. 相关系数矩阵：可以通过计算独立变量之间的相关系数，判断它们之间的关系强度。

当相关系数超过0.8或-0.8时，可以视为存在高度相关性，即可能存在多重共线性问题。

2. 方差扩大因子（VIF）：VIF是用来检验自变量之间是否存在共线性的指标。

计算每一个自变量的VIF值，当VIF值大于10或者更高时，可以视为存在多重共线性。

3. 条件数（Condition index）：条件数也是一种用来检验多重共线性的指标。

它度量了回归矩阵的奇异性或者相对不稳定性。

当条件数超过30时，可以视为存在多重共线性。

4. 特征值（Eigenvalues）：通过计算特征值，可以判断回归矩阵的奇异性。

如果存在特征值接近于零的情况，可能存在多重共线性。

以上是常用的多重共线性检验方法，可以根据实际情况选择合适的方法进行检验。

二、多重共线性的处理在检测到存在多重共线性问题后，可以采取以下几种方式进行处理：1. 去除相关性强的变量：在存在高度相关变量的情况下，可以选择去除其中一个或多个相关性较强的变量。

2. 聚合相关变量：将相关性强的变量进行加权平均，得到一个新的变量来替代原来的变量。

3. 主成分分析（PCA）：主成分分析是一种降维技术，可以将相关性强的多个变量合并成为一个或多个无关的主成分。

4. 岭回归（Ridge Regression）：岭回归是一种缓解多重共线性的方法，通过加入一个正则化项，来使得共线性变量的系数估计更加稳定。

5. Lasso回归（Lasso Regression）：Lasso回归也是一种缓解多重共线性的方法，通过对系数进行稀疏化，来选择重要的变量。

山西大学实验报告实验报告题目：多重共线性问题的检验和处理学院：专业：课程名称：计量经济学学号：学生姓名：教师名称：崔海燕上课时间：一、实验目的：熟悉和掌握Eviews在多重共线性模型中的应用，掌握多重共线性问题的检验和处理。

二、实验原理：1、综合统计检验法；2、相关系数矩阵判断；3、逐步回归法；三、实验步骤：（一）新建工作文件并保存打开Eviews软件，在主菜单栏点击File\new\workfile，输入start date1978和end date 2006并点击确认，点击save键，输入文件名进行保存。

（二）输入并编辑数据在主菜单栏点击Quick键，选择empty\group新建空数据栏，根据理论和经验分析，影响粮食生产（Y）的主要因素有农业化肥施用量（X1）、粮食播种面积（X2）、成灾面积（X3）、农业机械总动力（X4）和农业劳动力（X5），其中成灾面积的符号为负，其余均应为正。

下表给出了1983——2000中国粮食生产的相关数据。

点击name键进行命名，选择默认名称Group01,保存文件。

Y X1 X2 X3 X4 X5 1983 38728 1660 114047 16209 18022 31151 1984 40731 1740 112884 15264 19497 30868 1985 37911 1776 108845 22705 20913 31130 1986 39151 1931 110933 23656 22950 31254 1987 40208 1999 111268 20393 24836 31663 1988 39408 2142 110123 23945 26575 32249 1989 40755 2357 112205 24449 28067 33225 1990 44624 2590 113466 17819 28708 38914 1991 43529 2806 112314 27814 29389 39098 1992 44264 2930 110560 25895 30308 38669 1993 45649 3152 110509 23133 31817 37680 1994 44510 3318 109544 31383 33802 36628 1995 46662 3594 110060 22267 36118 35530 1996 50454 3828 112548 21233 38547 34820 1997 49417 3981 112912 30309 42016 34840 1998 51230 4084 113787 25181 45208 35177 1999 50839 4124 113161 26731 48996 35768 2000 46218 4146 108463 34374 52574 36043 2001 45264 4254 106080 31793 55172 36513 2002 45706 4339 103891 27319 57930 36870 2003 43070 4412 99410 32516 60387 365462004 46947 4637 101606 16297 64028 35269 2005 48402 4766 104278 19966 68398 33970 2006 49804 4928 104958 24632 72522 32561 2007 50160 5108 105638 25064 76590 31444 （三）用普通最小二乘法估计模型参数用最小二乘法估计模型参数。

多重共线性问题及解决方法概念所谓多重共线性（Multicollinearity）是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。

一般来说，由于经济数据的限制使得模型设计不当，导致设计矩阵中解释变量间存在普遍的相关关系。

后果参数估计失去其意义检验与检验目前常用的多重共线性诊断方法有： 1.自变量的相关系数矩阵R诊断法：研究变量的两两相关分析，如果自变量间的二元相关系数值很大，则认为存在多重共线性。

但无确定的标准判断相关系数的大小与共线性的关系。

有时，相关系数值不大，也不能排除多重共线性的可能。

2.方差膨胀因子（the variance inflation factor，VIF)诊断法：方差膨胀因子表达式为：VIFi=1/（1-R2i)。

其中Ri为自变量xi对其余自变量作回归分析的复相关系数。

当VIFi很大时，表明自变量间存在多重共线性。

该诊断方法也存在临界值不易确定的问题，在应用时须慎重。

3.容忍值（Tolerance，简记为Tol）法：容忍值实际上是VIF的倒数，即Tol＝1/VIF。

其取值在0～1之间，Tol越接近1，说明自变量间的共线性越弱。

在应用时一般先预先指定一个Tol 值，容忍值小于指定值的变量不能进入方程，从而保证进入方程的变量的相关系数矩阵为非奇异阵，计算结果具有稳定性。

但是，有的自变量即使通过了容忍性检验进入方程，仍可导致结果的不稳定。

4.多元决定系数值诊断法：假定多元回归模型p个自变量，其多元决定系数为R2y（X1，X2,…，Xp）。

分别构成不含其中某个自变量（Xi,i=1,2,…，p）的p个回归模型，并应用最小二乘法准则拟合回归方程，求出它们各自的决定系数R2i（i=1,2,…，p）。

如果其中最大的一个R2k 与R2Y很接近，就表明该自变量在模型中对多元决定系数的影响不大，说明该变量对Y总变异的解释能力可由其他自变量代替。

实验名称：多重共线性的检验与处理实验时间：2011.12.10实验要求：主要是学习多重共线性的检验与处理，主要是研究解释变量与其余解释变量之间有严重多重共线性的模型，分析变量之间的相关系数。

通过具体案例建立模型，然后估计参数，求出相关的数据。

再对模型进行检验，看数据之间是否存在多重共线性。

最后利用所求出的模型来进行修正。

实验内容：实例：我国钢材供应量分析通过分析我国改革开放以来（1978－1997）钢材供应量的历史资料，可以建立一个单一方程模型。

根据理论及对现实情况的认识，影响我国钢材供应量 Y（万吨）的主要因素有：原油产量X1（万吨），生铁产量X2（万吨），原煤产量X3（万吨），电力产量X4（亿千瓦小时），固定资产投资X5(亿元)，国内生产总值X6(亿元)，铁路运输量X7（万吨）。

（一）建立我国钢材供应量的计量经济模型：（二）估计模型参数，结果为：Dependent Variable: YMethod: Least SquaresDate: 11/02/09 Time: 16:09Sample: 1978 1997Included observations: 20Variable Coefficient Std. Error t-Statistic Prob.C 139.2362 718.2493 0.193855 0.8495X1 -0.051954 0.090753 -0.572483 0.5776X2 0.127532 0.132466 0.962751 0.3547X3 -24.29427 97.48792 -0.249203 0.8074X4 0.863283 0.186798 4.621475 0.0006X5 0.330914 0.105592 3.133889 0.0086X6 -0.070015 0.025490 -2.746755 0.0177X7 0.002305 0.019087 0.120780 0.9059R-squared 0.999222 Mean dependent var 5153.350Adjusted R-squared 0.998768 S.D. dependent var 2511.950S.E. of regression 88.17626 Akaike info criterion 12.08573Sum squared resid 93300.63 Schwarz criterion 12.48402Log likelihood -112.8573 F-statistic 2201.081Durbin-Watson stat 1.703427 Prob(F-statistic) 0.000000由此可见，该模型可绝系数很高，F检验值2201.081，明显显著。