力的分解唯一解
- 格式:doc
- 大小:106.00 KB
- 文档页数:3



力的分解基本知识点与练习题基本知识点一、分力的概念1、几个力,如果它们共同产生的效果跟作用在物体上的一个力产生的效果相同,则这几个力就叫做那个力的分力(那个力就叫做这几个力的合力)。
2、分力与合力是等效替代关系,其相同之处是作用效果相同;不同之处是不能同时出现,在受力分析或有关力的计算中不能重复考虑。
二、力的分解1、力的分解的概念:求一个已知力的分力叫做力的分解。
2、力的分解是力的合成的逆运算。
同样遵守力的平行四边形定则:如果把已知力F作为平行四边形的对角线,那么,与力F共点的平行四边形的两个邻边就表示力F的两个分力F1和F2。
3、力的分解的特点是:同一个力,若没有其他限制,可以分解为无数对大小、方向不同的力(因为对于同一条对角线.可以作出无数个不同的平行四边形),通常根据力的作用效果分解力才有实际意义。
4、按力的效果分解力F的一般方法步骤:(1)根据物体(或结点)所处的状态分析力的作用效果(2)根据力的作用效果,确定两个实际分力的方向;(3)根据两个分力的方向画出平行四边形;(4)根据平行四边形定则,利用学过的几何知识求两个分力的大小。
也可根据数学知识用计算法。
三、对一个已知力进行分解的几种常见的情况和力的分解的定解问题将一个力F分解为两个分力,根据力的平行四边形法则,是以这个力F为平行四边形的一条对角线作一个平行四边形。
在无附加条件限制时可作无数个不同的平行四边形。
这说明两个力的合力可唯一确定,一个力的两个分力不是唯一的。
要确定一个力的两个分力,一定有定解条件。
假设合力F一定1、当俩个分力F1已知,求另一个分力F2,如图F2有唯一解。
2、当俩个分力F 1, F2的方向已知,求这俩个力,如图F1, F2有唯一解3、当俩个分力F1, F2的大小已知,求解这俩个力。
A、当F1F2一组解。
B、F1F,无解。
C、F1F,俩个解。
4、当一个分力的方向已知,另一个大小未知。
①2sinθ,无解。
②2sinθ,一个解。






力的合成与分解知识要点归纳一、力的合成1.合力与分力:如果几个力共同作用产生的效果与某一个力单独作用时的效果相同,则这一个力为那几个力的,那几个力为这一个力的.2.共点力:几个力都作用在物体的同一点,或者它们的作用线相交于一点,这几个力叫做共点力.3.力的合成:求几个力的的过程.4.平行四边形定则:两个力合成时,以表示这两个力的线段为作平行四边形,这两个邻边之间的就表示合力的大小和方向.二、力的分解1.力的分解:求一个力的的过程,力的分解与力的合成互为.2.矢量运算法则:(1)平行四边形定则(2)三角形定则:把两个矢量的首尾顺次连结起来,第一个矢量的首到第二个矢量的尾的为合矢量.3.力的分解的两种方法1)力的效果分解法①根据力的实际作用效果确定两个实际分力的方向;②再根据两个实际分力方向画出平行四边形;③最后由平行四边形和数学知识(如正弦定理、余弦定理、三角形相似等)求出两分力的大小.2)正交分解法①正交分解方法:把一个力分解为互相垂直的两个分力,特别是物体受多个力作用时,把物体受到的各力都分解到互相垂直的两个方向上去,然后分别求出每个方向上力的代数和.②利用正交分解法解题的步骤首先:正确选择直角坐标系,通常选择共点力的作用点为坐标原点,直角坐标系的选择应使尽量多的力在坐标轴上.其次:正交分解各力,即分别将各力投影在坐标轴上,然后求各力在x轴和y 轴上的分力的合力F x 和F y :F x =F 1x +F 2x +F 3x +…,F y =F 1y +F 2y+F 3y +…再次:求合力的大小F =错误! ,确定合力的方向与x 轴夹角为θ=arctan F y F x. 4.将一个力分解的几种情况:①已知合力和一个分力的大小与方向:有唯一解②已知合力和两个分力的方向:有唯一解③已知合力和两个分力的大小(两分力不平行):当F1+F2<F 时无解;当F1+F2>F 时有两组解④已知一个分力F 1的方向和另一个分力F 2的大小,对力F 进行分解,如图4所示则有三种可能:(F 1与F 的夹角为θ) 当F 2〈F sin θ时无解;当F 2=F sin θ或F 2≥F 时有一组解;当F sin θ〈F 2<F 时有两组解.5.注意:(1)合力可能大于分力,可能等于分力,也可能小于分力的大小。

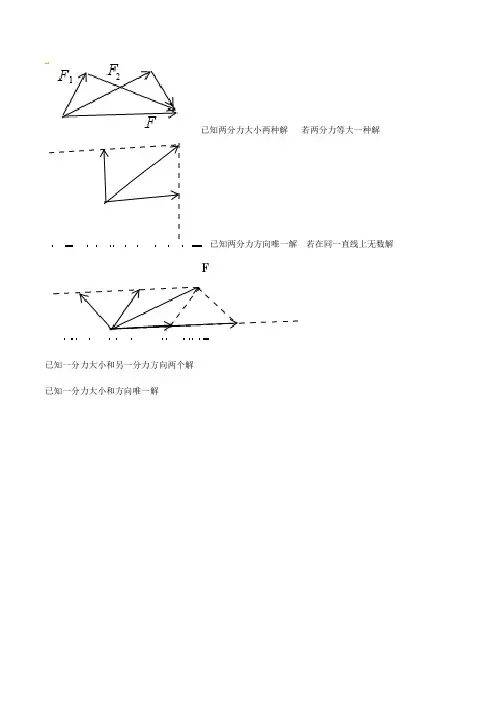
已知两分力大小两种解若两分力等大一种解
已知两分力方向唯一解若在同一直线上无数解
F
已知一分力大小和另一分力方向两个解
已知一分力大小和方向唯一解
力的分解的几种常见情形:
1、已知合力和两分力的方向.有唯一解.类似于已知两角夹边可以确定三角形
2、已知合力F和一个分力F1.有唯一解.类似于已知两边夹角可以确定三角形
3、已知合力和两分力的大小.类似于已知三边可以确定三角形
1当F1+F2> F时有两组解;
2当F1+F2= F时有唯一的一组解;
3当F1+F2< F时无解;
4、已知合力F和一个分力F1的方向F1与F的夹角为α及分力F2的大小.
用图示法和三角形知识分析:
①当F2<Fsinα时,圆与F l无交点,说明此时F l无解,如图 a所示.
②当F2=Fsinα时,圆与F l相切,说明此时F l只有一解,如图 b所示.
③当Fsinα<F2< F时,圆与F l有两交点,此时F l有两解,如图 c所示.
④当F2≥F时.圆与F l只有一个交点,此时F l只有一解,如图 d所示.。
(1)已知合力F 和两个不平行分力的方向
其解是唯一的
(2)已知合力F 和一个分力的大小、方向F
1
F 2F F
1F 其解是唯一的
力的分解中,解的唯一性讨论:
2
F
(3)已知合力F 和一个分力F 1的方向和另一个分力F 2的大小当F 2<F sin θ时,当F 2=F sin θ时,当F sin θ<F 2<F 时,当F 2>F 时,F 1F θF
1F θ090
<θ当F 2>F 时,有唯一解;其余均无解;
090≥θ无解;分解是唯一的;分解不唯一,有两解;分解也是唯一的;
(4)已知合力F 和两个分力的大小F 1、F 2无解;有唯一解;有两对解;或F 1+F 2<F 时,若F <F 1-F 2或F 1+F 2=F 时,若F 1-F 2=F 若F 1-F 2<F <F 1+F 2时,分别以F 的始端、末端为圆心,以F 1、F 2为半径作圆,两圆有两个交点,所以F 分解为F 1、F 2有两种情况.。
学案8力的分解[目标定位] 1.知道什么是力的分解,知道力的分解同样遵守平行四边形定则.2.理解力的分解原则,并会用作图法和计算法求分力.3.知道力的三角形定则,会区分矢量和标量.4.会用正交分解法求合力.一、力的分解[问题设计]王昊同学假期里去旅游,他正拖着行李箱去检票,如图1所示.王昊对箱子有一个斜向上的拉力,这个力对箱子产生了什么效果?图1答案王昊对箱子斜向上的拉力产生了两个效果:水平方向使箱子前进,竖直方向将箱子向上提起.[要点提炼]1.力的分解(1)定义:已知一个力求它的分力的过程叫做力的分解.(2)分解法则:力的分解是力的合成的逆运算,遵守力的平行四边形定则.2.对一个已知力的分解可依据力的实际效果来确定:(1)依据力的实际作用效果确定两个分力的方向.(2)依据两个分力的方向作出力的平行四边形.(3)利用数学学问解三角形,分析、计算分力的大小.3.力的分解的争辩(1)假如没有限制,一个力可分解为很多对大小、方向不同的分力.(2)有限制条件的力的分解①已知合力和两个分力的方向时,有唯一解.(如图2所示)图2②已知合力和一个分力的大小和方向时,有唯一解.(如图3所示)图3(3)已知合力F以及一个分力F1的方向和另一个分力F2的大小时,若F与F1的夹角为α,有下面几种可能:图4①当F sin α<F2<F时,有两解,如图4甲所示.②当F2=F sin α时,有唯一解,如图乙所示.③当F2<F sin α时,无解,如图丙所示.④当F2>F时,有唯一解,如图丁所示.二、力的正交分解法1.正交分解的目的:当物体受到多个力作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不便利,为此先将各力正交分解,然后再合成.2.正交分解法求合力的步骤(1)建立坐标系:以共点力的作用点为坐标原点建立直角坐标系,直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上.(2)正交分解各力,即将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图5所示.图5(3)分别求出x轴、y轴上各分力的矢量和,即:F x=F1x+F2x+F3x+…F y =F 1y +F 2y +F 3y +…(4)求共点力的合力:合力大小F =F 2x +F 2y ,合力的方向与x 轴的夹角为α,则tan α=F yF x . 三、矢量相加的法则 1.三角形定则(1)内容:如图6所示,把两个矢量首尾相接,从第一个矢量的始端指向其次个矢量的末端的有向线段就表示合矢量的大小和方向,这就是矢量相加的三角形定则.图6(2)实质:平行四边形定则的简化.(如图7所示)图72.矢量和标量(1)矢量既有大小又有方向,相加时遵从平行四边形定则(或三角形定则). (2)标量只有大小,没有方向,相加时依据算术法则. 留意 矢量和标量的最本质的区分是运算法则不同.一、按力的作用效果分解例1 如图8甲所示,在一个直角木支架上,用塑料垫板作斜面,将一用橡皮筋拉着的小车放在斜面上(如图乙),观看塑料垫板和橡皮筋的形变.图8(1)小车重力对斜面和橡皮筋产生了哪些作用效果?假如没有小车重力的作用,还会有这些作用效果吗?(2)请依据重力产生的两个效果将重力分解,并求两分力的大小.答案 (1)斜面上小车重力产生了两个效果:一是使小车压紧斜面,二是使小车沿斜面下滑,拉伸橡皮筋.不会.(2)重力的分解如图所示设斜面的倾角为θ(忽视斜面的形变).由几何关系知∠DOE=θ.由三角函数可得:F1=mg sin α,F2=mg cos α.针对训练如图9所示,轻杆与柱子之间用铰链连接,杆的末端吊着一个重为30 N的物体,轻绳与水平轻杆之间的夹角为θ=30°,求轻绳和轻杆各受多大的力?图9答案60 N52 N解析重物对O点的拉力F=G,产生两个作用效果:一个是沿绳方向拉轻绳,一个是沿杆方向压杆(因轻杆处于静止时杆所受的弹力肯定沿着杆,否则会引起杆的转动),作平行四边形如图所示,由几何关系解得F1=Gsin θ=60 NF2=Gtan θ≈52 N二、有限制条件的力的分解例2按下列两种状况把一个竖直向下的180 N的力分解为两个分力.图10(1)一个分力在水平方向上,并等于240 N,求另一个分力的大小和方向.(2)一个分力在水平方向上,另一个分力与竖直方向的夹角为30°斜向下(如图10所示),求两个分力的大小.解析(1)力的分解如图所示.F 2=F 2+F 21=300 N设F 2与F 的夹角为θ,则 tan θ=F 1F =43,解得θ=53°(2)力的分解如图所示. F 1=F tan 30°=180×33N =60 3 N F 2=F cos 30°=18032N =120 3 N答案 (1)300 N 与竖直方向夹角为53° (2)水平方向分力的大小为60 3 N ,斜向下的分力的大小为120 3 N 三、力的正交分解法例3 如图11所示,水平地面上有一重60 N 的物体,在与水平方向成30°角斜向上、大小为20 N 的拉力F 作用下匀速运动,求地面对物体的支持力和摩擦力的大小.图11解析 对物体进行受力分析,如图所示,物体受重力G 、支持力F N 、拉力F 、摩擦力F f .建立直角坐标系, 对力进行正交分解得: y 方向: F N +F sin 30°-G =0① x 方向:F f -F cos 30°=0② 由①②得:F N =50 N ,F f =10 3 N. 答案 50 N 10 3 N1.力的分解:已知一个力求它的分力的过程.力的分解遵循平行四边形定则. 2.力的分解有唯一解的条件 (1)已知两个分力的方向.(2)已知一个分力的大小和方向. 3.力的分解方法(1)按力的实际作用效果分解. (2)正交分解法以共点力的作用点为原点建立直角坐标系(让尽量多的力在坐标轴上),把不在坐标轴上的力分解到x 轴、y 轴上,然后分别求出x 轴和y 轴上的合力F x 和F y ,则共点力的合力大小F =F 2x +F 2y ,合力方向与x 轴夹角为α,tan α=F yF x . 4.矢量相加的法则平行四边形定则、三角形定则.1.(按力的作用效果分解)在图12中,AB 、AC 两光滑斜面相互垂直,AC 与水平面成30°.假如把球O 的重力G 依据其作用效果分解,则两个分力的大小分别为( )图12A.12G ,32G B.33G ,3G C.23G ,22G D.22G ,32G 答案 A解析 对球所受重力进行分解如图所示,由几何关系得F 1=G sin 60°=32G ,F 2=G sin 30°=12G ,A 正确.2.(有限制条件的力的分解)甲、乙两人用绳子拉船,使船沿OO ′方向航行,甲用1 000 N 的力拉绳子,方向如图13所示,要使船沿OO ′方向航行,乙的拉力最小值为( )图13A.500 3 N B.500 NC.1 000 N D.400 N答案B解析要使船沿OO′方向航行,甲和乙的拉力的合力方向必需沿OO′方向.如图所示,作平行四边形可知,当乙拉船的力的方向垂直于OO′时,乙的拉力F乙最小,其最小值为F乙min=F甲sin 30°=1 000×12N=500 N,故B正确.3.(正交分解法)如图14所示,放在水平面上的物体A用轻绳通过光滑定滑轮连接另一物体B,并静止,这时A受到水平面的支持力为F N,摩擦力为F f,若把A向右移动一些后,A 仍静止,则()图14A.F N将增大B.F f将增大C.轻绳拉力将减小D.物体A所受合力将增大答案AB解析物体A受力分析如图,系统处于静止状态,绳子的拉力不变,始终等于B的重力,即F=m B g,A所受合力为零,故C、D均错;当A向右移动时,θ角减小,F N=m A g-F sin θ,F f=F cos θ,由此可得,F N、F f均增大,所以A、B正确.题组一对力的分解的理解1.若将一个力F分解为两个力F1、F2,则下列说法正确的是()A.F是物体实际受到的力B.F1、F2不是物体实际受到的力C.物体同时受到F、F1、F2三个力的作用D.F1、F2共同作用的效果与F相同答案ABD2.把一个力分解为两个力时()A.一个分力变大时,另一个分力肯定要变小B.两个分力不能同时变大C.无论如何分解,两个分力不能同时小于这个力的一半D.无论如何分解,两个分力不能同时大于这个力的2倍答案C解析设把一个力F分解为F1、F2两个分力,当F1、F2在一条直线上且方向相反时,则有F=|F1-F2|,当F1变大时,F2也变大,A、B错.F1、F2可以同时大于F的2倍,D错.当将F沿一条直线分解为两个方向相同的力F1、F2时,则有F=F1+F2,可知F1、F2不行能同时小于12F,C对.3.下列说法中正确的是()A.一个2 N的力能分解为7 N和4 N的两个分力B.一个2 N的力能分解为7 N和9 N的两个分力C.一个6 N的力能分解为3 N和4 N的两个分力D.一个8 N的力能分解为4 N和3 N的两个分力答案BC题组二有限制条件的力的分解4.下列说法正确的是()A.已知合力大小、方向,则其分力必为确定值B.已知合力大小、方向和一个分力的大小、方向,则另一个分力必为确定值C.分力数目确定后,若已知各分力大小、方向,可依据平行四边形定则求出总的合力D.若合力为确定值,两分力方向已知,依据平行四边形定则肯定可以求出这两个分力的大小答案BCD解析已知合力大小、方向,其分力有很多组,A错.若已知合力大小、方向和一个分力的大小、方向,则依据平行四边形定则,另一分力为确定值,B对.若分力确定后,可依据平行四边形定则,求出总的合力,C 对.合力为确定值,两分力的方向已知,则两分力是唯一的.5.将一个有确定方向的力F =10 N 分解成两个分力,已知一个分力有确定的方向,与F 成30°夹角,另一个分力的大小为6 N ,则在分解时( ) A .有很多组解 B .有两组解 C .有唯一解 D .无解答案 B解析 由三角形定则作图如图所示,由几何学问知另一分力的最小值F 2′=F sin 30°=10×12 N =5 N ,而题中分力的大小为6 N ,大于最小值5 N ,小于F =10 N ,所以有两组解. 题组三 按力的作用效果分解6.如图1为某同学设计的一个小试验.他将细绳的一端系在手指上(B 处),绳的另一端系在直杆的A 端,杆的另一端C 顶在掌心上,组成一个“三角支架”.在杆的A 端悬挂不同重物,并保持静止.通过试验会感受到( )图1A .绳子是被拉伸的,杆是被压缩的B .杆对手掌施加作用力的方向沿杆由C 指向A C .绳对手指施加作用力的方向沿绳由B 指向AD .所挂重物质量越大,绳和杆对手的作用力也越大 答案 ACD解析 重物重力的作用效果,一方面拉紧绳,另一方面使杆压紧手掌,所以重力可以分解为沿绳方向的力F 1和垂直于掌心方向的力F 2,如图所示.由几何学问得F 1=Gcos θ,F 2=G tan θ,若所挂重物质量变大,则F 1、F 2都变大,选项A 、C 、D 正确.7.如图2所示,将绳子的一端系在汽车上,另一端系在等高的树干上,两端点间绳长为10 m .用300 N 的拉力把水平绳子的中点往下拉离原位置0.5 m ,不考虑绳子的重力和绳子的伸长量,则绳子作用在汽车上的力的大小为( )图2 A.1 500 N B.6 000 N C.300 N D.1 500 3 N 答案A解析由题意可知绳子与水平方向的夹角正弦值为sin α=0.5 5=0.1,所以绳子的作用力为F绳=F2sin α=1 500 N,A项正确,B、C、D项错误.8.如图3所示,三段不行伸长的细绳,OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,其中OB是水平的,A端、B端固定在水平天花板上和竖直墙上.若渐渐增加C 端所挂重物的质量,则最先断的绳是()图3A.必定是OA B.必定是OBC.必定是OC D.可能是OB,也可能是OC答案A解析OC下悬挂重物,它对O点的拉力等于重物的重力G.OC绳的拉力产生两个效果:使OB在O点受到水平向左的力F1,使OA在O点受到沿绳子方向斜向下的力F2,F1、F2是G的两个分力.由平行四边形定则可作出力的分解图如图所示,当渐渐增大所挂物体的质量时,哪根绳受的拉力最大则哪根最先断.从图中可知:表示F2的有向线段最长,F2分力最大,故OA绳最先断.题组四力的正交分解9.如图4所示,质量为m的等边三棱柱静止在水平放置的斜面上.已知三棱柱与斜面之间的动摩擦因数为μ,斜面的倾角为30°,则斜面对三棱柱的支持力与摩擦力的大小分别为()图4 A.32mg 和12mg B.12mg 和32mg C.12mg 和12μmg D.32mg 和32mg 答案 A解析 依据重力mg 的作用效果,可分解为沿斜面对下的分力F 1和使三棱柱压紧斜面的力F 2,依据几何关系得F 1=mg sin 30°=12mg , F 2=mg cos 30°=32mg , 由于,F 1与三棱柱所受静摩擦力大小相等,F 2与斜面对三棱柱的支持力大小相等,因此,选项A 正确.10.如图5所示,甲、乙、丙三个物体质量相同,与地面的动摩擦因数相同,受到三个大小相同的作用力F ,当它们滑动时,受到的摩擦力大小是( )图5A .甲、乙、丙所受摩擦力相同B .甲受到的摩擦力最大C .乙受到的摩擦力最大D .丙受到的摩擦力最大答案 C解析 题图中三个物体对地面的压力分别为F N 甲=mg -F sin θ,F N 乙=mg +F sin θ,F N 丙=mg ,因它们均相对地面滑动,由F f =μF N 知,F f 乙>F f 丙>F f 甲,故C 正确.11.如图6所示,质量为m 的物块与水平面之间的动摩擦因数为μ,现用斜向下与竖直方向夹角为θ的推力作用在物块上,使物块在水平面上匀速移动,求推力的大小.(重力加速度为g )图6答案 μmg cos θ-μsin θ解析 对物块受力分析如图所示将物块受到的力沿水平和竖直方向分解,依据平衡条件有水平方向:F cos θ=F f ①竖直方向:F N =mg +F sin θ②F f =μF N ③由①②③得F =μmg cos θ-μsin θ12.如图7所示,物体的质量m =4.4 kg ,用与竖直方向成θ=37°的斜向右上方的推力把该物体压在竖直墙壁上,并使它沿墙壁在竖直方向上做匀速直线运动.物体与墙壁间的动摩擦因数μ=0.5,取重力加速度g =10 N/kg ,求推力F 的大小.(sin 37°=0.6,cos 37°=0.8)图7答案 88 N 或40 N解析 若物体向上做匀速直线运动,则受力分析如图甲所示.F cos θ=mg +F fF sin θ=F NF f =μF N故推力F =mg cos θ-μsin θ= 4.4×100.8-0.5×0.6N =88 N若物体向下做匀速直线运动,受力分析如图乙所示. F cos θ+F f =mgF sin θ=F NF f =μF N故推力F =mg cos θ+μsin θ= 4.4×100.8+0.5×0.6 N =40 N。
力的分解常用的方法剖析:1.正交分解法(1)定义:把一个力分解为互相垂直的分力的方法.(2)优点:把物体所受的不同方向的各个力都分解到相互垂直的两个方向上去,然后再求每个方向的分力的代数和,这样就把复杂的矢量运算转化成了简单的代数运算,最后再求两个互成90o的力的合力就简单多了.(3)运用正交分解法解题的步骤:1正确选择直角坐标系,通常选择共点力的作用点为坐标原点,直角坐标x、y的选择可按以下原则去确定:a.尽可能使更多的力落在坐标轴上.b.沿物体运动方向或加速度方向设置一个坐标轴.c.若各种设置效果一样,则沿水平方向和竖直方向设置两坐标轴.2正交分解各力,即分别将各力投影到坐标轴上,分别求x轴和y轴各力投影的合力Fx和Fy,其中,;3求Fx和Fy的合力即为共点力的合力合力大小:,合力的方向与x轴夹角:.2.按问题的需要进行分解(1)已知合力和两个分力的方向,求分力的大小.如图2-2-5甲已知力F和α、β,显然所做出的平行四边形是唯一确定的,即两个分力的大小也唯一确定.(2)已知合力、一个分力的大小和方向,求令一个分力的大小和方向.如图2-2-5乙,已知F、F1和α,显然此平行四边形也被唯一确定,即F2的大小和方向(角度β)也被唯一确定了.(3)已知合力、一个分力的方向和另一个分力的大小,即已知F、α(F与F1的夹角)和F2的大小,求F1的大小和F2的方向,有如下几种情况:F>F2>Fsinα时,有两个解;F2=Fsinα时,有唯一解;F2<Fsinα时,无解,因为此时无法组成力的平行四边形;F2≥F时,有唯一解.【例题3】如图2-2-7甲所示,电灯的重力,绳与顶板间的夹角为绳水平,则绳所受的拉力;绳所受的拉力.解析: 查力的平衡、力的合成与分解.先分析物理现象:为什么绳AO,BO受到拉力呢?原因是由于OC绳受到电灯的拉力才使AO,BO绳张紧产生拉力,因此OC绳的拉力产生了两个效果,一是沿OA向下的拉紧AO的分力F1,二是沿BO向左的拉紧BO绳的分力F2,画出平行四边形如图2-2-7乙所示,因为OC拉力等于电灯重力,因此,由几何关系得:答案:【变式训练3】如图2-2-8所示,用轻质三角支架悬挂重物,已知AB杆所受的最大压力为2000N,AC 绳所受的最大拉力为1000N,α 角为30o.为了不使支架断裂,则所悬的重物应当满足。
力的分解Ⅰ力的分解的几种典型情况将一个力按一定条件分解时合力可能能按要求进行分解,即有解,也可能不能按要求进行分解,即无解。
分析是否有解的方法是看代表合力的有向线段与代表分力的有向线段能否按要求构成平行四边形,如果能构成平行四边形,说明有解;如果它们不能构成平行四边形,说明无解。
典型的情况有以下几种:(1)已知合力和两个分力的方向时,有唯一解,如下图所示。
(2)已知合力和一个分力的大小和方向时,有唯一解,如下图所示。
(3)已知合力以及一个分力的大小和另一个分力的方向时,有下面几种可能:如图所示,①当Fsin θ<F2<F时,有两解。
②当F2=Fsin θ时,有唯一解。
③当F2<Fsin θ时,无解。
④当F2>F时,有唯一解。
小试牛刀:例:如图所示,物体静止在光滑水平面上,力F作用于物体上的O点,现要使物体受到由O指向O′方向的合力(F与OO′都在同一平面内,与OO′间夹角为θ)。
那么,必须同时再加一个力,这个力的最小值()A.Fcos θB.Fsin θC.Ftan θ D.Fcot θ【答案】B【解析】已知合力F合的方向由O指向O′,但大小不确定,又已知一个分力F的大小和方向,确定另一个分力(设为Fx)的最小值。
根据三角形定则可画出一个任意情况,如图甲所示。
从图中可看出,Fx的大小就是过F的箭头向直线OO′上所引直线的长度,在不考虑合力大小的情况下,欲使Fx最小,应使Fx与直线OO′垂直,如图乙所示,此时Fx=Fsin θ。
Ⅱ按实际效果进行分解1.把一个力分解为两个力,从理论上讲有无数组解。
因为同一条对角线可以构成的平行四边形有无穷多个(如图所示),这样分解是没有实际意义的,实际分解时,按力的作用效果可分解为两个确定的分力。
2.按实际效果分解力的一般思路3.按实际效果分解的几个实例:实例分析地面上物体受斜向上的拉力F,拉力F一方面使物体沿水平地面前进,另一方面向上提物体,因此拉力F可分解为水平向前的力F1和竖直向上的力F2。
已知两分力大小(两种解) 若两分力等大(一种解)
已知两分力方向(唯一解)若在同一直线上(无数解)
F
已知一分力大小和另一分力方向(两个解)
已知一分力大小和方向(唯一解)
力的分解的几种常见情形:
1、已知合力和两分力的方向.有唯一解. (类似于已知两角夹边可以确定三角形)
2、已知合力F和一个分力F1.有唯一解.(类似于已知两边夹角可以确定三角形)
3、已知合力和两分力的大小.(类似于已知三边可以确定三角形)
(1)当F 1+F2> F时有两组解;
(2)当F1+F2= F时有唯一的一组解;
(3)当F1+F2< F时无解。
4、已知合力F和一个分力F1的方向(F1与F的夹角为α)及分力F2的大小.
用图示法和三角形知识分析:
①当F2<Fsinα时,圆与Fl无交点,说明此时F l无解,如图 (a)所示.
②当F2=Fsinα时,圆与F l相切,说明此时F l只有一解,如图 (b)所示.
③当Fsinα<F2< F时,圆与Fl有两交点,此时F l有两解,如图 (c)所示.
④当F2≥F时.圆与F l只有一个交点,此时F l只有一解,如图(d)所示.。