第二十一讲:§6.5磁场对运动电荷和载流导线的作用(一、二、三)
- 格式:doc
- 大小:114.00 KB
- 文档页数:4





6–5 磁场对运动电荷和载流导线的作用一 带电粒子在电场和磁场中所受的力电场力E qF =e磁场力(洛仑兹力)B q F ⨯=v m大小 θυsin B q F m =只能改变速度方向运动电荷在电场和磁场中受的力B q E q F ⨯+=v 例1 一质子沿着与磁场垂直的方向运动, 在某点它的速率为16s m 101.3-⋅⨯。
由实验测得这时质子所受的洛仑兹力为N 104.714-⨯。
求该点的磁感强度的大小。
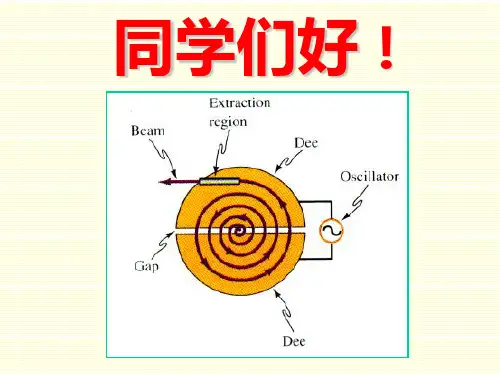
解:T 15.0T 101.3106.1104.761914=⨯⨯⨯⨯==--v q F B 二 带电粒子在磁场中的运动1. 0υ与B 平行或反平行 0=m F ,c =υ2. 0υ 与B 垂直,回旋半径和回旋频率 B ⊥0vR m B q 200v v = 回旋半径:qBm R 0v = 回旋周期:qBm R T π2π20==v ∙0υ B 粒子做直线运动回旋频率:mqB T f π21== 3. 0υ 与B 成θ角,磁聚焦B q F ⨯=v m⊥+=v v v //θcos v v //=θsin v v =⊥qBm R ⊥=v qBm T π2= 螺距qBm d π2cos θv T v //== 磁聚焦在均匀磁场中某点 A 发射一束初速相差不大的带电粒子,它们的V 与B 之间的夹角θ不尽相同,但都较小,这些粒子沿半径不同的螺旋线运动,因螺距近似相等,都相交于屏上同一点,此现象称之为磁聚焦应用 电子光学,电子显微镜等三 带电粒子在电场和磁场中的运动1. 质谱仪速度选择器B e E e ⨯=vBE =vRm B q 2v v =' vR B q m '=2. 回旋加速器频率与半径无关mqB f π2=到半圆盒边缘时mqBR 0=v 2k 21v m E = mR B q E 22022k = 例2 有一回旋加 速器,他 的交变 电压的 频率为Hz 10126⨯,半圆形电极的半径为0.532m 。





6-5 磁场对运动电荷和载流导线的作用四 安培力1 安培定律、安培力洛伦兹力B e f ⨯-=d m v大小:θsin d m B e f v =θsin d d d lB S ne F v =S ne I d v =φθsin d sin d d lB I lB I F ==磁场对电流元的作用力B l I F ⨯=d d —安培定律,F d —安培力有限长载流导线所受的安培力B l I F F ll ⨯==⎰⎰d d 例1 如图一通有电流I 的闭合回路放在磁感应强度为B 的均匀磁场中,回路平面与磁感强度B 垂直。
回路由直导线 AB 和半径为 R 的圆弧导线 BCA 组成,电流为顺时针方向,求磁场作用于闭合导线的力。
解:j B AB I F -=102=x F⎰=θsin d 2l BI F y⎰-=00π2d sin θθθθBIr Fj AB BI j r BI F ==)cos 2(02θj AB BI F -=1021=+=F F F例2 求图中不规则的平面载流导线在均匀磁场中所受的力,已知B 和I 。
解:B l I F ⨯=d dθθsin d sin d d l BI F F x ==θθcos d cos d d l BI F F y ==0d d 00===⎰⎰y BI F F x x BIl x BI F F ly y ===⎰⎰0d d j BIl F F y ==结论 任意平面载流导线在均匀磁场中所受的力,与其始点和终点相同的载流直导线所受的磁场力相同。
例3 半径为R 载有电流I 2的导体圆环与电流为I 1的长直导线放在同一平面内, 直导线与圆心相距为 d ,且 R < d 两者间绝缘,求作用在圆电流上的磁场力。
解:θμcos π210R d I B += θμcos d π2d d 2102R d l I I l BI F +== θd d R l =θθμcos d π2d 210R d R I I F += θθθμθcos d cos π2cos d d 210R d R I I F F x +== θθθμθcos d sin π2sin d d 210R d R I I F F y +== ⎰+=π20210cos d cos π2θθθμR d R I I F x )1(22210R d d I I --=μ 0cos d sin π2π20210=+=⎰θθθμR d RI I F y i R d dI I i F F x )1(22210--==μ2 无限长两平行载流直导线间的相互作用力1121dl I B dF =,2212dl I B dF =a I B πμ2202=,a I B πμ2101=导线1、2单位长度上所受的磁力为:a I I dl dF πμ221011=,aI I dl dF πμ221022= 电流单位“安培”的定义:放在真空中的两条无限长平行直导线,各通有相等的稳恒电流,当导线相距1米,每一导线每米长度上受力为2×10-7牛顿时,各导线中的电流强度为1安培。
第二十一讲:§6.5磁场对运动电荷和载流导线的作用(一、二、三)
一、洛伦磁力:运动电荷在磁场中所受的力
1、表达式:q m ⨯=υ 满足右手螺旋关系
2、讨论:①0 q ,m 与 ⨯υ 同向;
②0 q ,m 与 ⨯υ 反向;
洛伦磁力与速度垂直,因而不做功。
它不能改变运动电荷的速度大小,只能改变速度方向,使其运动方向发生改变。
二、带电粒子在磁场中的运动 设有一均匀磁场,磁感应强度B ,带电粒子以初速度0进入磁场,根据牛顿定律,有
dt
d m q m υυ=⨯= (6-30) 1、0//B
由(6-30)式,0=m F ,带电粒子在磁场
不受力的作用,将作匀速直线运动。
2、0┴B
此时,带电粒子在磁场中作匀速圆周运动
如图所示: ①回旋半径:R m B q F m 200υυ== qB
m R 0υ=⇒ ②回旋周期:qB
m qB m R
T πυυπυπ222000===
③回旋频率:m
qB T f π21==
3、0与B 成任意夹角θ 此时,可将0υ分解为
θυυcos 0//= θυυs i n 0=⊥ ①回旋半径:R m B q F m 2⊥⊥==υυ qB
m qB m R θυυsin 0==⇒⊥ ②回旋周期:qB
m qB m R
T πυυπυπ222===⊥⊥⊥ 结果同上 ③旋距:qB m T h πθ
υυ2cos 0//== P222例题6-5
三、霍尔
在导体两侧出现电势差的现象,称为霍尔效应。
霍尔效应是磁电效应的一种,即带电粒子在磁场和电场在运动所产生的效应。
1、霍尔电势差 21U U U H -=
b BI U H ∝ b
BI R U H H =⇒ ⑴
2、霍尔系数
①二力平衡: qE B q =υ E B =⇒υ ⑵
②电流与其他物理量的关系:ab qn S qn I υυ== nqb I a =
υ ⑶ ③霍尔电势差:b
IB nq B nqb I Ba Ea U U U H 121==
==-=υ ⑷ 由⑴、⑷可推出
nq R H 1= 讨论:0 q 0 H R ;0 q 0 H R ;
利用霍尔效应的霍尔元件可以用来控制转速、压力;还可以控制电流,是自动控制的一个重要元件。
由于通电导线周围存在磁场,其大小与导线中的电流成正比,故可以利用霍尔元件测量出磁场,就可确定导线电流的大小I B ∝。
利用这一原理可以设计制成霍尔电流传感器。
其优点是不与被测电路发生电接触,不影响被测电路,不消耗被测电源的功率,特别适合于大电流传感。
四、洛伦磁力在科学与工程技术中的应用实例
五、安培力
小结:磁场对运动电荷的作用(一、二、三)
作业:P256 2-28;2-29;2-30;
预习:§6.6磁场力的功
第二十一讲:§6.5磁场对运动电荷和载流导线的作用(一、二、三) 作业P256
6-28 由题设
K B V B V e B V e F x y y x )(-=⨯=
)N (1024.610)03.0315.02(106.1146
19K K --⨯=⨯⨯-⨯-⨯-=
6-29 由题设质子沿x ,y 轴的速度分量分别为1616s m 103,s m 102--⋅⨯=⋅⨯=y x V V ,故质子作螺旋运动的半径为
m 109.308
.0106.11031067.12195
27---⨯=⨯⨯⨯⨯⨯==eB mV R y
螺距为 08
.0106.1102101.922195
31⨯⨯⨯⨯⨯⨯===--ππeB mV T V h x x m 164.0=
6-30 因为霍尔电压为
b
IB ne U H 1=
故待测磁场为 2
3
19245101015.0106.110102.4----⨯⨯⨯⨯⨯⨯==I neb U B H T 101.0=。