下载文档原格式
基于MATLAB的自适应均衡器的研究毕业论自适应均衡器（Adaptive Equalizer）是一种用于消除信号传输中的失真影响的信号处理器。
在通信系统和数码信号处理中，信号在传输过程中容易受到噪声干扰和信号失真的影响，从而导致接收端的信号质量下降。
自适应均衡器通过根据接收端的反馈信息，调整均衡器的参数来补偿信号传输中的失真影响，从而提高信号质量。
MATLAB是一种广泛应用于科学和工程领域的高级计算机语言和环境。
它提供了丰富的工具和函数库，可以方便地进行信号处理和模拟仿真。
基于MATLAB的自适应均衡器研究可以通过建立模型、仿真实验和性能评估来实现。
首先，在MATLAB中可以通过建立自适应均衡器模型来进行研究。
自适应均衡器的基本原理是根据接收信号和已知的传输信号之间的差异，调整均衡器的系数来补偿信号失真。
在MATLAB中，可以根据特定的信道模型和均衡算法来实现自适应均衡器模型。
其次，通过进行仿真实验可以验证自适应均衡器的性能。
在MATLAB 中，可以生成各种类型的信号，并通过添加噪声和失真来模拟信号传输中的实际情况。
然后，使用自适应均衡器模型来对仿真信号进行处理，并比较处理前后的信号质量。
通过观察误码率、信号噪声比等指标，可以评估自适应均衡器的性能。
最后，可以使用MATLAB进行自适应均衡器的性能分析和优化。
通过调整均衡器的参数和算法，可以优化自适应均衡器的性能。
MATLAB提供了各种工具和函数库，如优化算法工具箱、信号处理工具箱等，可以帮助研究人员快速分析和优化自适应均衡器的性能。
总之，基于MATLAB的自适应均衡器的研究可以通过建立模型、进行仿真实验和性能评估来实现。
MATLAB提供了丰富的工具和函数库，可以方便地进行信号处理和模拟仿真，从而帮助研究人员深入了解和优化自适应均衡器的工作原理和性能。
基于MATLAB的数字滤波器设计摘要：通过Matlab 强大的信号处理功能，分析数字均衡器的设计要求，对各种数字音频信号进行滤波处理，设计出一种比较合理的数字滤波器，并在此基础上设计一种均衡器，最后对该数字滤波器和均衡器进行综合测试并改进，使其达到要求的指标。
关键词： MATLAB；数字滤波器；均衡器一、概述随着数字化技术的快速、深入发展，人们对数字化电子产品所产生的图像、图形以及声音等质量的要求越来越高。
在实时数字处理过程中，与D/A 和A/D 转换相关的模拟信号重构过程是决定数字系统输出质量的关键。
在声音的拾取过程及通过音响设备的传送过程中，由于设备或器件的原因，其幅度对频率的响应往往不一致，这样就达不到原来的效果，往往需要对目标信号进行滤波处理，以满足用户对信号的要求。
MATLAB 是一个数据分析和处理功能十分强大的工程实用软件，它的滤波器设计工具箱为实现声音信号的数字滤波提供了十分方便的函数和命令。
本文将介绍基于MATLAB设计出的一种实用的数字滤波器，并对其功能进行扩展，设计出一种均衡器。
滤波器的种类很多，按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。
低通滤波器：它允许信号中的低频或直流分量通过，抑制高频分量或干扰和噪声。
高通滤波器：它允许信号中的高频分量通过，抑制低频或直流分量。
带通滤波器：它允许一定频段的信号通过，抑制低于或高于该频段的信号、干扰和噪声。
带阻滤波器：它抑制一定频段内的信号，允许该频段以外的信号通过。
上述每种滤波器又可以分为模拟滤波器和数字滤波器。
如果滤波器的输入输出都是数字信号，则这样的滤波器称之为数字滤波器，它通常通过一定的运算关系改变输入信号所含频率成分的相对比例或者滤除某些频率成分来实现滤波。
根据数字滤波器冲激响应的时域特性，可将数字滤波器分为两种，即无限长冲激响应（IIR）滤波器和有限长冲激响应（FIR）滤波器。
根据数字信号处理的一般理论，IIR滤波器的特征是具有无限持续时间的冲激响应，而FIR滤波器使冲激响应只能持续一定的时间。
基于Matlab的数字滤波器设计及均衡器设计1数字滤波器设计背景及目的数字滤波器是一个离散时间系统，是一种按预定的算法，将输入离散时间信号转换为所要求的输出离散时间信号的特定功能装置。
数字滤波器具有高精度、高可靠性、可程控改变特性或复用、便于集成等优点。
数字滤波器在语言信号处理、图像信号处理、医学生物信号处理以及其他应用领域都得到了广泛应用。
数字滤波器有低通、高通、带通、带阻和全通等类型。
它可以是时不变的或时变的、因果的或非因果的、线性的或非线性的。
应用最广的是线性、时不变数字滤波器，以及FIR滤波器。
本次设计的目的是在Matlab R2007a的软件平台上，应用所学知识，设计一款FIR数字滤波器，要求有便于用户操作的用户界面，能完成低通、高通、带通及带阻等常用滤波功能。
2数字滤波器设计原理数字滤波器可以按所处理信号的维数分为一维、二维或多维数字滤波器。
一维数字滤波器处理的信号为单变量函数序列，例如时间函数的抽样值。
二维或多维数字滤波器处理的信号为两个或多个变量函数序列。
例如，二维图像离散信号是平面坐标上的抽样值。
本次设计的滤波器属于一维数字滤波器。
图1 信号变换数字滤波器的优点是利用差分方程可求离散系统的瞬态解，如下图2所示。
图2 滤波器优点FIR滤波器又称为有限脉冲响应滤波器，FIR就来源于名词“有限脉冲响应”的英文单词首字符缩写。
FIR传递函数：脉冲响应函数：由于h(k)是一个有限长度的序列，故FIR滤波器称为有限脉冲响应滤波器。
FIR滤波器的滤波公式：y(k)=h(0)x(k-m/2)+h(1)x(k-m/2+1) +...+h(m) x(k+m/2)FIR滤波器系数脉冲响应函数设计方法如下其中低通、高通、带通及带阻的设计原理如下图所示。
3设计内容7.3 搭建GUI界面Matlab环境下的图形用户界面（GUI）是由窗口、光标、按键、菜单、文字说明等对象（Objects）构成的一个用户界面。
电子信息系综合课程设计基于Matlab的自适应均衡器设计专业名称通信工程班级学号学生姓名指导教师设计时间2010.12.20~2011.1.7课程设计任务书专业：学号：学生姓名（签名）：设计题目：基于Matlab的自适应均衡器设计一、设计实验条件实验室，Matlab软件二、设计任务及要求1. 课题要求系统学习时域均衡原理，掌握理论知识；2. 首先进行时域均衡原理和算法设计，再在所用的仿真软件Matlab上对设计进行仿真分析，最后写实验报告；3. 对整个系统设计进行回顾，总结心得。
三、设计报告的内容1.设计题目与设计任务（设计任务书）2.前言（绪论）(设计的目的、意义等)3.设计主体（各部分设计内容、分析、结论等）4.结束语（设计的收获、体会等）5.参考资料四、设计时间与安排1、设计时间：3周2、设计时间安排：熟悉实验设备、收集资料: 4天设计图纸、实验、计算、程序编写调试: 7天编写课程设计报告: 3天答辩: 1天基于Matlab的自适应均衡器设计一、设计目的及意义：通过本学期通信原理课程的学习，主要对数字信号系统的通信原理、传输机制等有了系统深入的了解。
而实践性的课程设计能够起到提高综合运用能力，加强理论知识的学习，提高实验技术，启发创造新思想的效果。
此次课程设计是自适应均衡器设计。
我们按照查找资料、软件选择、系统设计、仿真实现、结果优化这一流程进行。
不仅使我们进一步巩固了课程知识，也提高了我们分析问题、解决问题的能力。
二、设计主体：1 、设计原理数字信号经过这样的信道传输以后，由于受到了信道的非理想特性的影响，在接收端就会产生码间干扰(ISI)，使系统误码率上升，严重情况下使系统无法继续正常工作。
理论和实践证明，在接收系统中插入一种滤波器，可以校正和补偿系统特性，减少码间干扰的影响。
这种起补偿作用的滤波器称为均衡器。
时域均衡是利用均衡器产生的时间波形去直接校正已畸变的波形，使包括均衡器在内的整个系统的冲击响应满无码间串扰条件。
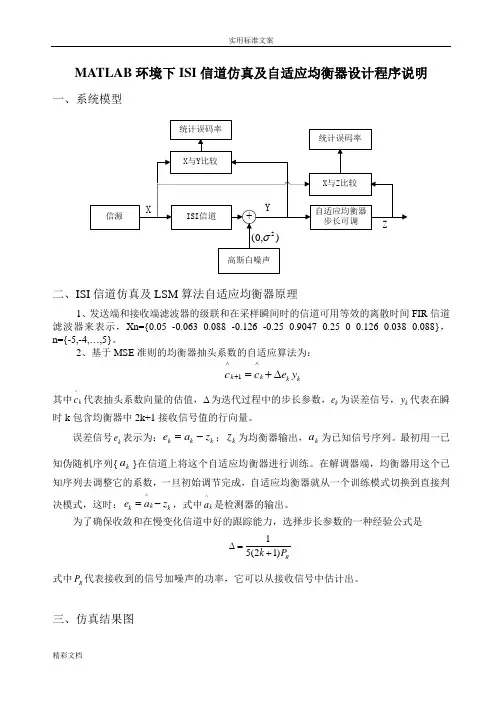
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示，Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088}，n={-5,-4,…,5}。
2、基于MSE 准则的均衡器抽头系数的自适应算法为：^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值，∆为迭代过程中的步长参数，k e 为误差信号，k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为：k k k e a z =-；k z 为均衡器输出，k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端，均衡器用这个已知序列去调整它的系数，一旦初始调节完成，自适应均衡器就从一个训练模式切换到直接判决模式，这时：^k k k e a z =-，式中^k a 是检测器的输出。
为了确保收敛和在慢变化信道中好的跟踪能力，选择步长参数的一种经验公式是15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率，它可以从接收信号中估计出。
三、仿真结果图四、结论分析从结果图中我们可以看出，在信噪比逐渐增大的过程中，未经均衡器均衡的差错率没有明显改善，可知系统中始终存在码间干扰造成的误码；经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下，均衡器均衡之后的误码率并没有明显改善，甚至没有未均衡的差错率低，这主要是因为噪声为随机信号，功率大时对源信号影响较大，而且均衡器不易跟踪；当我们把均衡器的步长调低后，跟踪能力增强，差错率降低。
附源程序代码：main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_in_dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR_in_dB)[y,len]=channel(info,SNR_in_dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信号码元if (y(i)<0), %判决译码elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码，统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡，得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器，误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器，并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后，得到的误码率end;semilogy(SNR_in_dB,Pe,'blacko-'); %自适应均衡器均衡之后，误码率结果图hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器，并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后，得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后，误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡，步长detla=0.11',...'经自适应均衡器均衡，步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数，则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数，可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_actual_isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道，相当于信号序列与信道模型序列作卷积%需要指出，此时码元序列长度变为N+len-1，译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss.m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参，则均方为0，标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数，则标准差为输入实参，均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lms_equalizer.m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元，一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。
电子信息工程学院《DSP技术及应用》课程设计报告题目：自适应均衡器的设计专业班级：通信工程专业10级通信B班二〇一三年六月十日目录一、设计目的 (1)二、设计要求 (1)三、设计原理及方案 (2)四、软件流程 (3)五、调试分析 (9)六、设计总结 (10)七、参考文献 (10)设计目的通过本学期课程的学习，我们主要对数字信号系统的通信原理、传输机制等有了深入的了解。
而实践性的课程设计能够起到提高综合运用能力，提高实验技术，启发创造新思想的效果。
我们小组此次课程设计是自适应均衡器设计，通过查找资料，我们了解到在一个实际的通信系统中，由于多径传输、信道衰落等影响，在接收端也会产生严重的码间串扰。
串扰造成严重影响时，必须对整个系统的传递函数进行校正,使其接近无失真传输条件。
为了提高通信系统的性能，一般在接收端采用均衡技术。
由于信道具有随机性、时变性，因此我们设计自适应均衡器，使其能够实时地跟踪无线通信信道的时变特性，根据信道响应自动调整滤波器抽头系数。
图1公式1 我们决定使用的LMS 算法是目前使用很广泛的自适应均衡算法，同时我们按照查找资料、系统设计、仿真实现、结果优化这一流程进行。
不仅使我们进一步巩固了课程知识，也提高了我们分析问题、解决问题的能力。
二、设计要求1、熟练掌握自适应滤波器的原理和LMS 算法的理论知识；2、学会运用matlab 软件，生成并对该信号进二进制序列信号和正弦信号，并模拟一个码间串扰信道，使信号通过码间串扰信道，之后对其进行加噪处理。
比较经过均衡器和未经均衡的效果随信噪比的变化。
3、完成以二进制序列信号和正弦信号为输入信号设计自适应均衡器的基础上，实现改变LMS 算法的步长进而改变自适应均衡器的抽头系数来观察信号的均方误差随步长的变化。
4、完成对归一化LMS 算法的研究，使经过信道的信号通过可以自定义NLMS 算法次数的自适应均衡器，观察信号的均方误差的变化曲线。
5、完成声音信号的采集，研究声音信号的时域波形和频域波形，对声音信号分别加高频噪声和通过模拟信道，使处理过的信号通过巴特沃斯滤波器和自适应均衡器，分析均衡器的效果。
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示，Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088}，n={-5,-4,…,5}。
2、基于MSE 准则的均衡器抽头系数的自适应算法为：^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值，∆为迭代过程中的步长参数，k e 为误差信号，k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为：k k k e a z =-；k z 为均衡器输出，k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端，均衡器用这个已知序列去调整它的系数，一旦初始调节完成，自适应均衡器就从一个训练模式切换到直接判决模式，这时：^k k k e a z =-，式中^k a 是检测器的输出。
为了确保收敛和在慢变化信道中好的跟踪能力，选择步长参数的一种经验公式是15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率，它可以从接收信号中估计出。
三、仿真结果图四、结论分析从结果图中我们可以看出，在信噪比逐渐增大的过程中，未经均衡器均衡的差错率没有明显改善，可知系统中始终存在码间干扰造成的误码；经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下，均衡器均衡之后的误码率并没有明显改善，甚至没有未均衡的差错率低，这主要是因为噪声为随机信号，功率大时对源信号影响较大，而且均衡器不易跟踪；当我们把均衡器的步长调低后，跟踪能力增强，差错率降低。
附源程序代码：main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_in_dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR_in_dB)[y,len]=channel(info,SNR_in_dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信号码元if (y(i)<0), %判决译码elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码，统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡，得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器，误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器，并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后，得到的误码率end;semilogy(SNR_in_dB,Pe,'blacko-'); %自适应均衡器均衡之后，误码率结果图hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器，并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后，得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后，误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡，步长detla=0.11',...'经自适应均衡器均衡，步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数，则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数，可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_actual_isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道，相当于信号序列与信道模型序列作卷积%需要指出，此时码元序列长度变为N+len-1，译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss.m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参，则均方为0，标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数，则标准差为输入实参，均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lms_equalizer.m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元，一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。
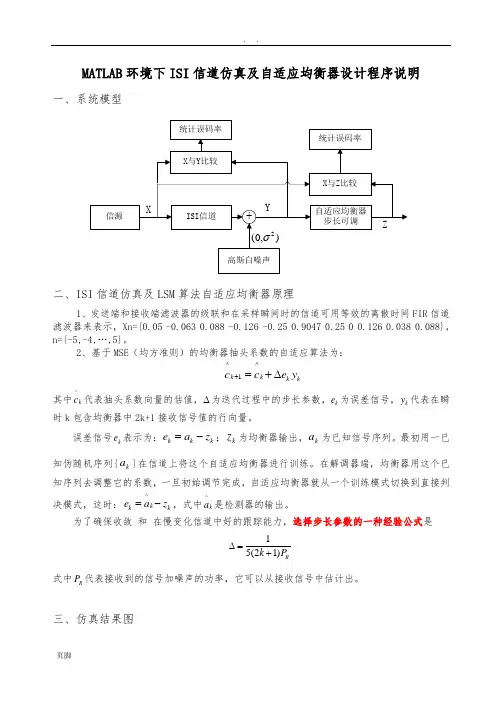
MATLAB 环境下ISI 信道仿真及自适应均衡器设计程序说明一、系统模型二、ISI 信道仿真及LSM 算法自适应均衡器原理1、发送端和接收端滤波器的级联和在采样瞬间时的信道可用等效的离散时间FIR 信道滤波器来表示，Xn={0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088}，n={-5,-4,…,5}。
2、基于MSE （均方准则）的均衡器抽头系数的自适应算法为：^^1k k k k c c e y +=+∆其中^k c 代表抽头系数向量的估值，∆为迭代过程中的步长参数，k e 为误差信号，k y 代表在瞬时k 包含均衡器中2k+1接收信号值的行向量。
误差信号k e 表示为：k k k e a z =-；k z 为均衡器输出，k a 为已知信号序列。
最初用一已知伪随机序列{k a }在信道上将这个自适应均衡器进行训练。
在解调器端，均衡器用这个已知序列去调整它的系数，一旦初始调节完成，自适应均衡器就从一个训练模式切换到直接判决模式，这时：^k k k e a z =-，式中^k a 是检测器的输出。
为了确保收敛 和 在慢变化信道中好的跟踪能力，选择步长参数的一种经验公式是15(21)R k P ∆=+ 式中R P 代表接收到的信号加噪声的功率，它可以从接收信号中估计出。
三、仿真结果图四、结论分析从结果图中我们可以看出，在信噪比逐渐增大的过程中，未经均衡器均衡的差错率没有明显改善，可知系统中始终存在码间干扰造成的误码；经均衡器均衡后的差错率则有明显改善。
但我们同时也可以看到在信噪比较低情况下，均衡器均衡之后的误码率并没有明显改善，甚至没有未均衡的差错率低，这主要是因为噪声为随机信号，功率大时对源信号影响较大，而且均衡器不易跟踪；当我们把均衡器的步长调低后，跟踪能力增强，差错率降低。
附源程序代码：main_plot.mclear;clc;echo off;close all;N=10000; %指定信号序列长度info=random_binary(N); %产生二进制信号序列SNR_ in _dB=8:1:18; %AWGN信道信噪比for j=1:length(SNR _in_ dB)[y, len ]=channel(info, SNR _in _dB(j)); %通过既有码间干扰又有白噪声信道numoferr=0; %初始误码统计数for i=len+1:N+len, %从第len个码元开始为真实信元if (y(i)<0), %判决译码decis=-1;elsedecis=1;end;if (decis~=info(i-5)), %判断是否误码，统计误码码元个数numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 未经均衡器均衡，得到的误码率end;semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器，误码率结果图hold on;delta_1=0.11; %指定自适应均衡器的步长delta_2=0.09; %指定自适应均衡器的步长for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_1); %通过自适应均衡器，并设置步长为0.11 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后，得到的误码率end;semilogy(SNR _in _ dB, Pe ,'blacko-'); %自适应均衡器均衡之后，误码率结果图 hold on;for j=1:length(SNR_in_dB)y=channel(info,SNR_in_dB(j)); %通过信道z=lms_equalizer(y,info,delta_2); %通过自适应均衡器，并设置步长为0.09 numoferr=0;for i=1:N,if (z(i)<0),decis=-1;elsedecis=1;end;if (decis~=info(i)),numoferr=numoferr+1;end;end;Pe(j)=numoferr/N; % 经自适应均衡器均衡后，得到的误码率end;semilogy(SNR_in_dB,Pe,'blue.-'); %自适应均衡器均衡之后，误码率结果图hold on;xlabel('SNR in dB');ylabel('Pe');title('ISI信道自适应均衡系统仿真');legend('未经均衡器均衡','经自适应均衡器均衡，步长detla=0.11',...'经自适应均衡器均衡，步长detla=0.09');random_binary.m%产生二进制信源随机序列function [info]=random_binary(N)if nargin == 0, %如果没有输入参数，则指定信息序列为10000个码元N=10000;end;for i=1:N,temp=rand;if (temp<0.5),info(i)=-1; % 1/2的概率输出为-1elseinfo(i)=1; % 1/2的概率输出为1endend;channel.m%模拟既有码间干扰又有高斯白噪声的信道function [y,len]=channel(x,snr_in_dB)SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换sigma=1/sqrt(2*SNR); %高斯白噪声的标准差%指定信道的ISI参数，可以看出此信道质量还是比较差的actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];len_ actual _isi=(length(actual_isi)-1)/2;len=len_actual_isi;y=conv(actual_isi,x); %信号通过信道，相当于信号序列与信道模型序列作卷积%需要指出，此时码元序列长度变为N+len-1，译码时我们从第len个码元开始到N+len个结束for i=1:2:size(y,2),[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声end;y=y+noise; %叠加噪声gngauss . m%产生高斯白噪声function [gsrv1,gsrv2]=gngauss(m,sgma)if nargin == 0, %如果没有输入实参，则均方为0，标准差为1m=0; sgma=1;elseif nargin == 1, %如果输入实参为1个参数，则标准差为输入实参，均值为0 sgma=m; m=0;end;u=rand;z=sgma*(sqrt(2*log(1/(1-u))));u=rand;gsrv1=m+z*cos(2*pi*u);gsrv2=m+z*sin(2*pi*u);lm _equalizer .m%LSM算法自适应滤波器实现function [z]=lms_equalizer(y,info,delta)estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数K=5;for k=1:size(y,2)-2*K,y_k=y(k:k+2*K); %获取码元，一次11个z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和e_k=info(k)-z_k; %误差估计estimated_c=estimated_c+delta*e_k*y_k; %计算校正抽头系数z(k)=z_k; %均衡后输出的码元序列end;。
毕业设计（论文）自适应均衡器的设计与仿真摘要在移动通信领域中，码间干扰始终是影响通信质量的主要因素之一。
为了提高通信质量，减少码间干扰，在接收端通常采用均衡技术抵消信道的影响。
由于信道响应是随着时间变化的，通常采用自适应均衡器。
自适应均衡器能够自动的调节系数从而跟踪信道，成为通信系统中一项关键的技术。
本篇论文在对无线通信信道进行研究的基础上，阐述了信道产生码间干扰的原因以及无码间干扰的条件，介绍了奈奎斯特第一准则和时域均衡的原理。
深入研究了均衡器的结构和自适应算法，在均衡器的结构中主要介绍了4种自适应均衡器结构即线性横向均衡器、线性格型均衡器、判决反馈均衡器和分数间隔均衡器，并对这几种结构进行了比较。
对于系数调整算法主要介绍了常用的几种算法，包括LMS算法、RLS算法以及盲均衡常用的恒模算法(CMA)，并讨论了它们各自的优缺点。
最后选用线性横向均衡器结构与上述3种系数调整算法，利用MATLAB进行仿真，并对结果进行分析与比较。
关键字：自适应均衡器，LMS，RLS，CMA ，MATLABAbstractIn the field of mobile communications, the inter-symbol interferences (ISI) is always one of the primary factor which effects transmission. Adaptive equalization is mainly solution of dealing with ISI. Equalizers are often used to combat the influence of channels for improving communication’s quality and decreasing ISI in receivers. Sometimes, channel response varies due to time, the adaptive equalizer is always necessary. Equalizer coefficients can be automatically adjusted to track the channel as a key communication system technology.On the basis of studying on wireless communication channel, this paper discusses the reasons of resulting inter-symbol interference (ISI) and without conditions, introduces Nyquist first rule and the theory of adaptive equalizers. The equalizer structures and the adaptive algorithm are particularly studied in this paper. Mainly introducing and comparing four adaptive equalizer structures, such as linear horizontal equalizer, line personality type equalizer, decision feedback equalizer, fractionally spaced equalizers. Then we research the algorithms of the adaptive equalizer which are often used, including LMS, RLS, CMA, and discuss their respective advantages and disadvantages. Finally, we choose different adaptive equalizer structures and algorithms, and use the MATALB tool to simulate, at the end of this paper we analyze and compare the results.Keywords: adaptive equalizer, LMS, RLS, CAM, MATLAB目录摘要 (I)ABSTRACT (II)目录 (III)第一章绪论 (1)1.1引言 (1)1.2国内(外)研究现状 (1)1.3论文研究的内容及主要工作 (2)第二章信道、码间干扰及均衡技术 (3)2.1信道 (3)2.1.1 恒参信道 (4)2.1.2 变参信道 (4)2.2通信信道模型 (6)2.3码间干扰 (7)2.4自适应均衡的原理与特点 (10)2.5本章小结 (11)第三章均衡器结构 (12)3.1自适应均衡简介 (12)3.2均衡器的分类 (12)3.3线性横向均衡器结构(LTE) (13)3.4线性格型均衡器(LLE) (14)3.5判决反馈均衡器(DFE) (15)3.6分数间隔均衡器(FSE) (17)3.7本章总结 (21)第四章自适应均衡算法的理论基础 (22)4.1最小均衡误差算法(LMS) (22)4.2递归最小二乘算法(RLS) (25)4.3盲均衡算法 (27)4.4本章小结 (30)第五章均衡器的仿真与实现 (31)5.1采用线性横向均衡器与LMS算法 (31)5.2采用线性横向均衡器与RLS算法 (31)5.3利用恒模算法和线性横向均衡器 (32)总结 (35)参考文献 (36)致谢 (37)附录 (38)第一章绪论1.1引言通常信道特性是一个复杂的函数，它可能包括各种线性失真、非线性失真、交调失真、衰落等。
电子信息系综合课程设计基于Matlab的自适应均衡器设计专业名称通信工程班级学号学生姓名指导教师设计时间2010.12.20~2011.1.7课程设计任务书专业：学号：学生姓名（签名）：设计题目：基于Matlab的自适应均衡器设计一、设计实验条件实验室，Matlab软件二、设计任务及要求1. 课题要求系统学习时域均衡原理，掌握理论知识；2. 首先进行时域均衡原理和算法设计，再在所用的仿真软件Matlab上对设计进行仿真分析，最后写实验报告；3. 对整个系统设计进行回顾，总结心得。
三、设计报告的内容1.设计题目与设计任务（设计任务书）2.前言（绪论）(设计的目的、意义等)3.设计主体（各部分设计内容、分析、结论等）4.结束语（设计的收获、体会等）5.参考资料四、设计时间与安排1、设计时间：3周2、设计时间安排：熟悉实验设备、收集资料: 4天设计图纸、实验、计算、程序编写调试: 7天编写课程设计报告: 3天答辩: 1天基于Matlab的自适应均衡器设计一、设计目的及意义：通过本学期通信原理课程的学习，主要对数字信号系统的通信原理、传输机制等有了系统深入的了解。
而实践性的课程设计能够起到提高综合运用能力，加强理论知识的学习，提高实验技术，启发创造新思想的效果。
此次课程设计是自适应均衡器设计。
我们按照查找资料、软件选择、系统设计、仿真实现、结果优化这一流程进行。
不仅使我们进一步巩固了课程知识，也提高了我们分析问题、解决问题的能力。
二、设计主体：1 、设计原理数字信号经过这样的信道传输以后，由于受到了信道的非理想特性的影响，在接收端就会产生码间干扰(ISI)，使系统误码率上升，严重情况下使系统无法继续正常工作。
理论和实践证明，在接收系统中插入一种滤波器，可以校正和补偿系统特性，减少码间干扰的影响。
这种起补偿作用的滤波器称为均衡器。
时域均衡是利用均衡器产生的时间波形去直接校正已畸变的波形，使包括均衡器在内的整个系统的冲击响应满无码间串扰条件。
频域均衡是从校正系统频率特性出发，使包括均衡器的基带系统的总特性满足无失真传输条件；频域均衡在信道特性不变，且在传输低速数据时是适用的。
而时域均衡可以根据信道特性的变化进行调整，能够有效地减小码间串扰，故在高速数据传输中得以广泛应用。
图1数字基带传输系统在实际中，当数字基带传输系统（如图1）的特性()()ωωωωRTGCGH)()(=不满足奈奎斯特第一准则时，就会产生有码间串扰的响应波形。
现在我们来证明：如果在接收滤波器和抽样判决之间插入一个称之为横向滤波器的可调滤波器，其冲激响应为∑∞-∞=-=n SnT nT t C t h )()(δ其中，ωωπωππd e nTH T T C s SST jn T T iSSSn ⎰∑-+=)(2nC 完全依赖于H(ω)，那么，理论上就可消除抽样时刻上的码间串扰。
由 上式可以看出，这里的()t h T 是图2所示网络的单位冲激响应。
该网络是有无限多的按横向排列的迟延单元sT 和抽头加权系数nC 组成的，因此成为横向滤波器。
它的功能是利用它产生的无限多个响应波形之和，将接收滤波器输出端抽样时刻上有码间串扰的响应波形变换成抽样时刻上无码间串扰的响应波形。
由于很想滤波器的均衡原理是建立在响应波形上的，故把这种均衡成为时域均衡。
图2横向滤波器不难看出，横向滤波器的特性将取决于各抽头系数nC 。
如果nC 是可调整的，则图3所示的滤波器是通用的；特别是当nC 可自动调整时，则它能够适应信道特性的变化，可以动态校正系统的事件响应。
图3有限长横向滤波器及其输入和输出波形理论上，无限长的横向滤波器可以完全消除抽样时刻上的码间串扰，但实际中是不可能实现的。
因为，不仅均衡器的长度受限制，并且系数nC 的调整准确度也受到限制。
如果nC 的调整准确度可不到保证，即使增加长度也不不会获得显著的效果。
因此，有必要进一步讨论有限长横向滤波器的抽头增益调整问题。
设一个具有2N+1个抽头的横向滤波器，如图3（a ）所示，其单位冲激响应为()t e ，则有∑-=-=NNi SiiT t C t e )()(δ有设它的输入为)(t x ，)(t x 是被均衡的对象，并设它没有附加噪声，如图3（b ）所示，则均衡后输出波形()t y 为∑-=-=*=NNi SiiT t x C t e t x t y )()()()(在抽样时刻SkT t = (设系统无延时时)上，有∑-=-=NNi ik i k xC y上式说明，均衡器在第k 个抽样时刻上的样值ky 将有2N+1个iC 与ik x -乘积之和来决定。
显然，其中除0y 以外的所有ky 都属于波形失真引起的码间串扰。
当输入波形)(t x 给定，及各种可能的ik x -确定是，通过调整iC 使指定的ky 等于零时容易办到的，但同时要求所有的ky （除k=0外）都等于零却是一件很难的事。
这也说明，利用有限长的横向滤波器减小码间串扰是可能的，但完全消除是不可能的。
为了反映这些失真的大小，我们可采用最小均方和迫零算法准则来衡量。
本实验采用最小均方误差算法（LMS ）。
LMS （Least Mean Square ）算法最早由Widrow 于1960年建立。
采用最小均方算法的均衡器比迫零算法均衡器要稳定一些，它所采用的准则是使均衡器的期望输出值和实际输出值之间的均方误差(MSE)最小化的准则。
由Wiener 滤波理论可知，滤波器的最优抽头系数矢量可表示为xdxx opt r R W 1-=式中xx R 是输入信号矢量()n x 的互相关函数，()n x r xd 是输入信号矢量与期望信号矢量()n d 的互相关函数。
直接求解式此式的运算量非常大，尤其当滤波器的抽头系数个数比较多时。
考虑如图4所示的自适应FIR 滤波器：)(n y 1-z 1-z 1-z1-z)1(-n y )(~n x ∑)(1n w )(2n w )(2n w L -)(1n w L -⨯⨯⨯⨯⨯)1(--L n y )(0n w ……图4 自适应FIR 滤波器令()()()()()n X W n d n y n d n e H -=-=表示滤波器在n 时刻的误差，并定义均方误差()()[]()()⎥⎦⎤⎢⎣⎡-==⎰22n x W n d E n e E n J H de为代价函数。
由梯度的定义可以得出，代价函数相对于滤波器抽头系数矢量w 梯度为()()(){}n e k n x E n J k *--=∇2()()()[]{}1,...1,0,2-=*---=M k n x W n d k n x E H ，定义梯度矢量为()()()()[]TM defn J n J n J n J 110,....,,-∇∇∇=∇以及输入矢量和抽头系数矢量：()()()()[]TM n x n x n x n x 1.....1+--=()()()()[]TM n w n w n w n w 110.....-=则此式可以写作以下矢量形式：()()()()[]{}n w X n d n x E n J H -*-=∇2()n w R r xx xd 22+-= 最广泛使用的自适应算法形式为“下降算法”：()()()()n v n n w n w μ+-=1式中()n w 是第n 步迭代的系数矢量，()n μ是第n 步迭代的更新步长，而v(n)是第n 步迭代的更新方向矢量。
最常用的下降法为梯度下降法，又称最陡下降法。
在这种算法里，更新方向矢量v(n)取作第n-1 次迭代的代价函数J （n-1）的负梯度，即最陡下降法的统一形式为()()()()1211-∇--=n J n n w n w μ 系数21为了使得到的更新公式更加简单可得抽头系数矢量的更新公式为()()()()()11--+-=n w R r n n w n w xx xd μ从上式中可以看出，滤波器抽头系数矢量的更新迭代与xd r 和xx R 有关，而实际的信号处理过程中，xd r 和xx R 都不是能够先验知道的，因此通常用梯度的估计值()1-∇∧n J 来代替()1-∇n J .()()()()()()[]n w n x n x n d n x n J H-*-=∇∧2可得()()()()()()()()[]n w n x n X n d n x n n w n w H-*+-=μ1()()()()n x n e n n w *+-=μ1 其中()()()n y n d n e -=为滤波器输出与期望信号的误差函数。
上式就是LMS 算法抽头系数的更新公式，容易验证。
()()n J n J ∇∇∧是的无偏估计，通过上面的讨论可以总结出LMS 算法的具体步骤如下： 步骤l ：初始化抽头系数矢量()[]0,....0,0==n n w T；步骤2 ：当n=n+1时计算滤波器输出()()n x w n y H =， 计算误差函数()()()n y n d n e -=，更新滤波器抽头系数矢量()()()()(),1n x n e n n w n w *+-=μ 关于上面的LMS 算法有以下几点注释：注释l ：若取()=n μ常数，则称为基本LMS 算法。
注释2 ：若取()()(),02,0(,>∈+=ββμ），其中a n x n x an H 则的到归一化LMS 算法。
注释3 ：在功率归一化算法中，取()()()可由的方差表示其中,,22n x n an x xσσμ=()()n e n xx2221+-=λσσ递推计算，这里)1,0(∈λ为遗忘因子，由0<a<M2确定，而M 是滤波器阶数. 注释4 ：当期望信号未知时，步骤2中的d(n)可直接用判决器的实际输出()n d ∧代替。
本实验中选取滤波器阶数order=63，调整步长u=0.02，均为经验值。
2 、Matlab 仿真过程 1.定义一个随机信道c=0.4; x1=c*rand(); x2=c*rand();x3=c*rand();%信道参数isi=[1，x1，x2，x3];snr=10; %AWGN信道信噪比2.定义滤波器各参数order=63; %滤波器阶数len=1000; %训练序列长度u=0.02; %调整步长M=(order-1)/2;N=len+length(isi)-1;e=zeros(1，N);error=e;y=zeros(1，N); %FIR滤波器输出3.信道均衡过程for i=1:100x=sign(rand(1，len)-0.5);%采用PN码作为训练序列noise=randn(1，N)/10.^(snr/10);%AWGNy=conv(isi，x)+noise;%输出wk=zeros(1，order);%横向滤波器系数for n=order:N-M+1 %LMS算法y1=y(n+M-1:-1:n-M-1);d1=wk*y1';e(n)=x(n)-d1;wk=wk+u*e(n)*y1;e(n)=10*log10(abs(e(n)));endqerror=error+e;end4.得到横向滤波器系数wk输出结果:wk =Columns 1 through 9-0.0058 0.0297 0.0283 0.0247 -0.0147 -0.0118 0.0385 -0.0348 0.0095Columns 10 through 180.0422 0.0321 0.0236 0.0126 -0.0068 -0.0310 0.0094 0.0207 -0.0136Columns 19 through 270.0354 0.0016 -0.0281 0.0181 0.0014 0.0073 -0.0104 0.0038 0.0422Columns 28 through 360.0149 0.0396 0.0150 0.9751 -0.2937 -0.2446 0.1236 0.0825 -0.0315Columns 37 through 45-0.0098 -0.0055 0.0035 -0.0426 -0.0316 0.0045 0.0007 -0.0574 0.0115Columns 46 through 540.0346 -0.0578 0.0389 -0.0503 -0.0110 0.0133 0.0500 -0.0114 -0.0143Columns 55 through 63-0.0055 -0.0214 0.0119 0.0058 -0.0181 -0.0184 -0.0392 0.0115 -0.02725.计算自适应均衡器误差收敛性error=error(order:N-M+1)/100;%误差值t=1:length(error);plot(t，error);title('误差收敛曲线');ylabel('误差dB');xlabel('n');02004006008001000-12-10-8-6-4-2误差收敛曲线误差d Bn图5误差收敛曲线6. 随机信号通过理想均衡信道M = 4;msg = randint(1500，1，M); %产生一个1500 x 1 在[0，M-1]区域内的随机整数序列modmsg = qammod(msg ，M); %进行qam 调制的映射 trainlen = 500; %定义训练序列的帧长chan = [.986; .845; .237; .123+.31i]; %定义信道参量 filtmsg = filter(chan ，1，modmsg); % 模拟信道变化 eq1 = lineareq(8， lms(0.01));%生成均衡器对象 eq1.SigConst = qammod([0:M-1]，M); % 设置星座图[symbolest ，yd] = equalize(eq1，filtmsg ，modmsg(1:trainlen));h = scatterplot(filtmsg ，1，trainlen ，'bx'); hold on; %以蓝星画出未经过均衡的信号scatterplot(symbolest ，1，trainlen ，'g.'，h); %在原图的基础上以绿色画出经过均衡后的信号scatterplot(eq1.SigConst ，1，0，'k*'，h); %在原图的基础上以黄色标出理想星座图legend('Filtered signal'，'Equalized signal'， 'Ideal signal constellation'); hold off; % 计算误码率demodmsg_noeq = qamdemod(filtmsg ，M); %解调未均衡的码字 demodmsg = qamdemod(yd ，M); %解调已均衡的码字[nnoeq ，rnoeq] = symerr(demodmsg_noeq(trainlen+1:end)，...对比未均衡信号和样本信号的误码和误码率msg(trainlen+1:end));[neq ，req] = symerr(demodmsg(trainlen+1:end)，...msg(trainlen+1:end)); %对比均衡信号和样本信号的误码和误码率 disp('Symbol error rates with and without equalizer:') disp([req rnoeq])-2-1012-2.5-2-1.5-1-0.500.511.522.5Q u a d r a t u r eIn-PhaseScatter plotFiltered signal Equalized signalIdeal signal constellation图6信号星座图输出结果: Symbol error rates with and without equalizer:0 0.32303、实验结果分析输入信号通过参数可调的数字滤波器后产生输出信号，将其与期望相应进行比较，形成误差信号，并以此通过LMS算法对滤波器参数进行逐步调整，最终使误差均方值最小，并得到自适应均衡器各阶参数。
