第八章计算长度
- 格式:ppt
- 大小:321.50 KB
- 文档页数:31

数学初中教材第八章三角形与三角函数在初中数学教材的第八章中,我们将学习有关三角形与三角函数的知识。
本章内容涵盖了三角形的基本概念、性质以及与三角函数的关系。
通过学习本章内容,我们可以更好地理解和应用三角形和三角函数的知识。
一、三角形的基本概念与性质在初中数学中,我们首先学习了三角形的基本概念与性质。
三角形是由三条边和三个角所组成的图形,我们通常用大写字母A、B、C来表示三个角,用小写字母a、b、c来表示三条边。
根据三角形的边长关系,我们可以将三角形分为等边三角形、等腰三角形和普通三角形。
等边三角形的三条边长度相等,等腰三角形的两条边长度相等,普通三角形的三条边长度各不相等。
除了边长关系外,我们还学习了三角形的角度关系。
根据角度的大小,三角形可以分为锐角三角形、直角三角形和钝角三角形。
在直角三角形中,一个角为90度,而在锐角三角形中,所有角度都小于90度,钝角三角形则有一个角大于90度。
二、三角函数的概念与性质在学习了三角形的基本概念与性质后,我们进一步学习了三角函数的概念与性质。
三角函数是描述角度与边长关系的函数,其中常用的三角函数包括正弦函数、余弦函数和正切函数。
正弦函数是指一个角的对边与斜边的比值,通常用sin表示。
余弦函数是指一个角的邻边与斜边的比值,通常用cos表示。
正切函数是指一个角的对边与邻边的比值,通常用tan表示。
通过三角函数的性质,我们可以进一步研究三角形的性质。
例如,根据正弦定理和余弦定理,我们可以推导出三角形内角和、外角和以及边长的关系。
这些性质对于解决实际问题非常重要。
三、三角形的计算应用作为数学的一个重要分支,三角形的知识经常在实际生活中得到应用。
例如,在建筑设计、航海导航、地质勘测等领域,我们经常需要利用三角形的知识来计算距离、角度等问题。
在实际计算中,我们可以通过应用三角函数来解决各种三角形相关的计算问题。
例如,已知一个角和两条边的长度,我们可以利用正弦定理或余弦定理来计算出其他未知边或角的大小。

抛物线焦点弦长公式3个关于抛物线焦点弦的弦长公式在高中教材第八章中有关于已知倾斜角的焦点弦,求焦点弦的弦长的问题,其中只介绍了开口向右时的焦点弦的长度计算问题:(1)已知:抛物线的方程为,过焦点F的弦AB交抛物线于AB两点,且弦AB的倾斜角为,求弦AB的长。
解:由题意可设直线AB的方程为将其代入抛物线方程整理得:,且设A,B两点的坐标为则:。
当时,斜率不存在,,|AB|=2p.即为通径而如果抛物线的焦点位置发生变化,则以上弦长公式成立吗?这只能代表开口向右时的弦长计算公式,其他几种情况不尽相同。
现在我们来探讨这个问题。
(2)已知:抛物线的方程为,过焦点的弦AB交抛物线于A,B两点,直线AB倾斜角为,求弦AB的长。
解:设A,B的坐标为,斜率为k,而焦点坐标为,故AB的方程为,将其代入抛物线的方程整理得:从而。
弦长为:即为通径。
而与(1)的结果一样,与(2)的结果一样,但是(1)与(2)的两种表达式不一样,为了统一这两种不同的表达式,只须作很小的改动即可。
现将改动陈述于下:(3)已知:抛物线的方程为,过焦点F的弦AB交抛物线于A,B两点,且弦AB与抛物线的对称轴的夹角为,求弦AB的长。
解:由题意可设直线AB的方程为将其代入抛物线方程整理得:。
若倾斜角,则;若倾斜角则。
设A,B两点的坐标为则:。
而,故;当时,,|AB|=2p.即为通径。
而与(3)的结果一样同理:(4)已知:抛物线的方程为,过焦点的弦AB交抛物线于A,B两点,直线AB与抛物线的对称轴的夹角为,求弦AB的长。
解:设A,B的坐标为,若倾斜角为,斜率为k。
则,而焦点坐标为。
故AB的方程为,将其代入抛物线的方程整理得:从而。
弦长为:当倾斜角,则;当倾斜角则所以恒成立。
当时,,|AB|=2p.即为通径。
而与(4)的结果一样。
故只要直线AB与抛物线的对称轴的夹角为,那么不论抛物线的开口向上,向下,向左还是向右,过焦点的弦的弦长都可以用一个公式表示,即。

长方形周长教案公开课第一章:长方形周长的概念1.1 导入:通过展示生活中的长方形物品(如门、窗户、书籍等),引导学生观察长方形的特点,引发对长方形周长的思考。
1.2 讲解:长方形周长是指长方形四条边的总长度。
用字母C表示周长,计算公式为C = 2L + 2W,其中L表示长方形的长,W表示长方形的宽。
1.3 互动:让学生举例说明生活中常见的长方形物品,并计算它们的周长。
1.4 练习:给出一些长方形的长和宽,让学生计算它们的周长。
第二章:长方形周长的计算方法2.1 导入:通过上一章的学习,引导学生思考如何快速计算长方形周长。
2.2 讲解:长方形周长的计算方法有多种,如直接计算法、分解法、翻转法等。
2.3 互动:让学生尝试使用不同的方法计算同一长方形的周长,并交流比较哪种方法更快更简便。
2.4 练习:给出一些长方形的长和宽,让学生选择合适的方法计算它们的周长。
第三章:长方形周长的应用3.1 导入:通过展示一些实际问题,引导学生思考长方形周长在生活中的应用。
3.2 讲解:长方形周长可以应用于计算物体的表面积、围栏的周长、衣服的尺寸等。
3.3 互动:让学生举例说明长方形周长在日常生活中的应用,并计算相应的数值。
3.4 练习:给出一些实际问题,让学生计算长方形周长的应用。
第四章:长方形周长的扩展4.1 导入:引导学生思考长方形周长的扩展问题,如如何计算长方形群组的周长。
4.2 讲解:长方形群组的周长可以通过计算每个长方形的周长之和来得到。
4.3 互动:让学生尝试计算多个长方形组合在一起的周长,并交流解题策略。
4.4 练习:给出一些长方形组合,让学生计算它们的周长。
第五章:长方形周长的综合练习5.1 导入:通过展示一些综合性的题目,引导学生思考如何综合运用长方形周长的知识。
5.2 讲解:长方形周长的综合练习可以涉及多个知识点,如面积、角度等。
5.3 互动:让学生尝试解决一些综合性的题目,并交流解题思路。
5.4 练习:给出一些综合性的题目,让学生独立解决并计算长方形周长。

建筑CAD第八章的计算单选题及答案(计算单项选择题)注意:选项(abcd)后面数字是一道题对这题的的评分,也就是答案,如果是0,是错误的,.就不要选择。
top/默认广东课程04/第8章、建筑施工图绘制/计算(单选)计算(单选)将长度和角度精度设置为小数点后四位,绘制以下图形,求剖面线区域的面积()。
A. 673522.1316 100B. 673522.1361 0C. 673522.1613 0D. 673522.3161 0计算(单选)将长度和角度精度设置为小数点后四位,绘制以下图形,求剖面线区域的面积()。
A. 105720.0541 100B. 105720.0514 0C. 105720.0415 0D. 105720.0414 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中阴影部分的面积()。
A. 639333.3331 0B. 639333.3332 0C. 639333.3333 100D. 639333.3334 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中蓝色阴影部分的周长()。
A. 12124.8472 100B. 12124.8473 0C. 12124.8474 0D. 12124.8475 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中A.B.C三点所围成的三角形的周长()。
A. 2581.9818 100B. 2581.9819 0C. 2581.9820 0D. 2581.9821 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中房屋整体的周长()。
A. 194.6795 100B. 194.6796 0C. 194.6797 0D. 194.6798 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中红色砖墙的面积()。
A. 301527.4354 0B. 301527.4355 100C. 301527.4356 0D. 301527.4357 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中书桌整体面积()。


长度计算大班教案一、教学目标1. 知识目标:学生能够正确使用标准度量衡单位对长度进行计算。
2. 能力目标:学生能够灵活运用所学的长度计算方法解决实际生活问题。
3. 情感目标:培养学生的观察力、思考力和团队合作精神。
二、教学重难点1. 教学重点:帮助学生理解并正确使用长度计量单位进行计算。
2. 教学难点:培养学生的应用能力,使其能够运用所学的知识解决实际问题。
三、教学准备1. 教具准备:长度计量工具(尺子、卷尺等)、实物(书本、铅笔等)。
2. 教材准备:相关的课程教材和学案。
四、教学过程步骤一:导入向学生展示一尺子和一张A4纸,提问:“你们知道尺子的长度是多少吗?纸的长度是多少?”引导学生回忆并巩固尺寸和长度的概念。
步骤二:学习1. 学习长度计量单位通过展示和讲解,引导学生认识并记忆长度计量单位的名称和符号。
例如:厘米(cm)、米(m)、千米(km)。
2. 探索长度计量单位的换算关系引导学生进行探究,使用尺子测量教室中各物体的长度,并记录在黑板上。
然后帮助学生发现各物体的长度单位之间的换算关系。
促使他们理解1米(m)= 100厘米(cm),1千米(km)= 1000米(m)。
3. 进行练习组织学生进行练习,包括长度单位间的换算和长度计算的应用题。
步骤三:巩固和拓展1. 游戏:计算比赛将全班分成小组,每组选择一名代表进行长度计算比赛。
根据题目,学生使用所学的长度计算方法进行计算,比赛时间为5分钟。
最后检查答案,确认无误后颁发胜利证书和奖励。
2. 拓展应用引导学生将所学的长度计算方法应用到实际问题中,如测量校园内某条道路的长度或家中某个房间的面积。
五、课堂总结学生通过本节课的学习,掌握了长度计算的方法和技巧,能够准确使用长度计量单位进行计算。
同时,培养了学生的观察力和思考力,提高了他们的团队合作能力。
六、课后作业1. 完成课堂练习题。
2. 自主选择一个实际场景,运用所学的长度计算方法进行测量和计算。
七、教学反思本节课通过导入、学习、巩固和拓展的步骤,有针对性地培养了学生对长度计量单位的理解和计算能力。


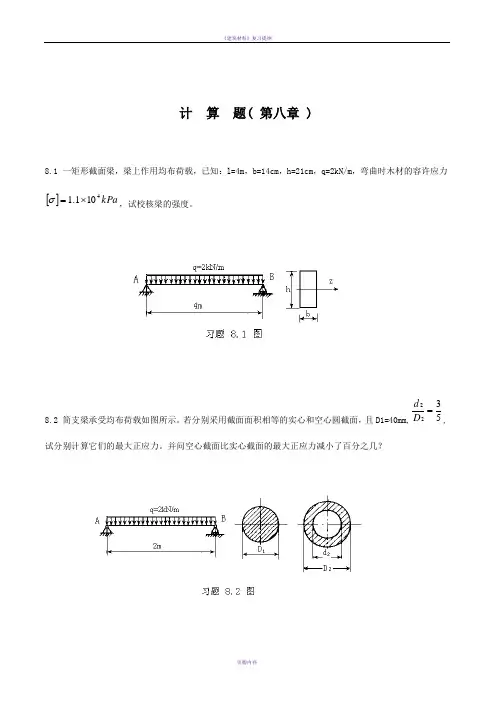
计 算 题( 第八章 )8.1 一矩形截面梁,梁上作用均布荷载,已知:l=4m ,b=14cm ,h=21cm ,q=2kN/m ,弯曲时木材的容许应力[]kPa 4101.1⨯=σ,试校核梁的强度。
8.2 简支梁承受均布荷载如图所示。
若分别采用截面面积相等的实心和空心圆截面,且D1=40mm,5322=D d ,试分别计算它们的最大正应力。
并问空心截面比实心截面的最大正应力减小了百分之几?8.3 图示悬臂梁,横截面为矩形,承受载荷F1与F2作用,且F1=2F2=5kN。
试计算梁内的最大弯曲正应力,及该应力所在截面上K点处的弯曲正应力。
8.4 图示梁,由No-22槽钢制成,弯矩M=80N·m,并位于纵向对称面(即x-y平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
提示:有关槽钢的几何性质可从附录中查得。
8.5 图示变截面梁,自由端承受荷载F作用,梁的尺寸l,b与h均为已知。
试计算梁内的最大弯曲正应力。
8.6 图示截面梁,横截面上剪力FQ=300kN,试计算:(a)图中截面上的最大剪应力和A点的剪应力;(b)图中腹板上的最大剪应力,以及腹板与翼缘交界处的剪应力。
8.7 图示矩形截面木梁,许用应力[σ]=10Mpa。
(1)试根据强度要求确定截面尺寸b。
(2)若在截面A处钻一直径为d=60mm的圆孔(不考虑应力集中),试问是否安全。
8.8 一对称T形截面的外伸梁,梁上作用均布荷载,梁的截面如图所示。
已知:mkNqml/8,5.1==,求梁截面中的的最大拉应力和最大压应力。
8.9 欲从直径为d的圆木中截取一矩形截面梁,试从强度角度求出矩形截面最合理的高h和宽b。
8.10 图示外伸梁,承受荷载F作用。
已知荷载F=20kN,许用应力[σ]=160Mpa,许用剪应力[τ]=90Mpa。
请选择工字钢型号。
8.11一铸铁梁,其截面如图所示,已知许用压应力为许用拉应力的4倍,即[σc]=4[σt]。

五年级数学上册全册教案(人教版)第一章:小数乘法教学目标:1. 理解小数乘法的意义,掌握小数乘法的基本运算方法。
2. 能够正确进行小数乘法的计算。
教学内容:1. 小数乘法的意义和运算方法。
2. 小数乘法的计算法则。
教学步骤:1. 引入小数乘法的概念,通过实际例题让学生理解小数乘法的意义。
2. 讲解小数乘法的运算方法,引导学生进行实际计算。
3. 总结小数乘法的计算法则,让学生能够独立进行计算。
教学评价:1. 通过课堂练习,检查学生对小数乘法的理解程度。
2. 通过课后作业,评估学生小数乘法的计算能力。
第二章:小数除法教学目标:1. 理解小数除法的意义,掌握小数除法的基本运算方法。
2. 能够正确进行小数除法的计算。
教学内容:1. 小数除法的意义和运算方法。
2. 小数除法的计算法则。
1. 引入小数除法的概念,通过实际例题让学生理解小数除法的意义。
2. 讲解小数除法的运算方法,引导学生进行实际计算。
3. 总结小数除法的计算法则,让学生能够独立进行计算。
教学评价:1. 通过课堂练习,检查学生对小数除法的理解程度。
2. 通过课后作业,评估学生小数除法的计算能力。
第三章:分数乘法教学目标:1. 理解分数乘法的意义,掌握分数乘法的基本运算方法。
2. 能够正确进行分数乘法的计算。
教学内容:1. 分数乘法的意义和运算方法。
2. 分数乘法的计算法则。
教学步骤:1. 引入分数乘法的概念,通过实际例题让学生理解分数乘法的意义。
2. 讲解分数乘法的运算方法,引导学生进行实际计算。
3. 总结分数乘法的计算法则,让学生能够独立进行计算。
教学评价:1. 通过课堂练习,检查学生对分数乘法的理解程度。
2. 通过课后作业,评估学生分数乘法的计算能力。
第四章:分数除法1. 理解分数除法的意义,掌握分数除法的基本运算方法。
2. 能够正确进行分数除法的计算。
教学内容:1. 分数除法的意义和运算方法。
2. 分数除法的计算法则。
教学步骤:1. 引入分数除法的概念,通过实际例题让学生理解分数除法的意义。
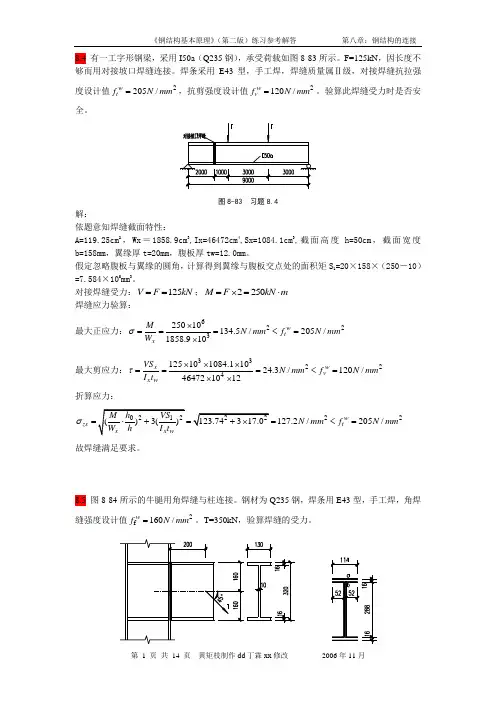
8.4 有一工字形钢梁,采用I50a (Q235钢),承受荷载如图8-83所示。
F=125kN ,因长度不够而用对接坡口焊缝连接。
焊条采用E43型,手工焊,焊缝质量属Ⅱ级,对接焊缝抗拉强度设计值2205/w t f N mm =,抗剪强度设计值2120/w v f N mm =。
验算此焊缝受力时是否安全。
图8-83 习题8.4解:依题意知焊缝截面特性:A=119.25cm 2,Wx =1858.9cm 3,Ix=46472cm 4,Sx=1084.1cm 3,截面高度h=50cm ,截面宽度b=158mm ,翼缘厚t=20mm ,腹板厚tw=12.0mm 。
假定忽略腹板与翼缘的圆角,计算得到翼缘与腹板交点处的面积矩S 1=20×158×(250-10)=7.584×105mm 3。
对接焊缝受力:125V F kN ==;2250M F kN m =⨯=⋅ 焊缝应力验算:最大正应力:622325010134.5/205/1858.910w t x M N mm f N mm W σ⨯===<=⨯ 最大剪应力:33224125101084.11024.3/120/464721012w x v x w VS N mm f N mm I t τ⨯⨯⨯===<=⨯⨯ 折算应力:22127.2/205/w zs t N mm f N mm σ=<= 故焊缝满足要求。
8.5 图8-84所示的牛腿用角焊缝与柱连接。
钢材为Q235钢,焊条用E43型,手工焊,角焊缝强度设计值2f 160/w f N mm =。
T=350kN ,验算焊缝的受力。
图8-84 习题8.5 图8-84-1 焊缝截面计算简图解:(注:焊缝上下翼缘长度114mm 有些问题,应取2130210110l tmm -=-⨯=,黄钜枝06年6月19日)如图8-84-1,截面特性计算如下:2(11425242882)0.75667.2f A h mm =⨯+⨯+⨯⨯= 228820.73225.6w f A h mm =⨯⨯=32741288288[2882114(16)252()4]0.77.913101222f f I h mm =⨯⨯+⨯+⨯+⨯⨯⨯=⨯焊缝受力:247.52N kN ==;247.52V kN ==; 49.5M V e kN m =⋅=⋅ 应力验算:危险点为a 、b 两点,下面分别验算: 对a 点: 32247.51043.67/5667.2N aN N mm A σ⨯===62749.510160100.09/7.91310M a af My N mm I σ⨯⨯===⨯ 2243.67100.09143.76/195.2/N Mw a a f f N mm f N mm σσβ+=+=<=对b 点:32247.51076.73/3225.6V bw V N mm A τ⨯=== 243.67/N Nb a N mm σσ==62749.51014490.16/7.91310M b bf My N mm I σ⨯⨯===⨯22133.87/160/w f N mm f N mm =<=故焊缝强度满足要求。
《建筑力学》第8章计算题计 算 题( 第八章 )8.1 一矩形截面梁,梁上作用均布荷载,已知:l=4m ,b=14cm ,h=21cm ,q=2kN/m ,弯曲时木材的容许应力[]kPa 4101.1⨯=σ,试校核梁的强度。
8.2 简支梁承受均布荷载如图所示。
若分别采用截面面积相等的实心和空心圆截面,且D1=40mm,5322=D d ,试分别计算它们的最大正应力。
并问空心截面比实心截面的最大正应力减小了百分之几?8.3 图示悬臂梁,横截面为矩形,承受载荷F1与F2作用,且F1=2F2=5kN。
试计算梁内的最大弯曲正应力,及该应力所在截面上K点处的弯曲正应力。
8.4 图示梁,由No-22槽钢制成,弯矩M=80N·m,并位于纵向对称面(即x-y平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
提示:有关槽钢的几何性质可从附录中查得。
8.5 图示变截面梁,自由端承受荷载F作用,梁的尺寸l,b与h均为已知。
试计算梁内的最大弯曲正应力。
8.6 图示截面梁,横截面上剪力FQ=300kN,试计算:(a)图中截面上的最大剪应力和A点的剪应力;(b)图中腹板上的最大剪应力,以及腹板与翼缘交界处的剪应力。
8.7 图示矩形截面木梁,许用应力[σ]=10Mpa。
(1)试根据强度要求确定截面尺寸b。
(2)若在截面A处钻一直径为d=60mm的圆孔(不考虑应力集中),试问是否安全。
8.8 一对称T形截面的外伸梁,梁上作用均布荷载,梁的截面如图所示。
已知:m,=,求梁截面中的5.1=8l/qkNm的最大拉应力和最大压应力。
8.9 欲从直径为d的圆木中截取一矩形截面梁,试从强度角度求出矩形截面最合理的高h和宽b。
8.10 图示外伸梁,承受荷载F作用。
已知荷载F=20kN,许用应力[σ]=160Mpa,许用剪应力[τ]=90Mpa。
请选择工字钢型号。
8.11一铸铁梁,其截面如图所示,已知许用压应力为许用拉应力的4倍,即[σc]=4[σt]。
《长度和时间的测量》教案第一章:长度测量1.1 目标:让学生了解并掌握长度测量的基本工具和方法。
1.2 内容:1.2.1 长度测量工具:尺子、卷尺、测量带等。
1.2.2 测量方法:直接测量、累加测量、换算测量等。
1.3 教学活动:1.3.1 讲解长度测量工具的使用方法及注意事项。
1.3.2 演示长度测量的实际操作。
1.3.3 学生分组进行长度测量练习,教师巡回指导。
1.4 作业:1.4.1 学生独立完成长度测量练习题。
第二章:时间测量2.1 目标:让学生了解并掌握时间测量的基本工具和方法。
2.2 内容:2.2.1 时间测量工具:秒表、计时器、钟表等。
2.2.2 测量方法:直接测量、累积测量等。
2.3 教学活动:2.3.1 讲解时间测量工具的使用方法及注意事项。
2.3.2 演示时间测量的实际操作。
2.3.3 学生分组进行时间测量练习,教师巡回指导。
2.4 作业:第三章:长度和时间的关系3.1 目标:让学生了解长度和时间的关系,并能够运用其解决实际问题。
3.2 内容:3.2.1 长度和时间的关系:速度、频率等。
3.2.2 实际问题:长度和时间的关系在生活中的应用,如行程、周期等。
3.3 教学活动:3.3.1 讲解长度和时间的关系及其应用。
3.3.2 学生进行长度和时间关系的实际测量,如测量物体运动速度等。
3.3.3 分析测量结果,解决实际问题。
3.4 作业:3.4.1 学生独立完成长度和时间关系练习题。
第四章:长度和时间测量在实际中的应用4.1 目标:让学生了解长度和时间测量在实际中的应用,提高其测量技能。
4.2 内容:4.2.1 实际应用:工程测量、地理测量、生产测量等。
4.2.2 测量技能:精确测量、快速测量等。
4.3 教学活动:4.3.1 讲解长度和时间测量在实际中的应用。
4.3.2 学生进行实际测量操作,如测量教室长度、宽度等。
4.3.3 分析测量结果,提高测量技能。
4.4 作业:第五章:长度和时间测量实验5.1 目标:让学生通过实验,巩固长度和时间测量的知识和技能。