第一章 有限元基础1
- 格式:ppt
- 大小:1.22 MB
- 文档页数:37



有限元分析基础第一章有限元法概述在机械设计中,人们常常运用材料力学、结构力学等理论知识分析机械零构件的强度、刚度和稳定性问题。
但对一些复杂的零构件,这种分析常常就必须对其受力状态和边界条件进行简化。
否则力学分析将无法进行。
但这种简化的处理常常导致计算结果与实际相差甚远,有时甚至失去了分析的意义。
所以过去设计经验和类比占有较大比重。
因为这个原因,人们也常常在设计中选择较大的安全系数。
如此也就造成所设计的机械结构整体尺寸和重量偏大,而局部薄弱环节强度和刚度又不足的设计缺陷。
近年来,数值计算机在工程分析上的成功运用,产生了一门全新、高效的工程计算分析学科——有限元分析方法。
该方法彻底改变了传统工程分析中的做法。
使计算精度和计算领域大大改善。
§1.1 有限元方法的发展历史、现状和将来一,历史有限元法的起源应追溯到上世纪40年代(20世纪40年代)。
1943年R.Courant从数学的角度提出了有限元法的基本观点。
50年代中期在对飞机结构的分析中,诞生了结构分析的矩阵方法。
1960年R.W.Clough在分析弹性力学平面问题时引入了“Finite Element Method”这一术语,从而标志着有限元法的思想在力学分析中的广泛推广。
60、70年代计算机技术的发展,极大地促进了有限元法的发展。
具体表现在:1)由弹性力学的平面问题扩展到空间、板壳问题。
2)由静力平衡问题——稳定性和动力学分析问题。
3)由弹性问题——弹塑性、粘弹性等问题。
二,现状现在有限元分析法的应用领域已经由开始时的固体力学,扩展到流体力学、传热学和电磁力学等多个传统的领域。
已经形成了一种非常成熟的数值分析计算方法。
大型的商业化有限元分析软件也是层出不穷,如:SAP系列的代表SAP2000(Structure Analysis Program)美国安世软件公司的ANSYS大型综合有限元分析软件美国航天航空局的NASTRAN系列软件除此以外,还有MASTER、ALGO、ABIQUES、ADINA、COSMOS等。






有限元分析基础第⼀讲第⼀章有限元的基本根念Basic Concepts of the Finite Element Method1.1引⾔(introduction)有限元(FEM 或FEA)是⼀种获取近似边值问题的计算⽅法。
边值问题(boundary valueproblems, 场问题field problem )是⼀种数学问题(mathematical problems)(在所研究的区域,⼀些相关变量满⾜微分⽅程如物理⽅程、位移协调⽅程等且满⾜特定的区域边界)。
边值问题也称为场问题,场是指我们研究的区域,并代表⼀种物理模型。
场变量是满⾜微分⽅程的相关变量,边界条件代表场变量在场边界上特定的值(物理边界转化为数学边界)。
根据所分析物理问题的不同,场变量包括位移、温度、热量等。
1.2有限元法的基本思路 (how does the finite element methods work)有限元法的基本思路可以归结为:将连续系统分割成有限个分区或单元,对每个单元提出⼀个近似解,再将所有单元按标准⽅法组合成⼀个与原有系统近似的系统。
下⾯⽤在⾃重作⽤下的等截⾯直杆来说明有限元法的思路。
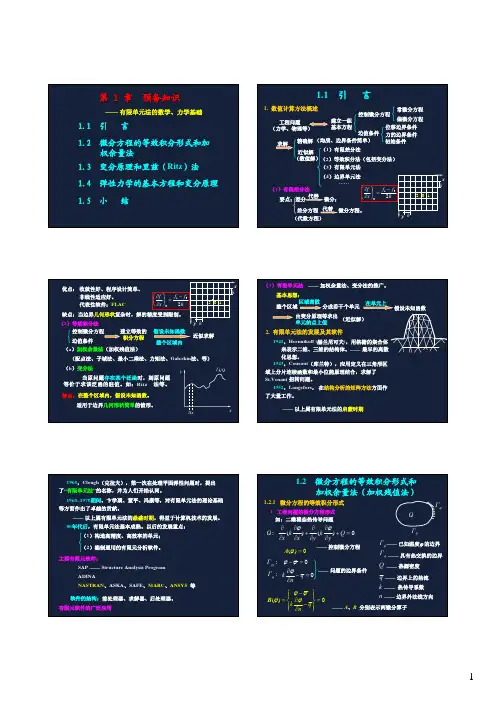
等截⾯直杆在⾃重作⽤下的材料⼒学解答图1.1 受⾃重作⽤的等截⾯直杆图1.2 离散后的直杆受⾃重作⽤的等截⾯直杆如图所⽰,杆的长度为L ,截⾯积为A ,弹性模量为E ,单位长度的重量为q ,杆的内⼒为N 。
试求:杆的位移分布,杆的应变和应⼒。
)()(x L q x N -=EAdxx L q EA dx x N x dL )()()(-==-==x x Lx EA q EA dx x N x u 02)2()()((1))(x L EAq dx du x -==ε )(x L AqE x x -==εσ等截⾯直杆在⾃重作⽤下的有限元法解答 (1) 离散化如图1.2所⽰,将直杆划分成n 个有限段,有限段之间通过⼀个铰接点连接。

§1有限元的基础理论§1-1 概述有限元法是一种数值计算的近似方法。
早在40年代初期就已有人提出,但当时由于没有计算工具而搁置,一直到50年代中期,高速数字电子计算机的出现和发展为有限元法的应用提供了重要的物质条件,才使有限元法得以迅速发展。
有限元法在西方起源于飞机和导弹的结构设计,发表这方面文章最早而且最有影响的是西德的J.H.Argyris教授,于1954–1955年间,他在《Aircraft engineering》上发表了许多有关这方面的论文,并在此基础上写成了《能量原理与结构分析》,此书成为有限元法的理论基础。
美国的M.T.Turner,R.W.Clough,H.C.Martin和L.J.Topp等人于1956年发表了一篇题为《复杂结构的刚度和挠度分析》一文,此文提出了计算复杂结构刚度影响系数的方法,说明了如何利用计算机进行分析。
美国教授R.W.Clough于1960年在一篇介绍平面应力分析的论文中,首次提出了有限元法的名字。
1965年英国的O.C.Zienliewice教授及其合作者解决了将有限元应用于所有场的问题,使有限元法的应用范围更加广泛。
有限元法的优点很多,其中最突出的优点是应用范围广。
发展至今,不仅能解决静态的、平面的、最简单的杆系结构,而且还可以解决空间问题、板壳问题、结构的稳定性问题、动力学问题、弹塑性问题和粘弹性问题、疲劳和脆性断裂问题以及结构的优化设计问题。
而且不论物体的结构形式和边界条件如何复杂,也不论材料的性质和外载荷的情况如何,原则上都能应用。
§1-2 有限元的基础理论有限元法的基本思路和基本原则以结构力学中的位移法为基础,把复杂的结构或连续体看成有限个单元的组合,各单元彼此在节点处连接而组成整体。
把连续体分成有限个单元和节点,称为离散化。
先对单元进行特性分析,然后根据各节点处的平衡和协调条件建立方程,综合后作整体分析。
这样一分一合,先离散再综合的过程,就是把复杂结构或连续体的计算问题转化为简单单元的分析与综合的问题。