当前位置：文档之家 › 粘性流体力学第六章(6-2)讲解

粘性流体力学第六章(6-2)讲解

  • 格式：ppt
  • 大小：1.35 MB
  • 文档页数：57

下载文档原格式

  / 57

合集下载

流体力学第6章讲解

流体力学第6章讲解


2、射孔的形状，圆孔口和方孔显然其扩张的情况不会相同。不同的射口形状有 不
同的实验值。用φ表示这个影响因素， 对圆断面射流 φ＝3.4，长条缝射孔 φ＝2.44。
圆孔综口合射这流两：个t影g响因素K：x k＝Kφα 3.4a
x
R 1 3.4 as 3.4( as 0.294)
r0
vm
vm r0 1
1
v0 R
2
1
[(11.5 )2 ]2d
0
9
第二节圆断面射流的运动分析
1
n
1
n
[(1 1.5 )2 ] d Bn; [(1 1.5 )2 ] d Cn
0
0
n
1
1.5
2
2.5
3
Bn
0.0985
0.064
0.0464
0.0359
0.0286
第一节无限空间淹没紊流射流特性
二、紊流系数a及几何特征
其斜率即：tga＝常数＝k。 对于不同的条件，k值是不同的常数，也叫实验常数。 通过实验发现，k值的影响因素有两个主要的因素：
1、射孔出口截面上气流的紊流强度。 紊流强度的大小用紊流系数a（A）来表示：a大紊流的强度就大，因此，紊
流 系数的大小可以反映出射流的扩张能力，所以，a也叫表征射流流动结构的 特征系数。另一方面，由于a反映的是射流混合能力的大小，因此，a还可以反 映孔口出口截面上的速度均匀程度。a越小，则混合能力越差，说明流速越均匀 。
二、断面流量Q
R
微环面的流量表达式 Q 2vydy Q0 r02v0
0
主体段：
R
Q
v r 0
y
y
2 ( )( )d( )
流体力学第六章流体节流与缝隙流动

流体力学第六章流体节流与缝隙流动

第六章流体节流与缝隙流动(了解各种节流及缝隙流动现象，理解影响流量的因素，理解偏心状缝。

掌握气蚀现象。

) §6.1 流体的节流节流：管道内流体流经断面突然缩小的截面后，又进入和以前一样断面的管道，致使压力下降的现象，称为节流。

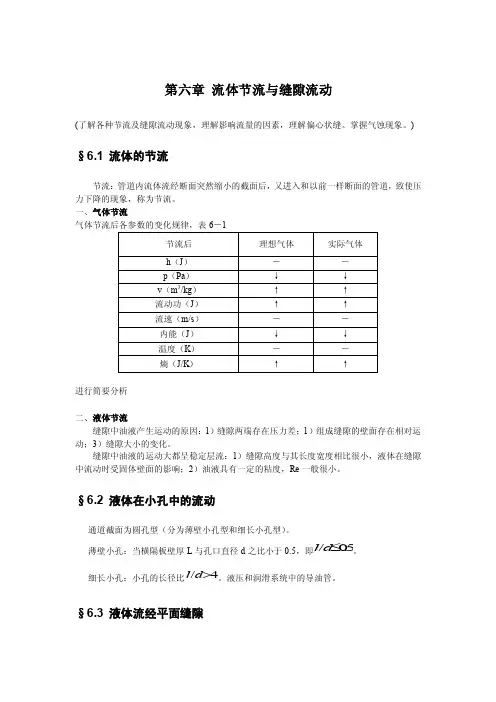
一、气体节流气体节流后各参数的变化规律，表6－1进行简要分析二、液体节流缝隙中油液产生运动的原因：1）缝隙两端存在压力差；1）组成缝隙的壁面存在相对运动；3）缝隙大小的变化。

缝隙中油液的运动大都呈稳定层流：1）缝隙高度与其长度宽度相比很小，液体在缝隙中流动时受固体壁面的影响；2）油液具有一定的粘度，Re一般很小。

§6.2 液体在小孔中的流动通道截面为圆孔型（分为薄壁小孔型和细长小孔型）。

l d≤。

薄壁小孔：当横隔板壁厚L与孔口直径d之比小于0.5，即/0.5l d>。

液压和润滑系统中的导油管。

细长小孔：小孔的长径比/4§6.3 液体流经平面缝隙平面缝隙：由两平行平面夹成的缝隙。

齿轮泵齿顶与泵壳之间的油液运动，柴油机中滑块与导板之间的油液流动。

结论：1）缝隙中液体流速按抛物线规律分布的；2）流经平面缝隙的流量与缝隙厚度δ的三次方成正比，和动力粘度μ成反比。

§6.4 液体流经同心环状缝隙同心环状缝隙：由内外两个同心圆柱面所围成的缝隙。

结论：流经平面缝隙的流量与缝隙厚度δ的三次方成正比。

§6.5 液体流经偏心环状缝隙偏心环状缝隙：在船舶机械中的环状缝隙，当运动部件装配不当或工作受力不均时，同心环状缝隙就变成偏心环状缝隙。

结论：流经偏心环状缝隙的流量与偏心距成正比，偏心距最大时，泄漏量为同心环状缝隙的2.5倍。

§6.6 液体流经具有相对运动的平行面缝隙喷油泵中的柱塞泵。

类型：（1、2、3）1）平行剪切流动∆=p，由于液体粘滞性，通过平行板的运动液体运动。

2）压差流动液体的运动，在缝隙两端的压差作用下实现。

3）压差与剪切流动的合成液体的运动，在缝隙两端的压差和平行剪切力的作用下共同实现。

流体力学第二版(蔡增基)第六章

流体力学第二版(蔡增基)第六章

②是否存在速度势函数?若存在，求出其表达式。 【解】（1）由不可压流体平面流动的连续性方程
ux u y (4 x) (4 y) 0 x y x y
该流动满足连续性方程。 （2）由于是平面流动
x y 0
1 u y u x 1 4 y 4 x z 0 2 x y 2 x y 该流动为无旋流动，存在速度势函数。
u y x u x y
平面流动为无旋流动。
平面无旋流动的速度势函数为： d u xdx u y dy 平面无旋流动的拉普拉斯方程：
2 x
2

2 y
2
0
【例2】有一不可压流体平面流动的速度分布为
u x 4 x，u y 4 y；
①该平面流动是否满足连续性方程；
o
D
C
E
把对角线EOF的旋转角速度定义为整个流 E' 体微团在xoy面的旋转角速度，用 z 表示。
1 u y u x 2 y x 1 u u y x z 2 z x
EOF的旋转角速度可看成是AOC和BOD角速度的平均：
左侧中心点沿x方向的流速为：
u x左 u x u x dx x 2
dz dy
u x dx x 2
dx
u x右 u x 右侧中心点沿x方向的流速为：
dt时间内沿x方向流入和流出的净体积流量为：
dQx (u x
dQx u x dxdydz dt x
如图（a）所示，虽然流体微团运动轨迹是圆形，但由 于微团本身不旋转，故它是无旋流动；
在图 (b)中，虽然流体微团运动轨迹是直线，但微团绕 自身轴线旋转，故它是有旋流动。
流体力学讲义第六章流动阻力及能量损失2

流体力学讲义第六章流动阻力及能量损失2

流体⼒学讲义第六章流动阻⼒及能量损失2第六章流动阻⼒及能量损失本章主要研究恒定流动时，流动阻⼒和⽔头损失的规律。

对于粘性流体的两种流态——层流与紊流，通常可⽤下临界雷诺数来判别，它在管道与渠道内流动的阻⼒规律和⽔头损失的计算⽅法是不同的。

对于流速，圆管层流为旋转抛物⾯分布，⽽圆管紊流的粘性底层为线性分布，紊流核⼼区为对数规律分布或指数规律分布。

对于⽔头损失的计算，层流不⽤分区，⽽紊流通常需分为⽔⼒光滑管区、⽔⼒粗糙管区及过渡区来考虑。

本章最后还阐述了有关的边界层、绕流阻⼒及紊流扩散等概念。

第⼀节流态判别⼀、两种流态的运动特征1883年英国物理学家雷诺（Reynolds O.）通过试验观察到液体中存在层流和紊流两种流态。

1.层流层流（laminar flow），亦称⽚流：是指流体质点不相互混杂，流体作有序的成层流动。

特点：（1）有序性。

⽔流呈层状流动，各层的质点互不混掺，质点作有序的直线运动。

（2）粘性占主要作⽤，遵循⽜顿内摩擦定律。

（3）能量损失与流速的⼀次⽅成正⽐。

（4）在流速较⼩且雷诺数Re较⼩时发⽣。

2.紊流紊流（turbulent flow），亦称湍流：是指局部速度、压⼒等⼒学量在时间和空间中发⽣不规则脉动的流体运动。

特点：（1）⽆序性、随机性、有旋性、混掺性。

流体质点不再成层流动，⽽是呈现不规则紊动，流层间质点相互混掺，为⽆序的随机运动。

（2）紊流受粘性和紊动的共同作⽤。

（3）⽔头损失与流速的1.75~2次⽅成正⽐。

（4）在流速较⼤且雷诺数较⼤时发⽣。

⼆、雷诺实验如图6-1所⽰，实验曲线分为三部分：（1）ab段：当υ<υc时，流动为稳定的层流。

（2）ef段：当υ>υ''时，流动只能是紊流。

（3）be段：当υc<υ<υ''时，流动可能是层流（bc段），也可能是紊流（bde段），取决于⽔流的原来状态。

图6-1图6-2实验结果（图6-2）的数学表达式层流：m1=1.0, h f=k1v , 即沿程⽔头损失与流线的⼀次⽅成正⽐。

流体力学第六章

流体力学第六章


积分常数C1、C2由边界条件确定。
C1 exp( h) C2 exp( h) 0
消去一个常数
C C1 exp(h) C 2 exp(h) 2 C exp ( z h) exp ( z h) Cch ( z h) 2 Cch ( z h)sin x cos t 在 z0
t x x y y z
自由面上的运动边界条件
波浪问题的基本方程和边界条件：
2φ
2φ x
2

2φ y
2
1 t 2
n 0

z p pa

2
2
0
运动学方程 动力学方程

gz 0
=+

pa C (t ) dt
1 p pa gz 0 t 2
在自由面上： z , p pa
1 g 0 t 2
在自由面上：
z ( x, y, t ) , z z ( x x, y y, t t )
流体质点的速度 ：
Ach ( z h) u cos x cos t x shh
w Ash ( z h) sin x cos t z shh
波数和频率之间的关系
Ach ( z h) sin x cos t shh
z0
0 在 z h z g 0 在 z 0 t
Ach ( z h) sin x cos t shh
2 gthh
流体质点的运动轨迹（有限水深）：
u w
Ach ( z h) sh h Ash ( z h) sh h
第六章粘性流体动力学基础

第六章粘性流体动力学基础

第六章 粘性流体动力学基础实际流体都是有粘性的，只有当粘性力与惯性力相比很小时，才能忽略粘性力而采用“理想流体”这个简单的理想模型。

支配粘性流体运动的方程比理想流体的基本方程复杂得多，因此粘性流体动力学问题的求解比理想流体动力学问题更加复杂、困难。

本章的目的在于介绍粘性流体动力学的一些基本知识。

§1 雷诺数（Re ）——粘性对于流动的影响的大小的度量粘性流体运动方程为：⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+=z y x Dt D z y x p p p f V ρ1 在x 方向的投影为：⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+∂∂z p y p x p f z u w y u v x u u t u zx yx xx x ρ1 这里以xu u ∂∂作为惯性力的代表； y p yx ∂∂ρ1作为粘性力项的代表，其大小为⎪⎪⎭⎫ ⎝⎛∂∂∂∂y u y μρ1。

下面以圆球的粘性流体绕流为例，来估算作用在单位质量流体上的惯性力和粘性力的量阶：（插圆球绕流图）L 为所研究问题的特征长度；∞V 为特征速度；∞ρ为特征密度；∞μ为特征粘性系数。

u 的量阶为∞V ；x u ∂∂的量阶为L V ∞； 22yu ∂∂的量阶为L V 2∞， 则： 作用在单位质量流体上的惯性力的量阶为：LV 2∞ 作用在单位质量流体上的粘性力的量阶为：2L V ∞∞∞ρμ 粘性力惯性力～22L V L V ∞∞∞∞ρμ＝∞∞v L V ＝∞Re Re 称为雷诺数（Reynolds 数），它的物理意义是作用在流体上的惯性力与粘性力的比值的度量。

Re 数是粘性流体动力学中最重要的无量纲参数，它在粘性流体动力学中所占地位与无粘气体动力学的M 数相当。

在不同Re 数范围内的粘性流体运动可以有完全不同的性质，下面以圆柱绕流为例看不同Re 数范围内的圆柱绕流运动。

（插圆柱绕流图）总之：Re 增加，粘性影响变弱，当Re 》1时，对于某些问题，如无分离绕流物体的升力问题，可忽略粘性影响，采用“理想流体”模型。

流体力学 第6章

流体力学 第6章


6.5 紊流运动
紊流的形成过程
选定流层
6.5 紊流运动
紊流的形成过程
6.5 紊流运动
紊流的形成过程
6.5 紊流运动
紊流的形成过程
6.5 紊流运动
紊流的形成过程
6.5 紊流运动
紊流的形成过程
6.5 紊流运动
紊流的形成过程
6.5 紊流运动
紊流的形成过程
6.5 紊流运动
13600 ( 1) 0.3 4.23m 900
设为层流
4Q v 2 2.73m/s d
6.4 圆管中的层流运动
64 l v2 hf vd d 2 g
解得
2 gd 2 hf 8.54106 m 2 /s 64lv
7.69103 Pa s
【解】 列细管测量段前、后 断面的伯努利方程
p1 p2 hf g g
p1 p2 p1 p2 hf g g g
6.4 圆管中的层流运动
p1 g (h hp ) p2 gh p hp p1 p2 ( p ) ghp
h
p p1 p2 hf ( 1)hp g g
2r0
w v 8
6.3 沿程水头损失与剪应力的关系
w v 8
w 定义 v
—— 壁剪切速度，则
v v

8
(6 -11)
上式表明了为沿程阻力系数λ和壁面剪应力τw的关系 式。
6.4 圆管中的层流运动
6.4.1 流动特征
①有序性：水流呈层状流动，各层的质点互不掺混， 质点作有序的直线运动。
6.2.2 雷诺数 1. 圆管流雷诺数
第6章 粘性流体层流流动

第6章 粘性流体层流流动


将傅里叶定律,内能关系式以及牛顿流体的应力 张量表示式全部代入可以得到:
v (ρcT ) v v ∫V t dV + ∫A ρcTv dA ∫A kgrad (T ) dA v v (v o )dV = ∫ pdiv (v )dV + ∫ ΦdV = ∫ T:
2 2 vr 2 v z 1 vθ vr + + 2 + 2 + 2 r r θ z r Φ=μ 2 2 2 v 1 vr 1 v z vθ v z vr r θ + + + + + z r z r r r θ r θ
Re =
vd ρ
μ
=
vd
υ
对应于临界流速的雷诺数成为临界雷诺数.大量的实验表明 虽然管径和流体介质不同时,临界流速不同,但临界雷诺数 基本在一个确定的范围:2000-2300. Re<2000, 层流; Re>2000, 紊流
层流和紊流 层流 流动特性 阻力特性 判断准则 壁面 速度 紊流
互不干扰,各自 互相掺混杂乱无 成层 章 m=1 M=1.75~2 Re<2000,Rec 与粗糙度无关 速度 Re>2000,Rec 与粗糙度有关 瞬时值=时均值 +脉动值
p1 p 2
γ
lg h f = lg K + m lg v
层流时 h f = lg K 1 + lg v h f = K 1v
沿程损失与断面平均流速 成正比.
二,两种流动形态的判别标准
由雷诺实验知,层流和紊流可以直接用临界速度来判别, 但是临界速度随管径的大小和流体的种类而改变.因此 流态与流速,管道直径,粘性有关.雷诺定义了一个无 量纲数
流体力学第六章_伯努利积分和动量定理

流体力学第六章_伯努利积分和动量定理




m gΔh g ( z4 z3 ) ( m 1)gΔh ( c)

[例4.6] 文丘利流量计：沿总流的伯努利方程(3-3) 由连续性方程
V2 A1 V1 A2
( d)
将(d)式代入(c)式 ,整理后可得大管的平均速度为
V1 k 2 g h
上式中
( m / ) 1 k 2 ( A / A ) 1 1 2
动能 重力势能
2
(沿流线)
压强势能
b) 拉格朗日积分
rotv 0 , v grad
V grad P 0 2 t
2
V P F (t ) t 2
2
c) 伯努利-拉格朗日积分
V ~ V C 2
不可压缩重流体
2
V p C 2
2
可压缩均熵流体
V p C 2 1
2
说明1：
伯努利方程的限制条件 ①沿流线
1V12
2
条件的放宽
沿流束
gz1 p1


2V22
2
gz 2
p2

(沿流束)
②定常流
不定常流
（取α1＝α2＝1）
2 v V12 p1 V22 p2 gz1 gz2 ds 1 t 2 2
1/ 2
k称为流速系数，文丘利管的流量公式为
Q kA1 2 g h
沿流线伯努利方程的限制条件无粘性流体粘性流体gzgz无粘性流体粘性流体不可压缩流体可压缩流体常数62伯努利积分和拉格朗日积分的应用很大的容器表明自由面a静止不动从而这是个定常问题分析
流体力学第六章 势流理论

流体力学第六章 势流理论


破坏了压力分布对ｙ轴的对称性
１. ２. 物体周围的流场无界 ３. 物体周围流场中不存在源、汇、涡等奇点 ４. 物体作等速直线运动 ５. 物体表面流动没有分离
若其中的任一条件被破坏，则物体即将遭受到 流体的作用力（阻力或升力）。
由达朗贝尔谬理，可分析物体在流体中运动 时可能受力的种类及其本质。
§６-3 绕圆柱体的有环量流动－麦格鲁斯效应
等势线：圆心在ｘ轴上，与ｙ轴相切的一组圆。
这些圆与ψ＝const正交
注意：
偶极子的轴线和方向
轴线：源和汇所在的直线
方向：由汇指向源的方向
图6-8（b）
偶极子的方向
为ｘ轴负向
四、点涡（环流）
点涡：无界流场中坐标原点处一无穷长直线涡，
方向垂直于x0y平面，与xoy平面的交点 诱导速度沿点涡为中心的圆周切线方向，大小
2.物面条件: 圆柱表面不可穿透，即
r=ｒ0处，有 Vｎ= Vｒ=０， 或ｒ=ｒ0 的圆周是一条流线。
边界条件的数学表达式
（a）无穷远条件：
ｒ ∞
Vx V0 Vy 0
或
（ｂ）物面条件：
Vr V0 cos V V0 sin
r = r０，vｎ= vr=０或r = r０处ψ=０ （零流线）
均匀流和偶极子迭加后的速度势和流函数为:
Q x cos1 2 r2
极坐标下： M cos
2 r
（６-１0）
直角坐标下：
M
2
x x2 y2
（６-11）
对于流函数：
1
2
Q
2
(1
2)
Q
2
( )
这里：r2＝ x Sinθ1
所以
x sin 1
流体力学第6章流体运动微分方程

流体力学第6章流体运动微分方程

代入式(5)可得
b p C1 2 x
C2 0
38
于是得速度分布
1 p 2 vx (by y ) 2 x
(2)上板以匀速U沿x方向运动 这时的边界条件为
vx | y 0 0, vx | y b U
39
代入式(5)可得
U b p C1 b 2 x
若此流场满足连续性方程和无旋条件，试求
A，B，C，D所满足的条件。不计重力影响。
13
解：由连续方程可知
u=Ax+By, v=Cx+Dy, w=0
u v 0 x y
则有
A D 0
又由于流动无旋，则有
则有
u v y x B C 0
14
练习： 有一个三维不可压流场，已知其x向和y向的分 速度为
yy
x
dx
17
对流体微团应用牛顿第二定律，则沿x轴 方向的运动微分方程为
xx f x dxdydz xx dydz ( xx dx)dydz x yx yx dzdx ( yx dy)dzdx zx dxdy y zx Dv x ( zx dz)dxdy dxdydz z Dt
代入上式的第一式并整理得：
20
Dv x vx vx vx 1 p fx ( 2 2 2 ) Dt x x y z
2 2 2
同 理 Dv z 1 p 2vz 2vz 2vz 得 fz ( 2 2 2 ) Dt z x y z
v x v y 0 x y
9
例题：不可压缩流体的二维平面流动，y方向 的速度分量为 2 y
v y yx
试求x方向的速度分量，假定x=0时，vx=0。

第六章 层流对流换热


u max
= − r02 4μ
d ( p + ρ gh ) dL
（6－8）
由于旋转抛物体的体积恰好等于它的外切圆柱体体积的一半，因此，平均流速等于最大流速 的一半，即
U
=
1 2
u max
= − r02 8μ
d ( p + ρ gh ) dL
（6－9）
同时，无量纲速度的分布为
φ= u U
=
⎡ 2 ⎢1
ρc
p
(
w
∂T ∂r
+u
∂T ) ∂x
=
λ
(
∂ 2T ∂r 2
+
1 r
∂T ∂r
+
∂ 2T ∂x 2
)
（6－15）
因为是充分发展的层流流动，故 w = 0 ， ∂ T ∂x
沿x
不再变化，
∂2T ∂x2
=0
，上述能量方
程即成为
ρc
pu
∂T ∂x
=λ r
∂ (r ∂T ) ，根据 ∂T
∂r ∂r
∂x
=
d T~ dx
3
流动，由于流体的物性不随温度变化，即动量方程与能量方程之间没有藕合作用，因而可以
先求速度场，后求温度场，而速度场已由上述方法求得，
再利用能量方程就可求出温度分布。
三、 恒热流密度时对流换热系数的确定
t
tw
tm
恒热流密度下的换热，如电加热、辐射加热、以及换
tc
热器中单位面积换热量为常量的情况，其温度（壁温、容
和u
=
2U
⎡ ⎢1 ⎣
−
(
r r0
)2
⎤ ⎥ ⎦

第六章 流体力学课后答案

第六章 液体力学6-1 有一个长方体形的水库，长200 m ，宽150 m ，水深10 m ，求水对水库底面和侧面的压力。

解：水对水库底面的压力为：()()391 1.0109.810150200 2.910F ghS N ρ==⨯⨯⨯⨯⨯=⨯侧面的压力应如下求得：在侧面上建立如图所示的坐标系，在y 处取侧面窄条dy ，此侧面窄条所受的压力为：dF glydy ρ=整个侧面所受的压力可以表示为：2012hF glydy glh ρρ==⎰对于10h m =、200l m =的侧面：()2721'9.8102F glh N ρ==⨯ 对于10h m =、150l m =的侧面：()2721''7.4102F glh N ρ==⨯侧面的总压力为：()82222'2'' 3.410F F F N =+=⨯6-2 有三个底面积相同但形状各异的容器，分别盛上高度相同的水，如题图所示，根据静止流体压强的概念，三个容器底面的压强是相同的，所以每个容器底面所受的水的压力也是相同的，水对底面压力是由水的重量引起的，但是三个容器中所盛的水的重量显然不等，请对这个似乎矛盾的结果作出解释。

答：三个容器底面的压强是相同的，但流体对容器内壁的压强并不是容器对其支撑面的压强，容器对其支撑面的压力等于水与容器本身重量之和。

因此，容器对其支撑面的压强是不同的。

如蓝球内壁的压强要比蓝球对支撑面的压强要大得多。

6-3 在35.010s ⨯的时间内通过管子截面的二氧化碳气体(看作为理想流体)的质量为0.51 kg 。

已知该气体的密度为37.5kg m -⋅ ，管子的直径为2.0 cm ，求二氧化碳气体在管子里的平均流速。

解： 单位时间内流过管子截面的二氧化碳气体的体积，即流量为：53130.511.36107.5 5.010V m Q m s t ρ--===⨯⋅⨯⨯平均流速为：()521221.3610 4.3103.14 1.010V Q v m s S ----⨯===⨯⋅⨯⨯ 6-4 当水从水笼头缓慢流出而自由下落时，水流随位置的下降而变细，何故？如果水笼头管口的内直径为d ，水流出的速率为0v ，求在水笼头出口以下h 处水流的直径。

工程流体力学 第6章 粘性流体管道内流动

de 2ab ab
第6章 粘性流体管道内流动
6.4 管内流动的两种损失
不可压粘性流体的总流伯努利方程：
V12 p1 V22 p2 1 gz1 2 gz2 hw 2 2
hw——单位重量流体损失的能量。
1.沿程（水头）损失
渐变流中由于流体微团、层间、流体与管壁间粘性摩擦引
教学内容
第0章 绪论 第1章 流体的主要物理性质 第2章 流体静力学 第3章 流体流动的基本方程 第4章 旋涡理论和势流理论 第5章 相似理论与量纲分析 第6章 粘性流体管内流动 第7章 粘性流体绕物体的流动
第6章 粘性流体管内流动
6.1 粘性流体中的应力分析
理想流体—无粘性，无切向应力； 实际流体—有粘性，存在切向应力，表现为阻碍流体运动的 摩擦力，消耗机械能。
是t时刻的脉动速度但脉动速度的时均量为零即u010tuudtt?在横向也存在横向脉动且第6章粘性流体管道内流动在横向yz也存在横向脉动且0vw依上法湍流中有瞬时压强p时均压强脉动压强p且pppp01tppdtt?010tppdtt?若湍流中各物理量的时均值如不随时间而变仅是空间点的函数即uvwp?第6章粘性流体管道内流动随时间而变仅是间点的函数即uuxyzppxyz?则被称为恒定的湍流运动但湍流的瞬时运动总是非恒定的
时，随着 当逐渐加大玻璃管内流速到达某一上临界值 Vcr 玻璃管内流速的再增大，颜色水与周围清水混合，使整个圆管 都带有颜色，表明此时质点的运动轨迹极不规则，各层质点相 互掺混，称这种流动状态为湍流。
从层流到湍
流的转捩阶段称
为过渡流，一般 将它作为湍流的 初级阶段。
第6章 粘性流体管道内流动
6.3.2 层流和湍流
6.2 不可压缩粘性流体的运动微分方程

第六章流体动压润滑ppt课件

数学运算方便所作的简化；
以上假设中的前四个对于一般流体润滑问 题后， 四基 个本 假上 设是 是正为确简的化。而引入的，只能有条 件地使用，在某些工况下必须加以修正。
Reynolds方程
方程的推导
运用上述假设，由Navier-Stokes方程和连续方程可以直 接推导出Reynolds方程。但是，为了了解流体润滑中的物理 现象，以及考虑到零件润滑的具体情况，可以采用流体力学 中微元体分析方法推导Reynolds方程。
u 1 p 2 x
z2 zh
U h
U0
z h
U0
(6-5)
右图表示流速u沿Z方向的分布。它由三 部分组成：式(6-5)中的
第三项表示整个润滑膜以U0运动，沿膜 厚方向即Z向各点的速度相同。
第二项则是流速沿膜厚方向按三角形分 布，它代表由于各表面的相对滑动速度 (Uh-U0)引起的流动，所以称为“速度流 动”。 第一项为抛物线分布，它表示由 p 引 起的流动，故称为“压力流动”。x
p 0 x
( h3 p ) 6 (Uh) y y x
Reynolds方程---方程应用
Reynolds方程是润滑理论中的基本方程，流体润滑状 态下的主要特性，都可以通过求解这一方程后推导出来。 ①压力分布p
当运动速度和润滑剂粘度已知时，对于给定的间隙形 态h(x,y)和边界条件，将Reyno1ds方程积分，即可求得压 力分布p(x,y) 。 ②载荷量W
端表示产生润滑压力的各种效应。将其右端展开，各项物理意义如下:
U h ，V h
x
y
动压效应
h U ，h V
x
y
Uh ，Vh
x
y
(h
0
)
h t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ui ui ui 2k 2 t xi
(6－37）
4
式中k为湍动能 ( k 1 uiui ) ，如果 t 是一个标量， 2 u i 2 0 那么 u u 0 ，而实际上 uiui k 。 i i xi 3 为此Boussinesq修正（6－35），提出对于三维湍流
第六章 湍流基本理论
第一节 第二节 第三节 第四节 第五节 第六节 第七节 湍流的基本特征和统计平均方法 湍流连续方程和雷诺方程 湍流能量方程 雷诺平均统计模式 湍流的相关函数和谱分析 拟序结构 湍流大涡数值模拟
1
第四节 雷诺平均统计模式
在雷诺方程中的不封闭量是雷诺应力，因此统计模式的 目标是封闭雷诺平均方程，建立足够的雷诺应力方程组（代 数的、微分的或一般泛函形式的）使得平均运动方程可解。 雷诺统计模式以大量的试验观测为基础，通过量纲分析、 张量分析和其他手段，包含合理的推理和猜测，提出假设， 建立模型，然后与试验对比，进行进一步的修正和精确化。 迄今为止的湍流模拟没有一个是建立在完全严密的理论基础 上，因此也称之为湍流的半经验理论。目前虽然没有建立适 用于任何流动条件的通用湍流模式的前景，但针对各种具体 流动，已成功地发展了一些模型，它们在工程技术应用中发 挥着越来越大的作用。 目前的湍流统计模式主要有两类:湍流涡粘模式和雷诺应 力模式。
*
lm i kx2 t i kx2v*
(6－41）
阻力。
w是壁面摩擦
10
在边界层的外层（核心区）：
lm o 1
(6－42）
t o 2 v *
2 0.06 ~ 0.075 ， 式中o表示外层，1 0.075~ 0.09， 为间隙因子。
(6－40）
根据实验研究可以得到以下几点： a、由试验得到的 lm ，不象假设的那样为流体微团的 尺寸，而是与流动的平均尺度一样的量级。 b 、lm 不 是 空 间 常 数 。 在 边 界 层 中 根 据 尼 古 拉 兹 和 Klebanoff试验，在内层（壁面区）
w v , 式中i表示内层，k=0.40~0.41，
5
（2）混合长度理论
Prandtl混合长度理论依然从Boussinesq的假设 出发，对于二维湍流，令：
u1 t t x2
式中 t 为湍流雷诺切应力，并 t 认为与湍流的脉动 速度与混合长度lm的乘积成正比
t u1 lm
混合长度lm类比于气体分子运动的自由行程，在lm一段 特征长度之内湍流微团保持自己的动量不变。
2

由于u1 ~ u1 , 所以微团从 x2 l 运动到 x2 时 u1 0, u 2 0 ，也就是说 u1 和 u 2 是异号的。 还可以认为 u 2 ~ u1，这是因为当 x2 l 处的微团 到达点 x2 时，恰巧在 x2 l 微团的左边时，就会产 生碰撞，而产生横向运动 u1 ，这样 u2 ~ u1 。同样, 当两个微团到达 x2 点时向相反运动时，周围的微团会 向中间补充也会产生 u 2 。
u1 u1 u1 u2 t t x2 x2 对三维流动 ui u j ui u j t Dij t x j xi
(6－34）
2 t Sij
(6－35）
3
应力张量表示
ij pij t Dij
(6－36）
t t 其中： t 湍流动力粘性系数，或称涡旋粘性系数， 是湍流运动粘性系数。 上述假设所以能提出是基于对湍流脉动引起的动量 交换与气体分子运动引起的粘性切应力进行简单的类比 的结果。对于 一般在定温下可认为是常数，但 t不 是常量，因为湍流的动量交换取决于湍流的平均运动。 流动只在一个方向上有明确的速度梯度时，可以认 为 t 是个标量。在一般情况下，当i=j时
2 ui u j k ij t D.A测得在圆柱尾迹的充分湍流区， t 0.0164U0d ,(U0 是来流速度，d是圆柱直径）。 Hinze J.O.在空气的圆截面射流中测得 t 0.0116U p d （UP是射流入射速度，d是射流孔径）。当UP＝40m/s ， d=25mm，则 t 0.0116m2 / s 大约是空气 的1000倍。
8
d u1 u1 u1 x2 l u1 x2 l dx2
图6－7 u2 的产生
认为
u2

d u1 常数 l dx2
12
2 du 1 du 1 u1 u 2 l m dx 2 dx 2
(6－39）
9
t lm
2
du1 dx2
6
图6－6 混合长度与脉 动速度
对于图中二维不可压定常湍流：
ux2 l ux2 ux2 l
假设微团从 x2 l 或 x 2 l 运动至 x2，对于 x2 来讲， 脉动速度 u 2 0 或 u 2 0 ，
7
du1 ( x2 ) u1 x2 l u1 x2 l ... ... dx2 x x
2
1、湍流涡粘模式
涡粘模式理论是目前工程中常用的模式，它的表达 式和分子粘性类似，因此比较容易将N－S方程数值解 法推广到雷诺平均方程的计算中来。
(1)、涡粘性模型
布西内斯克（Boussinesq J.,1877）提出二维湍流 的雷诺应力与粘性应力作用相似的假设，即局部的雷 诺应力与平均速度梯度成正比：
Van Driest（1959）年提出在内层：
kx2 1 exp x 2 25.3v