2008年高考试题——数学文(全国卷2)

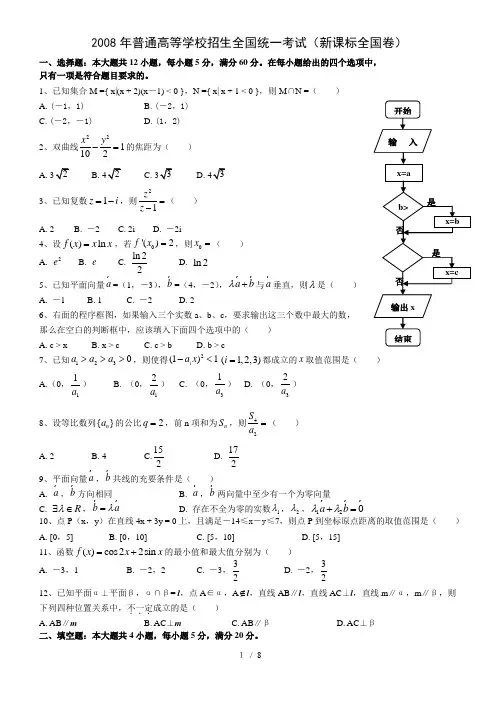
2008年普通高等学校招生全国统一考试（新课标全国卷）一、选择题：本大题共12小题，每小题5分，满分60分。

在每小题给出的四个选项中， 只有一项是符合题目要求的。

1、已知集合M ={ x|(x + 2)(x －1) < 0 }，N ={ x| x + 1 < 0 }，则M ∩N =（ ） A. (－1，1) B. (－2，1)C. (－2，－1)D. (1，2)2、双曲线221102x y -=的焦距为（ ）3、已知复数1z i =-，则21z z =-（ ） A. 2B. －2C. 2iD. －2i4、设()ln f x x x =，若0'()2f x =，则0x =（ ）A. 2e B. e C. ln 22D. ln 25、已知平面向量a r =（1，－3），b r =（4，－2），a b λ+r r 与a r垂直，则λ是（ ）A. －1B. 1C. －2D. 26、右面的程序框图，如果输入三个实数a 、b 、c ，要求输出这三个数中最大的数， 那么在空白的判断框中，应该填入下面四个选项中的（ ） A. c > xB. x > cC. c > bD. b > c7、已知1230a a a >>>，则使得2(1)1i a x -<(1,2,3)i =都成立的x 取值范围是（ ）A.（0，11a ） B. （0，12a ） C. （0，31a ） D. （0，32a ）8、设等比数列{}n a 的公比2q =，前n 项和为n S ，则42S a =（ ） A. 2 B. 4 C.152D.1729、平面向量a r ，b r共线的充要条件是（ ）A. a r ，b r 方向相同B. a r ，b r 两向量中至少有一个为零向量C. R λ∃∈， b a λ=r rD. 存在不全为零的实数1λ，2λ，120a b λλ+=r r r10、点P （x ，y ）在直线4x + 3y = 0上，且满足－14≤x －y ≤7，则点P 到坐标原点距离的取值范围是（ ） A. [0，5]B. [0，10]C. [5，10]D. [5，15]11、函数()cos 22sin f x x x =+的最小值和最大值分别为（ ）A. －3，1B. －2，2C. －3，32 D. －2，3212、已知平面α⊥平面β，α∩β= l ，点A ∈α，A ∉l ，直线AB ∥l ，直线AC ⊥l ，直线m ∥α，m ∥β，则下列四种位置关系中，不一定．．．成立的是（ ） A. AB ∥m B. AC ⊥m C. AB ∥βD. AC ⊥β二、填空题：本大题共4小题，每小题5分，满分20分。

2008年普通高等学校招生全国统一考试文科数学（必修+选修Ⅰ）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分．第I 卷1至2页，第II 卷3至9页．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷考生注意： 1．答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ，并贴好条形码．请认真核准条形码上的准考证号、姓名和科目． 2．每小题选出答案后，用2Ｂ铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．在试题卷上作答无效．．．．．．．．．．3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 参考公式： 如果事件A B ，互斥，那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ，相互独立，那么 其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是P ，那么34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(01,2)k k n kn n P k C P P k n -=-= ，，，一、选择题1．函数y = ） A ．{|1}x x ≤B ．{|0}x x ≥C ．{|10}x x x ≥或≤D ．{|01}x x ≤≤2．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图像可能是（ ）A ．B ．C ．D ．3．512x ⎛⎫+ ⎪⎝⎭的展开式中2x 的系数为（ ）A ．10B ．5C ．52D ．14．曲线324y x x =-+在点(13)，处的切线的倾斜角为（ ） A ．30°B ．45°C ．60°D ．120°5．在ABC △中，AB c = ，AC b = ．若点D 满足2BD DC = ，则AD=（ ）A ．2133b c + B ．5233c b -C ．2133b c - D ．1233b c +6．2(sin cos )1y x x =--是（ ） A ．最小正周期为2π的偶函数 B ．最小正周期为2π的奇函数 C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数7．已知等比数列{}n a 满足122336a a a a +=+=，，则7a =（ ） A ．64B ．81C ．128D ．2438．若函数()y f x =的图象与函数1y =的图象关于直线y x =对称，则()f x =（ ） A ．22ex -B ．2e xC ．21ex +D ．2+2ex9．为得到函数πcos 3y x ⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin y x =的图像（ ） A ．向左平移π6个长度单位 B ．向右平移π6个长度单位 C ．向左平移5π6个长度单位 D ．向右平移5π6个长度单位10．若直线1x y a b+=与圆221x y +=有公共点，则（ ）A ．221a b +≤B ．221a b +≥ C ．22111a b+≤D ．2211a b +≥1 11．已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 内的射影为ABC △的中心，则1AB 与底面ABC 所成角的正弦值等于（ ）A ．13B C D ．2312．将1，2，3填入33⨯的方格中，要求每行、每列都没有重复数字，下面是一种填法，则不同的填写方法共有（ ）A ．6种B ．12种C ．24种D ．48种2008年普通高等学校招生全国统一考试文科数学（必修+选修Ⅰ）第Ⅱ卷注意事项：1．答题前，考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，然后贴好条形码．请认真核准条形码上的准考证号、姓名和科目．2．第Ⅱ卷共7页，请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，在试题卷上作答无效．．．．．．．．．． 3．本卷共10小题，共90分．二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上．（注意：在试题卷上作答无效．．．．．．．．．） 13．若x y ，满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩，，，≥≥≤≤则2z x y =-的最大值为 ．14．已知抛物线21y ax =-的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 ． 15．在ABC △中，90A ∠=，3tan 4B =．若以A B ，为焦点的椭圆经过点C ，则该椭圆的离心率e = ．16．已知菱形ABCD 中，2AB =，120A ∠=，沿对角线BD 将ABD △折起，使二面角A BD C --为120 ，则点A 到BCD △所在平面的距离等于 ．三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 设ABC △的内角A B C ，，所对的边长分别为a b c ，，，且cos 3a B =，sin 4b A =． （Ⅰ）求边长a ；（Ⅱ）若ABC △的面积10S =，求ABC △的周长l ．18．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 四棱锥A BCDE -中，底面BCDE 为矩形，侧面ABC ⊥底面BCDE ，2BC =，CD =AB AC =．（Ⅰ）证明：AD CE ⊥；（Ⅱ）设侧面ABC 为等边三角形，求二面角C AD E --的大小．19．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 在数列{}n a 中，11a =，122n n n a a +=+． （Ⅰ）设12nn n a b -=．证明：数列{}n b 是等差数列； （Ⅱ）求数列{}n a 的前n 项和n S ． 20．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 已知5只动物中有1只患有某种疾病，需要通过化验血液来确定患病的动物．血液化验结果呈阳性的即为患病动物，呈阴性即没患病．下面是两种化验方案： 方案甲：逐个化验，直到能确定患病动物为止．方案乙：先任取3只，将它们的血液混在一起化验．若结果呈阳性则表明患病动物为这3只中的1只，然后再逐个化验，直到能确定患病动物为止；若结果呈阴性则在另外2只中任取1只化验．求依方案甲所需化验次数不少于依方案乙所需化验次数的概率．CDE AB21．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 已知函数32()1f x x ax x =+++，a ∈R ． （Ⅰ）讨论函数()f x 的单调区间；（Ⅱ）设函数()f x 在区间2133⎛⎫-- ⎪⎝⎭，内是减函数，求a 的取值范围． 22．（本小题满分12分）（注意：在试题卷上作答无效．．．．．．．．．） 双曲线的中心为原点O ，焦点在x 轴上，两条渐近线分别为12l l ，，经过右焦点F 垂直于1l 的直线分别交12l l ，于A B ，两点．已知OA AB OB 、、成等差数列，且BF 与FA同向． （Ⅰ）求双曲线的离心率；（Ⅱ）设AB 被双曲线所截得的线段的长为4，求双曲线的方程．2008年普通高等学校招生全国统一考试 文科数学（必修+选修Ⅰ）参考答案一、1．D 2．A 3．C 4．B 5．A 6．D 7．A 8．A 9．C 10．D 11．B 12．B二、13．9 14．12 15．12 16三、17．解：（1）由cos 3a B =与sin 4b A =两式相除，有：3cos cos cos cot 4sin sin sin a B a B b BB b A A b B b ==== 又通过cos 3a B =知：cos 0B >，则3cos 5B =，4sin 5B =，则5a =．（2）由1sin 2S ac B =，得到5c =．由222cos 2a c b B ac+-=，解得：b =最后10l =+18．解：（1）取BC 中点F ，连接DF 交CE 于点O ， AB AC =， ∴AF BC ⊥，又面ABC ⊥面BCDE ， ∴AF ⊥面BCDE ， ∴AF CE ⊥．tan tan 2CED FDC ∠=∠=， ∴90OED ODE ∠+∠= ，90DOE ∴∠= ，即CE DF ⊥，CE ∴⊥面ADF ， CE AD ∴⊥．（2）在面ACD 内过C 点做AD 的垂线，垂足为G ． CG AD ⊥，CE AD ⊥， AD ∴⊥面CEG ， EG AD ∴⊥，则CGE ∠即为所求二面角．AC CD CG AD ==，DG =，EG ==，CE =则222cos 2CG GE CE CGE CG GE +-∠==πarccos CGE ∴∠=-⎝⎭．19．解：（1）122n n n a a +=+，11122n nn n a a +-=+， 11n n b b +=+，则n b 为等差数列，11b =，n b n =，12n n a n -=．（2）01211222(1)22n n n S n n --=+++-+12121222(1)22n n n S n n -=+++-+两式相减，得01121222221n n n n n S n n -=---=-+ ．20．解：设1A 、2A 分别表示依方案甲需化验1次、2次。

2008年普通高等学校招生全国统一考试数学（文史类）（北京卷）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至9页，共150分．考试时间120分钟．考试结束，将本试卷和答题卡一并交回．第Ⅰ卷（选择题 共40分）注意事项： 1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案．不能答在试卷上．一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．若集合{|23}A x x =-≤≤，{|14}B x x x =<->或，则集合A B 等于（ ）A ．{}|34x x x >或≤ B ．{}|13x x -<≤ C ．{}|34x x <≤D ．{}|21x x --<≤2．若372log πlog 6log 0.8a b c ===，，，则（ ） A ．a b c >>B ．b a c >>C ．c a b >>D ．b c a >>3．“双曲线的方程为221916x y -=”是“双曲线的准线方程为95x =±”的（ ） A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件4．已知ABC △中，a =b =60B =，那么角A 等于（ ）A ．135B ．90C ．45D ．305．函数2()(1)1(1)f x x x =-+<的反函数为（ ）A ．1()11)fx x -=>B ．1()11)fx x -=>C ．1()11)f x x -=+≥D ．1()11)f x x -=-≥6．若实数x y ，满足1000x y x y x ⎧-+⎪+⎨⎪⎩，，，≥≥≤则2z x y =+的最小值是（ ）A ．0B ．12C ．1D ．27．已知等差数列{}n a 中，26a =，515a =，若2n n b a =，则数列{}n b 的前5项和等于（ ） A ．30B ．45C ．90D ．1868．如图，动点P 在正方体1111ABCD A B C D -的对角线1BD 上，过点P 作垂直于平面11BB D D 的直线，与正方体表面相交于M N ，．设B P x =，MN y =，则函数()y f x =的图象大致是（ ）A BC DMNP A 1B 1C 1D 12008年普通高等学校招生全国统一考试数学（文史类）（北京卷）第Ⅱ卷（共110分）注意事项：1．用钢笔或圆珠笔将答案直接写在试卷上．2．答卷前将密封线内的项目填写清楚．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在题中横线上． 9．若角α的终边经过点(12)P -，，则tan 2α的值为 ． 10．不等式112x x ->+的解集是 ． 11．已知向量a 与b 的夹角为120，且4==a b ，那么a b 的值为 ．12．5231x x ⎛⎫+ ⎪⎝⎭的展开式中常数项为 ；各项系数之和为 ．（用数字作答）13．如图，函数()f x 的图象是折线段ABC ，其中A B C ，，的坐标分别为(04)(20)(64)，，，，，，则((0))f f = ；函数()f x 在1x =处的导数(1)f '= ．14．已知函数2()cos f x x x =-，对于ππ22⎡⎤-⎢⎥⎣⎦，上的任意12x x ，，有如下条件：①12x x >； ②2212x x >； ③12x x >．其中能使12()()f x f x >恒成立的条件序号是 ．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（本小题共13分）已知函数2π()sin sin 2f x x x x ωωω⎛⎫=+ ⎪⎝⎭（0ω>）的最小正周期为π． （Ⅰ）求ω的值；（Ⅱ）求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦，上的取值范围．16．（本小题共14分）如图，在三棱锥P ABC -中，2AC BC ==，90ACB ∠=，AP BP AB ==，PC AC ⊥． （Ⅰ）求证：PC AB ⊥；（Ⅱ）求二面角B AP C --的大小． 17．（本小题共13分）已知函数32()3(0)f x x ax bx c b =+++≠，且()()2g x f x =-是奇函数． （Ⅰ）求a ，c 的值；（Ⅱ）求函数()f x 的单调区间．18．（本小题共13分）甲、乙等五名奥运志愿者被随机地分到A B C D ，，，四个不同的岗位服务，每个岗位至少有一名志愿者．（Ⅰ）求甲、乙两人同时参加A 岗位服务的概率； （Ⅱ）求甲、乙两人不在同一个岗位服务的概率． 19．（本小题共14分） 已知ABC △的顶点A B ，在椭圆2234x y +=上，C 在直线2l y x =+：上，且AB l ∥． （Ⅰ）当AB 边通过坐标原点O 时，求AB 的长及ABC △的面积； （Ⅱ）当90ABC ∠=，且斜边AC 的长最大时，求AB 所在直线的方程． 20．（本小题共13分）数列{}n a 满足11a =，21()n n a n n a λ+=+-（12n =，，），λ是常数． （Ⅰ）当21a =-时，求λ及3a 的值；（Ⅱ）数列{}n a 是否可能为等差数列？若可能，求出它的通项公式；若不可能，说明理由； （Ⅲ）求λ的取值范围，使得存在正整数m ，当n m >时总有0n a <．ACBP2008年普通高等学校招生全国统一考试数学（文史类）（北京卷）参考答案一、选择题（本大题共8小题，每小题5分，共40分）1．D 2．A 3．A 4．C 5．B 6．A 7．C 8．B二、填空题（本大题共6小题，每小题5分，共30分）9．4310．{}|2x x <-11．8-12．10 3213．2 2-14．②三、解答题（本大题共6小题，共80分） 15．（共13分） 解：（Ⅰ）1cos 2()22x f x x ωω-=11sin 2cos 2222x x ωω=-+π1sin 262x ω⎛⎫=-+ ⎪⎝⎭． 因为函数()f x 的最小正周期为π，且0ω>， 所以2ππ2ω=，解得1ω=． （Ⅱ）由（Ⅰ）得π1()sin 262f x x ⎛⎫=-+ ⎪⎝⎭． 因为2π03x ≤≤， 所以ππ7π2666x --≤≤，所以1πsin 2126x ⎛⎫-- ⎪⎝⎭≤≤． 因此π130sin 2622x ⎛⎫-+ ⎪⎝⎭≤≤，即()f x 的取值范围为302⎡⎤⎢⎥⎣⎦，． 16．（共14分）解法一：（Ⅰ）取AB 中点D ，连结PD CD ，． AP BP =， PD AB ∴⊥． AC BC =， CD AB ∴⊥． PD CD D =，ACBDPAB ∴⊥平面PCD ． PC ⊂平面PCD ， PC AB ∴⊥．（Ⅱ）AC BC =，AP BP =， APC BPC ∴△≌△． 又PC AC ⊥， PC BC ∴⊥．又90ACB ∠=，即AC BC ⊥，且ACPC C =，BC ∴⊥平面PAC ．取AP 中点E ．连结BE CE ，． AB BP =，BE AP ∴⊥．EC 是BE 在平面PAC 内的射影， CE AP ∴⊥．BEC ∴∠是二面角B AP C --的平面角．在BCE △中，90BCE ∠=，2BC =，BE AB ==sin 3BC BEC BE ∴∠==． ∴二面角B AP C --的大小为arcsin3． 解法二：（Ⅰ）AC BC =，AP BP =， APC BPC ∴△≌△． 又PC AC ⊥， PC BC ∴⊥． AC BC C =，PC ∴⊥平面ABC ． AB ⊂平面ABC ， PC AB ∴⊥．（Ⅱ）如图，以C 为原点建立空间直角坐标系C xyz -．则(000)(020)(200)C A B ，，，，，，，，． 设(00)P t ，，．PB AB ==，2t ∴=，(002)P ，，． ACBEPy取AP 中点E ，连结BE CE ，．AC PC =，AB BP =，CE AP ∴⊥，BE AP ⊥．BEC ∴∠是二面角B AP C --的平面角．(011)E ，，，(011)EC =--，，，(211)EB =--，，，cos 26EC EB BEC EC EB∴∠===． ∴二面角B AP C --的大小为arccos17．（共13分）解：（Ⅰ）因为函数()()2g x f x =-为奇函数，所以，对任意的x ∈R ，()()g x g x -=-，即()2()2f x f x --=-+． 又32()3f x x ax bx c =+++所以32323232x ax bx c x ax bx c -+-+-=----+． 所以22a a c c =-⎧⎨-=-+⎩，．解得02a c ==，．（Ⅱ）由（Ⅰ）得3()32f x x bx =++．所以2()33(0)f x x b b '=+≠．当0b <时，由()0f x '=得x =x 变化时，()f x '的变化情况如下表：所以，当0b <时，函数()f x 在(-∞，上单调递增，在(上单调递减，在)+∞上单调递增．当0b >时，()0f x '>，所以函数()f x 在()-∞+∞，上单调递增． 18．（共13分）解：（Ⅰ）记甲、乙两人同时参加A 岗位服务为事件A E ，那么3324541()40A A P E C A ==，即甲、乙两人同时参加A 岗位服务的概率是140． （Ⅱ）设甲、乙两人同时参加同一岗位服务为事件E ，那么4424541()10A P E C A ==，所以，甲、乙两人不在同一岗位服务的概率是9()1()10P E P E =-=． 19．（共14分）解：（Ⅰ）因为AB l ∥，且AB 边通过点(00)，，所以AB 所在直线的方程为y x =．设A B ，两点坐标分别为1122()()x y x y ，，，． 由2234x y y x⎧+=⎨=⎩，得1x =±．所以12AB x =-=．又因为AB 边上的高h 等于原点到直线l 的距离．所以h =122ABC S AB h ==△． （Ⅱ）设AB 所在直线的方程为y x m =+，由2234x y y x m⎧+=⎨=+⎩，得2246340x mx m ++-=． 因为A B ，在椭圆上， 所以212640m ∆=-+>．设A B ，两点坐标分别为1122()()x y x y ，，，， 则1232mx x +=-，212344m x x -=，所以12AB x =-=．又因为BC 的长等于点(0)m ，到直线l 的距离，即BC =所以22222210(1)11AC AB BC m m m =+=--+=-++． 所以当1m =-时，AC 边最长，（这时12640∆=-+>） 此时AB 所在直线的方程为1y x =-． 20．（共13分）解：（Ⅰ）由于21()(12)n n a n n a n λ+=+-=，，，且11a =． 所以当21a =-时，得12λ-=-， 故3λ=．从而23(223)(1)3a =+-⨯-=-．（Ⅱ）数列{}n a 不可能为等差数列，证明如下：由11a =，21()n n a n n a λ+=+-得22a λ=-，3(6)(2)a λλ=--，4(12)(6)(2)a λλλ=---．若存在λ，使{}n a 为等差数列，则3221a a a a -=-，即(5)(2)1λλλ--=-， 解得3λ=．于是2112a a λ-=-=-，43(11)(6)(2)24a a λλλ-=---=-． 这与{}n a 为等差数列矛盾．所以，对任意λ，{}n a 都不可能是等差数列．（Ⅲ）记2(12)n b n n n λ=+-=，，，根据题意可知，10b <且0n b ≠，即2λ>且2*()n n n λ≠+∈N ，这时总存在*0n ∈N ，满足：当0n n ≥时，0n b >；当01n n -≤时，0n b <．所以由1n n n a b a +=及110a =>可知，若0n 为偶数，则00n a <，从而当0n n >时，0n a <；若0n 为奇数，则00n a >，从而当0n n >时0n a >．因此“存在*m ∈N ，当n m >时总有0n a <”的充分必要条件是：0n 为偶数，记02(12)n k k ==，，，则λ满足22221(2)20(21)210k k b k k b k k λλ-⎧=+->⎪⎨=-+--<⎪⎩． 故λ的取值范围是22*4242()k k k k k λ-<<+∈N ．。

2008 年全国统一高考数学试卷（文科）（全国卷Ⅱ）一、选择题（共12 小题，每小题5 分，满分60 分）1．（5 分）若sinα＜0 且tanα＞0，则α是（）A．第一象限角B．第二象限角C．第三象限角D．第四象限角2．（5 分）设集合M={m∈Z|﹣3＜m＜2}，N={n∈Z|﹣1≤n≤3}，则M∩N=（）A．{0，1} B．{﹣1，0，1}C．{0，1，2} D．{﹣1，0，1，2}3．（5 分）原点到直线x+2y﹣5=0 的距离为（）A．1 B．C．2D．4．（5分）函数f（x）=﹣x 的图象关于（）A．y 轴对称B．直线y=﹣x 对称C．坐标原点对称D．直线y=x 对称5．（5 分）若x∈（e﹣1，1），a=lnx，b=2lnx，c=ln3x，则（）A．a＜b＜c B．c＜a＜b C．b＜a＜c D．b＜c＜a6．（5 分）设变量x，y 满足约束条件：，则z=x﹣3y 的最小值（）A．﹣2 B．﹣4 C．﹣6 D．﹣87．（5 分）设曲线y=ax2在点（1，a）处的切线与直线2x﹣y﹣6=0 平行，则a= （）A．1 B．C．D．﹣18．（5 分）正四棱锥的侧棱长为，侧棱与底面所成的角为60°，则该棱锥的体积为（）A．3 B．6 C．9 D．189．（5分）的展开式中x 的系数是（）A．﹣4 B．﹣3 C．3 D．410．（5 分）函数f（x）=sinx﹣cosx 的最大值为（）A．1 B．C．D．211．（5 分）设△ABC 是等腰三角形，∠ABC=120°，则以A，B 为焦点且过点C 的双曲线的离心率为（）A．B．C．D．12．（5 分）已知球的半径为2，相互垂直的两个平面分别截球面得两个圆，若两圆的公共弦长为2，则两圆的圆心距等于（）A．1 B．C．D．2二、填空题（共4 小题，每小题5 分，满分20 分）13．（5分）设向量，若向量与向量共线，则λ=．14．（5 分）从10 名男同学，6 名女同学中选3 名参加体能测试，则选到的3 名同学中既有男同学又有女同学的不同选法共有种（用数字作答）15．（5 分）已知F 是抛物线C：y2=4x 的焦点，A，B 是C 上的两个点，线段AB 的中点为M（2，2），则△ABF 的面积等于．16．（5 分）平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件①；充要条件②．（写出你认为正确的两个充要条件）三、解答题（共6 小题，满分70 分）17．（10 分）在△ABC 中，cosA=﹣，cosB=．（I）求sinC 的值；（II）设BC=5，求△ABC 的面积．18．（12 分）等差数列{a n}中，a4=10 且a3，a6，a10 成等比数列，求数列{a n}前20 项的和S20．19．（12 分）甲、乙两人进行射击比赛，在一轮比赛中，甲、乙各射击一发子弹．根据以往资料知，甲击中8 环，9 环，10 环的概率分别为0.6，0.3，0.1，乙击中8 环，9 环，10 环的概率分别为0.4，0.4，0.2．设甲、乙的射击相互独立．（I）求在一轮比赛中甲击中的环数多于乙击中环数的概率；（II）求在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数的概率．20．（12 分）如图，正四棱柱ABCD﹣A1B1C1D1 中，AA1=2AB=4，点E 在CC1 上且C1E=3EC．（I）证明：A1C⊥平面BED；（II）求二面角A1﹣DE﹣B 的大小．21．（12 分）设a∈R，函数f（x）=ax3﹣3x2．（I）若x=2 是函数y=f（x）的极值点，求a 的值；（II）若函数g（x）=f（x）+f′（x），x∈[0，2]，在x=0 处取得最大值，求a 的取值范围．22．（12 分）设椭圆中心在坐标原点，A（2，0），B（0，1）是它的两个顶点，直线y=kx（k＞0）与AB 相交于点D，与椭圆相交于E、F 两点．（I）若，求k 的值；（II）求四边形AEBF 面积的最大值．2008 年全国统一高考数学试卷（文科）（全国卷Ⅱ）参考答案与试题解析一、选择题（共12 小题，每小题5 分，满分60 分）1．（5 分）若sinα＜0 且tanα＞0，则α是（）A．第一象限角B．第二象限角C．第三象限角D．第四象限角【考点】GC：三角函数值的符号．【分析】由正弦和正切的符号确定角的象限，当正弦值小于零时，角在第三四象限，当正切值大于零，角在第一三象限，要同时满足这两个条件，角的位置是第三象限，实际上我们解的是不等式组．【解答】解：sinα＜0，α在三、四象限；tanα＞0，α在一、三象限．故选：C．【点评】记住角在各象限的三角函数符号是解题的关键，可用口诀帮助记忆：一全部，二正弦，三切值，四余弦，它们在上面所述的象限为正2．（5 分）设集合M={m∈Z|﹣3＜m＜2}，N={n∈Z|﹣1≤n≤3}，则M∩N=（）A．{0，1} B．{﹣1，0，1} C．{0，1，2} D．{﹣1，0，1，2}【考点】1E：交集及其运算．【分析】由题意知集合M={m∈z|﹣3＜m＜2}，N={n∈z|﹣1≤n≤3}，然后根据交集的定义和运算法则进行计算．【解答】解：∵M={﹣2，﹣1，0，1}，N={﹣1，0，1，2，3}，∴M∩N={﹣1，0，1}，故选：B．【点评】此题主要考查集合和交集的定义及其运算法则，是一道比较基础的题．3．（5 分）原点到直线x+2y﹣5=0 的距离为（）A．1 B．C．2 D．【考点】IT：点到直线的距离公式．【分析】用点到直线的距离公式直接求解．【解答】解析：．故选：D．【点评】点到直线的距离公式是高考考点，是同学学习的重点，本题是基础题．4．（5 分）函数f（x）=﹣x 的图象关于（）A．y 轴对称B．直线y=﹣x 对称C．坐标原点对称D．直线y=x 对称【考点】3M：奇偶函数图象的对称性．【分析】根据函数f（x）的奇偶性即可得到答案．【解答】解：∵f（﹣x）=﹣+x=﹣f（x）∴是奇函数，所以f（x）的图象关于原点对称故选：C．【点评】本题主要考查函数奇偶性的性质，是高考必考题型．5．（5 分）若x∈（e﹣1，1），a=lnx，b=2lnx，c=ln3x，则（）A．a＜b＜c B．c＜a＜b C．b＜a＜c D．b＜c＜a【考点】4M：对数值大小的比较．【分析】根据函数的单调性，求a 的范围，用比较法，比较a、b 和a、c 的大小．【解答】解：因为a=lnx 在（0，+∞）上单调递增，故当x∈（e﹣1，1）时，a∈（﹣1，0），于是b﹣a=2lnx﹣lnx=lnx＜0，从而b＜a．又a﹣c=lnx﹣ln3x=a（1+a）（1﹣a）＜0，从而a＜c．综上所述，b＜a＜c．故选：C．【点评】对数值的大小，一般要用对数的性质，比较法，以及0 或1 的应用，本题是基础题．6．（5 分）设变量x，y 满足约束条件：，则z=x﹣3y 的最小值（）A．﹣2 B．﹣4 C．﹣6 D．﹣8【考点】7C：简单线性规划．【专题】11：计算题．【分析】我们先画出满足约束条件：的平面区域，求出平面区域的各角点，然后将角点坐标代入目标函数，比较后，即可得到目标函数z=x﹣3y 的最小值．【解答】解：根据题意，画出可行域与目标函数线如图所示，由图可知目标函数在点（﹣2，2）取最小值﹣8故选：D．【点评】用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．7．（5 分）设曲线y=ax2在点（1，a）处的切线与直线2x﹣y﹣6=0 平行，则a= （）A．1 B．C．D．﹣1【考点】6H：利用导数研究曲线上某点切线方程．【分析】利用曲线在切点处的导数为斜率求曲线的切线斜率；利用直线平行它们的斜率相等列方程求解．【解答】解：y'=2ax，于是切线的斜率k=y'|x=1=2a，∵切线与直线2x﹣y﹣6=0 平行∴有2a=2∴a=1故选：A．【点评】本题考查导数的几何意义：曲线在切点处的导数值是切线的斜率．8．（5 分）正四棱锥的侧棱长为，侧棱与底面所成的角为60°，则该棱锥的体积为（）A．3 B．6 C．9 D．18【考点】LF：棱柱、棱锥、棱台的体积．【专题】11：计算题．【分析】先求正四棱锥的高，再求正四棱锥的底面边长，然后求其体积．【解答】解：高，又因底面正方形的对角线等于，∴底面积为，∴体积故选：B．【点评】本题考查直线与平面所成的角，棱锥的体积，注意在底面积的计算时，要注意多思则少算．9．（5 分）的展开式中x 的系数是（）A．﹣4 B．﹣3 C．3 D．4【考点】DA：二项式定理．【分析】先利用平方差公式化简代数式，再利用二项展开式的通项公式求出第r+1 项，令x 的指数为1 求得展开式中x 的系数．【解答】解：=（1﹣x）4（1﹣x）4的展开式的通项为T r+1=C4r（﹣x）r=（﹣1）r C4r x r令r=1 得展开式中x 的系数为﹣4故选：A．【点评】本题考查二项展开式的通项公式是解决二项展开式的特定想问题的工具．10．（5 分）函数f（x）=sinx﹣cosx 的最大值为（）A．1 B．C．D．2【考点】H4：正弦函数的定义域和值域；HJ：函数y=Asin（ωx+φ）的图象变换．【专题】11：计算题．【分析】根据两角和与差的正弦公式进行化简，即可得到答案．【解答】解：，所以最大值是故选：B．【点评】本题主要考查两角和与差的正弦公式和正弦函数的最值问题．三角函数中化为一个角的三角函数问题是三角函数在高考中的热点问题．11．（5 分）设△ABC 是等腰三角形，∠ABC=120°，则以A，B 为焦点且过点C 的双曲线的离心率为（）A．B．C．D．【考点】KC：双曲线的性质．【专题】11：计算题；16：压轴题．【分析】根据题设条件可知2c=|AB|，所以，由双曲线的定义能够求出2a，从而导出双曲线的离心率．【解答】解：由题意2c=|AB|，所以，由双曲线的定义，有，∴故选：B．【点评】本题考查双曲线的有关性质和双曲线定义的应用．12．（5 分）已知球的半径为2，相互垂直的两个平面分别截球面得两个圆，若两圆的公共弦长为2，则两圆的圆心距等于（）A．1 B．C．D．2【考点】LG：球的体积和表面积．【专题】11：计算题；5F：空间位置关系与距离．【分析】求解本题，可以从三个圆心上找关系，构建矩形利用对角线相等即可求解出答案．【解答】解：设两圆的圆心分别为O1、O2，球心为O，公共弦为AB，其中点为E，则OO1EO2 为矩形，于是对角线O1O2=OE，而OE==，∴O1O2=故选：C．【点评】本题考查球的有关概念，两平面垂直的性质，是基础题．10 610 6 10 6 10 6二、填空题（共 4 小题，每小题 5 分，满分 20 分） 13．（5 分）设向量 ，若向量与向量共线，则 λ= 2 ．【考点】96：平行向量（共线）．【分析】用向量共线的充要条件：它们的坐标交叉相乘相等列方程解． 【解答】解：∵a=（1，2），b=（2，3）， ∴λα+b=（λ，2λ）+（2，3）=（λ+2，2λ+3）． ∵向量 λα+b 与向量 c=（﹣4，﹣7）共线， ∴﹣7（λ+2）+4（2λ+3）=0， ∴λ=2． 故答案为 2【点评】考查两向量共线的充要条件．14．（5 分）从 10 名男同学，6 名女同学中选 3 名参加体能测试，则选到的 3 名同学中既有男同学又有女同学的不同选法共有 420种（用数字作答）【考点】D5：组合及组合数公式． 【专题】11：计算题；32：分类讨论．【分析】由题意分类：①男同学选 1 人，女同学中选 2 人，确定选法；②男同学 选 2 人，女同学中选 1 人，确定选法；然后求和即可．【解答】解：由题意共有两类不同选法，①男同学选 1 人，女同学中选 2 人，不同选法 C 1C 2=150； ②男同学选 2 人，女同学中选 1 人，不同选法 C 2C 1=270；共有：C 1C 2+C 2C 1=150+270=420 故答案为：420【点评】本题考查组合及组合数公式，考查分类讨论思想，是基础题．15．（5 分）已知 F 是抛物线 C ：y 2=4x 的焦点，A ，B 是 C 上的两个点，线段 AB， 的中点为 M （2，2），则△ABF 的面积等于 2 ．【考点】K8：抛物线的性质．【专题】5D ：圆锥曲线的定义、性质与方程． 【分析】设 A （x 1，y 1），B （x 2，y 2），则=4x 2，两式相减可得：（y 1+y 2）（y 1﹣y 2）=4（x 1﹣x 2），利用中点坐标公式、斜率计算公式可得 k AB ，可得直线 AB 的方程为：y ﹣2=x ﹣2，化为 y=x ，与抛物线方程联立可得 A ，B 的坐标，利用弦长公式可得|AB |，再利用点到直线的距离公式可得点 F 到直线 AB 的距离 d ，利用三角形面积公式求得答案．【解答】解：∵F 是抛物线 C ：y 2=4x 的焦点，∴F （1，0）．设 A （x 1，y 1），B （x 2，y 2），则， =4x 2，两式相减可得：（y 1+y 2）（y 1﹣y 2）=4（x 1﹣x 2）， ∵线段 AB 的中点为 M （2，2），∴y 1+y 2=2×2=4，又=k AB ，4k AB =4，解得 k AB =1，∴直线 AB 的方程为：y ﹣2=x ﹣2，化为 y=x ，联立 ，解得，，∴|AB |==4．点 F 到直线 AB 的距离 d=，∴S △ABF ===2，故答案为：2．【点评】本题主要考查了直线与抛物线相交问题弦长问题、“点差法”、点到直线的距离公式、三角形的面积计算公式，考查了推理能力与计算能力，属于难题．16．（5 分）平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件①三组对面分别平行的四棱柱为平行六面体；充要条件②平行六面体的对角线交于一点，并且在交点处互相平分；．（写出你认为正确的两个充要条件）【考点】29：充分条件、必要条件、充要条件；L2：棱柱的结构特征．【专题】16：压轴题；21：阅读型．【分析】本题考查的知识点是充要条件的定义及棱柱的结构特征及类比推理，由平行六面体与平行四边形的定义相似，故我们可以类比平行四边形的性质，类比推断平行六面体的性质．【解答】解：类比平行四边形的性质：两组对边分别平行的四边形为平行四边形，则我们类比得到：三组对面分别平行的四棱柱为平行六面体．类比平行四边形的性质：两条对角线互相平分，则我们类比得到：平行六面体的对角线交于一点，并且在交点处互相平分；故答案为：三组对面分别平行的四棱柱为平行六面体；平行六面体的对角线交于一点，并且在交点处互相平分；【点评】类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．三、解答题（共6 小题，满分70 分）17．（10 分）在△ABC 中，cosA=﹣，cosB=．（I）求sinC 的值；（II）设BC=5，求△ABC 的面积．【考点】GG：同角三角函数间的基本关系；GP：两角和与差的三角函数．【专题】11：计算题．【分析】（Ⅰ）先利用同角三角函数的基本关系求得sinA 和sinB 的值，进而根据sinC=sin（A+B）利用正弦的两角和公式求得答案．（Ⅱ）先利用正弦定理求得AC，进而利用三角形面积公式求得三角形的面积．【解答】解：（Ⅰ）∵在△ABC 中，A+B+C=180°，sinC=sin（180﹣（A+B））=sin（A+B）由，得，由，得．所以．（Ⅱ）由正弦定理得．所以△ABC 的面积S=BC•AC•sinC=×5××=．【点评】本题主要考查了同角三角函数的基本关系的应用和正弦的两角和公式的应用．考查了学生对三角函数基础知识的理解和灵活运用．18．（12 分）等差数列{a n}中，a4=10 且a3，a6，a10 成等比数列，求数列{a n}前20 项的和S20．【考点】85：等差数列的前n 项和．【专题】54：等差数列与等比数列．【分析】先设数列{a n}的公差为d，根据a3，a6，a10 成等比数列可知a3a10=a62，把d 和a4 代入求得d 的值．再根据a4 求得a1，最后把d 和a1 代入S20 即可得到答案．【解答】解：设数列{a n}的公差为d，则a3=a4﹣d=10﹣d，a6=a4+2d=10+2d，a10=a4+6d=10+6d．由a3，a6，a10 成等比数列得a3a10=a62，即（10﹣d）（10+6d）=（10+2d）2，整理得10d2﹣10d=0，解得d=0 或d=1．当d=0 时，S20=20a4=200．当d=1 时，a1=a4﹣3d=10﹣3×1=7，于是=20×7+190=330．【点评】本题主要考查了等差数列和等比数列的性质．属基础题．19．（12 分）甲、乙两人进行射击比赛，在一轮比赛中，甲、乙各射击一发子弹．根据以往资料知，甲击中8 环，9 环，10 环的概率分别为0.6，0.3，0.1，乙击中8 环，9 环，10 环的概率分别为0.4，0.4，0.2．设甲、乙的射击相互独立．（I）求在一轮比赛中甲击中的环数多于乙击中环数的概率；（II）求在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数的概率．【考点】C8：相互独立事件和相互独立事件的概率乘法公式．【专题】11：计算题．【分析】（Ⅰ）甲、乙的射击相互独立，在一轮比赛中甲击中的环数多于乙击中环数包括三种情况，用事件分别表示为A=A1•B1+A2•B1+A2•B2，且这三种情况是互斥的，根据互斥事件和相互独立事件的概率公式得到结果．（Ⅱ）由题意知在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数表示三轮中恰有两轮或三轮甲击中环数多于乙击中的环数，这两种情况是互斥的，根据互斥事件和相互独立事件的概率公式得到结果．【解答】解：记A1，A2 分别表示甲击中9 环，10 环，B1，B2 分别表示乙击中8环，9 环，A 表示在一轮比赛中甲击中的环数多于乙击中的环数，B 表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数，C1，C2 分别表示三轮中恰有两轮，三轮甲击中环数多于乙击中的环数．（I）甲、乙的射击相互独立在一轮比赛中甲击中的环数多于乙击中环数包括三种情况，用事件分别表示为A=A1•B1+A2•B1+A2•B2，且这三种情况是互斥的，根据互斥事件和相互独立事件的概率公式得到∴P（A）=P（A1•B1+A2•B1+A2•B2）=P（A1•B1）+P（A2•B1）+P（A2•B2）=P（A1）•P（B1）+P（A2）•P（B1）+P（A2）•P（B2）=0.3×0.4+0.1×0.4+0.1×0.4=0.2．（II）由题意知在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数表示三轮中恰有两轮或三轮甲击中环数多于乙击中的环数，这两种情况是互斥的，即B=C1+C2，∵P（C1）=C32[P（A）]2[1﹣P（A）]=3×0.22×（1﹣0.2）=0.096，P（C2）=[P（A）]3=0.23=0.008，∴P（B）=P（C1+C2）=P（C1）+P（C2）=0.096+0.008=0.104．【点评】考查运用概率知识解决实际问题的能力，包括应用互斥事件和相互独立事件的概率，相互独立事件是指两事件发生的概率互不影响，这是可以作为一个解答题的题目，是一个典型的概率题．20．（12 分）如图，正四棱柱ABCD﹣A1B1C1D1 中，AA1=2AB=4，点E 在CC1 上且C1E=3EC．（I）证明：A1C⊥平面BED；（II）求二面角A1﹣DE﹣B 的大小．【考点】LW：直线与平面垂直；MJ：二面角的平面角及求法．【专题】14：证明题；15：综合题；35：转化思想．【分析】法一：（Ⅰ）要证A1C⊥平面BED，只需证明A1C 与平面BED 内两条相交直线BD，EF 都垂直；（Ⅱ）作GH⊥DE，垂足为H，连接A1H，说明∠A1HG 是二面角A1﹣DE﹣B 的平面角，然后解三角形，求二面角A1﹣DE﹣B 的大小．法二：建立空间直角坐标系，（Ⅰ）求出，证明A1C⊥平面DBE．（Ⅱ）求出 平面 DA 1E 和平面 DEB 的法向量，求二者的数量积可求二面角 A 1﹣ DE ﹣B 的大小． 【解答】解：解法一：依题设知 AB=2，CE=1．（I ） 连接 AC 交 BD 于点 F ，则BD ⊥AC ．由三垂线定理知，BD ⊥A 1C ．（3 分）在平面 A 1CA 内，连接 EF 交 A 1C 于点 G ， 由于，故 Rt △A 1AC ∽Rt △FCE ，∠AA 1C=∠CFE ，∠CFE 与∠FCA 1 互余．于是 A 1C ⊥EF ．A 1C 与平面 BED 内两条相交直线 BD ，EF 都垂直，所以 A 1C ⊥平面 BED ．（6 分）（II ） 作 GH ⊥DE ，垂足为 H ，连接 A 1H ．由三垂线定理知 A 1H ⊥DE ，故∠A 1HG 是二面角 A 1﹣DE ﹣B 的平面角．（8 分），． ，又， ．．所以二面角 A 1﹣DE ﹣B 的大小为．（（12 分））解法二：以 D 为坐标原点，射线 DA 为 x 轴的正半轴，建立如图所示直角坐标系 D ﹣xyz ．依题设，B （2，2，0），C （0，2，0），E （0，2，1），A 1（2，0，4）．，．（3 分）（Ⅰ）因为，，故 A 1C ⊥BD ，A 1C ⊥DE ． 又 DB ∩DE=D ，所以 A 1C ⊥平面 DBE ．（6 分）（Ⅱ）设向量=（x ，y ，z ）是平面 DA 1E 的法向量，则，．，．故2y+z=0，2x+4z=0．令y=1，则z=﹣2，x=4，=（4，1，﹣2）．（9 分）等于二面角A1 ﹣DE﹣B 的平面角，所以二面角A1﹣DE﹣B 的大小为．（12分）【点评】本题考查直线与平面垂直的判定，二面角的求法，考查空间想象能力，逻辑思维能力，是中档题．21．（12 分）设a∈R，函数f（x）=ax3﹣3x2．（I）若x=2 是函数y=f（x）的极值点，求a 的值；（II）若函数g（x）=f（x）+f′（x），x∈[0，2]，在x=0 处取得最大值，求a 的取值范围．【考点】6C：函数在某点取得极值的条件；6D：利用导数研究函数的极值；6E：利用导数研究函数的最值．【专题】16：压轴题．【分析】（Ⅰ）导函数在x=2 处为零求a，是必要不充分条件故要注意检验（Ⅱ）利用最大值g（0）大于等于g（2）求出a 的范围也是必要不充分条件注意检验【解答】解：（Ⅰ）f'（x）=3ax2﹣6x=3x（ax﹣2）．因为x=2 是函数y=f（x）的极值点，所以f'（2）=0，即6（2a﹣2）=0，因此a=1．经验证，当a=1 时，x=2 是函数y=f（x）的极值点．（Ⅱ）由题设，g（x）=ax3﹣3x2+3ax2﹣6x=ax2（x+3）﹣3x（x+2）．当g（x）在区间[0，2]上的最大值为g（0）时，g（0）≥g（2），即0≥20a﹣24．故得．反之，当时，对任意x ∈ [0 ，2] ，==≤0，而g（0）=0，故g（x）在区间[0，2]上的最大值为g（0）．综上，a 的取值范围为．【点评】当函数连续且可导，极值点处的导数等于零是此点为极值点的必要不充分条件，所以解题时一定注意检验．22．（12 分）设椭圆中心在坐标原点，A（2，0），B（0，1）是它的两个顶点，直线y=kx（k＞0）与AB 相交于点D，与椭圆相交于E、F 两点．（I）若，求k 的值；（II）求四边形AEBF 面积的最大值．【考点】96：平行向量（共线）；KH：直线与圆锥曲线的综合．【专题】11：计算题；16：压轴题．【分析】（1）依题可得椭圆的方程，设直线AB，EF 的方程分别为x+2y=2，y=kx，D（x0，kx0），E（x1，kx1），F（x2，kx2），且x1，x2 满足方程（1+4k2）x2=4，进而求得x2 的表达式，进而根据求得x0 的表达式，由D 在AB 上知x0+2kx0=2，进而求得x0 的另一个表达式，两个表达式相等求得k．（Ⅱ）由题设可知|BO|和|AO|的值，设y1=kx1，y2=kx2，进而可表示出四边形AEBF 的面积进而根据基本不等式的性质求得最大值．【解答】解：（Ⅰ）依题设得椭圆的方程为，直线AB，EF 的方程分别为x+2y=2，y=kx（k＞0）．如图，设D（x0，kx0），E（x1，kx1），F（x2，kx2），其中x1＜x2，且x1，x2 满足方程（1+4k2）x2=4，故．①由知x0﹣x1=6（x2﹣x0），得；由D 在AB 上知x0+2kx0=2，得．所以，化简得24k2﹣25k+6=0，解得或．（Ⅱ）由题设，|BO|=1，|AO|=2．由（Ⅰ）知，E（x1，kx1），F（x2，kx2），不妨设y1=kx1，y2=kx2，由①得x2＞0，根据E 与F 关于原点对称可知y2=﹣y1＞0，故四边形AEBF 的面积为S=S△OBE +S△OBF+S△OAE+S△OAF=•（﹣y1）==x2+2y2= = = ，当x2=2y2时，上式取等号．所以S 的最大值为．【点评】本题主要考查了直线与圆锥曲线的综合问题．直线与圆锥曲线的综合问题是支撑圆锥曲线知识体系的重点内容，问题的解决具有入口宽、方法灵活多样等，而不同的解题途径其运算量繁简差别很大．。

2008年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分、第Ⅰ卷1至2页、第Ⅱ卷3至10页、 考试结束后，将本试卷和答题卡一并交回、第Ⅰ卷注意事项：1、答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上、2、每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑、如需改动，用橡皮擦干净后，再选涂其它答案标号、不能答在试题卷上、3、本卷共12小题，每小题5分，共60分、在每小题给出的四个选项中，只有一项是符合题目要求的、 参考公式：如果事件A B ，互斥，那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ，相互独立，那么 其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么 34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率 其中R 表示球的半径()(1)(012)k k n kk n P k C p p k n -=-=，，，，一、选择题1、若sin 0α<且tan 0α>是，则α是（ ）A 、第一象限角B 、 第二象限角C 、 第三象限角D 、 第四象限角2、设集合{|32}M m m =∈-<<Z ，{|13}N n n MN =∈-=Z 则，≤≤（ ）A 、{}01，B 、{}101-，，C 、{}012，，D 、{}1012-，，，3、原点到直线052=-+y x 的距离为（ ）A 、1B 、3C 、2D 、54、函数1()f x x x=-的图像关于（ ）A 、y 轴对称B 、 直线x y -=对称C 、 坐标原点对称D 、 直线x y =对称5、若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ ）A 、a <b <cB 、c <a <bC 、 b <a <cD 、 b <c <a6、设变量x y ，满足约束条件：222y x x y x ⎧⎪+⎨⎪-⎩，，．≥≤≥，则y x z 3-=的最小值为（ ）A 、2-B 、4-C 、6-D 、8-7、设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （ ）A 、1B 、12C 、12-D 、1-8、正四棱锥的侧棱长为32，侧棱与底面所成的角为︒60，则该棱锥的体积为（ ）A 、3B 、6C 、9D 、189、44)1()1(x x +-的展开式中x 的系数是（ ）A 、4-B 、3-C 、3D 、410、函数x x x f cos sin )(-=的最大值为（ ）A 、1B 、2 C 、3D 、211、设ABC △是等腰三角形，120ABC ∠=，则以A B ，为焦点且过点C 的双曲线的离心率为（ ）A 、221+ B 、231+ C 、 21+ D 、31+12、已知球的半径为2，相互垂直的两个平面分别截球面得两个圆、若两圆的公共弦长为2，则两圆的圆心距等于（ ）A 、1B 、2C 、3D 、22008年普通高等学校招生全国统一考试文科数学(必修+选修I)第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分、把答案填在题中横线上、13、设向量(12)(23)==，，，a b ，若向量λ+a b 与向量(47)=--，c 共线，则=λ 、 14、从10名男同学，6名女同学中选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的不同选法共有 种（用数字作答）15、已知F 是抛物线24C y x =：的焦点，A B ，是C 上的两个点，线段AB 的中点为(22)M ，，则ABF △的面积等于 、16、平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件① ； 充要条件② 、 （写出你认为正确的两个充要条件）三、解答题：本大题共6小题，共70分、解答应写出文字说明，证明过程或演算步骤、 17、（本小题满分10分） 在ABC △中，5cos 13A =-，3cos 5B =、 （Ⅰ）求sinC 的值；（Ⅱ）设5BC =，求ABC △的面积、 18、（本小题满分12分）等差数列{}n a 中，410a =且3610a a a ，，成等比数列，求数列{}n a 前20项的和20S 、19、（本小题满分12分）甲、乙两人进行射击比赛，在一轮比赛中，甲、乙各射击一发子弹、根据以往资料知，甲击中8环，9环，10环的概率分别为0.6，0.3，0.1，乙击中8环，9环，10环的概率分别为0.4，0.4，0.2、设甲、乙的射击相互独立、（Ⅰ）求在一轮比赛中甲击中的环数多于乙击中环数的概率；（Ⅱ）求在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数的概率、 20、（本小题满分12分）如图，正四棱柱1111ABCD A BC D -中，124AA AB ==，点E 在1CC 上且EC E C 31=、 （Ⅰ）证明：1AC ⊥平面BED ； （Ⅱ）求二面角1A DE B --的大小、 21、（本小题满分12分）设a ∈R ，函数233)(x ax x f -=、（Ⅰ）若2=x 是函数)(x f y =的极值点，求a 的值；（Ⅱ）若函数()()()[02]g x f x f x x '=+∈，，，在0=x 处取得最大值，求a 的取值范围、 22、（本小题满分12分）设椭圆中心在坐标原点，(20)(01)A B ，，，是它的两个顶点，直线)0(>=k kx y 与AB 相交于点D ，与椭圆相交于E 、F 两点、 （Ⅰ）若6ED DF =，求k 的值； （Ⅱ）求四边形AEBF 面积的最大值、AB CD EA 1B 1C 1D 12008年普通高等学校招生全国统一考试 文科数学试题（必修+选修Ⅰ）参考答案和评分参考评分说明：1、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要 考查内容比照评分参考制订相应的评分细则、2、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和 难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分、3、解答右端所注分数，表示考生正确做到这一步应得的累加分数、4、只给整数分数、选择题不给中间分、一、选择题1、C2、B3、D4、C5、C6、D7、A8、B9、A 10、B 11、B 12、C 二、填空题13、2 14、420 15、216、两组相对侧面分别平行；一组相对侧面平行且全等；对角线交于一点；底面是平行四边形、注：上面给出了四个充要条件、如果考生写出其他正确答案，同样给分、 三、解答题 17、解：（Ⅰ）由5cos 13A =-，得12sin 13A =， 由3cos 5B =，得4sin 5B =、 ··········································································· 2分所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=、 ····································· 5分（Ⅱ）由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯===、 ··········································· 8分 所以ABC △的面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=、 ····················· 10分18、解：设数列{}n a 的公差为d ，则3410a a d d =-=-， 642102a a d d =+=+，104由3610a a a ，，成等比数列得23106a a a =，即2(10)(106)(102)d d d -+=+， 整理得210100d d -=，解得0d =或1d =、······················································································· 7分 当0d =时，20420200S a ==、 ······································································ 9分 当1d =时，14310317a a d =-=-⨯=， 于是2012019202S a d ⨯=+207190330=⨯+=、 ············································· 12分 19、解：记12A A ，分别表示甲击中9环，10环，12B B ，分别表示乙击中8环，9环，A 表示在一轮比赛中甲击中的环数多于乙击中的环数，B 表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数，12C C ，分别表示三轮中恰有两轮，三轮甲击中环数多于乙击中的环数、（Ⅰ）112122A A B A B A B =∙+∙+∙，····························································· 2分 112122()()P A P A B A B A B =++ 112122()()()P A B P A B P A B =++112122()()()()()()P A P B P A P B P A P B =++0.30.40.10.40.10.40.2=⨯+⨯+⨯=、 ····························································· 6分（Ⅱ）12B C C =+， ······················································································ 8分22213()[()][1()]30.2(10.2)0.096P C C P A P A =-=⨯⨯-=，332()[()]0.20.008P C P A ===，1212()()()()0.0960.0080.104P B P C C P C P C =+=+=+=、 ··························· 12分 20、解法一：依题设，2AB =，1CE =、（Ⅰ）连结AC 交BD 于点F ，则BD AC ⊥、1在平面1ACA 内，连结EF 交1AC 于点G ，由于1AA ACFC CE== 故1Rt Rt A AC FCE △∽△，1AAC CFE ∠=∠， CFE ∠与1FCA ∠互余、于是1AC EF ⊥、 1AC 与平面BED 内两条相交直线BD EF ，都垂直， 所以1AC ⊥平面BED 、 ·················································································· 6分 （Ⅱ）作GH DE ⊥，垂足为H ，连结1A H 、由三垂线定理知1A H DE ⊥，故1A HG ∠是二面角1A DE B --的平面角、························································ 8分EF =CE CF CG EF ⨯==EG ==、 13EG EF =，13EF FD GH DE ⨯=⨯=又1AC ==113AG AC CG =-=、11tan A GA HG HG∠== 所以二面角1A DE B --的大小为 ················································· 12分 解法二：以D 为坐标原点，射线DA 为x 轴的正半轴， 建立如图所示直角坐标系D xyz -、依题设，1(220)(020)(021)(204)B C E A ，，，，，，，，，，，、AB CDEA 1B 1C 1D 1 FH G(021)(220)DE DB ==，，，，，，11(224)(204)AC DA =--=，，，，，、 ······························ 3分 （Ⅰ）因为10AC DB =，10AC DE =， 故1AC BD ⊥，1AC DE ⊥、 又DBDE D =，所以1AC ⊥平面DBE 、 ·················································································· 6分 （Ⅱ）设向量()x y z =，，n 是平面1DA E 的法向量，则DE ⊥n ，1DA ⊥n 、故20y z +=，240x z +=、令1y =，则2z =-，4x =，(412)=-，，n 、 ····················································· 9分1AC <>，n 等于二面角1A DE B --的平面角， 11114cos 42AC AC AC <>==，nn n 所以二面角1A DE B --的大小为、 ················································· 12分 21、解：（Ⅰ）2()363(2)f x ax x x ax '=-=-、因为2x =是函数()y f x =的极值点，所以(2)0f '=，即6(22)0a -=，因此1a =、 经验证，当1a =时，2x =是函数()y f x =的极值点、 ········································· 4分 （Ⅱ）由题设，3222()336(3)3(2)g x ax x ax x ax x x x =-+-=+-+、当()g x 在区间[02]，上的最大值为(0)g 时， (0)(2)g g ≥，即02024a -≥、故得65a ≤、 ································································································ 9分 反之，当65a ≤时，对任意[02]x ∈，，26()(3)3(2)5g x x x x x +-+≤23(210)5xx x =+- 3(25)(2)5xx x =+- 0≤，而(0)0g =，故()g x 在区间[02]，上的最大值为(0)g 、综上，a 的取值范围为65⎛⎤-∞ ⎥⎝⎦，、 ··································································· 12分22、（Ⅰ）解：依题设得椭圆的方程为2214x y +=， 直线AB EF ，的方程分别为22x y +=，(0)y kx k =>、 ····································· 2分 如图，设001122()()()D x kx E x kx F x kx ，，，，，，其中12x x <， 且12x x ，满足方程22(14)4k x +=，故21x x =-=、①由6ED DF =知01206()x x x x -=-，得021215(6)77x x x x =+==； 由D 在AB 上知0022x kx +=，得0212x k=+、 所以212k =+， 化简得2242560k k -+=，解得23k =或38k =、 ······················································································ 6分 （Ⅱ）解法一：根据点到直线的距离公式和①式知，点E F ，到AB 的距离分别为1h ==2h ==······················································· 9分又AB ==AEBF 的面积为121()2S AB h h =+ 1525(14k =+==≤当21k =，即当12k =时，上式取等号、所以S 的最大值为 ························ 12分 解法二：由题设，1BO =，2AO =、设11y kx =，22y kx =，由①得20x >，210y y =->， 故四边形AEBF 的面积为BEF AEF S S S =+△△222x y =+ ···································································································· 9分===当222x y =时，上式取等号、所以S 的最大值为 ······································· 12分。

2008年高考全国数学（Ⅱ）卷试题、试卷分析及2009年高考走势试卷研究组：王春清康纯芳牛福利李海洋曲茹张传锋徐颖执笔人：徐颖一、2008年高考试题总体评价2008年是全国高考均使用新课程卷的第四个年头，自主命题的省份也延续了2006年的16个省份。

除了考试中心命制的、供部分省市使用的全国（Ⅰ、Ⅱ、Ⅲ）卷外，自主命题的省份均进行了独立命题。

在这些试卷中，除了江西、山西和广东省数学文理合用一张卷外，其余包括三套全国卷在内的数学试卷均是文理分开的。

这样，2008年全国高考数学，共命制试题35套。

说明了伴随着课程改革的不断深入，高考改革也正在全国范围内迅速推进，预示着高考制度改革的春天即将到来。

今年是我省使用新课程卷的第五个年头，选用的仍是全国统一试卷（Ⅱ）。

从整体上来看，试题背景公平，面貌平和，易于入手。

基本保持了新课程卷8年来的一些基本做法。

特别是与近几年的试卷相比，出现了“五稳”的态势和“二新”的格局。

“五稳”。

即：稳在内容要求上，稳在试卷结构上，稳在题型、题量上，稳在各部分内容以及新增内容的分值比例上，稳在难易程度上，稳在应用题的落脚点上。

基础题、中档题、难题的分数比例分配上，08年基本达到（而不是理论上达到）：5：3：2的比例。

“二新”，即：新在文科与理科试卷进一步分化，相同题、姊妹题的分数减少，不同题的分数增加，预示着命题者对向不同方向发展的学生，在数学素养方面的不同要求；新在难题（或曰能力题）的考查角度上，即在考查学生演绎推理的同时，注重了合情推理的考查，即观察、判断、猜想、类比推理等推理能力的考查（如理、文的12题），并从考查学生思维品质的严谨性和周密性入手（不苛求其深刻性），着力于对学生综合能力（包括阅读理解能力（如理19题））——运算能力、分析和解决问题能力，以及创新精神和实践能力的考查。

从而使08年的全国数学（Ⅱ）卷基本保持了近几年的命题风格，即：“难易适度、结构平稳、梯度合理、知情并重、新旧交融”，突显了“能力立意”的主导思想，体现了新课程的新理念——人人学有用的数学、人人学必要的数学、不同的人在数学上获得不同的发展。

2008年高考全国数学（Ⅱ）卷试题、试卷分析及2009年高考走势试卷研究组：王春清康纯芳牛福利李海洋曲茹张传锋徐颖执笔人：徐颖一、2008年高考试题总体评价2008年是全国高考均使用新课程卷的第四个年头，自主命题的省份也延续了2006年的16个省份。

除了考试中心命制的、供部分省市使用的全国（Ⅰ、Ⅱ、Ⅲ）卷外，自主命题的省份均进行了独立命题。

在这些试卷中，除了江西、山西和广东省数学文理合用一张卷外，其余包括三套全国卷在内的数学试卷均是文理分开的。

这样，2008年全国高考数学，共命制试题35套。

说明了伴随着课程改革的不断深入，高考改革也正在全国范围内迅速推进，预示着高考制度改革的春天即将到来。

今年是我省使用新课程卷的第五个年头，选用的仍是全国统一试卷（Ⅱ）。

从整体上来看，试题背景公平，面貌平和，易于入手。

基本保持了新课程卷8年来的一些基本做法。

特别是与近几年的试卷相比，出现了“五稳”的态势和“二新”的格局。

“五稳”。

即：稳在内容要求上，稳在试卷结构上，稳在题型、题量上，稳在各部分内容以及新增内容的分值比例上，稳在难易程度上，稳在应用题的落脚点上。

基础题、中档题、难题的分数比例分配上，08年基本达到（而不是理论上达到）：5：3：2的比例。

“二新”，即：新在文科与理科试卷进一步分化，相同题、姊妹题的分数减少，不同题的分数增加，预示着命题者对向不同方向发展的学生，在数学素养方面的不同要求；新在难题（或曰能力题）的考查角度上，即在考查学生演绎推理的同时，注重了合情推理的考查，即观察、判断、猜想、类比推理等推理能力的考查（如理、文的12题），并从考查学生思维品质的严谨性和周密性入手（不苛求其深刻性），着力于对学生综合能力（包括阅读理解能力（如理19题））——运算能力、分析和解决问题能力，以及创新精神和实践能力的考查。

从而使08年的全国数学（Ⅱ）卷基本保持了近几年的命题风格，即：“难易适度、结构平稳、梯度合理、知情并重、新旧交融”，突显了“能力立意”的主导思想，体现了新课程的新理念——人人学有用的数学、人人学必要的数学、不同的人在数学上获得不同的发展。

2008年普通高等学校招生全国统一考试语文试卷（全国Ⅱ）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至4页，第Ⅱ卷5至9页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项1．答题前，考生在答题卡上务必用直径0.5毫米黑色签字笔将自己的姓名、准考证号填写清楚,并帖好条形码。

请认真核准条形码的准考证号、姓名和科目。

2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

在试题卷上作答无效。

3．本试卷共10小题，每小题3分，共30分。

在每小题给出的四个悬想中，只有一项符合要求。

一、（12分，每小题3分）1．下列词语中加点的字，读音全都正确的一组是A.迸．发（bèng）不掘不挠．（ráo）怆．然（chuàng）婀．娜多姿（ē）。

B.跻．身（jī）岿．然不动（kuī）女娲．（wō）谆．谆教导（zhūn）C.恫吓．（xià）病入膏肓．（huāng）浣．衣（huàn）神情尴尬．（gà）D.粗糙．（cāo）徘徊．观望（huái）糟粕．（pò）锲．而不舍（qiè）2．下列各句中，加点的成语使用不恰当的一项是A.新来的王老师为人不苟言笑，同事们一般都产跟他嘻嘻哈俣，只有谭校长有时还会跟他开点无伤大雅．．．．的玩笑。

B.近几年，来中国演出的外国艺术团络绎不绝．．．．，不过人们对俄罗斯芭蕾舞团的《天鹅湖》还是情有独钟，屡看不厌。

C.美国博物馆的收费可谓各尽所能．．．．：有的一部分收费，有的分时段收费，还有的是否交费、交费多少由参观者自行决定。

D.中、日、韩三国参加这次围棋比赛的运动员，水平都在伯仲之间．．．．，谁能胜出，就要看谁具有更好的竞技状态和心理素质了。

3．下列各句中，没有语病的一句是A.金乌炭雕工艺精湛，采用纯天然颜料着色，具有高雅、时尚、个性的艺术享受，还能吸附有毒有害气体，是一种环保艺术品。