社2024pdfcontents •绪论•线性规划•整数规划•动态规划•图与网络分析•存储论•排队论目录01绪论运筹学的起源与发展起源运筹学起源于20世纪30年代，最初是应用在军事领域，旨在研究和解决军事策略和资源分配问题。
发展随着计算机技术的飞速发展和数学理论的不断完善，运筹学逐渐从军事领域扩展到经济、管理、工程等各个领域，并形成了完整的学科体系。
运筹学的定义与特点定义运筹学是一门应用数学、计算机科学和经济学等多学科交叉的综合性学科，旨在通过数学建模、优化算法和计算机技术等方法，对复杂系统进行优化决策。
特点运筹学具有多学科交叉性、广泛应用性、理论性与实践性相结合等特点。
它注重定量分析和实证研究，强调优化决策和系统效率。
经济领域运筹学在经济管理、市场预测、投资决策等方面有广泛应用，如生产计划、库存管理、物流运输等。
社会领域运筹学在社会服务、城市规划、医疗卫生等方面也有应用，如交通规划、教育资源分配等。
工程领域运筹学在工程设计、施工计划、质量控制等方面提供优化方法和技术支持。
军事领域运筹学在军事战略制定、作战计划优化、后勤资源分配等方面发挥重要作用。
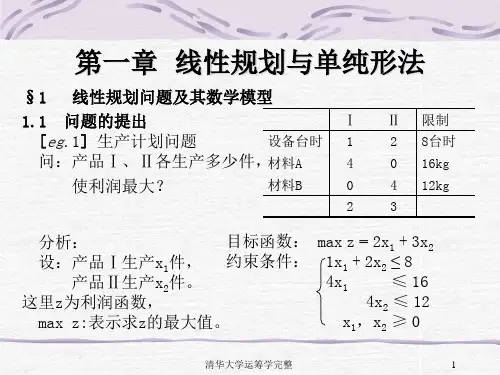
运筹学的应用领域02线性规划线性规划问题的数学模型目标函数线性规划问题中需要优化的目标，通常表示为决策变量的线性函数。
约束条件限制决策变量取值的条件，通常表示为决策变量的线性不等式或等式。
决策变量线性规划问题中需要确定的未知量，通常表示为向量形式。
可行域满足所有约束条件的决策变量取值范围所构成的区域。
最优解使目标函数达到最优值的决策变量取值点。
目标函数等值线目标函数取不同值时对应的决策变量取值点所连成的曲线。
线性规划问题的图解法满足所有约束条件且基变量取非负值的决策变量取值点。
初始基可行解通过不断更换基变量和非基变量，使目标函数值不断改善的过程。
迭代过程判断当前基可行解是否为最优解的方法，通常通过计算检验数来实现。
最优性检验单纯形法如何合理安排生产计划以最小化成本或最大化利润。
