《信号与系统》郑君里第二章习题解答
- 格式:pdf
- 大小:105.21 KB
- 文档页数:7
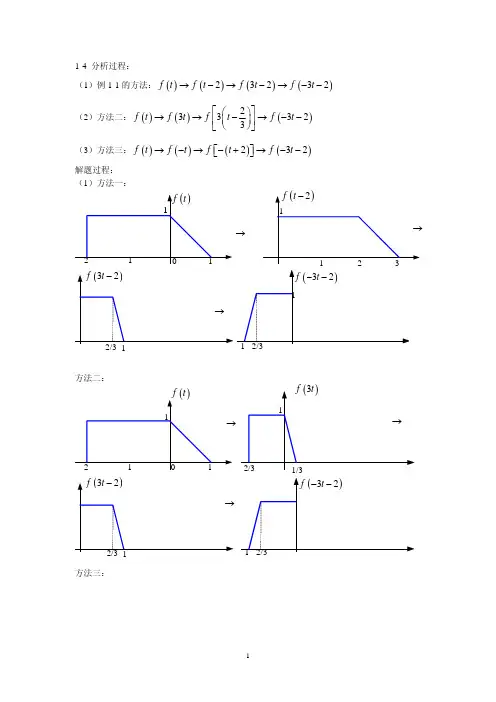



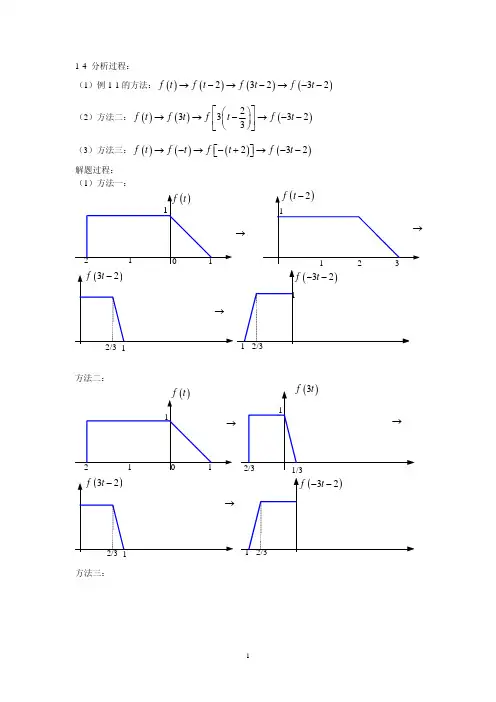
郑君⾥的信号与系统的第⼆三章习题参考解B 第⼆章习题参考解2-2,试画出下列信号波形,从中可得出何结论。
其中t -∞<<∞t1=0:1/200:8;>> y1=sin(0.5*pi*t1);>> subplot(4,1,1),plot(t1,y1),title('sin(0.5*pi*t1)u(t1)的⼀段'),grid >> t2=1:1/200:8;>> y2=sin(0.5*pi*t2);>> subplot(4,1,2),plot(t2,y2),title('sin(0.5*pi*t)u(t2-1)的⼀段'),grid >> y3=sin(0.5*pi*(t1-1));>> subplot(4,1,3),plot(t1,y3),title('sin(0.5*pi*(t1-1))u(t)的⼀段'),grid >> y4=sin(0.5*pi*(t2-1));>> subplot(4,1,4),plot(t2,y4),title('sin(0.5*pi*(t2-1))u(t2-1)的⼀段'),grid 解:⽤MA TLAB 作图如上。
从中可看出:1,周期信号Sin 与单位阶跃信号相乘,得到⾮周期信号。
2,1sin()()2t u t π与1sin[(1)](1)2t u t π--是向右移动1。
⽽1sin[(1)]()2t u t π-与1sin()()2t u t π只是sin 的起始相位不同。
2-12,⼰知序列(0.8)2302,3(){k k k k x k -≤≤<>=1,⽤阶跃信号的截取特性表⽰X (k );解:()(0.8)[(2)4()]kx k u k u k =+--2,⽤加权单位脉冲序列表⽰X(k)。
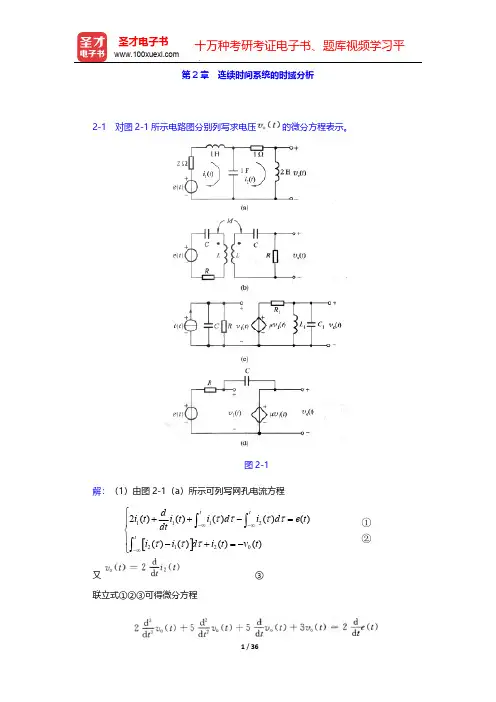


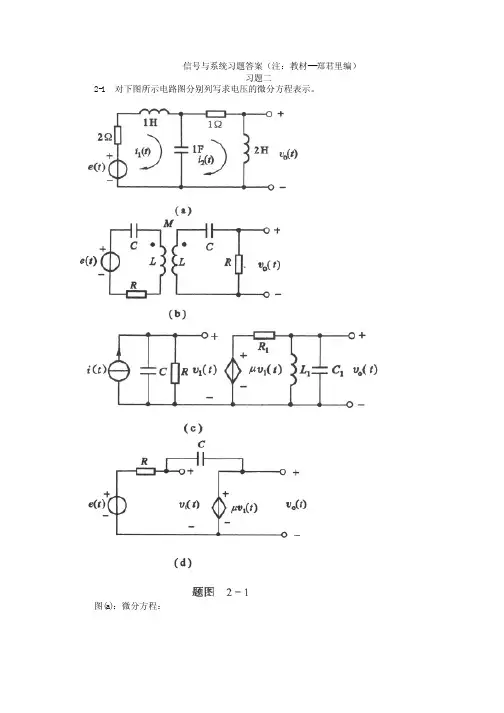
第二章 连续时间系统的时域分析第一讲 微分方程的建立与求解一、微分方程的建立与求解对电路系统建立微分方程,其各支路的电流、电压将为两种约束所支配: 1.来自连接方式的约束:KVL 和KIL ,与元件的性质无关。
2.来自元件伏安关系的约束:与元件的连接方式无关。
例2-1 如图2-1所示电路,激励信号为,求输出信号。
电路起始电压为零。
图2-1解以输出电压为响应变量,列回路电压方程:所以齐次解为:。
因激励信号为,若,则,将其代入微分方程:所以,从而求得完全解:由于电路起始电压为零并且输入不是冲激信号,所以电容两端电压不会发生跳变,,从而若,则特解为,将其代入微分方程,并利用起始条件求出系数,从而得到:二、起始条件的跳变——从到1.系统的状态(起始与初始状态)(1)系统的状态:系统在某一时刻的状态是一组必须知道的最少量的数据,利用这组数据和系统的模型以及该时刻接入的激励信号,就能够完全确定系统任何时刻的响应。
由于激励信号的接入,系统响应及其各阶导数可能在t=0时刻发生跳变,所以以表示激励接入之前的瞬时,而以表示激励接入以后的瞬时。
(2)起始状态:,它决定了零输入响应,在激励接入之前的瞬时t=系统的状态,它总结了计算未来响应所需要的过去的全部信息。
(3)初始状态:跳变量,它决定了零状态响应,在激励接入之后的瞬时系统的状态。
(4)初始条件:它决定了完全响应。
这三个量的关系是:。
2.初始条件的确定(换路定律)电容电压和电感电流在换路(电路接通、断开、接线突变、电路参数突变、电源突变)瞬间前后不能发生突变,即是连续的。
时不变:时变:例电路如图2-2所示,t=0以前开关位于"1"已进入稳态,t=0时刻,开关自"1"转至"2"。
(1)试从物理概念判断、和、。
(2)写出t>0时间内描述系统的微分方程式,求的完全响应。
图2-2解(1)换路前电路处于稳态电感相当于短路,电感电流,电容相当于开路= 0,= = 0。

第二章 连续时间系统的时域分析经典法:双零法卷积积分法:求零状态响应求解系统响应→定初始条件满足换路定则起始点有跳变:求跳变量零输入响应:用经典法求解零状态响应:卷积积分法求解()()()()⎩⎨⎧==-+-+0000L L c c i i u u例题•例题1:连续时间系统求解(经典法,双零法) •例题2:求冲激响应(n >m ) •例题3:求冲激响应(n <m ) •例题4:求系统的零状态响应 •例题5:卷积 •例题6:系统互联例2-1分析在求解系统的完全响应时,要用到有关的三个量是: :起始状态,它决定零输入响应;()()()()()()()()()强迫响应。
状态响应,自由响应,并指出零输入响应,零,求系统的全响应,已知 系统的微分方程为描述某t u t e r r t e t t e t r t t r t t r =='=+=++--,00,206d d 22d d 3d d LTI 22()-0)(k r ⎩⎨⎧状态变量描述法输出描述法—输入建立系统的数学模型:跳变量,它决定零状态响应; :初始条件,它决定完全响应;这三个量之间的关系是 分别利用 求零状态响应和完全响应,需先确定微分方程的特解。
解:方法一:利用 先来求完全响应,再求零输入响应,零状态响应等于完全响应减去零输入响应。
方法二:用方法一求零输入响应后,利用跳变量 来求零状态响应,零状态响应加上零输入响应等于完全响应。
本题也可以用卷积积分求系统的零状态响应。
方法一1. 完全响应 该完全响应是方程 (1)方程(1)的特征方程为 特征根为 方程(1)的齐次解为因为方程(1)在t >0时,可写为 (2)显然,方程(1)的特解可设为常数D ,把D 代入方程(2)求得 所以方程(1)的解为下面由冲激函数匹配法定初始条件 由冲激函数匹配法定初始条件 据方程(1)可设代入方程(1),得匹配方程两端的 ,及其各阶导数项,得 所以,所以系统的完全响应为()+0)(k zsr ()+0)(k r ()()()+-+=-000)()()(k zs k k r r r ()()++00)()(k k zs r r ,()()代入原方程有将t u t e =()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()++'0,0r r ()()++''0,0zs zs r r ()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()的解且满足00,20='=--r r 0232=++αα2121-=-=αα,()t t e A e A t r 221--+=()()()()t u t r t t r tt r 62d d 3d d 22=++3=D ()3221++=--tt e A e A t r ()()()t u b t a t t r ∆+=δ22d d ()()t u a t t r ∆=d d ()无跳变t r ()()()()()()t u t t r t u a t u b t a 6223+=+∆+∆+δδ2=a ()t δ()()22000=+=+'='-+a r r ()()200==-+r r ()()代入把20,20=='++r r ()3221++=--t t e A e A t r 1,021-==A A 得()0 32≥+-=-t e t r t ()t r zi 再求零输入响应2.求零输入响应 (3)(3)式的特征根为 方程(3)的齐次解即系统的零输入响应为所以,系统的零输入响应为 下面求零状态响应零状态响应=完全响应—零输入响应,即 因为特解为3,所以强迫响应是3,自由响应是方法二(5)以上分析可用下面的数学过程描述 代入(5)式 根据在t =0时刻,微分方程两端的 及其各阶导数应该平衡相等,得 于是t >0时,方程为 齐次解为 ,特解为3,于是有所以,系统的零状态响应为方法一求出系统的零输入响应为()是方程响应因为激励为零,零输入t r zi ()()()02d 3d d 22=++t r dt t r t t r ()()()()()()的解.,且满足 0000 2000='='='===--+--+r r r r r r zi zi zi zi 2121-=-=αα,()t t zi e B e B t r 221--+=()()式解得,代入,由)4(0020='=++zi zi r r 2,421-==B B ()0 242≥-=--t e e t r t t zi ()0 342≥++-=--t e e t r t t zs t t e e 24--+-()是方程零状态响应t r zs ()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()的解且满足000='=--zs zs r r ()项由于上式等号右边有t δ()应含有冲激函数,,故t r zs "()将发生跳变,即从而t r zs '()()-+'≠'00zs zs r r ()处是连续的.在而0=t t r zs ()()()()()t u a t r t t u b t a t r tzs zs∆=+∆+=+d d ,d d 22δ()()()()()()t u t t r t u a t u b t a 6223+=+∆+∆+δδ()t δ2=a ()()()()002000===+'='-+-+zs zs zs zs r r a r r ()()()()t u t r t t r t t r 62d d 3d d 22=++ 221t t e D e D --+()3221++=--t t zi e D e D t r ()()得由初始条件0,200=='++zs zs r r 1,421=-=D D ()0) ( 342≥++-=--t e e t r t t zs ()0 242≥-=--t e e t r t t zi完全响应=零状态响应+零输入响应,即例2-2冲激响应是系统对单位冲激信号激励时的零状态响应。
《信号与系统》习题与答案第一章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。
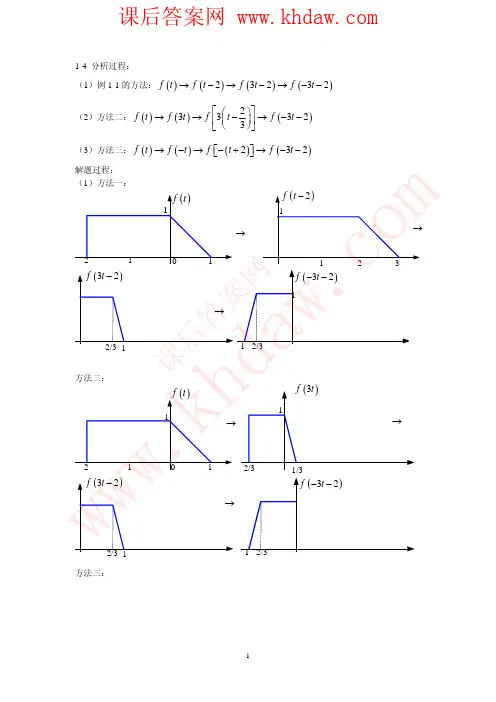
1.2 已知信号[])2()1()1()(--++=t u t u t t f ,画出)32(+-t f 的波形。
1.3已知信号[])2()1()1()(--++=t u t u t t f ,试求它的直流分量。
答案:01.4 已知信号[])2()1()1()(--++=t u t u t t f ,试求它的奇分量和偶分量。
答案:偶分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号⎩⎨⎧=20)(tt f≥<t t 是否是奇异信号。
答案:二阶以上导数不连续,是奇异信号。
1.6 已知)(t f 是有界信号,且当∞→t 时0)(→t f ,试问)(t f 是否是能量有限信号。
答案:不一定。
1.7 对一连续三角信号进行抽样,每周期抽样8点,求抽样所得离散三角序列的离散角频率。
答案:4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三角信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
比较和说明两波形的差别,为什么? (1) t t f 4cos)(1π= (2)t t f 415cos)(2π= 答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1) t C t B t A t f 9cos 7cos 4sin )(++= 答案:是周期函数,周期π2=T 。
(2) n j d n f 8e)(π-= 答案:是周期信号,周期16=N1.10 求下列表达式的函数值(1) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f - (2) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f(3) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00>t 时为1;当00<t 时为0 (4) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00<t 时为1;当00>t 时为0 (5) ⎰∞∞--++dt t t e t )2()(δ; 答案:2e 2- (6) ⎰∞∞--+dt t t t )6()sin (πδ; 答案:2/16/+π(7)[]⎰∞∞----dt t t t e t j )()2(0δδω; 答案:0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果(1) tt e t r d )(d )(=; 答案:线性,时不变,因果 (2) )()()(t u t e t r =; 答案:线性,时变,因果(3) [])()(sin )(t u t e t r =; 答案:非线性,时变,因果 (4) )1()(t e t r -=; 答案:线性,时变,非因果 (5) )2()(t e t r =; 答案:线性,时变,非因果 (6) )()(2t e r r =; 答案:非线性,时不变,因果 1.12 试证明:)()0(')(')0()(')(t f t f t t f δδδ-=。
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
《信号与系统》习题与答案第一章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。
1.2 已知信号[])2()1()1()(--++=t u t u t t f ,画出)32(+-t f 的波形。
1.3已知信号[])2()1()1()(--++=t u t u t t f ,试求它的直流分量。
答案:01.4 已知信号[])2()1()1()(--++=t u t u t t f ,试求它的奇分量和偶分量。
答案:偶分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号⎩⎨⎧=20)(t t f 0≥<t t 是否是奇异信号。
答案:二阶以上导数不连续,是奇异信号。
1.6 已知)(t f 是有界信号,且当∞→t 时0)(→t f ,试问)(t f 是否是能量有限信号。
答案:不一定。
1.7 对一连续三角信号进行抽样,每周期抽样8点,求抽样所得离散三角序列的离散角频率。
答案:4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三角信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
比较和说明两波形的差别,为什么? (1) t t f 4cos)(1π= (2)t t f 415cos)(2π= 答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1) t C t B t A t f 9cos 7cos 4sin )(++= 答案:是周期函数,周期π2=T 。
(2) n j d n f 8e)(π-= 答案:是周期信号,周期16=N1.10 求下列表达式的函数值(1) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f - (2) ⎰∞∞--dt t t t f )()(0δ; 答案:)(0t f(3) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00>t 时为1;当00<t 时为0 (4) ⎰∞∞---dt t t u t t )2()(00δ; 答案:当00<t 时为1;当00>t 时为0 (5)⎰∞∞--++dt t t e t )2()(δ; 答案:2e 2-(6) ⎰∞∞--+dt t t t )6()sin (πδ; 答案:2/16/+π(7)[]⎰∞∞----dt t t t e t j )()2(0δδω; 答案:0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果(1) tt e t r d )(d )(=; 答案:线性,时不变,因果 (2) )()()(t u t e t r =; 答案:线性,时变,因果 (3) [])()(sin )(t u t e t r =; 答案:非线性,时变,因果 (4) )1()(t e t r -=; 答案:线性,时变,非因果 (5) )2()(t e t r =; 答案:线性,时变,非因果 (6) )()(2t e r r =; 答案:非线性,时不变,因果1.12 试证明:)()0(')(')0()(')(t f t f t t f δδδ-=。