天大物理化学第五版 第五章 化学平衡

目录第一章 气体的pVT 关系 ...................................................................... 1 第二章 热力学第一定律 ..................................................................... 9 第三章 热力学第二定律 .................................................................... 29 第四章 多组分系统热力学 ................................................................ 56 第五章 化学平衡 ................................................................................ 66 第六章 相平衡 (82)第一章 气体的pVT 关系1-1物质的体膨胀系数V α与等温压缩系数T κ的定义如下：1 1TT p V p V V T V V ⎪⎪⎭⎫⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂=κα 试导出理想气体的V α、T κ与压力、温度的关系？解：对于理想气体，pV=nRT111 )/(11-=⋅=⋅=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T TVV p nR V T p nRT V T V V p p V α 1211 )/(11-=⋅=⋅=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=p p V V p nRT V p p nRT V p V V TT T κ 1-2 气柜内有121.6kPa 、27℃的氯乙烯（C 2H 3Cl ）气体300m 3，若以每小时90kg 的流量输往使用车间，试问贮存的气体能用多少小时？解：设氯乙烯为理想气体，气柜内氯乙烯的物质的量为mol RT pV n 623.1461815.300314.8300106.1213=⨯⨯⨯==每小时90kg 的流量折合p 摩尔数为 133153.144145.621090109032-⋅=⨯=⨯=h mol M v Cl H Cn/v=（14618.623÷1441.153）=10.144小时1-3 0℃、101.325kPa 的条件常称为气体的标准状况。

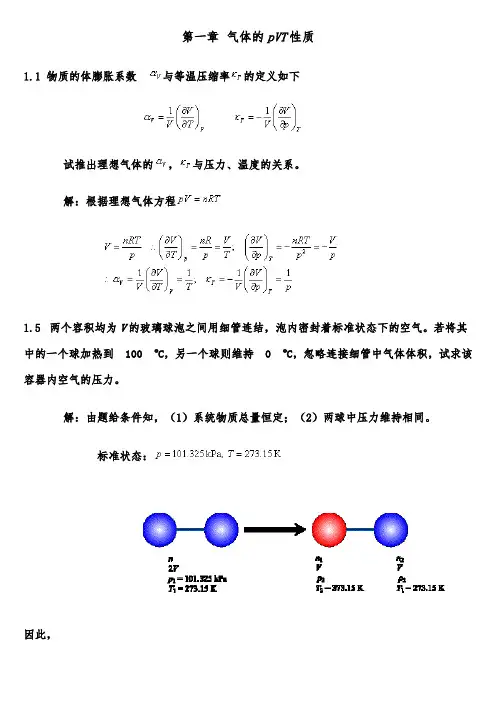
第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的，与压力、温度的关系。

解：根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结，泡内密封着标准状态下的空气。

若将其中的一个球加热到100 ︒C，另一个球则维持0 ︒C，忽略连接细管中气体体积，试求该容器内空气的压力。

解：由题给条件知，（1）系统物质总量恒定；（2）两球中压力维持相同。

标准状态：因此，1.9 如图所示，一带隔板的容器内，两侧分别有同温同压的氢气与氮气，二者均可视为理想气体。

（1）保持容器内温度恒定时抽去隔板，且隔板本身的体积可忽略不计，试求两种气体混合后的压力。

（2）隔板抽取前后，H2及N2的摩尔体积是否相同？（3）隔板抽取后，混合气体中H2及N2的分压立之比以及它们的分体积各为若干？解：（1）等温混合后即在上述条件下混合，系统的压力认为。

（2）混合气体中某组分的摩尔体积怎样定义？（3）根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气，为进行实验时确保安全，采用同样温度的纯氮进行置换，步骤如下：向釜内通氮气直到4倍于空气的压力，尔后将釜内混合气体排出直至恢复常压。

重复三次。

求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。

解：分析：每次通氮气后至排气恢复至常压p，混合气体的摩尔分数不变。

设第一次充氮气前，系统中氧的摩尔分数为，充氮气后，系统中氧的摩尔分数为，则，。

重复上面的过程，第n次充氮气后，系统的摩尔分数为，因此。

1.13 今有0 C，40.530 kPa的N2气体，分别用理想气体状态方程及van der Waals方程计算其摩尔体积。

实验值为。

解：用理想气体状态方程计算用van der Waals计算，查表得知，对于N2气（附录七），用MatLab fzero函数求得该方程的解为也可以用直接迭代法，，取初值，迭代十次结果1.16 25 ︒C时饱和了水蒸气的湿乙炔气体（即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压）总压力为138.7 kPa，于恒定总压下冷却到10 ︒C，使部分水蒸气凝结为水。

第五章第五章化学平衡问题：1.在一定条件下，反应物能否按预期的反应变成产物？2.如何提高产物的量？3.在一定条件下，反应的极限产率为多少？4.极限产率怎样随条件变化？研究的内容：1.化学平衡是研究化学反应方向和限度的关键。

2.本章讨论应用热力学第二定律的平衡条件来处理化学平衡问题。

3.将用热力学方法推导化学平衡时温度、压力、组成间的关系，并计算平衡组成。

4.如何改变条件可得到更大的产率？将通过热力学计算讨论温度、压力、组成等条件如何影响平衡。

1、摩尔反应Gibbs 函数与化学反应亲和势§5.1化学反应的等温方程在T，p一定的条件下，对0 = ΣνB B的化学反应进行时，∆r G m与系统组成的关系。

吉布斯函数判据:∆≤pT,G< 自发= 平衡（恒T，p，及W ’= 0）定义：()5.1.1a ∆mr G A −=表示在恒T ，p ，及W ’= 0时，化学反应进行的推动力。

≥T,p A > 正向自发= 平衡< 逆向自发（恒T ，p ，及W ’= 0）化学反应亲和势（简称亲和势）由吉布斯判据：2.∆r G m 与反应进度的关系，平衡条件某一化学反应0 = Σv B B ，在恒T ，p 下：()5.1.2a d d BBB ∑=n µG ξνn d d B B =Q ()5.1.2b d d BB B ∑=ξµνG ()∑==⎟⎠⎞⎜⎝⎛∂∂B B B m r 5.1.3∆µνG ξG pT,()5.1.1b ∆m r pT,ξG G A ⎟⎠⎞⎜⎝⎛∂∂−=−=定义{G }N 2(g) +3H 2(g) = 2NH 3(g)恒T ，p 下，均相化学反应0 = Σv B B ，如：0⎛⎞∂<⎜⎟∂ξ⎝⎠T,pG 0⎛⎞∂>⎜⎟∂ξ⎝⎠T,pG 0⎛⎞∂=⎜⎟∂ξ⎝⎠T,pG {G }{ξ}反应系统G～ξ关系示意图A>0A<0A=03.化学反应的等温方程恒T 、恒p ，且W´= 0时，对于理想气体间的化学反应∑=BB B 0ν其任一组分的化学势是：⎟⎟⎠⎞⎜⎜⎝⎛+=p p RT µµB B B ln ()5.1.4a ln ∆B B B B B B m r ⎟⎟⎠⎞⎜⎜⎝⎛+=∑∑p p νRT µνG ∑=BB B mr ∆µνG 代入BBB B B B ln ln ννp p RT RT p p ⎛⎞⎛⎞=∑∏⎜⎟⎜⎟⎝⎠⎝⎠()r m B BB∆ 5.1.5G νµ=∑压力商J p它仅是温度的函数。

物理化学上册第五版天津大学出版社第五章化学平衡习题答案5-1 在某恒定的温度和压力下，取mol n 10=的A （g ）进行如下反应：)()(g B g A =若θθμμA B =，试证明，当反应进度mol 5.0=ξ时，系统的吉布斯函数G 值为最小，这时A ，B 间达到化学平衡。

证明：)()(g B g A =设开始时，A 的物质的量为0,A n ，B 的物质的量为0,B n ，而反应过程中A 、B 的物质的量分别为A n 与B n ，此时系统的吉布斯函数为ξμμd dG B B )(-=设反应从A 开始时mol n A 10=，当反应进度mol 5.0=ξ时，mol 5.0n n B A ==，mol nBB1=∑，p 5.0p p B A ==及θθμμA B =代入上式得)}ln ln (){( )}ln ()ln ({)(=-+-=+-+=-=ξμμξνμνμξμμθθθθd p RT p RT d p RT p RT d dG A B A B A A B B B B或 0,=⎪⎪⎭⎫⎝⎛∂∂-=pT G A ξ 这就证明了若θθμμA B =，反应进度mol 5.0=ξ时，系统的吉布斯函数G 值为最小，此时0,=⎪⎪⎭⎫⎝⎛∂∂-=pT G A ξ，A ，B 间达到化学平衡。

5-2 已知四氧化二氮的分解反应)(42g O N )(22g NO在298.15K 时，θmrG ∆175.4-⋅=mol kJ 。

试判断在此温度及下列条件下，反应进行的自发方向：（1）)1000( ),100(242kPa NO kPa O N ；（2）)100( ),1000(242kPa NO kPa O N ；（3）)200( ),300(242kPa NO kPa O N 。

解：1454.0K ,9283.1)15.298314.8/(1075.4/ln 3=-=⨯⨯-=∆-=θθθRT G K m r（1）100100/100)100/1000(/)/(22422===θθp p p p J O N NO p ， ,θK J p >反应向左； （2）1.0100/1000)100/100(/)/(22422===θθp p p p J O N NO p ， ,θK J p <反应向右； （3）333.1100/300)100/200(/)/(22422===θθp p p p J O N NO p， ,θK J p >反应向左。

第五章 化学平衡5－1．在某恒定的温度和压力下，取n 0﹦1mol 的A (g )进行如下化学反应：A (g )B (g )若0B μ﹦0A μ，试证明，当反应进度﹦0.5mol 时，系统的吉布斯函数G 值为最小，这时A ，B 间达到化学平衡。

解： 设反应进度为变量A (g )B (g )t ﹦0 n A , 0﹦n 0 0 0﹦0t ﹦t 平 n A n B﹦BBn ν n B ﹦B，n A ﹦n 0－n B ﹦n 0－B，n ﹦n A ＋n B ﹦n 0气体的组成为：y A ﹦A n n ﹦00B n n νξ-﹦01n ξ-，y B ﹦B nn﹦0n ξ各气体的分压为：p A ﹦py A ﹦0(1)p n ξ-，p B ﹦py B ﹦p n ξ各气体的化学势与的关系为：0000ln ln (1)A A AA p p RT RT p p n ξμμμ=+=+- 0000lnln B B B B p p RT RT p p n ξμμμ=+=+⋅ 由 G ＝n AA＋n BB＝(n A 0A μ＋n B 0B μ)＋00ln(1)A p n RT p n ξ-＋00ln B p n RT p n ξ⋅ ＝[n 0－A μ＋0B μ]＋n 00lnpRT p ＋00()ln(1)n RT n ξξ--＋0ln RT n ξξ 因为 0B μ﹦0A μ，则G ＝n 0(0A μ＋0lnpRT p )＋00()ln(1)n RT n ξξ--＋0ln RT n ξξ ,0()ln T p G RT n ξξξ∂=∂- 20,20()()T p n RT Gn ξξξ∂=-∂-＜0 令 ,()0T p Gξ∂=∂011n ξξξξ==-- ﹦0.5 此时系统的G 值最小。

5－2．已知四氧化二氮的分解反应 N 2O 4 (g) 2 NO 2(g )在298.15 K 时，0r m G ∆＝4.75kJ ·mol －1。

第五章 化学平衡5－1．在某恒定的温度和压力下，取n 0﹦1mol 的A (g )进行如下化学反应：A (g )垐?噲? B (g ) 若0B μ﹦0A μ，试证明，当反应进度﹦时，系统的吉布斯函数G 值为最小，这时A ，B 间达到化学平衡。

解： 设反应进度为变量A (g )垐?噲?B (g )t ﹦0 n A , 0﹦n 0 0 0﹦0 t ﹦t 平 n A n B ﹦BBn ν n B ﹦B ，n A ﹦n 0－n B ﹦n 0－B ，n ﹦n A ＋n B ﹦n 0气体的组成为：y A ﹦A n n ﹦00B n n νξ-﹦01n ξ-，y B ﹦B nn﹦0n ξ各气体的分压为：p A ﹦py A ﹦0(1)p n ξ-，p B ﹦py B ﹦p n ξ各气体的化学势与的关系为：0000ln ln (1)A A AA p p RT RT p p n ξμμμ=+=+- 0000lnln B B B B p p RT RT p p n ξμμμ=+=+⋅ 由 G ＝n AA ＋n BB ＝(n A 0A μ＋n B 0B μ)＋00ln(1)A p n RT p n ξ-＋00ln B p n RT p n ξ⋅ ＝[n 0－0A μ＋0B μ]＋n 00lnpRT p ＋00()ln(1)n RT n ξξ--＋0ln RT n ξξ 因为 0B μ﹦0A μ，则G ＝n 0(0A μ＋0lnpRT p)＋00()ln(1)n RT n ξξ--＋0ln RT n ξξ ,0()ln T p G RT n ξξξ∂=∂- 20,20()()T p n RT Gn ξξξ∂=-∂-＜0 令 ,()0T p Gξ∂=∂011n ξξξξ==-- ﹦ 此时系统的G 值最小。

5－2．已知四氧化二氮的分解反应 N 2O 4 (g )垐?噲? 2 NO 2(g )在 K 时，0r m G ∆＝·mol －1。

目　录第1章　气体的pVT关系1.1　复习笔记1.2　课后习题详解1.3　名校考研真题详解第2章　热力学第一定律2.1　复习笔记2.2　课后习题详解2.3　名校考研真题详解第3章　热力学第二定律3.1　复习笔记3.2　课后习题详解3.3　名校考研真题详解第4章　多组分系统热力学4.1　复习笔记4.2　课后习题详解4.3　名校考研真题详解第5章　化学平衡5.1　复习笔记5.2　课后习题详解5.3　名校考研真题详解第6章　相平衡6.1　复习笔记6.2　课后习题详解6.3　名校考研真题详解第7章　电化学7.1　复习笔记7.2　课后习题详解7.3　名校考研真题详解第8章　量子力学基础8.1　复习笔记8.2　课后习题详解8.3　名校考研真题详解第9章　统计热力学初步9.1　复习笔记9.2　课后习题详解9.3　名校考研真题详解第10章　界面现象10.1　复习笔记10.2　课后习题详解10.3　名校考研真题详解第11章　化学动力学11.1　复习笔记11.2　课后习题详解11.3　名校考研真题详解第12章　胶体化学12.1　复习笔记12.2　课后习题详解答：分散相粒子直径d介于1～1000nm范围内的高分散系统称为胶体系统。

胶体系统的主要特征：高分散性、多相性和热力学不稳定性。

答：在暗室中，将一束经过聚集的光线投射到胶体系统上，在与入射光垂直的方向上，可观察到一个发亮的光锥，称为丁泽尔效应。

丁泽尔效应的实质是胶体粒子对光的散射。

可见光的波长在400～760nm的范围内，而一般胶体粒子的尺寸为1～1000nm。

当可见光投射到胶体系统时，如胶体粒子的直径小于可见光波长，则发生光的散射现象，产生丁泽尔效应。

答：胶体粒子带电、溶剂化作用和布朗运动是溶胶稳定存在的三个重要原因。

（1）胶体粒子表面通过以下两种方式而带电：①固体表面从溶液中有选择性地吸附某种离子而带电；②固体表面上的某些分子、原子在溶液中发生解离，使固体表面带电。