第7章稳恒磁场分析
- 格式:doc
- 大小:421.50 KB
- 文档页数:10






第7章 稳恒磁场7-1 如图,一个处在真空中的弓形平面载流线圈acba ,acb 为半径cm 2=R 的圆弧,ab 为圆弧对应的弦,圆心角090aob ∠=,A 40=I ,试求圆心O 点的磁感应强度的大小和方向。
解 由例7-1 线段ba 的磁感应强度 o o 40140(cos45-cos135) =410T4π0.02cos45B μ-=⨯⨯︒方向垂直纸面向外。
由例7-2 圆弧acb 的磁感应强度4002π1402 3.1410T 2π2420.02I μB R μ-==⨯=⨯方向垂直纸面向内。
4120.8610TB B B -=-=⨯方向垂直纸面向外。
7-2 将载流长直导线弯成如图所示的形状,求圆心O 点处磁感应强度。
解 如图,将导线分成1(左侧导线)、2(半圆导线)、3(右侧导线)三部分,设各部分在O 点处产生的磁感应强度分别为1B 、2B 、3B 。
根据叠加原理可知,O 点处磁感应强度321B B B B++=。
01=B024I B Rμ=,方向垂直于纸面向里034πI B Rμ=,方向垂直于纸面向里O 点处磁感应强度大小为习题7-1图0O 23(1π)4πIB B B Rμ=+=+ ,方向垂直于纸面向里。
7-3 一圆形载流导线圆心处的磁感应强度为1B ,若保持导线中的电流强度不变,而将导线变成正方形,此时回路中心处的磁感应强度为2B ,试求21:B B解 设导线长度为l ,为圆环时, 2πl R = 001π2I I B R l μμ==为正方形时,边长为4l,由例7-100024(cos 45cos135)4π8IB lμ=⨯-=⨯212 :πB B =7-4 如图所示,一宽为a 的薄长金属板,均匀地分布电流I ,试求在薄板所在平面、距板的一边为a 的点P 处的磁感应强度。
解 取解用图示电流元,其宽度为d r ,距板下边缘距离为r ,其在P 点处激发的磁感应强度大小为00d d d 2π22π(2)II r B (a r)a r aμμ==--,方向垂直于纸面向外。


稳恒磁场小结稳恒磁场是指磁场的大小和方向都不随时间而变化的磁场。
在物理学中,磁场的产生是由电荷运动而引起的,因此稳恒磁场可以通过电流来产生。
在这篇文章中,我们将讨论稳恒磁场的性质、产生、应用及相关实验等内容。
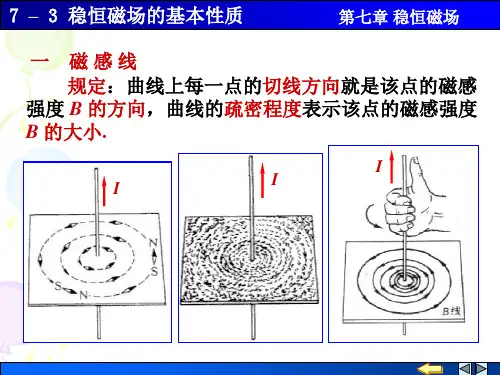
稳恒磁场可以被表示为磁感应强度B,B的方向与磁力线相同。
磁力线是从磁北极流向磁南极的。
磁北极与磁南极的定义与地球上的地理北极和地理南极不同。
在磁力线中,磁感应强度越强,磁力线越密集。
在稳恒磁场中,磁场与电流有一个简单的关系。
电流与磁场的方向关系可以由安培定则来确定。
安培定则的核心思想是:当一条电流元素通过一点时,该电流元素造成的磁场再该点的贡献方向与电流元素方向的右手定则相同。
该定则可以通过实验验证。
另外,稳恒磁场还有一个重要的特性:在稳恒磁场中,不会存在单独的磁极。
总有一个磁极与之相对应。
这一特性被称为“磁偶极子”的性质。
稳恒磁场可以通过电流来产生。
当电荷经过导线时,它会产生磁场。
当电流在圆环上流动时,会产生一个垂直于圆环平面的磁场。
在物理学实验中,通常使用初始磁场为零的可调电阻来产生电流。
通常使用Hall电效应来测量电阻中电流的强度。
在Hall电效应中,将电阻放在强磁场中,当电流通过电阻时,电阻中的电子会受到洛伦兹力的影响,使得电阻中的电子发生偏转,最终在一个方向上聚积起来。
这个方向与电流方向垂直,并形成Hall电压。
由于稳恒磁场的特性,它在许多领域中都有应用。
在现代物理学中,稳恒磁场用于粒子加速器中的磁铁,可以帮助加速器中的粒子定向行进。
磁共振成像是另一个使用稳恒磁场的重要技术。
在磁共振成像中,磁场中的氢原子核可以被用于诊断人体内部的病变。
磁场中的氢原子核的性质是由磁场强度的大小和方向所决定的,因此磁共振成像需要一个非常稳定的磁场。
在物理学中,稳恒磁场还可以用来研究磁性材料和磁性现象。
通过使用稳恒磁场,可以测量磁材料的磁场和演示磁现象。
此外,稳恒磁场还可以用来研究交变磁场的行为,在许多相对论简化模型中,也常使用稳恒磁场。
第七章 练习题1、在磁感强度为B的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n与B 的夹角为α ,则通过半球面S的磁通量(取弯面向外为正)为(A) πr 2B .. (B) 2 πr 2B . (C) -πr 2B sin α. (D) -πr 2B cos α.2、如图所示,电流I 由长直导线1经a 点流入由电阻均匀的导线构成的正方形线框,由b 点流出,经长直导线2返回电源(导线1、2的延长线均通过O 点).设载流导线1、2和正方形线框中的电流在框中心O 点产生的磁感强度分别用 1B 、2B、3B 表示,则O点的磁感强度大小 (A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0、B 3≠ 0,但0321=++B B B. (C) B ≠ 0,因为虽然021=+B B,但B 3≠ 0.(D) B ≠ 0,因为虽然B 3= 0,但021≠+B B.3、通有电流I 的无限长直导线有如图三种形状,则P ,Q ,O 各点磁感强度的大小B P ,B Q ,B O 间的关系为: (A) B P > B Q > B O . (B) B Q > B P > B O . (C) B Q > B O > B P . (D) B O > B Q > B P .4、磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R ,x 坐标轴垂直圆筒轴线,原点在中心轴线上.图(A)~(E)哪一条曲线表示B -x 的关系?[ ]5、如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分⎰⋅Ll B d 等于(A) I 0μ. (B)I 031μ. (C) 4/0I μ. (D) 3/20I μ.IBxOR (D )Bx O R(C )BxO R (E )电流筒6、如图,在一固定的载流大平板附近有一载流小线框能自由转动或平动.线框平面与大平板垂直.大平板的电流与线框中电流方向如图所示,则通电线框的运动情况对着从大平板看是: (A) 靠近大平板. (B) 顺时针转动.(C) 逆时针转动.(D) 离开大平板向外运动.7、在一根通有电流I 的长直导线旁,与之共面地放着一个长、宽各为a 和b 的矩形线框,线框的长边与载流长直导线平行,且二者相距为b ,如图所示.在此情形中,线框内的磁通量Φ =______________.8、如图所示,在真空中有一半圆形闭合线圈,半径为a ,流过稳恒电流I ,则圆心O 处的电流元l Id 所受的安培力F d 的大小为____,方向________.9、有一根质量为m ,长为l 的直导线,放在磁感强度为 B的均匀磁场中B的方向在水平面内,导线中电流方向如图所示,当导 线所受磁力与重力平衡时,导线中电流I =___________________.10、图示为三种不同的磁介质的B ~H 关系曲线,其中虚线表示的是B = μ0H 的关系.说明a 、b 、c 各代表哪一类磁介质的B ~H 关系曲线:a 代表____________________的B ~H 关系曲线.b 代表____________________的B ~H 关系曲线.c 代表____________________的B ~H 关系曲线.11、AA '和CC '为两个正交地放置的圆形线圈,其圆心相重合.AA '线圈半径为20.0 cm ,共10匝,通有电流10.0 A ;而CC '线圈的半径为10.0 cm ,共20匝,通有电流 5.0 A .求两线圈公共中心O 点的磁感强度的大小和方向.(μ0 =4π×10-7 N ·A -2)12、如图所示,一无限长载流平板宽度为a ,线电流密度(即沿x 方向单位长度上的电流)为δ ,求与平板共面且距平板一边为b 的任意点P 的磁感强度.I 1I 2IlI dIB13、螺绕环中心周长l = 10 cm ,环上均匀密绕线圈N = 200匝,线圈中通有电流I = 0.1 A .管内充满相对磁导率μr = 4200的磁介质.求管内磁场强度和磁感强度的大小.14、一根同轴线由半径为R 1的长导线和套在它外面的内半径为R 2、外半径为R 3的同轴导体圆筒组成.中间充满磁导率为μ的各向同性均匀非铁磁绝缘材料,如图.传导电流I 沿导线向上流去,由圆筒向下流回,在它们的截面上电流都是均匀分布的.求同轴线内外的磁感强度大小B 的分布.答案:一 选择题1、D2、A3、D4、B5、D6、B7、2ln 20πIaμ 8、a l I 4/d 20μ 垂直电流元背向半圆弧(即向左)9、)/(lB mg10、铁磁质、 顺磁质、 抗磁质 11、解:AA '线圈在O 点所产生的磁感强度002502μμ==AAA A r I NB (方向垂直AA '平面)CC '线圈在O 点所产生的磁感强度 005002μμ==CCC C r I N B (方向垂直CC '平面)O 点的合磁感强度 42/1221002.7)(-⨯=+=C AB B B T B 的方向在和AA '、CC '都垂直的平面内,和CC '平面的夹角︒==-4.63tg1AC B B θC A12、解:利用无限长载流直导线的公式求解.(1) 取离P 点为x 宽度为d x 的无限长载流细条,它的电流 x i d d δ=(2) 这载流长条在P 点产生的磁感应强度 xiB π=2d d 0μxxπ=2d 0δμ 方向垂直纸面向里.(3) 所有载流长条在P 点产生的磁感强度的方向都相同,所以载流平板在P点产生的磁感强度==⎰B B d ⎰+πba bxdx x20δμbb a x+π=ln20δμ 方向垂直纸面向里.13、解: ===l NI nI H /200 A/m===H H B r μμμ0 1.06 T14、解:由安培环路定理:∑⎰⋅=iI l Hd0< r <R 1区域: 212/2R Ir rH =π 212R Ir H π=, 2102R Ir B π=μR 1< r <R 2区域: I rH =π2rI H π=2, rIB π=2μR 2< r <R 3区域: )()(22223222R R R r I I rH ---=π )1(22223222R R R r rI H ---π=)1(2222322200RR R r rIH B ---π==μμr >R 3区域: H = 0,B = 0。
第6章恒定磁场习题6.1 毕奥—萨伐尔定律一.选择题( )1、宽为a ,厚度可以忽略不计的无限长扁平载流金属片,如图6.1.1所示,中心轴线上方一点P 的磁感应强度的方向是(A) 沿y 轴正向. (B )沿z 轴负向.(B) (C) 沿y 轴负向. (D) 沿x 轴正向.( )2、两无限长载流导线,如图6.1.2放置,则坐标原点的磁感应强度的大小和方向分别为:(A)2μ0 I / (2 π a ) ,在yz 面内,与y 成45︒角. (B)2μ0 I / (2 π a ) ,在yz 面内,与y 成135︒角. (C)2μ0 I / (2 π a ) ,在xy 面内,与x 成45︒角.(D)2μ0 I / (2 π a ) ,在zx 面内,与z 成45︒角. ( )3、一无限长载流导线,弯成如图6.1.3所示的形状,其中ABCD 段在x O y平面内,BCD 弧是半径为R 的半圆弧,DE 段平行于O z 轴,则圆心处的磁感应强度为(A) j μ0 I / (4 π R ) + k [μ0 I / (4 π R )-μ0 I / (4R )] .(B) j μ0 I / (4 π R ) -k [μ0 I / (4 π R ) + μ0 I / (4R )] . (C) j μ0 I / (4 π R ) + k [μ0 I / (4 π R )+μ0 I / (4R )] . (D) j μ0 I / (4 π R ) -k [μ0 I / (4 π R )-μ0 I / (4R )] .( )4、一电流元i d l 位于直角坐标系原点,电流沿Z 轴方向,空间点P ( x , y , z )的磁感应强度沿x 轴的分量是:(A) 0.(B) –(μ0 / 4π)i y d l / ( x 2 + y 2 +z 2 )3/2 . (C) –(μ0 / 4π)i x d l / ( x 2 + y 2 +z 2 )3/2 .(D) –(μ0 / 4π)i y d l / ( x 2 + y 2 +z 2 ) .( )5、电流I 由长直导线1 沿垂直bc 边方向经a 点流入一电阻均匀分布的正三角形线框,再由b 点沿垂直ac 边方向流出,经长直导线2 返回电源 (如图6.1.4),若载流直导线1、2和三角形框在框中心O 点产生的磁感应强度分别用B 1 、B 2和B 3 表示,则O 点的磁感应强度大小 (A) B = 0,因为B 1 = B 2 = B 3 = 0 .(B) B = 0,因为虽然B 1 ≠0,B 2 ≠0,但 B 1 +B 2 = 0 ,B 3 = 0. (C) B ≠ 0,因为虽然B 3 =0,但B 1 +B 2 ≠ 0. (D) B ≠ 0,因为虽然B 1 +B 2 = 0,但B 3 ≠0 . ( )6、如图6.1.5,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷.此正方形以角速度ω 绕AC 轴旋转时,在中心O 点产生的磁感强度大小为B 1;此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感强度的大小为B 2,则B 1与B 2间的关系为(A) B 1 = B 2. (B) B 1 = 2B 2. (C) B 1 =21B 2. (D) B 1 = B 2 /4. ( )7、边长为 l 的正方形线圈中通有电流I ,此线圈在A 点(见图6.1.6)产生的磁感强度B 为 (A)l Iπ420μ. (B) l Iπ220μ (C) lIπ02μ. (D) 以上均不对. ( )8、如图6.1.7所示,电流从a 点分两路通过对称的圆环形分路,汇合于b 点.若ca 、bd 都沿环的径向,· ·xyz -aaII O图6.1.2y -R · · xz R I IO A BC DE图6.1.3 12 O a bcI I图6.1.4图6.1.5AII 图6.1.6则在环形分路的环心处的磁感强度(A) 方向垂直环形分路所在平面且指向纸内. (B) 方向垂直环形分路所在平面且指向纸外. (C) 方向在环形分路所在平面,且指向b . (D) 方向在环形分路所在平面内,且指向a . (E) 为零.( )9、在一平面内,有两条垂直交叉但相互绝缘的导线,流过每条导线的电流i 的大小相等,其方向如图6.1.8所示.问哪些区域中有某些点的磁感强度B 可能为零? (A) 仅在象限Ⅰ. (B) 仅在象限Ⅱ. (C) 仅在象限Ⅰ,Ⅲ. (D) 仅在象限Ⅰ,Ⅳ.(E) 仅在象限Ⅱ,Ⅳ.二.填空题 1、氢原子中的电子,以速度v 在半径r 的圆周上作匀速圆周运动,它等效于一圆电流,其电流I 用v 、r 、e (电子电量)表示的关系式为I = ,此圆电流在中心产生的磁场为B= ,它的磁矩为p m = .2、真空中稳恒电流I 流过两个半径分别为R 1 、R 2的同心半圆形导线,两半圆导线间由沿直径的直导线连接,电流沿直导线流入 (1) 如果两个半圆面共面,如图6. 1.9 (1),圆心O 点磁感应强度B 0 的大小为 ,方向为 ; (2) 如果两个半圆面正交,如图6.1.9(2),则圆心O 点磁感应强度B 0 的大小为 ,B 0的方向与y 轴的夹角为 .3、求图6.1.10中各图P 点的磁感强度B 的大小和方向三.计算题1、 如图,将一导线由内向外密绕成内半径为R 1 ,外半径为R 2 的圆形平面线圈,共有N 匝,设电流为I ,求此园形平面载流线圈在中心O 处产生的磁感应强度的大小.II · O O · I I x yz R 1R 2R 2 R 1 (1)(2)图6.1.91 2a bOI I · ·cI db a图6.1.7图6.1.8I aI2P IP a a图6.1.102.、宽为b的无限长平面导体薄板,通过电流为I,电流沿板宽度方向均匀分布,求:(1)在薄板平面内,离板的一边距离为b的M点处的磁感应强度;(2)通过板的中线并与板面垂直的直线上的一点N处的磁感应强度,N点到板面的距离为x。
3、在半径R=1cm的无限长半圆柱形金属薄片中,有电流I=5A自下而上通过,如图所示,试求圆柱轴线上一的磁感应强度。
点P4、一个塑料圆盘,半径为R,电荷q均匀分布于表面,圆盘绕通过圆心垂直盘面的轴转动,角速度为ω。
求圆盘中心处的磁感应强度。
一.选择题()1、图6.2.1为磁场B中的一袋形曲面,曲面的边缘为一半径等于R的圆,此圆面的平面与磁感应强度B的方向成π/6角,则此袋形曲面的磁通量Φm(设袋形曲面的法线向外)为(A) πR 2B . (B)3πR 2B/2.(C) πR 2B /2 . (D) -πR 2B /2 .( )2、如图6.2.2所示,XY 平面内有两相距为L 的无限长直载流导线,电流的大小相等,方向相同且平行于X 轴,距坐标原点均为a ,Z 轴上有一点P 距两电流均为2a ,则P 点的磁感应强度B(A) 大小为3μ0I /(4πa ),方向沿Z 轴正向. (B) 大小为μ0I /(4πa ),方向沿Z 轴正向.(C) 大小为3μ0I /(4πa ),方向沿Y 轴正向. (D) 大小为3μ0I /(4πa ),方向沿Y 轴负向.( )3、磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R ,x 坐标轴垂直圆筒轴线,原点在中心轴线上.图6.2.3中(A)~(D)哪一条曲线表示B -x 的关系?( )4、若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布 (A) 不能用安培环路定理来计算. (B) 可以直接用安培环路定理求出. (C) 只能用毕奥-萨伐尔定律求出. (D) 可以用安培环路定理和磁感强度的叠加原理求出.( )5、如图6.2.4所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ和面上各点的磁感应强度B 将如何变化?(A )Φ增大,B 也增大;(B )Φ不变,B 也不变; (C )Φ增大,B 不变;(D )Φ不变,B 增大。
( )6、磁场的高斯定理⎰⎰=⋅0S d B ϖϖ说明了下面的哪些叙述是正确的?a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(A )ad ; (B )ac ; (C )cd ; (D )ab 。
( )8、如图6.2.5所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ和面上各点的磁感应强度B 将如何变化?(A )Φ增大,B 也增大;(B )Φ不变,B 也不变; (C )Φ增大,B 不变; (D )Φ不变,B 增大。
( )9、 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,如图6.2.6所示,则在圆心o 处的磁感应强度大小为多少? (A )0; (B )R I 2/0μ; (C )R I 2/20μ;(D )R I /0μ。
二.填空题1、其圆心重合,相互正交的,半径均为R 的两平面圆形线圈,匝数均为N ,电流均为I ,且接触点处相互绝缘,如图6.2.7所示,则圆心O 处磁感应强度的矢量式为 .·P O xy z -a a 2a 2a II 图6.2.2图6.2.3IS图6.2.4 IS图6.2.5 II o图6.2.62、 一带正电荷q 的粒子以速率v 从X 负方向飞过来向X 正方向飞去,当它经过坐标原点时,在X 轴上的x0处的磁感应强度矢量表达式为 ,在Y 轴上的y 0处的磁感应强度矢量表达式为. 3、如图 6.2.8所示,真空中有两圆形电流I 1 和 I 2 和三个环路L 1 L 2 L 3,则安培环路定律的表达式为l B d 1⋅⎰L = , l B d 2⋅⎰L = ,l B d 3⋅⎰L = .4、如图6.2.9所示,均匀磁场的磁感应强度为B =0.2T ,方向沿x 轴正方向,则通过abod 面的磁通量为_________,通过befo 面的磁通量为__________ ,通过aefd 面的磁通量为_______ 。
三.计算题1、二条长直载流导线与一长方形线圈共面,如图所示.已知a = b = c = 10cm ,l = 10m ,I 1 = I 2 = 100A ,求通过线圈的磁通量.2、同轴电缆由导体圆柱和一同轴导体薄圆筒构成,电流I 从一导体流入,从另一导体流出,且导体上电流均匀分布在其横截面积上,设圆柱半径为R 1,圆筒半径为R 2,如图所示.求: (1)磁感应强度B 的分布;(2)在圆柱和圆筒之间单位长度截面的磁通量为多少?图6.2.72图6.2.830习题6.3 磁感应强度 洛伦兹力一.选择题( )1、一个动量为p 电子,沿图6.3.1所示的方向入射并能穿过一个宽度为D 、磁感应强度为B (方向垂直纸面向外)的均匀磁场区域,则该电子出射方向和入射方向间的夹角为(A) α=arccos(eBD/p ). (B) α=arcsin(eBD/p ). (C) α=arcsin[BD /(ep )]. (D) α=arccos[BD/(e p )]. ( )2、一均匀磁场,其磁感应强度方向垂直于纸面,两带电粒子在该磁场中的运动轨迹如图6.3.2所示,则(A) 两粒子的电荷必然同号.(B) 粒子的电荷可以同号也可以异号.(C) 两粒子的动量大小必然不同.(D) 两粒子的运动周期必然不同.( )3、一运动电荷q ,质量为m ,以初速v 0进入均匀磁场,若 v 0与磁场方向的夹角为α,则 (A) 其动能改变,动量不变. (B) 其动能和动量都改变.(C) 其动能不变,动量改变. (D) 其动能、动量都不变.( )4、两个电子a 和b 同时由电子枪射出,垂直进入均匀磁场,速率分别为v 和2v ,经磁场偏转后,它们是(A)a 、b 同时回到出发点. (B) a 、b 都不会回到出发点. (C) a 先回到出发点. (D) b 先回到出发点.( )5、 如图6.3.3所示两个比荷(q/m )相同的带导号电荷的粒子,以不同的初速度v 1和 v 2(v 1>v 2)射入匀强磁场B 中,设T 1 、T 2分别为两粒子作圆周运动的周期,则以下结论正确的是:(A) T 1 = T 2,q 1和q 2都向顺时针方向旋转; (B) T 1 = T 2,q 1和q 2都向逆时针方向旋转(C) T 1 ≠ T 2,q 1向顺时针方向旋转,q 2向逆时针方向旋转; (D) T 1 = T 2,q 1向顺时针方向旋转,q 2向逆时针方向旋转; 二.填空题1、一电子在B =2×10-3T 的磁场中沿半径为R =2×10-2m 、螺距为h =5.0×10-2m 的螺旋运动,如图 6.3.4所示,则磁场的方向 , 电子速度大小为 .2、 磁场中某点处的磁感应强度B =0.40i -0.20j (T), 一电子以速度v =0.50×106i +1.0×106j(m/s)通过该点,则作用于该电子上的磁场力F = .3、在匀强磁场中,电子以速率v =8.0×105m/s 作半径R =0.5cm 的圆周运动.则磁场的磁感应强度的大小B = .三.计算题1.如图所示,一平面塑料圆盘,半径为R ,表面均匀带电,电荷面密度为σ,假定盘绕其轴线OO '以角速度ω转动,磁场B 垂直于轴线OO ',求圆盘所受磁力矩的大小。