AE 最短路径分析

network analyst 最短路径算法Network Analyst是ArcGIS的一个扩展工具，可以用于求解最短路径。

在ArcGIS中使用Network Analyst求解最短路径的步骤如下：1. 加载模块：点击菜单栏中【自定义】-【拓展模块】，在弹出菜单中勾选Network Analyst模块即可加载该模块。

2. 启动【Network Analyst】工具条：若工具栏内显示为【交通网络】，则证明系统已经自动识别了该网络模型，并把它作为默认的网络分析对象。

3. 启动路径分析：点击【Network Analyst】工具条上的【network analyst】按钮，在下拉菜单中选择【新建路径】，之后会显示【network analyst】面板（如未显示，可点击工具栏上红圈中显示的按钮）。

此时，图层列表内新添了【路径】图层。

4. 设置停靠点：在【network analyst】面板中选择【停靠点】，然后点击工具条上的【创建网络位置工具】，在图面上的路径分析起点和终点各点击一次，这两个点会被同步添加到【network analyst】面板的【停靠点】项目下。

5. 设置障碍：例如某条路正在维修不能通行。

在【Network analyst】面板中选择【点障碍Point barriers】，然后点击【Network Analyst】工具条上的，再点击图面上的障碍路段，该路段会标记一个障碍标志。

6. 设置分析属性：点击【Network analyst】面板右上角的【属性】按钮，显示【图层属性】对话框。

切换到【分析设置】选项卡，将【阻抗】设为【路程（米）】或【车行时间（分钟）】，意味着根据车行时间来计算最短路径，点【确定】完成设置。

7. 路径求解：点击【network analyst】工具条上的【求解】工具，即可得到计算结果。

8. 查看详细数据：右键【network analyst】面板中【路径】项下的路线【图形选择1-图形选择2】，在弹出菜单中选择【属性】，显示【属性】对话框。

最短路径知识点总结最短路径问题的核心思想是通过某种策略找到两个节点之间的最短路径。

在图的表示方法上，最短路径问题通常使用邻接矩阵或邻接表来表示图的结构。

多种最短路径算法也可以适用于不同的图模型，包括有向图、无向图、带权图等。

常用的最短路径算法包括Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。

下面将对这些算法进行介绍和总结。

Dijkstra算法是一种解决单源最短路径问题的贪心算法。

它的核心思想是通过不断地确定距离源点距离最短的顶点来逐步扩展已知的最短路径集合。

具体步骤包括：初始化距离数组，设置起点距离为0，其他顶点距离为无穷大；选择未访问顶点中距离最短的顶点，并将其标记为已访问；更新与该顶点相邻的顶点的距离；不断重复以上步骤直到所有顶点都被访问。

Dijkstra算法的时间复杂度为O(V^2)，其中V表示顶点的个数。

当图比较大时，可以使用堆优化的Dijkstra算法，将时间复杂度优化到O((V+E)logV)。

Bellman-Ford算法是一种解决单源最短路径问题的动态规划算法。

它的核心思想是通过对所有边进行松弛操作，不断更新顶点的最短路径估计值。

具体步骤包括：初始化距离数组，设置起点距离为0，其他顶点距离为无穷大；循环遍历所有边，不断进行松弛操作，直到没有发生变化为止。

Bellman-Ford算法的时间复杂度为O(VE)，其中V表示顶点的个数，E表示边的个数。

这个算法可以解决包含负权边的图的最短路径问题，而Dijkstra算法则无法处理负权边。

Floyd-Warshall算法是一种解决多源最短路径问题的动态规划算法。

它的核心思想是通过对所有顶点之间的距离进行不断更新，找到所有顶点之间的最短路径。

具体步骤包括：初始化距离矩阵，设置顶点之间的距离为边的权重，若没有直接相连的边则设置为无穷大；循环遍历所有顶点，尝试将每个顶点作为中转点，并尝试更新所有顶点对之间的距离。

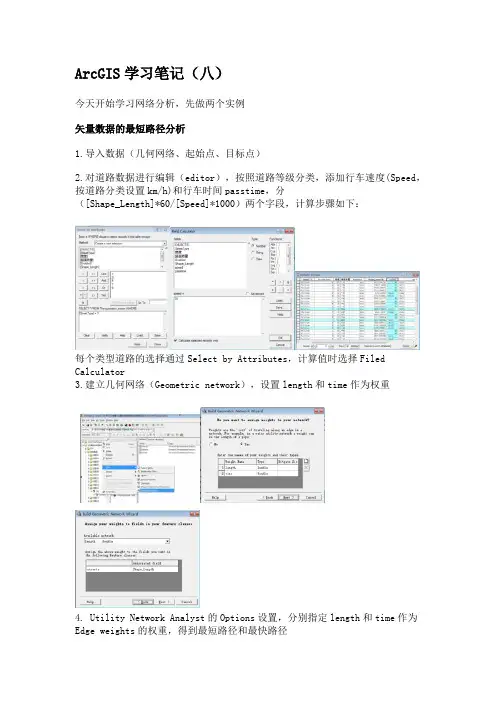
ArcGIS学习笔记（八）今天开始学习网络分析，先做两个实例矢量数据的最短路径分析1.导入数据（几何网络、起始点、目标点）2.对道路数据进行编辑（editor），按照道路等级分类，添加行车速度(Speed，按道路分类设置km/h)和行车时间passtime，分（[Shape_Length]*60/[Speed]*1000）两个字段，计算步骤如下：每个类型道路的选择通过Select by Attributes，计算值时选择Filed Calculator3.建立几何网络（Geometric network），设置length和time作为权重4. Utility Network Analyst的Options设置，分别指定length和time作为Edge weights的权重，得到最短路径和最快路径5.选择起始点和目标点得到路径图，可以设置障碍（临时性的选择和数据库的交汇点或通道的Enabled设置）时间最短和路程最短，还可以在左下角看到总计算值，单位为分钟和米。

栅格数据的最短路径分析1. 数据准备（DEM，起始点和目标点，河流数据等）2. 给出条件（成本最少，路径最短，避开河流），成本权重3. 计算DEM的坡度数据（slope）和起伏度数据（Neighborhood statistics）4. 按统一标准重分类，如1-10起伏度分级图和河流分级图5. 栅格加权计算cost=river+(slope*p1+rough*p2)6. 起始点（Distance to）成本计算（Cost weighted）生成distance，并创建成本方向图direction到目标点（Path to）的最短路径成本距离图成本方向图最终结果如图：明天详细学习网络分析，。

《最短路径问题》的反思及应用编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（《最短路径问题》的反思及应用）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为《最短路径问题》的反思及应用的全部内容。

《最短路径问题》的反思及应用我们知道，有效地开发和利用课本,对于学生的学习具有重要的意义。

学生对于课本上例题或习题能否吃透，直接影响着学生的学习效果。

因此教师要引导学生挖掘教材，引导学生进行反思,从中领悟问题解决过程的数学内涵.有这样一个问题：如图1所示，牧马人从地出发,到一条笔直的河边饮马,然后到地.牧马人到河边的什A l B么地方饮马，可使所走的路径最短?分析我们把河边近似看做一条直线 (如图2)，为直线上的一个动点，那么，上面的l P l问题可以转化为：当点在直线的什么位置时，与的和最小。

P l AP PB如图3所示，作点关于直线的对称点，连接，交直线于点，则点就是牧马AB l P PB l'B'人到河边饮马的位置。

事实上，点与点的线段最短，由对称性质知，，因为=PB PB'B A'AB'，即点到点、的距离之和最小。

+=+=P A BPA PB PA PB AB''上述路径问题，是利用轴对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离，基本思路是运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长。

从解题过程不难看出，本题蕴含着三个数学思想方法：数学模型思想，转化思想，对称思想.如果学生一旦认识或明白这些思想方法,就能举一反三,再复杂的问题也会迎刃而解。

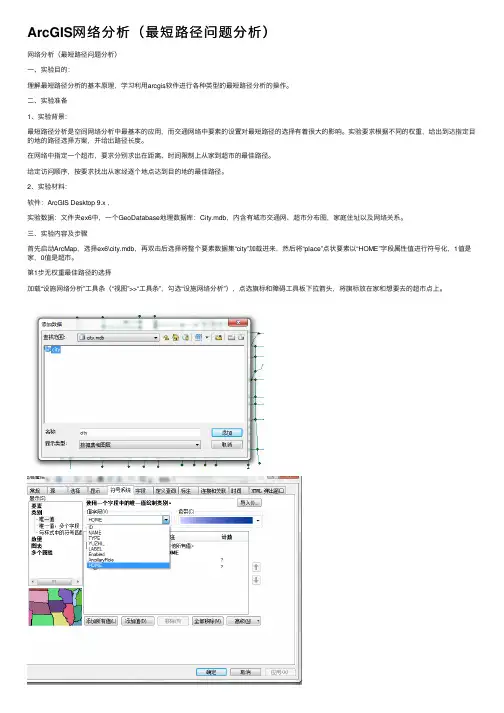
ArcGIS⽹络分析（最短路径问题分析）⽹络分析（最短路径问题分析）⼀、实验⽬的：理解最短路径分析的基本原理，学习利⽤arcgis软件进⾏各种类型的最短路径分析的操作。

⼆、实验准备1、实验背景：最短路径分析是空间⽹络分析中最基本的应⽤，⽽交通⽹络中要素的设置对最短路径的选择有着很⼤的影响。

实验要求根据不同的权重，给出到达指定⽬的地的路径选择⽅案，并给出路径长度。

在⽹络中指定⼀个超市，要求分别求出在距离、时间限制上从家到超市的最佳路径。

给定访问顺序，按要求找出从家经逐个地点达到⽬的地的最佳路径。

2、实验材料：软件：ArcGIS Desktop 9.x ，实验数据：⽂件夹ex6中，⼀个GeoDatabase地理数据库：City.mdb，内含有城市交通⽹、超市分布图，家庭住址以及⽹络关系。

三、实验内容及步骤⾸先启动ArcMap，选择ex6\city.mdb，再双击后选择将整个要素数据集“city”加载进来，然后将“place”点状要素以“HOME”字段属性值进⾏符号化，1值是家，0值是超市。

第1步⽆权重最佳路径的选择加载“设施⽹络分析”⼯具条（“视图”>>“⼯具条”，勾选“设施⽹络分析”），点选旗标和障碍⼯具板下拉箭头，将旗标放在家和想要去的超市点上。

第2步加权最佳路径选择在设施⽹络分析⼯具条上，点选旗标和障碍⼯具板下拉箭头，将旗标放在家和想去的某个超市点上。

选择“分析”下拉菜单，选择“选项”按钮，打开“分析选项”对话框，选择“权重”标签页，在“边权重”上，全部选择长度“length”权重属性。

点选“追踪任务”下拉菜单选择“查找路径”。

单击“执⾏”键，则以长度为⽐重为基础的最短路径将显⽰出来，这条路径的总成本将显⽰在状态列。

上述是通过距离的远近选择⽽得到的最佳路径，⽽不同类型的道路由于道路车流量的问题，有时候要选择时间较短的路径，同样可以利⽤⽹络分析进⾏获得最佳路径。

第3步按要求和顺序逐个对⽬的点的路径的实现在设施⽹络分析⼯具条上，点选旗标和障碍⼯具板下拉箭头，将旗标按照车辆访问的顺序逐个放在点上。

最短路径算法分析2随着计算机和地理信息科学的发展,地理信息系统因其强大的功能得到日益广泛和深入的应用。

网络分析作为GIS最主要的功能之一,在电子导航、交通旅游、城市规划以及电力、通讯等各种管网、管线的布局设计中发挥了重要的作用,通用的网络分析功能包括路径分析、资源分配、连通分析、流分析等。

网络分析中最基本和最关键的问题是最短路径问题,它作为许多领域中选择最优问题的基础,在交通网络分析系统中占有重要地位。

从道路网络模型的角度看,最短路径分析就是在指定道路网络的两节点间找出一条阻碍强度最小的路径。

根据阻碍强度的不同定义,最短路径不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。

相应地,最短路径问题就成为最快路径问题、最低费用问题等。

因此,城市道路网作为一种大型网络设施有其本身的特征。

它一方面包含网络本身的拓扑特征;另一方面还包含了大量反应地理位置特征的几何数据。

本文根据道路网的特点,运用GIS网络分析功能对道路网络模型、道路的权重选择以及快速寻求路网中两节点间的最短路径算法分别进行了研究。

1 道路网模型及权重设置1.1 道路网模型建立城市道路网主要由众多道路相交、相连构成。

在纵横交织、错综复杂的道路网络中,道路间的地理位置关系相当复杂,一条道路可能与若干条道路相交相连,且其相交相连的模式复杂。

为了避免过多地考虑道路间的拓扑关系,抽取道路网中道路交叉路口作为分析对象,并对道路以交叉路口为结点进行分割,成为路段。

这样,整个网络图将由交叉路口点和路段组成,并定义交叉路口点为网络的结点,路段为网络的弧。

从而建立基于路段连接的网络模型,其模型形式表述为:式中,RW代表道路网络;N代表结点集;R代表路段集合,其元素为有序对,表示由结点x到结点y存在一条有向通路;LR代表路段长度集合,其元素表示有向路段的加权长度。

其中,路段的加权长度是指根据目标函数要求,综合各种动态实时信息和静态属性信息后所得的路段参数,而并非真实意义下的长度。

AE运动路径调整技巧解析在Adobe After Effects（以下简称AE）中，运动路径是控制图层运动的关键要素之一。

正确调整运动路径可以使图层动画更加流畅、自然，并增强视觉效果。

本文将介绍一些实用的AE运动路径调整技巧，帮助读者提升动画制作的能力。

一、运动路径基础知识在开始分析运动路径调整技巧之前，我们先来了解一些基本的运动路径概念。

1. 运动路径是指图层在二维或三维空间中的移动轨迹。

2. 关键帧是控制图层运动的关键点，每个关键帧对应一个具体的位置信息。

3. 在AE中，可以通过调整关键帧之间的插值来改变图层的运动速度和路径形状。

二、调整运动路径的技巧1. 平滑运动当图层在运动过程中出现抖动或突然停顿的情况时，可以通过平滑运动路径来改善。

具体操作如下：（1）选中关键帧，并右键点击“关键帧助手”中的“空间调整器”。

（2）在弹出的空间调整器面板中，可以看到每个关键帧的位置和曲线。

通过调整曲线的形状，使得连续的关键帧之间的过渡更加平滑，从而实现平滑运动效果。

2. 更改速度和时间有时候，我们希望图层的速度在运动过程中有所变化，或者调整图层的运动时长。

以下是一些实用技巧：（1）选中关键帧，并右键点击“关键帧助手”中的“速度图”。

（2）在弹出的速度图面板中，可以通过调整速度图曲线的形状来改变图层运动的速度。

拉伸或压缩曲线的区域可以控制图层运动的快慢。

（3）若想调整图层的运动时长，可以选中关键帧并拖动以增加或减少关键帧之间的间隔。

3. 创建自定义路径除了直线和曲线路径外，AE还提供了一些自定义路径的工具。

以下是几种常用的自定义路径技巧：（1）贝塞尔路径：在创建形状图层或调整图层路径时，我们可以使用贝塞尔路径工具来创建更加复杂的路径形状。

（2）蒙特卡洛路径：该路径可以模拟粒子在空间中的随机运动轨迹，常用于创造自然效果或特殊视觉效果。

（3）描边路径：运用此技巧可以通过在图层中添加描边并在路径上进行调整，从而创造出柔和的形状变化或图形动画。

算法最短路径最短路径算法是一种在图中寻找两个节点之间最短路径的方法。

它在许多实际应用中都有广泛的应用，比如导航系统、网络路由和物流规划等。

本文将介绍几种常见的最短路径算法，并对它们的原理和应用进行详细解析。

一、Dijkstra算法Dijkstra算法是最短路径算法中最常用的一种。

它通过不断更新起始节点到其他节点的距离，逐步找到最短路径。

具体步骤如下：1. 初始化起始节点的距离为0，其他节点的距离为无穷大。

2. 选择距离起始节点最近的节点，并标记为已访问。

3. 更新与该节点相邻节点的距离，如果经过该节点到达相邻节点的距离更短，则更新距离。

4. 重复步骤2和3，直到所有节点都被访问过或者没有可更新的节点。

Dijkstra算法的时间复杂度为O(V^2)，其中V为节点的数量。

它适用于没有负权边的图，可以求解单源最短路径问题。

二、Bellman-Ford算法Bellman-Ford算法是一种可以处理带有负权边的图的最短路径算法。

它通过对所有边进行松弛操作，逐步逼近最短路径。

具体步骤如下：1. 初始化起始节点的距离为0，其他节点的距离为无穷大。

2. 对所有边进行V-1次松弛操作，其中V为节点的数量。

3. 检查是否存在负权环，如果存在，则说明图中存在无穷小的最短路径，算法结束。

Bellman-Ford算法的时间复杂度为O(VE)，其中V为节点的数量，E为边的数量。

它适用于解决单源最短路径问题，并且可以处理带有负权边的图。

三、Floyd-Warshall算法Floyd-Warshall算法是一种可以求解任意两个节点之间最短路径的算法。

它通过动态规划的思想，逐步更新节点之间的距离。

具体步骤如下：1. 初始化节点之间的距离矩阵，如果两个节点之间有直接边，则距离为边的权重，否则为无穷大。

2. 对于每一个节点k，遍历所有节点对(i, j)，如果经过节点k的路径比直接路径更短，则更新距离矩阵中的值。

3. 重复步骤2，直到所有节点对的距离都被更新。

点选路障点IPoint BipNew;if (B_ipPoints == null){B_ipPoints = new MultipointClass();}BipNew =axMapControl1.ActiveView.ScreenDisplay.DisplayTransformation.ToMapPoi nt(e.x, e.y);object o1 = Type.Missing;B_ipPoints.AddPoint(BipNew, ref o1, ref o1);IRgbColor Bcolor = new RgbColorClass();Bcolor.Red = 0;Bcolor.Green = 0;Bcolor.Blue = 0;IElement Belement = new MarkerElementClass();ISimpleMarkerSymbol Bsms = new SimpleMarkerSymbolClass();Bsms.Color = Bcolor as IColor;Bsms.Size = 20;Belement.Geometry =axMapControl1.ActiveView.ScreenDisplay.DisplayTransformation.ToMapPoi nt(e.x, e.y);pGC1.AddElement(Belement, 0);axMapControl1.ActiveView.PartialRefresh(esriViewDrawPhase.esriViewGra phics, null, null);int intEdgeUserClassID;int intEdgeUserID;int intEdgeUserSubID;int intEdgeID;IPoint ipFoundEdgePoint;double dblEdgePercent;INetwork ipNetwork = m_work;INetElements ipNetElements = ipNetwork as INetElements;int intCount = B_ipPoints.PointCount;//这里的points有值吗？//定义一个边线旗数组for (int i = 0; i < intCount; i++){IPoint ipEdgePoint = B_ipPoints.get_Point(i);//查找输入点的最近的边线m_ipPointToEID.GetNearestEdge(ipEdgePoint, out intEdgeID, out ipFoundEdgePoint, out dblEdgePercent);//输入一点，返回改点最近的边线ipNetElements.QueryIDs(intEdgeID, esriElementType.esriETEdge, out intEdgeUserClassID,out intEdgeUserID, out intEdgeUserSubID);int FeatClassID = intEdgeUserClassID;int FeatID = intEdgeUserID;m_selSetBarriers.Add(FeatClassID, FeatID);axMapControl1.ActiveView.PartialRefresh(esriViewDrawPhase.esriViewGra phics, null, null);}最后生成有路障的最短路径事件Form_Main.SolvePath("Distance");//先解析路径textBox1.Text = Form_Main.m_dblPathCost .ToString ();IPolyline ipPolyResult = Form_Main.PathPolyLine();//最后返回最短路径Form_Main.clicked = false;IRgbColor color = new RgbColorClass();color.Blue = 255;IElement element_Distance = new LineElementClass();ISimpleLineSymbol sls = new SimpleLineSymbolClass(); sls.Color = color;sls.Style = esriSimpleLineStyle.esriSLSSolid;sls.Width = 3;element_Distance.Geometry = ipPolyResult;ILineElement lineElement_2 =(ILineElement)element_Distance;lineElement_2.Symbol = sls;Form_Main.pGC.AddElement(element_Distance, 1);Form_Main.Form_Main_MapControl.ActiveView.PartialRefresh(esriViewDraw Phase.esriViewGraphics, null, null);//解决路径方法public static void SolvePath(string WeightName){try{int intEdgeUserClassID;int intEdgeUserID;int intEdgeUserSubID;int intEdgeID;IPoint ipFoundEdgePoint;double dblEdgePercent;ITraceFlowSolverGEN ipTraceFlowSolver = new TraceFlowSolverClass() as ITraceFlowSolverGEN;INetSolver ipNetSolver = ipTraceFlowSolver as INetSolver;INetwork ipNetwork = m_work;ipNetSolver.SourceNetwork = ipNetwork;ipNetSolver.SelectionSetBarriers = m_selSetBarriers;//添加路障INetElements ipNetElements = ipNetwork as INetElements;int intCount = m_ipPoints.PointCount;//这里的points有值吗？//定义一个边线旗数组IEdgeFlag[] pEdgeFlagList = newEdgeFlagClass[intCount];for (int i = 0; i < intCount; i++){INetFlag ipNetFlag = new EdgeFlagClass() as INetFlag;IPoint ipEdgePoint = m_ipPoints.get_Point(i);//查找输入点的最近的边线m_ipPointToEID.GetNearestEdge(ipEdgePoint, out intEdgeID, out ipFoundEdgePoint, out dblEdgePercent);ipNetElements.QueryIDs(intEdgeID, esriElementType.esriETEdge, out intEdgeUserClassID, out intEdgeUserID, out intEdgeUserSubID);erClassID = intEdgeUserClassID;erID = intEdgeUserID;erSubID = intEdgeUserSubID;IEdgeFlag pTemp = (IEdgeFlag)(ipNetFlag as IEdgeFlag);pEdgeFlagList[i] = pTemp;}ipTraceFlowSolver.PutEdgeOrigins(ref pEdgeFlagList);INetSchema ipNetSchema = ipNetwork as INetSchema;INetWeight ipNetWeight =ipNetSchema.get_WeightByName(WeightName);INetSolverWeights ipNetSolverWeights = ipTraceFlowSolver as INetSolverWeights;ipNetSolverWeights.FromToEdgeWeight = ipNetWeight;//开始边线的权重ipNetSolverWeights.ToFromEdgeWeight = ipNetWeight;//终止边线的权重object[] vaRes = new object[intCount - 1];//通过findpath得到边线和交汇点的集合ipTraceFlowSolver.FindPath(esriFlowMethod.esriFMConnected,esriShortestPathObjFn.esriSPObjFnMinSum,out m_ipEnumNetEID_Junctions, out m_ipEnumNetEID_Edges, intCount - 1, ref vaRes);//计算元素成本m_dblPathCost = 0;for (int i = 0; i < vaRes.Length; i++){double m_Va = (double)vaRes[i];m_dblPathCost = m_dblPathCost + m_Va;}m_ipPolyline = null;}catch (Exception ex){Console.WriteLine(ex.Message);}}//返回路径的几何体方法public static IPolyline PathPolyLine(){IEIDInfo ipEIDInfo;IGeometry ipGeometry;if (m_ipPolyline != null)return m_ipPolyline;m_ipPolyline = new PolylineClass();IGeometryCollection ipNewGeometryColl = m_ipPolyline as IGeometryCollection;//引用传递ISpatialReference ipSpatialReference =Form_Main_MapControl.SpatialReference;IEIDHelper ipEIDHelper = new EIDHelperClass();ipEIDHelper.GeometricNetwork = m_ipGeometricNetwork;ipEIDHelper.OutputSpatialReference = ipSpatialReference; ipEIDHelper.ReturnGeometries = true;IEnumEIDInfo ipEnumEIDInfo =ipEIDHelper.CreateEnumEIDInfo(m_ipEnumNetEID_Edges);int count = ipEnumEIDInfo.Count;ipEnumEIDInfo.Reset();for (int i = 0; i < count; i++){ipEIDInfo = ipEnumEIDInfo.Next();ipGeometry = ipEIDInfo.Geometry;ipNewGeometryColl.AddGeometryCollection(ipGeometry as IGeometryCollection);}return m_ipPolyline;}。

最短路径求最值12个模型详解最短路径求最值是指要在最小的距离内求出最优的结果。

最短路径求最值的12个模型如下：1. 旅行商问题（TSP）：旅行商问题是求解对给定城市进行最佳巡回路径的一种最优化问题。

2. 最大流最小割：最大流最小割是一种最优化问题，它是用最小的割点将一个连通图分割成两部分，使得最大的流量在这两部分之间流动的最优化问题。

3. 关键路径算法：关键路径算法是一种运用于解决项目计划问题的最优化算法，它寻找出在所有可能路径中，最短的项目路径作为最终的项目安排。

4. 迪杰斯特拉算法：迪杰斯特拉算法是一种最短路径搜索算法，它通过控制向图中每个点的距离，来求出从指定点出发到达目的地最短的距离。

5. 弗洛伊德算法：弗洛伊德算法是一种求解最短路径的算法，通过使用动态规划的方法，它可以在网络中快速求出最短路径。

6. 贝尔曼-福德算法：贝尔曼-福德算法是一种求解最短路径的算法，它利用宽度优先和深度优先搜索结合的方法，求出网络中任意两点之间的最短路径。

7. 克鲁斯卡尔算法：克鲁斯卡尔算法是一种解决最短路径问题的算法，它通过比较每条边的权值来求解8.斐波那契堆：斐波那契堆是一种运用斐波那契算法实现最小堆和最大堆结构的数据结构，可以帮助快速查找最大和最小值。

9. A*算法：A*算法是一种运用heuristics函数的最优化搜索算法，它可以快速的找到最短的路径。

10. Dijkstra–Scholten算法：Dijkstra–Scholten算法是一种在复杂网络环境中求解最短路径的算法，它采用端到端的方法求出最适合的路径。

11. Bellman-Ford算法：Bellman-Ford算法是一种最短路径算法，它将路径最优化的目标写成一个系统的线性方程，并利用动态规划技术解决这类问题。

12. Johnson算法：Johnson算法是一种运用反向算法实现最短路径搜索的方法，它由索引器和搜索器两部分组成，索引器会根据输入的起点和终点，快速计算出最短路径并输出。

最短路径规划问题归纳总结
最短路径规划是一种常见的优化问题，在很多应用领域都有广泛的应用。

其目标是在给定的图中找到从起始节点到目标节点的最短路径。

常见的最短路径算法
1. Dijkstra算法
Dijkstra算法是最常用的最短路径算法之一，适用于没有负权边的图。

它以贪心的方式逐步扩展最短路径集合，直到找到目标节点的最短路径。

2. Bellman-Ford算法
Bellman-Ford算法是一种处理负权边的最短路径算法。

它通过迭代更新节点的最短路径估计来找到最短路径。

3. Floyd-Warshall算法
Floyd-Warshall算法适用于解决所有节点之间的最短路径问题。

它通过动态规划的方式计算任意两个节点之间的最短路径。

4. A*算法
A*算法是一种启发式搜索算法，常用于求解图中的最短路径。

它通过估计目标节点到当前节点的代价来引导搜索，以减少搜索空间。

最短路径问题的应用
最短路径规划在许多领域都有广泛的应用，包括：
1. 导航系统：根据当前位置和目的地，通过最短路径规划确定
导航路线。

2. 网络路由：在计算机网络中，通过最短路径规划确定数据包
的传输路径。

3. 物流运输：在物流管理中，通过最短路径规划确定货物的最
佳配送路径。

4. 交通规划：通过最短路径规划优化交通流量，减少拥堵和行程时间。

总结
最短路径规划问题是一个重要且常见的优化问题，有多种算法可以用于求解。

根据具体情况和问题要求，可以选择适合的算法来解决最短路径规划问题，并将其应用于不同领域的具体场景中。

AE开发之基于几何网络的最短路径分析1、实习目的本次实习目的在于熟练掌握ArcGIS Engine开发工具并能够通过C#语言在VS 2010开发环境中完成查询几何网络的最短路径分析的功能。

2、实习时间2015年5月23日星期六3、实习容3.1实验环境操作系统：Windows 2007二次开发平台：VS 2010开发环境、ArcGIS Desktop10.0、AE开发组件3.2实验任务完成基于几何网络分析的最短路径查询功能，即实现通过在几何网络地图中指定起始点，能够查询经过起始点的最短路线，并能够通过缩放功能在地图窗口居中显示。

3.3实验步骤3.3.1新建项目选择\文件\新建项目，如图选择项目类型中Visual C#，再选择Windows Application，记为“FindShortPath”，点击确定。

3.3.2添加控件3.3.3控件绑定因为添加的控件只是单独存在，但是程序需要各控件间协同工作，因此要进行控件绑定。

3.3.4创建几何网络1.在ArcCataLog中新建个人地理数据库—“甘地的个人地理数据库”，然后新建要素数据集“road”，接着，鼠标右键选择要素数据集“road”，选择“导入要素类”，导入需要创建几何网络的要素类“主要公路”，输出要素类的名字改为“road”，如下图所示:2.鼠标右键选择要素数据集“road”，选择新建“几何网络”，则出现“新建几何网络”对话框，作如下图所示的一系列设置，最终得到几何网络“road_Net”。

至此，得到几何网络“road_Net”，如下图所示:3.3.5代码实现最短路径分析①设置ToolStrip1②添加代码private IActiveView m_ipActiveView;private IMap m_ipMap;//地图控件中地图private IGraphicsContainer pGC;//图形对象private bool clicked = false;int clickedcount = 0;private double m_dblPathCost = 0;private IGeometricNetwork m_ipGeometricNetwork;private IPointCollection m_ipPoints;//输入点集合private IPointToEID m_ipPointToEID;private IEnumNetEID m_ipEnumNetEID_Junctions;private IEnumNetEID m_ipEnumNetEID_Edges;private IPolyline m_ipPolyline;private IMapControl3 mapctrlMainMap = null;private void Form1_Load(object sender, EventArgs e){//对象初始化mapctrlMainMap = (IMapControl3)this.axMapControl1.Object;m_ipActiveView = axMapControl1.ActiveView;m_ipMap = m_ipActiveView.FocusMap;clicked = false;pGC = m_ipMap as IGraphicsContainer;}private void Findpath_Click(object sender, EventArgs e){mapctrlMainMap.CurrentTool = null;//设置鼠标样式axMapControl1.MousePointer = esriControlsMousePointer.esriPointerCrosshair;if (yerCount == 0){MessageBox.Show("请先加载几何网络数据！");return;}m_ipActiveView = axMapControl1.ActiveView;m_ipMap = m_ipActiveView.FocusMap;clicked = false;pGC = m_ipMap as IGraphicsContainer;ILayer ipLayer = m_ipMap.get_Layer(0);IFeatureLayer ipFeatureLayer = ipLayer as IFeatureLayer;IFeatureDataset ipFDS = ipFeatureLayer.FeatureClass.FeatureDataset;OpenFeatureDatasetNetwork(ipFDS);clicked = true;clickedcount = 0;pGC.DeleteAllElements();}private void SolvePath_Click(object sender, EventArgs e){axMapControl1.MousePointer = esriControlsMousePointer.esriPointerDefault;if (SolvePathGan("Weight"))//先解析路径{IPolyline ipPolyResult = PathPolyLine();//最后返回最短路径clicked = false;if (ipPolyResult.IsEmpty){MessageBox.Show("没有路径可到!!");}else{IRgbColor color = new RgbColorClass();color.Red = 255;color.Blue = 64;color.Green = 128;LineElementClass element = new LineElementClass();ILineSymbol linesymbol = new SimpleLineSymbolClass();linesymbol.Color = color as IColor;linesymbol.Width = 3;element.Geometry = m_ipPolyline;element.Symbol = linesymbol;pGC.AddElement(element, 0);m_ipActiveView.PartialRefresh(esriViewDrawPhase.esriViewGraphics, null, null);axMapControl1.FlashShape(element.Geometry);MessageBox.Show("路径经过" + m_ipEnumNetEID_Edges.Count + "条线" + "\r\n" + "经过节点数为" + m_ipEnumNetEID_Junctions.Count + "\r\n" + "路线长度为" + m_ipPolyline.Length.ToString("#######.##") + "\r\n", "几何路径信息");}}}//路径缩放功能private void SuoFang_Click(object sender, EventArgs e){if (m_ipPolyline == null){MessageBox.Show("当前没有执行路径查询！！！请确认！");}else{this.axMapControl1.Extent = m_ipPolyline.Envelope;}}#region 自定义路径查询函数public void OpenFeatureDatasetNetwork(IFeatureDataset FeatureDataset){CloseWorkspace();if (!InitializeNetworkAndMap(FeatureDataset))Console.WriteLine("打开network出错");}//关闭工作空间private void CloseWorkspace(){m_ipGeometricNetwork = null;m_ipPoints = null;m_ipPointToEID = null;m_ipEnumNetEID_Junctions = null;m_ipEnumNetEID_Edges = null;m_ipPolyline = null;}//初始化几何网络和地图private bool InitializeNetworkAndMap(IFeatureDataset FeatureDataset){IFeatureClassContainer ipFeatureClassContainer;IFeatureClass ipFeatureClass;IGeoDataset ipGeoDataset;ILayer ipLayer;IFeatureLayer ipFeatureLayer;IEnvelope ipEnvelope, ipMaxEnvelope;double dblSearchTol;INetworkCollection ipNetworkCollection = FeatureDataset as INetworkCollection;int count = ipNetworkCollection.GeometricNetworkCount;//获取第一个几何网络工作空间m_ipGeometricNetwork = ipNetworkCollection.get_GeometricNetwork(0);INetwork ipNetwork = m_work;if (m_ipMap != null){ipFeatureClassContainer = m_ipGeometricNetwork as IFeatureClassContainer;count = ipFeatureClassContainer.ClassCount;for (int i = 0; i < count; i++){ipFeatureClass = ipFeatureClassContainer.get_Class(i);ipFeatureLayer = new FeatureLayerClass();ipFeatureLayer.FeatureClass = ipFeatureClass;for (int j = 0; j < m_yerCount; j++){if (m_ipMap.get_Layer(j).Name.ToUpper() == .ToUpper()){continue;}}}}count = m_yerCount;ipMaxEnvelope = new EnvelopeClass();for (int i = 0; i < count; i++){ipLayer = m_ipMap.get_Layer(i);ipFeatureLayer = ipLayer as IFeatureLayer;ipGeoDataset = ipFeatureLayer as IGeoDataset;ipEnvelope = ipGeoDataset.Extent;ipMaxEnvelope.Union(ipEnvelope);}m_ipPointToEID = new PointToEIDClass();m_ipPointToEID.SourceMap = m_ipMap;m_ipPointToEID.GeometricNetwork = m_ipGeometricNetwork;double dblWidth = ipMaxEnvelope.Width;double dblHeight = ipMaxEnvelope.Height;if (dblWidth > dblHeight)dblSearchTol = dblWidth / 100;elsedblSearchTol = dblHeight / 100;m_ipPointToEID.SnapTolerance = dblSearchTol;return true;}//返回路径的几何体public IPolyline PathPolyLine(){IEIDInfo ipEIDInfo;IGeometry ipGeometry;if (m_ipPolyline != null) return m_ipPolyline;m_ipPolyline = new PolylineClass();IGeometryCollection ipNewGeometryColl = m_ipPolyline as IGeometryCollection;//引用传递ISpatialReference ipSpatialReference = m_ipMap.SpatialReference;IEIDHelper ipEIDHelper = new EIDHelper();ipEIDHelper.GeometricNetwork = m_ipGeometricNetwork;ipEIDHelper.OutputSpatialReference = ipSpatialReference;ipEIDHelper.ReturnGeometries = true;IEnumEIDInfo ipEnumEIDInfo = ipEIDHelper.CreateEnumEIDInfo(m_ipEnumNetEID_Edges);int count = ipEnumEIDInfo.Count;ipEnumEIDInfo.Reset();for (int i = 0; i < count; i++){string[] info;info = new string[count];ipEIDInfo = ipEnumEIDInfo.Next();ipGeometry = ipEIDInfo.Geometry;ipNewGeometryColl.AddGeometryCollection(ipGeometry as IGeometryCollection);info[i] = m_ipPolyline.Length.ToString();}return m_ipPolyline;}public bool SolvePathGan(string WeightName){try{int intJunctionUserClassID;int intJunctionUserID;int intJunctionUserSubID;int intJunctionID;IPoint ipFoundJunctionPoint;ITraceFlowSolverGEN ipTraceFlowSolver = new TraceFlowSolver() as ITraceFlowSolverGEN;INetSolver ipNetSolver = ipTraceFlowSolver as INetSolver;if (m_ipGeometricNetwork == null){return false;}INetwork ipNetwork = m_work;ipNetSolver.SourceNetwork = ipNetwork;INetElements ipNetElements = ipNetwork as INetElements;if (m_ipPoints == null){ MessageBox.Show("请选择点!!"); return false; }int intCount = m_ipPoints.PointCount;//这里的points 有值吗？////定义一个边线旗数组//*********最近点***************//////////IJunctionFlag[] pJunctionFlagList = new JunctionFlag[intCount];for (int i = 0; i < intCount; i++){INetFlag ipNetFlag = new JunctionFlag() as INetFlag;IPoint ipJunctionPoint = m_ipPoints.get_Point(i);//查找输入点的最近的网络点m_ipPointToEID.GetNearestJunction(ipJunctionPoint, out intJunctionID, out ipFoundJunctionPoint);ipNetElements.QueryIDs(intJunctionID, esriElementType.esriETJunction, out intJunctionUserClassID, out intJunctionUserID, out intJunctionUserSubID);erClassID = intJunctionUserClassID;erID = intJunctionUserID;erSubID = intJunctionUserSubID;IJunctionFlag pTemp = (IJunctionFlag)(ipNetFlag as IJunctionFlag);pJunctionFlagList[i] = pTemp;}ipTraceFlowSolver.PutJunctionOrigins(ref pJunctionFlagList);INetSchema ipNetSchema = ipNetwork as INetSchema;INetWeight ipNetWeight = ipNetSchema.get_WeightByName(WeightName);INetSolverWeights ipNetSolverWeights = ipTraceFlowSolver as INetSolverWeights;ipNetSolverWeights.FromToEdgeWeight = ipNetWeight;//开始边线的权重ipNetSolverWeights.ToFromEdgeWeight = ipNetWeight;//终止边线的权重object[] vaRes = new object[intCount - 1];//通过findpath得到边线和交汇点的集合ipTraceFlowSolver.FindPath(esriFlowMethod.esriFMConnected,esriShortestPathObjFn.esriSPObjFnMinSum,outm_ipEnumNetEID_Junctions, out m_ipEnumNetEID_Edges, intCount - 1, ref vaRes);m_dblPathCost = 0;for (int i = 0; i < vaRes.Length; i++){double m_Va = (double)vaRes[i];m_dblPathCost = m_dblPathCost + m_Va;}m_ipPolyline = null;return true;}catch (Exception ex){Console.WriteLine(ex.Message); return false;}#endregion}private void axMapControl1_OnMouseDown(object sender, IMapControlEvents2_OnMouseDownEvent e){if (clicked != true)return;IPoint ipNew;if (m_ipPoints == null){m_ipPoints = new Multipoint();}ipNew = m_ipActiveView.ScreenDisplay.DisplayTransformation.ToMapPoint(e.x, e.y);object o = Type.Missing;m_ipPoints.AddPoint(ipNew, ref o, ref o);IElement element;ITextElement textelement = new TextElementClass();element = textelement as IElement;clickedcount++;textelement.Text = clickedcount.ToString();element.Geometry = m_ipActiveView.ScreenDisplay.DisplayTransformation.ToMapPoint(e.x, e.y);pGC.AddElement(element, 0);m_ipActiveView.PartialRefresh(esriViewDrawPhase.esriViewGraphics, null, null);}3.4实验结果在得到的窗口中加载“甘地的个人地理数据库”（在压缩包中有）中的几何网络“road_Net”，将几何网络地图加载到地图显示窗口中，如下图所示：点击图标添加起始点，效果如下图：然后点击图标，计算最短路径，效果如下图：最后点击图标得到最短路径的缩放，效果如下图：这样就完成了最短路径的查询分析和显示的功能。

最短路径分析可行性分析最短路径分析是一种在图形或网络中找到最短路径的技术。

这种分析方法可以应用于各种场景，如交通规划、GPS导航、电信网络、物流配送等。

在进行最短路径分析之前，我们需要先构建一个图形或网络模型，然后使用适当的算法来计算最短路径。

在进行最短路径分析之前，我们需要进行可行性分析。

可行性分析是评估和判断一个方法或决策是否可行、合理、可实施的过程。

对于最短路径分析，主要从技术可行性、经济可行性和社会可行性三个方面进行分析。

首先，技术可行性是指是否存在适当的技术和工具来进行最短路径分析。

对于小规模的网络或图形，如城市中的交通路网，使用常规算法如迪杰斯特拉或A*等算法可以很方便地求解最短路径问题。

对于大规模复杂的网络，如全球互联网或物流网络，需要使用更高级的算法和技术，如分布式计算、并行计算或机器学习等方法。

因此，在进行最短路径分析前，需要确认是否有合适的技术和工具来应用。

其次，经济可行性是指进行最短路径分析的成本是否可接受。

成本包括软件工具的费用、计算资源的费用、数据采集和处理的费用等。

通常情况下，最短路径分析需要依赖地理信息系统（GIS）等软件工具，这些工具通常需要支付一定的许可费用。

另外，进行最短路径分析可能需要大量的计算资源，包括计算机、服务器等，并且可能需要支付相应的电费、维护费用等。

此外，数据的采集和处理也需要相应的费用，如地理数据的采集和处理、电信数据的获取等。

因此，在进行最短路径分析之前，需要综合考虑是否有足够的经济资源来支持。

最后，社会可行性是指进行最短路径分析是否对社会有积极的影响。

最短路径分析常应用于交通规划、物流配送等领域，可以提高交通效率、减少交通拥堵、减少能源消耗等，对于城市和社会发展具有重要意义。

然而，最短路径分析可能会涉及个人隐私和数据安全等问题，例如GPS导航、电信网络分析可能会涉及个人位置信息、通信记录等敏感信息的收集和处理。

因此，在进行最短路径分析之前，需要充分考虑和解决相关的隐私和安全问题。

最短路径的七种类型嘿，朋友们！今天咱们来聊聊最短路径的七种类型，就像探索七个神秘的宝藏通道一样。

首先是直线型最短路径，这就像是两点之间的“爱情直通车”，没有弯弯绕绕，直接就奔着目标去了。

仿佛是射出的箭，毫不犹豫，只朝着靶心飞。

要是现实生活里所有的事情都像直线型最短路径这么简单就好了，那我们都能像超级英雄一样，“嗖”的一下就到达目的地，什么堵车、绕路都不存在。

然后是折线型最短路径，这可有点像小调皮鬼走的路。

它不是一条直线，而是折来折去，就像在迷宫里乱窜的小老鼠，看似东奔西跑，但其实每一段折线都是精心计算后的选择，就为了能以最短的距离到达终点。

这就好比你去超市，本来想直接拿东西就走，结果被促销的小摊位吸引，绕了几个弯，但最后还是很快找到了收银台。

再说说曲线型最短路径，这简直是艺术大师的杰作。

它像一条灵动的丝带在空中飘舞，虽然弯弯曲曲，但每一处弯曲都充满了智慧。

就像一个优雅的舞者，看似舞步复杂，实则每一步都在向着舞台的中心靠近，它是在空间里玩一场优美的距离游戏。

阶梯型最短路径呢，感觉像是在爬楼梯去天堂。

一步一个台阶，稳扎稳打，虽然看起来是一级一级的，但是整体上却是最省力气、最短距离的方式。

这就像我们玩游戏时，按部就班地完成一个个任务关卡，最后成功通关，而且还是用了最聪明的办法。

还有跳跃型最短路径，这就像是超级马里奥一样，跳过那些不必要的障碍，直接跳到关键的平台上。

充满了冒险和刺激，就像一个武林高手，施展轻功，从这个山头直接跳到那个山头，只挑最关键的落脚点，一下子就把距离缩短了。

树形最短路径就像是一棵大树的枝干伸展，从树干到树枝再到细枝末节，每一条路径都是为了把营养以最快的速度传递到树叶。

它错综复杂却又有条不紊，就像一个大家族的关系网，看似复杂，其实内部有着最有效的联络方式。

最后是混合型最短路径，这可是个大杂烩啊。

就像一个厨师把前面所有的做菜方法混合在一起，做出了一道绝世佳肴。

它综合了各种路径的优点，在不同的情况下灵活切换，就像一个多面手，遇到什么问题就用什么方式解决，总是能以最短的路径达到最终的目的。

/gishomeC#+AE 几何网络的最短路径publicvoid SolvePath(IMap _pMap, IGeometricNetwork _pGeometricNetwork, string _pWeightName, IPointCollection _pPoints, double _pDist, ref IPolyline _pPolyline, refdouble _pPathCost){try{// 这4个参数其实就是一个定位Element的指标int intEdgeUserClassID;int intEdgeUserID;int intEdgeUserSubID;int intEdgeID;IPoint pFoundEdgePoint;double dblEdgePercent;ITraceFlowSolverGEN pTraceFlowSolver = new TraceFlowSolverClass() as ITraceFlowSolverGEN;INetSolver pNetSolver = pTraceFlowSolver as INetSolver;//操作是针对逻辑网络的,INetwork是逻辑网络INetwork pNetwork = _work;pNetSolver.SourceNetwork = pNetwork;INetElements pNetElements = pNetwork as INetElements;int pCount = _pPoints.PointCount;//定义一个边线旗数组IEdgeFlag[] pEdgeFlagList = new EdgeFlagClass[pCount];IPointToEID pPointToEID = new PointToEIDClass();pPointToEID.SourceMap = _pMap;pPointToEID.GeometricNetwork = _pGeometricNetwork;pPointToEID.SnapTolerance = _pDist;for (int i = 0; i < pCount; i++){INetFlag pNetFlag = new EdgeFlagClass() as INetFlag;IPoint pEdgePoint = _pPoints.get_Point(i);//查找输入点的最近的边线pPointToEID.GetNearestEdge(pEdgePoint, out intEdgeID, out pFoundEdgePoint, out dblEdgePercent);pNetElements.QueryIDs(intEdgeID, esriElementType.esriETEdge, out intEdgeUserClassID, out intEdgeUserID, out intEdgeUserSubID);erClassID = intEdgeUserClassID;erID = intEdgeUserID;erSubID = intEdgeUserSubID;IEdgeFlag pTemp = (IEdgeFlag)(pNetFlag as IEdgeFlag);pEdgeFlagList = pTemp;}pTraceFlowSolver.PutEdgeOrigins(ref pEdgeFlagList);INetSchema pNetSchema = pNetwork as INetSchema;INetWeight pNetWeight = pNetSchema.get_WeightByName(_pWeightName);INetSolverWeightsGEN pNetSolverWeights = pTraceFlowSolver as INetSolverWeightsGEN;pNetSolverWeights.FromToEdgeWeight = pNetWeight;//开始边线的权重pNetSolverWeights.ToFromEdgeWeight = pNetWeight;//终止边线的权重object[] pRes = newobject[pCount - 1];//通过FindPath得到边线和交汇点的集合IEnumNetEID pEnumNetEID_Junctions;IEnumNetEID pEnumNetEID_Edges;pTraceFlowSolver.FindPath(esriFlowMethod.esriFMConnected,esriShortestPathObjFn.esriSPObjFnMinSum,out pEnumNetEID_Junctions, out pEnumNetEID_Edges, pCount - 1, ref pRes);//计算元素成本_pPathCost = 0;for (int i = 0; i < pRes.Length; i++){double m_Va = (double)pRes;_pPathCost = _pPathCost + m_Va;}IGeometryCollection pNewGeometryColl = _pPolyline as IGeometryCollection;//QI ISpatialReference pSpatialReference = _pMap.SpatialReference;IEIDHelper pEIDHelper = new EIDHelperClass();pEIDHelper.GeometricNetwork = _pGeometricNetwork;pEIDHelper.OutputSpatialReference = pSpatialReference;pEIDHelper.ReturnGeometries = true;IEnumEIDInfo pEnumEIDInfo = pEIDHelper.CreateEnumEIDInfo(pEnumNetEID_Edges); int Count = pEnumEIDInfo.Count;pEnumEIDInfo.Reset();for (int i = 0; i < Count; i++){IEIDInfo pEIDInfo = pEnumEIDInfo.Next();IGeometry pGeometry = pEIDInfo.Geometry;pNewGeometryColl.AddGeometryCollection(pGeometry as IGeometryCollection); }}catch (Exception ex){Console.WriteLine(ex.Message);}}复制代码结果如下：红色的表示结果。

最短路径需求分析报告根据百度查资料，问同学，交流，听课，我完成了本次作业，下面是我这次作业的主要过程和经历的一些过程的问题和解决方式。

由于是完成作业以后再截的图，所以并不是十分详细，但是我会争取表达清楚我的意思，之前在制作的过程中也有过做一步，截一张图，但是总有出错的时候，使我不得不重新制作，所以就不再做一步，截一张图了，望老师谅解。

以及不足和可以改进的地方欢迎各位看过我过程的人们提出宝贵意见和与我交流学习，谢谢。

首先找到一张清晰，简明的地铁图十分重要，太过复杂的在画线，描点方面都会显得十分繁琐而且影响心情，我完成作业过程中失败很多次之后，我发现先描地铁线会比先描点更好，为接下去的步骤制作可以化繁为简，甚至是一个承下的前提，所以先描线，描线的时候要细致，认真，线条要美观，自己看上去也舒服。

1.首先在arccatalog里创造两个shapefile文件，分别是地铁站点和地铁线路。

2.在arcmap里打开你的地铁图和你生成的两个shapefile文件，开始画线描点，用editor toolbar来完成，无论是画线和描点，都要启用editor目录下的snapping，在vertex上打勾，这样在描线的时候交叉的线的焦点会重合，比手动肯定精准更多，也是为了寻最短路径时，解决换乘问题，这一步做好，这个问题已经解决了一半，描点使用snapping，是为了站点会与路线完美重合,在整个过程中，描点，画线是最重要的步骤，做好这两步，剩下的步骤其实十分简单。

3.画完线之后，肯定会有至少2条地铁线相交的线段，这是地铁中换成的站点，用editor toolbar工具里的split tool工具进行打断，首先要用select features选中一条线路，再选择split tool在相交点进行打断，打断之后，再用select features进行选择该线路的时候就不会全部选中，而是只会选择一段，因为被打断的缘故。

如法炮制，把所有相交线路按照上述方法，以换成点为打断点全部一一打断，这样，换成问题就解决了。

最短路径算法（Dijkstra、Floyd）总结最短路径算法是图算法中比较重要的组成部分，在《算法导论》中有比较详细的阐述和证明。

很长时间没在看过图算法的内容，在接触到增强学习后，复习了下A*算法，故对最短路径算法进行一下简单的总结，A*算法将会另外开一篇文章。

Dijkstra和Floyd算法是最为经典的两个针对无向图进行最短路径求取的算法，本文先对这两个算法进行回顾和总结。

Dijkstra算法如上图，现在我们要求从源点AA开始求取图中其它点的最短路径。

具体过程是：（1）. 将AA放入最后的结果中RetRet；（2）. 选取与AA距离最短的点，显然是CC，更新AA经过CC到其它与CC有直接连接的点的距离，更新的规则上面已经说过，以BB为例，A?BA->B的距离大于A?C?BA->C->B的距离，所以更新A?BA->B的距离为5。

同时，AA到DEDE初始是无穷大（图的存储约定），所以更新AA到DEFDEF 的距离分别为{6、7}，并加入最后的结果中，Ret={A,C}Ret={A,C}；（3）. 由于CC已经被选取，在下一次选择距离AA最短的点时就不再考虑CC，那么这次选择显然就是BB，比较还没加入RetRet且和BB直接连接的点（C、D）（C、D），更新规则和上面一样，最后将BB加入到RetRet 中，这时Ret={A,C,B}Ret={A,C,B};（4）. 以此类推，选择DD并更新和DD直接相连的点，并加入到RetRet 中。

最后Ret={A,C,B,D,E,F}Ret={A,C,B,D,E,F},这便是源点AA到图中所有点的最短路径，例如求A?EA->E的最短路径便是A?C?B?D?EA-C-B-D-E。

简易代码如下（因为手头电脑问题，并没有运行检查正确性）：const int MAXINT = INT_MAX; --图中不直接连接的点的权重定义const int MAXNUM = 6; --图中的节点数目int dst[MAXNUM]; --存放源点到其它点的距离int prev[MAXNUM]; --存放路径int G[MAXNUM][MAXNUM]; --图的邻接矩阵void Dijstra(int v0)bool used[MAXNUM]; -- 判断图中节点时候已经被加入最后的结果中，初始为falseint node_num = MAXNUM;for(int i = 1; i=n; i++)dst[i] = G[v0][i]; --从邻接矩阵中获取距离信息used[i] = false;if( MAXINT == dst[i] )prev[i] = -1;prev[i] = v0; -- 设置源点直接连接的点的前驱为源点dst[v0] = 0; -- 源点到源点的距离设置为0used[v0] = true; --标记源点已经被加入最后的结果中for(int i = 2; i = n; i++){int mindst = MAXINT;int u = v0;for(int j = 1; j = n; j++) -- 选取目前距离矩阵中与源点最短距离的点if( (!used[j]) dst[j] mindst){mindst = dst[j];used[u] = true; --将该点加入到最后结果中for(int j = 1; j = n; ++j)if( (!used[j]) G[u][j] MAXINT)if(dst[u]+G[u][j] dst[j])dst[j] = dst[u]+G[u][j]; -- 更新距离pre[j] = u; -- 设置前驱Floyd算法Dijkstra算法是解决单源最短路径算法，当需要解决图中任意两点的最短路径时，Dijkstra则需要多次计算，而且，当图中存在负的边权重时，Dijkstra则显得无能为力。