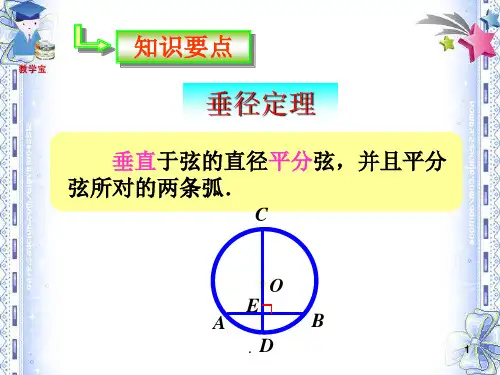
垂直于弦的直径什么是垂直于弦的直径？在圆的几何学中，直径是两个在圆周上相对点之间的线段，并且经过圆心。
而垂直于弦的直径是指与给定弦垂直的直径。
换句话说，如果一个直径与某条弦垂直相交，那么它就是垂直于弦的直径。
特性和性质1.垂直于弦的直径的性质之一是它们互相垂直。
这意味着，如果两条直径都是垂直于同一条弦，那么这两条直径相互垂直。
2.对于一个给定的圆和一条弦，只有一个垂直于该弦的直径。
这是因为直径经过圆心，且圆心位于弦的垂直平分线上。
3.垂直于弦的直径被称为弦的直径。
这是因为垂直于弦的直径通过弦的中点，并将弦一分为二。
4.对于一个给定的圆，以及圆心处的一点，存在唯一的垂直于通过该点的弦的直径。
这是因为垂直于弦的直径经过圆心。
如何证明一条直径垂直于弦？要证明一条直径垂直于弦，可以使用以下步骤：1.假设有一个圆，以及一条弦和它的中点。
我们需要证明通过该中点的直径是垂直于弦。
2.通过指定的弦的两个端点和圆心绘制弧。
3.连接弧的两个端点与圆心，形成两条半径。
4.根据性质，半径与圆周相切于弦的端点。
5.通过弦的中点绘制一条水平线段，并通过圆心绘制一条垂直线段。
6.证明水平线段与垂直线段相交于直径的一点。
7.由于水平线段与弦平行，且垂直线段与弧相切于弦的端点，因此直径与弦垂直相交。
8.因此，通过弦的中点的直径是垂直于弦的。
垂直于弦的直径的应用垂直于弦的直径的概念在几何学和数学中具有广泛的应用。
以下是几个具体的应用场景：1.圆锥与割线问题：当我们考虑一个锥体与平面相交时，垂直于割线的直径对于计算截面的半径和圆锥的体积非常有用。
2.弦截矩关系：根据垂直于弦的直径的性质，我们可以推导出弦的截矩公式。
截矩是描述截面形状的一个参数，它对于材料的强度和性能分析非常重要。
3.三角函数与圆：在三角函数中，正弦值、余弦值和正切值等与圆相关的概念经常涉及到垂直于弦的直径。
这些概念为我们理解三角函数的图像、计算角度和边长提供了基础。
