辅助线正解

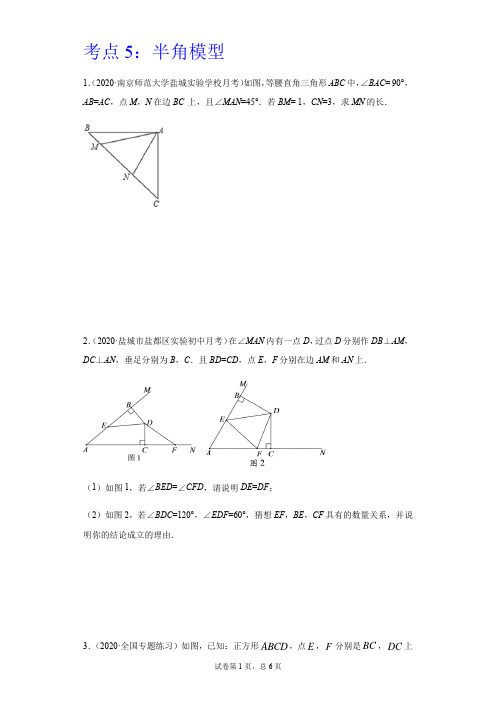
考点5：半角模型1．（2020·南京师范大学盐城实验学校月考）如图，等腰直角三角形ABC中，∠BAC= 90°，AB=AC，点M，N在边BC上，且∠MAN=45°．若BM= 1，CN=3，求MN的长．2．（2020·盐城市盐都区实验初中月考）在∠MAN内有一点D，过点D分别作DB⊥AM，DC⊥AN，垂足分别为B，C．且BD=CD，点E，F分别在边AM和AN上．（1）如图1，若∠BED=∠CFD，请说明DE=DF；（2）如图2，若∠BDC=120°，∠EDF=60°，猜想EF，BE，CF具有的数量关系，并说明你的结论成立的理由．3．（2020·全国专题练习）如图，已知：正方形ABCD，点E，F分别是BC，DC上的点，连接AE ，AF ，EF ，且45EAF ∠=︒，求证：BE DF EF +=．4．（2020·山东济南·期末）如图，正方形ABCD 中，E 、F 分别在边BC 、CD 上，且∠EAF ＝45°，连接EF ，这种模型属于“半角模型”中的一类，在解决“半角模型”问题时，旋转是一种常用的分析思路．例如图中∠ADF 与∠ABG 可以看作绕点A 旋转90°的关系．这可以证明结论“EF ＝BE ＋DF ”，请补充辅助线的作法，并写出证明过程．（1）延长CB 到点G ，使BG ＝ ，连接AG ； （2）证明：EF ＝BE ＋DF5．如图，在正方形ABCD 中，E 、F 是对角线BD 上两点，将ADF 绕点A 顺时针旋转90︒ 后，得到ABM ，连接EM ，AE ，且使得45∠=︒MAE ．（1）求证：=ME EF ；（2）求证：222EF BE DF =+.6．如图所示，在ABC ∆中，30A B ∠=∠=︒，60MCN ∠=︒，MCN ∠的两边交AB 边于E ，F 两点，将MCN ∠绕C 点旋转（1）画出BCF ∆绕点C 顺时针旋转120︒后的ACK ∆； （2）在（1）中，若222AE EF BF +=，求证：2BF CF =；（3）在（2）的条件下，若31AC =+，直接写出EF 的长.7．正方形ABCD 的边长为3，E 、F 分别是AB 、BC 边上的点,且∠EDF=45°.将∠DAE 绕点D 逆时针旋转90°，得到∠DCM.（1）求证：EF=FM（2）当AE=1时，求EF 的长．8．（2019·全国初二专题练习）如图：E 、F 分别是正方形ABCD 的边CD 、DA 上一点，且CE+AF=EF ，请你用旋转的方法求∠EBF 的大小．9．（2020·陕西期末）如图，AB AD BC DC ===，90C D ABE BAD ∠=∠=∠=∠=︒，点E 、F 分别在边BC 、CD 上，45EAF ∠=︒，过点A 作GAB FAD ∠=∠，且点G 在CB 的延长线上．（1）GAB ∆与FAD ∆全等吗？为什么？ （2）若2DF =，3BE =，求EF 的长．10．（2020·重庆北碚·初三其他）已知：正方形ABCD 中，45MAN ∠=，MAN ∠绕点A 顺时针旋转，它的两边分别交CB DC ，（或它们的延长线）于点M N ，． 当MAN ∠绕点A 旋转到BM DN =时（如图1），易证BM DN MN +=．（1）当MAN ∠绕点A 旋转到BM DN ≠时（如图2），线段,BM DN 和MN 之间有怎样的数量关系？写出猜想，并加以证明．（2）当MAN 绕点A 旋转到如图3的位置时，线段,BM DN 和MN 之间又有怎样的数量关系？请直接写出你的猜想．参考答案1．解：如图，过点C作CE⊥BC，垂足为点C，截取CE，使CE＝BM．连接AE、EN．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°．∵CE⊥BC，∴∠ACE＝∠B＝45°．在△ABM和△ACE中AB ACB ACE BM CE⎧∠⎪∠⎪⎨⎩＝＝＝，∴△ABM≌△ACE（SAS）．∴AM＝AE，∠BAM＝∠CAE．∵∠BAC＝90°，∠MAN＝45°，∴∠BAM＋∠CAN＝45°．于是，由∠BAM＝∠CAE，得∠MAN＝∠EAN ＝45°．在△MAN和△EAN中AM AEMAN EAN AN AN⎪∠⎪⎩∠⎧⎨＝＝＝，∴△MAN≌△EAN（SAS）．∴MN＝EN．在Rt△ENC中，由勾股定理，得EN2＝EC2＋NC2．∴MN2＝BM2＋NC2．∵BM＝1，CN＝3，∴MN2＝12＋32，∴MN．2．【详解】（1）∵DB⊥AM，DC⊥AN，∴∠DBE=∠DCF=90°．在△BDE和△CDF中，∵,,,BED CFDDBE DCFBD CD∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE≌△CDF（AAS）．∴DE=DF．（2）过点D作∠CDG=∠BDE，交AN于点G．在△BDE和△CDG中，∵ ,,,EBD GCD BD CD BDE CDG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ △BDE ≌△CDG （ASA ） ∴DE =DG ，BE =CG ． ∵∠BDC =120°，∠EDF =60°， ∴ ∠BDE+∠CDF =60°． ∴ ∠FDG =∠CDG +∠CDF =60°．∴ ∠EDF =∠GDF ． 在△EDF 和△GDF 中，,,,DE DG EDF GDF DF DF =⎧⎪∠=∠⎨⎪=⎩∴ △EDF ≌△GDF （SAS ）． ∴ EF =FG ．∴ EF =FC +CG =FC +BE ．3．【详解】如解图，将ABE △绕点A 逆时针旋转90︒至ADG 的位置，使AB 与AD 重合．∠AG AE =，,DAG BAE DG BE ∠=∠=． ∠45EAF ∠=︒．∠904545GAF DAG DAF BAE DAF BAD EAF ∠=∠+∠=∠+∠=∠-∠=︒-︒=︒， ∠EAF GAF ∠=∠． 在AGF 和AEF 中，,AG AEGAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩， ∠()AGF AEF SAS △≌△．∠EF GF =．∠GF DG DF BE DF =+=+， ∠BE DF EF +=．4．解：（1）根据旋转的性质知BG=DF ，从而得到辅助线的做法：延长CB 到点G ，使BG=DF ，连接AG ；（2）∵四边形ABCD 为正方形， ∴AB=AD ，∠ADF=∠ABE=∠ABG=90°， 在∠ADF 和∠ABG 中AD AB ADF ABG DF BG =⎧⎪∠=∠⎨⎪=⎩∴∠ADF ∠∠ABG （SAS ）， ∴AF=AG ，∠DAF=∠GAB ， ∵∠EAF=45°， ∴∠DAF+∠EAB=45°， ∴∠GAB+∠EAB=45°， ∴∠GAE=∠EAF =45°， 在∠AGE 和∠AFE 中0AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩∴∠ADF ∠∠ABG （SAS ）， ∴GE=EF ，∴EF ＝GE=BE+GB=BE ＋DF 5．【详解】证明：（1）∵将ADF 绕点A 顺时针旋转90°后，得到ABM ，∴MB DF ＝，AM AF ＝，∠∠BAM DAF ＝， MA AF ∴⊥， 45∠︒MAE ＝， 45∴∠︒EAF ＝，∴∠∠MAE FAE ＝，在△AME 和AFE △中AM AF MAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩， ()AME AFE SAS ∴≅，∴=ME EF ；（2）由（1）得：=ME EF ， 在Rt MBE 中，222+MB BE ME =， 又∵MB DF =，222∴+EF BE DF =．（1）作图如图所示（2）证明：连结KE ，作KH ⊥AC 于H ，如图，∵∠A=∠B=30°，∠MCN=60°， ∴∠ACB=120°， ∴∠ACE+∠BCF=60°，∵△BCF 绕点C 顺时针旋转120゜后的△ACK ，∴BF=AK ，∠KCA=∠FCB ，CK=CF ，∠KAC=∠B=30°， ∴∠KCE=∠KCA+∠ACE=∠FCB+∠ACE=60°， ∴∠KCE=∠FCE ， 在△CKE 和△CFE 中CK CF KCE FCE CE CE ⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△CKE ≌△CFE ，∵AE2+EF2=BF2，∴AE2+KE2=AK2，∴△AEK为直角三角形，∴∠AEK=90°，∴∠KEC=∠FEC=45°，∴∠BCF=180°-45°-60°-30°=45°，∴∠KCA=45°，设KH=a，在Rt△KHC中，a；在Rt△KHA中，AK=2a，∴AK：KC=2a，∴BF：，即CF；（3）设KH=a，在Rt△KHC中，HC=a；在Rt△KHA中，a，∴，解得a=1，∴AK=2a=2，在Rt△AEK中，∠KAE=∠KAC+∠CAE=60°，∴∠AKE=30°，∴AE=12AK=1，∴∴ 7．【详解】(1)∠∠DAE 逆时针旋转90°得到∠DCM ∠DE=DM ∠EDM=90° ∠∠EDF + ∠FDM=90° ∠∠EDF=45°∠∠FDM =∠EDM=45° ∠ DF= DF ∠∠DEF∠∠DMF ∠ EF=MF …（2） 设EF=x ∠AE=CM=1 ∠ BF=BM -MF=BM -EF=4-x ∠ EB=2在Rt∠EBF 中，由勾股定理得222EB BF EF += 即2222(4)x x +-=解之，得 52x =8．解：将∠BCE 以B 为旋转中心，逆时针旋转90º，使BC 落在BA 边上，得∠BAM ，则∠MBE=90º，AM=CE,BM=BE,因为CE ＋AF ＝EF ，所以MF ＝EF ，又BF=BF,所以∠FBM∠∠FBE,所以∠MBF=∠EBF, 所以∠EBF=9．【详解】 解：（1）∵90D ABE ∠=∠=︒，点G 在CB的延长线上， ∴∠ABG =∠D =90°， 在△GAB 和△F AD 中，∵GAB FAD ∠=∠，AB =AD ，∠ABG =∠D ， ∴△GAB ≌△F AD （ASA ）； （2）∵△GAB ≌△F AD ， ∴AG =AF ，GB =DF ，∵90BAD ∠=︒，45EAF ∠=︒， ∴∠BAE +∠DAF =45°，∴∠BAE +∠GAB =45°，即∠GAE =45°， ∴∠GAE =∠EAF ， 在△GAE 和△F AE 中，∵AG =AF ，∠GAE =∠EAF ，AE =AE ， ∴△GAE ≌△F AE （SAS ）， ∴GE =EF ，∵GE =GB +BE =DF +BE =2+3=5， ∴EF =5．10．【详解】（1）BM+DN=MN 成立．证明：如图，把△ADN 绕点A 顺时针旋转90°，得到△ABE ，则可证得E 、B 、M 三点共线．∴∠EAM=90°-∠NAM=90°-45°=45°， 又∵∠NAM=45°， ∴在△AEM 与△ANM 中，AE ANEAM NAM AM AM ⎪∠⎪⎩∠⎧⎨＝＝＝ ∴△AEM ≌△ANM （SAS ）， ∴ME=MN ，∵ME=BE+BM=DN+BM ， ∴DN+BM=MN ； （2）DN -BM=MN ．在线段DN 上截取DQ=BM ，如图，在△ADQ 与△ABM 中，∵AD AB ADQ ABM DQ BM ⎪∠⎪⎩∠⎧⎨＝＝＝， ∴△ADQ ≌△ABM （SAS ）， ∴∠DAQ=∠BAM ， ∴∠QAN=∠MAN ． 在△AMN 和△AQN 中，AQ AM QAN MAN AN AN ⎪∠⎪⎩∠⎧⎨＝＝＝ ∴△AMN ≌△AQN （SAS ）， ∴MN=QN ， ∴DN -BM=MN ．。

初中辅助线102种方法初中数学中的辅助线是指在解题过程中为了简化计算或证明关系而引入的辅助线条。

它可以帮助我们更好地理解问题，找到解题的思路和方法。

下面我将介绍一些常见的初中数学辅助线的方法共102种，希望对你的学习有所帮助。

一、简化计算型：1.使用除法计算2.使用平均数计算3.使用倍数计算4.使用分数计算5.使用比例计算6.使用公式计算7.使用近似值计算8.使用合并计算9.使用反向计算10.使用等差数列计算11.使用等比数列计算12.使用余数计算13.使用开平方计算14.使用全等三角形计算15.使用相似三角形计算16.使用三角函数计算17.使用面积计算18.使用体积计算19.使用平行四边形计算20.使用正方形计算21.使用等腰三角形计算22.使用垂直角计算23.使用圆的性质计算24.使用直角三角形计算二、求证关系型：25.使用数轴求证结论26.使用等距离线段求证结论27.使用相似三角形求证结论28.使用画图法求证结论29.使用平行四边形的性质求证结论30.使用正方形的性质求证结论31.使用相等线段求证结论32.使用角度和为180度求证结论33.使用角度和为360度求证结论34.使用锐角三角形角度关系求证结论35.使用直角三角形角度关系求证结论36.使用分割线段求证结论37.使用等腰三角形角度关系求证结论38.使用辅助角求证结论39.使用辅助线段求证结论40.使用同位角性质求证结论41.使用对称性求证结论42.使用对称图形求证结论43.使用等腰梯形性质求证结论44.使用等腰三角形线段关系求证结论45.使用四边形对角线性质求证结论46.使用圆的性质求证结论47.使用辐角关系求证结论48.使用有序数对求证结论49.使用矩形性质求证结论50.使用三角形内接圆性质求证结论51.使用七巧板求证结论52.使用抽屉原理求证结论53.使用排列组合求证结论三、解决线型：54.使用重要线段求解问题55.使用重要角度求解问题56.使用等距离线段求解问题57.使用正方形对称性求解问题58.使用等腰三角形求解问题59.使用平行四边形求解问题60.使用零点、对称点、最大值最小值求解问题61.使用相交弦、弧求解问题62.使用切线求解问题63.使用对称点求解问题64.使用相等线段求解问题65.使用等距离点求解问题66.使用同位角性质求解问题67.使用相似三角形求解问题68.使用全等三角形求解问题70.使用角度和为180度求解问题71.使用角度和为360度求解问题72.使用锐角三角形角度关系求解问题73.使用直角三角形角度关系求解问题74.使用同位角性质求解问题75.使用等腰三角形角度关系求解问题76.使用辅助角求解问题77.使用辅助线段求解问题78.使用分割线段求解问题79.使用等腰梯形性质求解问题80.使用对角线性质求解问题81.使用折角求解问题82.使用相似图形求解问题83.使用正方形的对称性求解问题84.使用等腰三角形线段关系求解问题85.使用三角形内角和为180度求解问题86.使用辐角关系求解问题87.使用无理方程求解问题89.使用矩形的性质求解问题90.使用弧长和面积关系求解问题91.使用正多边形的性质求解问题92.使用等腰梯形的性质求解问题93.使用命题与真值求解问题94.使用夹角的性质求解问题95.使用相对坐标求解问题96.使用中点定理求解问题97.使用边长关系求解问题98.使用距离公式求解问题99.使用勾股定理求解问题100.使用平行四边形的对角线性质求解问题101.使用足分线关系求解问题102.使用线段积关系求解问题以上便是初中辅助线的102种方法，覆盖了数学中常见的辅助线方法，可以帮助你更好地理解和解决数学问题。

初中数学辅助线添加技巧：弦图勾股的几个重要证明方法证法一（赵爽证明）：以a 、b 为直角边（b >a ），以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于12ab ．把这四个直角三角形拼成如图所示形状．c b aHG F EDCBA∵ Rt △DAH ≌ Rt △ABE ， ∴ ∠HDA = ∠EAB ． ∵ ∠HAD + ∠HAD = 90º， ∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c 2． ∵ EF = FG =GH =HE = b ―a ，∠HEF = 90º．∴ EFGH 是一个边长为b ―a 的正方形，它的面积等于()2b a -． ∴()22142ab b a c ⨯+-= ．∴ 222a b c +=．证法二（邹元治证明）：以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于12ab ． 把这四个直角三角形拼成如图所示形状，使A 、E 、B三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上．cb a HGFED CBA∵ Rt △HAE ≌ Rt △EBF ， ∴ ∠AHE = ∠BEF ． ∵ ∠AEH + ∠AHE = 90º，∴ ∠AEH + ∠BEF = 90º． ∴ ∠HEF = 180º―90º= 90º．∴ 四边形EFGH 是一个边长为c 的正方形．它的面积等于c 2． ∵ Rt △GDH ≌ Rt △HAE ， ∴ ∠HGD =∠EHA ． ∵ ∠HGD + ∠GHD = 90º， ∴ ∠EHA + ∠GHD = 90º． 又∵ ∠GHE = 90º， ∴ ∠DHA = 90º+ 90º= 180º．∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2a b +． ∴ ()22142a b ab c +=⨯+．∴ 222a b c +=．证法三（陈杰证明）：直角边长分别为a 、b 的四个三角形全等，斜边长为c ，图中有3个正方形边长分别为a 、b 、c ，设整个图形的面积为S ．c b a Ic b a HGF EDCBA∵△ABH ≌ △HEF ， ∴BAH EHF ∠=∠，∴90BAH AHB EHF AHB ∠+∠=∠+∠=︒， ∴90AHF ∠=︒，∴四边形AHFI 是正方形．∵2222122S a b ab a b ab =++⨯=++，22122S c ab c ab =+⨯=+，∴222a b ab c ab ++=+， ∴222a b c +=．证法四（1876年美国总统Garfield 证明）：c b a cb ED C BA以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于12ab ．把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上． ∵ Rt △EAD ≌ Rt △CBE ， ∴ ∠ADE = ∠BEC ． ∵ ∠AED + ∠ADE = 90º， ∴ ∠AED + ∠BEC = 90º． ∴ ∠DEC = 180º―90º= 90º． ∴ △DEC 是一个等腰直角三角形， 它的面积等于212c ．又∵ ∠DAE = 90º， ∠EBC = 90º， ∴ AD ∥BC ．∴ ABCD 是一个直角梯形，它的面积等于()212a b +． ∴()221112222a b ab c +=⨯+． ∴222a b c +=．证法五（总统证法变形）：如图，矩形ABCD 绕点A 顺时针旋转90º至AB'C'D'的位置，连接CC'．设,,AB a BC b AC c ===．B'C'D'c b aD C BA∵四边形BCC'D'为直角梯形，∴()()2122'D'a b S BC C'D'BD'+=+=梯形BCC ． ∵Rt Rt ABC AB'C'△≌△， ∴BAC B'AC'∠=∠．∴2211122222ABC CAC'D'AC''D'c abS S S S ab c ab +=++=++=△△△梯形BCC ． ∴()22222a b c ab++=．∴222a b c +=．证法六（梅文鼎证明）：作四个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ． 把它们拼成如图那样的一个多边形，使D 、E 、F 在一条直线上． 过C 作AC 的延长线交DF 于点P ．a b c a b c a bc P cb a HG F E DC BA∵ D 、E 、F 在一条直线上，且Rt △GEF ≌ Rt △EBD ， ∴ ∠EGF = ∠BED ， ∵ ∠EGF + ∠GEF = 90°， ∴ ∠BED + ∠GEF = 90°， ∴ ∠BEG =180º―90º= 90º． 又∵ AB = BE = EG = GA = c ， ∴ ABEG 是一个边长为c 的正方形． ∴ ∠ABC + ∠CBE = 90º． ∵ Rt △ABC ≌ Rt △EBD ， ∴ ∠ABC = ∠EBD ． ∴ ∠EBD + ∠CBE = 90º． 即∠CBD = 90º．又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a ． ∴ BDPC 是一个边长为a 的正方形． 同理，HPFG 是一个边长为b 的正方形．设多边形GHCBE 的面积为S ，则222112,222a b S ab c S ab +=+⨯=+⨯∴222a b c +=．勾股定理的证明方法较多，这是其中的几种．方法总结：勾股定理的证明方法是多样的，而其中的多种方法是具有共性的． 观察上面的证明方法可发现：每个图形中都可以提炼出一个相同的模型——三垂直全等模型．如下图所示．三垂直全等模型其实是从弦图中衍生出来的一个模型，当我们解直角三角形或者正方形的试题时，在很多情况下我们可以考虑构造弦图来解决，有时候是完整的弦图，有时只需一半弦图——三垂直全等模型．图a 与图b 是三垂直全等模型经过直角三角形位置变化之后所得到的另外两个有三垂直和全等三角形的图形，在做题时可参考．图b图a典例精析例1．（1）图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC ＝6，BC ＝5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图9-2所示的“数学风车”，则这个风车的外围周长是 ．图1CBA（2）如图，直线l 上有三个正方形a ，b ，c ，若a ，c 的面积是5和11，则b 的面积为 ．b a cCEDBA解：（1）76；（2）16例2如图1——图3，两个正方形如下图并列排列，要求剪两刀，使之拼成一个新的正方形．（1）如图1，若正方形边长分别为1、2，请在图中画出剪切线；（2）如图2，若正方形的边长分别为a 、b （a >b ），请画出剪切线并标出各边的长度； （3）若要求剪三刀拼成一个正方形，请在图3中画出剪切线．图3图2图1解：（1）、（2）、（3）的剪切线如图a 、图b 、图c 所示：图c图b图a点拨：图c 是证明勾股定理中非常有名的“朱青出入图”． 例3．如图，已知ADBC ，ABE △和CDF △是等腰直角三角形，90,2,5EAB FDC AD BC ∠=∠=︒==，求四边形AEDF 的面积．CFEDBA解：分别过点E 、B 作EN AD ⊥，BM AD ⊥交DA 的延长线于点N 、M ，分别过点F 、C 作FP AD ⊥，CQ AD ⊥，交AD 及AD 延长线于点P 、Q ．NM QP CFEDBAAED ADF EAFD S S S =+△△四边形 ()111222AD EN AD FP AD EN FP =+=+ ∵△AEB 和△FDC 都是等腰直角三角形， ∴90,,EAB FDC AE AB DF CD ∠=∠=︒==． ∵EN AD ⊥，BM AD ⊥，FP AD ⊥，CQ AD ⊥， ∴90BMN ENA FPD DQC ∠=∠=∠=∠=︒． ∴,ENA MBA FPD QCD ∠=∠∠=∠． ∴,ENA AMB FPD DQC △≌△△≌△． ∴,EN AM FP DQ ==．∴EN FP AM DQ MQ AD +=+=-． ∵ADBC ，BM CQ ，且90BMN ∠=︒，∴四边形BMQC 是矩形． ∴BC MQ =． ∵5,2BC AD ==，∴523EN FP +=-=． ∴12332EAFD S =⨯⨯=四边形．例4． 如图1，在Rt △ABC 中，∠ACB =90°，BC =a ，AC =b ，以其各边向外作正方形，得到一个凸六边形DEFGHI ．（1）求这个六边形的面积；（2）试判断线段EF 、GH 、DI 能否构成三角形，若能，探求该三角形的面积与△ABC 面积的关系；若不能，请说明理由．ZY XW 图3图2图1A B C H ID EF GAB C HI D E FGH P IC GFEDB A解：（1）如上图2，作出正方形ABDE 的内弦图，则易知四个直角三角形全等． 则AZ WB AF ==，那么AWB AZE DYE BXD ABC S S S S S ====△△△△△．又∵,,EAF EAZ DBI DBX GCH ABC S S S S S S ===△△△△△△，且AEF ABC CGH BID S S S S ===△△△△，4ABC AFGC BCHI ABDE DEFGHI S S S S S =+++△正方形正方形正方形六边形 222142a b c ab =+++⨯22222a b ab =++．（2）线段EF 、GH 、DI 能构成三角形． 如图3，过点F 作FPGH 交AC 于点P ，连接EP 、IP ，易证四边形FPHG 是平行四边形，PHI ACB △≌△， ∴四边形PIDE 也是平行四边形． 那么,AFP GCH BID APE △≌△△≌△．∴EF 、GH 、DI 可能构成三角形，即EPF △，面积为3ABC S △．点拨：以三角形三边为边向外分别作正方形的题型，可能构造弦图或者作平行线构造平行四边形，利用弦图的性质，三角形全等或者面积关系来解题．例5． 将矩形ABCD 纸片沿对角线AC 剪开，得到△ABC 和△A′C′D ，如图1所示．将△A′C′D 的顶点A′与点A 重合，并绕点A 按逆时针方向旋转，使点D 、A (A′)、B 在同一条直线上，如图2所示．观察图2可知：与BC 相等的线段是 ，∠CAC′= °． 问题探究如图3，△ABC 中，AG ⊥BC 于点G ，以A 为直角顶点，分别以AB 、AC 为直角边，向△ABC 外作等腰Rt △ABE 和等腰Rt △ACF ，过点E 、F 作射线GA 的垂线，垂足分别为P 、Q ． 试探究EP 与FQ 之间的数量关系，并证明你的结论．AB CEFG PQ图3解：情景观察：AD 或A′D ；90． 问题探究：结论：EP =FQ ． 证明：∵△ABE 是等腰三角形， ∴AB =AE ，∠BAE=90°． ∴∠BAG +∠EAP =90°． ∵AG ⊥BC ，∴∠BAG +∠ABG =90°， ∴∠ABG =∠EAP ． ∵EP ⊥AG ，∴∠AGB =∠EPA =90°， ∴Rt △ABG ≌Rt △EAP ． ∴AG =EP ．同理AG =FQ ． ∴EP =FQ ． 举一反三如图，梯形ABCD 中，AD ∥BC ，分别以两腰AB 、CD 为边向两边作正方形ABGE 和正方形DCHF ．设线段AD 的垂直平分线l 交线段EF 于点M ，EP ⊥l 于点P ，FQ ⊥l 于点Q ．求证：EP =FQ ．图1 图2C'A'B A DCABCDBCD A (A')C'HNM QP Ll CGFEDBA点拨：这两道题图形较复杂，但解题的思路很清晰，仍是构造三垂直全等模型，添加了辅助线问题就迎刃而解了．例6． 如图，直角梯形ABCD 中，AD ∥BC ，∠ADC =90°，l 是AD 的垂直平分线，交AD 于点M ，以腰AB 为边作正方形ABFE ，EP ⊥l 于点P ．求证：2EP +AD =2CD ．M P l CFED BA解：作AH BC ⊥于点H ，延长EP 交AH 于点G ．54321M PlCFEDBA∵l 是AD 的垂直平分线， ∴1,2AM DM AD l AH ==．又∵ABCD 是梯形， ∴90C D ∠=∠=︒． ∴四边形AHCD 是矩形， ∴AH CD =． 又∵PE l ⊥，∴EH AH ⊥，∴四边形AGPM 是矩形， ∴12GP AM AD ==， ∴1290∠=∠=︒． ∴3490∠+∠=︒．在正方形ABFE 中，,90AB AE BAE =∠=︒， ∴4590∠+∠=︒． ∴35∠=∠．∵12∠=∠，35∠=∠，AB EA =， ∴ABH EAG △≌△．∴AH EG =，即CD AH EG ==．∴12CD GP PE AD PE =+=+，即22CD AD PE =+． 例7．如图，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD =2，BC =3，设BCD α∠=，以D 为旋转中心，将腰DC 逆时针旋转90°至DE ．CEDBA（1）当45α=︒时，求EAD △的面积； （2）当30α=︒时，求EAD △的面积；（3）当090α︒<<︒，猜想EAD △的面积与α的大小有无关系？若有关，写出EAD △的面积S 与α的关系式；若无关，请说明理由．解：（1）当45α=︒时，90BCE ∠=︒．延长AD 交DE 于点G ，则AG CE ⊥，点G 是CE 中点，CG EDBA∴四边形ABCG 是矩形，EG =DG =1． ∴112122EAD S AD EG ==⨯⨯△． （2）当30α=︒时，延长AD 交CE 于点G ，过点E 作EH AG ⊥于点H ．HCG ED BA∵30α=︒，∴30CDG ∠=︒，60EDG ∠=︒，DE CD ==． 在Rt EHD △中，12DH DE ==， ∴1， ∴112122EAD S AD EH ==⨯⨯△． （3）分别过E 、C 两点作AD 的垂线，交AD 延长线于点F 、G ，HCG ED BA∴90EFG AGC ∠=∠=︒， ∵,ADBC AB BC ⊥，∴90B BAD ∠=∠=︒， B BAD AGC ∠=∠=∠，∴四边形ABCG 是矩形． ∴3AG BC ==， ∴321DG =-=， ∵90CDE ∠=︒， ∴90CDG EDG ∠+∠=︒， ∵90CDG DCG ∠+∠=︒，∴DCG EDG ∠=∠， ∵CD DE =， ∴CDG DEF △≌△， ∴1DE DG ==， ∴112122EAD S AD EF ==⨯⨯△． ∴EAD △的面积与α的大小无关． 跟踪训练1．如图，点C 为线段AB 上一点，正方形ADEF 和正方形BCDG 的面积分别为10cm 2和5cm 2，则△EDG 的面积为 cm 2．CGFEDBA2．四边形ABCD 是正方形，直线1l ，2l ，3l 分别通过A 、B 、C 三点，且123l l l ，若1l 与2l 的距离为5，2l 与3l 的距离为7，则正方形ABCD 的面积为 ．CDBA3．在正方形ABCD 中，点G 为BC 上任意一点，连接AG ，过B 、D 两点分别作,BE AG DF AG ⊥⊥，垂足分别为E 、F 两点．探究线段EF 、DF 、BE 三者之间的关系，并证明你的结论．CGFEDBA4．我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”，如图1，图2由弦图变化得到，它是用八个全等的直角三角形拼接而成．记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为1S，2S，3S．若12310S S S++=，则2S的值是．5．如图，平面直角坐标系xOy中，点A、B的坐标分别为A（4，0），B（0，—4），P为y轴上B点下方一点，PB=m（m>0），以AP为边作等腰直角三角形APM，其中PM=PA，点M落在第四象限．（1）求直线AB的解析式；（2）用含m 的代数式表示点M 的坐标；（3）若直线MB 与x 轴交于点Q ，判断点Q 的坐标是否随m 的变化而变化？写出你的结论，并说明理由．例6．如图，Rt △PQR 的直角边为5厘米，9厘米．问图中3个正方形面积之和比4个三角形面积之和大多少？95RQ P FEDCBA7．（1）四年一度的国际数学家大会于2002年8月20日在北京召开．大会会标如图1所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积为13，每个直角三角形两直角边的和是5，求中间小正方形的面积．（2）现有一张长为6．5厘米，宽为2厘米的纸片，如图2，请你将它分割成6块，再拼成一个正方形（要求：先在图2中画出分割线，再画出拼成的正方形并标明相应数据）．图2图1中考前瞻如图1至图3，点C 为定线段AB 外一动点，以AC 、BC 为边分别向外侧作正方形CADF 和正方形CBEG ，分别作1DD AB ⊥、1EE AB ⊥，垂足分别为1D 、1E ．当C 的位置在直线AB 的同侧变化过程中，（1）如图1，当∠ACB ＝90°，AC =4，BC =3时，求11DD EE +的值；（2）求证：如图2，不论C 的位置在直线AB 的同侧怎样变化，11DD EE +的值为定值； （3）求证：如图3，不论C 的位置在直线AB 的同侧怎样变化，线段DE 的中点M 为定点．图3图2图1A1E 1GAD 1BE 1E GC FD E 1D 1GFEDC B A。

平行四边形几何辅助线专题详解1 平行四边形知识框架{分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4个点的坐标平行四边形的面积{利用面积解决问题方程思想构造中位线{连接法{连接两中点知一中点，取另一中点知两中点，构双中位线倍长法{倍长垂直于角平分线的线段倍长线段 方法1 分类讨论思想分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4点坐标一、动态讨论解题技巧：点在线段的不同位置，也会造成不同的结果 （1）1个点的移动如下图，1个点C 在直线AB 上移动，会出现3种情况：①在线段AB 左侧；②在线段AB 当中；③在线段AB 右侧，具体见例1.（2）2个点的移动如下图，2个点C、D在线段AB上移动（C、D两点在AB中），会出现2种情况：①点C在点D的左侧；②点C在点D的右侧，具体见例2.例1.▱ABCD的内角∠BCD的平分线CE交射线DA于点E，若AE=3，DE=4，求▱ABCD的周长。

例2.在▱ABCD中，AD=8，AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，且EF=2，求AB的长。

二、高的位置的讨论解题技巧：在平行四边形中作高，会出现2种情况：①在图形内；②在图形外。

（1）过点作下（上）侧边的高如下图，过点A作▱ABCD下侧的边CD上的高AE。

因▱ABCD倾斜方向的变化，高会存在两种情况，具体见例1（2）过点右（左）侧边的高如下图，过点B作▱ABCD的右侧边AD上的高AE。

因▱ABCD倾斜大小的变化，高会存在两种情况，具体见例2上述两种情况实质是同一种情况经过翻折后得到的，为同一种情况。

例1.在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，若AB=5，BC=6，求CE的值。

例2.在▱ABCD中，AD=BD=4，BE是AD边上的高，∠EBD=30°，求△ABD的面积。

初中数学中考复习考点知识与题型专题讲解专题20全等三角形的辅助线问题【考点题型】考点题型一连接两点做辅助线典例1．把正方形ABCD绕着点A，按顺时针方向旋转得到正方形AEFG，边FG与BC 交于点H（如图）．试问线段HG与线段HB相等吗？请先观察猜想，然后再证明你的猜想．【解析】试题分析：要证明HG与HB是否相等，可以把线段放在两个三角形中证明这两个三角形全等，或放在一个三角形中证明这个三角形是等腰三角形，而图中没有这样的三角形，因此需要作辅助线，构造三角形．试题解析：HG=HB，证法1：连接AH，∵四边形ABCD，AEFG都是正方形，∴∠B=∠G=90°，由题意知AG=AB，又AH=AH，∴Rt△AGH≌Rt△ABH（HL），∴HG=HB．证法2：连接GB，∵四边形ABCD，AEFG都是正方形，∴∠ABC=∠AGF=90°，由题意知AB=AG，∴∠AGB=∠ABG，∴∠HGB=∠HBG，∴HG=HB．变式1-1．已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形画出图形,写出结论不证明.【答案】（1）见解析；（2）见解析【分析】(1)先连接AD，构造全等三角形：△BED和△AFD．AD是等腰直角三角形ABC底边上的中线，所以有∠CAD=∠BAD=45°，AD=BD=CD，而∠B=∠C=45°，所以∠B=∠DAF，再加上BE=AF，AD=BD，可证出：△BED≌△AFD，从而得出DE=DF，∠BDE=∠ADF，从而得出∠EDF=90°，即△DEF是等腰直角三角形；(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.【详解】解：（1）连结AD ,∵AB=AC ,∠BAC=90°,D为BC中点,∴AD⊥BC ,BD=AD ,∴∠B=∠BAD=∠DAC=45°,又∵BE=AF ,∴△BDE≌△ADF（SAS）,∴ED=FD ,∠BDE=∠ADF,∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,∴△DEF为等腰直角三角形.（2）连结AD∵AB=AC ,∠BAC=90°,D 为BC 中点 , ∴AD=BD ,AD ⊥BC ,∴∠DAC=∠ABD=45°, ∴∠DAF=∠DBE=135°, 又∵AF=BE ,∴△DAF ≌△DBE （SAS ）,∴FD=ED ,∠FDA=∠EDB,∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°. ∴△DEF 为等腰直角三角形.变式1-2．如图，以O 为直角顶点作两个等腰直角三角形Rt OAB 和Rt OCD △，且点C 在线段AB 上（A B 、除外），求证：222AC BC CD +=【答案】证明见解析【分析】连接BD ，证明△AOC ≌△BOD （SAS ），得到△CBD 为直角三角形，再由勾股定理即可证明．【详解】解：连接BD ，∵△AOB 与△COD 为等腰直角三角形，∴AO=BO ，CO=DO ，∠AOB=∠COD=90°，∠A=∠ABO=45°，∴∠AOC+∠BOC=∠BOD+∠BOC∴∠AOC=∠BOD ，在△AOC 与△BOD 中，AO BO AOC BOD CO DO =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△BOD （SAS ）∴∠A=∠OBD=45°，AC=BD ，∴∠ABO+∠OBD=90°，即∠CBD=90°，∴在Rt △CBD 中，222BD BC CD +=即222AC BC CD +=．考点题型二全等三角形 -倍长中线模型典例2．已知，在Rt ABC △中，90BAC ∠=︒，点D 为边AB 的中点，AE CD ⊥分别交CD ，BC 于点F ，E ．（1）如图1，①若AB AC =，请直接写出EAC BCD ∠-∠=______；②连接DE ，若2AE DE =，求证：DEB AEC ∠=∠；（2）如图2，连接FB ，若FB AC =，试探究线段CF 和DF 之间的数量关系，并说明理由．【答案】（1）①45°；②见解析；（2）2CF DF =，理由见解析【分析】（1）①利用直角三角形两个锐角相加得90︒和三角形的外角等于不相邻的两个内角和的性质结合题干已知即可解题．②延长ED 至点G ，使得DG DE =，连接AG ，从而可证明ADG ≌BDE （SAS ），再利用全等的性质，可知DGA DEB ∠=∠，即可知道//AG BC ，所以GAE AEC ∠=∠，根据题干又可得到AE EG =，所以DGA GAE ∠=∠，从而得出结论．（2）延长CD 至点H ，使得DH DF =，连接BH ，从而可证明HDB ≌FDA △（SAS ），再利用全等的性质，可知BH AF =，90H AFD AFC ∠=∠=∠=︒，根据题干即可证明Rt HBF △≌Rt FAC △（HL ），即得出结论．【详解】（1）①∵90EAC ACD ∠+∠=︒，90AEC BCD ∠+∠=︒∴EAC BCD AEC ACD ∠-∠=∠-∠∵90EAC BAE ∠+∠=︒∴ACD BAE ∠=∠又∵AEC B BAE ∠=∠+∠∴EAC BCD B BAE ACD ∠-∠=∠+∠-∠∴45EAC BCD B ∠-∠=∠=︒故答案为45︒．②如图，延长ED 至点G ，使得DG DE =，连接AG ，∵点D 为AB 的中点，∴BD AD =，又∵ADG BDE ∠=∠，∴ADG ≌BDE ，∴DGA DEB ∠=∠，∴//AG BC ，∴GAE AEC ∠=∠，又∵2AE DE =，∴AE EG =，∴DGA GAE ∠=∠，∴DEB AEC ∠=∠．（2）2CF DF =．如图，延长CD 至点H ，使得DH DF =，连接BH ，∵AD BD =，ADF BDH ∠=∠，∴HDB ≌FDA △，∴BH AF =，90H AFD AFC ∠=∠=∠=︒，∵BF AC =．∴Rt HBF △≌Rt FAC △，∴2CF HF DF ==．变式2-1．某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．（探究与发现）（1）如图1，AD 是ABC 的中线，延长AD 至点E ，使ED AD =，连接BE ，证明：ACD EBD △≌△．（理解与应用）（2）如图2，EP 是DEF 的中线，若5EF =，3DE =，设EP x =，则x 的取值范围是________．（3）如图3，AD 是ABC 的中线，E 、F 分别在AB 、AC 上，且DE DF ⊥，求证：BE CF EF +>．【答案】（1）见解析；（2）14x <<；（3）见解析【分析】（1）根据全等三角形的判定即可得到结论；（2）延长EP 至点Q ，使PQ PE =，连接FQ ，根据全等三角形的性质得到3FQ DE ==，根据三角形的三边关系即可得到结论；（3）延长FD 至G ，使得GD DF =，连接BG ，EG ，结合前面的做题思路，利用三角形三边关系判断即可．【详解】（1）证明：CD BD =，ADC EDB ∠=∠，AD ED =，ACD EBD ∴≌，（2）14x <<；如图，延长EP 至点Q ，使PQ PE =，连接FQ ，在PDE ∆与PQF ∆中，PE PQ EPD QPF PD PF =⎧⎪∠=∠⎨⎪=⎩，PEP QFP ∴∆≅∆，3FQ DE ∴==，在EFQ ∆中，EF FQ QE EF FQ -<<+，即53253x -<<+， x 的取值范围是14x <<；故答案为：14x <<；（3）延长FD 至G ，使得GD DF =，连接BG ，EG ，在DFC △和DGB 中，DF DG =，CDF BDG ∠=∠，DC DB =，(SAS)DFC DGB ∴≌，BG CF ∴=，在EDF 和EDG △中，DF DG =，90FDE GDE ∠=∠=︒，DE DE =，(SAS)EDF EDG ∴≌，EF EG ∴=，在BEG 中，两边之和大于第三边，BG BE EG ∴+>，又EF EG =，BG CF =，BE CF EF ∴+>变式2-2．倍长中线的思想在丁倍长某条线段（被延长的线段a 要满足两个条件：①线段a 一个端点是图中一条线段b 的中点；②线段a 与这条线段b 不共线)，然后进行连接，构造三角形全等，再进一步将某些线段进行等量代换，再证明全等或其他的结论，从而解决问题．（应用举例）如图（1），已知：AD 为ABC ∆的中线，求证：2AB AC AD +>．简证：如图（2），延长AD 到E ，使得DE AD =，连接CE ，易证ABD ECD ∆≅∆，得AB =，在ACE ∆中，AC CE +>，2AB AC AD +>．（问题解决）（1）如图（3），在ABC ∆中，AD 是BC 边上的中线，E 是AD 上一点，且BE AC =，延长BE 交AC 于F ，求证：AF EF =．（2）如图（4），在ABC ∆中，90,A D ∠=︒是BC 边的中点，E F 、分别在边AB AC 、上，DE DF ⊥，若3,4BE CF ==，求EF 的长．（3）如图（5），AD 是ABC ∆的中线，,AB AE AC AF ==，且90BAE FAC ∠=∠=︒，请直接写出AD 与EF 的数量关系_及位置关系_．【答案】,CE AE ；（1）详见解析；（2）5；（3）2EF AD =，EF AD ⊥【应用举例】由全等的性质可得AB=EC ，由三角形三边关系可得AC+CE>AE ，即AB+AC>2AD ；故答案为EC ，AE ；【问题解决】（1）由题意不难得到,ACD GBD ∆≅∆所以∠BGD=∠BED=∠AEF=∠DAC ，∴有AF=EF ；（2）延长ED 到G ，使DG=ED ，连结CG 、FG ，不难得到EF=FG ，另同（1）有△BDE ≌△CDG ，所以∠FCG=∠FCD+∠GCD=∠FCD+∠EBD=90°，CG=BE=3，由勾股定理可得FG 即EF 的长；（3）由全等三角形的性质可以得到解答．【详解】【应用举例】,CE AE【问题解决】()1如图()1延长AD 到G ，使得,DG AD =连接,BG易证,ACD GBD ∆≅∆得,BG AC G DAC =∠=∠，,BE AC =,BE BG ∴=,G BEG ∴∠=∠,BEG AEF ∠=∠,AEF EAC ∴∠=∠AF EF ∴=．()2如图()2，延长ED 到G ，使得,DG ED =连接,CG FG 、易证,BDE CDG ∆≅∆得,,CG BE ED GD B DCG ==∠=∠，,DE DF ⊥DF ∴垂直平分,EG,FE FG ∴=90,A ∠=︒90,B ACB ∴∠+∠=︒90,DCG ACB ∴∠+∠=︒即90,FCG ∠=︒在Rt FCG ∆中，3,4CG BE CF ===，5,FG ∴=5,EF ∴=()32EF AD EF AD =⊥，，理由如下：如图3，延长AD 到G ，使AD=DG ，延长DA 交EF 于P ，连结BG ，则不难得到△BGD≌△CAD，∴BG=AC，∠GBD=∠ACD，∠DGB=∠DAC，又AF=AC，∴BG=AF，∴∠ABG=∠ABD+∠GBD=∠ABD+∠ACD=180°-∠BAC=∠EAF，∴在△ABG和△EAF中，AB AEABG EAF BG AF=⎧⎪∠=∠⎨⎪=⎩，∴△ABG≌△EAF，∴EF=AG=2AD，∠EFA=∠DGB=∠DAC，∵∠DAC+∠PAF=180°-∠FAC=180°-90°=90°，∴∠EFA+∠PAF=90°，∴∠APF=90°，∴EF⊥AD ．考点题型三全等三角形–旋转模型典例3．在Rt△ABC中，∠ABC=90°，∠BAC＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△AED，点B、C的对应点分别是E、D.(1)如图1，当点E恰好在AC上时，求∠CDE的度数；(2)如图2，若α=60°时，点F是边AC中点，求证：四边形BFDE是平行四边形.【答案】（1）15°；（2）证明见解析.【分析】（1）如图1，利用旋转的性质得CA＝DA，∠CAD＝∠BAC＝30°，∠DEA＝∠ABC＝90°，再根据等腰三角形的性质求出∠ADC，从而计算出∠CDE的度数；（2）如图2，利用直角三角形斜边上的中线性质得到BF＝12AC，利用含30度的直角三角形三边的关系得到BC＝12AC，则BF＝BC，再根据旋转的性质得到∠BAE＝∠CAD＝60°，AB＝AE，AC＝AD ，DE＝BC，从而得到DE＝BF，△ACD和△BAE为等边三角形，接着由△AFD≌△CBA得到DF＝BA，然后根据平行四边形的判定方法得到结论．【详解】解：（1）如图1，∵△ABC绕点A顺时针旋转α得到△AED，点E恰好在AC上，∴∠CAD＝∠BAC＝30°，∠DEA＝∠ABC＝90°，∵CA＝DA，∴∠ACD＝∠ADC＝12（180°−30°）＝75°，∠ADE=90°-30°=60°，∴∠CDE＝75°−60°＝15°；（2）证明：如图2，∵点F是边AC中点，∴BF＝12 AC，∵∠BAC＝30°，∴BC＝12 AC，∴BF＝BC，∵△ABC绕点A顺时针旋转60°得到△AED，∴∠BAE＝∠CAD＝60°，AB＝AE，AC＝AD，DE＝BC，∴DE＝BF，△ACD和△BAE为等边三角形，∴BE＝AB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△AFD≌△CBA，∴DF＝BA，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．变式3-1．给出定义，若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．（1）在你学过的特殊四边形中，写出两种勾股四边形的名称；（2）如图，将△ABC绕顶点B按顺时针方向旋转60°得到△DBE，连接AD，DC，CE，已知∠DCB=30°．①求证：△BCE是等边三角形；②求证：DC2+BC2=AC2，即四边形ABCD是勾股四边形．【答案】(1)正方形、矩形、直角梯形均可；(2)①证明见解析②证明见解析【分析】（1）根据定义和特殊四边形的性质，则有矩形或正方形或直角梯形；（2）①首先证明△ABC≌△DBE，得出AC=DE，BC=BE，连接CE，进一步得出△BCE 为等边三角形；②利用等边三角形的性质，进一步得出△DCE是直角三角形，问题得解．【详解】解：（1）正方形、矩形、直角梯形均可；（2）①∵△ABC≌△DBE，∴BC=BE，∵∠CBE=60°，∴△BCE是等边三角形；②∵△ABC≌△DBE，∴BE=BC，AC=ED；∴△BCE为等边三角形，∴BC=CE，∠BCE=60°，∵∠DCB=30°，∴∠DCE=90°，在Rt △DCE 中，DC 2+CE 2=DE 2，∴DC 2+BC 2=AC 2．变式3-2．如图，在ABC △中，90BAC ∠=︒，E 为边BC 上的点，且AB AE =，D 为线段BE 的中点，过点E 作EF AE ⊥，过点A 作AF BC ，且AF 、EF 相交于点F .（1）求证：C BAD ∠=∠（2）求证：AC EF =【答案】（1）见解析；（2）见解析【分析】（1）由等腰三角形的性质可得AD ⊥BC ，由余角的性质可得∠C=∠BAD ；（2）由“ASA”可证△ABC ≌△EAF ，可得AC=EF ．【详解】（1）如图∵AB AE =，∴ABE ∆是等腰三角形 又∵D 为BE 的中点， ∴AD BE ⊥（等腰三角形三线合一） 在Rt ABC ∆和Rt DBA ∆中， ∵B 为公共角，90BAC BDA ∠=∠=︒， ∴C BAD ∠=∠.另解：∵D 为BE 的中点， ∵BD ED =，又AB AE =，AD AD =， ∴ADB ADE ∆≅∆，∴ADB ADE ∠=∠，又180ADB ADE ∠+∠=︒， ∴90ADB ADE ∠=∠=︒ ∴AD BC ⊥，在Rt ABC ∆和Rt DBA ∆中， ∵B 为公共角，90BAC BDA ∠=∠=︒， ∴C BAD ∠=∠.（2）∵AF BC ，∴EAF AEB ∠=∠，∵AB AE =，∴ABE AEB ∠=∠，∴EAF ABC ∠=∠，又∵90BAC AEF ∠=∠=∠︒， ∴BAC AEF ∆≅∆，∴AC EF =.考点题型四全等三角形– 垂线模型典例4．在△ABC 中，∠ACB ＝90°，AC ＝BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E ．(1)当直线MN 绕点C 旋转到图1的位置时，求证：△ADC ≌△CEB ；(2)当直线MN 绕点C 旋转到图2的位置时，试问DE 、AD 、BE 的等量关系?并说明理由． 【答案】（1）见解析；（2）DE=AD-BE ，理由见解析【分析】（1）由已知推出∠ADC=∠BEC=90°，因为∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，推出∠DAC=∠BCE ，根据AAS 即可得到答案；（2）与（1）证法类似可证出∠ACD=∠EBC ，能推出△ADC ≌△CEB ，得到AD=CE ，CD=BE ，即可得到答案．【详解】解：（1）证明：如图1，∵AD ⊥DE ，BE ⊥DE ，∴∠ADC=∠BEC=90°，∵∠ACB=90°，∴∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，∴∠DAC=∠BCE ，在△ADC 和△CEB 中， CDA BEC DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△CEB （AAS ）；（2）结论：DE=AD-BE ．理由：如图2，∵BE ⊥EC ，AD ⊥CE ，∴∠ADC=∠BEC=90°，∴∠EBC+∠ECB=90°，∵∠ACB=90°，∴∠ECB+∠ACE=90°，∴∠ACD=∠EBC ，在△ADC 和△CEB 中，ACD CBE ADC BEC AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△CEB （AAS ），∴AD=CE ，CD=BE ，∴DE=EC-CD=AD-BE ．变式4-1．在直角三角形ABC 中，90,30︒︒∠=∠=ACB BAC ，分别以AB 、AC 为边在ABC ∆外侧作等边ABE ∆和等边ACD ∆，DE 交AB 于点F ，求证：=EF FD .【答案】详见解析【分析】过点E 作EG AB ⊥于点G ，则有1122AG BG AE AB ===，再证 ()SAS ACB EGA ≅，得到EG AC =.从而得到90DAF DAC CAB ∠=∠+∠=︒，所以(AAS)ADF GEF ≅，即可完成证明。

全等三角形常见辅助线作法【例1】.已知：如图6, 4BCE、△ACO分别是以8E、为斜边的直角三角形，且= ACDE是等边三角形.求证：△ A3c是等边三角形.【例2】、如图，已知BC>AB, AD=DCo BD 平分NABC。

求证：ZA+ZC=180°.线段的数量关系: 通过添加辅助线构造全等三角形转移线段到一个三角形中证明线段相等。

1、倍长中线法【例.3］如图，己知在△ABC中，ZC = 90°, ZB = 30°, A。

平分NB4C,交BC于点D.求证：BD = 2CD证明：延长DC到E,使得CE=CD,联结AEZC=90°A AC ± CDVCD=CEAD=AEVZB=30° ZC=90°ZBAC=60°YAD 平分NBACJ ZBAD=30°A DB=DA ZADE=60°VDB=DA：.BD=DE/. BD=2DC4B D笫3题•/ ZADE=60° AD=AEA △ ADE为等边三角形，AD=DE【例4.】如图，。

是AABC的边上的点，且CD = AB, ZADB = ZBAD, AE是AARD的中线。

求证：AC = 2AEo 证明：延长AE至IJ点F,使得EF=AE联结DF在4ABE和4FDE中BE=DEZAEB=ZFEDAE=FE/.△ABE 也AFDE (SAS) A AB=FD ZABE=ZFDE VAB=DCJ FD = DCZADC=ZABD+ZBAD ZADB = ZBAD，ZADC=ZABD+ZBDA VZABE=ZFDE・・・NADONADB+NFDE即ZADC= ZADF ffiAADF 和AADC 中AD=AD< ZADF= ZADC、DF =DC・•・△ ADF也ADC(SAS) AAF=ACAC=2AE【变式练习】、如图，AABC中，BD二DOAC, E是DC的中点，求证：AD平分NBAE.【小结】熟悉法一、法三“倍长中线”的辅助线包含的基本图形“八字型”和“倍长中线”两种基本操作方法, 倍长中线，或者倍长过中点的一条线段以后的对于解决含有过中点线段有很好的效果。

保送生黄怀毅：用坚持实现梦想(图)黄怀毅敲开梦想中清华大学的大门，收到期盼中的录取通知书，来自泉州五中的黄怀毅，凭借全国高中数学联赛的优异成绩成为清华大学软件学院的保送生。

勤奋认真、不懈拼搏，是黄怀毅多年来坚持的学习和生活方式。

他用自己坚定的步伐，努力迈向梦想，创造辉煌。

数学：坚定的追求黄怀毅从小学开始，对知识就有着热切的渴望，对数学更是有着特别的追求。

谈到这份与数学的不解之缘，他提到，“我一直对数学有着无由的钟爱，这也离不开数学老师给予我的鼓励和帮助”。

他对数学的这种奇妙感觉一直持续着。

上了初中，开始更加认真钻研数学，并且和同学一起讨论，提升学习能力的同时，更体会了合作和分享的快乐。

“在初二年的一次练习中，我曾与另一个一起学习数学竞赛的非常要好的同学用六条辅助线合作做出一道正解有十几条辅助线的几何题，那种兴奋的心情无以言表！那种经历含苞待放下的瞬间绽放不也能说是一种生命的极致！在这种时候，我领会了一种合作的重要价值，这比一个人做出一道题的快乐更可贵，这还包含一种合作的快乐，分享的快乐，又有如一遇知己，心有灵犀，正是漫漫人生中一段最美丽的片段。

”步入高中，他愈发坚定了自己对数学的追求。

他与几个一起读数学竞赛的朋友合作，竞争，一起为了同一个梦想不断努力朝前进。

“我们渴望在全国高中数学联赛中发挥出自己最好的水平。

最后，我拿到了梦寐以求的一等奖。

是数学，让我们团聚在一起；是数学，让我们找到了知己。

人不一定要有终点的美丽，在过程中留下过奋斗的足迹，也可以是生命的一道风景！”数学已经成了他生活的一部分，这份对数学坚定的追求令他收获了友谊，收获了荣誉，更助他进入了梦想的清华大学。

长跑：坚持到习惯黄怀毅的坚持不仅仅表现在学业上，生活中的他也是一个坚持不懈的人。

在提到长跑兴趣时，他如是说，“我坚信，不必有出众的才华，不需有华丽的外表，只要你有一双完整的腿，你就能奔跑！”初二，他人生中第一次尝试跑长跑，他把这当作是对自己的一种考验，是自己给自己下达的命令。

八年级上册数学几何辅助线经典题一、概述在数学几何学科中，辅助线是解决问题的重要方法之一。

在八年级上册数学教材中，有许多经典的数学几何辅助线题目，通过这些题目的练习，可以帮助学生更好地掌握辅助线的运用方法，提高解题能力。

本文将针对八年级上册数学几何辅助线经典题进行详细介绍和解析。

二、题目一：相似三角形的辅助线应用题目描述：如图所示，∠ABC=∠ACD=90°，AB=4cm，AC=6cm，CD=9cm，求AD的长度。

解析：根据题目给出的信息，我们可以通过绘制辅助线来解决这道题。

连接BD并延长至E点，使得BE=BC。

接下来，连接AE，可得到相似三角形ABE与ACD。

根据相似三角形的性质，我们可以得出以下等式：AB/AC=BE/AD，即4/6=4/(4+AD)。

通过解方程，可以求得AD=8cm。

三、题目二：三角形中的中位线问题题目描述：如图所示，△ABC中，D为AB的中点，E为AC的中点，连接DE，求证：DE//BC。

解析：这道题目考察了中位线的性质和应用。

根据△ABC的性质，可以得出AD=DC，AE=EB，通过连接DE可以得到四边形ADBE。

根据四边形的性质，可以得出ADBE是一个平行四边形，而平行四边形的对角线互相平分，因此DE//BC。

四、题目三：正方形中的选点问题题目描述：如图所示，ABCD为正方形，E为BC的中点，连接AE，求证：AE⊥CD。

解析：这道题目是典型的正方形中的选点问题。

首先根据正方形的性质可以得出AB⊥BC，BC⊥CD，AD⊥DC，因此AD//BC。

接下来连接AE，并可得到△ADE与△CDE，由△ADE≌△CDE，可得出AE⊥CD。

五、结语通过以上三道典型的数学几何辅助线经典题目的解析，我们可以看到辅助线在解决问题中的重要作用。

通过练习和掌握这些经典题目，不仅可以提高学生的数学运算能力，还可以加深对数学几何知识的理解。

希望学生能够在课堂上认真学习，多加练习，提高自己的解题能力，取得好成绩。

辅助线——解正方形题必杀技江苏 徐灯书在解与正方形有关的问题时，通常要作适当的辅助线来牵线搭桥．辅助线是我们成功解题的“桥梁”．一、添加辅助线构造等腰三角形例1 把正方形ABCD 绕着点A ，按顺时针方向旋转得到正方形AEFG ，边FG 与BC 交于点H （如图1）．试问线段HG 与线段HB 相等吗？请先观察、猜想，然后再说明你猜想的正确性．图1分析：猜想HG HB =，证明线段相等的思路通常是证明两线段所在的三角形全等或判定两线段所在的三角形为等腰三角形．本题应考虑等腰三角形的等角对等边予以说明较为简捷．解：HG HB =．理由：连接GB ．因为四边形ABCD 、AEFG 都是正方形，所以90ABC AGF ∠=∠=．由题意知AB AG =．所以AGB ABG ∠=∠．所以HGB HBG ∠=∠．所以HG HB =．二、作对角线例2 如图2，在正方形ABCD 中，P 为对角线BD 上一点，BE PC ⊥，垂足为E ，4AP =，3BE =，则BPC △的面积是 ．图2分析：根据正方形的对角线相等且互相垂直平分，知4AP PC ==，从而易求BPC △的面积．解：连接AC ，因为四边形ABCD 是正方形，所以对角线AC 与BD 互相垂直平分．所以4AP PC ==． 所以1143622BPC S PC BE =⋅=⨯⨯=△． 三、作平行线例3 如图3，P 为正方形ABCD 边BC 延长线上的一点，E 为DP 的中点，DP 的垂直平分线交边DC 于M ，交边AB 的延长线于N ．试说明DP MN =．图3分析：欲判定DP MN =，联想到全等三角形是判定线段或角相等的重要手段，从而考虑过M 作MH BC ∥，通过判定DPC MNH △≌△来实现．解：在正方形ABCD 中，AB BC CD ==，90ABC BCD ∠=∠=．过M 作MH BC ∥交AB 于点H ，则四边形HBCM 是矩形．所以MH BC CD ==，90MHN ∠=．因为18090DCP BCD ∠=-∠=，所以DCP MHN ∠=∠．因为90P PDC +∠=，90PDC DME ∠+∠=，所以DME P ∠=∠．而DME NMC ∠=∠，N NMC ∠=∠，所以N P ∠=∠．所以DPC MNH △≌△．所以DP MN =．四、截长补短例 4 如图4，E 是正方形ABCD 的边BC 上一点，F 是DC 的延长线上一点，且BAE FAE ∠=∠，试猜想线段BE 、DF 、AF 的数量关系，并说明你的理由．图4分析：借助刻度尺测量，知BE DF AF +=．考虑利用延长法（将一短线段延长，使整条线段等于两短线段的和，再说明整条线段等于长线段）来说明．即将FD 延长至E '，使DE BE '=，只需再推出AFE '△是等腰三角形，即可寻找线段BE 、DF 、AF 的数量关系．解：猜想BE DF AF +=．理由：将FD 延长至E '，使DE BE '=，连接AE '．由正方形的性质知，90ABE ADE '∠=∠=，AB AD =．所以ABE ADE '△≌△．所以BAE DAE '∠=∠，AEB E '∠=∠．由于BAE FAE ∠=∠，而BAE DAE '∠=∠，所以EAF DAE '∠=∠．所以DAE FAE '∠=∠．由AD BC ∥，知AEB DAE ∠=∠，所以AEB FAE '∠=∠，即E FAE ''∠=∠．所以E F AF '=．故BE DF AF +=．。