三角函数诱导公式及经典记忆方法
- 格式:doc
- 大小:215.00 KB
- 文档页数:9

三角函数诱导公式及推导-CAL-FENGHAI.-(YICAI)-Company One1三角函数诱导公式:所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
常用公式:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)= tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)= cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)= cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαsin(π/2-α)=cosαcos(π/2+α)=-sinαcos(π/2-α)=sinαtan(π/2+α)=-cotαtan(π/2-α)=cotαcot(π/2+α)=-tanαcot(π/2-α)=tanα推算公式:3π/2 ±α与α的三角函数值之间的关系:sin(3π/2+α)=-cosαsin(3π/2-α)=-cosαcos(3π/2+α)=sinαcos(3π/2-α)=-sinαtan(3π/2+α)=-cotαtan(3π/2-α)=cotαcot(3π/2+α)=-tanαcot(3π/2-α)=tanα诱导公式记忆口诀:“奇变偶不变,符号看象限”。

三角函数诱导公式:所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
常用公式:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)=-cosαtan(π+α)= tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)= cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)= cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαsin(π/2-α)=cosαcos(π/2+α)=-sinαcos(π/2-α)=sinαtan(π/2+α)=-cotαtan(π/2-α)=cotαcot(π/2+α)=-tanαcot(π/2-α)=tanα推算公式:3π/2 ±α与α的三角函数值之间的关系:sin(3π/2+α)=-cosαsin(3π/2-α)=-cosαcos(3π/2+α)=sinαcos(3π/2-α)=-sinαtan(3π/2+α)=-cotαtan(3π/2-α)=cotαcot(3π/2+α)=-tanαcot(3π/2-α)=tanα诱导公式记忆口诀:“奇变偶不变,符号看象限”。

诱导公式记忆口诀诱导公式大家知道它的记忆方式有哪些吗?哪个可以帮助你记得又快又准?下面是店铺给大家整理的诱导公式记忆口诀,供大家参阅!诱导公式记忆口诀规律公式一到公式五函数名未改变,公式六函数名发生改变。
公式一到公式五可简记为:函数名不变,符号看象限。
即α+k·360°(k∈Z),﹣α,180°±α,360°-α的三角函数值,等于α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号。
上面这些诱导公式可以概括为:对于kπ/2±α(k∈Z)的三角函数值,①当k是偶数时,得到α的同名函数值,即函数名不改变;②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan。
(奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号。
(符号看象限)例如:sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。
当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。
所以sin(2π-α)=-sinα口诀奇变偶不变,符号看象限。
注:奇变偶不变(对k而言,指k取奇数或偶数),符号看象限(看原函数,同时可把α看成是锐角)。
公式右边的符号为把α视为锐角时,角k·360°+α(k∈Z),-α、180°±α,360°-α所在象限的原三角函数值的符号可记忆:水平诱导名不变;符号看象限。
各种三角函数在四个象限的符号如何判断,也可以记住口诀“一全正;二正弦(余割);三两切;四余弦(正割)”.这十二字口诀的意思就是说:第一象限内任何一个角的三角函数值都是“+”;第二象限内只有正弦和余割是“+”,其余全部是“-”;第三象限内只有正切和余切是“+”,其余函数是“-”;第四象限内只有正割和余弦是“+”,其余全部是“-”。

1 / 1
诱导公式的记忆口诀
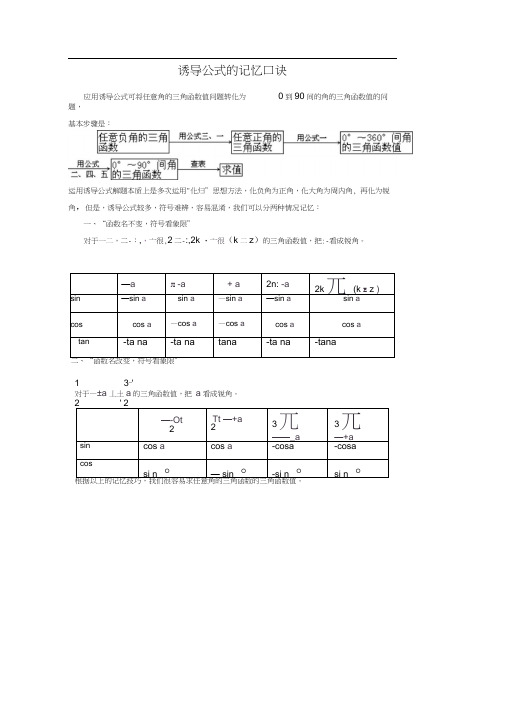
应用诱导公式可将任意角的三角函数值问题转化为 0到 90间的角的三角函数值的问题,基本步骤是:
运用诱导公式解题本质上是多次运用“化归”思想方法,化负角为正角,化大角为周内角,再化为锐角,但是,诱导公式较多,符号难辨,容易混淆,我们可以分两种情况记忆:
一、“函数名不变,符号看象限”
对于)(2,2,,,z k k ∈+-+--απαπαπαπα的三角函数值,把α看成锐角。
二、“函数名改变,符号看象限” 对于απ
απ
±±3,
的三角函数值,把α看成锐角。
根据以上的记忆技巧,我们很容易求任意角的三角函数的三角函数值。

八个诱导公式的口诀在咱们学习三角函数的时候,那八个诱导公式就像是一道道小关卡,不过别担心,我这儿有一套超棒的口诀来帮你轻松应对!“奇变偶不变,符号看象限。
”这简简单单的八个字,可是蕴含着大大的学问呢!先来说说“奇变偶不变”。
啥意思呢?就是当咱们的角度加上或者减去的是π/2 的奇数倍,比如π/2、3π/2 等等,函数名称就得变,正弦变余弦,余弦变正弦,正切变余切,余切变正切。
要是加上或者减去的是π/2 的偶数倍,像π、2π 这些,那函数名称就不变啦。
再看“符号看象限”。
这就更有意思啦!比如说,咱们要计算sin(π/2 + α) ,那咱们先把α 当成锐角,π/2 + α 就在第二象限。
第二象限正弦是正的,所以sin(π/2 + α) 就等于cosα 。
我记得之前给一个学生讲这个的时候,他总是迷糊,怎么都搞不清楚。
我就给他举了个特别形象的例子。
假设α 是一个正在欢快玩耍的小朋友,π/2 呢,就像是一个大转盘,每次加上或者减去它,小朋友的状态就会发生变化。
如果是奇数倍的转盘,小朋友就得换身衣服,从正弦小朋友变成余弦小朋友,或者从正切小朋友变成余切小朋友。
如果是偶数倍的转盘,小朋友就还是原来的样子,只是心情可能会变。
而这个心情是好是坏,就得看他转到了哪个象限。
咱们再来看具体的公式。
sin(-α)= -sinα ,这就好像α 小朋友心情不好,生闷气了,负负得正,心情就好了,所以符号是负的。
cos(-α)=cosα ,α 小朋友心情不错,没有变化,所以符号是正的。
sin(π - α) = sinα ,这就像是α 小朋友玩累了,睡了一觉,醒来还是那个快乐的自己,所以函数不变,符号也是正的。
cos(π - α) = -cosα ,α 小朋友做了个噩梦,心情糟糕了,所以符号变成负的。
sin(π + α) = -sinα ,α 小朋友被噩梦吓哭了,心情超级差,所以符号是负的。
cos(π + α) = -cosα ,α 小朋友一直哭一直哭,心情怎么都好不起来,所以符号还是负的。
诱导公式一、三种三角函数(sin cos tan)的函数值正负象限分布情况(基础内容)sinαcosαtanα(cotα)二、诱导公式(对所有的三角函数都适用)(一)负角变正角看该三角函数第四象限的符号。
例sin(﹣30°)=﹣sin30°cos(﹣50°)=cos50°tan(﹣80°)=﹣tan80°(二)π的偶数倍角的转换。
(α看做锐角,切记!!!否则结果是错误的)1.+α,看该三角函数第一象限符号(α看做锐角,即使α是钝角也当做锐角)2.-α,看该三角函数第四象限符号(α看做锐角,即使α是钝角也当做锐角)此时三角函数转换前后的三角函数(sin cos tan)并没有变化。
例sin(4π+α)=sinαtan(﹣4π-α)=﹣tanαcos400°=cos(180°*2+40°)=cos40°sin(﹣480°)=sin(﹣180°*2-60°)=﹣sin60°注:π的偶数倍的转换,其实就是讲角化成2kπ±α的形式,而2Kπ就相当于一个终边在X轴正半轴的角,之后再利用旋转的知识对±α进行运算。
(另一种理解方式)(三)π的奇数倍角的转换。
(α看做锐角,切记!!!否则结果是错误的)1.+α,看该三角函数第三象限符号(α看做锐角,即使α是钝角也当做锐角)2.-α,看该三角函数第二象限符号(α看做锐角,即使α是钝角也当做锐角)此时三角函数转换前后的三角函数(sin cos tan)并没有变化。
例cos495°=cos(3*180°-45°)=﹣cos45°Sin870°=sin(5*180°-30°)=sin30°注:π的奇数倍的转换,其实就是讲角化成kπ±α的形式,而Kπ就相当于一个终边在X轴负半轴的角,之后再利用旋转的知识对±α进行运算。
三角函数诱导公式大全三角函数诱导公式三角函数诱导公式一:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα三角函数诱导公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα三角函数诱导公式三:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα三角函数诱导公式四:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)三角函数诱导公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα三角函数诱导公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)2诱导公式作用及用法一、三角函数诱导公式的作用:可以将任意角的三角函数转化为锐角三角函数。
诱导公式是指三角函数中,利用周期性将角度比较大的三角函数,转换为角度比较小的三角函数的公式。
接下来给大家分享三角函数常用的诱导公式及记忆口诀。
三角函数的诱导公式诱导公式一:终边相同的角的同一三角函数的值相等设α为任意锐角,弧度制下的角的表示:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)诱导公式二:π+α的三角函数值与α的三角函数值之间的关系设α为任意角,弧度制下的角的表示:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα诱导公式三:任意角α与-α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα诱导公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系sin(π-α)=sinαcos(π-α)=-cosαcot(π-α)=-cotα诱导公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα诱导公式六:π/2±α及3π/2±α与α的三角函数值之间的关系sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotα三角函数诱导公式记忆口诀奇变偶不变,符号看象限。
三角函数诱导公式及记忆方法一、同角三角函数的基本关系式(一)基本关系1、倒数关系tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=12、商的关系sinα/cosα=tanαsecα/cscα=tanαcosα/sinα=cotαcscα/secα=cotα3、平方关系sin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α(二)同角三角函数关系六角形记忆法构造以"上弦、中切、下割;左正、右余、中间1"的正六边形为模型。
1、倒数关系对角线上两个函数互为倒数;2、商数关系六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。
(主要是两条虚线两端的三角函数值的乘积,下面4个也存在这种关系。
)。
由此,可得商数关系式。
3、平方关系在带有阴影线的三角形中,上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。
二、诱导公式的本质所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
(一)常用的诱导公式1、公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα,k∈z cos(2kπ+α)=cosα,k∈ztan(2kπ+α)=tanα,k∈z cot(2kπ+α)=cotα,k∈zsec(2kπ+α)=secα,k∈z csc(2kπ+α)=cscα,k∈z2、公式二:α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosαtan(π+α)= tanα cot(π+α)= cotαsec (π+α) =—secα csc (π+α) =—cscα3、公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)=-sinα cos (-α)= cosα tan (-α)=-tanα cot (-α)=-cotα sec (—α) = secα csc (—α) =—cscα4、公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin (π-α)= sinα cos (π-α)=-cosαtan (π-α)=-tanα cot (π-α)=-cotαsec (π—α) =—secα csc (π—α) = cscα5、公式五:利用公式一和公式三可以得2π-α与α的三角函数值之间的关系:sin (2π-α)=-sinα cos (2π-α)= cosαtan (2π-α)=-tanα cot (2π-α)=-cotαsec (2π—α) = secα csc (2π—α) =—cscα6、公式六:2π+α与α的三角函数值之间的关系:sin (2π+α)= cosα cos (2π+α)=-sinαtan (2π+α)=-cotα cot (2π+α)=-tanα sec (2π+α) =—cscα csc (2π+α) =secα7、公式七:2π-α与α的三角函数值之间的关系:sin (2π-α)= cosα cos (2π-α)=sinαtan (2π-α)= cotα cot (2π-α)=tanαsec (2π—α) = cscα csc (2π—α) =secα8、推算公式:23π+α与α的三角函数值之间的关系: sin (23π+α)=-cosα cos (23π+α)= sinα tan (23π+α)=-cotα cot (23π+α)=-tanα sec (23π+α) = cscα csc (23π+α) =—secα9、推算公式:23π—α与α的三角函数值之间的关系: sin (23π-α)=-cosα cos (23π-α)=-sinαtan (23π-α)= cotα cot (23π-α)= tanαsec (23π-α) =—cscα csc (23π—α) =—secα诱导公式记忆口诀:“奇变偶不变,符号看象限”。
“奇、偶”指的是2π的倍数的奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。
(反之亦然成立)“符号看象限”的含义是:把角α看做锐角,不考虑α角所在象限,看n·(π/2)±α是第几象限角,从而得到等式右边是正号还是负号。
符号判断口诀:“一全正;二正弦;三两切;四余弦”。
这十二字口诀的意思就是说:第一象限内任何一个角的四种三角函数值都是“+”;第二象限内只有正弦是“+”,其余全部是“-”;第三象限内只有正切和余切是“+”,其余全部是“-”;第四象限内只有余弦是“+”,其余全部是“-”。
“ASCT”意即为“all(全部)”、“sin”、“tan”、“cos”(二)其他三角函数知识1、两角和差公式sin(α+β)= sinαcosβ+cosαsinβsin(α-β)= sinαcosβ-cosαsinβcos(α+β)= cosαcosβ-sinαsinβcos(α-β)= cosαcosβ+sinαsinβtan(α+β)=(tanα+tanβ )/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)2、二倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2αtan2α=αα2tan -12tan 3、半角的正弦、余弦和正切公式sin 22α=2cos -1α cos 22α=2cos 1α+ tan 22α=ααcos 1cos -1+ tan 2α=ααsin cos -1=ααcos 1sin + 4、万能公式sinα=2tan 122tan2αα+ cosα=2tan 12tan -122αα+ tanα=2tan -122tan2αα5、三倍角的正弦、余弦和正切公式sin3α=3sinα-4sin 3α cos3α=4cos 3α-3cosαta n3α=α—α—α233tan 1tan 3tan 6、三角函数的和差化积公式 sinα+sinβ=2sin 2βα+·cos 2β—α sinα-sinβ=2cos 2βα+·sin 2β—αcosα+cosβ= 2cos 2βα+·cos 2β—α cosα-cosβ=-2sin 2βα+·sin 2β—α7、三角函数的积化和差公式sinα·cosβ=21[sin(α+β)+sin(α-β)]cosα·sinβ=21 [sin(α+β)-sin(α-β)] cosα·cosβ=21 [cos(α+β)+cos(α-β)] sinα·sinβ=-21 [cos(α+β)-cos(α-β)] 三、公式推导过程 (一)万能公式推导 sin2α=2sinαcosα=αααα22sin cos cos sin 2+ (因为cos 2α+sin 2α=1) 再把上面的分式上下同除cos 2α,可得sin2α=2tan 122tan2αα+ 然后用2α代替α即可。
同理可推导余弦的万能公式。
正切的万能公式可通过正弦比余弦得到。
(二)三倍角公式推导tan3α=ααcos3sin3=αα—ααααααcos sin2sin cos2sin 2cos cos sin2+=αα—αα—αα—ααααcos sin 2sin cos cos sin sin cos cos sin 22222+ 上下同除以cos 3α,得:tan3α=α—α—α233tan 1tan 3tan sin3α=sin(2α+α)=sin2αcosα+cos2αsinα=2sinαcos 2α+(1-2sin 2α)sinα =2sinα-2sin 3α+sinα-2sin 3α =3sinα-4sin 3αcos3α=cos(2α+α)=cos2αcosα-sin2αsinα=(2cos 2α-1)cosα-2cosαsin 2α =2cos 3α-cosα+(2cosα-2cos 3α) =4cos 3α-3cosα 即 sin3α=3sinα-4sin 3α cos3α=4cos 3α-3cosα (三)和差化积公式推导首先,我们知道sin(α+β)=sin αcos β+cos αsin β, sin(α-β)=sin αcos β-cos αsin β我们把两式相加就得到sin(α+β)+sin(α-β)=2sin αcos β所以,sin αcos β=2sin sin β)—(αβ)(α++同理,若把两式相减,就得到cos αsin β=2sin sin β)—(α—β)(α+同样的,我们还知道cos(α+β)=cos αcos β-sin αsin β,cos(α-β)=cos αcos β+sin αsin β所以,把两式相加,我们就可以得到cos(α+β)+cos(α-β)=2cos αcos β所以我们就得到,cos αcos β=2cos cos β)—(αβ)(α++同理,两式相减我们就得到sin αsin β= —2cos cos β)—(α—β)(α+这样,我们就得到了积化和差的四个公式:sin αcos β=2sin sin β)—(αβ)(α++cos αsin β=2sin sin β)—(α—β)(α+cos αcos β= 2cos cos β)—(αβ)(α++sin αsin β=-2cos cos β)—(α—β)(α+好,有了积化和差的四个公式以后,我们只需一个变形,就可以得到和差化积的四个公式.我们把上述四个公式中的α+b 设为x, α-β设为y,那么α=2y x +, β=2yx - 把α,β分别用x,y 表示就可以得到和差化积的四个公式: sinx+siny=2sin 2y x +cos 2yx - sinx-siny=2cos 2y x +sin 2y x - cosx+cosy=2cos2y x +cos 2y x - cosx-cosy=—2sin2y x +sin 2yx -。