高新一中八年级数学下册自学导案(42)

☆ 高新一中八年级数学下册自学导案（38）课题：一、 温故引新：1．要使△ABC ∽△A ＇B ＇C ＇（1）若∠A ＝∠A ，则需添加的条件是 。

（2）若BC B'C' ＝ACA'C'＝K ，则需添加的条件是 。

2．若△ABC ∽△A ＇B ＇C ＇，则有 。

3．什么叫做相似多边形 ；相似多边形的对应角 _____ ，各对应边________ 。

二．明确目标：1．经历探索相似多边形的性质的过程，发展积极的情感态度价值观和探索精神。

2. 理解并掌握相似三角形对应高的比，角平分线的比，中线的比等于相似比并能用它解决 简单的问题.， 三．探究新知： （一）自主探究1．某技术工人准备按照比例尺3:4的图纸制作三角形零件, 如图1,图纸上的△ ABC 表示该零件的横断面△ A’B’C’ （1）B A AB ''＝ ，C B BC ''＝ , C A AC''＝ （2）△ABC 与△A ′B ′C ′相似吗？ 如果相似，请说明理由，并指出它们的相似比.（3）在图中你还能找出相似三角形吗？ （图1） （4）DC CD''等于多少？你是怎么做的？ 2．联系拓广【练1】．如图，已知△ABC ∽△A ’B ’C ’ ，△ABC 与△D'C'B'A'DBCAC'B'CA ’B ’C ’相似比为k,AE ，A ’E ’是对应 中线，求证：【练2】．如图，已知△ABC ∽△A’B’C’中，△ABC 与△A ’B ’C ’相似比为k, AF ，A ’F ’是对应角平分线。

求证：（二）形成概念相似三角形的性质：（三）学以致用1．如果两个相似三角形的对应高的比为2:3，那么对应角平分线的比是_ _ ，对应边上的中线的比是______ ,那么两个三角形的相似比是 。

2．如图△ABC ∽△A ’B ’C ’，对应中线AD ＝6cm ，A ’D ’＝10cm ，则△ABC 与A ’B ’C ’的相似比是 。

课题：一、情境创设：超级女生李宇春，不仅人长的漂亮，歌唱的好，人缘更好。

她美丽善良；她温柔可爱；她飒爽英姿；她无所不能。

人们都喜欢她。

在这段48字的介绍中，哪个字出现次数最多？有几次？二、明确目标：1、理解频数、频率等概念，会对一组数据进行统计，并列出相应的统计图表。

2、能根据数据处理的结果，做出合理的判断与预测，从而解决实际问题，并在这一过程中体会统计对决策的作用。

3、.通过统计数据，制成各种图表，增强学生对生活中所见到的统计图表进行数据处理和评判的主动意识。

三、探究新知：（一）自主探究阅读课本P184-185并回答问题（1）（2）（3）（二）形成概念频数：频率：频率=频数/总次数（三）学以致用1．一组数据“3.5.5.3.3”中“5”出现的频数为____频率为____。

2.一次语文测验，100名学生中有36人得了优秀，则优秀人数的频数为____频率为_____。

3。

完成课本P186做一做、议一议Array四．拓展提升1. 在对某班的一次英语测验成绩进行统计分析中，各分数段的人数如图所示（分数取正整数，满分100分）．（1）该班有多少名学生．（2）69.5～79.5分这一组的频数是多少？频率是多少？2．你们喜爱球类体育运动吗？请从下面几项中选出你最喜爱的球类运动项目。

A、篮球B、排球C、足球D、羽毛球E、乒乓球（每小组分别请一位同学到黑板上进行统计，将每位同学最喜爱的球类运动用字母表示出来。

列出统计表并画出适当的统计图）五、学后检测1．近几年，人们的环保意识逐渐增强，“白色污染”现象越来越受到人们的重视.下表是李昕同学对自己的家庭某一周内丢弃的塑料袋数目的统计：请你帮李昕估算一下，照这样下去，李昕家一年大约要丢弃__个塑料袋（一年按365天计算）. 2．光明中学环保小组对某区8个餐厅一天的快餐饭盒使用个数做调查，结果如下：125 115 140 270 110 120 100 140①这8个餐厅平均每个餐厅一天使用饭盒________个.②根据样本平均估算，若该区有餐厅62个，则一天共使用饭盒________个.3．为了迎接2010年世博会，某单位举办了英语培训班.100名职工在一个月内参加英语培训的次数如下表所示：这个月每个职工平均参加英语培训的次数为________.4. 对某班的一次数学测验成绩进行统计分析，各分数段的人数如图所示（分数取正整数，满分为100分）．请根据图形回答下列问题：①该班有名学生；②70～79分这一组的频数是 ，频率是 ． 六、学后反思40～49 50～59 60～69 70～79 80～8990～99 成绩/。

课题：一元一次不等式和一元一次不等式组的分类复习题一、不等式的概念和性质 （一）不等式的概念（1）例1：已知①1=+y x ；②y x >；③y x 2+；④12≥-y x ；⑤0<x 其中属于不等式的有（ ）A. 2个B. 3个C. 4个D. 5个（2）例2：在01322>+-y y ，0122=++y y ，26-<-，272ab ，1232-+x x ，0312<--y y ，6557+≥+x x 中，是一元一次不等式的是 （二）不等式的性质： 1、例：如果不等式1)1(->-a x a 的解集是1<x ，那么a 的取值范围是 。

2、练习：⑴已知关于x 的不等式2)1(>-x a 的解集为ax -<12则a 的取值范围是 。

⑵如果0<<n m 那么下列结论错误的是（ ） A. 99-<-n m B. n m ->- C. m n 11> D. 1>nm ⑶若10<<a ，则2a ，a1，a 之间的大小关系是 。

⑷如果a<b ，那么（ ）A. 2a ＜2bB. 2b ab <C. 2a ＜abD. －2a ＞－2b ⑸如图所示，对a ，b ，c 三种物体的重量判断正确的是（ ）A. a<cB. a<bC. a>cD. b<c ⑹若1>ba，则下列各式正确的是（） A. a>b B. a<b C. ab>0 D. 以上答案都不对⑺已知ab ＜0，ab 2>0,且a ＋b ＜0，下列四个答案中正确的是（ ） A.1->b a B. 1-<b a C. 1>b a D. 1<ba⑻如果ab ＜0，且a －b ＜0，则a 、b 的符号是（ ）A. a ＞0，b ＞0B. a ＜0，b ＜0C. a ＜0，b ＞0D. a ＞0，b ＜0一元一次不等式和一元一次不等式组的复习第1页共16页⑼如果－a 2b ＞0且a ＜0，那么下列式子中，正确的是（ ） A. ab 2＞0 B. a 2＋ab ＞0 C.a ＋b ＞0 D.02>ab⑽当a ＜0，b ＞0，a ＋b ＞0时，把a 、b 、－a 、－b 四个数用“＜”连接是 ⑾若y x >，则ay ax >,那么一定有（ ） A. a ＞0 B. a ＜0 C. a ≥0 D. a ≤0 ⑿若y x >则ay ax ≤，那么一定有（ ） A. a ＞0 B. a ＜0 C. a ≥0 D. a ≤0 ⒀若y x <，则y a x a 22<那么一定有（ ） A. a>0 B. a<0 C. a ≠0 D. a 是任意实数 ⒁若4a ＞5a 成立，那么一定有（ ）A. a ＞0B. a ＜0C. a ≥0D. a ≤0⒂已知x ＜0，－1<y ＜0，将x ，xy ，xy 2从小到大依次排列 。

课题：一、 温故引新1．要证明两直线平行，有哪些方法?2．几何推理证明的思路是否是唯一的?能举例说明吗?3．你能否将上一节的1个公理，2个定理的条件与结论互换吗? 二．明确目标：1．理解掌握平行线的性质公理和定理，会用它们进行推理。

２．了解平行线的性质定理与判定定理的区别，能在推理过程中正确运用，进一步熟悉掌握推理过程的规范的书写方法及格式. 三．探究新知：1平行线的第一个性质（公理）：两直线平行，同位角相等 想一想：利用这个公理，你能证明哪些熟悉的结论？ 2．证明定理：两直线平行，内错角相等。

证明的步骤（1）根据题意，画出相应的图形。

（2）根据题意，结合图形，写出已知、求证。

（3）写出推理过程。

定理：两条平行线被第三条直线所截，内错角相等。

简写：两直线平行，内错角相等。

3．证明定理：两直线平行，同旁内角互补。

⎩⎨⎧，内错角相等利用定理：两直线平行，同位角相等利用公理：两直线平行两种方法 定理：两条平行线被第三条直线所截，同旁内角互补。

简写：两直线平行，同旁内角互补。

四、拓展与提高1.如图，ＢＤ平分∠ＡＤＣ，ＤＥ∥ＡＢ，试说明△ＤＥＢ的形状，并说明理由。

CEDAB2．过△ABC的顶点C任作一直线，与边AB及中线AD分别交于点F和E，求证：AE∶ED=2AF∶FB.3．如下图，△ABC中，AD∥BC，连结CD交AB于E，且AE∶EB=1∶3，过E作EF∥BC，交AC于F，S△ADE=2cm2，求S△BCE，S△AEF.4．下图中，E为平行四边形ABCD的对角线AC上一点，AE∶EC=1∶3，BE的延长线交CD的延长线于G，交AD于F，求证：BF ∶FG=1∶2.四．学后检测1．⒈ 如图，已知，AB ∥FG ，AC ∥EH ，BG = CH ，求证：EF ∥BC⒉ 如图，已知，ΔABC 中，DE ∥BC ，DF ∥AC ，求证：BFDEDF AE DB AD ==ACBEFGHACDBE3． 如图，已知四边形ABCD 是平行四边形，FC = 5.4cm ，XE = 2.7 cm ，BE = 3.2 cm ，求DC 的长；4．如图，在⊿ABC 中，AD 平分∠BAC ，CE ⊥AD ，BF ⊥AD ，求证：ACABCE BFABC DEFABCD EF5．如图，在⊿ABC 中，AD 是∠BAC 的外角平分线，CE ∥AB ，求证AC AD DE AB •=•2．如图，已知平行四边形ABCD 中，M 是BC 边的中点，E 为AB 延长线上的一点，且BE =12AB ，EM 的延长线交AC 于N ，交CD 于F ，求证：（1）BE = CF ；（2）求ANE CNF S S ∆∆:的值；ABCDEFABCD FMNE学后反思。

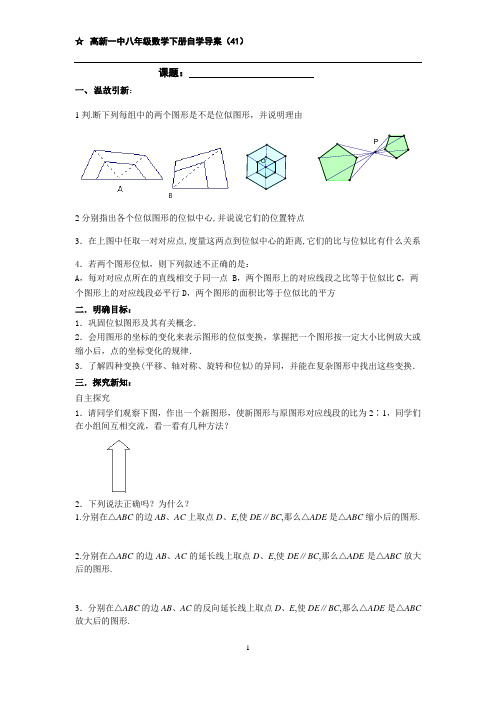
课题：一、 温故引新：1判.断下列每组中的两个图形是不是位似图形，并说明理由2分别指出各个位似图形的位似中心,并说说它们的位置特点3．在上图中任取一对对应点,度量这两点到位似中心的距离,它们的比与位似比有什么关系4．若两个图形位似，则下列叙述不正确的是：A ，每对对应点所在的直线相交于同一点B ，两个图形上的对应线段之比等于位似比C ，两个图形上的对应线段必平行D ，两个图形的面积比等于位似比的平方二．明确目标：1．巩固位似图形及其有关概念．2．会用图形的坐标的变化来表示图形的位似变换，掌握把一个图形按一定大小比例放大或缩小后，点的坐标变化的规律．3．了解四种变换(平移、轴对称、旋转和位似)的异同，并能在复杂图形中找出这些变换．三．探究新知：自主探究1．请同学们观察下图，作出一个新图形，使新图形与原图形对应线段的比为2∶1，同学们在小组间互相交流，看一看有几种方法？2．下列说法正确吗？为什么？1.分别在△ABC 的边AB 、AC 上取点D 、E ,使DE ∥BC ,那么△ADE 是△ABC 缩小后的图形.2.分别在△ABC 的边AB 、AC 的延长线上取点D 、E ,使DE ∥BC ,那么△ADE 是△ABC 放大后的图形.3．分别在△ABC 的边AB 、AC 的反向延长线上取点D 、E ,使DE ∥BC ,那么△ADE 是△ABC 放大后的图形.四．拓展提升探究1．如图，△ABC三个顶点坐标分别为A(2，3)，B(2，1)，C(6，2)，①将△ABC向左平移三个单位得到△A1B 1C1，写出A1、B1、C1三点的坐标；②写出△ABC关于x轴对称的△A2B 2C2三个顶点A2、B2、C2的坐标；③将△ABC绕点O旋转180°得到△A3B3C3，写出A3、B3、C3三点的坐标．探究2①如图，在平面直角坐标系中，有两点A(6，3)，B(6，0)．以原点O为位似中心，相似比为3：1，把线段AB缩小．观察对应点之间坐标的变化，你有什么发现？②如图，△ABC三个顶点坐标分别为A(2，3)，B(2，1)，C(6，2)，以点O为位似中心，相似比为1：2，将△ABC放大，观察对应顶点坐标的变化，你有什么发现？探究3。

课题：一．基础回顾：(1)什么是一元一次不等式组、一元一次不等式的解集?(2)一元一次不等式一组的解法及确定解集的方法是什么/二．明确目标：1、巩固复习一元一次不等式组的解法；2．含有字母的二元一次方程组的解的讨论及字母的取值范围。

三．探索新知：（一）温故知新1．解下列不等式组,并把解集在数轴上表示出来.(1)3150728xx x->⎧⎨-<⎩(2)224315xx+<⎧⎨-≥⎩(3)21113112xxx-+>-⎧⎪⎨+-≥⎪⎩2．完成课本P30引例，若x取正整数呢？3.完成课本P30例2、例3解：4.完成课本P30-31议一议、随堂练习（二）自主探究 1.当2(m-3)< 103m -时,求关于x 的不等式(5)4m x ->x-m 的解集.2.a 为何值时，方程组⎩⎨⎧=+=+63488y x ay x 的解是正数？3．已知不等式4()0.5 5.81213x a x x x -<+⎧⎪+⎨>-⎪⎩的解集为2x <，求a 的取值范围。

四．拓展与探究：1．若不等式组2113x ax <⎧⎪-⎨>⎪⎩无解，则a 的取值范围是。

练习：（1）若不等式组⎩⎨⎧-<+>232a x a x 无解，求a 的取值范围。

（2）若关于x 的不等式组12x x m -≤<⎧⎨>⎩有解，求m 的范围。

2.若关于x 的不等式组61540x xx m +⎧>+⎪⎨⎪+<⎩的解集为4x <，求m 的取值范围。

3.已知不等式组2123x a x b -<⎧⎨->⎩的解集为-1<x<1,则(a+1)(b-1)的值等于多少?五．检测反馈：1.下列不等式组中，解集是2<x <3的不等式组是（ ）A.⎩⎨⎧>>23x xB.⎩⎨⎧<>23x x C.⎩⎨⎧><23x xD.⎩⎨⎧<<23x x2.不等式组⎩⎨⎧+≤-+<24722x x x x 的解集在数轴上表示正确的是（ ）3.若a >b ,则不等式⎩⎨⎧≤<a x ax 的解集为（ ） A. x ≤bB .x <a C. b ≤x <a D.无解4.不等式组⎩⎨⎧>-<+mx x x 148的解集是x >3，则m 的取值范围是（ ）A. m =3B. m ≥3C. m ≤3D. m <35. 不等式组⎪⎩⎪⎨⎧<≥->521x x x 的解集是_______.6. 如果关于x 的不等式组⎩⎨⎧-<+>232a x a x 无解，则常数a 的取值范围是________.7. 如果三角形的三边长分别是3 cm 、（1－2a ） cm 、8 cm ，那么a 的取值范围是________. 8.如果关于x 、y 的方程组⎩⎨⎧=+=-ay x y x 53102的解满足x >0且y <0,请确定实数a 的取值范围.9.某企业现有工人80人，平均每人每年可创产值a 元.为适应市场经济改革，现决定从中分流一部分人员从事服务行业.分流后企业工人平均每人每年创造产值可增加30%，服务行业人员平均每人每年可创产值2.5a 元.要使分流后企业工人的全年总产值不低于原来全年总产值，而且服务行业人员全年创产值不低于原企业全年总产值的一半.假设你是企业管理者，请你确定分流到服务行业的人数.10． 试确定以下不等式组的解集:(1)求不等式组2(6)32151132x x x x -<-⎧⎪-+⎨-≤⎪⎩的整数解.(2)解不等式组25344(31)5(21)132x x x x x x⎧⎪-<+⎪-<+⎨⎪-⎪≥⎩ (3) 0503010x y x x x -<⎧⎪-<⎪⎨+>⎪⎪+>⎩参 考 答 案1. C2. C3. A4. C5. 2≤x ＜56. a ≤27. －5＜a ＜－28.解方程组⎩⎨⎧=+=-ay x y x 53102得这个方程组的解是⎩⎨⎧-=+=622a y a x∵x ＞0且y ＜0， ∴⎩⎨⎧<->+06202a a 解得：－2＜a ＜39.解：设分流x 人从事服务行业，则剩余（80－x )人从事企业生产.根据题意得：⎪⎩⎪⎨⎧⨯≥≥-+a ax a x a 80215.280)80(%)301(即⎩⎨⎧≥≤a ax a ax 405.2243.1 ∴⎪⎩⎪⎨⎧≥≤1613618x x 又∵x 是整数∴x =16,17或18即可分流16人或17人、18人去从事服务行业.10．解:(1)不等式组的整数解为-1,0,1,2,3,4. (2)解集为-9<x ≤25. (3)解集为-1<x<5. 六．学后反思。

课题：一、温故引新：1。

相似多边形.定义：————————————————————————————————————————叫做相似多边形.2．记法：如多边形ABCDEF和多边形A1B1C1D1E1F1 相似，记作。

3. 相似比：————————————————————————————————叫做相似比.4.相似多边形的性质：如果两个多边形相似，那么它们的对应角——————，对应边—————。

5．问题：所有的等腰三角形都相似吗？所有的等边三角形呢？怎样的两个三角形相似？二．明确目标：1．通过一些具体的情境和应用深化对相似三角形的理解和认识2．进一步体会数学内容之间的内在联系，初步认识特殊与一般之间的辩证关系，提高学生学习数学三．探究新知：（一）自主探究如果ΔABC 与ΔA′B′C′`中，AB：A′B′=BC：B′C′=AC：A′C′=3：1，且∠A=∠A′，∠B=∠B′，∠C=∠C′，那么ΔABC 与ΔA`B`C`的相似吗？为什么？（二）形成概念1．相似三角形定义：————————————————————————————————————————叫做相似三角形.2．记法：如ΔABC和多边形ΔA1B1C1相似，记作。

3. 相似比：————————————————————————————————叫做相似比.4.相似多边形的性质：如果两个多边形相似，那么它们的对应角——————，对应边—————。

（三）学以致用1．议一议（1）两个全等三角形一定相似吗？为什么？（2） 两个直角三角形一定相似吗？两个等腰直角三角形呢？为什么 2．完成课本P128例1、例23。

完成课本P129随堂练习四．拓展提升例3．（3）如图，正方形ABCD ，AC 、BD 相交于O ，OE ⊥BC 于E,则图中与 ΔCOE 相似的三角形的个数有（ ） A 2B 4C 8D 9例4．正方形ABCD 的边BC 在等腰直角三角形PQR 的斜边QR 上，•其余两个顶点A ，D 在PQ ，PR 上，求。

数据的收集与处理小结与思考一、知识框架图:(二)复习反馈1.为了考察某地初中毕业生数学升学考试情况，从中抽查了100名学生考试成绩，在这个问题中，样本容量是___________．2．为了解某种产品的质量，从中抽取出300个产品进行检验．在这个问题中，300个产品的质量叫做( )A ．总体B ．个体C ．样本D ．样本容量3．在样本方差的计算公式s 2＝101［(x 1-20)2＋(x 2-20)2＋…＋(x 10-20)2］中，数字10和20分别表示样本的( )A ．容量、方差B ．平均数、容量C ．容量、平均数D ．标准差、平均数4．已知数据7，3，11，3，1，8，那么这组数据的众数是___________．5．若3，4，5，6，x 1，x 2，x 3的平均数是12，则x 1＋x 2＋x 3＝___________．6．从观测所得的数据中取出m 个x 1，n 个x 2，p 个x 3组成一个样本，那么这个样本的平均数是( )A ．3321x x x ++ B ．p n m x x x ++++321 C ．3321px nx mx ++ D ．p n m px nx mx ++++321 7．总体方差是表示总体的___________的特征数．8．样本3，-4，0，-1，2的方差是___________．9．绘制频数分布直方图时，各个小长方形的高等于相应各组的（ ）A ．组距B ．频数C ．频率D ．平均数10.为了调查班级中对新班主任老师的印象，下列更具有代表性的样本是（ ）A ．调查前十名的学生B.调查后十名的学生C.调查单号学号的学生D.调查全体男同学11. 一组数据：2-，1-，0，x ，1的平均数是0，则x =____,方差=2S ______. 12.如果样本方差[]242322212)2()2()2()2(41-+-+-+-=x x x x S ，那么这个样本的平均数为_________.样本容量为________.13．数据501，502，503，504，505，506，507，508，509的标准差是（ ）A 、B 、C 、D 、114.为了考察某商店一年中每天的营业额，从中抽查了30天的营业额.其中总体是____________________________________,个体是_________________________,样本是______________________,样本容量是____________.15.下列任务，你认为采用什么调查方式更合适？（1） 了解一批日光灯管的使用寿命；（2） 了解一个小区的业主对物业公司的满意程度；（3） 了解本班学生对目前台湾形势的认识情况；16．某农科所在8个试验点对甲、乙两种玉米进行对比试验，这两种玉米在各试验点的亩产量如下(单位：千克)：甲：450 460 450 430 450 460 440 460乙：440 470 460 440 430 450 470 440在这些试验点甲、乙两种玉米哪一种产量比较稳定？二、复习典例例1．一家电脑生产厂家在某城市三个经销本厂产品的大商场调查，产品的销量占这三个大商场同类产品销量的40%．由此在广告中宣传，他们的产品在国内同类产品的销售量占40%．请你根据所学的统计知识，判断该宣传中的数据是否可靠：________，理由是________．例2.若一组数据x1、x2……x n，的平均值为x，方差为s2，求下列各组数据的平均值和方差.(1) x1+a,x2+a,……,x n+a; (2)ax1,ax2, …,ax n; (3) ax1+b,ax2+b, …,ax n+b.提示：先写出平均值和方差的公式，然后再套用公式求出新数据的平均值和方差.总结：（1）把一组数据每一个数都加上或减去同一个数，它的平均值也要加上或减去同一个数，而方差不变.(2)把一组数据每一个数都扩大或缩小a倍，它的平均值也扩大或缩小a倍，而方差要扩大或缩小a2倍.对应训练：1.已知：y1,y2,y3的平均值为y，方差为s2.（1）y1-1,y2-1,y3-1的平均值________方差________;（2）-3y1，-3y2，-3y3的平均值________方差________;（3）2y1+5,2y2+5,2y3+5的平均值________方差________;2.已知样本x1、x2……x n的方差是2，则样本3x1+5,3x2+5,3x3+5,……3x n+5的方差是（）3．学生李明通过计算（A），（B），（C），（D）四组数据的方差后，发现有三组数据的方差相同，则方差不同的一组数据是（）A.102，103，105，107，108B.12，13，15，17，18C．1，4，9，25，36 D.2112,2113,2115,2117,2118例3.某校要从小王和小李两名同学中挑选一人参加全国数学竞赛，在最近的五次选拔考试中，他俩的成绩分别如下表：（2）在这五次考试中，成绩比较稳定的是谁？若将80分以上（含80分）的成绩视为优秀，则小王、小李在这五次考试中的优秀率各是多少？（3）历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为应选谁参加比赛比较合适？说明理由.三、检测：1.样本方差越小，说明（ ）A 、样本容量越小B 、样本容量越大C 、样本波动越大D 、样本波动越小2．在数据统计中，能反映一组数据变化范围大小的指标是（ ）A 、极差B 、方差C 、标准差D 、以上都不对3．能反映一组数据与其平均值的离散程度的是（ ）A 、极差和方差B 、极差和标准差C 、方差和标准差D 、以上都不对4．已知甲、乙两个样本（样本容量一样大），若甲样本的方差是0.4，乙样本的方差是0.2,那么比较甲、乙两个样本的波动大小的结果是（ ）A 、甲样本的波动比乙大B 、乙样本的波动比甲大C 、甲、乙的波动一样大D 、无法比较5.已知321,,x x x 的平均数=x 10，方差=2S 3，则3212,2,2x x x 的平均数为____，方差为________.6.如果一组数据的极差是80，若画图前确定组距是9，则组数是（ ）A 、7组B 、8组C 、9组D 、10组7.如果给定数组中每一个数都减去同一非零常数，则数据的（ ）A 、平均数改变，方差不变B 、平均数改变，方差改变C、平均数不变，方差不变D、平均数不变，方差改变四、拓展：为选派一名学生参加全市实践活动技能竞赛,A、B两位同学在学校实践基地现场进行加工直径为20mm的零件的测试，他俩各加式的10个零件的相关数据依次如下图所示（单位：mm）。

课题：一．基础回顾：1．分式的定义： 。

2.分式有意义的条件 ；分式值为零的条件： 。

3．回忆学过的分数基本性质，判断下列各对式子是否相等?为什么? (1)474373⨯⨯和；(2) ）（）（和252252-⨯-⨯；(3) 030232⨯⨯和； (4) 262464÷÷和；(5) 131232++和； 分数的基本性质：二．明确目标：。

1．使学生掌握分式的基本性质，并能熟练运用基本性质进行分式“等值”变形。

2．了解分式约分的步骤和依据，掌握分式约分的方法；了解最简分式的意义，能将分式化为最简分式.3．通过分数与分式的比较，培养学生类比联想的思维习惯和思想方法。

三．探究新知：（一）、自主探究：63=21的依据是什么？你认为分式a a 2与21相等吗？m n n 2与mn 呢？ 想一想：（二）、类比归纳 分式的基本性质：。

用式子表示是：①,M B M A B A ⨯⨯=（M ≠0 ） ②,MB M A B A ÷÷=（M ≠0）【注意：这里面的A 、B 、M 均为整式。

】 （三）、学以致用1．完成课本P80-P81例2、例3。

解： 解：分式的约分：2。

完成课本P69“做一做”和“议一议”最简分式： 。

3。

化简分式：（1）3232636c ab c b a ；（2）)1(8)1(22a ab a a --；（3）2222996b a b ab a -+-；（4）12124++-a a a5．完成课本P71想一想、随堂练习。

6．不改变分式的值，使下列分式的分子与分母都不含“—”：（1）b a 32--； （2）mn -； （3）b a 3-- 四．拓展提升例1、不改变分式的值，使下列分式的分子与分母的最高次项的系数是正数：（1）221x x -； （2）233yy y y +-； （3）323b b a a --例2、 不改变分式的值，把下列各式的分子与分母中各项的系数都化为整数： y x 7.03.0)1( (2)y x y x -+21131 (3) b a b a -+7.05.02.0例3、先约分，再求值： 22323444abb a a ab a +--，其中a=-2,b=-0.5例4、（1）实数a 、b 满足ab =1，记M =a +11+b +11,N =a a +1+bb +1，比较M 、N 的大小. （2）巳知实数x 满足4x 2一4 x+1=0，求代数式数2x ＋x 21的值。

课题：一元一次不等式和一元一次不等式组复习 一、知识结构网络二、基本知识点回顾1. 一般的,____________________________________________________叫做不等式。

注意：①不等式中常出现的符号是“<”、“≤”、“>”、“≥”（还有“≠”）②理解“非负数”、“非正数”、“不大于”、“不小于”、“至少”、“至多”等 ③根据文字列不等式，如“ x 与17的和比它的5倍小”列式为_______________;2. 不等式的基本性质：基本性质1 _______________________________________________________________； 基本性质2 _______________________________________________________________；基本性质3_______________________________________________________________。

例如：如果y x <，那么x+5___y+5 ，3x___3y ，-2x___-2y 3. 一元一次不等式和一元一次不等式组①区分不等式的解和解集：3=x 是82<x 的解，不等式82<x 的解集是4<x 。

②__________________________________________________叫做一元一次不等式。

一般地，关于同一个未知数的几个一元一次不等式合在一起就组成一元一次不等式组。

③数轴上表示不等式的解集：一，注意方向；二，注意实心与空心的区别；5.31≤<-x④会解一元一次不等式(组)（注意：解题的步骤）x<22-3-2-15431y如：①623-<-x x ； ②3722xx -≥-；③⎩⎨⎧<-+>2.015.013.02.0x x x 4. 一元一次不等式与一次函数的关系⑴作出函数22+=x y 的图像，观察图像回答下列问题： ①x 取何值时，0=y ？ ②x 取何值时，0>y ？ ③x 取何值时，0<y ？ ④x 取何值时，2≥y ？⑵根据给出的两个函数图象回答问题：①当______x 时，21y y > ②当______x 时，21y y ≤。