下载文档原格式
全排列算法讨论2你非常自豪.但这也许是适当的时候提醒自己谦虚的妤处.既然都到了这个地步了,何不再走多一步,翻一下书看看,也许你找到的方法已经早有别人发现了.果真是这样的话,你,一个无知的白痴,到处大吹大擂自己的发明是会被笑话的.于是你找出了封尘的电脑和数学教科书.找到了排列组合一章,开始细读.终于你找到了这样的一幅图画：[4321][3421][321][3241][21][231].[3214][213].[1][321].[21][231].[ 213].书中写到,要产生一个排列其实可以用这样一个方法："先选一个数1,然后第二个数2可以放在1的前面或是后面.而每一个放法都会产生一个2位数,对于每一个这样的两位数,第三个数3,都可以放在它的前面,中间,或是最后；如此产生一个3位数；而每一个3位数,第4位数都可以插入到这3个数的任何一个空位中,如此类推.书中还列出了一个程式范例呢！并声这个方法要和已知的最快的算排列的方法速度相若.你急不可待地开始把书中的描述实现.用Python,你很快又得到了一个全新的程式：1#permute6.py2def permute(seq)：3 seqn=[seq.pop()4 while seq：5 newseq=6 new=seq.pop()7#print"seq：",seq,'seqn',seqn,'new',new8 for iin range(len(seqn))：9 item=seqn[i]10 for jin range(len(item)+1)：11 newseq.append(''.join([item[：j],new,item[j：]]))12seqn=newseq13#print'newseq',newseq14 return seqn1516importsys,calc17seq=list(sys.argv[1])18where=int(sys.argv[2])19thelist=perm ute(seq)20print'Got',len(thelist),'items.'21calc.calc(thelist,where)测试结果如下：$time cpython permute6.py 1234567 4Got 5040 items.Maximum at 6531742,product 4846002 real 0m0.167s user 0m0.150s sys 0m0.020s哇塞！书中自有黄金屋咧！想不到这个才是最快的算法.你开始感到要击败这次的对手不是不件容易的事,而且现在已经很晚了,你身心也都被疲倦所包围著.你绝望地看著这个新的程式码和它那美妙的结构,作出最后的尝试：待续.守夜人：Got 24items.['1234','2134','2314','2341','1324','3124','3214','3241','1342' ,'3142','3412','3421','1243','2143','2413','2431','1423','4123','4213 ','4231','1432','4132','4312','4321']上面就是permute7.py产生的四位数字排列结果,你细心地反覆观看,终于看出了一些端倪：其实所产生的排列是有一种对称性的,第一个和最后一个是完全次序相反的,而第二个又和倒数第二个完全相反.利用这些对称性,也许你可以把计算时间打个对折哟.而你研究了一下程式的实现方法后你发现只要改一行！就可以实现这样的功能：就是第一行seqn=[seq.pop()]改成seqn=[seq.pop()+seq.pop()].这样你就实现了只产生其中一半的排列,尔后你只要把这个列表中的元素都掉个就完成了整个排列.程式如下1#permute7.py2def permute(seq)：3 seqn=[seq.pop()+seq.pop()]4 while seq：5 newseq=6 new=seq.pop()7#print"seq：",seq,'seqn',seqn,'new',new8 for iin range(len(seqn))：9item=seqn[i]10 for jin range(len(item)+1)：11newseq.append(''.join([item[：j],new,item[j：]]))12seqn=newseq13#print'newseq',newseq14 return seqn1516importsys,calc17seq=list(sys.argv[1])18where=int(sys.argv[2])19thelist=perm ute(seq)20print'Got',len(thelist),'items.'21print thelist22#这个等一下再探讨23#calc.calc2(thelist,where)测试数据表示果然这个改良了的程式要比原来快了刚好一倍.这次应该足够了.但是要得到整个排列的话要把这半个列表重抄一次而且每个元素都要反过来："1234"-"4321".但是在Python之中的字串并没有反序的函数,因此你必须先把字串变成列表,再反过来,然而list.reverse()这个函数偏偏很讨厌的不会传回任何值(因为它是in-place的缘故),所以你要用i=list(item)；i.reverse；i=''.join(i)；这个复杂的方法.你想了想,这个做法大概会把原来只做一半排列所省下来的时间都浪费掉了.你思考半天,终于决定重写calc.py部份以便直接利用已知的半个列表.#！python#calc.py def calc(seq,where)：maximum,max_item=0,for iin seq：product=int(i[：where])*int(i[where：])if product maximum：maximum,max_item=product,i elif product==maximum：max_item+=','+i print"Maximum at",max_item,",product",maximum def calc2(seq,where)：maximum,max_item=0,for iin seq：product=int(i[：where])*int(i[where：])if product maximum：maximum,max_item=product,i elif product==maximum：max_item+=','+irev=list(i)rev.reverse()i=''.join(rev)product=int(i[：where])*int(i[where：])if product maximum：maximum,max_item=product,i elif product==maximum：max_item+=','+i print"Maximumat",max_item,",product",maximum当然你保留了以前的函数calc而只是新加一个专门给permute7.py调用的calc2函数.你试了一下速度,成功了比permute6.py快了一丁点.虽然只是这一点儿点儿,你也觉得快活无比.因为又一次,你为一个大家都觉得好的方法做出了改良.虽然你知道在这个阶段如果你把calc.py整合到排列产生器中也许会得更好的提速效果,但你觉得现在这样已经可以很多人都认同你的能力了.而且能把一个高效的排列产生器独开来也许是聪明的做法,因为将来你一定会再用它的.你看了一下所有的程式,从permute1.py到permute7.py,再做了一次速度的检定.反正是最后一次了,干脆做个大的吧.$ti me python permute2.py 123456789 5Got 362880 items.Maximum at 875319642,product 843973902 real 0m 46.478s user 0m 46.020s sys0m0.430s$time python permute3.py 123456789 5Got 362880 items.Maximum at 875319642,product 843973902 real 0m 38.997s user 0m 38.600s sys0m0.400s$time python permute4.py 123456789 5Got 362880 items.Maximum at 875319642,product 843973902 real 0m 33.845s user 0m 33.460s sys0m0.380s$time python permute5.py 123456789 5Got 362880 items.Maximum at 875319642,product 843973902 real 0m 10.681s user 0m 10.530s sys0m0.150s$time python permute6.py 123456789 5Got 362880 items.Maximum at 875319642,product 843973902 real 0m8.279s user 0m8.110s sys0m0.170s$time cpython permute7.py 123456789 5Got 181440 items.Maximum at 875319642,product 843973902 real 0m7.827s user 0m7.650s sys0m0.180s嗯,很不错.最快的要比原先快上近七倍呢！于是你打算明天一有空便把这个最好的公式贴到网上去,让更多人分享.你很放心地去睡觉了.但是不知为了什么,你总觉得有些事烦扰著你,还有什么不妥的地方呢?你实在想不到了,迷迷糊糊地抱著迷惑不安的心情入梦.终于你忍不住爬了起床,再一次回到电脑屏幕前.你想到了一个致命的问题,对于很大很大的排列,permute7.py还是会尝试一下子把所有的排列都做出来,不用多久电脑资源就会被耗光的.你也许要另想一个方法,每次只做一个排列.但你是否可以把所有的排列用1,2,3,4的方法数出来呢?你看著教科书上的那幅图画,这样的树状结构应该有办法的,你对自己说.慢慢读著书上的文字.设想有n个数字,先取第一个数字.再取第二个数字,第二个数可以放在第一个数的左或右面,就是有0,1两个选择.再取第三个数,放到前面选好的两个数字中,可以放在最左,中间,最右,就是有0,1,2三个选择.嗯,很自然吗.忽然你想到了二进位,八进位那些数系转换关系."我可以设计这样一个数,.xyz,其中个位数z是二进位的,也就是放第二个数的两个位置；十位数y 是三进位的,化表放第三个数字的三个位子,然后百位数是四进位,千位数是五进位的,依以类推."没错,这样设计的话,如果0表示放于最左面的话,则"2021"这个数就代表了排列五个元素(abcde),取一个a,然后第二个b放在a的右面成ab,取c放到最右面成为abc,取d放到最左面成dabc；最后e放到中间去成为daebc.至于"2021"这个特别的设计的数可以用.+x*4+y*3+z*2这样的计算来映对到自然数的数列上去.没错了,如求4个数的4！=24个排列,第18个排列可以这样求得,18除2,余数是0,所以第二个数放在第一个数的左面；然后商9再除3,余数0,所以第三个数于在头两个数的最左；最后3除以4,余数是3,因此第四个数要放在前三个数的第4个空位,也就是最右面.利用这个方法,你就不必先求出整个排列才能开始计算.尽管这好像牺牲了时间,但省下了大量的空间.你完全可以算出1000个数的最大排列方法,纵使那可能要用去几个月的运算.你更高兴的是用这个方法,你可以把整个计算拆开成为一个一个的部份：譬如说求10！=3628800个排列,你大可以把1到1000000让一部电脑做,1000001到2000001让另一部来做.大家的工作并不重覆,这等于实现并行运算了！啊哈！妙极了！忽然你灵光一闪,对了,这个不正是permute4.py的算法吗！你昨天还久思不得其解呢,现在你已经完全明白了.呜,虽然这么好的算法原来不是你原创的,但是你仍然异常兴奋.因为你的思路竟和那些大牛们互相吻合.你渐渐记起了当你还在玩DOS游戏机的年代,曾有个古怪的人向你吹嘘过某个电脑扑克游戏中用了一个威力很大的洗牌法,多么的快而且公平,不必怕黑客们用已知的随机数表来出千.现在你猜到了,那个算法很可能就是眼下这一个了.有52张牌,如果要预先算出52！个排列才能洗牌可真要命呢.你觉得舒服多了,你整理了一下程式,打算把结果告诉大家.然而刚才的不安感又重新来袭.你再看了一次最后也应该是最棒的程式,心中安慰自己道："千万不要跌进低等程式员的的陷阱,他们疯也似的不断追求,郤从来不知道自己的目标,也不知道什么才是好.完美的设计不在于你无法添加新的功能,完美的设计是再也不能精简现有的功能."你觉得permute7.py已迫近了这一个极限.但你内心深处并没有因此而舒坦开来,一种悬空的感觉自足下升起.也许是你太累了,于是者你决定闭目养神数分钟再开始上网,可惜你很快地迷迷糊糊地进入了梦境.待续.终篇：你做了一个梦,梦中你看到阿凡提骑著他那出名的毛驴来到你面前并向你提出挑战："除非你解答了我的难题,不然我的驴子会不停在你耳边嘶叫令你无法睡好！问题是：把数字56789放到*里得出最大的的乘积."你发出会心的微笑,正想祭出你的permute7.py之时忽然想起阿凡提是不可能懂得电脑编程的！你心中登时凉了一大截：阿凡提的方法一定不必用电脑算出所有的排列方法,并很快的得知答案的.随著一声震天的驴嘶,你惊醒了,发现原来你伏在电脑桌上睡去了,不小心压著了键盘上的方向键而令你的电脑发出了痛苦的BEEP声.回想梦境,你打算暂时离开电脑,回到问题本身上来：怎样才能"看"出最大的乘积呢?你拿出纸笔,开始计算：假设五个数为[a][c]*[d][e],展开的话成为a*100*d*10+a*100*e*1+b*10*d*10+b*10*e*1+c*1*d*10+c*1*e*1这个可以写成一个矩阵：d ea 1000 100 b100 10 c10 1你这样想到：在整个答案中,a带来的页献是一个百位数加上一个十位数,而d的页献是一个百位数加十位数加个位数,因此d要比a更重要.要取得最大的积则一定要把56789中最大的9放在d的位置,然后是a,如此类推.为了方便计算,你干脆用对数来记数100=10e2,用2来代表好了,因此：d ea 32 b2 1c 10计算每一行或列的和,把它称为该数的基值,我们得到a=5,b=3,c=1,d=6,e=3.咦?b和e的基值是一样的,怎么办！你思考著："啊哈！因为我们用了对数,而log(1)=0因此把b和e之间的微小分别给忽略了！"好吧,试把每个数都加大一个,得到：d ea 43 b3 2c 21这样基数变成了：a=7,b=5,c=3,d=9,e=6.这些基数代表了该位置的重要性,可以按大小分予不同的数字.好,按基数的大小来分配数字你得到了865*97.一对答案,哟！不一样！正确解是875*96.哪里不对了呢?仔细分析下来,你发现b和e互换了.换的原因是这样的：b的页献：b*d*100+b*e*10 e的页献：e*a*100+e*b*10+e*c粗看的话e的页献要大一些,但因为我们把9配给了d而8配给了a,因此最终的结果是b的实际页献要比e大.由于e和b的基数只相差在e*c这个个位数乘积上,d和a之间的分配结果把这个小的差异覆盖掉了.你考虑著："要把这样的覆盖也算上去的话,也许可以做一个二阶基数.如b*d的基数是100,但是由于d的基数为9,那b的二阶基数可以算成9,代表和b 相关的是一个较为重要的数；同样e*a的基数是也是100但由于a的基数只是7,因此e的二阶基数只是7而已.这样就可以得出b要比e更重要了."于是你有了一个想法：先写出相关矩阵,然后计算每个数的基数和二阶基数,再进行排序,当两个基数很接近时就用二阶基数来判别哪个较重要.嗯,你觉得自己聪明极了,于是开始验算,但很快又发现其实b和e的二阶基数原来也是一样的！大家都是15.也许我们要用一个三阶基数才能分辨他们.你又想了一些新的二阶基数的定义,有些的确给出正确的答案,但你渐渐觉得这一切并不很妥当.因为就算能计出56789,但是在更多的排列,如7位数甚至9位数的排列你怎样保证答案也一定准确呢,而两个基数到底怎样才算是比较接近呢?仔细审视你的方法,用对数来表示乃至直接相加来求所谓的基数统统都是即兴的,毫不严谨.或者要真正解决他们必需要把每一种情况都算进来,而那样做的话必然要计算n！那么多次！说到底还是要算排列的.你有些失望,但暗中觉得松了一口气,因为到底是permute7.py得到最后的胜利.你伸了一下懒腰,原来天都快亮了.这时你感到有些饿,便去拿了半个凉馒头,冲了一些可可.你对著空空的萤光屏,静静地坐了大概十分钟,然后答案进入你的脑海,谜团被解开了.你的方法是求出所有位置的"重要性"(用你的语言就是求基数),然后依次把最大的数字分配给最重要的位置.但是位置的重要性是和其他位置纠缠在一起的,因此一次过算出所有位置的重要性必须考虑大量不同的组合排列,并不实际.但是,我们其实可以每次只求第一个最大的基数的位置(abc*de的情况下最大的基数是d),这个最大的基数是没有争议的.当求得这个位置时,干脆把最大的数字放到该位子上,然后再求一次基数,找出接下来最大的位子,这个位子也是无可争议的.如此一来,原来求5个数字的全排列成就简化为5次简单的回圈.一个求Factorial(n)的问题变成了n次循环！啊哈！你精神大好,从另一个角度切入：假如5个数字一样,11111,最大的乘积只能是111*11,现在容许改大一个数,改哪个会使结果最大?211*11,121*11,112*11,111*21,111*12?答案是111*21,也就是d的位置.好,把d替换成9.问题变成5个数字,111*91,改一个数(除了9),改哪一个?211*91,121*91,112*91,111*19?答案是211*91,也就是a的位置.好,替换成8.依此类推,答案正正是875*96.你重开电脑,很快地把新方法输入程式,并改名为wise.py.1def solve(seq,where)：2 n=len(seq)3 seq.sort()4 seq.reverse()5 table=[for iin range(n)]6 left,right=where,n-where7leftr=long('1'*left)8 rightr=long('1'*right)9 flag=10 for itemin[int(x)for xin seq]：11 for iin range(left)：12 table[left-i-1]=(leftr+10*i)*rightr13 for iin range(right)：14 table[right-i+where-1]=leftr*(rightr+10*i)15 for iin flag：16 table[i]=017tablesorted=table[：]18 tablesorted.sort()19maxindex=table.index(tablesorted[-1])20 if maxindex=where：21rightr=rightr+(item-1)*10*(right-maxindex+where-1)22 else：23leftr=leftr+(item-1)*10*(left-maxindex-1)24flag.append(maxindex)25#print maxindex,leftr,rightr26 returnleftr,rightr2728importsys29leftr,rightr=solve(list(sys.argv[1]),int(sys.argv[2]))30print"Ma ximum at",leftr,rightr,',product',leftr*rightr你验算了一下结果,完全正确！这时你好奇地再次time了一下程式的速度$time python permute7.py 123456789 5Got 181440 items.Maximum at 875319642,product 843973902 real 0m7.827s user 0m7.650s sys0m0.180s$time python wise2.py 123456789 5Maximum at 875319642,product 843973902 real 0m0.042s user 0m0.010s sys 0m0.030s哇！快了近两百倍！当然了.如果算更多位的排列会快更多,因为wise.py 跳离了n！的限制.你现在觉得舒服多了.你真的解了这个问题.你不再怕有人会写出更快10倍的程式了.你既有了"聪明"的答案(软解)来对付阿凡提和他的驴子,而在硬解方面,你也自信有世界第一流的排列产生器.你完全满足了,你不再感到疲累,心中疑犹一扫而空.这时你身体感到一阵震栗但心中却喜乐无穷,你第一次感受到了编程之道的洗礼.并且,你学会了所有程式大师都有的态度：我没法用中文来形容,这种态度叫做"to hack".你知道只要你熟练并保持这种态度来面对生命中的难题,你很快就可以满师出山了.你最后一次浏览了一下你的程式码,发现在wise.py中,其实每一个循环完成后,最重要的位置和最次要的位子都是不容争议的,因此大可放心地替换两个数字而不是一个,那程式可以再快一倍.不过你觉得现在己经很够了,你颇有禅机地自言自语道："我已经找到明月,再纠缠只下去只是妄执于指月的手而已."你熟练地登出系统并关上电脑,你知道这次你可以真正安心地睡一觉了.哎哟！天已亮了,今天是礼拜一,你要上班的.喔！又要被老板说上班一条虫,下班一条龙.惨.全篇完.课后检讨：一)在上面的故事中,我们看到了解决编程问题的五个方法.把问题规范成一个普遍的形式,这样更容易和别人交流以及找相关资料.自己尝试找答案.在网上搜寻更好的答案.想一个方法来打败这个更好的答案.翻查教科书或是文献,从基本开始思考有没有最好的解.这些书能被选成教本一定有它的原因.研究问题的特殊情况,也许会有别出心裁的巧妙方法.二)故事中每个程式都只有二三十行大小,说明Python语言表达力强且语意很浓缩,做为快速开发或是测算自己的想法都是非常好的.三)Python程式浓缩之余,它的语言也异常的清晰.回看上面的程式,你会发现它们全都不难明白.这说明Python程式更加容易维护.四)在故事中,我们有很大的篇幅是在讨论方法而只有小部份是在描述Python的语言特性.这证明Python更适合用来教授编程的概念.事实上,Python的作者Guido和很多人都认为Python是电脑教育的首选语言.教师可以让学生静静地思考,学通运算的法则；而不是上来就疯狂地敲打键盘,并要记住一大堆电脑语言的古怪特徵.五)整个故事围绕于算法的改进而较少碰到Python程式的优化问题.也许在续集中(如果有的话),我们要尝试一下在固定的算法及尽量少改动程式码的条件下,提高Python程式的效率.我暂时想到的方法包括：利用较新和较快的语法.如yield,generator.用Python的自带优化选项以及内建模组.用第三方的扩展模组,如Numpy,Scipy.用编译方式代替解释,如freeze,py2exe.用JIT类的方法,如Psyco.用Thread,在多CPU的机器上平行运算.最后一样要大改程式了,用C来做扩展.更有'to hack'感觉的,修改Python主干程式,加入像string.reverse()这样的辅助函数.六)文中所用的测试硬件：CPU：Pentium III 866 RAM：128 MB文中所用的测试软件：Slackware Linux：9.0 Linux Kernel：2.4.2 GCC：3.2.2 Python：修改过的2.1.3七)啃凉馒头对脑筋有帮助.八)如果你能想到更好的方法,欢迎联络本人：glace_at_(本文第一次发表在技术论坛)搜寻页面或尝试以下动作：附加档案,删除页面,本页连结图特别声明：1：资料来源于互联网，版权归属原作者2：资料内容属于网络意见，与本账号立场无关3：如有侵权，请告知，立即删除。
全排列的⼏种算法全排列，我们⾼中时就学过，数学上很简单，可是⽤计算机的算法实现还是有点味道的，今天我将我碰到的⼏种算法如数奉上，欢迎交流！第⼀种：递归最常见的也是最好理解的⽅法：简单点：⽐如"a" ,"b","c"全排列，可以看做事"a" +"b","c"的全排列及"b"+ "a","c"的全排列及"c" + "a","b"的全排列也就是说，遍历原数组中的每个元素，让剩余的元素全排列，这样就找到规律了。
代码如下：public static void main(String[] args) {char buf[]={'a','b','c','d'};perm(buf,0,buf.length-1);}public static void perm(char[] buf,int start,int end){if(start==end){//当只要求对数组中⼀个字母进⾏全排列时，只要就按该数组输出即可（特殊情况）for(int i=0;i<=end;i++){System.out.print(buf[i]);}System.out.println();}else{//多个字母全排列（普遍情况）for(int i=start;i<=end;i++){//（让指针start分别指向每⼀个数）char temp=buf[start];//交换数组第⼀个元素与后续的元素buf[start]=buf[i];buf[i]=temp;perm(buf,start+1,end);//后续元素递归全排列temp=buf[start];//将交换后的数组还原buf[start]=buf[i];buf[i]=temp;}}}第⼆中⽅法：也是递归，但是和第⼀种有所区别，算法：将数据分为两部分，递归将数据从左侧移右侧实现全排列⽐较抽象，如list abcd，遍历每⼀个数，将每个数放到⼀个新的list中,并将该元素从原list删除，然后将剩下的元素继续遍历每个元素继续放到新的list ⾥，这样，当list的长度为原list长度，或者原list长度为0时打印结果！下⾯是简单的⽰意图：// abcd//bcd a//cd ab//d abc//abcd//c abd//abdc//bd ac//d acb//acbd//b acd//acdb//bc ad ...//acd b ...//abd c ...//abc d ...源代码如下：private static void sort(List datas, List target) {//System.out.println("size="+datas.size());if (datas.size()==0) {for (Object obj : target)System.out.print(obj+" ");System.out.print(" ");return;}for (int i = 0; i < datas.size(); i++) {List newDatas = new ArrayList(datas);List newTarget = new ArrayList(target);newTarget.add(newDatas.get(i));newDatas.remove(i);sort(newDatas, newTarget);}}public static void main(String[] args) {List list = new ArrayList();for(int i=0;i<5;i++){list.add(i+1);}sort(list, new ArrayList());}第三种⽅法：⾮递归直接上代码：public static void main(String[] args) {int[] arr = new int[]{1,2,3,4,5,6};for(int i :arr){System.out.print(i + " ");}System.out.println();int totalnum = 1;while(NextNumber(arr,arr.length)){for(int i :arr){System.out.print(i + " ");}System.out.println();totalnum ++;}System.out.println("Total Num: " + totalnum);}private static Boolean NextNumber(int[] arr, int n){//数组最后⼀个元素位置int lastIndex = n-1;//从右向左确定第⼀个数字（前⾯的数字⽐它⼩）int firstIndex = lastIndex;for(;arr[firstIndex-1]>arr[firstIndex];firstIndex--){if(firstIndex == 1){//已经轮询完毕,此数已经是最⼤的那个数return false;}}//从右向左确定⼀个交换数（此数⽐arr[firstIndex]⼩且⽐arr[firstIndex-1]⼤）int swapIndex = lastIndex;for(;swapIndex > firstIndex;swapIndex--){if(arr[swapIndex] < arr[firstIndex] && arr[swapIndex] > arr[firstIndex-1]){break;}}//交换数字swap(arr,firstIndex-1,swapIndex);//将firstIndex右边的数字排序for(;firstIndex < lastIndex;firstIndex++,lastIndex--){if(arr[firstIndex] > arr[lastIndex]){swap(arr,firstIndex,lastIndex);}}return true;}private static void swap(int[] arr,int i, int j){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}如果此⽂对你有帮助，请留个⾔，新⼈需要打架的⽀持和⿎励！。
1.5全排列的生成算法全排列的生成算法就是对于给定的字符集，用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。
这里介绍全排列算法四种：(A)字典序法(B)递增进位制数法(C)递减进位制数法(D)邻位对换法1.5.1字典序法对给定的字符集中的字符规定了一个先后关系，在此基础上规定两个全排列的先后是从左到右逐个比较对应的字符的先后。
[例]字符集{1,2,3},较小的数字较先,这样按字典序生成的全排列是:123,132,213,231,312,321。
[注意] 一个全排列可看做一个字符串，字符串可有前缀、后缀。
1）生成给定全排列的下一个排列所谓一个的下一个就是这一个与下一个之间没有其他的。
这就要求这一个与下一个有尽可能长的共同前缀，也即变化限制在尽可能短的后缀上。
[例]839647521是1--9的排列。
1—9的排列最前面的是123456789，最后面的是987654321，从右向左扫描若都是增的，就到了987654321，也就没有下一个了。
否则找出第一次出现下降的位置。
/1.5.2递增进位制数法1)由排列求中介数在字典序法中，中介数的各位是由排列数的位决定的.中介数位的下标与排列的位的下标一致。
在递增进位制数法中，中介数的各位是由排列中的数字决定的。
即中介数中各位的下标与排列中的数字(2—n)一致。
可看出n-1位的进位链。
右端位逢2进1，右起第2位逢3进1，…，右起第i位逢i+1进1，i=1,2,…,n-1. 这样的中介数我们称为递增进位制数。
上面是由中介数求排列。
由序号（十进制数）求中介数（递增进位制数）如下：m=m1,0≤m≤n!-1m1=2m2+kn-1,0≤kn-1≤1m2=3m3+kn-2,0≤kn-2≤2……………mn-2=(n-1)mn-1+k2,0≤k2≤n-2mn-1=k1,0≤k1≤n-1p1p2…pn←→(k1k2…kn-1)↑←→m在字典序法中由中介数求排列比较麻烦，我们可以通过另外定义递增进位制数加以改进。
数学排列组合题的解题思路和方法数学排列组合题是高中数学中的重要内容之一，也是考试中常出现的题型。
解决这类题目需要掌握一定的思路和方法。
本文将介绍数学排列组合题的解题思路和方法，帮助读者更好地应对这类题目。
一、排列组合的基本概念在开始讨论解题思路和方法之前，我们先来回顾一下排列组合的基本概念。
排列是指从一组元素中选取若干个元素按一定的顺序排列的方式。
排列的公式为P(n, m)，表示从n个元素中选取m个元素排列的方式数。
组合是指从一组元素中选取若干个元素不考虑顺序的方式。
组合的公式为C(n, m)，表示从n个元素中选取m个元素组合的方式数。
在解决排列组合问题时，我们需要根据题目的要求确定使用排列还是组合的方式，并结合具体情况来计算。
二、解题思路和方法1. 确定题目要求在解决排列组合题时，首先要仔细阅读题目，理解题目的要求。
明确题目要求是使用排列还是组合的方式，以及需要计算的具体数值。
2. 确定元素个数根据题目的描述，确定参与排列组合的元素个数。
通常题目中会给出元素的个数，但也有一些题目需要根据题意进行推断。
3. 确定排列还是组合根据题目的要求，确定是使用排列还是组合的方式。
如果题目要求考虑元素的顺序，则使用排列；如果题目不考虑元素的顺序，则使用组合。
4. 计算排列组合的方式数根据确定的元素个数和使用的排列组合方式，计算出排列组合的方式数。
使用相应的公式，将元素个数代入公式中进行计算。
5. 考虑特殊情况有些排列组合题目中可能存在特殊情况，需要进行额外的考虑。
例如，题目中可能要求某些元素不能重复使用，或者要求某些元素必须同时出现等。
在解题过程中，要注意这些特殊情况，并根据题目要求进行相应的调整。
6. 检查和回答问题在计算出排列组合的方式数后，要对结果进行检查，确保计算的准确性。
同时，根据题目的要求，回答问题，给出最终的答案。
三、实例分析为了更好地理解解题思路和方法，我们来看一个具体的例子。
例题：某班有10名学生，其中3名男生和7名女生，从中选取3名学生组成一支代表队，要求队伍中至少有一名男生，有多少种不同的选择方式？解题思路和方法：1. 确定题目要求：从10名学生中选取3名学生组成代表队，要求队伍中至少有一名男生。
⼀⽂搞懂全排列、组合、⼦集问题微信搜⼀搜：【bigsai】获取更多肝货知识春风⼗⾥，感谢有你前⾔Hello，⼤家好，我是bigsai，long time no see！在刷题和⾯试过程中，我们经常遇到⼀些排列组合类的问题，⽽全排列、组合、⼦集等问题更是⾮常经典问题。
本篇⽂章就带你彻底搞懂全排列！求全排列？全排列即：n个元素取n个元素(所有元素)的所有排列组合情况。
求组合？组合即：n个元素取m个元素的所有组合情况(⾮排列)。
求⼦集？⼦集即：n个元素的所有⼦集(所有可能的组合情况)。
总的来说全排列数值个数是所有元素，不同的是排列顺序；⽽组合是选取固定个数的组合情况(不看排列)；⼦集是对组合拓展，所有可能的组合情况(同不考虑排列)。
当然，这三种问题，有相似之处⼜略有所不同，我们接触到的全排列可能更多，所以你可以把组合和⼦集问题认为是全排列的拓展变形。
且问题可能会遇到待处理字符是否有重复的情况。
采取不同的策略去去重也是相当关键和重要的！在各个问题的具体求解上⽅法可能不少，在全排列上最流⾏的就是邻⾥互换法和回溯法，⽽其他的组合和⼦集问题是经典回溯问题。
⽽本篇最重要和基础的就是要掌握这两种⽅法实现的⽆重复全排列，其他的都是基于这个进⾏变换和拓展。
全排列问题全排列，元素总数为最⼤，不同是排列的顺序。
⽆重复序列的全排列这个问题刚好在是原题的，⼤家学完可以去a试试。
问题描述：给定⼀个没有重复数字的序列，返回其所有可能的全排列。
⽰例：输⼊: [1,2,3]输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]回溯法实现⽆重复全排列回溯算法⽤来解决搜索问题，⽽全排列刚好也是⼀种搜索问题，先回顾⼀下什么是回溯算法：回溯算法实际上⼀个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满⾜求解条件时，就“回溯”返回，尝试别的路径.⽽全排列刚好可以使⽤试探的⽅法去枚举所有中可能性。
常见的算法问题全排列在我参加蓝桥杯时发现⼤多数问题都可以采⽤暴⼒破解所以这个时候我就想进⾏⼀下总结：关于全排列问题的通⽤解法，⽐如：（⽆重复全排列）（有重复的选取）（从N个数中选取m个数然后进⾏排列的问题）我这⾥尝试总结⼀下：⽐如⼀般问题喜欢问1-9有多少种全排列，那么代码如下import java.util.Stack;public class Test1 {//应对全排列问题//分为三种情况：⽆重复的全排列有重复的全排列全排列挑选出任意数字的全排列//这⾥写的是⽆重复的全排列//⽐如1-9的全排列private static int count=0;public static void main(String[] args) {Stack<Integer> stack =new Stack<Integer>();for(int i=1;i<=9;i++){stack.push(i);fun(stack);stack.pop();}System.out.println(count);}private static void fun(Stack<Integer> stack) {if(stack.size()==9){count++;return;}for(int j=1;j<=9;j++){if(!stack.contains(j)){stack.push(j);fun(stack);stack.pop();}}}}关于这个全排列我才⽤的stack来做从1-9个数据中随机选取4个数据结果如下我们需要注意的是考虑前⾯对其那么后⾯就不⼀定会对齐import java.util.ArrayList;//这⾥我希望⽐如从1-9中选取4个数出来进⾏组合//这⾥的组合是只考虑组合不考虑顺序public class Test1B {//设置⼀个全局变量⽤来存储需要存储的数据private static ArrayList<Integer> arrayList = new ArrayList<Integer>();private static int count=0;public static void main(String[] args) {//待选数组int[] A={1,2,3,4,5,6,7,8,9};//选取数据的个数int k=4;if(k>A.length||k<=0){return;}//存储位置存储数组的下标待选数据个数fun(A,0,k);System.out.println(count);}private static void fun(int[] A, int index, int k) {if(k==1){for(int i=index;i<A.length;i++){arrayList.add(A[i]);System.out.println(arrayList.toString()+"");count++;arrayList.remove((Object)A[i]);}}else if(k>1){for(int i=index;i<A.length;i++){arrayList.add(A[i]);//k值需要减少因为随着载⼊数据必然会带来K值下降 i值增加fun(A, i+1, k-1);arrayList.remove((Object)A[i]);}}else{return;}}}然后是从1-9中选取四个数的全排列import java.util.ArrayList;//去重复的排列从1-9中挑选出是四个数进⾏排列public class Test1D {private static ArrayList<Integer> arrayList =new ArrayList<Integer>();private static int count=0;public static void main(String[] args) {int[] A={1,2,3,4,5,6,7,8,9};int k=4;fun(k,A);System.out.println(count);}private static void fun(int k, int[] A) {if(k==1){for(int i=0;i<A.length;i++){arrayList.add(A[i]);System.out.println(arrayList.toString());arrayList.remove((Object)A[i]);count++;}}else if(k>1){for(int i=0;i<A.length;i++){arrayList.add(A[i]);fun(k-1, removElement(A));arrayList.remove((Object)A[i]);}}else{return;}}//这个函数的⽬的⽐较数组和Arraylist中那个重叠如果重叠就将数组中的数据去掉private static int[] removElement(int[] A) {ArrayList<Integer> list = new ArrayList<Integer>();for(int i=0;i<A.length;i++){//遍历数组//表⽰不存在boolean exit=true;for(int j=0;j<arrayList.size();j++){//遍历arraylistif(A[i]==arrayList.get(j)){exit=false;break;}}if(exit){list.add(A[i]);}}int[] B=new int[list.size()];for(int m=0;m<list.size();m++){B[m]=list.get(m);}return B;}}然后是不去重的从1-9中选取4个数每个数可以重复四次的排列import java.util.ArrayList;public class Test1E {private static ArrayList<Integer> arrayList =new ArrayList<Integer>();private static int count=0;public static void main(String[] args) {int[] A ={1,2,3,4,5,6,7,8,9};int k=4;fun(0,k,A);System.out.println(count);}private static void fun(int index, int k, int[] A) {if(k==1){for(int i=0;i<A.length;i++){arrayList.add(A[i]);System.out.println(arrayList.toString());arrayList.remove(arrayList.size()-1);count++;}}else if(k>1){for(int i=0;i<A.length;i++){arrayList.add(A[i]);fun(i, k-1, A);arrayList.remove(arrayList.size()-1);}}else{return;}}}好了⼀般的排列问题解决了希望对你有所帮助。
排列题型及解题方法
排列题型是数学和逻辑题目中常见的一类题型，主要考察的是对元素排列顺序的理解和应用。
解题方法主要基于排列的定义和性质，以及一定的逻辑推理能力。
排列题型的常见形式有：
1.全排列：给定n个不同的元素，求其所有可能的排列方式。
2.有限制条件的排列：在给定n个元素中，某些元素不能相邻或必须相邻，求满足条
件的排列方式。
3.分组排列：将n个元素分成m组，每组元素数量有一定限制，求满足条件的分组方
式。
针对这些题型，可以采取以下解题方法：
1.穷举法：对于元素数量较少的情况，可以直接通过穷举所有可能的情况来求解。
2.排列公式：对于全排列问题，可以使用排列公式P(n,m) = n! / (n-m)!，其中n是总元
素数量，m是选择的元素数量。
3.分治法：对于有限制条件的排列问题，可以将问题拆分成多个子问题，分别求解后
再合并结果。
4.插空法：对于元素之间不能相邻的问题，可以先将没有限制的元素进行排列，然后
在它们之间和两端的空隙中插入有限制的元素。
5.捆绑法：对于元素之间必须相邻的问题，可以将这些元素看作一个整体进行排列，
然后再考虑整体内部的排列。
6.分组法：对于分组排列问题，可以先将元素分成满足条件的组，然后再对组进行排
列。
在解题过程中，还需要注意一些细节问题，如避免重复计数、正确处理边界情况等。
通过不断练习和总结，可以提高解决排列题型的能力。
全排列的⼏种实现（含字典序排列算法分析） 始于⼀个很简单的问题：⽣成｛0，1，2，3，...，n-1｝的n！种排列，即全排列问题。
下⾯介绍⼏种全排列的实现，以及探讨⼀下其解题思路。
基于枚举/递归的⽅法思路： 基于枚举的⽅法，也可以说是基于递归的⽅法，此⽅法的思路是先将全排列问题的约束进⾏放松，形成⼀个较容易解决的新问题，解新问题，再对新问题进⾏约束，解出当前问题。
以上全排列问题是⽣成｛0，1，2，...，n-1｝的n！个排列，隐含的⼀个约束是这个n个位置上的数必须是给出的集合中的数，不能重复使⽤。
当我们将此约束放松的时候，问题就变成了n个位置每个位置上有0~n-1种可能出现的数字，列出所有n n种数列，即在每⼀位上枚举所有的可能。
新问题的算法⾮常简单：private Integer[] perm;private void permut(int pos, int n) {if (pos == n) {for (int i = 0; i < perm.length; i++) {System.out.print(perm[i]);}System.out.println();return;}for (int i = 0; i < n; i++) {perm[pos] = i;permut(pos+1, n);}} ⽽我们实际的问题只要保证每⼀位上的数字在其他位置上没有使⽤过就⾏了。
private boolean[] used;private Integer[] perm;private void permut(int pos, int n) {if (pos == n) {for (int i = 0; i < perm.length; i++) {System.out.print(perm[i]);}System.out.println();return;} //针对perm的第pos个位置，究竟使⽤0~n-1中的哪⼀个进⾏循环for (int i = 0; i < n; i++) {if (used[i] == false) {perm[pos] = i;used[i] = true; //i已经被使⽤了，所以把标志位设置为Truepermut(pos+1, n);used[i] = false; //使⽤完之后要把标志复位}}} 或者完全按递归是思想，对｛0，1，2，...，n-1｝进⾏排列，分别将每个位置交换到最前⾯位，之后全排列剩下的位：private static void PermutationList(int fromIndex, int endIndex){if (fromIndex == endIndex)Output();else{for (int index = fromIndex; index <= endIndex; ++index){// 此处排序主要是为了⽣成字典序全排列，否则递归会打乱字典序Sort(fromIndex, endIndex);Swap(fromIndex, index);PermutationList(fromIndex + 1, endIndex);Swap(fromIndex, index);}}}基于字典序的⽅法 基于字典序的⽅法，⽣成给定全排列的下⼀个排列，所谓⼀个的下⼀个就是这⼀个与下⼀个之间没有其他的。
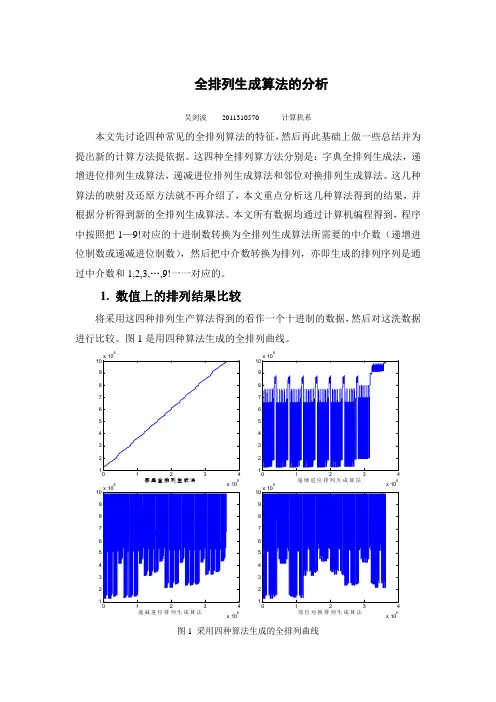
全排列问题的求解算法及相关应用李曼生(兰州师范高等专科学校数学系,甘肃兰州730030)摘要:给出了1至n全排列问题的二种求解算法,分析了该问题在栈中的应用。
关键词:算法;栈;数据结构中图分类号:TG3861引言在很多问题求解中,都会用到1...n各种全排列,我们知道1...n自然数的全排列共有n!种,那么如何设计算法用计算机打印出1...n的所有全排列呢?当n是某一个固定值时,可以轻而易举地通过n重循环算法完成此功能。
但是要对任意n值实现算法,却并不容易实现。
本文给出了二种实现此功能的算法,分析了算法的时间复杂度,并介绍了具体应用的例子。
2求解算法以下算法均用delphi语句描述。
2.1算法1:用数组模拟n重循环该算法设立一个数组a,来模拟n重循环的n 个循环控制变量,每次循环时判断n个循环控制变量是否完全不同,如果不同则是一个全排列。
循环完一次以后,要改变最内层循环的循环控制变量值,内层循环完以后,再进行外层循环。
在数组a中,a [1]表示最外层循环控制变量,a[n]表示最内层循环控制变量。
a的初值如下设置:a[1]a[2]a[3]...a[n]123...nprocedure p(n:integer);var a:array[1..100]of integer;con:boolean;i,j,k,m:longint;op:string;//储存字符串输出beginfor i:=1to n do a[i]:=i;//为a赋初值m:=0;//计数全排列的数量while a[1]<n+1do//n重循环begincon:=true;j:=1;while(j<=n)and con dobeginfor k:=1to j-1doif a[k]=a[j]then con:=false;j:=j+1end;//判断a数组中n个循环控制变量是否不同if con then//con为真,输出a数组中全排列beginm:=m+1;//全排列的数量加1op:=..;for i:=1to n doop:=op+..+inttostr(a[i]);//输出opend;k:=n;//最内层循环a[k]:=a[k]+1;//最内层循环控制变量加1if a[k]>n then//最内层循环完毕begin//依次修改各循环控制变量while(a[k]>n)and(k>1)dobegink:=k-1;a[k]:=a[K]+1;end;k:=k+1;while k<=n dobegin第21卷第4期2005年4月甘肃科技Gansu Science and T echnologyV ol.21No.4Apr il.2005a[k]:=1;k:=k+1;end;end;end;//n重循环endend;//过程p结束该算法是用数组模拟一个n重循环,其时间复杂度是o(nn),算法虽然通过给a赋初值的办法,减少了很多循环次数,但不影响算法的整个时间复杂度。
全排列编程算法
全排列是一种组合问题，通常使用递归算法来实现。
以下是一个使用递归的Python示例，用于生成给定列表的所有可能排列：
```python
def permute(nums):
def backtrack(start):
if start == len(nums) - 1:
result.append(nums.copy())
return
for i in range(start, len(nums)):
nums[start], nums[i] = nums[i], nums[start]
backtrack(start + 1)
nums[start], nums[i] = nums[i], nums[start]
result = []
backtrack(0)
return result
# 示例
nums = [1, 2, 3]
result = permute(nums)
print(result)
```
在这个例子中，`permute` 函数使用了嵌套的`backtrack` 函数来实现递归。
在每一层递归中，它通过交换元素的位置来生成不同的排列。
`start` 参数表示当前递归的起始位置，当`start` 达到列表的最后一个元素时，将当前排列添加到结果列表中。
你可以将不同的列表传递给`permute` 函数，以生成它们的全排列。
例如，对于输入`[1, 2, 3]`，输出将是所有可能的排列，如`[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 2, 1], [3, 1, 2]]`。
排列与组合问题的解题方法排列与组合是数学中重要的组合数学问题，常用于解决计数和选择问题。
在排列与组合中，排列是指从一组元素中选取若干个按特定顺序排列的方式；而组合则是指从一组元素中选取若干个无序的方式。
解决排列与组合问题的方法有很多，下面将介绍一些常用的解题方法。
一、排列问题的解题方法1. 全排列方法：全排列是指对给定的一组元素进行全面排列，确保每个元素都排在不同的位置上。
全排列问题可以通过递归算法来解决。
具体步骤如下：1）选取第一个元素作为排列的首位；2）将剩余的元素进行全排列；3）将选取的元素与全排列的结果进行组合。
2. 循环方法：循环方法是指通过循环遍历的方式来求解排列问题。
具体步骤如下：1）确定排列的元素个数和位置；2）通过循环遍历的方式确定每个位置上的元素。
3. 递归方法：递归方法是指通过递归函数的调用来求解排列问题。
递归方法可以将一个问题分解为更小的子问题，并通过递归调用来解决子问题。
具体步骤如下：1）选取第一个元素作为排列的首位；2）将剩余的元素进行递归调用，求解子问题的排列；3）将选取的元素与子问题的排列进行组合。
二、组合问题的解题方法1. 递推公式法：递推公式法是一种求解组合问题的常用方法。
通过递推公式，可以将大的组合问题分解为更小的子问题，并通过递归调用来解决子问题。
具体步骤如下：1）确定组合的元素个数和位置；2）通过递推公式计算每个位置上的元素。
2. 数学公式法：数学公式法是指通过数学公式来求解组合问题。
常用的组合公式有排列组合公式、二项式定理等。
通过应用数学公式，可以快速计算组合问题的解。
具体步骤如下：1）确定组合的元素个数和位置；2）通过数学公式计算每个位置上的元素。
3. 动态规划法：动态规划法是一种求解组合问题的高效算法。
通过定义递推关系和初始条件，可以通过动态规划的方式求解组合问题。
具体步骤如下：1）定义递推关系和初始条件；2）通过递推公式计算每个位置上的元素。
总结：排列与组合问题的解题方法有很多种，选择合适的方法取决于具体的问题和求解的要求。
全排列算法全排列算法2009年10月20日星期二下午 08:39全排列的生成算法就是对于给定的字符集，用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。
任何n个字符集的排列都可以与1,n的n个数字的排列一一对应，因此在此就以n个数字的排列为例说明排列的生成法。
n个字符的全体排列之间存在一个确定的线性顺序关系。
所有的排列中除最后一个排列外，都有一个后继;除第一个排列外，都有一个前驱。
每个排列的后继都可以从它的前驱经过最少的变化而得到，全排列的生成算法就是从第一个排列开始逐个生成所有的排列的方法。
全排列的生成法通常有以下几种:字典序法递增进位数制法递减进位数制法邻位交换法递归类算法1.字典序法字典序法中，对于数字1、2、3......n的排列，不同排列的先后关系是从左到右逐个比较对应的数字的先后来决定的。
例如对于5个数字的排列12354和12345，排列12345在前，排列12354在后。
按照这样的规定，5个数字的所有的排列中最前面的是12345，最后面的是54321。
字典序算法如下:设P是1,n的一个全排列:p=p1p2......pn=p1p2......pj-1pjpj+1......pk-1pkpk+1......pn1)从排列的右端开始，找出第一个比右边数字小的数字的序号j(j从左端开始计算)，即 j=max{i|pi<pi+1}2)在pj的右边的数字中，找出所有比pj大的数中最小的数字pk，即k=max{i|pi>pj}(右边的数从右至左是递增的，因此k是所有大于pj的数字中序号最大者)3)对换pi，pk4)再将pj+1......pk-1pkpk+1pn倒转得到排列p’’=p1p2.....pj-1pjpn.....pk+1pkpk-1.....pj+1，这就是排列p的下一个下一个排列。
例如839647521是数字1,9的一个排列。
从它生成下一个排列的步骤如下: 自右至左找出排列中第一个比右边数字小的数字4 839647521在该数字后的数字中找出比4大的数中最小的一个5 839647521将5与4交换 839657421将7421倒转 839651247所以839647521的下一个排列是839651247。
本文为原创，如需转载，请注明作者和出处，谢谢！全排列是将一组数按一定顺序进行排列，如果这组数有n个，那么全排列数为n!个。
现以{1, 2, 3, 4, 5}为例说明如何编写全排列的递归算法。
1、首先看最后两个数4, 5。
它们的全排列为4 5和5 4, 即以4开头的5的全排列和以5开头的4的全排列。
由于一个数的全排列就是其本身，从而得到以上结果。
2、再看后三个数3, 4, 5。
它们的全排列为3 4 5、3 5 4、 4 3 5、 4 53、 53 4、 54 3 六组数。
即以3开头的和4,5的全排列的组合、以4开头的和3,5的全排列的组合和以5开头的和3,4的全排列的组合.从而可以推断，设一组数p = {r1, r2, r3, ... ,rn}, 全排列为perm(p)，pn = p - {rn}。
因此perm(p) = r1perm(p1), r2perm(p2), r3perm(p3), ... , rnperm(pn)。
当n = 1时perm(p} = r1。
为了更容易理解，将整组数中的所有的数分别与第一个数交换，这样就总是在处理后n-1个数的全排列。
算法如下：#include <stdio.h>int n =0;void swap(int *a, int *b){int m;m = *a;*a = *b;*b = m;}void perm(int list[], int k, int m){int i;if(k > m){for(i =0; i <= m; i++) printf("%d ", list[i]);printf("\n");n++;}else{for(i = k; i <= m; i++){swap(&list[k], &list[i]); perm(list, k +1, m); swap(&list[k], &list[i]);}}}int m ain(){int list[] = {1, 2, 3, 4, 5};perm(list, 0, 4);printf("total:%d\n", n);return0;}谁有更高效的递归和非递归算法，请回贴。
排列组合问题的类型及解答策略排列组合问题是概率论的一个重要内容，常见于数学和统计学的相关考试中。
它涉及将一组元素按照一定的规则进行排列或组合，从而求解出不同可能性的个数。
在数学领域中，排列与组合属于不同的问题类型，需要采用不同的解答策略。
首先，我们来讨论排列问题。
排列指的是从给定的一组元素中按照一定顺序选取若干个元素，形成一个有序的排列。
对于排列问题，常见的求解策略有全排列和有限排列两种。
全排列问题是指将给定的所有元素进行排列，即对于每一个元素都有可能处于不同的位置。
解答全排列问题时，可以使用递归算法。
首先确定第一个位置的元素，然后将剩余的元素进行全排列，依次确定后面的位置，直到所有元素都被排列。
全排列问题的解答策略比较直接，但对于元素较多的情况下，可能会导致运行时间较长。
有限排列问题是指从给定的一组元素中选取若干个元素进行排列，但排列的长度有限制，即不一定需要将所有元素都排列出来。
解答有限排列问题时，可以使用递归算法或迭代算法。
递归算法的思路与全排列问题类似，需要确定每个位置的元素，但要考虑到排列的长度限制。
迭代算法则可以通过循环来实现，每次选取一个元素并确定位置，直到达到排列长度限制或所有元素都被选取。
接下来，我们讨论组合问题。
组合指的是从给定的一组元素中选取若干个元素，形成一个无序的组合。
对于组合问题，常见的求解策略有全组合和有限组合两种。
全组合问题是指将给定的所有元素进行组合，即对于每一个元素都有可能被选取或不被选取。
解答全组合问题时，可以使用位运算的思想。
假设元素个数为n，可以使用n位二进制数表示每个元素的选取状态，0表示不选取，1表示选取。
通过遍历所有可能的二进制数，即可得到全组合的解。
有限组合问题是指从给定的一组元素中选取若干个元素进行组合，但组合的个数有限制。
解答有限组合问题时，可以使用递归算法或迭代算法。
递归算法的思路是从第一个元素开始选取，然后对剩余元素进行组合，依次确定后面的元素，直到达到组合个数限制或所有元素都被选取。
一、填空题1、算法的复杂性是算法效率2、的度量，是评价算法优劣的重要依据。
1、设n为正整数，利用大“O(·)”记号，将下列程序段的执行时间表示为n的函数，则下面程序段的时间复杂度为O(n)2、。
i=1; k=0;while(i<n) { k=k+10*i;i++; }3、计算机的资源最重要的是时间和空间资源。
因而，算法的复杂性有时间复杂度和空间复杂度之分。
3、f(n)= 6×2n+n2，f(n)的渐进性态f(n)= O( 2n4、 )5、递归是指函数直接或者间接通过一些语句调用自身。
4、分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立6、且与原问题相同。
二、选择题（本题20分，每小题2分）1、分支限界法与回溯法都是在问题的解空间树T上搜索问题的解,二者( B )。
A.求解目标不同,搜索方式相同B.求解目标不同,搜索方式也不同C.求解目标相同,搜索方式不同D.求解目标相同,搜索方式也相同2、回溯法在解空间树T上的搜索方式是( A)。
A.深度优先B.广度优先C.最小耗费优先D.活结点优先3、在对问题的解空间树进行搜索的方法中,一个活结点最多有一次机会成为活结点的是( B )。
A.回溯法B.分支限界法C.回溯法和分支限界法D.回溯法求解子集树问题4、以下关于判定问题难易处理的叙述中正确的是( C )。
A.可以由多项式时间算法求解的问题是难处理的B.需要超过多项式时间算法求解的问题是易处理的C.可以由多项式时间算法求解的问题是易处理的D.需要超过多项式时间算法求解的问题是不能处理的5、设f(N),g(N)是定义在正数集上的正函数,如果存在正的常数C和自然数N0,使得当N≥N0时有f(N)≤Cg(N),则称函数f(N)当N充分大时有上界g(N),记作f(N)=O(g(N)),即f(N)的阶( A )g(N)的阶。
A.不高于B.不低于C.等价于D.逼近6、对于含有n个元素的子集树问题,最坏情况下其解空间的叶结点数目为( B )。
