欧拉方程推导

03
欧拉公式的证明
利用三角函数的性质进行证明
总结词
利用三角函数的周期性和对称性，通 过一系列的等式变换，推导出欧拉公 式。
详细描述
首先，利用三角函数的周期性和对称 性，将角函数转化为指数形式。然 后，通过一系列的等式变换，将指数 形式转化为欧拉公式。
利用复数的性质进行证明
总结词
利用复数的共轭和模的性质，通过代数运算 和等式变换，推导出欧拉公式。
快速傅里叶变换（FFT）
欧拉公式在快速傅里叶变换算法中有重要应用， 该算法用于信号处理和频谱分析等领域。
加密算法的实现
欧拉公式可以用于实现一些加密算法，例如 RSA公钥加密算法。
并行计算中的向量旋转
在并行计算中，欧拉公式可以用于实现向量的旋转操作，提高计算效率。
THANKS
感谢观看
欧拉公式的应用场景
01
在物理学中，欧拉公式被广泛应用于波动方程、电磁学、量子 力学等领域。
02
在工程学中，欧拉公式被用于信号处理、控制系统等领域。
在金融学中，欧拉公式被用于计算复利、评估风险等。
03
02
欧拉公式的推导过程
利用三角函数的性质进行推导
总结词
利用三角函数的周期性和对称性，通过一系列的恒等变换，推导出欧拉公式。
04
欧拉公式的变种和推广
欧拉恒等式
总结词
欧拉恒等式是数学中一个重要的恒等式，它 表示三角函数和指数函数之间的关系。
详细描述
欧拉恒等式是数学中一个重要的恒等式，它 表示三角函数和指数函数之间的关系。这个 恒等式在数学分析、复变函数、微分方程等 领域有着广泛的应用。通过欧拉恒等式，我 们可以将三角函数转化为指数函数，从而简

欧拉公式的推导
欧拉公式是由瑞士数学家拉斐尔·欧拉提出的一个有关多边形面积与边数的公式，是一个
显示复杂性的表达式，被用在多边形计算中。

拉斐尔·欧拉公式可用来快速计算多边形面积。

它主要用于几何图形和多边形概念的研究，从而确定图形的大小和形状。

拉斐尔·欧拉发现，多边形面积可以表示为多边形边数乘以一半周长，减去多边形内部夹
角的和，这种观点形成拉斐尔·欧拉公式，公式的原理是由钝角三角形的面积来派生出来的。

拉斐尔·欧拉定理的数学表达式如下：
S=1/2 (n x c) - ( Σ θ )
其中，S代表多边形的面积，n代表多边形的边数，c代表多边形的周长，θ表示多边形内部所有夹角的和。

拉斐尔·欧拉公式是一个非线性的计算公式，以方便和简单的方式计算任意多边形的面积，包括三角形，四边形，五边形等等，这是一个重要的数学原理，有助于理解多边形的几何
学计算。

经过拉斐尔·欧拉的费力调查和发现，他终于得出了多边形面积与边数之间的关系，并利
用这一关系表示出欧拉公式。

拉斐尔·欧拉公式一直被许多数学家们转化为新的数学表达
式使用，用以表示多边形的面积运算。

拉斐尔·欧拉公式‘被应用于从小学到大学，从总体
分析到详细测量，甚至是机器人多边形数学分析等方面。

拉斐尔·欧拉公式可以更有效地解决几何问题，是几何测量的一个重要工具、这也被应用
到各种工程领域中，它能够用最简洁的方式表达多边形的面积计算。

拉斐尔•欧拉的贡献
也帮助人们用数学的方式去研究多边形，几何学，他的贡献也为人类几何学的发展增添了浓厚的历史气息。

欧拉方程推导全过程嘿，数学爱好者们！今天我要带大家走进一个超级有趣的数学世界，那就是欧拉方程的推导。

这可不像在公园散步那么简单，但也绝不是无法攀登的高山，只要跟着我一步一步来，保准你能搞明白。

咱先来说说什么是欧拉方程。

想象一下，在数学这个大王国里，有一个神秘的方程式，就像一颗璀璨的明珠，它把指数函数、三角函数这些看似不太相关的家伙巧妙地联系在了一起。

这就是欧拉方程，$e^{ix} = \cos x + i\sin x$，其中$e$是自然常数，$i$是虚数单位，$x$是一个实数。

这个方程就像一把魔法钥匙，能打开很多数学难题的大门呢。

那咱们怎么推导这个神奇的方程呢？咱们得从泰勒级数这个有力的工具开始。

泰勒级数就像是一个超级放大镜，可以把一个函数展开成无穷项的多项式。

对于指数函数$e^x$，它的泰勒级数展开式是：$e^x = 1 + x + \frac{x^2}{2!}+ \frac{x^3}{3!}+ \frac{x^4}{4!}+ \cdots$。

这个式子看起来有点吓人，但是别怕，咱们一点点分析。

这里的$n!$就是$n$的阶乘，也就是从$1$乘到$n$。

再来看三角函数$\cos x$和$\sin x$的泰勒级数展开式。

$\cos x = 1 - \frac{x^2}{2!}+ \frac{x^4}{4!}- \frac{x^6}{6!}+ \cdots$，$\sin x = x - \frac{x^3}{3!}+ \frac{x^5}{5!}- \frac{x^7}{7!}+ \cdots$。

现在咱们把$x$换成$ix$代入到$e^x$的泰勒级数展开式中。

$e^{ix} = 1 + ix + \frac{(ix)^2}{2!}+ \frac{(ix)^3}{3!}+ \frac{(ix)^4}{4!}+ \cdots$。

那这个式子要怎么化简呢？咱们来仔细瞧瞧。

$(ix)^2 = -x^2$，$(ix)^3 = -ix^3$，$(ix)^4 = x^4$等等。

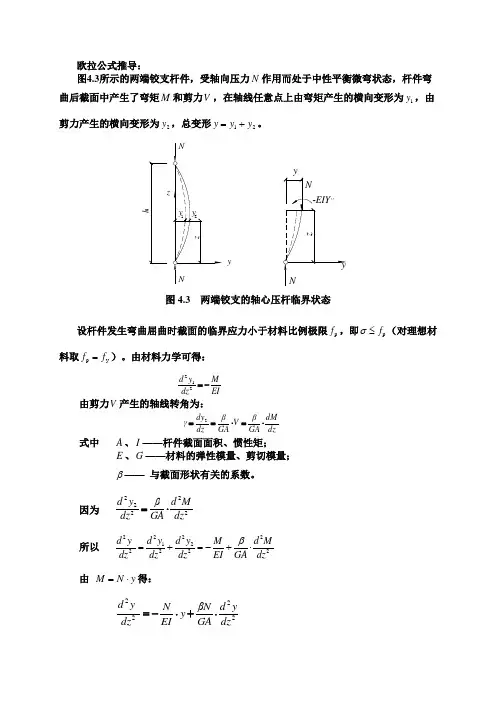
欧拉公式推导：图4.3所示的两端铰支杆件，受轴向压力N 作用而处于中性平衡微弯状态，杆件弯曲后截面中产生了弯矩M 和剪力V ，在轴线任意点上由弯矩产生的横向变形为1y ，由剪力产生的横向变形为2y ，总变形21y y y +=。

y图4.3 两端铰支的轴心压杆临界状态设杆件发生弯曲屈曲时截面的临界应力小于材料比例极限p f ，即p f ≤σ（对理想材料取y p f f =）。

由材料力学可得：EI M dz y d -=212 由剪力V 产生的轴线转角为：dz dM GA V GA dzdy ⋅=⋅==ββγ2 式中 A 、I ——杆件截面面积、惯性矩；E 、G ——材料的弹性模量、剪切模量； β—— 与截面形状有关的系数。

因为 22222dz M d GA dz y d ⋅=β 所以 2222122222d y d y d y M d M dz dz dz EI GA dzβ=+=-+⋅ 由 y N M ⋅=得：2222dzy d GA N y EI N dz yd ⋅+⋅-=β01=⋅+⎪⎭⎫ ⎝⎛-''y EIN GA N y β 令 ⎪⎭⎫ ⎝⎛-=GA N EI Nk β12得常系数线性二阶齐次方程 20y k y ''+=其通解为：sin cos y A kz B kz =+由边界条件：;0,0==y z 0=B ，kz A y sin =。

再由0,==y l z 得：0sin =kl A上式成立的条件是0=A 或0sin =kl ，其中0=A 表示杆件不出现任何变形，与杆件微弯的假设不符。

由0sin =kl ，得πn kl =（=n 1，2，3…），取最小值=n 1，得π=kl ，即2221N k N l EI GA πβ==⎛⎫- ⎪⎝⎭由此式解出N ，即为中性平衡的临界力cr N12222222211Ι11γππβππ⋅+⋅=⋅+⋅=lΕΙl ΕGA l ΕΙl ΕΙN cr （4.6） 临界状态时杆件截面的平均应力称为临界应力cr σ1222211γλπλπσ⋅+⋅==ΕΑΕA N cr cr （4.7）式中 1γ——单位剪力时杆件的轴线转角，)/(1GA βγ=；l ——两端铰支杆得长度；λ——杆件的长细比，i l /=λ；i ——杆件截面对应于屈曲轴的回转半径，A I i /=。

欧拉动力学方程推导欧拉动力学方程推导作为物理学必修的内容，欧拉动力学方程常常被各类研究者所关注。

欧拉动力学方程是描述物体在运动过程中受到各个力作用所导致的运动变化规律。

下面，我们将进行欧拉动力学方程的详细推导，以便让读者更加深入了解物理学的这部分内容。

1. 初步摆放对于欧拉动力学方程的推导，第一步是明确出力的平衡关系，也就是万有引力定律。

万有引力定律的核心是万有引力定律公式，即F=Gm_1m_2/r^2。

其中，F表示两个物体之间的力，G是万有引力常数，m_1和m_2分别是两个物体的质量，r是两个物体距离的距离。

2. 重心位置计算另外，需要求出物体的重心位置，以便在计算过程中进行更加精准的计算。

重心位置是物体的质量分布情况的简化结果。

具体的求解过程可以从物体几何结构上出发进行计算。

3. 动能定理应用在具备力的平衡关系和物体重心位置的计算结果后，我们还需要应用动能定理进行计算。

动能定理描述的是物体在做功时能量的变化规律。

物体在运动过程中由于受到外力的作用而发生的速度变化，同时产生的动能变化会导致物体做功。

4. 应用欧拉动力学方程最后，我们需要应用欧拉动力学方程，进行力的平衡关系的进一步推导。

欧拉动力学方程的核心是对所受到的力进行平衡分析，从而得出物体的加速度变化规律。

在欧拉动力学方程的具体应用中，需要注意对不同物体所受到的力进行区分，并且进行相应的求解。

总之，欧拉动力学方程的推导需要对力的平衡关系、重心位置计算、动能定理和欧拉动力学方程等各个方面进行分析。

通过深入研究这些内容，读者将会对欧拉动力学方程和物理学的各个细节问题有更加深入的认识和理解。

牛顿-欧拉方程向量法推导
欧拉方程(Euler equations)，是欧拉运动定律的定量描述，该定律为：
)]([1b
b b b b b I M I Ω⨯Ω-=Ω-& 其中b Ω为体坐标系下的角速度，b I 为体坐标系下的转动惯量，b M 为体坐标系下的外力矩。

欧拉方程通常与牛顿的平移运动方程被一起写出，称为牛顿-欧拉方程(Newton-Euler equations)，此处只推导欧拉方程。

在不考虑外力矩时，约束条件为惯性坐标系的角动量守恒（非体坐标系的角动量守恒），即有：
0/)(=Ωdt RI d b b
其中R 为旋转矩阵。

拆解有：
0=Ω+Ωb
b b b RI I R && 0)(=Ω+Ω⨯Ωb
b b b b I I & 最后可得：
b
b b b b I I /)(Ω⨯Ω-=Ω& 加入外力矩后可得完整的欧拉方程：
)]([1b
b b b b b I M I Ω⨯Ω-=Ω-&。

因式分解欧拉公式推导因式分解可是数学里的一个有趣“魔法”，而欧拉公式更是数学世界中的一颗璀璨明珠。

今天咱们就来聊聊因式分解欧拉公式的推导，准备好和我一起走进这个神奇的数学世界了吗？先来说说什么是因式分解。

就好比把一个大蛋糕切成小块，因式分解就是把一个复杂的多项式，分解成几个简单的式子相乘的形式。

比如说，$x^2 - 1$ 就可以分解成 $(x + 1)(x - 1)$ 。

那欧拉公式是啥呢？它长这样：$e^{ix} = \cos x + i\sin x$ 。

这里的$e$ 是自然常数，约等于 2.718 ，$i$ 是虚数单位，满足 $i^2 = -1$ 。

咱们开始推导啦！假设我们有一个复数 $z = \cos x + i\sin x$ ，对它求导，可得：$z^\prime = -\sin x + i\cos x$然后，我们把 $i$ 乘到 $z$ 上，得到：$iz = i\cos x - \sin x$嘿，您瞧瞧，这 $iz$ 不就正好是 $z^\prime$ 嘛！这就说明 $z$ 满足一个微分方程：$z^\prime = iz$ 。

解这个微分方程，您猜怎么着？它的解就是 $z = e^{ix}$ 。

所以，我们就得到了欧拉公式：$e^{ix} = \cos x + i\sin x$ 。

这推导过程是不是还挺神奇的？我想起之前给学生们讲这部分内容的时候，有个学生瞪着大眼睛，一脸迷茫地问我：“老师，这欧拉公式到底有啥用啊？”我笑着跟他说：“孩子，就好比你有一把神奇的钥匙，这欧拉公式就是能打开很多数学难题大门的那把钥匙。

”比如说，在计算一些复杂的积分时，欧拉公式就能大显身手。

还有在研究波动现象，像声波、光波的时候，欧拉公式也能帮我们更好地理解和分析。

数学的世界就是这样，一个公式的推导，可能看起来复杂，但当您真正理解了它，就会发现其中的美妙和乐趣。

就像探索一个神秘的宝藏，每一步的发现都让人兴奋不已。

希望通过这次的讲解，能让您对因式分解欧拉公式的推导有更清晰的认识，感受到数学的魅力。

【数学科普】欧拉公式的推导
欧拉公式是数学中一个非常重要的公式，它连接了三角函数和复数。

以下是欧拉公式的推导过程：
第一步，我们设z=x+yi，其中x 和y 是实数，i 是虚数单位，满足i2=−1。

第二步，根据复数的三角形式，我们可以将z 写
成ρ(cosθ+isinθ)的形式，其中ρ=x2+y2，
θ是z 在复平面上的辐角。

第三步，根据三角函数的加法公式，我们有：
cos(A+B)=cosAcosB−sinAsinB
sin(A+B)=sinAcosB+cosAsinB
第四步，令A=θ，B=2nπ（其中n 是整数），则：cos(A+B)=cos(θ+2nπ)=cosθ
sin(A+B)=sin(θ+2nπ)=sinθ
第五步，由于ρ和θ是z 的极坐标表示中的两个变量，我们可以将ρ和θ分别替换
为r 和t，其中r=∣z∣。

第六步，根据第五步的替换，我们可以得到：
z=r(cost+isint)
第七步，根据复数的模长和辐角，我们有：
r=∣z∣=x2+y2
t=arctan(xy)
第八步，将第七步中的r 和t 代入第六步中的公式，得到：
z=r(cost+isint)
综上，我们得到了欧拉公式：
z=x+yi=r(cost+isint)。

欧拉公式19种证明欧拉公式是数学中的一个重要公式，它的表达式为e^(ix)=cos(x)+i*sin(x)，其中e表示自然对数的底数2.71828…，i表示虚数单位。

欧拉公式有多种证明方法，下面我们将介绍其中19种常见的证明方法。

1. 泰勒级数证明法：利用泰勒级数展开式展开e^(ix)和cos(x)+i*sin(x)，然后将它们相等的系数进行比较，即可得出欧拉公式。

2. 复合函数证明法：将e^(ix)看作复数函数f(x)=e^x，将cos(x)和sin(x)看作f(x)的实部和虚部，则有f(ix)=cos(x)+i*sin(x)，即e^(ix)=cos(x)+i*sin(x)。

3. 微积分证明法：将欧拉公式两边分别对x求导，得到ie^(ix)=-sin(x)+i*cos(x)，再将其两边同时乘以i，即可得到欧拉公式。

4. 积分证明法：将欧拉公式两边同时积分，得到e^(ix)/i=-sin(x)/i+cos(x)，再将其两边同时乘以i，即可得到欧拉公式。

5. 欧拉级数证明法：将e^(ix)和cos(x)+i*sin(x)的泰勒级数展开式进行对比，即可得到欧拉公式。

6. 幂级数证明法：将e^(ix)和cos(x)+i*sin(x)的幂级数展开式进行对比，即可得到欧拉公式。

7. 矩阵证明法：构造一个2x2矩阵，使其特征值为e^(ix)和e^(-ix)，然后求解该矩阵的本征向量，即可得到欧拉公式。

8. 矩阵幂证明法：将e^(ix)表示为矩阵的形式，然后对该矩阵进行幂运算，即可得到欧拉公式。

9. 极限证明法：将e^(ix)表示为极限的形式，然后通过极限的性质推导出欧拉公式。

10. 解微分方程证明法：将e^(ix)看作微分方程y'=iy的解，并利用欧拉公式将其转化为y=cos(x)+i*sin(x)，即可得到欧拉公式。

11. 解偏微分方程证明法：将e^(ix)看作偏微分方程u_t+iu_x=0的解，并利用欧拉公式将其转化为u=cos(x-t)+i*sin(x-t)，即可得到欧拉公式。

欧拉方程推导过程欧拉方程是数学中的一个重要概念，它描述了函数的一些基本性质。

欧拉方程是由瑞士数学家欧拉在18世纪提出的，它在微积分、物理学、工程学等领域都有广泛应用。

本文将详细介绍欧拉方程的推导过程。

一、函数的定义在推导欧拉方程之前，我们首先需要了解函数的定义。

函数是一种映射关系，它将一个自变量映射到一个因变量上。

具体来说，如果有两个集合X和Y，那么一个函数f可以表示为：f:X→Y其中X是自变量集合，Y是因变量集合。

对于任意一个x∈X，f(x)表示x在函数f下的取值。

二、泰勒公式泰勒公式是微积分中的一个重要定理，它描述了函数在某一点附近可以用多项式逼近的性质。

具体来说，如果有一个n+1次可导函数f(x)，那么对于任意实数x0和正整数n，有：f(x)=f(x0)+\frac{f'(x0)}{1!}(x-x0)+\frac{f''(x0)}{2!}(x-x0)^2+...+\frac{f^{(n)}(x0)}{n!}(x-x0)^n+R_n(x)其中Rn(x)是余项，它表示了函数f(x)在x0处的误差。

当x趋近于x0时，余项Rn(x)的大小趋近于0，因此可以用泰勒公式来近似表示函数f(x)。

三、欧拉方程的定义欧拉方程是描述函数性质的一个重要方程，它具有如下形式：a_0y(x)+a_1y'(x)+a_2y''(x)+...+a_ny^{(n)}(x)=f(x)其中a0,a1,...,an和f(x)都是已知函数或常数。

这个方程中的n称为方程的阶数。

四、欧拉方程推导过程现在我们来推导欧拉方程。

假设有一个二阶线性微分方程：ay''(x)+by'(x)+cy(x)=f(x)其中a,b,c和f(x)都是已知函数或常数。

我们需要将这个微分方程转化为欧拉方程。

首先，我们令y=e^(mx)，其中m是一个常数。

对于这个函数，有：y'=me^(mx)y''=m^2e^(mx)将上述结果代入原微分方程中，得到：am^2e^(mx)+bme^(mx)+ce^(mx)=f(x)将e^(mx)提取出来，并除以a，得到：m^2+\frac{b}{a}m+\frac{c}{a}=\frac{f(x)}{a}e^{-mx}现在我们令z=e^(mx)，则有：m=\frac{\ln z}{x}将上述结果代入欧拉方程中，得到：\frac{d^2}{dx^2}(z)=\frac{1}{x^2}\left(\frac{d}{dz}\right)^2(z)-\frac{1}{x}\left(\frac{d}{dz}\right)(z)这就是欧拉方程的一般形式。

a ≤ t ≤b
引Hale Waihona Puke 1对任意x > 0及任意正数n, 有 (1 + x) n < e nx
引理2 则
设s > 0，t为非负实数, 序列{ai }满足递推不等式 ai +1 ≤ (1 + s ) ai + t ai +1 ≤ e
( i +1) s
t t ( + a0 ) s s
定理2
若函数f (t , y )在凸区域D = {(t , y ) | a ≤ t ≤ b, f (t , y1 ) f (t , y2 ) ≤ L y1 y2
∞ < y < +∞}上关于变量t , y都满足李普希兹条件,即 则欧拉法的整体截断误差为 hM L (b a ) Ei +1 ≤ (e 1) 2L f ′′(t ) .
其中, M = max
a ≤t ≤b
作业 教材P198 习题1、2
§9-1 欧拉法
一、欧拉公式的推导
对一阶方程的初值问题
dy = f (t , y ) dt y ( a ) = y0 a≤t ≤b (1)
假设式(1)的唯一解y (t )在[a, b]上有二次连续导数, 则对i = 0,1, L, n 1, 作泰勒展开得 (ti +1 ti ) 2 y (ti +1 ) = y (ti ) + (ti +1 ti ) y′(ti ) + y′′(ξ i ) 2! 其中, ti < ξ i < ti +1 , i = 0,1, L, n 1 (2)
ti+1 ti
f (t , y (t ))dt
所以

欧拉恒等式推导全过程全文共四篇示例，供读者参考第一篇示例：欧拉恒等式，也被称为欧拉公式，是数学家欧拉在18世纪提出的一个重要公式。

它是以自然对数e、圆周率π、虚数单位i和三角函数之间的关系而闻名于世。

欧拉恒等式的形式如下：e^(iπ) + 1 = 0这个看似简单的公式实际上蕴含了许多深刻的数学道理，是数学中的一块宝藏。

接下来，我们将从简单的数学概念开始，逐步推导欧拉恒等式的全过程。

我们需要了解几个基本的数学定义。

自然对数e是一个重要的常数，它是一个无穷不循环小数，约等于2.71828。

圆周率π是另一个重要的常数，它是一个无理数，约等于3.14159。

虚数单位i是一个虚数，定义为i^2 = -1。

我们知道，欧拉公式涉及到三个重要的数学常数：e、π和i。

我们回顾一下复指数函数。

复指数函数的定义如下：e^(ix) = cos(x) + i sin(x)e是自然对数的底，i是虚数单位，x是一个实数，cos(x)和sin(x)分别是x的余弦和正弦函数。

现在，我们来推导欧拉恒等式。

我们让x等于π，代入上面的复指数函数公式中：根据三角函数的性质，cos(π) = -1，sin(π) = 0，所以：将上式代入欧拉恒等式中得：所以欧拉恒等式得证。

通过这个推导过程，我们可以看到欧拉公式的美妙之处。

它将自然对数e、圆周率π、虚数单位i和三角函数之间的关系巧妙地结合在一起，展现了数学的精密和美丽。

这个公式在数学、物理、工程等领域都有着重要的应用，是数学家们智慧的结晶。

希望通过这篇文章，读者们能更加深入地了解欧拉恒等式的推导过程，感受数学的奥秘和魅力。

第二篇示例：欧拉恒等式是数学中著名的公式之一，它将指数函数、三角函数和虚数单位e、i和π联系在一起。

这个公式的推导过程非常有趣，充满了数学上的魅力和美感。

本文将带领读者一步一步地揭开欧拉恒等式的面纱。

我们需要了解几个重要的数学概念。

一是自然对数e，定义为极限\[\lim_{n \to \infty} (1 + \frac{1}{n})^n\]，近似值约为2.71828；二是虚数单位i，定义为\[\sqrt{-1}\]；三是圆周率π，它是一个无理数，近似为3.14159。

欧拉拉格朗日方程推导欧拉-拉格朗日方程（Euler-Lagrange equation）是用于描述物理系统的经典力学问题的定律，它的推导基于变分原理和拉格朗日函数。

在物理学中，我们经常需要找到一个系统的最优路径，即该路径下其中一物理量的变分问题。

为此，拉格朗日引入了一个新的函数，即拉格朗日函数（Lagrange function），它是系统的广义坐标（generalized coordinates）和广义速度（generalized velocities）的函数，记作L(q, q ̇)。

广义坐标是指描述系统的自由度的坐标，坐标的个数与系统自由度的数量相等。

广义速度是广义坐标对时间的导数。

这个拉格朗日函数可以看作系统的动能（kinetic energy）和势能（potential energy）的代数和。

我们希望通过求解拉格朗日函数的变分问题，来得到系统的最优路径。

变分问题的解就是能够使拉格朗日函数满足对应的极值条件的路径。

这个变分问题可以用欧拉方程来描述。

首先，我们需要定义一个定义域中的路径，路径上的点可以由广义坐标 q 的函数表示，即 q(t)。

接下来，引入一个新的函数，广义速度v(t)，它表示路径上其中一点的广义坐标 q 对时间的导数，即 v(t) =dq(t)/dt。

这个函数可以用来表示路径上其中一点的切矢量。

在此基础上，我们可以定义一个新的函数，即作用量（action），记作S。

作用量是广义坐标 q 和广义速度 v 的函数，定义为路径上各个点的拉格朗日函数在时间间隔 t1 到 t2 上的积分：S[q(t)] = ∫L(q, v) dt, t1到t2上式描述了广义坐标和广义速度在整个路径上的变化，我们希望找到一个路径使得作用量最小化。

为了求解这个变分问题，我们需要引入变分运算符（variational operator），记作δ。

变分运算符作用在函数上得到函数的变分值（函数的微小变化）。

对于一些函数 f(x)，它的变分值可以表示为：δf(x)=f(x+δx)-f(x)其中，δx是函数x的变分值。

流体欧拉方程流体力学是研究流体运动规律或流体静力学问题的一门学科。

欧拉方程是描述无黏流动的基本方程之一。

下面我们就来了解一下流体欧拉方程吧。

一、欧拉方程的定义和作用欧拉方程是描述无黏流动的基本方程之一，它是由欧拉基于质量守恒与动量守恒定律得出的。

欧拉方程的作用是描述流体在宏观上的运动规律，对于大规模的流体运动问题具有非常重要的意义。

二、欧拉方程的形式和推导欧拉方程可以写为：∂ρ/∂t + ∇·(ρu) = 0∂u/∂t +(u·∇)u + (1/ρ)∇p = f其中，ρ是流体的密度，u是流体的速度，p是流体的压强，f是流体所受到的外力。

这两个方程分别代表了质量守恒方程和动量守恒方程。

欧拉方程的推导基于牛顿第二定律：F=ma，也就是力等于质量乘以加速度。

在流体力学中，力是由压强和粘性力组成的。

将牛顿第二定律写成流体力学中的形式，就可以得到欧拉方程。

三、欧拉方程的应用欧拉方程可以应用于各种流体运动问题中，例如：1. 定常流：在定常流中，流体的速度和压强在整个流场中保持不变，因此可以通过欧拉方程来描述流体的运动规律。

2. 喷流：喷流是一种流体由高压区域流向低压区域的运动方式，在喷流问题中，欧拉方程可以用来描述流体在各个位置的速度和压强等参数的变化规律。

3. 涡流：涡流是一种流体圆周运动的形式，在涡流问题中，欧拉方程可以用来描述流体圆周运动的速度和压强等参数的变化规律。

四、欧拉方程的局限性欧拉方程是一种描述无黏流动的基本方程，因此只适用于无黏流动问题。

在黏性流体中，由于黏性力的存在，欧拉方程并不能完全描述流体的运动，需要补充其他方程进行描述。

此外，欧拉方程还忽略了流体内部的微观结构，因此只适用于宏观问题，对于微观问题的描述必须采用其他的理论。

简述欧拉方程的基本原理
欧拉方程是描述自由刚体在物体绕某一固定轴进行转动时运动状态的方程。

它是由瑞士数学家欧拉所提出的。

欧拉方程的基本原理可以概括为以下两点：
1. 刚体转动的惯性力矩与外力矩之和等于角加速度乘以转动惯量。

这个原理可以表示为：
I · α = Σ τ
其中，I为刚体的转动惯量，α为角加速度，τ为外力对刚体的合力矩。

这个原理说明了刚体转动的惯性作用与外力作用之间的关系。

2. 刚体转动的动力学方程可以由欧拉方程推导而来。

假设刚体绕一个固定轴进行转动，欧拉方程可以表示为：
I · α = Σ τ
M = I · ω
这里，ω为角速度，M为转动惯量相对于转动轴的矩。

这个原理说明了角加速度与角速度之间的关系。

欧拉方程的基本原理可以用于分析刚体转动时的运动状态，以及预测与控制刚体的转动行为。

欧拉方程推导过程概述欧拉方程（Euler’s equation）是描述流体运动的基本方程之一，它是由瑞士数学家欧拉（Leonhard Euler）在18世纪提出的。

欧拉方程在流体力学、空气动力学等领域具有广泛的应用。

本文将介绍欧拉方程的推导过程，以及一些相关的概念。

基本假设在推导欧拉方程之前，我们需要先明确一些基本假设和定义： 1. 流体是连续的：假设流体是连续、无限可分的。

这意味着我们可以对流体的性质进行连续的观察和分析。

2. 流体是可压缩的：假设流体在运动过程中可以发生密度的变化。

3. 流体满足牛顿力学：假设流体的运动可以用牛顿力学描述，即满足牛顿第二定律。

推导过程为了推导欧拉方程，我们首先需要从基本假设出发，利用牛顿第二定律来描述流体运动。

1. 守恒方程守恒方程是流体力学中的基本方程，描述了质量、动量和能量的守恒。

在欧拉方程的推导中，我们主要关注质量守恒和动量守恒。

1.1 质量守恒质量守恒可以表达为以下形式：∂ρ+∇⋅(ρv)=0∂t其中，ρ表示流体的密度，v表示流体的速度。

该方程描述了密度在空间和时间上的变化。

1.2 动量守恒动量守恒可以表达为以下形式：ρ(∂v ∂t+v ⋅∇v)=−∇p +∇⋅T +ρg 其中，p 表示流体的压强，T 表示应力张量，g 表示重力加速度。

该方程描述了流体的动量在空间和时间上的变化。

2. 应力张量欧拉方程中的应力张量T 描述了流体内部的相互作用力。

它可以通过牛顿第二定律和基本假设推导得到。

2.1 应力张量的定义应力张量是一个二阶张量，它描述了流体内部各点沿不同方向的力和应变之间的关系。

在流体力学中，应力张量可以表示为：T ij =−pδij +σij其中，p 是流体的压强，δij 是克罗内克（Kronecker ）δ符号，σij 是剪切应力张量。

2.2 应力张量的推导为了推导应力张量，我们考虑流体中某一点的受力情况。

由牛顿第二定律可知，该点受到的合力等于质量乘以加速度：F =ma将质量表示为体积乘以密度m =ρV ，并将加速度表示为速度的时间导数a =dv dt ，可以得到：F =ρV dv dt将体积表示为面积乘以厚度V =SΔz ，并将速度的导数表示为时间的偏导数dv dt =∂v ∂t ，可以得到：F =ρSΔz ∂v ∂t当体积趋近于0时，左侧的合力可以表达为面积上的应力乘以面积元dS，即F= TdS。

欧拉公式推导和差化积全文共四篇示例，供读者参考第一篇示例：欧拉公式是数学中非常著名的公式之一，它将自然对数的底e与虚数单位i联系在一起，形成了一个非常优雅的数学表达式。

欧拉公式的推导过程虽然较为复杂，但其中的一些技巧和方法却是非常值得我们学习和掌握的。

在这篇文章中，我们将介绍欧拉公式的推导过程，并结合差化积的技巧来更好地理解这个公式的美妙之处。

让我们来回顾一下欧拉公式的表达式：e^(iθ) = cosθ + i·sinθ这个公式将自然对数的底e的指数函数与三角函数cos和sin联系在了一起，展现了数学中的一种美丽的关系。

那么，这个公式是如何推导出来的呢？接下来，我们将通过一系列的推导过程来揭示这个谜底。

我们从泰勒级数展开开始。

泰勒级数是用一个无限多个项的无穷级数来表示一个函数的方法，我们可以将任意一个函数表示成一个无穷级数的形式。

对于指数函数e^x来说，它的泰勒级数展开形式如下：e^x = 1 + x + x^2/2! + x^3/3! + x^4/4! + ...接着，我们将x替换为iθ，即e^(iθ)，得到：接下来，我们来考虑sinθ和cosθ的泰勒级数展开形式。

根据三角函数的性质，我们可以知道：将sinθ和cosθ的泰勒级数展开形式代入到e^(iθ)的泰勒级数展开中，我们可以得到：接下来，让我们结合差化积的技巧来更好地理解欧拉公式的美妙之处。

差化积是一种用于化简三角函数乘积的技巧，其中利用了三角函数的加法公式和乘法公式。

在欧拉公式中，我们可以利用差化积的技巧将cosθ和sinθ的乘积进行化简，进一步证明欧拉公式的正确性。

在欧拉公式中，我们知道e^(iθ) = cosθ + i·sinθ，我们可以将cosθ和sinθ用e^(iθ)的形式来表示：cosθ = (e^(iθ) + e^(-iθ))/2sinθ = (e^(iθ) - e^(-iθ))/(2i)接着，我们将cosθ和sinθ的乘积进行差化积的化简：= i(e^(2iθ) - e^(-2iθ))/4= i(sin2θ)/2通过差化积的技巧，我们成功地将cosθ和sinθ的乘积进行了化简，最终得到了i(sin2θ)/2的形式。