超经典带电粒子在磁场中的偏转(几何关系)
- 格式:doc
- 大小:92.50 KB
- 文档页数:6

第十二讲磁场对运动电荷的作用带电粒子在磁场中的偏转1.磁场对运动电荷的作用力称为洛仑兹力。
通电直导体在磁场中所受的安培力的实质是磁场作用于导体内的运动电荷的洛仑兹力的合力。
据此,可以推导出,当电荷速度方向与磁场方向垂直时,洛仑兹力的计算公式为。
①当时,。
即磁场对静止的电荷无作用力,磁场只对运动电荷有作用力。
这与电场对其中的静止电荷或运动电荷总有电场力作用是不同的。
对①式中的v,应理解为电荷相对于磁场的运动速度。
当v的大小改变时,洛仑兹力大小也改变。
当电荷运动方向与磁场方向相同或相反,即v与B平行时,由实验可知,。
所以只有当v与B不平行时,运动电荷才受洛仑兹力。
当电荷运动方向与磁场方向夹角为θ时,电荷所受洛仑兹力计算公式为。
2.洛仑兹力的方向,仍用左手定则来判断。
判断时,让磁感线穿入手心,四指指向正电荷运动方向(或负电荷运动方向的反方向),大拇指指向就是洛仑兹力方向。
洛仑兹力的方向具有这样的特点:无论对v与B是否垂直,洛仑兹力总是同时垂直于电荷运动方向与磁场方向。
因此,洛仑兹力不能改变速度的大小,也始终不对电荷做功。
3.一个不计重力的带电粒子,以与磁场垂直的速度进入匀强磁场。
由于它所受的洛仑兹力方向同时垂直于磁场和速度方向,带电粒子只能在垂直于磁场方向的平面内运动。
而且洛仑兹力只改变它的运动方向,不改变它的速度大小,于是该带电粒子在匀强磁场中做匀速圆周运动。
洛仑兹力提供了它作匀速圆周运动所需要的向心力。
4.带电粒子作匀速圆周运动的半径和周期:由可得带电粒子作匀速圆周运动的半径公式:,带电粒子在匀强磁场中作匀速圆周运动的半径大小,是由粒子的质量、带电量、磁感强度以及粒子速度四个因素决定的。
若同种粒子(或荷质比相同的粒子)在同一磁场中作匀速圆周运动时,它们的半径与粒子速度大小成正比。
由得周期公式,周期是由带电粒子的质量、电量、磁感强度三个因素决定的,与速率的大小无关。
5.质谱仪:是测量带电粒子的质量和分析同位素的重要工具。



一、知识归纳1、 带电粒子在电场中运动 (1)匀加速运动:2022121mv mv qU t -=注意1:求解时间时,用运动学公式注意2:求解某一方向运动时,也可利用动能定理(2)类平抛运动: ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=====-==+======αθtan 22tan 21212102002022220x yt v at v at v v mv mv y d U q qEy y v v at v dm Uqm Eq a at y tv x y y o y 或2、带电粒子在磁场中运动(1)匀速直线运动:利用平衡条件。
(2)匀速圆周运动:⎪⎪⎪⎩⎪⎪⎪⎨⎧=====⇒=Bq mT t Bq mv R T Bq mv R R v m qvB θπθππ2222,其中R 、θ主要通过几何关系确定。
注意1:确定圆心方法:利用三角函数、勾股定理等注意2:确定圆心角方法:利用速度的偏转角等于圆周运动的圆心角等 3、圆周运动的圆心确定方法法1:已知轨迹上两点的速度方向 法2:已知轨迹上的两点和其中一点的速度方向 法3:已知轨迹上一点的速度方向和半径R 法4:已知轨迹上的两点和半径R 4、带电粒子在有界磁场中运动的极值问题(1)刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切。
(2)当速度v 一定时,弧长(或弦长)越大,圆周角越大,则时间越长。
5、对称规律解题法(1)从同一边界射入的粒子,又从同一边界射出时,速度与边界的夹角相等。
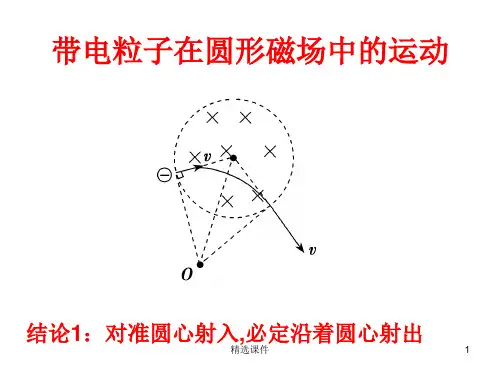
(2)在圆形磁场区域内,沿径向射入的粒子,一定沿径向射出。
(3)在圆形磁场区域内,不沿径向射入的粒子,也满足对称性。
1. 关于带负电的粒子(重力可忽略不计),下面说法中准确的是① 沿电场线方向飞入匀强电场,电场力做功,动能增加 ② 垂直电场线方向飞入匀强电场,电场力做功,动能增加 ③ 垂直磁感线方向飞入匀强磁场,磁场力不做功,动能不变 ④ 沿磁感线方向飞入匀强磁场,磁场力做功,动能增加 A. ①② B. ②③ C. ③④ D. ①④2、如图9,两个初速度大小相同的同种离子a 和b ,从O 点沿垂直磁场方向进入匀强磁场,最后打到屏P 上。

高考物理带电粒子在磁场中偏转带电粒子在磁场中偏转的求解策略带电粒子在磁场中偏转问题是历年高考的重点问题,同时也是热点问题。
总结考试中的诸多失误,集中在对这类问题的解法缺乏规律性的认识。
为此本文就求解这类题型的某些规律归纳如下。
一、基本思想因为洛伦兹力F始终与速度v垂直,即F只改变速度方向而不改变速度的大小,所以运动电荷垂直磁感线进入匀强磁场且仅受洛伦兹力时,一定做匀速圆周运动,由洛伦磁力提供向心力,即F qvB mv R==2/。
带电粒子在磁场中运动问题大致可分两种情况:1. 做完整的圆周运动(在无界磁场或有界磁场中);2. 做一段圆弧运动(一般在有界磁场中)。
无论何种情况,其关键均在圆心、半径的确定上。
二、思路和方法1. 找圆心方法1:若已知粒子轨迹上的两点的速度方向,则可根据洛伦兹力F⊥v,分别确定两点处洛伦兹力F的方向,其交点即为圆心。
方法2:若已知粒子轨迹上的两点和其中一点的速度方向,则可作出此两点的连线(即过这两点的圆弧的弦)的中垂线,再画出已知点v的垂线,中垂线与垂线的交点即为圆心。
方法3:若已知粒子轨迹上的两点和能求得的半径R ,则可作出此两点连线的中垂线,从连线的端点到中垂线上的距离为R 的点即为圆心。
方法4:若已知粒子入射方向和出射方向,及轨迹半径R ,但不知粒子的运动轨迹,则可作出此两速度方向夹角的平分线,在角平分线上与两速度方向直线的距离为R 的点即为圆心。
方法5:若已知粒子圆周运动轨迹上的两条弦,则两条弦的中垂线的交点即为圆心。
2. 求半径圆心确定下来后,半径也随之确定。
一般可运用平面几何知识来求半径的长度。
3. 画轨迹在圆心和半径确定后可根据左手定则和题意画出粒子在磁场中的轨迹图。
4. 应用对称规律从一边界射入的粒子,若从同一边界射出时,则速度与边界的夹角相等;在圆形磁场区域内,若粒子沿径向射入,则必沿径向射出。
三、实例分析例1. 如图1所示,两电子沿MN 方向射入两平行直线间的匀强磁场,并分别以v v 12、的速度射出磁场。



高考回归复习—电磁场之带电粒子在电、磁场中的偏转模型1.如图所示,在平面直角坐标系xoy 的第二象限内有平行于y 轴的匀强电场,电场强度大小为E ,方向沿y 轴负方向。
在第一、四象限内有一个半径为R 的圆,圆心坐标为(R ,0),圆内有方向垂直于xoy 平面向里的匀强磁场。
一带正电的粒子(不计重力),以速度为v 0从第二象限的P 点,沿平行于x 轴正方向射入电场,通过坐标原点O 进入第四象限,速度方向与x 轴正方向成30︒,最后从Q 点平行于y 轴离开磁场,已知P 点的横坐标为2-h 。
求:(1)带电粒子的比荷q m; (2)圆内磁场的磁感应强度B 的大小;(3)带电粒子从P 点进入电场到从Q 点射出磁场的总时间。
2.物理学中,常用电场或磁场控制带电粒子的运动轨迹。
如图所示,质量为m ,电量为e 电子,由静止开始经电压U 加速后,从枪口P 沿直线OM 射出,若要求电子能击中偏离OM 方向α角、与枪口相距d 的靶Q ,不计电子的重力。
试求在以下两种情况下,所需的匀强磁场B 的大小和匀强电场E 的大小。
(1)若空间有垂直纸面向里的匀强磁场;(2)若空间有在纸面内且垂直于PQ 斜向上的匀强电场。
3.如图所示,在直角坐标系xOy 的第一象限内存在匀强磁场,磁场方向垂直于xOy 面向里,第四象限内存在沿y 轴正方向的匀强电场,电场强度大小为E ,磁场与电场图中均未画出。
一质量为m 、带电荷量为+q 的粒子自y 轴的P 点沿x 轴正方向射入第四象限,经x 轴上的Q 点进入第一象限。
已知P 点坐标为(0,-l ),Q 点坐标为(2l ,0),不计粒子重力。
O(1)求粒子经过Q点时速度的大小和方向;(2)若粒子在第一象限的磁场中运动一段时间后以垂直y轴的方向进入第二象限,求磁感应强度B的大小。
4.如图所示,两平行金属板AB中间有互相垂直的匀强电场和匀强磁场。
A板带正电荷,B板带等量负电荷,电场强度为E;磁场方向垂直纸面向里,磁感应强度为B1。


带电粒子在磁场中的偏转运动带电粒子在磁场中的偏转运动是物理中一个重要的现象,它在电磁学和粒子物理学中发挥着重要作用。
本文将从宏观角度和微观角度两方面探讨带电粒子在磁场中的偏转运动。
一、宏观角度从宏观角度来看,当一个带电粒子进入一个外磁场时,由于带电粒子的电荷与外磁场之间的相互作用,带电粒子将会受到一个力的作用。
这个力被称为洛伦兹力,它的方向垂直于带电粒子的运动方向和磁场方向,并遵循右手定则。
洛伦兹力的大小与带电粒子的电荷、速度以及磁场的强度有关。
根据洛伦兹力的作用,带电粒子将会在磁场中发生偏转运动。
偏转的路径将取决于带电粒子的质量、电荷、速度以及磁场的强度、方向。
如果带电粒子的速度与磁场方向垂直,那么它将做一个圆周运动;如果带电粒子的速度与磁场方向有夹角,那么它将做一个螺旋状的运动。
在实际应用中,带电粒子在磁场中的偏转运动被广泛应用于粒子加速器、磁共振成像等领域。
通过控制磁场的强度和方向,可以实现对带电粒子的运动轨迹的控制,从而对粒子进行加速、聚焦和瞄准等操作。
二、微观角度从微观角度来看,带电粒子在磁场中的偏转运动可以通过洛伦兹力与带电粒子的运动方程相结合来描述。
根据经典电动力学理论,带电粒子在外磁场中会受到洛伦兹力的作用,其运动方程可以写作:m*a = q*v×B其中,m是带电粒子的质量,a是带电粒子的加速度,q是带电粒子的电荷量,v是带电粒子的速度,B是外磁场的磁感应强度。
从上述运动方程可以看出,带电粒子在磁场中的偏转运动与带电粒子的电荷量、质量、速度以及磁场的强度有关。
在量子力学中,我们知道带电粒子的运动是离散的,具有量子性质。
因此,在微观尺度下,带电粒子在磁场中的偏转运动需要通过量子力学的方法进行分析和描述。
通过量子力学的框架,我们可以利用薛定谔方程来描述带电粒子在磁场中的运动。
薛定谔方程将考虑波粒二象性的带电粒子视为波函数,描述了带电粒子的时间演化和空间分布。
在外磁场的作用下,带电粒子的波函数将发生相应的演化和变化,从而影响带电粒子的运动轨迹。
带电粒子在磁场中偏转的求解策略带电粒子在磁场中偏转问题是历年高考的重点问题,同时也是热点问题。
总结考试中的诸多失误,集中在对这类问题的解法缺乏规律性的认识。
为此本文就求解这类题型的某些规律归纳如下。
一、基本思想因为洛伦兹力F始终与速度v垂直,即F只改变速度方向而不改变速度的大小,所以运动电荷垂直磁感线进入匀强磁场且仅受洛伦兹力时,一定做匀速圆周运动,由洛伦磁力提供向心力,即F€qvB€mv2/R。
带电粒子在磁场中运动问题大致可分两种情况:1.做完整的圆周运动(在无界磁场或有界磁场中);2.做一段圆弧运动(一般在有界磁场中)。
无论何种情况,其关键均在圆心、半径的确定上。
二、思路和方法1.找圆心方法1:若已知粒子轨迹上的两点的速度方向,则可根据洛伦兹力F丄v,分别确定两点处洛伦兹力F的方向,其交点即为圆心。
方法2:若已知粒子轨迹上的两点和其中一点的速度方向,则可作出此两点的连线(即过这两点的圆弧的弦)的中垂线,再画出已知点v的垂线,中垂线与垂线的交点即为圆心。
方法3:若已知粒子轨迹上的两点和能求得的半径R,则可作出此两点连线的中垂线,从连线的端点到中垂线上的距离为R的点即为圆心。
方法4:若已知粒子入射方向和出射方向,及轨迹半径R,但不知粒子的运动轨迹,则可作出此两速度方向夹角的平分线,在角平分线上与两速度方向直线的距离为R的点即为圆心。
方法5:若已知粒子圆周运动轨迹上的两条弦,则两条弦的中垂线的交点即为圆心。
2.求半径圆心确定下来后,半径也随之确定。
一般可运用平面几何知识来求半径的长度。
3.画轨迹在圆心和半径确定后可根据左手定则和题意画出粒子在磁场中的轨迹图。
4.应用对称规律从一边界射入的粒子,若从同一边界射出时,则速度与边界的夹角相等;在圆形磁场区域内,若粒子沿径向射入,则必沿径向射出。
三、实例分析例1.如图1所示,两电子沿MN方向射入两平行直线间的匀强磁场,并分别以v、v12的速度射出磁场。
则v:v是多少?两电子通过匀强磁场所需时间之比t:t是多少?1212M—*MXXX X XXX X图1解析:利用上述方法1;可确定出两电子轨迹的圆心O]和圆心。
物理经典模型(五:磁场偏转)[概述]:带电粒子在垂直进入匀强磁场做匀速圆周运动。
但从近年的高考来看,带电粒子垂直进入有界磁场中发生偏转更多,其中运动的空间还可以是组合形式的,如匀强磁场与真空组合、匀强磁场、匀强电场组合等,这样就引发出临界问题、数学等诸多综合性问题。
[要点]:从圆的完整性来看:完整的圆周运动和一段圆弧运动,即不完整的圆周运动。
无论何种问题,其重点均在圆心、半径的确定上,而绝大多数的问题不是一个循环就能够得出结果的,需要有一个从定性到定量的过程。
回旋模型三步解题法:①画轨迹:已知轨迹上的两点位置及其中一点的速度方向;已知轨迹上的一点位置及其速度方向和另外一条速度方向线。
②定圆心:(1)已知入射点、出射点、入射方向和出射方向时,可通过入射点和出射点分别作垂直于入射方向和出射方向的直线,两条直线的交点就是圆弧轨道的圆心(如图甲所示,图中P为入射点,M为出射点).(2)已知入射方向、入射点和出射点的位置时,可以通过入射点作入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆弧轨迹的圆心(如图乙所示,P为入射点,M为出射点).③找联系:③利用带电粒子只受洛伦兹力时遵循的半径及周期公式联系速度与轨道半径相联系:往往构成一个直角三角形,可用几何知识(勾股定理或用三角函数)已知角度与圆心角相联系:常用的结论是“一个角两边分别与另一个角的两个边垂直,两角相等”;圆心角与速度偏向角的关系;时间与周期相联系:(或)带电粒子在有界磁场中运动的几种常见情形(1)直线边界(进出磁场具有对称性,如图所示) (2)平行边界(存在临界条件,如图所示)(3)圆形边界(沿径向射入必沿径向射出,如图所示)[误区]:洛伦兹力永远与速度垂直、不做功;重力、电场力做功与路径无关,只由初末位置决定,当重力、电场力做功不为零时,粒子动能变化。
因而洛伦兹力也随速率的变化而变化,洛伦兹力的变化导致了所受合外力变化,从而引起加速度变化,使粒子做变加速运动。
带电粒子在磁场中的偏转角带电粒子在磁场中的偏转角,这个话题一听就让人有点头大,感觉好像跟高深的物理学挂钩,离我们平常人的世界有点远。
不过,要是我们把它聊得轻松一点,大家其实会发现,原来这个东西还挺有意思的!就好像是玩一个“粒子版的过山车”,只不过这个过山车是隐形的,而且它只在看不见的磁场里转来转去。
你想啊,带电粒子就像是颗“小小的电荷炸弹”,在我们的眼皮底下“咻”的一声就飞来飞去了。
它本来是直直地跑着的,突然就被磁场吸引,偏离了原来的轨迹。
哦!你是不是已经开始觉得好像有点意思了?别急,咱们慢慢来。
这个“偏转角”就是你把那颗“炸弹”放进磁场里,它跑了跑,最后偏离了原来的方向,那个偏离的角度,就是“偏转角”。
这个偏转角说白了就是磁场和粒子之间的一种“默契”。
你想啊,磁场一出现,它就像是个老大的指挥官,给带电粒子下达了一个命令:“喂,走这边!”然后粒子就按照指挥跑了。
这个角度有多大呢?哎呀,这个就得看磁场有多强啦!磁场强,粒子跑得越偏;磁场弱,粒子就跑得没那么远。
再说了,粒子的速度也很重要。
速度快了,它好像跑得飞快,偏离的角度可能就小一点;速度慢了,它就像是给磁场“牵着鼻子走”,偏转角自然大一点。
是不是感觉像是在讲一个跑酷的故事?有个粒子,原本它的路线就这么定了,结果一遇上了一个障碍物(也就是磁场),它就不得不改变方向。
这个障碍物,可能是特别强的磁场,也可能是个“温柔一点”的小磁场,不管是什么样的场,它一出现,这颗小小的粒子就得乖乖改变路线了。
你可能会好奇,为什么偏转角跟粒子的速度、磁场的强度、甚至粒子的电荷量都有关?嗯,这就有点像开车的道理了。
你开车速度快,遇到拐弯的时候自然就不容易甩尾,转弯半径大;而如果你开得慢,转弯的时候就容易大摇大摆地跑偏了。
同样的,带电粒子也要看它速度有多快,磁场有多强。
你要是速度够快,磁场一给它一个小推力,它就转得特别小,几乎看不出来;要是它慢了,磁场就给它施点劲儿,嘿,它的轨迹就转得更明显。
超经典带电粒子在磁场中的偏转(做了这些不用在做其他的题了)1.如图所示,一束电子(电量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为θ=300。
(不计电子重力)求:(1) 电子的质量m=(2) 电子在磁场中的运动时间t=2.三个速度不同的同一种带电粒子,沿同一方向从图中长方形区域的匀强磁场上边缘射入,当它们从下边缘飞出时,对入射方向的偏角分别为90°、60°、30°,则它们在磁场中的运动时间之比为___。
3.如图所示,在半径为r的圆形区域内,有一个匀强磁场,一带电粒子以速度v0从M点沿半径方向射入磁场区,并由N点射出,O点为圆心,∠MON=120°,求粒子在磁场区的偏转半径R及在磁场区中的运动时间。
(粒子重力不计)4.长为L 的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁场强度为B ,板间距离也为L ,板不带电,现有质量为m ,电量为q 的带正电粒子(不计重力),从左边极板间中点处垂直磁场以速度v 平行极板射入磁场,欲使粒子不打在极板上,则粒子入射速度v 应满足什么条件5.如图所示,比荷为e/m 的电子垂直射入宽为d ,磁感应强度为B 的匀强磁场区域,则电子能穿过这个区域至少应具有的初速度v0大小为多少6.如图所示,匀强磁场的磁感应强度为B ,宽度为d ,边界为CD 和EF 。
一电子从CD 边界外侧以速率V0垂直射入匀强磁场,入射方向与CD 边界间夹角为θ。
已知电子的质量为m ,电量为e ,为使电子能从磁场的另一侧EF 射出,求电子的速率V0至少多大vL L B7.一匀强磁场,磁场方向垂直于xy 平面,在xy 平面上,磁场分布在以O 为中心的一个圆形区域内。
一个质量为m 、电荷为q 的带电粒子,由原点O 开始运动,初速为v ,方向沿x 正方向。
后来,粒子经过y 轴上的P 点,此时速度方向与y 轴的夹角为30º,P 到O 的距离为L ,如图所示。
超经典带电粒子在磁场中的偏转(做了这些不用在做其他的题了)
1.如图所示,一束电子(电量为e)以速度v垂直射入磁感应强度为B、宽度为d
的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为θ=300。
(不计电
子重力)求:
(1) 电子的质量m=?
(2) 电子在磁场中的运动时间t=?
2.三个速度不同的同一种带电粒子,沿同一方向从图中长方形区域的匀强磁场上边缘射入,当它们从下边缘飞出时,对入射方向的偏角分别为90°、60°、30°,则它们在磁场中的运动时间之比为___。
3.如图所示,在半径为r的圆形区域内,有一个匀强磁场,一带电粒子
以速度v0从M点沿半径方向射入磁场区,并由N点射出,O点为圆
心,∠MON=120°,求粒子在磁场区的偏转半径R 及在磁场区中的运动时间。
(粒子重力不计) 4.长为L 的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁场
强度为B ,板间距离也为L ,板不带电,现有质量为m ,电量为q 的带
正电粒子(不计重力),从左边极板间中点处垂直磁场以速度v 平行极
板射入磁场,欲使粒子不打在极板上,则粒子入射速度v 应满足什么条
件? 5.如图所示,比荷为e/m 的电子垂直射入宽为d ,磁感应强度为B 的
匀强磁场区域,则电子能穿过这个区域至少应具有的初速度v0大小为
多少?
v L
L B
6.如图所示,匀强磁场的磁感应强度为B ,宽度为d ,边界为CD 和EF 。
一电子从CD 边界外侧以速率V0垂直射入匀强磁场,入射方向与CD 边
界间夹角为θ。
已知电子的质量为m ,电量为e ,为使电子能从磁场的
另一侧EF 射出,求电子的速率V0至少多大?
7.一匀强磁场,磁场方向垂直于xy 平面,在xy 平面上,磁场分布在以
O 为中心的一个圆形区域内。
一个质量为m 、电荷为q 的带电粒子,
由原点O 开始运动,初速为v ,方向沿x 正方向。
后来,粒子经过y 轴
上的P 点,此时速度方向与y 轴的夹角为30º,P 到O 的距离为L ,如
图所示。
不计重力的影响。
求磁场的磁感强度B 的大小和xy 平面上磁
场区域的半径R 。
× × × × × ×
× × × × × ×
× × × C D E F m e θ V d
解:粒子在磁场中受洛伦兹力作用,作匀速圆周运动,设半径为r
①
据此并由题意知,粒子在磁场中的轨迹的圆心C必在y轴上,且P点在磁场区之外。
过P点沿速度方向作延长线,它与x轴相交于Q点,作圆弧过O点与x轴相切,并且与PQ相切,切点A即粒子离开磁场区的地点。
这样也圆弧轨迹的圆心C,如图所示:
由图中几何关系得:L=3r ②
由①②求得:③
图中OA的长度即圆形磁场区的半径R,由图中几何关系得:
④
:半径为R的圆形区域内有一匀强磁场,圆心为O,如图所示。
一质量
为m、带电量为q的粒子从圆形边界上M点以速度v对准圆心O入射,
从N点射出磁场,速度方向偏转了600。
求:
(1)磁感应强度B的大小;
(2)改变磁感强度大小,可使得粒子在磁场中运动的时间减半,问此时的磁感强度B1 ;(写出B1与B的关系式)
(3)若粒子在由M运动到N的过程中突然改变磁感强度大小为B2 ,可使得粒子被束缚在磁场中,求B2的最小值?
答案
(1)设粒子在磁场中作圆周运动的半径为r,
据qBv = mv2/r (1分)
其中r = R·cot300 (2分)
代入得(1分)
(2)粒子在磁场中做圆周运动的周期,若速度偏转的角度为θ,
则有,由题意,第一次θ = 600,那么第二次θ1 = 300(2分)在直角三角形中,tan150 = R / r1? = qRB1 / mv ,tan300 = R / r? = qRB / mv ,
联立解得(2分,简化后的结果为)
(3)分析知,当粒子运动到圆弧MN的中点时,有最大的回旋半径,设为r2 ,
则2 r2 = r – R ,得到(2分)gkstk 代入得(2分)。