浙教版八年级下数学竞赛练习卷(1)

初二数学竞赛试卷姓名 得分一、填空题（每小题3分，共30分）1．当x 时，x 23-有意义，x 时12+-x 有意义 2．当x= 时，分式1036522-++-x x x x 的值为零。

3．已知方程02)6(92=-++-k x k x 有两个相等的实数根，则k= 这两个相等的根是 4．如图，在△ABC 中，AB=AC ，EF 是AB 的垂直平分线，若BC=10，△BFC 的周长为22，则△ABC 的周长是5．若实数a,b 满足039)2(22=+-+-a ab a 则a= b=6．若 —2<x<2 化简=--+-x x x 34427．若322-+-a ax x 是一个完全平方式，则a 的值8．已知 521=+x x ，则=-xx 19．m 为 时，关于x 的方程234222+=-+-x x mx x 会产生增根10．如图，若直角三角形两直角边上的中线ＡＥ，ＢＤ的长分别为５和102 则斜边ＡＢ＝A BCEF C D E二、选择题（每小题３分，共３０分）１．已知方程032=+-x kx 有两个实数根，则k 的取值范围---------------------（ ）A 0121≠≤k k 且 B 121≥k C 121≤k D 0121≠<k k 且 2．如果等腰三角形的两条边长是方程01222=+-x x 的两个根，则它的周长是（ ）A 123123-+或B 123+C 123-D 122+3．三角形内有一点，这点到三个顶点的距离相等，则这个点一定三角形的--（ ）A 三边垂直平分线的交点B 三条中线的交点C 三条高线的交点D 三条内角平分线的交点 4．计算56145614--+的值------------------------------------------------------（ ）A 1 B5 C 52 D 55．一项工程，甲队独做需用m 天，乙队独做需用n 天，若甲，乙两队合作完成这项工程，所需天数------------------------------------------------------------------------------（ ）A n m 11+B mn n m +C n m mn +D n m +6．已知，b a b a +=+111那么baa b +等于------------------------------------------------（ ）A —1B 1C —2D 2 7．若0<a<1，则a a aa +⨯+÷-+11)11(2122可化简为--------------------------------（ ） Aa a+-11 B 11+-a a C 21a - D 12-a 8．已知542c b a ==则cb a cb a +--+2的值------------------------------------------------------（ ）A 1B 3C 921D 1139．如图，S △ABC=6，BD ：DC=3：5，AK ：KD=4：5，则 S △CDK=------------------（ ）A 15B 12.5C 7.5D 14.510．若yx y yx y y x +--==则51,31等于-----------------------------------------（ ）A 31B 3C 31- D —3三．解答题1． 解方程：（每小题5分，共10分）（1）0242142222=+-+---xx x x x x（2）1211)10)(9(1)1(1)1(1=+++⋅⋅⋅+++-x x x x x x2．方程0)2443()1(2222=++++++b ab a x a x 有实根，求a,b 的值（10分）3．甲乙两车分别从A ，B 两地相向而行，已知甲车比乙车早出发15分钟，甲，乙两车的速度比2：3，相遇时甲车比乙车少走6千米，并且乙车从B 地到A 地需要211小时，求A ，B 两地相距的距离为多少千米？（10分）4．如图，Rt △ABC 中 ∠C=90o，D 为AB 上点，作DE ⊥BC 于E ，若BE=AC ，BD=21，DE+BC=1求证：∠ABC=30o （10分）ACEB D。

绝密★启用前浙教版2018-2019学年八年级数学竞赛试卷A题号一二三总分得分注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）请点击修改第I卷的文字说明评卷人得分一．选择题（共8小题，3*8=24）1．设a=﹣（﹣2）2，b=﹣（﹣3）3，c=﹣（﹣42），则﹣[a﹣（b﹣c）]=（）A．15 B．7 C．﹣39 D．472．方程的解是x=（）A．B．﹣C．D．﹣3．以下三个判断中，正确的判断的个数是（）（1）x2+3x﹣1=0，则x3﹣10x=﹣3（2）若b+c﹣a=2+，c+a﹣b=4﹣，a+b﹣c=﹣2，则a4+b4+c4﹣2（a2b2+b2c2+c2a2）=﹣11 （3）若a2=a1q，a3=a2q，a4=a3q，则a1+a2+a3+a4=（q≠1）A．0 B．1 C．2 D．34．如图，D，E，F为等边三角形ABC三边中点，AE、BF、CD交于O，DE，EF，FD为三条中位线，则图中能数出不同的直角三角形的个数是（）A．36 B．32 C．30 D．285．5名学生身高两两不同，把他们按从高到低排列，设前三名的平均身高为a米，后两名的平均身高为b米．又前两名的平均身高为c米，后三名的平均身高为d米，则（）A．B．C．D．以上都不对6．把红珠、蓝珠各四颗串成一条（项链可以旋转，翻转），则实质不同的串法数是（）A．6 B．7 C．8 D．107．能整除任意5个连续整数之和的最大整数是（）A．1 B．2 C．3 D．58．一个屏幕封闭图形，只要有一条边不是直线段，就称为曲边形，例如圆、弓形、扇形等都是曲边形，则如图中，可以数出（）个不同的曲边形．A．42 B．36 C．30 D．28第Ⅱ卷（非选择题）请点击修改第Ⅱ卷的文字说明评卷人得分二．填空题（共8小题，3*8=24）9．已知a﹣b=4，ab+c2+4=0，则a+b+c的值为．10．已知，则的值为．11．在平面直角坐标系中，点P[m（m+1），m﹣1]（m为实数）不可能在第象限．12．有一只手表每小时比准确时间慢3分钟，若在清晨4：30与准确时间对准，则当天上午手表指示的时间是10：50，准确时间应该是．13．如图，P是平行四边形ABCD内一点，且S△P AB=5，S△P AD=2，则阴影部分的面积为．14．若10个数据的平均数是，平方和是10，则方差是．15．若直线323x+457y=1103与直线177x+543y=897的交点坐标是（a，b），则a2+2004b2的值是．16．某校组织师生春游，如果单独租用45座客车若干辆，刚好坐满；如果单独租用60座客车，可以少租一辆，且余30个座位．则该校去参加春游的人数为；若已知45座客车的租金为每辆250元，60座客车租金为每辆300元，这次春游同时租用这两种客车，其中60座客车比45座客车多租1辆，所以租金比单独一种客车要节省，按这种方案需要租金元．评卷人得分三．解答题（共4小题，52分）17．（10分）已知关于x、y的方程组：，求出所有整数a，使得方程组有整数解（即x、y都是整数），并求出所有的整数解．18．（12分）求出所有的正整数n，使得12+22+32+42+…+n2﹣（n+1）2﹣（n+2）2﹣（n+3）2﹣…﹣（2n﹣1）2﹣（2n）2=﹣10115.（参考公式：1+2+3+4+…+n=）19．（15分）某市为了节约用水，规定：每户每月用水量不超过最低限量am3时，只付基本费8元和定额损耗费c元（c≤5）；若用水量超过am3时，除了付同上的基本费和损耗费外，超过部分每1m3付b元的超额费．根据上表的表格中的数据，求a、b、c．20．（15分）如图，把一张长10cm，宽8cm的长方形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．（1）要使无盖长方体盒子的底面积为48cm2，那么剪去的正方形的边长为多少？（2）你认为折合而成的无盖长方体盒子的侧面积有可能等于52cm2吗？请说明理由；（3）如果把长方形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的长方形，然后折合成一个有盖的长方体盒子，那么它的侧面积（指的是高为剪去的正方形边长的长方体的侧面积）可以达到30cm2吗？请说明理由．参考答案与试题解析1．解：a=﹣（﹣2）2=﹣4，b=﹣（﹣3）3=27，c=﹣（﹣42）=16，∴﹣[a﹣（b﹣c）]，=﹣[﹣4﹣（27﹣16）]，=15．故选：A．2．解：移项合并同类项得：﹣[﹣（﹣1﹣x）﹣]=，∴﹣（﹣1﹣x）﹣=﹣，移项合并同类项得：﹣（﹣1﹣x）=，∴﹣1﹣x=﹣，∴x=﹣，故选：D．3．解：（1）x3﹣10x=x（x2﹣10）=x（1﹣3x﹣10）=﹣3（x2+3x）=﹣3，故（1）正确；（2）a4+b4+c4﹣2（a2b2+b2c2+c2a2）=（a2﹣b2﹣c2）2﹣4b2c2=（a2﹣b2﹣c2+2bc）（a2﹣b2﹣c2﹣2bc）=（a+b﹣c）（a﹣b+c）（a+b+c）（a﹣b﹣c）又知b+c﹣a=2+，c+a﹣b=4﹣，a+b﹣c=﹣2，可得a+b+c=4+，故a4+b4+c4﹣2（a2b2+b2c2+c2a2）=﹣11，故（2）正确；（3）当q=1时，a1+a2+a3+a4=4a1，当q≠1时，a1+a2+a3+a4=，故（3）正确，正确的有3个，故选D．4．解：①∵DE，EF，FD为等边△ABC三条中位线，∴AB=AC=BC，∴EF AB，ED AC，∴四边形CEDF是菱形，∴EF⊥CD，∴在菱形CEDF中有6个不同的直角三角形：Rt△CEG、Rt△CFG、Rt△DGE、Rt△DFG、Rt△EOG、Rt△FOG；同理，在菱形ADEF、菱形BEFD中各有6个不同的直角三角形；②∵D为等边三角形ABC三边中点，∴CD⊥AB，∴△ADC、△BDC、AOD、△BOD是直角三角形；同理，以BF、AE为直角边的三角形各有4个；综上所述，图中能数出的直角三角形由6×3+4×3=30（个）；故选：C．5．解：∵3a+2b=2c+3d，∵a＞d，∴2a+2b＜2c+2d，∴a+b＜c+d，∴＜，即＞，故选：B．6．解：①第一个●和第二个●两珠间隔0个蓝珠，即●●…；②第一个●和第二个●两珠间隔1个蓝珠，即●○●…；③第一个●和第二个●两珠间隔2个蓝珠，即●○○●…；④第一个●和第二个●两珠间隔3个蓝珠，即●○○○●…；⑤第一个●和第二个●两珠间隔4个蓝珠，即●○○○○●…；⑥第二个●和第三个●两珠间隔2个蓝珠，即●●○○…；⑦第二个●和第三个●两珠间隔3个蓝珠，即●●○○○…；⑧第二个●和第三个●两珠间隔4个蓝珠，即●●○○○○••；∵项链可以旋转，翻转，∴第三个●和第四个●两珠间隔珠的情况和第一和第二红珠间隔相同，以此类推…∴共8种方法．故选：C．7．解：设五个连续整数分别为a﹣2，a﹣1，a，a+1，a+2，所以这五个数的和为a﹣2+a﹣1+a+a+1+a+2=5a，因为5a是5的倍数，所以不论a为何值，五个连续整数的和都可以被5整除．故选：D．8．解：数曲边形，一定要有弧，五角星把圆周分成5个弧，我们按含有1个弧、2个弧、…、5个弧来分类，仅含1个弧有两种情况，每种情况按5个弧转一圈各有5个曲边形，共有5+5个；仅含2个弧可以分相连和不相连2种情况，相连的2个弧，按5个弧转一圈有5个曲边形；不相连的2个弧，似乎又有2种情况，按5个弧转一圈各有5个曲边形，但实际上转圈数时这两种情况是重复的，故不相连的2个弧可数出5个曲边形；仅含3个弧可以分相连和不相连2种情况，每种情况按5个弧转一圈可数出有5个曲边形，共有5+5个；仅含4个弧的情况，每种情况按5个弧转一圈可数出有5个曲边形；含全部5个弧的情况，1个曲边形．综上，一共有5+5+5+5+5+5+5+1=36个．故选：B．9．解：∵a﹣b=4，∴a=b+4，代入ab+c2+4=0，可得（b+4）b+c2+4=0，（b+2）2+c2=0，∴b=﹣2，c=0，∴a=b+4=2．∴a+b+c=0．故答案为：0．10．解：根据非负数性质可知a﹣1=0且ab﹣2=0解得a=1 b=2则原式=裂项得；故答案为11．解：（1）当m（m+1）＞0时，有或，所以m＞0或m＜﹣1，因此m﹣1＞﹣1或m﹣1＜﹣2，即P[m（m+1），m﹣1]可能经过第一或四象限．（2）当m（m+1）＜0时，有或，所以﹣1＜m＜0，因此﹣2＜m﹣1＜﹣1，即P[m（m+1），m﹣1]经过第三象限．综合得，P[m（m+1），m﹣1]不经过第二象限．12．解：设标准时间经过了x分钟，则57：60=380：x．解得x=400．400分钟合6小时40分钟，再加4小时30分钟=11小时10分钟．所以准确时间应该是11：10．故应填：11：10．13解：∵S△P AB+S△PCD=S▱ABCD=S△ACD，∴S△ACD﹣S△PCD=S△P AB，则S△P AC=S△ACD﹣S△PCD﹣S△P AD，=S△P AB﹣S△P AD，=5﹣2，=3．故答案为：3．14．解：方差S2=[（x1﹣）2+（x2﹣）2+…+（x n﹣）2]=[x12+x22+…+x n2﹣2（x1+x2+…+x n）+n2]=[x12+x22+…+x n2﹣2×n+n2]=[x12+x22+…+x n2]﹣2=×10﹣（）2=．故填．15．解：把323x+457y=1103与177x+543y=897联立，解得，∴a=2，b=1，因此a2+2004b2=2008．故答案为：2008．16．解：设该校去参加春游的人数为a人，则有，解得：a=270设租用45座客车x辆，则租用60座客车（x+1）辆，由题意若单独租45座客车需要270÷45=6辆，租金250×6=1500元，若单独租60座客车需要（270+30）÷60=5辆，租金300×5=1500元，则有：，解得：2≤x＜∵x为正整数∴x=2即租45座客车2辆，60座客车3辆，此时租金为：250×2+300×3=1400（元）．故答案为270，1400．17．解：解原方程组得，，假设x=1时，可求得a=﹣7，y=﹣1；同样设x为其他整数，a、y的值都不能为整数，∴原方程组的整数解为．18．解：原式可化为：12﹣（n+1）2+22﹣（n+2）2+…n2﹣（2n）2=﹣10115，﹣n（n+2）﹣n（n+4）﹣n（n+6）﹣…﹣n（3n）=﹣10115，﹣n（n+2+n+4+n+6+…+3n﹣2+3n）=﹣10115，﹣n3﹣2n（1+2+3+…+n）=﹣10115，﹣n3﹣2n（）=﹣10115，2n3+n2=10115∴n=17．19．解：设每月用水量为xm3，支付水费为y元．则y=，由题意知：0＜c≤5∴8＜8+c≤13从表中可知，第二、三月份的水费均大于13元，故用水量15m3、22m3均大于最低限量am3，将x=15，x=22分别代入②式，得解得b=2，2a=c+19 ⑤再分析一月份的用水量是否超过最低限量，不妨设9＞a，将x=9代入②，得9=8+2（9﹣a）+c，即2a=c+17 ⑥⑥与⑤矛盾．故9≤a，则一月份的付款方式应选①式，则8+c=9，∴c=1代入⑤式得，a=10．答：a=10，b=2，c=1．20．解：（1）设剪去的正方形边长为xcm，由题意，得（10﹣2x）（8﹣2x）=48，即x2﹣9x+8=0解得x1=8（不合题意，舍去），x2=1．∴剪去的正方形的边长为1cm．…（2分）（2）折合而成的无盖长方体盒子的侧面积不可能等于52 cm2，理由如下：设剪去的正方形边长为xcm，由题意，得2[x（10﹣2x）+x（8﹣2x）]=52…（2分）整理得2x2﹣9x+13=0∵△=b2﹣4ac=81﹣4×2×13＜0，∴原方程没有实数解．即折合而成的无盖长方体盒子的侧面积不可能等于52 cm2．…（2分）（3）设剪去的正方形边长为xcm，若按图1所示的方法剪折，解方程，得该方程没有实数解．…（3分）若按图2所示的方法剪折，解方程，得．∴当按图2所示的方法剪去的正方形边长为cm或3cm时，能使得到的有盖长方体盒子的侧面积达到30 cm2．…（3分）。

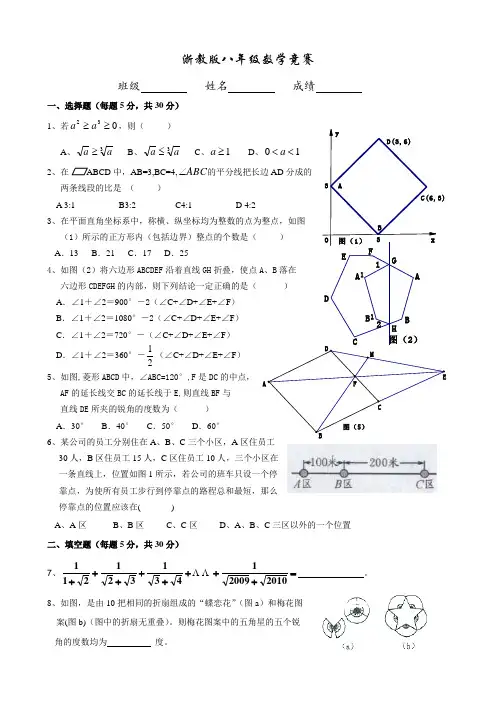
A浙教版八年级数学竞赛班级 姓名 成绩一、选择题（每题5分，共30分） 1、若032≥≥a a ，则（ ）A 、3a a ≥B 、3a a ≤C 、1≥aD 、10<<a 2、在中，AB=3,BC=4,ABC ∠的平分线把长边AD 分成的 两条线段的比是 （ ）A 3:1 B3:2 C4:1 D 4:23、在平面直角坐标系中，称横、纵坐标均为整数的点为整点，如图 （1）所示的正方形内（包括边界）整点的个数是（ ） A ．13 B ．21 C ．17 D ．254、如图（2）将六边形ABCDEF 沿着直线GH 折叠，使点A 、B 落在 六边形CDEFGH 的内部，则下列结论一定正确的是（ ） A ．∠1＋∠2＝900°－2（∠C+∠D+∠E+∠F ） B ．∠1＋∠2＝1080°－2（∠C+∠D+∠E+∠F ） C ．∠1＋∠2＝720°－（∠C+∠D+∠E+∠F ）D ．∠1＋∠2＝360°－12（∠C+∠D+∠E+∠F ）5、如图,菱形ABCD 中，∠ABC=120°,F 是DC 的中点， AF 的延长线交BC 的延长线于E,则直线BF 与 直线DE 所夹的锐角的度数为（ ） A ．30° B ．40° C ．50° D ．60°6、某公司的员工分别住在A 、B 、C 三个小区，A 区住员工 30人，B 区住员工15人，C 区住员工10人，三个小区在 一条直线上，位置如图1所示，若公司的班车只设一个停 靠点，为使所有员工步行到停靠点的路程总和最短，那么 停靠点的位置应该在( )A 、A 区B 、B 区C 、C 区D 、A 、B 、C 三区以外的一个位置 二、填空题（每题5分，共30分） 7、=++++++++201020091431321211 。

8、如图，是由10把相同的折扇组成的“蝶恋花”（图a ）和梅花图 案(图b)（图中的折扇无重叠）。

2020-2021学年浙江省八年级下学期数学竞赛卷1 一．选择题（共8小题）1．设a＝﹣2，则代数式a3+4a2﹣a+6的值为（）A．6B．4C．2+2D．2﹣2【解答】解：∵a＝﹣2，∴（a+2）2＝（）2，即a2+4a＝1，∴a3+4a2﹣a+6＝a（a2+4a）﹣a+6＝a×1﹣a+6＝6．故选：A．2．关于x的方程x2﹣bx+4＝0有两个相等的正实数根，则b的值为（）A．4B．﹣4C．﹣4或4D．0【解答】解：∵关于x的方程x2+bx+4＝0有两个相等的正实数根，∴△＝b2﹣4×1×4＝b2﹣16＝0，解得：b＝4．故选：A．3．如图所示，∠A+∠B+∠C+∠D+∠E+∠F+∠G＝（）A．360°B．450°C．540°D．720°【解答】解：如图，在四边形ACEH中，∠A+∠C+∠E+∠1＝360°，在四边形BDFP中，∠B+∠D+∠F+∠2＝360°，∵180°﹣∠1+180°﹣∠2+∠G＝180°，∴∠A+∠C+∠E+∠1+∠B+∠D+∠F+∠2+180°﹣∠1+180°﹣∠2+∠G＝360°+360°+180°，∴∠A+∠B+∠C+∠D+∠E+∠F+∠G＝360°+180°＝540°．故选：C．4．如图，在Rt△ABC中，∠C＝90°，AC＝3，以AB为一边向三角形外作正方形ABEF，正方形的中心为O，且OC＝4，那么BC的长等于（）A．3B．5C．2D．【解答】解：如图，作EQ⊥x轴，以C为坐标原点建立直角坐标系，CB为x轴，CA为y轴，则A（0，3）．设B（x，0），由于O点为以AB一边向三角形外作正方形ABEF的中心，∴AB＝BE，∠ABE＝90°，∵∠ACB＝90°，∴∠BAC+∠ABC＝90°，∠ABC+∠EBQ＝90°，∴∠BAC＝∠EBQ，在△ABC和△BEQ中，∴△ACB≌△BQE（AAS），∴AC＝BQ＝3，BC＝EQ，设BC＝EQ＝x，∴O为AE中点，∴OM为梯形ACQE的中位线，∴OM＝，又∵CM＝CQ＝，∴O点坐标为（，），根据题意得：OC＝4＝，解得x＝5，则BC＝5．故选：B．5．如图正方形ABCD的顶点A在第二象限y＝图象上，点B、点C分别在x轴、y轴负半轴上，点D在第一象限直线y＝x的图象上，若S阴影＝，则k的值为（）A．﹣1B．C．D．﹣2【解答】解：如图，过点A作AG⊥x轴，过点D作DE⊥x轴，作DF⊥AG交y轴于H，∴四边形DHOE是矩形∵∠ADC＝∠HDE＝90°∴∠ADC﹣∠FDC＝∠HDE﹣∠FDC∴∠ADF＝∠CDE，∵点D在第一象限直线y＝x的图象上，∴DH＝DE，且∠ADF＝∠CDE，∠DHM＝∠DEN∴△DHM≌△DEN（ASA）∴S△DHM＝S△DNE，∴＝S四边形DHOE＝DH×DE∴DH＝DE＝同理可证：△AFD≌△BGA≌△COB≌△DHC∴AF＝HD＝BG＝OC，AG＝DF＝BO＝HC∴OC＝HD＝＝AF＝BG∴CH＝∴AG＝＝BO∴GO＝∴点A坐标（﹣，）∴k＝﹣×＝﹣故选：B．6．如图，在平行四边形ABCD中，BC＝2AB，CE⊥AB于E，F为AD的中点，若∠AEF＝54°，则∠B＝（）A．54°B．60°C．66°D．72°【解答】解：过F作FG∥AB∥CD，交BC于G；则四边形ABGF是平行四边形，所以AF＝BG，即G是BC的中点；连接EG，在Rt△BEC中，EG是斜边上的中线，则BG＝GE＝FG＝BC；∵AE∥FG，∴∠EFG＝∠AEF＝∠FEG＝54°，∴∠AEG＝∠AEF+∠FEG＝108°，∴∠B＝∠BEG＝180°﹣108°＝72°．故选：D．7．若m是关于x的方程x2﹣2020x+1＝0的根，则（m2﹣2020m+4）•（m2﹣2020m﹣5）的值为（）A．18B．﹣18C．20D．﹣20【解答】解：∵m是关于x的方程x2﹣2020x+1＝0的根，∴m2﹣2020m+1＝0，∴m2﹣2020m＝﹣1，∴（m2﹣2020m+4）•（m2﹣2020m﹣5）＝（﹣1+4）×（1﹣5）＝﹣18．故选：B．8．如图，四边形OABC为平行四边形，A在x轴上，且∠AOC＝60°，反比例函数y＝（k ＞0）在第一象限内过点C，且与AB交于点E．若E为AB的中点，且S△OCE＝8，则OC的长为（）A．8B．4C．D．【解答】解：过点C作CD⊥x轴于点D，过点E作EF⊥x轴于点F，如图：∵四边形OABC为平行四边形，∴OC＝AB，OC∥AB，∴∠EAF＝∠AOC＝60°，在Rt△COD中，∵∠DOC＝60°，∴∠DOC＝30°，设OD＝t，则CD＝t，OC＝AB＝2t，在Rt△EAF中，∵∠EAF＝60°，AE＝AB＝t，∴AF＝，EF＝AF＝t，∵点C与点E都在反比例函数y＝的图象上，∴OD×CD＝OF×EF，∴OF＝＝2t，∴OA＝2t﹣＝t，∴S四边形OABC＝2S△OCE，∴t×t＝2×8，∴解得：t＝（舍负），∴OC＝．故选：D．二．填空题（共6小题）9．已知关于x的一元二次方程（1﹣2k）x2﹣2x﹣1＝0有两个不相等的实数根，则k 的取值范围﹣3≤k＜4且k≠．【解答】解：∵关于x的一元二次方程（1﹣2k）x2﹣2x﹣1＝0有两个不相等的实数根，∴，解得：﹣3≤k＜4且k≠．故答案为：﹣3≤k＜4且k≠．10．若＜0，化简﹣﹣3的结果为﹣2x．【解答】解：由题意得，或，解得，﹣2＜x＜，则原式＝|5﹣3x|﹣|x﹣2|﹣3＝5﹣3x﹣2+x﹣3＝﹣2x，故答案为：﹣2x．11．如图，双曲线y＝（x＞0）的图象上．△OA1B1，△A1A2B2，…，△A n﹣1A n B n均为正三角形，过B1作B1C⊥x轴于C，过B2作B2D⊥x轴于D，则点A n的坐标为（，0）．【解答】解：∵点B1，B2在双曲线y＝（x＞0）的图象上，∴OC•B1C＝3，∵△OA1B1，△A1A2B2，…，△A n﹣1A n B n均为正三角形，∴B1C＝OC，∴OC＝，∴OA1＝2，∴；连接OB2，则OD•B2D＝3，∵OD＝OA1+A1D＝2+，，∴∴，∴，同理可得，，…由上可知，．故答案为：（，0）．12．P是正方形ABCD内一点，AB＝5，P A＝，PC＝5，则PB＝或2．【解答】解：如图所示，∴PB＝＝或PB＝＝2，故答案为：或2．13．已知x1，x2，x3，x4，x5为正整数，任取四个数求和，只能得到44，45，46，47这样四个结果，则这5个数的众数是11．【解答】解：根据题意，设这个重复的和为z，可得：（x1+x2+x3+x4+x5）×4＝44+45+46+47+z，可得：z＝46，可得五个数据之和为57，所以五个数据为：10，11，12，13，11，故答案为：1114．如图，已知直线y＝kx（k＞0）分别交反比例函数y＝和y＝在第一象限的图象于点A，B，过点B作BD⊥x轴于点D，交y＝的图象于点C，连接AC．若△ABC是等腰三角形，则k的值是或．【解答】解：∵点B是y＝kx和y＝的交点，y＝kx＝，∴点B坐标为（，2），同理可求出点A的坐标为（，），∵BD⊥x轴，∴点C横坐标为，纵坐标为，∴BA＝，AC＝，BC＝，∴BA2﹣AC2＝k＞0，∴BA≠AC，若△ABC是等腰三角形，①当AB＝BC时，则＝，解得：k＝±（舍去负值）；②当AC＝BC时，同理可得：k＝；故答案为：或．三．解答题（共4小题）15．已知x﹣y＝6，，求的值．【解答】解：∵x﹣y＝6，∴，∴，∵+＝•+•＝（+）＝9，∴，即，∴＝（﹣）＝×＝4．16．已知实数a，b，c满足：a+b+c＝2，abc＝4．（1）求a，b，c中的最大者的最小值；（2）求|a|+|b|+|c|的最小值．【解答】解：（1）不妨设a是a，b，c中的最大者，即a≥b，a≥c，由题设知a＞0，且b+c＝2﹣a，．于是b，c是一元二次方程的两实根，≥0，a3﹣4a2+4a﹣16≥0，（a2+4）（a﹣4）≥0．所以a≥4．又当a＝4，b＝c＝﹣1时，满足题意．故a，b，c中最大者的最小值为4．（2）因为abc＞0，所以a，b，c为全大于0或一正二负．①若a，b，c均大于0，则由（1）知，a，b，c中的最大者不小于4，这与a+b+c＝2矛盾．②若a，b，c为或一正二负，设a＞0，b＜0，c＜0，则|a|+|b|+|c|＝a﹣b﹣c＝a﹣（2﹣a）＝2a﹣2，由（1）知a≥4，故2a﹣2≥6，当a＝4，b＝c＝﹣1时，满足题设条件且使得不等式等号成立．故|a|+|b|+|c|的最小值为6．17．如图，四边形ABCD是矩形，E是对角线BD上不同于B、D的任意一点，AF＝BE，∠DAF＝∠CBD．（1）求证：△ADF≌△BCE；（2）求证：四边形ABEF是平行四边形；（3）试确定当点E在什么位置时，四边形AEDF为菱形？并说明理由．【解答】（1）证明：∵四边形ABCD是矩形，∴AD＝BC，在△ADF和△BCE中，，∴△ADF≌△BCE（SAS）；（2）证明：∵四边形ABCD是矩形，∴AD∥BC，∠BAD＝90°，∴∠DBC＝∠ADB，∵∠DAF＝∠CBD，∴∠DAF＝∠ADB，∴AF∥BE，∵AF＝BE，∴四边形ABEF是平行四边形；（3）解：当E为BD的中点时，四边形AEDF变为菱形，理由如下：如图所示：∵E为BD的中点，∠BAD＝90°，∴AE＝BE＝DE，∵AF＝BE，AF∥BD，∴AF∥DE，AF＝DE，AF＝AE，∴四边形AEDF是平行四边形，∴四边形AEDF是菱形．18．请你利用直角坐标平面上任意两点（x1，y1），（x2，y2）间的距离公式d＝解答下列问题：已知：反比例函数y＝与正比例函数y＝x的图象交于A，B两点（A在第一象限），点F1（﹣2，﹣2），F2（2，2）在直线y＝x上．设点P（x0，y0）是反比例函数y＝图象上的任意一点，记点P与F1，F2两点之间的距离之差d＝|PF1﹣PF2|．（1）试比较线段AB的长度与d的大小，并由此归纳出双曲线的一个重要定义（用简练的语言表述）．（2）现请你在反比例函数y＝第一象限内的分支上找一点P，使点P到F2（2，2）和点C（6，4）的距离之和最小，求点P的坐标．【解答】：解由y＝和y＝x组成的方程组可得A、B两点的坐标分别为，（，）、（﹣，﹣），线段AB的长度＝4．∵点P（x0，y0）是反比例函数y＝图象上一点，∴y0＝．∴PF1＝＝||，PF2＝＝||，∴d＝|PF1﹣PF2|＝|||﹣|||，当x0＞0时，d＝4；当x0＜0时，d＝4．因此，无论点P的位置如何，线段AB的长度与d一定相等．由此可知：到两个定点的距离之差（取正值）是定值的点的集合（轨迹）是双曲线．（2）由条件PF2＝PF1﹣4，知PF2+PC＝PF1+PC﹣4，由F1，﹣P，C三点共线时最小，此时可解得P（2，1）．。

浙教版八年级数学竞赛试题卷（一、精心选一选（本题有10个小题，每小题4分，共40分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在相应的括号内。

1． 不论x 、y 为何实数，346422+-+-y y xy x 的值总是 （ ）A.正数B.负数 C . 0 D. 非负数2． 一次函数y=ax-3a+1的图象必通过一定点,此定点坐标是 （ ） A. （1，3） B. （0，1） C. （3，1） D.（0，3）3．若关于x 的方程x 2-2k x-1=0有两个不相等的实数根，则直线y=kx +3必不经过 （ ）A. 第三象限B. 第四象限C. 第一、二象限D. 第三、四象限 4．某商品的进价是100元，标价为150元，商店要求以利润率不低于5%的售价打折出售，售货员最低可打 （ ）A.8折B. 7折C.6折D. 9折 5．梯形的两底角之和为900，上底长为5，下底长为11，则连结两底中点的线段长是 （ ）A. 3B.4C.5D.6 6．已知M （3，2）、N （1，-1），点P 在y 轴上，使PM+PN 最短，则点P 的坐标是（ ）A ．（0，21-） B. （0，0） C. （0，611） D.（0，41-）7．如果等腰三角形一腰上的高线等于腰长的一半,那么它的底角等于 （ ）A ．750 B. 150 C. 300 D 750或1508．如图,D 、E 分别是△ABC 的边BC 、AC 上的点，若AB=AC ，AD=AE ，∠α=300时，则∠CDE （ ） A ．150 B.300 C.450 D.2009．某商店有5袋面粉，各袋重量在25～30公斤之间，店里有一磅秤，但只有能称50～70公斤重量的秤砣，现要确定各袋面粉的重量，至少要称 （ ）A ．4次B ．5次C ．6次 D. 7次10．如图，正方形ABCD 的边长为2，点E 在AB 边上．四边形EFGB 也为正方形，设△AFC 的面积为S ，则 （ ） A ．S=2 B ．S=2.4 C ．S=4 D ．S 与BE 长度有关二．细心填一填（本题有10个小题，每小题4分，共40分）11．如果不等式组⎩⎨⎧<->-01a x x 无解，则a 的取值范围是____________12．如图的号码是由14位数字组成的，每一位数字写在下面的方格中，若任何相邻的三个数字之和都等于14，则x 的值等于13. 若一个数的平方根等于这个数的立方根，则这个数是14．.如图是2002年北京第24届国际数学家大会会标，它由4个全等 的直角三角形拼合而成，若图中大、小正方形的面积分别为13和1， 则直角三角形的较长直角边长为 .15．如图△ABC 中，AC ＞AB ，AB=4，AC=x ，AD 平分∠BAC ，BD ⊥AD 于D ，点E 是BC 的中点，DE=y ，则y 关于x 的 函数关系式为 16．已知1=-b a ，122-=-b a ，则=-20082008b a_________17.已知方程0119992001)2000(2=-⨯-x x 较大的根为α，方程0199919982=-+x x 较小的根为βαβ-则,的值是 。

八年级下数学竞赛试题浙八年级下数学竞赛试题浙版一、选择题（每题3分，共30分）1. 已知一个直角三角形的两个直角边分别为3和4，求斜边的长度。

A. 5B. 6C. 7D. 82. 一个数的立方根等于它本身，这个数可以是：A. 1B. -1C. 0D. 1和-13. 一个圆的半径为5，求圆的面积。

A. 25πB. 50πC. 75πD. 100π4. 下列哪个数是无理数？A. 3.14B. 0.333...C. πD. √25. 一个长方体的长、宽、高分别是2、3和4，求其体积。

A. 24B. 12C. 36D. 486. 如果一个数的相反数是-7，那么这个数是：A. 7B. -7C. 0D. 147. 一个数的绝对值是5，这个数可以是：A. 5B. -5C. 5或-5D. 08. 一个等腰三角形的两个底角相等，如果顶角为60°，求底角的大小。

A. 60°B. 45°C. 30°D. 90°9. 一个正六边形的内角是：A. 120°B. 108°C. 90°D. 60°10. 已知一个二次方程 \( ax^2 + bx + c = 0 \) 的解是2和-3，求\( b \) 的值。

A. -7B. -5C. 7D. 5二、填空题（每题4分，共20分）11. 一个数的平方根是4，这个数是________。

12. 一个数的绝对值是8，这个数可以是________。

13. 一个直角三角形的两个直角边分别是6和8，斜边的长度是________。

14. 一个数的立方是-27，这个数是________。

15. 一个圆的直径是10，这个圆的周长是________。

三、解答题（每题10分，共50分）16. 证明勾股定理：在一个直角三角形中，斜边的平方等于两直角边的平方和。

17. 解方程 \( 2x^2 - 7x + 3 = 0 \) 并求出解。

八年级数学竞赛试卷真题一．填空题（3′×8=24′）：1、如图，已知a ∥b ，∠1=40︒，则∠2=________度.2、在函数21-=x y 中，自变量x 的取值范围是3、有两名学员小林和小明练习射击，第一轮10枪打完后，两 人打靶的环数如图所示，通常新手的成绩不太稳定，那么 根据图中的信息，估计小林和小明两人中新手是 ．4、如图，在△ABC 中，AB=AC=32cm ，DE 是AB 的垂直平分线，分别交AB 、AC 于 D 、E 两点．若BC=21cm ，则△BCE 的周长是 cm ．5、如图，是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A 、B 、C 、D 的边长分别是3、5、2、3，则最大正方形E 的面积是 ．6、如图，已知函数b ax y +=和kx y =的图像交点P ，则可根据图像可得关于x 、y 的二元一次方程组的⎩⎨⎧=+=kx y bax y 的解是___________________．7、在数轴上截取从0至3的对应线段AB ，实数m 对应AB 上的点M ，如图1；将AB 折成正三角形，使点A ，B 重合于点P ，如图2；建立平面直角坐标系，平移此三角形，使它关于y 轴对称，且点P 的坐标为（0，2），PM 与x 轴交于点N （n ，0），如图3，当m ＝3时，则n ＝ ．（第1题图）bac21（第3题图）（第5题图）（第4题图）xyPy=ax+b y=kx-4-2（第6题图）8、如图，在ABC ∆中，AC AB =，40ABC ∠=︒，BD 是ABC ∠的平分线，延长BD 至E ，使DE AD =， 连结CE ，则ECA ∠的度数为 度．二、选择题（3′×10=30′）：11、若b a <，则下列各式中一定成立的是……………………………………………………( ) A ．0>-b a B ．0<-b a C ．0>ab D ．0<ab12、已知等腰三角形的一边长为4，另一边长为8，则它的周长是……………………………( )A ．12B ．16C ．20D ．16或2013、八年级（１）班50名学生的年龄统计结果如右表所示：则此班学生年龄的众数、中位数 分别为………………………………………………………………………………………… ()A ．14，14B ．15，14C ．14，15D ．15，1614、若点A (n ，2) 在y 轴上，则 点B (n －2 ，n +1) 在 ………………………………………( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限15、下列各图中，是立方体的表面展开图的是………………………………………………… ()A ．B ．C ．D ．16、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食,要爬行的最短路程(π取3) 是……………………………………………………………………………………………… ( )A ．20cmB ．10cmC ．14cmD ．无法确定17、一次函数b kx y +=的图象如图所示，当0<x 时，y 的取值范围是……………………( )A ．0<yB ．0>yC ．02<<-yD ．2-<y18、如果直线y ＝2x ＋m 与两坐标轴围成的三角形面积等于4，则m 的值是………(（第8题图） AB（第16题图）1-2xy（第17题图）年龄 13 14 15 16 人数422231DMCABP)A ．±3B ．3C ．±4D ．419、如图，是一个由几块相同的小正方体搭成的立体图形的三视图，则这堆立体图形中的小正方体共有…………………………………………………………………………………………… ( )块.主视图左视图俯视图A ．7或8B ．8或9C ． 9或10D ．10或1120、如图，点P 按A →B →C →M 的顺序在边长为1的正方形边上运动，M 是CD 边上的中点，设点P 经过的路程x 为自变量，△APM 的面积为y ，则函数y 的大致图像是………… ( )xy 0 1 22.5xy 0 1 2 2.5y 0 1 2 2.5y0 1 2 2.5三.解答题(共6小题，46分)19、（本题6分）解不等式组 ⎪⎩⎪⎨⎧≤+--+<-1215312)1(315x x x x 并求它的整数解。

八年级数学试卷一、选择题:(本题有10小题，每小题4分，共40分。

)1.如图，已知：AB ∥CD ，若∠1＝50°，则∠2的度数是（ ） A 、50° B 、60° C 、130° D 、120°2.以下各组数据能作为直角三角形三边长的是 （ ） A 、2，1，5 B 、5，11，12 C 、6，12，13 D 、5，12，133.已知等腰三角形一边是3，一边是6，则它的周长等于（ ）A ．12B ．15C ． 12 或15D ．18或154.如果用 表示1个立方体，用 表示两个立方体叠加，用 表示3个立方体叠加，那么下面右图由7个立方体叠成的几何体， 从正前方观察，可画出的平面图形是（ ）A C D5. 某体育用品商店新进一批运动服，每件进货价为120元，试销两天的情况如下为了增加销售量，你认为该店确定这批运动服单价时应更关心这组数据的（ ） A ．平均数 B ．中位数 C ．众数 D ．方差6.甲、乙两同学最近几次测验的平均分都是86分，但甲几次测验成绩的方差是0.61，乙的方差是1.72，由上述信息可知（ ）A 、甲的成绩比乙的好；B 、乙的成绩比甲好；C 、甲的成绩波动比乙的大；D 、乙的成绩波动比甲大。

7.下列调查，比较容易用普查方式的是（ ）A 、了解青田某中学学生体育中考的成绩B 了解青田县中小学生的近视率C 、了解青田县居民年人均收入D 、了解某一天离开青田县的人口流量8.下图可以沿线折叠成一个带数字的立方体，每三个带数字的面交于立方体的一个顶点，则相交于一个顶点的三个面上的数字之和最小是（ ）（A ） 7 （B ） 8 （C ） 9 （D ） 109.某校要了解八年级女生的体重，以掌握她们的身体发育情况，从八年级500名女生中抽出50名进行检测，就这个问题来说， 下面说法中正确的是（ ）A 、500名女生是总体B 、500名女生是个体C 、50是样本容量D 、500名女生是总体的一个样本 10.国庆假期中，小华与同学到休博园去玩探宝游戏，按照探宝图，他们从门口A 处出发先往东走8千米，又往北走2千米，遇到障碍后又往西走3千米，再折向北走到6千米处往东拐，仅走了1千米，就找到了宝藏，则门口A 到藏宝点B 的直线距售价（元） 280 250 220 200 160 件数 2 4 7 18 5_C_ A第7题 学校 班级 姓名 考号16 38 AB21 2 36 4 5 _ B_ D_1 _ 2左视图主视图俯视图 离是（ ）千米。

湖州四中八（下）竞赛题姓名 班级一、化简计算（每小题4分） 1. 14425081010⨯⨯.. 2.521312321⨯÷；3. 2484554+-+ 4 、2332326--5. 3)154276485(÷+- 6、(231⎛+ ⎝7、⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛+121580325.12712 8、(()2771+--二、选择适当的方法解方程（每小题4分） 9、； 10、.11、12、13、； 14、15、； 16、17、18、解关于x 的一元二次方程：()0012422≠=--a ax x a19、02222=-+-n m mx x 20.()()2222222,06b a b ab a+=-+-+求21、用配方法求262+-x x 的最小值； 22、用配方法求1232++-x x 的最大值23、对于任意实数x ，试比较两代数x x x 42323--+1与10433++x x 的值的大小。

24、已知二次三项式2)6(92-++-m x m x 是一个完全平方式，试求m 的值.25、关于x 的一元二次方程()0422=+++kx k kx 有两个不相等的实数根，求k 的取值范围；26、已知()0053222≠=-+y xy y x ，求yx的值。

27.若142=++y xy x ，282=++x xy y ，则x+y 的值为28.如果012=-+x x ，那么代数式7223-+x x 的值。

29. 已知实数a 、b 满足条件： 求ab -的平方根。

30.某商店如果将进货价为8元的商品按每件10元售出，每天可销售200件，现在采用提高售价，减少进货量的方法增加利润，已知这种商品每涨价0.5元，其销量就减少10件;要使每天获得利润700元，请你帮忙确定售价。

绝密★启用前2018-2019学年浙教版八年级数学竞赛试题注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）请点击修改第I卷的文字说明一．选择题（共6小题，每小题4分，共24分）1．已知m为正整数，且关于x，y的二元一次方程组有整数解，则m2的值为（）A．4 B．1，4 C．1，4，49 D．无法确定2．已知+=3，则代数式的值为（）A．3 B．﹣2 C．﹣D．﹣3．正方形ABCD中，点P，Q分别是边AB，AD上的点，连接PQ、PC、QC，下列说法：①若∠PCQ=45°，则PB+QD=PQ；②若AP=AQ=，∠PCQ=36°，则；③若△PQC是正三角形，若PB=1，则AP=．其中正确的说法有（）A．3个B．2个C．1个D．0个4．10个互不相等的有理数，每9个的和都是“分母为22的既约真分数（分子与分母无公约数的真分数）”，则这10个有理数的和为（）A．B．C．D．5．如图所示，某工厂有三个住宅区，A，B，C各区分别住有职工30人，15人，10人，且这三点在一条大道上（A，B，C三点在同一直线上），已知AB=300米，BC=600米．为了方便职工上下班，该厂的接送车打算在此路段只设一个停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（）A．点A B．点B C．AB之间D．BC之间6．试卷上有6道选择题，每题有3个选项，结果阅卷老师发现，在所有卷子中任选3张答卷，都有一道题的选择互不相同，请问最多有（）人参加了这次考试．A．11 B．12 C．13 D．14第Ⅱ卷（非选择题）请点击修改第Ⅱ卷的文字说明二．填空题（共6小题，每小题4分，共24分）7．一条大河有A、B两个港口，水由A流向B，水流速度是4千米/时，甲、乙两船同时由A向B行驶，各自不停地在A、B之间往返航行．甲在静水中的速度是28千米/时，乙在静水中的速度是20千米/时，已知两船第二次迎面相遇与甲船第二次追上乙船（不算开始时甲、乙在A处的那一次）的地点相距40千米，则A、B两港口的距离为千米．8．在环行自行车赛场内，甲、乙、丙三人骑自行车进行训练，他们的速度是：甲每分钟圈，乙每分钟圈，丙每分钟圈，他们同时出发，起点如图所示（甲从A点出发，沿圆周逆时针运动；乙从B点出发，沿圆周逆时针运动；丙从C点出发，沿圆周顺时针运动），则出发后分三人第一次相遇．9．表2、表3是从表1中截取的一部分，则a+b=表1表2表310．杨辉是我国南宋时期杰出的数学家和教育家，下图是杨辉在公元1261年著作《详解九章算法》里面的一张图，即“杨辉三角”，该图中有很多规律，请仔细观察，解答下列问题：（1）图中给出了七行数字，根据构成规律，第8行中从右边数第3个数是；（2）利用不完全归纳法探索出第n行中的所有数字之和为．11．已知x、y、z满足，对于数a、[a]表示不大于a的最大整数，{a}=a﹣[a]，则10（x+y）+z的值为．12．甲、乙、丙三人进行智力抢答活动，规定：第一个问题由乙提出，由甲、丙抢答．以后在抢答过程中若甲答对1题，就可提6个问题，乙答对1题就可提5个问题，丙答对l题就可提4个问题，供另两人抢答．抢答结束后，总共有16个问题没有任何人答对，则甲、乙、丙答对的题数分别是．三．解答题（共4小题，52分）13．（12分）观察下列各式：13+23=1+8=9，而（1+2）2=9，∴13+23=（1+2）2；13+23+33=36，而（1+2+3）2=36，∴13+23+33=（1+2+3）2；13+23+33+43=100，而（1+2+3+4）2=100，∴13+23+33+43=（1+2+3+4）2；∴13+23+33+43+53=（）2=．根据以上规律填空：（1）13+23+33+…+n3=（）2=[]2．（2）猜想：113+123+133+143+153=．14．（12分）某中学的1号教学大楼共有4道门，其中两道正门大小相同，两道侧门也大小相同，安全检查时，对4道门进行了测试，当同时开启一道正门和两道侧门时，2分钟内可以通过560名学生，当同时开启一道正门和一道侧门时，4分钟内可通过800名学生．（1）求平均每分钟一道正门和一道侧门各可以通过多少名学生？（2）该中学的2号教学大楼，有和1号教学大楼相同的正门和侧门共5道，若这栋大楼的教室里最多有1920名学生，安全检查规定，在紧急情况下，全大楼学生应在4分钟内通过这5道门安全撤离，该栋大楼正门和侧门各有几道？15．（14分）如图1，小明将一张长方形纸片沿对角线剪开，得到两张三角形纸片（如图2）量得它们的斜边长为10cm，较小锐角为30°再将这两张三角形纸片摆成如图3的形状，但点B、C、F、D 在同一条直线上，且点C与点F重合（在图3至图6中统一用F表示）．小明在对这两张三角形纸片进行如下操作时遇到了三个问题，请你帮忙解决．（1）将图3中的△ABC沿BD向右平移到图4的位置，使点B与点F重合，请你求出平移的距离；（2）将图3中的△ABC绕点F顺时针方向旋转30°到图5的位置，A1F交DE于G，若DG=kEG，求k的值；（3）将图3中的△ABF沿直线AF翻折到图6的位置，AB1交DE于点H，请证明：AH=DH．16．（14分）探究问题：（1）阅读理解：①如图（A），在已知△ABC所在平面上存在一点P，使它到三角形顶点的距离之和最小，则称点P 为△ABC的费马点，此时P A+PB+PC的值为△ABC的费马距离；②如图（B），若四边形ABCD的四个顶点在同一圆上，则有AB•CD+BC•DA=AC•B D．此为托勒密定理；（2）知识迁移：①请你利用托勒密定理，解决如下问题：如图（C），已知点P为等边△ABC外接圆的上任意一点．求证：PB+PC=P A；②根据（2）①的结论，我们有如下探寻△ABC（其中∠A、∠B、∠C均小于120°）的费马点和费马距离的方法：第一步：如图（D），在△ABC的外部以BC为边长作等边△BCD及其外接圆；第二步：在上任取一点P′，连接P′A、P′B、P′C、P′D．易知P′A+P′B+P′C=P′A+（P′B+P′C）=P′A+；第三步：请你根据（1）①中定义，在图（D）中找出△ABC的费马点P，并请指出线段的长度即为△ABC的费马距离．（3）知识应用：2010年4月，我国西南地区出现了罕见的持续干旱现象，许多村庄出现了人、畜饮水困难，为解决老百姓的饮水问题，解放军某部来到云南某地打井取水．已知三村庄A、B、C构成了如图（E）所示的△ABC（其中∠A、∠B、∠C均小于120°），现选取一点P打水井，使从水井P到三村庄A、B、C所铺设的输水管总长度最小，求输水管总长度的最小值．参考答案与试题解析1．解：两式相加得：（3+m）x=10，则x=，代入第二个方程得：y=，当方程组有整数解时，3+m是10和15的公约数．∴3+m=±1或±5．即m=﹣2或﹣4或2或﹣8．又∵m是正整数，∴m=2，则m2=4．故选：A．2．解：+==3，即a+2b=6ab，则原式===﹣，故选：D．3．（1）证明：延长AB至点E，使BE=DQ，连接EC，AC，∵正方形ABCD，∴∠BCA=∠DCA=45°，CD=DA=AB=BC，∠D=∠EBC=90°，∴在△BEC和△DQC中，，∴△BEC≌△DQC（SAS），∴CE=CQ，∠BCE=∠DCQ，∵∠PCQ=45°，∴∠DCQ+∠PCB=45°，∴∠BCE+∠PCB=45°，即∠ECP=45°，∵在△PCE和△PCQ中，，∴△PCE≌△PCQ（SAS），∴PE=PQ，∵PE=PB+BE=PB+QD，∴PQ=PB+QD，（2）过点Q作∠PQC的角平分线，交PC于点E，∵正方形ABCD，∴∠A=∠D=∠B=90°，AD=AB=BC=CD，∵∠PCQ=36°，AP=AQ=，∴PQ=2，PB=QD，∴PE=PC﹣2，∵在△PBC和△QDC中，，∴△PBC≌△QDC（SAS），∴QC=PC，∴∠CPQ=∠CQP=72°，∴∠PQE=∠EQC=36°，∴QE=QP=EC=2，∵△QPE∽△CQP，∴PQ：QC=PE：PQ，即PQ2=PE•PC，∵PQ=2，∴PE•PC=4，∵PE=PC﹣2，∴PC2﹣2PC﹣4=0，解得：PC1=1﹣＜0（舍去），PC2=1+，∴PC=+1，（3）取PC的中点E，连接BE，做BM⊥PC于点M，∵正方形ABCD，∴BC=CD=AB=AD，∠D=∠B=∠A=∠BCD=90°，∵△PCQ为正三角形，∴QC=PQ=PC，∠QCP=60°，∵在Rt△PBC和Rt△QDC中，，∴Rt△PBC≌Rt△QDC（HL），∴∠BCP=∠DCQ=，PB=QD，∵E为PC的中点，∴BE=EC=PE=，∴∠BEM=30°，∴2BM=BE，∴4BM=PC，∵PC=AP，∴4BM=AP，∵BM⊥PC，∠BCP=15°，∴∠PBM=15°，∴△PBM∽△PCB，∴BP：PC=BM：BC，∵PB=1，∴BC=AB=AP+1，∴，∴AP2﹣AP﹣1=0，解得：AP1=1+，AP2=1﹣＜0（舍去），∴AP=+1，∴其中说法正确的共3个，故选：A．4．解：这10个有理数，每9个相加，一共得出另外10个数，由于原10个有理数互不相等，可以轻易得出它们相加后得出的另外10个数也是互不相等的，而这10个数根据题意都是分母22的既约真分数，而满足这个条件的真分数恰好正好有10个，∴这10项分别是：1/22，3/22，5/22，7/22，9/22，13/22，15/22，17/22，19/22，21/22．它们每一个都是原来10个有理数其中9个相加的和，那么，如果再把这10个以22为分母的真分数相加，得出来的结果必然是原来的10个有理数之和的9倍．所以，10个真分数相加得出结果为5，于是所求的10个有理数之和为5/9．故选：D．5．解：①以点A为停靠点，则所有人的路程的和=15×300+10×900=13500（米），②以点B为停靠点，则所有人的路程的和=30×300+10×600=15000（米），③以点C为停靠点，则所有人的路程的和=30×900+15×600=36000（米），④当在AB之间停靠时，设停靠点到A的距离是m，则（0＜m＜100），则所有人的路程的和是：30m+15（300﹣m）+10（900﹣m）=13500+5m＞13500，⑤当在BC之间停靠时，设停靠点到B的距离为n，则（0＜n＜200），则总路程为30（300+n）+15n+10（600﹣n）=15000+35n＞13500．∴该停靠点的位置应设在点A；故选：A．6．解：法一：第一道题有三个人分别选了1、2、3；第二道题他们三个人选了同一个答案（就是1吧，因为所有答案条件相同无所谓的），另外两个人选了2、3；第三道题他们五个人选了1，其他两个人选了2、3；第四题他们7个选1，另两个2、3；第五题他们9个选1，另两个2、3；第六题他们11个选1，另两个2、3；一共13人．只有这种情况才能保证随便三张卷子都有1题答案互不相同，这是抽屉定理中的穷举法．法二：首先只有一道试题时候最多3人，只有两道试题的时候最多4人，这个很容易用穷举法知道．现在，如果有14人做这道题的话，14人中任取3人的组合共有364种，根据抽屉原理，这里至少有122种取法第一题的答案相同．同样，在这122种取法中，至少41种取法第2题答案相同，接下来有14种取法第3题答案相同，5种取法第4题答案相同，这样根据两道题时候的情况，可以知道14人是不可能的，所以最多13人．7．解：设A、B两个港口的距离为d，甲顺水速度：28+4=32千米/时，甲逆水速度：28﹣4=24千米/时，乙顺水速度：20+4=24千米/时，乙逆水速度：20﹣4=16千米/时，第二次相遇地点：从A到B：甲速：乙速=32：24=4：3，甲到B，乙到E；甲从B到A，速度24，甲速：乙速=24：24=1：1，甲、乙在EB的中点F点第一次相遇；乙到B时，甲到E，这时甲速：乙速=24：16=3：2，甲到A点时，乙到C点；甲又从A顺水，这时甲速：乙速=32：16=2：1，所以甲、乙第二次相遇地点是AC处的点H，AH=×AB=AB=d，第二次追上地点：甲比乙多行1来回时第一次追上，多行2来回时第二次追上．甲行一个来回2AB时间+=d乙行一个来回2AB时间+=，一个来回甲比乙少用时间：﹣=，甲多行2来回的时间是：×2=，说明乙第二次被追上时行的来回数是：=4，甲第二次追上乙时，乙在第5个来回中，甲在第7个来回中．甲行6个来回时间是×6=，乙行4个来回时间是×4=，﹣=，从A到B甲少用时间：﹣=，说明第二次追上是在乙行到第五个来回的返回途中．﹣=，从B到A，甲比乙少用时间：﹣=，=，追上地点是从B到A的中点C处．根据题中条件，HC=40（千米），即=40，解得d=240千米．故答案为：240．8．解：设出发后x分钟后三人第一次相遇，由甲和乙相遇得：x=，解得：x=5，此时，甲逆时针行驶了=圈，当出发5分钟后，丙顺时针行驶了×5=圈，此时，甲乙丙第一次相遇．故答案为：5．9．解：表2中，∵15是5的3倍，24是6的4倍，∴a是5的6倍是30，或a是7的4倍是28，表3中，∵16是2的8倍，24是3的8倍，∴b是4的7倍是28，∴a+b=30+28=58或a+b=28+28=56．故答案为：58或56．10．解：（1）设第n行第2个数为a n（n≥2，n为正整数），第n行第3个数为b n（n≥3，n为正整数），观察，发现规律：∵a2=1，a3=2，a4=3，a5=4，a6=5，∴a n=n﹣1；∵b3=1，b4=3=1+2=b3+2，b5=6=3+3=b4+3，b6=10=6+4=b5+4，…，∴b n﹣b n﹣1=n﹣2，∴b n=b3+b4﹣b3+b5﹣b4+b6﹣b5+…+b n﹣b n﹣1=1+2+3+…+n﹣2=．当n=8时，b3==21；故答案为：21；（2）∵第1行数字之和1=20，第2行数字之和2=21，第3行数字之和4=22，第4行数字之和8=23，…∴第n行数字之和为2n﹣1．故答案为：2n﹣1．11．解：∵{a}=a﹣[a]，∴a={a}+[a]，∵①+②+③得：x+[x]+{x}+y+[y]+{y}+z+[z]+{z}=0.6，2x+2y+2z=0.6，x+y+z=0.3④，④﹣①得：{y}+[z]=1.2，所以{y}=0.2，[z]=1，④﹣②得：{x}+[y]=0.1，所以[y]=0，{x}=0.1，④﹣③得：[x]+{z}=﹣1，所以{z}=0，[x]=﹣1，∴x=[x]+{x}=﹣1+0.1=﹣0.9，y=[y]+{y}=0+0.2=0.2，z=[z]+{z}=1+0=1，∴10（x+y）+z=10×（﹣0.9+0.2）+1=﹣6．12．解：设甲、乙、丙答对得题数分别为x，y，z，根据题意列方程得，6x+5y+4z+1=x+y+z+16，整理得，5x+4y+3z=15，∵x，y，z为非负整数．∴x=1，y=1，z=2；或x=0，y=3，z=1．故答案为：（1，1，2）或（0，3，1）．13．解：由题意可知：13+23+33+43+53=（1+2+3+4+5）2=225（1）∵1+2+…+n=（1+n）+[2+（n﹣1）]+…+[+（n﹣+1）]=，∴13+23+33+…+n3=（1+2+…+n）2=[]2；（2）113+123+133+143+153=13+23+33+...+153﹣（13+23+33+ (103)=（1+2+…+15）2﹣（1+2+…+10）2=1202﹣552=11375．故答案为：1+2+3+4+5；225；1+2+…+n；；11375．14．解：（1）设平均每分钟一道正门可通过x名学生，一道侧门可以通过y名学生．则，解得．答：平均每分钟一道正门可通过120名学生，一道侧门可以通过80名学生；（2）设该栋大楼正门有m道，侧门有n道，则，解得．故该栋大楼正门有2道，侧门有3道．15．解：∵AB=DE=10，∠A=∠D=30°，∴FB=FE=5，∠B=∠FED=60°，FD=EF=5．（1）如图4，FC1=BF=5，所以△ABC沿BD向右平移的距离为5；（2）∵△ABC绕点F顺时针方向旋转30°到图5的位置，∴∠AF A1=30°，∴∠A1FD=60°，而∠D=30°，∴FG⊥CD，∴EG=EF=，∴DG=10﹣=，∴DG=3EG，∴k的值为3；（3）∵△ABF沿直线AF翻折到图6的位置，∴B1F=BF=EF，∠AB1F=∠B=60°，∴DB1=AE，∠DB1H=∠AEH=120°，而∠DHB1=∠AHE，在△DB1H与△AEH中，∵∠DB1H=∠AEH，DB1=AE，∠DHB1=∠AHE，∴△DB1H≌△AEH，∴AH=DH．16．（2）①证明：由托勒密定理可知PB•AC+PC•AB=P A•BC∵△ABC是等边三角形∴AB=AC=BC，∴PB+PC=P A，②P′D、AD，（3）解：如图，以BC为边长在△ABC的外部作等边△BCD，连接AD，则知线段AD的长即为最短距离．∵△BCD为等边三角形，BC=4，∴∠CBD=60°，BD=BC=4，∵∠ABC=30°，∴∠ABD=90°，在Rt△ABD中，∵AB=3，BD=4，∴AD===5（km），∴从水井P到三村庄A、B、C所铺设的输水管总长度的最小值为5km．。

2、类比1的计算过程，完成下面的计算：
⑴ =
4、计算
（1）
（2）
（3）
五、能力拓展
1、
2、先化简，再求值：
-10（-a3b2c）2· a·（bc）3-（2abc）3·（-a2b2c）2，其中a=-5，b=0.2，c=2。
（2）
=____________
a.观察⑴、⑵两题，并思考：
Ⅰ、⑴⑵两题属于_______与_______相乘。
⑦(－3xy)2=－6x2y2()
⑧(a3+b2)3=a9+b6( )
2．（口答）幂的运算的三个法则是什么？
3、光的速度约为 千米/秒，太阳光照射到地球上需要的时间大约是 秒，你知道地球与太阳的距离约是多少千米吗？（列出式子）
二、自主学习合作探究
探究：
1、
=________________
思考：计算过程中用到哪些运算律及运算性质？请写出来。
3、下面计算对不对？如果不对，应当怎样改正？
(1)3a3·2a2=6a6()(2)2x2·3x2=6x4()
(3)3x2·4x2=12x2()(4)5y3·3y5=15y15()
课
后
反
思
4、若2a=3，2b=5，2c=30，试用含a、b的式子表示c．
⑤(2x)4·(-3x2y)⑥（-xy2z3)4·（-x2y)3
2、计算
①（-2y）·(3xy5)②3x·5x2·(-x3y)
③(-2.5x)·(-4x)④x2yz·xyz3
⑤(2×105)(2×105)⑥(-2x)3(-4x2)
⑦xm+1y·6xym-1
③(－5a2b)·(－3a)·(－2ab2c)
反思：单项式与单项式相乘的结果仍是________________________________。

2013学年第二学期学科竞赛 八 年 级 数 学 试 卷一、选择题（每小题5分，共30分）1．若平行四边形的一边长为10，则它的两条对角线长可以是…………… （ ）A ．8和16B ．6和8C ．6和12D ．24和42．一组数据x 1，x 2，…，x n 的平均数为5，方差为16，其中n 是正整数，则另一组数据3x 1+2，3x 2+2，…，3x n +2的平均数和标准差分别是…………………………………… （ ）A ．15，144B ．17，144C ．17，12D ．7，163．已知一元二次方程01282=+-x x 的两个解恰好是等腰△ABC 的底边长和腰长，则△ABC 的周长为…………………………………………………… （ ）A ．14B ．10C ．11D ．14或104．三角形的三条边长分别为2、k 、4， 若k 满足方程361212622+--+-k k k k =0， 则k 的值为………………………………………………………………………… （ ）A ．2B ．3C ．3或4D ．2或3 5．如图四边形ABCD 中，∠BAD =125°，∠B =∠D =90°，在BC ，CD 上分别找一点M ，N ，使△AMN 周长最小时，则∠AMN +∠ANM 的度是…………………………………（ ）A ．130B ．120°C ．110°D ．100°6．如图，以Rt △BCA 的斜边BC 为一边在△BCA 的同侧作正方形BCEF ，设正方形的中心为O ， 连结AO ，如果AB =8，AO =122，那么AC 的长为……………………………（ ）A ．24B ．32C ．8D ．16（第5题图） （第6题图）二、填空题（每小题5分，共30分）.7．一个n 边形的内角和等于外角和的3倍，则n = ．8．函数121x y x x =---中，自变量x 的取值范围是_________________．9．要组织一次篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排28场比赛，则应邀请 支球队参加比赛． 10．已知实数a ，b 满足,24)3(2422a b a b a =+-+++-则a +b 的值是 ．11．如图，正方形ABCD 边长为2，AB ∥x 轴，AD ∥y 轴，顶点A 恰好落在双曲线y =x21上，边CD 、BC 分别交双曲线于点E 、F ，若线段AE 过原点，则S △AEF = ．12．如图，∠MON =90°，矩形ABCD 的顶点A 、B 分别在边OM 、ON 上，当B 在边ON 上运动时，A 随之在OM 上运动，矩形ABCD 的形状保持不变，其中AB =4，BC =2，运动过程中，点D 到点O 的最大距离为 ．（第11题图） （第12题图）三、解答题（共60分）13．（本题10分）已知在如图4×4的方格中，有一个格点三角形ABC （三个顶点均在格点上），其中AB =5，BC =22，AC =17.（1）请你在方格中画出该三角形；（2）求△ABC 中AC 边上的高的长（结果保留根号）.14．（本题12分）如图，矩形ABCD中，对角线AC与BD相交于点O，已知AB=6，BC=8，P是AD边上任意一点，作PE⊥AC于点E，PF⊥BD于点F.（1）求PE+PF长.（2）过O作OG⊥AC交AD于点G，求AG长.15．（本题12分）如图，在线段AB上任取一点E，在AB的同侧作等边△ADE和△BCE，连结CD，P、Q、M、N分别是AB、BC、CD、DA的中点.（1）判断四边形PQMN的形状，并证明你的结论；（2）若AE＝6，EB＝3，求此时四边形PQMN的周长（结果保留根号）16．（本题13分）如图，正比例函数y =x 21的图像与反比例函数y =)0( k x k 在第一象限的图像交于A 点，过A 点作x 轴的垂线，垂足为M ，已知△AOM 的面积为1，点B （－1，t ）为反比例函数在第三象限图像上的点.（1）试求出k 值及点B 的坐标.（2）在ｘ轴上是否存在点P ，使AB ＝AP ，请直接写出满足条件的点P 的坐标.（3）在y 轴上找一点P ，使｜PA －PB ｜的值 最大，并求出P 点坐标.17．（本题13分）阅读材料：一元二次方程根与系数有如下关系：若ｘ1，ｘ2是一元二次方程ax 2+bx +c =0(a ≠0)的两根，则ｘ1+ｘ2＝－a b ，ｘ1ｘ2＝ac ，这个定理人们称之为韦达定理. 例：若ｘ1，ｘ2是一元二次方程3x 2－7x +1=0的两根，则ｘ1+ｘ2＝37，ｘ1ｘ2＝31，反之，以ｘ1，ｘ2为两根的一元二次方程（二次项系数为1）为x 2－（ｘ1+ｘ2）x +ｘ1ｘ2=0. 例：以2和3为两根的一元二次方程（二次项系数为1）为x 2－5x +6=0. 仔细阅读上面材料，并解答下面问题：已知:实数a 、b 、c 满足a +b +c =2，abc =4.（1）求a 、b 、c 中最大者的最小值.（2）求｜a ｜+｜b ｜+｜c ｜的最小值.思路点拨：不妨设a ≥b ,a ≥c ，由条件得b +c =2－a ，bc =a4，构造以b 、c 为实根的一元二次方程.八年级数学参考答案 一、选择题（本题有6个小题，每小题5分，共30分） 1. 2. 3. 4. 5. 6.A C A BC B二、填空题（本题有6小题，每小题5分，共30分）7. 8 ; 8. 21＜x ≤1; 9. 810. 1; 11. 34; 12. 22+2;三、解答题（共 60分）13、 (本题10分)解：（1）△ABC 就是所求的三角形.（2）设AC 边上的高为ｈ.∵S △ABC ＝8－2－2－1＝3∴21AC ·ｈ＝3∴17ｈ＝6∴ｈ＝1717614、 (本题12分)解：（1）连结PO在矩形ABCD 中，AO ＝DO =21AC ，∠ABC ＝90°∴AC ＝2286 ＝10∴AO ＝DO ＝5∵S △AOD ＝S △AOP + S △DOP∴41S 矩＝21AO ·PE +21DO ·PF∴41 ×6×8＝21×5（PE +PF ） ∴PE +PF ＝524 （2）连结CG∵四边形ABCD 是矩形∴AO ＝CO ，∠ADC ＝90°， AD ＝BC ＝8， DC ＝AB ＝6∵OG ⊥AC∴GO 是AC 的中垂线∴CG ＝AG设AG ＝CG ＝ｘ，则DG ＝8－ｘ由勾股定理得：CG 2＝DG 2+CD 2∴ｘ2＝（8－ｘ）2+62 ∴ｘ＝425 15．（本题12分）证明：（1）四边形PQMN 是菱形，理由如下连结AC 、BD ．∵ PQ 为△ABC 的中位线，∴ PQ 21AC 同理 MN 21AC ．MQ 21BD ∴MN PQ ，∴ 四边形PQMN 为平行四边形．又∵△AEC 和△DEB 中，AE ＝DE ，EC ＝EB ，∠AED ＝60°＝∠CEB∴∠AEC ＝∠DEB ∴ △AEC ≌△DEB∴ AC ＝BD ，∴MN ＝MQ∴ 四边形PQMN 是菱形（2）过点D 作DF ⊥AB 于F ，则DF ＝又DF 2＋FB 2＝DB 2∴DB ＝∴由①知四边形PQMN 是菱形，可计算得周长是16．（本题13分）解：（1）∵△AOM 的面积为1， ∴21ｋ＝1，解得ｋ＝2，∴反比例函数的解析式为ｙ＝x2 把B （－1，ｔ）代入ｙ＝x2，解得ｔ＝－2 ∴B 点坐标为（－1，－2）.（2）存在.满足条件的点P 的坐标为（2＋17，0），（2－17，0）（3）作B 点关于ｙ轴的对称点C ，如图，则C 点坐标为（1，－2）∴PB ＝PC ， ∴｜PA －PB ｜＝｜PA －PC ｜≤AC∴当点P ，C ，A 共线时，｜PA －PB ｜的值最大.设直线AC 的解析式为y =mx +n ，把A （2,1），C （1，－2）代入，得直线AC 的解析式为y =3x －5.把ｘ＝0代入y =3x －5得ｙ＝－5， ∴P 点坐标为（0，－5）.17．（本题13分）解：（1）不妨设a ≥b ，a ≥c∵b +c =2－a , bc =a 4 ∴b ,c 为一元二次方程x 2－(2－a )x +a4=0的两个实根. ∴△＝（2－ａ）2－4×a 4≥0，即（ａ2＋4）（ａ－4）≥0，得 ａ≥4，当ａ＝4，ｂ＝ｃ＝－1时，ａ、ｂ、ｃ满足条件，故ａ、ｂ、ｃ中最大者的最小值为4.（2）ａ、ｂ、ｃ只可能一正二负，设ａ＞0，ｂ＜0，ｃ＜0，则｜ａ｜+｜ｂ｜+｜ｃ｜＝ａ－ｂ－ｃ＝2ａ－2，由（1）知ａ≥4，故2ａ－2≥6，当ａ＝4，ｂ＝ｃ＝－1时，ａ、ｂ、ｃ满足条件，且使｜ａ｜+｜ｂ｜+｜ｃ｜＝2ａ－2≥6中等号成立，故｜ａ｜+｜ｂ｜+｜ｃ｜的最小值为6.。

浙教版八年级第二学期五月份竞赛练习卷一、选择题1．下列图案都是由字母“m”经过变形、组合而成的，其中不是中心对称图形的是（ ）． ． ． ．A ．（2，1）和（-12，1）B ．（2，-1）和（-12，1）C ．（-2，1）和（12，1） D ．（-1，-2）和（-1，12）7．如图，在正五边形ABCDE 中，连接AC ，AD ，则∠CAD 的度数是（ ）A ．30°B ．36°C ．45°D ．60°8．在▱ABCD 中，M 为CD 的中点，如DC=2AD ，则AM 、BM 夹角度数是（ ） A ．90° B ．95° C ．85° D ．100°9．某班同学毕业时都将自己 的照片向全班其他同学各送一张表示留念，全班共送1035张照片，如果全班有x 名同学，根据题意，列出方程为（ ）A ．x （x+1）=1035B ．x （x-1）=1035×2C ．x （x-1）=1035D ．2x （x+1）=103510．定义：如果一元二次方程ax 2+bx+c=0（a≠0）满足a+b+c=0，那么我们称这个方程为“凤凰”方程．已知ax 2+bx+c=0（a≠0）是“凤凰”方程，且有两个相等的实数根，则下列结论正确的是（ ） A ．a=c B ．a=b C ．b=c D ．a=b=c 二、填空题11．如图，每个小正方形的边长为1，A 、B 、C 是小正方形的顶点，则∠ABC 的度数为________．ABC三、解答题19、某数学老师将本班学生的身高数据（精确到厘米）交给甲、乙两同学，要求他们各自独立地绘制一幅频数分布直方图，甲绘制的图如图１所示，乙绘制的图如图２所示．经检查确认，甲绘制的直方图是正确的，乙在整理数据与绘图过程中均有个别错误．（1）问该班学生有多少人？分组 分组 5 10 15 201117图1 图21（2）某同学身高为165厘米，他说：“我们班上比我高的人不超过”，他的说法正确吗？4（3）请指出乙在整理数据或绘图过程中所存在的一个．．错误．（4）设该班学生身高数据的中位数为a，试写出a的值20、如图，在平行四边形ABCD中，∠ABC=3∠A，点E在CD上，CE=1，EF⊥CD于E，AD=1，求BF的长．21．戒烟一小时，健康亿人行”．今年国际无烟日，小华就公众对在餐厅吸烟的态度进行了随机抽样调查，主要有四种态度：A．顾客出面制止；B．劝说进吸烟室；C．餐厅老板出面制止；D．无所谓．他将调查结果绘制了两幅不完整的统计图．请你根据图中的信息回答下列问题：（1）这次抽样的公众有人；（2）请将统计图①补充完整；（3）在统计图②中，“无所谓”部分所对应的圆心角是度；（4）若城区人口有20万人，估计赞成“餐厅老板出面制止”的有万人．并根据统计信息，谈谈自己的感想．（不超过30个字）22．如果关于x的一元二次方程(a-1)x a2+a+ax+1=0的一个整数根恰好是关于x的方程（m2+m）x2+3mx-3=0的一个根，试求a和m的值．23．已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．当∠MAN绕点A旋转到BM=DN时（如图1），易证BM+DN=MN．（1）当∠MAN绕点A旋转到BM≠DN时（如图2），线段BM、DN和MN之间有怎样的数量关系？写出猜想，并加以证明；（2）当∠MAN绕点A旋转到如图3的位置时，线段BM、DN和MN之间又有怎样的数量关系？请直接写出你的猜想．。

A B C D M N HE盐官片八年级数学竞赛试题（考试时间：90分钟，总分：120分）一、选择题（每小题3分，共42分）1、在下列八个数：3.1415926，0.151151115… ，10049，0.2， π1，7，722，327中，无理数的个数是 ( )A 2B 3C 4D 5 2、下列图形中，不是轴对称图形的是① ② ③ ④ ⑤A 、①⑤B 、②⑤C 、④⑤D 、①②3、如图，数轴上A B ，两点表示的数分别是1和2，点A 关于点B的对称点是点C ，则点C 所表示的数是（ ） A ．21-B ．12+C ．222-D ．221-4、已知|a|=5，2b =3，且ab>0，则a+b=（ ） A 、8 B 、—2 C 、8或—8 D 、2或—25、如图;已知,∠EAC=∠BAD,AC=AD,增加下列条件中的其中一个:①AB=AE,②BC=ED, ③∠C=∠D,④∠B=∠E; C其中能使△ABC ≌△AED 的个数有 E ( ) A. 4个 B. 3个. B A C. 2个 D. 1个 D 6、△ABC 中，A （—2，—3）、B （—1，—1）、C （0，1），将△ABC 绕B 点顺时针旋转90度，则点A 对应的点A`的坐标为（ ） A 、（3，0）B 、（3，1）C 、（4，1）D 、（4，0）7、直角坐标系中，A （1，1）在坐标轴上找点B 使 △AOB 为等腰三角形的点共有（ ）个Ａ、６ Ｂ、７ Ｃ、８ Ｄ、９8、如图,先将正方形纸片对折,折痕为MN,再把B 点折叠在 折痕MN 上,折痕为AE,点B 在MN 上的对应点为H,沿 AH 和DH 剪下,这样剪得的三角形中 ( )A ，AD DH AH ≠=B ，AD DH AH ==C ，DH AD AH ≠= D ，AD DH AH ≠≠9、如果一个三角形两边的平分线的交点在第三边上，则这个三角形是（ ）A 、锐角三角形B 、直角三角形C 、钝角三角形D 、不能确定10、已知点A 的坐标为(1，0)，点B 在直线y x =-上运动，当线段AB 最短时，点B 的坐标为A 、(0，0)B 、 11(,)22- C 、22(,)22- D 、 11(,)22-11、如图，等腰直角△ABC 中AB=AC ，将其按下图所示的方式折叠两次．第2次折叠第1次折叠C 'DDCBA 'A 'ABCCBA若DA ’＝1，给出下列说法： ①DC ’ 平分∠BDA ’； ②BA ’ 长为21+； ③△BC ’D 是等腰三角形； ④△CA ’D 的周长等于BC 的长． 其中正确的有（ ）（A ）1个 （B ）2个 （C ）3个 （D ）4个12、如图所示，∠AOB 是一个钢架，且∠AOB=10º， 为了使钢架更加牢固，需在内部添加一些钢管EF 、FG 、 GH …添加钢管的长度都与OE 相等，则最多能添加这 样的钢管的根数为（ ）A 、15B 、9C 、8D 、7 13、甲、乙两人骑车从学校出发，先上坡到距学校6千米的A 地，再下坡到距学校16千米的B 地，甲、乙两人行程y（千米）与时间x （小时）之间的函数关系如图所示．若甲、乙两人同时从B 地按原路返回到学校，返回时，甲和乙上、下坡的速度仍保持不变．则下列结论：①乙往返行程中的平均速度相同；②乙从学校出发45分钟后追上甲；③乙从B 地返回到学校用时1小时18分钟；④甲、乙返回时在下坡路段相遇．其中正确的结论有（ ） A ．②③ B ．①④ C ．①②④ D ．②③④ 14、如图，C 为线段AE 上一动点（不与点A ，E 重合），在AE 同侧分别作正三角形ABC 和正三角形CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ， BE 与CD 交于点Q ，连结PQ ．以下五个结论： ① AD =BE ；② PQ ∥AE ；③ AP =BQ ；④ DE =DP ；⑤ ∠AOB =60°．恒成立的有（ ）个．A 、1B 、2C 、3D 、4二、填空题（每小题3分，共18分）15、正数A 的平方根为2m －4与3m －1，则A 的值为__________。

八年级数学竞赛练习题一、选择题：1、方程431=-++x x 的整数解有（）A 、2个B 、3个C 、5个D 、无穷多个2、若等式98332-=--+x xx n x m 对任意的)3(±≠x x 恒成立，则=mn （）A 、8B 、－8C 、16D 、－16 3、若x ＞z ，y ＞z ，则下列各式中一定成立的是（）A 、x+y ＞4zB 、x+y ＞3zC 、x+y ＞2zD 、x+y ＞z4、规定[]a 表示不超过a 的最大整数。

当1-=x 时，代数式6323+-nx mx 的值为16，则=⎥⎦⎤⎢⎣⎡-n m 32（ ）。

A 、－4B 、－3C 、3D 、45、如图所示，在直角扇形ABC 内，分别以AB 和AC 为直径作半圆，两条半圆弧相交于点D ，整个图形被分成4321,,,S S S S 四部分，则42S S 和的大小关系是（）。

A 、42＜S SB 、42＝S SC 、42＞S SD 、无法确定6、初二（1）班共有35名学生，其中21的男生和31的女生骑自行车上学，那么该班骑自行车上学的学生的人数最少是（）。

A 、9B 、10C 、11D 、127、有A 、B 、C 三把刻度尺，它们的刻度都是从0到30个单位（单位长度各不相同），设三把尺子的0刻度和30刻度处到尺子边缘的长度可以忽略不计，现用其中的一把尺子量度另两把尺子的长度。

已知用C 尺量度，得A 尺比B 尺长6个单位；用A 尺量度，得B 尺比C 尺长10个单位；则用B 尺量度，A 尺比C 尺（）。

A 、长15个单位B 、短15个单位C 、长5个单位D 、短5个单位二、填空题：8、654321,,,,,x x x x x x 都是正数，且1165432=x x x x x x ，2265431=x x x x x x ，3365421=x xx x x x ，4465321=x x x x x x ，6564321=x x x x x x ，9654321=x xx x x x ，则=654321x x x x x x 。

初二数学竞赛试题一选择题：1、与18是同类二次根式的是（ ） A 243272112D C B2、数的大小关系是与5665大小都是无理数，不能比较D C B A 566556655665<=>3、在①线段②等边三角形③平行四边形④矩形⑤菱形⑥正方形这六种图形中，既是轴对称图形又是中心对称图形的有（ ）种A 3B 4C 5D 64、16的算术平方根是 （ ）A 4B 4±C 2D 2±5、在线段的比是 （ ）A 3:1 B3:2 C4:1 D 4:2二 填空题6 121的平方根是7 当a 时，式子a -3在实数范围内有意义。

8 在平行四边形ABCD 中，已知 140=∠+∠B A ,则B ∠的度数是9 若菱形两条对角线长分别是10cm 和24cm ，则此菱形的边长是 cm 10 8的倒数是11 已知一个矩形的长为1234，宽为32，则它面积相等的正方形的边长是 12 在实数范围内分解因式：=-32x中，AB=3,BC=4,ABC ∠的平分线把长边AD 分成的两条13 直角边长分别为6cm 和8cm 的直角三角形斜边上的中线长是 cm14 已知正方形的对角线长为2cm ，则其面积是 2cm15 若菱形的周长是，相邻的两个内角的度数比是1：2，那么这个菱形的较短的一条对角线的长是 cm 。

三 计算题 16 1476⨯⨯ 17 753131248+- 18x x x x 1246932-+ 19⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-5.0431381427四 简答题：知一个多边形的内角和是外角和的3倍，求这个多边形的边数。

21 已知x 、y 都是实数，且()0212=-++y x ，求xy 21的值。

五 画图题22画一个矩形ABCD ，使AB=2cm ，BC=3cm六 解答题23 已知1213+-a a 是最简二次根式，试求（34＋2a ）的算术平方根。

七 证明题24 如图，已知在直三角形ABC 中，ACB C ∠=∠,90 的平分线CD 交AB 于D,DF//BC,DE//AC.求证：四边形DECF 是正方形B C E F DA。

2013学年第二学期八年级综合知识竞赛数 学 试 卷一、选择题（每小题3分，共30分）1．下列图形中，既是轴对称图形又是中心对称图形的是（ ）A ．BC ． D2．如图，已知平行四边形ABCD 中，∠B ＝4∠A ，则∠C ＝（ ）A ．18ºB ．36ºC ．144ºD ．72º3．已知一组数据：12，5，9，5，14，下列说法不正确的是（ ）A.平均数是9B.中位数是9C.众数是5D.方差是54．若点P （a ，2）与Q （－1，b ）关于坐标原点对称，则a ，b 分别为（ ）A ．－1，2B ．1，－2C ．1，2D ．－1，－25.用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应该假设这个三角形中（ ）A.有一个内角小于60°B.每一个内角都小于60°C.有一个内角大于60°D.每一个内角都大于60°6、菱形具有而矩形不一定具有的性质是 ( )A ．内角和等于3600B ．对角相等C ．对角线互相垂直D ．对边平行且相等7.已知210k k <<,则是函数11-=x k y 和xk y 2=的图象大致是( )8.定义：如果一元二次方程)0(02≠=++a c bx ax 满足0=+-c b a ，我们称这个方程为“阿凡达”方程，已知02=++c bx ax 是阿凡达方程，且有两个相等的实数根，则下列正确的是（ ）A.b a =B.c a =C.c b a ==2D.c b =9、如图，已知△ABC 的面积为24，点D 在线段AC 上，点F 在线段BC 的延长线上，且4BF CF =，四边形DCFE 是平行四边形，则图中阴影部分的面积为（ ）．A ．8B ．6C ．4D ．310．如图，①②③④⑤五个平行四边形拼成一个含30º内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为26cm 2，四边形ABCD 面积是19cm 2，则①②③④四个平行四边形周长的总和为（ ）A ．64cmB ．48cmC ． 36cmD ．24cm二、填空题（每小题3分，共24分）11.使式子4x -有意义的条件是 。