第 十三 讲 全等三角形(5)

第十三讲轨迹、直角三角形全等的判定知识点：一、轨迹的意义：我们有时把符合某些条件的所有点的集合叫做。

二、三条基本轨迹：（1）和线段两个端点距离相等的点的轨迹是这条线段的。

（2）在一个角的内部（包括顶点）且到角两边距离相等的点的轨迹是这个角的。

（3）到定点的距离等于定长的点的轨迹是以这个定点为圆心、定长为半径的。

三、交轨法作图的概念：利用轨迹相交进行作图的方法叫做。

四、直角三角形全等的判定方法：如果两个直角三角形的和对应相等，那么这两个直角三角形全等。

（简称“H.L”）备注：证明普通三角形全等的方法也适合证明直角三角形全等。

例1.作图并说明符合条件的点的轨迹（不要求证明）（1）经过已知线段AB的两个端点的圆的圆心的轨迹。

（2）以已知线段AB为腰的等腰三角形ABC的顶点C的轨迹。

例2.电信部门要修建一座电视信号发射塔，如图，按照设计要求，发射塔到两个城镇A,B 的距离必须相等，到两条高速公路m,n的距离也必须相等，发射塔P应该修建在什么位置？例3.已知：如图△ABC中，BD⊥AC，CE⊥AB，BD、CE交于O点，且BD=CE 求证：OB=OC.例4.已知：Rt △ABC 中，∠ACB 是直角，D 是AB 上一点，BD=BC ，过D 作AB 的垂线交AC 于E ，求证：CD ⊥BE例5. 如图，在△ABC 中，AB ⊥AC ，且AB ＝AC ，点E 在AC 上，点D 在BA 的延长线上，AD ＝AE ．求证：（1）△ADC ≌△AEB ；（2）BE=CD ．课堂练习：1．使两个直角三角形全等的条件是（ ）A ．一个锐角对应相等B ．两个锐角对应相等C ．一条边对应相等 D.一直角边和斜边对应相等2．如图，BE 和CF 是△ABC 的高，它们相交于点O ，且BE=CD ，则图中有 对全等三角形，其中能根据“HL ”来判定三角形全等的有 对． 3．如图，有两个长度相同的滑梯（即BC ＝EF ），左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，则∠ABC ＋∠DFE ＝___________度．（第5题）ABCE D （第2题）O4. 如图，AD 为△ABC 的高，E 为AC 上一点，BE 交AD 于点F ，且有BF=AC ，FD=CD ．求证：BE ⊥AC ．5. 如图，△ABC 中，D 是BC 边的中点, AD 平分∠BAC ，DE ⊥AB 于E ，DF ⊥AC 于F .求证：（1）DE= DF ；（2）∠B =∠C6. 已知：如图，AC ⊥BC ，AD ⊥BD ，AD=BC ，CE ⊥AB ，DF ⊥AB ，垂足分别是E 、F求证：CE=DF.A BCE FABCE F课后练习：1.到∠AOB的两边距离相等的点的轨迹是。

13.5逆命题与逆定理1互逆命题与互逆定理(第1课时)一、基本目标1．理解逆命题与逆定理的意义，会写出一个命题的逆命题．2．会判断定理的逆命题的真假．二、重难点目标【教学重点】会写出一个命题的逆命题，会判断定理的逆命题的真假．【教学难点】写出一个命题的逆命题．环节1自学提纲，生成问题【5 min阅读】阅读教材P92～P93的内容，完成下面练习．【3 min反馈】一、互逆命题1．命题“两直线平行，内错角相等”的条件是两直线平行，结论是内错角相等．2．命题“内错角相等，两直线平行”的条件是内错角相等，结论是两直线平行．3．在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题．如果把其中一个命题叫做原命题，那么另一个命题就叫做它的逆命题．二、互逆定理1．“两直线平行，内错角相等”的逆命题是内错角相等，两直线平行．2．“对顶角相等”的逆命题是相等的角是对顶角．3．如果一个定理的逆命题也是定理，那么这两个定理叫做互逆定理，其中的一个定理叫做另一个定理的逆定理．环节2合作探究，解决问题活动1小组讨论(师生互学)【例题】写出下列各命题的逆命题，并判断其逆命题是真命题还是假命题，若是假命题，请举出一个反例说明．(1)两直线平行，同旁内角互补；(2)在同一平面内，垂直于同一条直线的两直线平行；(3)相等的角是内错角；(4)有一个角是60°的三角形是等边三角形．【互动探索】(引发学生思考)什么是逆命题？怎样举反例？【解答】(1)逆命题：同旁内角互补，两直线平行．是真命题．(2)逆命题：在同一平面内，如果两条直线平行，那么这两条直线垂直于同一条直线．是真命题．(3)逆命题：内错角相等．是假命题．反例：如图，∠1与∠2是内错角，但不相等．(4)逆命题：等边三角形有一个角是60°.是真命题．【互动总结】(学生总结，老师点评)说明命题为假命题的反例即为符合该命题条件而不符合该命题结论的例子，如(3)小题中的例子．活动2巩固练习(学生独学)1．下列命题的逆命题是真命题的是(C)A．全等三角形的周长相等B．对顶角相等C．等边三角形的三个角都是60°D．全等三角形的对应角相等2．写出“全等三角形的面积相等”的逆命题：面积相等的三角形全等．3．写出命题“有两角互余的三角形是直角三角形”的逆命题并证明．解：逆命题：直角三角形的两锐角互余．已知：在△ABC中，∠C＝90°.求证：∠A＋∠B＝90°.证明：∵∠A＋∠B＋∠C＝180°，∠C＝90°，∴∠A＋∠B＝90°，即∠A与∠B互余．环节3课堂小结，当堂达标(学生总结，老师点评)请完成本课时对应练习！2线段垂直平分线(第2课时)一、基本目标1．掌握线段垂直平分线的性质定理和判定定理．2．能灵活运用线段垂直平分线的性质定理和判定定理解题．二、重难点目标【教学重点】线段垂直平分线的性质定理和判定定理．【教学难点】灵活运用线段垂直平分线的性质定理和判定定理解题．环节1自学提纲，生成问题【5 min阅读】阅读教材P94～P95的内容，完成下面练习．【3 min反馈】1．如图，△ABC和△A′B′C′关于直线MN对称，点A′、B′、C′分别是点A、B、C的对称点，猜想一下线段AA′、BB′、CC′与直线MN有什么关系？解：AA′、BB′、CC′与直线MN垂直平分．2．线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等．3．线段垂直平分线的判定定理：到线段两端距离相等的点在线段的垂直平分线上．4．下列条件中，不能判定直线MN是线段AB的垂直平分线的是(C)A．MA＝MB，NA＝NBB．MA＝MB，MN⊥ABC．MA＝NA，MB＝NBD．MA＝MB，MN平分∠AMB5．三角形的三条垂直平分线交于一点．环节2合作探究，解决问题活动1小组讨论(师生互学)【例1】如图，在△ABC中，AB＝AC＝20 cm，DE垂直平分AB，垂足为点E，交AC 于点D.若△DBC的周长为35 cm，求BC的长．【互动探索】(引发学生思考)已知AB、AC的长和△DBC的周长，要求BC的长，先求什么？再求什么？【解答】∵DE垂直平分AB，∴AD＝BD.∵△DBC的周长＝BC＋BD＋CD＝35 cm，∴BC＋AD＋CD＝35 cm.∵AC＝AD＋DC＝20 cm，∴BC＝35－20＝15 (cm)．【互动总结】(学生总结，老师点评)利用线段垂直平分线的性质定理，可以实现线段之间的相互转化，从而求出未知线段的长．【例2】如图所示，在△ABC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，试说明AD与EF的关系．【互动探索】(引发学生思考)先利用角平分线的性质得出DE ＝DF ，再证△AED ≌△AFD ，从而找出AD 与EF 的关系．【解答】AD 垂直平分EF .证明如下： ∵AD 平分∠BAC ，DE ⊥AB ，DF ⊥AC ， ∴DE ＝DF ，∠AED ＝∠AFD ＝90°.在Rt △ADE 和Rt △ADF 中，∵⎩⎪⎨⎪⎧AD ＝AD ，DE ＝DF ，∴Rt △ADE ≌Rt △ADF ， ∴AE ＝AF ，∴A 、D 均在线段EF 的垂直平分线上，即直线AD 垂直平分线段EF .【互动总结】(学生总结，老师点评)证明线段的垂直平分线可以用定义法，也可用线段垂直平分线的判定定理．活动2 巩固练习(学生独学)1．三角形中，到三个顶点距离相等的点是( D ) A ．三条高线的交点 B ．三条中线的交点 C ．三条角平分线的交点 D ．三边垂直平分线的交点2．如图，△ABC 的两边AC 和BC 的垂直平分线分别交AB 于D 、E 两点，若AB 边的长为10 cm ，则△CDE 的周长为( A )A ．10 cmB ．20 cmC ．5 cmD ．不能确定3．如图，直线CD 是线段AB 的垂直平分线，P 为直线CD 上的一点，已知线段P A ＝5，则线段PB的长度为(B)A．6 B．5C．4 D．34．小明做了一个如图所示的风筝，其中EH＝FH，ED＝FD，小明说不用测量就知道DH是EF的垂直平分线．其中蕴含的道理是到线段两端距离相等的点在线段的垂直平分线上．活动3拓展延伸(学生对学)【例3】如图，在四边形ABCD中，AD∥BC，E为CD的中点，连结AE、BE，BE⊥AE，延长AE交BC的延长线于点F.求证：(1)FC＝AD；(2)AB＝BC＋AD.【互动探索】(1)根据AD∥BC可知∠ADC＝∠ECF，再根据E是CD的中点可证得△ADE≌△FCE，从而证得结论；(2)根据线段垂直平分线的性质判断出AB＝BF即可．【证明】(1)∵AD∥BC，∴∠ADC＝∠ECF.∵E是CD的中点，∴DE＝EC.又∵∠AED＝∠CEF，∴△ADE≌△FCE，∴FC＝AD.(2)∵△ADE≌△FCE，∴AE＝EF，AD＝CF.∵BE⊥AE，∴BE是线段AF的垂直平分线，∴AB＝BF＝BC＋CF.∵AD＝CF，∴AB＝BC＋AD.【互动总结】(学生总结，老师点评)本题是线段垂直平分线与全等三角形的综合应用，证得△ADE≌△FCE是解题的关键．环节3课堂小结，当堂达标(学生总结，老师点评)请完成本课时对应练习！3角平分线(第3课时)一、基本目标1．掌握角平分线的性质定理和判定定理．2．能灵活运用角平分线的性质定理和判定定理解题．二、重难点目标【教学重点】角平分线的性质定理和判定定理．【教学难点】灵活运用角平分线的性质定理和判定定理解题．环节1自学提纲，生成问题【5 min阅读】阅读教材P96～P98的内容，完成下面练习．【3 min反馈】1．角平分线上的点到角两边的距离相等．2．角的内部到角两边距离相等的点在角的平分线上．3．三角形的三条角平分线交于一点，这个交点一定在三角形内部，它到三角形三边距离相等．4．如图，AD⊥DC，AB⊥BC，若AB＝AD，∠DAB＝120°，则∠ACB的度数为30°.环节2合作探究，解决问题活动1小组讨论(师生对学)【例1】如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于点D，如果AC ＝3 cm，那么AE、AC、DE这三条线段之间有怎样的数量关系？请说明理由．【互动探索】(引发学生思考)根据“角平分线上的点到角两边距离相等”可得DE＝CE，从而可知AE 、AC 、DE 之间的数量关系．【解答】AE ＋DE ＝AC ＝3 cm.理由如下： ∵∠ACB ＝90°，BE 平分∠ABC ，DE ⊥AB ， ∴DE ＝CE ，由图可知，AC ＝AE ＋CE ， 所以AC ＝AE ＋DE ＝3 cm.【互动总结】(学生总结，老师点评)本题考查了“角平分线上的点到角两边距离相等”的性质，熟记性质是解题的关键．【例2】如图，P 是OC 上一点，PD ⊥OA 于点D ，PE ⊥OB 于点E ，F 、G 分别是OA 、OB 上的点，且PF ＝PG ，DF ＝EG .求证：OC 是∠AOB 的平分线．【互动探索】(引发学生思考)要证OC 是∠AOB 的平分线，需证PD ＝PE ，而通过证Rt △PFD ≌Rt △PGE 即可得PD ＝PE .【证明】∵PD ⊥OA ，PE ⊥OB ， ∴∠PDF ＝∠PEG ＝90°.在Rt △PFD 和Rt △PGE 中，∵⎩⎪⎨⎪⎧PE ＝PG ，DF ＝EC ，∴Rt △PFD ≌Rt △PGE (H.L.)， ∴PD ＝PE .∵P 是OC 上一点，PD ⊥OA ，PE ⊥OB ， ∴OC 是∠AOB 的平分线．【互动总结】(学生总结，老师点评)根据三角形全等得到PD ＝PE ，这样就把已知条件和角平分线的判定定理联系起来了．活动2巩固练习(学生独学)1．如图所示，在Rt△ACB中，∠C＝90°，AD平分∠BAC，若BC＝16，BD＝9，则点D到AB的距离是(D)A．10 B．9C．8 D．72．如图，直线l、l′、l″表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有(D)A．一处B．二处C．三处D．四处3．如图，∠B＝∠C＝90°，M是BC的中点，且DM平分∠ADC.(1)求证：AM平分∠DAB；(2)试说明线段DM与AM有怎样的位置关系？并证明你的结论．(1)证明：过点M 作ME ⊥AD 于点E . ∵DM 平分∠ADC ，∠C ＝90°，ME ⊥AD ， ∴MC ＝ME . ∵M 是BC 的中点， ∴BM ＝MC ＝ME .又∵∠B ＝90°，ME ⊥AD ， ∴AM 平分∠DAB .(2)解：AM ⊥DM .证明如下： ∵∠B ＝∠C ＝90°， ∴AB ∥DC ，∴∠BAD ＋∠ADC ＝180°.∵AM 平分∠DAB ，DM 平分∠ADC ， ∴∠MAD ＝12∠BAD ，∠MDA ＝12∠ADC ，∴∠MAD ＋∠MDA ＝90°， ∴∠AMD ＝90°， ∴AM ⊥DM .环节3 课堂小结，当堂达标 (学生总结，老师点评)请完成本课时对应练习！。

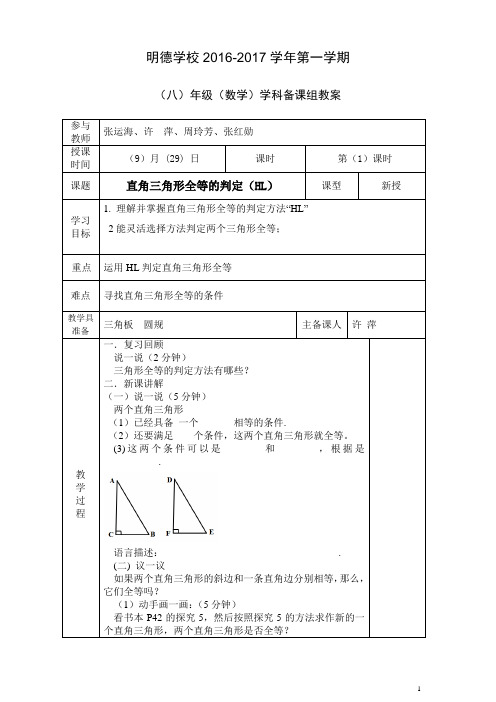
明德学校2016-2017学年第一学期（八）年级（数学）学科备课组教案参与教师张运海、许萍、周玲芳、张红勋授课时间（9）月 (29) 日课时第（1）课时课题直角三角形全等的判定（HL）课型新授学习目标1. 理解并掌握直角三角形全等的判定方法“HL”2能灵活选择方法判定两个三角形全等；重点运用HL判定直角三角形全等难点寻找直角三角形全等的条件教学具准备三角板圆规主备课人许萍教学过程一．复习回顾说一说（2分钟）三角形全等的判定方法有哪些？二．新课讲解（一）说一说（5分钟）两个直角三角形（1）已经具备一个_______相等的条件.（2）还要满足____个条件，这两个直角三角形就全等。

(3)这两个条件可以是________和________，根据是_________.语言描述：___________________________________. (二) 议一议如果两个直角三角形的斜边和一条直角边分别相等，那么，它们全等吗？（1）动手画一画：（5分钟）看书本P42的探究5，然后按照探究5的方法求作新的一个直角三角形，两个直角三角形是否全等？（2）得出结论：斜边和一条直角边分别相等的两个直角三角形全等（可以简写为“斜边、直角边”或“HL ” （3）几何语言（三）练一练（5分钟）如图,AC ⊥BC,BD ⊥AD ，垂足分别为C 、D, AC=BD. 求证：BC ﹦ADBA CD三、课堂检测(5分钟)1.如图，∠ABD=∠ACD=90°，BD=CD 求证： ∠BAD=∠CADDCBAC'B'A'C BA第1题 第2题 2.如图，已知在Rt △ABC 与Rt △A'B'C'中∠C=∠C'=90°,AC=A'C',BC=B'C',则Rt △ABC 与Rt △A'B'C'全等的根据是( ) A 、 HL B 、 ASA C 、 SAS D 、 SSA3.课本43页练习第2题课外作业学习辅导第27页： 第5课时课后 反思。