第六节测不准关系
- 格式:ppt
- 大小:75.51 KB
- 文档页数:4

《原子物理学》教学大纲课程性质:专业基础课程先修课程:力学、电磁学、光学总学时:60 学分:3.5理论学时:60 实验学时:实验纳入《近代物理实验》课程开课学院:物电学院适用专业:物理学大纲执笔人:凤尔银大纲编写时间:2007年元月教研室主任审核:凤尔银教学院长审定:一、说明1、课程的性质、地位和任务原子物理学为物理学专业的必修课,是物理学专业的一门重要基础课。
本课程的主要目标和任务是:以原子结构为中心,以实验事实为线索,了解原子和原子核层次的物质结构及运动和变化规律,揭示宏观现象与规律的本质。
介绍有关问题所需要的量子力学基本概念,阐述物质微观结构三个层次的物理过程、研究方法,培养创新思维。
使学生对物质世界有更深入的认识,获得在本课程领域内分析和处理一些最基本问题的初步能力。
2、课程教学的基本要求通过本课程的学习,力图使学生初步建立描述微观世界的物理图像,理解适应微观世界的新概念,掌握处理微观世界物理问题的新方法,为后续《量子力学》课程的学习打下一定的基础;本课程涉及知识面较广,讲授时要针对实际情况,对内容加以选择,尽量做到详略得当,让学生既能较全面,又能较深刻地理解和掌握。
课程教学中,要结合有关内容,适当将一些背景材料和物理学史引入教学,以利于加深对新知识的理解和把握。
同时,通过介绍二十世纪初物理学家,在解决经典物理学应用于微观粒子体系遇到困难时的大胆探索、勇于出新的思想脉络,使学生受到创新意识和创新精神方面的熏陶和教育,提高学生分析问题和解决问题的能力。
使学生了解物理学家对物质结构的实践——理论——再实践的认识过程,引导学生养成严谨、活跃、创新的思维方式和学习方法。
3、本课程的重点与难点重点:培养学生初步建立微观世界的物理图像,掌握描述原子结构的基本概念、基本原理和方法;掌握认识原子世界的基本规律,以便从思想和方法上做好准备,为今后学习量子力学打下基础。
难点:由于原子物理学课程是学生第一次系统的接触到的近代物理学的理论体系,它的许多概念、观点与学生长期形成的观念不相符合。

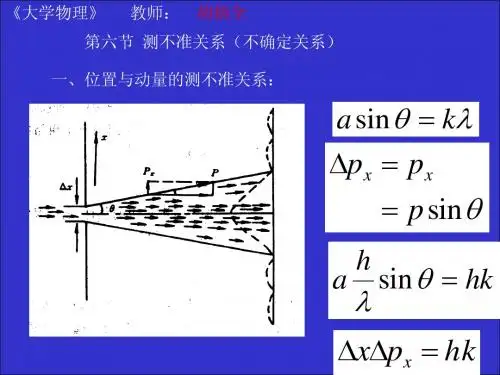
(图16.6a )一束水珠穿过单缝(图16.6b )一束光子穿过单狭缝§16.6 测不准原理在本教程即将结束时,再次强调微观粒子与宏观质点的不同特点.(一)宏观质点的位置坐标与动量的关系在经典力学中,一个宏观质点的运动状态,可用位置坐标、动量,以及运动轨道等概念来描述.已知一质点在某时刻的坐标和动量,以及它所在力场的性质,则可按牛顿运动定律求得它在任一时刻的坐标和动量,以及任一段时间内的运动轨道.看一个简单的例子,如(图16.6a ),设有一高压水枪,射出一束水注,沿着y 轴方向,垂直投射在一个宽为b 的单缝中.这束水珠穿过单缝后,冲击在垂直于y 轴的屏上Q 0点附近.(假设不计水珠所受重力,以及被缝的边缘阻挡的水珠).当缝的宽度b 缩小一些时,通过缝的水珠的位置总的来说都是互相接近一些的.当缝的宽度b 增大一些时,穿过缝的水珠的位置却是互相离开一些的.但是,不论缝中水珠的位置互相接近或离开,对它们的动量的大小和方向不会有影响.这是我们的常识可以得出的结论,也与经典力学一致.(二)光子的位置坐标与动量的关系如(图16.6b ),设有一束光子穿过宽度为a 的单狭缝.在屏上相当宽的范围,将出现衍射条纹.这就是第三篇§12.5所说的光的单缝衍射条纹,这是光的波粒二象性应有的结果.如(图16.6b ),设Q 1与Q -1为此单缝衍射条纹的第一级极小位置,则Q 1至Q -1范围内便是中央亮纹的位置.光波的大部分能量投射在中央亮纹,也就是说,穿过狭缝的光子,大多数到达中央亮纹.设Q 1所对应的偏角为1ϕ,此束光子的波长为λ,则按单缝衍射公式可得如下关系:〔单缝衍射第一级极小位置的偏角1ϕ〕 a sin 1ϕ=λ (16.6.1)此式表明:a 值较小,则1ϕ值较大.也就是说,当光子通过狭缝时,彼此的位置比较靠近,则它们射到屏上的分散范围就比较大.从光子的动量变化,也可看出它们的衍射情况.在进入狭缝时,光子的动量都等于p ,方向都与y 轴一致,即y p p=、0p x =.穿过狭缝射向中央亮纹的光子,它们的方向分散在偏角-1ϕ到1ϕ范围内.也就是说,从狭缝穿出的光子,它们的动量的x 轴分量x p ,其数值的分布范围为0≤x p ≤p sin 1ϕ.光子的x p 值之间的最大差值△x p =p sin 1ϕ-0=p sin 1ϕ.此△x p 称为x p 的测不准量.如果考虑到还有光子会射到中央亮纹以外,则x p 的测不准量△x p 的关系式应写成:△x p ≥p sin 1ϕ.光子在狭缝中的位置坐标x 之间的最大差值△x ,显然等于缝宽a .也就是说,x 的测不准量△x=a .⎥⎦⎤⎢⎣⎡∆∆x p x 与测不准量 λ=ϕ≥∆⋅∆ϕ≥∆=∆p s i np p x s i n p p ,x 1x 1x a a )3.6.16()2.6.16( 最后一式用到(16.6.1)式:a sin 1ϕ=λ.按德布罗意公式(16.1.5),p=h/λ,可将(16.6.3)式写成:〔△x 与△x p 的测不准关系〕 △x ·△x p ≥p λ=h (16.6.4)现在强调一下这个测不准关系式的重要意义.此式表明,△x 很小时,△x p 很大,△x 与△x p 的乘积必定大于常量h .这就是说,如果缩小狭缝的宽度a ,使得穿过狭缝光子的位置测不准量△x 缩小,则必定使得这些光子的动量分量测不准量△x p 增大.简单地说,光子的坐标x 测得越准确.它的动量分量x p 就测得越不准确.反过来,如果增大狭缝的宽度a ,按(16.6.1)式可知,a 增大,则1ϕ、sin 1ϕ、x p 和△x p 都会缩小.a 增大,△x=a 也增大.这表明,光子的动量分量x p 测得准确,它的坐标x 就测得不准确.(三)海森伯的测不准关系(或称不确定关系)如果用电子束代替上述的光子束,令电子束通过相应的单狭缝,也可测到电子波的单狭缝衍射条纹,也可从电子的波粒二象性关系式,导出测不准关系式(16.6.4).由于微观粒子都具有波粒二象性,因此,测不准关系式(16.6.4)对所有微观粒子都适用.比较(图16.6a )与(图16.6b )可知,测不准关系式(16.6.4)不适用于宏观质点.对宏观质点,可同时准确测定它的位置坐标与动量,可应用轨道的概念描述它的运动.宏观质点不具有波粒二象性,它的运动可用经典力学描述.测不准关系式(16.6.4)乃是只讲数量级的估算式子,式子中的普朗克常量可用h ,也可用 =h/2π表示.这个关系式不限于单狭缝衍射的简单例子,它可推广于微观粒子的一般运动情况:⎢⎣⎡测不准关系微观粒子的16.6.5) 这就是1927年初,德国年青物理学家海森堡提出的测不准原理❶.有的课本称上式为不确定度关系.(四)微观粒子的能量与时间的测不准关系设想有一束微观粒子,沿x 轴自由运动,其动量为p .按测不准关系式(16.6.5)可知:△x ·△x p ≥ , x p p = (16.6.6)设此自由微粒的速度v <<c ,则其能量E 与动量p 的关系为:v <<c ,E=m v 2/2=p 2/2m ,∴△E=p △p/m=v △p .此式代入(16.6.6)式得:△x ·△p=△x ·△E/v =△t ·△E ≥〔微观粒子的能量与时间的测不准关系〕△E ·△t ≥ (16.6.7)这个结论表明,微观粒子的能量与时间不可能同时进行准确的测量.比方说,氢原子在激发态的时间为10-8秒,可认为它的时间测不准量△t=10-8秒.代入(16.6.7)式便可得到❶《英汉物理学词汇》367页,科学出版社1975年版.它的能量测不准量△E:△E≥ /△t=1.05×10-34/10-8=1.05×10-26焦耳.这就是说,能量测不准量△E大于10-26焦.在(表15.3a)已列出,可见光光子的能量约为10-19焦.因此,氢原子发出的光谱线必定有一定的宽度.这结论已为实验所证实.(五)量子力学发展的艰辛历程❶❷1900年,普朗克为了从理论上说明热辐射的实验结果,提出了能量子的假设.这是牛顿以后自然哲学所经受的最巨大、最深刻的变革.从此以后人们不断地、严谨地探索微观粒子的客观性质.微观粒子的波粒二象性,它的波函数可表达几率密度,它的波动方程可导出四个量子数,它的位置坐标与动量、它的能量与时间都具有测不准关系,这一些主要结论互相一致,并都能纳入系统严密的量子力学中去.但是由于经典物理的辉煌成就,经典概念的深入人心,量子力学的发展过程是相当艰辛的.普朗克提出量子假设后,徘徊观望十几年,他企图把量子假设与经典理论调和起来,他首先起来反对爱因斯坦勇敢地推广量子理论.爱因斯坦是20世纪物理学两大重要发现(量子论与相对论)的元勋,是最受人们尊重的天才之一.但他与玻尔对量子力学的争论,是物理学史上持续时间最长、争论最激烈和最富有哲学意义的争论之一.玻尔是哥本哈根(丹麦首都)学派的领导人,他身边集结了一批极有才华的年青人,例如对波函数提出统计解释的玻恩,对微粒运动提出测不准关系的海森伯等.玻尔曾经提醒爱因斯坦,位置与动量、能量与时间的测不准关系,与他的相对论所说的时间要随运动系统而确定一样,都是人们不熟悉的客观规律.然而,爱因斯坦仍然认为一种完备的理论应该是决定论的,不应该用几率和测不准关系来表达微粒的运动.他多次设计理想实验,想证明测不准原理有错误,可是这些实验却证明测不准原理并无错误.由于对大多数学者接受的、哥本哈根学派量子理论的解释深感不满,爱因斯坦晚年,将自己置身于物理学发展的主流之外,一个人孤独而又艰难的跋涉着.哥本哈根学派的量子理论解释,也不是完美无缺的.物理学总要不断地向前发展,人类对自然规律的认识过程,总是不平坦的.〔例题16.6A〕试比较电子和质量为10g的子弹,在确定它们的位置时的不准量△x e和△x b.假定它们都沿x方向、以v=200m·s-1的速度运动,速度的测量误差在0.01%以内.〔解〕(1)由于v<<c,可知电子的质量m e=9.1×10-31kg.按题意,此电子的速度不准量△v=0.01%×v =10-4×200=2×10-2m/s,此电子的动量不准量△e p=m e△v=18.2×10-33kg·m/s.△v比v小得多,△e p也比e p=m e v小得多.代入测不准关系式(16.6.5)可得:△x e≥ /△e p=1.05×10-34/18.2×10-33=5.77×10-3m.已知原子的大小为10-10m数量级,上述电子的位置测不准量△x e比原子约大107倍.可知此电子的△e p较小,△x e就较大.此电子的动量测得准,位置就测不准.(2)按题意所述子弹的动量测不准量△b p可计算如下:❶杨建邺、止戈编著《杰出物理学家的失误》113—115,136—142页,1986年版.❷周世勋编《量子力学》399—405页,1961年版.△b p=m b△v=10×10-3×2×10-2=2.0×10-4kg·m/s.按测不准关系式(16.6.5),可求得此子弹的位置测不准量△x b:p 1.05×10-34/2×10-4=5.25×10-31m.△x b≥ /△b可知此子弹的△x b与△b p都很小,子弹的x b与b p可同时准确地测量.子弹是宏观物体,不具有波粒二象性,不受微观粒子测不准关系式(16.6.5)的限制.〔例题16.6B〕已知原子核线度的数量级为10-14米.假设电子被束缚在原子核内,试应用测不准关系估算此电子的动能有多大?〔解〕电子如果在原子核内,电子的位置不准量可认为是△x=10-14米.按照测不准关系式(16.6.5),此电子的动量不准量△p≥h/△x,即△p≥h/△x=6.63×10-34/10-14=6.63×10-20千克·米/秒.此电子的动量p不应小于△p,即p≥△p≥6.63×10-20千克·米/秒.按狭义相对论公式(见第一编〔附录4F〕)有:总能ε2=c2p2+20E,动能E k=ε-E0.由于cp≥3×108×6.63×10-20=1.99×10-11焦.此电子的静能E0=m0c2=9.1×10-31×9×1016=8.22×10-14焦.此静能E0远小于cp值,因此可略去E0,求得此电子的动能E k:E k=ε=cp≥1.99×10-11焦=124兆电子伏特.已知氘核的结合能为△E D=2.23兆电子伏特❶.上述电子的动能E k远大于△E D值,此电子会把氘核打碎.可知把电子关闭在一些原子核中是不可能的.❶程守洙、江之永主编《普通物理学》第三册(第三版)373—375页,1979年版.。



不确定关系(测不准关系)的表述和含义不确定关系(测不准关系)的表述和含义摘要:介绍了测不准关系的一些不同的表述和证明方法,对其中关于这一原理的认同和有争议的问题进行了比较与分析。
关键词:测不准关系;不确定度;量子理论;统计解释引言测不准关系是由量子力学基茌原理导出的一个重要推论,它是量子力学的一个基本原理,表明一个微观粒子的某些成对的物理量不可能同时具有确定的数值,例如位置与动量、时间和能量。
它反映了自然界的客观规律, 反映了微观粒子的波粒二象性的基本属性它在量子力学中占有重要的地位。
量子力学诞生至今约有80年了,作为一门基础理论已经相当成熟,在指导人类文明进步和学科发展方面发挥着重要的作用;但是,对量子力学基本理论的解释却一直存在着不同意见的争论,关于测不准关系的理解问题是争论的焦点之一。
本文对其中一些主要的有争议问题进行简要的介绍,并加以讨论。
1 几种主要的表述和证明方法测不准关系是海森堡在1927年提出的,他设想一种使用波长很短的γ射线的显微镜来最大限度地精确测定电子的位置,这种测量,依靠的是光子被电子的散射[康普顿(compt)散射。
海森堡在题为“关于最子理论的动力学和力学的直观内容”的论文中说[1]:“当测定…电子?位置的瞬间,也正是光产被电子散射的瞬问,电子的动量产生一个不连续的改变。
当所用的光的波长越小,即位置测定得越精确,这一改变就越大。
因此,在知道电子位置的瞬间,它的动量只能了解到对应于那一不连续改变的大小的程度。
于是,位置测定得越精确,动量就知道得越不精确,反之亦然。
在这种情况下,我们看到方程pq—qp=-ih的一种直接的物理解释。
这就是在文献中第一次出现的关于测不准关系的表述。
1929年,罗伯逊(Robertson)[2]在一篇短文中首次证明:两个厄密算符的标准偏差之积绝不会小于它们的对易子的平均的绝对值之半。
证明如下:设A和B是任意的两个厄密算符,C是它们的对易子,令A1=A一,B1=B 一,A和B的标准偏差分别为△A=1/2和△B=1/2。


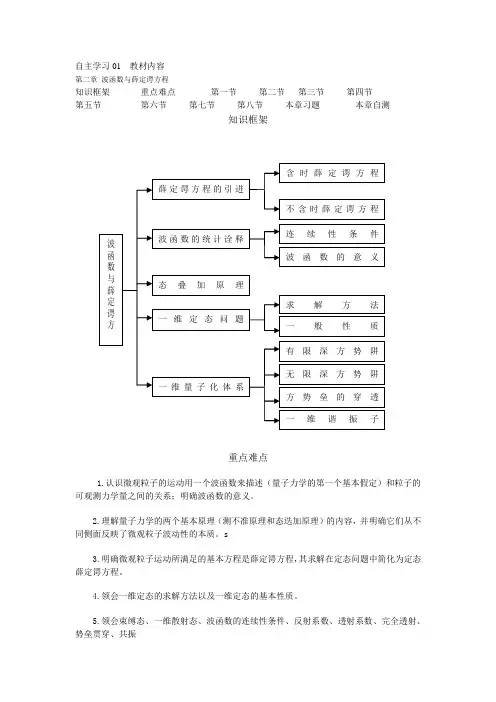
自主学习01 教材内容第二章波函数与薛定谔方程知识框架重点难点第一节第二节第三节第四节第五节第六节第七节第八节本章习题本章自测知识框架重点难点1.认识微观粒子的运动用一个波函数来描述(量子力学的第一个基本假定)和粒子的可观测力学量之间的关系;明确波函数的意义。
2.理解量子力学的两个基本原理(测不准原理和态迭加原理)的内容,并明确它们从不同侧面反映了微观粒子波动性的本质。
s3.明确微观粒子运动所满足的基本方程是薛定谔方程,其求解在定态问题中简化为定态薛定谔方程。
4.领会一维定态的求解方法以及一维定态的基本性质。
5.领会束缚态、一维散射态、波函数的连续性条件、反射系数、透射系数、完全透射、势垒贯穿、共振6.简明应用:定态薛定谔方程的求解、无限深方势阱、势、线性谐振子[本章教学难点]明确微观粒子运动所满足的基本方程是薛定谔方程,其求解在定态问题中简化为定态薛定谔方程。
掌握定态问题的求解方法,一维定态问题的一般性质。
2.1薛定谔方程的引进[本节要求]掌握一维势箱中粒子的薛定谔方程的求解方法及部分物理量的计算 [重点难点]1. 薛定谔方程的建立 2. 薛定谔方程的求解的过程 3. 物理量的计算 [本节内容]在经典力学中, 力学体系在t 时刻的状态由其坐标r 和相应的动量p 或速度v 决定, 其运动状态随时间的变化规律遵从牛顿运动方程. 如果我们知道力学体系的初始状态, 即可从牛顿方程求出体系在任一时刻的运动状态. 而微观粒子的量子态用波函数),(t r ψ描述,一旦),(t rψ确定,粒子的任何一个力学量的平均值以及它取各种可能测值的几率都完全确定, 那么量子态),(t rψ怎样随时间演化以及在各种具体情况下如何求出波函数呢? 薛定谔(E.Schrodinger,1926)提出的波动方程成功地解决了这个问题.下面从一个最简单的途径来引进这个方程.先讨论自由粒子情况.自由粒子能量与动量之间的关系是m p E 22=(1)由德布罗意关系,粒子的能量E 和动量p与跟粒子运动相联系的波的角频率ω和波矢k 之间有k p E==ω(2)也就是说,与具有一定能量E 和动量p 的粒子相联系的是平面单色波()()()()()Et r p i tr k i p ee t r -⋅-⋅==2/32/32121,ππψω (3)由此式可得ψψE t i =∂∂,ψψp i =∇-,ψψ222p =∇- (4)利用式(1),可以得出0)2()2(222=-=∇+∂∂ψψm p E m t i(5)对自由粒子的一般状态,波函数具有波包的形式,即许多平面单色波的叠加p d e p t r Et r p i 3)(23)()2(1),(-⋅⎰∞-∞+=ϕπψ (6)其中m p E 22=.可证 p d Ee p t i Et r p i 3)(23)()2(1-⋅⎰∞-∞+=∂∂ϕπψp d e p p Et r p i 3)(22322)()2(1-⋅⎰∞-∞+=∇-ϕπψ所以0)2)(()2(1)2(3)(22322=-∞-∞+=∇+∂∂-⋅⎰p d e m p E p m t i Et r p iϕπψ可见ψ仍满足方程(5) .所以式(5) 是自由粒子情况下波函数满足的方程.值得注意的是,如在经典能量动量关系(1)中作替换∇-=→∂∂→i p p ti E ˆ (7) 然后作用于波函数,就可得方程(5).其次考虑在势场)(r V中运动的粒子,按经典粒子的能量关系式 ()r V m p E+=22 (8)对上式作替换(7),并作用于波函数上,即得薛定谔方程),(ˆ),()(2),(22t r H t r r V m t r t i ψψψ≡⎥⎦⎤⎢⎣⎡+∇-=∂∂ (9)应该强调,薛定谔方程是量子力学最基本的方程,其地位与牛顿方程在经典力学中的地位相当,但这个方程是量子力学的一个基本假定,并不能从什么更根本的假定来证明它,其正确性,归根到底只能靠实践来检验. 另一方面, 薛定谔方程只含对时间的一阶导数, 为何可以描述波动过程呢? 在经典力学中, 波动方程022=∇-u a u tt 有周期性的解, 而热传导方程022=∇-u a u t 则描述不可逆过程, 没有周期性的解. 实际上,()t r k A u ω-⋅=cos 或()t r k A ω-⋅sin 都不满足热传导方程, 这是因为(以余弦函数为例)()()()πωωπωωωω+-⋅=-⋅-=∇⎪⎭⎫ ⎝⎛+-⋅=-⋅=∂∂=t r k A k t r k A k u t r k A t r k A t u u tcos cos 23cos sin 222 (10)这样t u 使相位增加23π,u 2∇使相位增加π,可见周期函数不可能满足热传导方程. 薛定谔方程虽然只含对时间的一阶导数, 但在t ∂∂ψ前面出现2πi e i =,正好使两者相位一致, 因而有周期性的解, 而且薛定谔方程中i 因子的出现, 使得波函数一般是复函数. 关于薛定谔方程的两点讨论: 1.定域的几率守恒对薛定谔方程(9)取复共轭,并注意到V V =*,得*)2(22ψψV m t i +∇-=∂∂-* (11))11()9(⨯-⨯*ψψ,得*)*(2*)*(2)*(2222ψψψψψψψψψψ∇-∇⋅∇-=∇-∇-=∂∂m mt i (12)令),(),(*t r t rψψρ= (13)*)ˆˆ*(21*)*(2ψψψψψψψψp pm m i j -=∇-∇-= (14)则式(12) 化为0=⋅∇+∂∂j t ρ(15)在空间闭区域V 中对上式积分,并根据高斯(Gauss )定理,得⎰⎰⋅-=S V s d j x d dt d 3ρ (16)上式左边代表在闭区域V 中找到粒子的总几率(或粒子数)在单位时间内的增加,而右边代表单位时间内通过封闭曲面S 而流入V 的几率(或粒子数).所以j具有几率流密度的意义.在式(16)中,让∞→V(全空间).对任何实际的波函数,是满足平方可积条件的,即∞→r 时,()εψ+-∝23r (0>ε).可证明,式(16)右边面积分趋于零.所以),(32=∞-∞+⎰x d t r dt d ψ从此式可见=∞-∞+⎰x d t r 32),( ψ常数 (与时间无关) (17)这与预期的一样,在全空间找到粒子的几率的总和应不随时间改变.波函数的归一化不随时间而改变.若在初始时刻波函数是归一化的,则在以后任何时刻都是归一化的.2.定态与能量本征值方程讨论一种常见而且极重要的情形,即势场V(r)不显含t.此时,薛定谔方程存在下列形式的解)()(),(t f r t rψψ= (18)代入薛定谔方程,分离变数后,得E r r V m r dt df t f i =⎥⎦⎤⎢⎣⎡+∇-=)()(2)(1)(122 ψψE 是既不依赖于t,也不依赖于r的常数,这样E i t f dt d -=)(ln所以iEt e t f -~)(.因此,得到形如下式的特解Etie r t r -=)(),(ψψ (19)其中)(rψ满足下列方程 ())()()(2ˆ22r E r r V m r H ψψψ=⎥⎦⎤⎢⎣⎡+∇-≡ (20)此式称为不含时间的薛定谔方程.形如(19)的波函数描述一个简谐振动,它的角频率是E =ω,按德布罗意关系,E 就是体系处于这个波函数所描述的状态时的能量.如果粒子初始时刻(t=0) 处于某一能量本征态()()r r Eψψ=0,,其中()r E ψ满足方程(20),若()r V 或Hˆ不显含时间t,容易验证()()()iEt r t r E -=exp ,ψψ满足含时薛定谔方程(9) ,并与初始时刻一样,()t r ,ψ也满足不含时薛定谔方程(20).也就是说,体系处于形如式(19)所描述的状态时,能量具有确定值.我们把这种具有确定能量值的状态称为定态,方程(20) 称为定态薛定谔方程.容易证明,粒子处于定态时,粒子在空间的几率密度()rρ、几率流密度()r j及任何不显含时间t 的力学量的平均值都不随时间而改变.数学上,把一个算符F ˆ作用于一个函数上而得到一个常数f 乘以该函数的方程,称为f 或算符F ˆ的本征方程,常数f 称为算符F ˆ的本征值.因此,定态薛定谔方程也称为能量或哈密顿算符H ˆ的本征值方程.设ψn 是体系哈密顿算符H ˆ的属于本征值E n 的本征函数,则体系的定态波函数为()()t iE n n ne r t r -=ψψ, (21)它也是含时薛定谔方程(9) 的特解,而含时薛定谔方程(9) 的一般解可表示为()()()t iE n n nn n n ne r c t r c t r -∑∑==ψψψ,, (22)它是若干定态波函数的叠加,按态叠加原理,当体系处于()t r , ψ态时,发现粒子处于()t r n ,ψ的几率为2nc .既然体系处于()t r ,ψ态时,其能量可以取各种不同的值,所以波函数(22) 不是定态波函数.在这种态下,粒子的几率密度()rρ和几率流密度()r j 都要随时间改变.除守恒量外,任何不显含时间t 的力学量的平均值也要随时间改变. 思考题1. 设()()()r c r c r E E 21210,ψ+ψ=ψ,问()0,r ψ是否为定态, 为什么? 求()t r , ψ. 答: ()0,r ψ不是定态.()()()t E iE t E iE e r c e r c t r 221121, ψ+ψ=ψ-.2. 计算r e ikr =ψ1和e ikr-=ψ2相应的几率流密度, 并由所得结果说明这两个波函数描述的是怎样传播的波.答:re r v mr k j 221==, 描述向外传播的球面波; r e r v j22-=, 描述向内传播的球面波.3. 粒子在一维势场中运动, 若所处的外场均匀但与时间有关, 即()()t V t x V =,,试用分离变量法求解一维薛定谔方程.答:()()⎥⎦⎤⎢⎣⎡+λ-μλ±⎰=ψt ds s V t i x ieAe t x 02,, 其中A 和λ为常数, 由归一化条件和初始条件确定.2.2 波函数的统计诠释[本节要求]认识微观粒子的运动用一个波函数来描述(量子力学的第一个基本假定)和粒子的可观测力学量之间的关系;波函数的平方给出了位置的测量结果;明确波函数的意义。

测量误差及不确定度的基础知识讲解测量误差及不确定度分析的基础知识物理实验是以测量为基础的。
测量可分为直接测量与间接测量,直接测量指无需对被测的量与其它实测的量进行函数关系的辅助计算而可直接得到被测量值的测量,间接测量指利用直接测量的量与被测量之间的已知函数关系经过计算从而得到被测量值的测量。
由于测量仪器、测量方法、测量环境、人员的观察力等种种因素的局限,测量是不能无限精确的,测量结果与客观存在的真值之间总是存在一定的差异,即存在测量误差。
因此分析测量中产生的各种误差,尽量消除或减小其影响,并对测量结果中未能消除的误差作出估计,给出测量结果的不确定度就是物理实验和科学实验中必不可少的工作。
为此我们必须了解误差的概念、特性、产生的原因及测量结果的不确定度的概念与估算方法等的有关知识。
误差的定义、分类及其处理方法一.误差的定义:测量结果与被测量的真值(或约定真值)之差叫做误差,记为:被测值的真值是一个理想的概念,一般说来真值是不知道的。
在实际测量中常用准确度高的实际值来作为约定真值,才能计算误差。
二.误差的分类及其处理方法:误差主要分为系统误差和随机误差。
系统误差:(1)定义:在同一被测量的多次测量过程中,绝对值和符号保持恒定或以可预知的方式变化的测量误差的分量。
(2)产生原因:① 仪器本身的缺陷或没按规定条件使用仪器而引起的误差(又称作仪器误差)例:电表的刻度不均匀---示值误差等臂天平的两臂实际不等---机构误差指针式电表使用前没调零---零位误差大气压强计未在标定条件下使用引起的系统误差等②测量所依据的理论公式本身的近似性、或实验条件不能达到理论公式的要求、或测量方法所带来的系统误差(又称作理论误差或方法误差)。
例:单摆运动方程小角度近似解引起的误差、伏安法测电阻时电表内阻引起的测量误差。
(3)分类及处理方法:根据误差的符号、绝对值确定与否分类如下:① 已定系统误差---绝对值和符号已经确定的系统误差分量,如零位误差、大气压强计室温下使用引起的误差、伏安法测电阻时电流表内接或外接引起的误差等;这类误差分量一般都要修正。

课程论文学院:物理电子工程学院专业:物理学年级: 2012级物理学班*名:***论文题目:测不准关系的理论推导成绩:2016 年 1 月 2 日目录摘要 (1)Abstract (1)1.引言 (1)2.历史发展 (1)3.测不准关系实验验证 (3)4.相关质疑 (3)5.意义 (4)5.1理论意义 (4)5.2现实意义 (4)6.总结 (4)参考文献 (4)测不准关系的理论推导学生姓名:李赵坤学号:20125041015学院:物理电子工程学院专业:物理学摘要:在量子力学里,测不准关系表明,粒子的位置与动量不可同时被确定,位置的不确定性与动量的不确定性遵守不等式。
一个微观粒子的某些物理量,如位置和动量,或方位角与动量矩,还有时间和能量等,不可能同时具有确定的数值,其中一个量越确定,另一个量的不确定程度就越大。
关键词:波粒二象性,不确定原理1引言测不准原理,又称“不确定性原理”、“不确定关系”,是量子力学中的一个重要关系,也是一个相当深奥的问题[1]。
表明粒子的位置与动量不可同时被确定,它反映了微观客体的特征。
即一个微观粒子的某些成对的物理量不可能同时具有确定的数值。
例如位置与动量、力一位角与角动量,其中一个量越确定,另一个量就越不确定。
它来源于物质的波粒二象性,测不准关系是从粒子的波动性中引出来的。
2历史发展1900年普朗克为了解释黑体辐射的实验规律提出能量量子化的概念;1905年爱因斯坦为了解释光电效应引入光子的概念;1913年玻尔提出的氢原子理论中运用光子概念构造了频率条件;1923年,德布罗意提出物质波假设:实物粒子与光相似,也具有波粒二象性。
1925年6月,维尔纳·海森堡发表论文《运动与机械关系的量子理论重新诠释》创立了矩阵力学。
旧量子论渐渐式微,现代量子力学正式开启[2]。
海森堡在论文里提出,只有在实验里能够观察到的物理量才具有物理意义,才可以用理论描述其物理行为。
海森堡抓住云室实验中观察电子径迹的问题进行思考。