判别分析实验报告 SPSS
- 格式:doc
- 大小:487.00 KB
- 文档页数:12


一、实验目的及要求:1、目的用SPSS软件实现判别分析及其应用.2、内容及要求用SPSS对实验数据利用Fisher判别法和贝叶斯判别法,建立判别函数并判定宿州、广安等13个地级市分别属于哪个管理水平类型。
二、仪器用具:三、实验方法与步骤:准备工作:把实验所用数据从Word文档复制到Excel,并进一步导入到SPSS 数据文件中,同时,由于只有当被解释变量是属性变量而解释变量是度量变量时,判别分析才适用,所以将城市管理的7个效率指数变量的变量类型改为“数值(N)”,度量标准改为“度量(S)”,以备接下来的分析。
四、实验结果与数据处理:表1 组均值的均等性的检验Wilks 的 Lambda F df1 df2 Sig.综合效率标准指数.582 23.022 2 64 .000 经济效率标准指数。
406 46.903 2 64 .000 结构效率标准指数.954 1。
560 2 64 .218 社会效率标准指数.796 8。
225 2 64 。
001 人员效率标准指数。
342 61。
645 2 64 。
000 发展效率标准指数。
308 71。
850 2 64 .000 环境效率标准指数。
913 3.054 2 64 .054表1是对各组均值是否相等的检验,由该表可以看出,在0。
05的显著性水平上我们不能拒绝结构效率标准指数和环境效率标准指数在三组的均值相等的假设,即认为除了结构效率标准指数和环境效率标准指数外,其余五个标准指数在三组的均值是有显著差异的。
表2 对数行列式group 秩对数行列式1 6 —33.4102 6 -33.1773 6 —40。
584汇聚的组内 6 -32.308 打印的行列式的秩和自然对数是组协方差矩阵的秩和自然对数。
表3 检验结果箱的 M 140.196F 近似。
2。
498df1 42df2 1990.001Sig. .000 对相等总体协方差矩阵的零假设进行检验。
以上是对各组协方差矩阵是否相等的Box’M检验,表2反映协方差矩阵的秩和行列式的对数值。
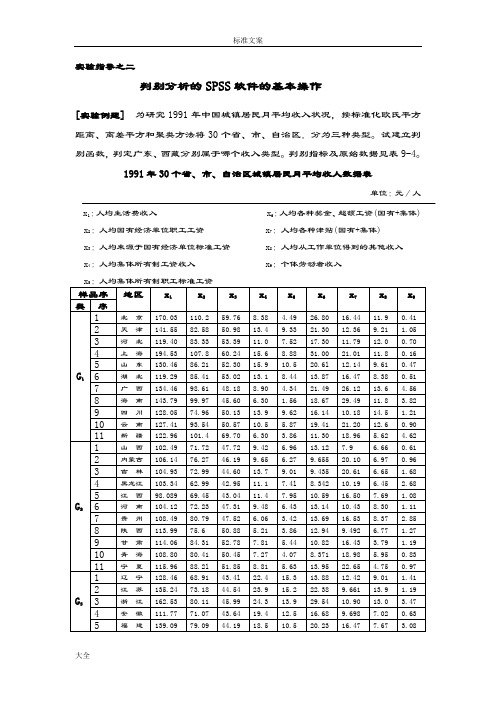
实验指导之二判别分析的SPSS软件的基本操作[实验例题]为研究1991年中国城镇居民月平均收入状况,按标准化欧氏平方距离、离差平方和聚类方法将30个省、市、自治区.分为三种类型。
试建立判别函数,判定广东、西藏分别属于哪个收入类型。
判别指标及原始数据见表9-4。
1991年30个省、市、自治区城镇居民月平均收人数据表单位:元/人 x1:人均生活费收入 x6:人均各种奖金、超额工资(国有+集体) x2:人均国有经济单位职工工资 x7:人均各种津贴(国有+集体)x3:人均来源于国有经济单位标准工资 x8:人均从工作单位得到的其他收入x4:人均集体所有制工资收入 x9:个体劳动者收入x5:人均集体所有制职工标准工资贝叶斯判别的SPSS操作方法:1. 建立数据文件2.单击Analyze→ Classify→ Discriminant,打开Discriminant Analysis 判别分析对话框如图1所示:图1 Discriminant Analysis判别分析对话框3.从对话框左侧的变量列表中选中进行判别分析的有关变量x1~x9进入Independents 框,作为判别分析的基础数据变量。
从对话框左侧的变量列表中选分组变量Group进入Grouping Variable 框,并点击Define Range...钮,在打开的Discriminant Analysis: Define Range对话框中,定义判别原始数据的类别数,由于原始数据分为3类,则在Minimum(最小值)处输入1,在Maximum(最大值)处输入3(见图2)。
选择后点击Continue按钮返回Discriminant Analysis主对话框。
图2 Define Range对话框4、选择分析方法✧Enter independent together 所有变量全部参与判别分析(系统默认)。
本例选择此项。
✧Use stepwise method 采用逐步判别法自动筛选变量。

【精品】多元统计分析--判别分析SPSS实验报告一、实验目的1.掌握判别分析的基本原理和应用方法;2.掌握SPSS软件进行判别分析的具体操作;3.通过一个实例,学习如何运用判别分析对指标进行判别。
二、实验内容三、实验原理1.判别分析基本原理:判别分析(Discriminant Analysis),是一种统计学中的分类技术,它是对变量进行归类的技术。
判别分析是用来确定一个对象或自变量集合属于哪一个预设类型或者组别的过程。
判别分析能够生成一个函数,将数据点映射到特定的类型上。
判别分析的应用领域非常广泛,主要应用于以下领域:(1)股票市场(预测股价的涨跌与时间、公司发展情况等因素的关系);(2)医学(区分疾病、患者状态等);(3)市场调查(确定客户类型、产品或服务喜好);(4)产业分析(区分有助于产品销售的市场决策因素);(5)经济学(预测月度或季度的经济指标)。
3.判别分析的主要应用步骤:(1)建立模型:首先选择和收集数据,将收集的数据分为训练集和测试集;(2)训练模型:使用训练数据建立模型;(3)评估模型:通过模型诊断来评估建立的模型的好坏;(4)应用模型:对新的数据建立模型并进行预测。
四、实验过程1. 上机操作:1)打开SPSS软件,加载数据文件;2)选择分类变量和连续变量;3)选择训练数据集;4)建立模型;5)预测实验数据集。
2. 操作步骤:SPSS分析的步骤如下:1)将数据输入SPSS软件,确保数据格式正确;2)选择Analyse- Classify- Discriminant;3)有两种不同的分类变量,单分类或多分类,如果你要解释一个特定的分类变量,选择单分类。
如果你不确定哪个分类变量最适合,请尝试不同的选项;4)选择两个或更个你认为与指定分类变量相关的连续变量;5)选择要用于判别分析的数据集;6)确定分类变量分类比率。
这可以在设置选项中完成;7)点击OK,开始进行分析;8)评估结果,包括汇总、判别函数、方差-方差贡献、判别矩阵;五、实验结果选取鸢尾花数据,经过训练,得到如下表所示的结果。


判别分析实验报告SPSS实验目的:判别分析(Discriminant Analysis)是一种经典的多元统计分析方法,用于解释和预测分类变量。
该实验旨在使用SPSS软件进行判别分析,探索一组变量对分类结果的贡献和预测能力。
实验步骤:1.数据收集:从一些公司的人力资源数据库中随机选择了200个员工作为样本,收集了以下变量:性别(男、女)、教育程度(本科、研究生、博士)、工龄(年)、绩效评分(0-5)、离职与否(是、否)。
2.数据清洗:检查数据中是否存在缺失值,并对缺失值进行处理。
删除离职与否变量中缺失值。
3.数据探索:使用SPSS进行描述性统计分析,了解样本的基本情况。
分别计算男女性别比例和各教育程度及离职状态的分布情况。
4. 变量选择:使用SPSS进行判别分析,将离职与否作为分类变量,性别、教育程度、工龄和绩效评分作为预测变量。
使用Wilks' Lambda检验选择预测变量,确定对分类结果的贡献。
5.判别函数计算:根据选择的预测变量,计算判别函数。
使用判别函数对样本进行分类,并计算分类结果的准确率。
实验结果:1.数据探索结果显示,样本中男女性别比例约为1:1,教育程度主要集中在本科和研究生,离职比例为14%。
2. 判别分析结果显示,Wilks' Lambda检验结果为0.632,p值小于0.05,说明选取的预测变量对分类结果有统计上显著的贡献。
3.计算得到的判别函数为D=-0.311(性别)+0.236(教育程度)+0.011(工龄)+0.585(绩效评分)。
4.使用判别函数对样本进行分类,分类准确率为81.5%。
其中,离职样本的分类准确率为75%,非离职样本的分类准确率为82%。
实验结论:通过判别分析实验,我们得出以下结论:1.性别、教育程度、工龄和绩效评分这四个变量对员工的离职与否有显著的预测能力。
2.预测变量中绩效评分对离职结果的贡献最大,说明绩效评分较低的员工更容易离职。
《SPSS统计软件应用》实验报告册20 - 20 学年第学期班级:学号:姓名:授课教师:实验教师:实验学时:实验组号:目录实验一SPSS的数据管理 (3)实验二描述性统计分析 (5)实验三均值检验 (6)实验四相关分析 (7)实验五因子分析 (8)实验六聚类分析 (11)实验七回归分析 (13)实验八判别分析 (14)实验一SPSS的数据管理一、实验目的1.熟悉SPSS的菜单和窗口界面,熟悉SPSS各种参数的设置;2.掌握SPSS的数据管理功能。
二、实验内容及步骤:1、定义spss数据结构。
下表是某大学的一个问卷调查,要求将问卷调查结果表示成spss可识别的数据文件,利用spss软件进行分析和处理。
练习:创建数据文件的结构,即数据文件的变量和定义变量的属性。
表1 大学教师基本情况调查表1.定义spss数据结构。
下表是某大学的一个问卷调查,要求将问卷调查结果表示成spss可识别的数据文件,利用spss软件进行分析和处理。
练习:创建数据文件的结构,即数据文件的变量和定义变量的属性。
实验步骤:(1)、打开定义变量的界面启动SPSS,进入主界面,单击图6-2所示的屏幕左下角的“Variable View”选项卡,打开定义变量的表格。
(2)、输入变量名,符合变量的命名规则在“Name”列的第一个单元格输入第一个变量名,如:“xm”。
(3)、确定变量类型,单击“Type”列的第一个单元格,如图6-3所示,SPSS的默认变量类型为数值型。
单击数值型变量后的“···”,弹出如图6-4所示的对话框,用户可以从该对话框中选择其他的变量类型。
(4)、设置字段值(5)、依次按要求输入完毕即可实验结果:实验分析:本实验,主要是按照要求一步一步来设置条件即可完满完成实验。
2 、高校提前录取名单的确定某高校今年对部分考生采取单独出题、提前录取的招生模式。
现有20名来自国内不同省市的考生报考该校,7个录取名额。
判别分析实验报告 SPSS一、实验目的判别分析是一种用于分类和预测的统计方法。
本次实验旨在通过使用 SPSS 软件,掌握判别分析的基本原理和操作流程,能够运用判别分析方法对实际数据进行分类,并对分类结果进行评估和解释。
二、实验数据本次实验使用的数据集包含了两个类别(类别 A 和类别 B)的样本,每个样本具有若干个特征变量,如年龄、收入、教育程度等。
数据集共有 200 个样本,其中类别 A 有 100 个样本,类别 B 有 100 个样本。
三、实验步骤1、数据导入首先,打开 SPSS 软件,选择“文件”菜单中的“打开”选项,将实验数据文件导入到 SPSS 中。
2、变量定义在 SPSS 数据视图中,对各个变量进行定义,包括变量名称、变量类型、变量标签等。
3、判别分析操作选择“分析”菜单中的“分类”子菜单,然后点击“判别分析”选项。
在弹出的判别分析对话框中,将类别变量选入“分组变量”框中,将其他特征变量选入“自变量”框中。
4、选择判别方法SPSS 提供了多种判别方法,如费希尔判别法、贝叶斯判别法等。
本次实验选择费希尔判别法。
5、模型评估在判别分析结果中,查看判别函数的系数、判别函数的显著性检验、分类结果的准确性等指标,以评估模型的性能。
四、实验结果与分析1、判别函数系数判别函数的系数反映了各个自变量对判别函数的贡献程度。
通过查看系数的大小和符号,可以了解各个变量在区分不同类别中的重要性。
例如,年龄变量的系数为正,说明年龄越大,越有可能属于某个类别;而收入变量的系数为负,说明收入越低,越有可能属于另一个类别。
2、判别函数的显著性检验通过对判别函数的显著性检验,可以判断判别函数是否能够有效地区分不同的类别。
如果检验结果显著,说明判别函数具有统计学意义,可以用于分类。
3、分类结果SPSS 会给出每个样本的分类结果,以及分类的准确性。
通过比较实际类别和预测类别,可以评估模型的分类效果。
如果分类准确性较高,说明模型能够较好地对样本进行分类;如果分类准确性较低,则需要进一步分析原因,可能是数据质量问题、变量选择不当或者判别方法不合适等。
实验课程名称: __多元统计分析--判别分析___准则判别归类,则可写成:⎪⎩⎪⎨⎧=>∈<∈),(),( ,),(),(,),(),(,21212211G X D G X D G X D G X D G X G X D G X D G X 当待判当当题目:表11.5的数据包含三种鸢尾的X2=萼片宽度与X4=花瓣的宽度的观测值。
对每种鸢尾有n1=n2=n3=50个观测值。
部分数据:第二部分:实验过程记录(可加页)(包括实验原始数据记录,实验现象记录,实验过程发现的问题等)散点图:图形→旧对话框→散点图,打开简单散点图子对话框;将想X2选入X轴变量,X4选入Y轴变量,将总体选入设置标记框中,点击确定。
判别分析:步骤:1、选择分析→分类→判别,打开判别分析子对话框。
2、选择变量“总体”,单击→,将其加入到分组变量栏中。
3、打开定义范围子对话框,最小值输入1,最大值输入3。
4、将变量“X2萼片宽度”、“X4花瓣的宽度”选入自变量栏中。
选择“一起输入自变量”的方法。
5、打开统计变量子对话框,选择均值、单变量ANOVA、Box’M、未标准化、组内协方差、分组协方差及总体协方差,单击继续。
6、打开分类子对话框,选择不考虑该个案时的分类,其余为默认值。
7、打开保存,选择所有的变量。
相关系数矩阵a总体萼片宽度X2 花瓣宽度X4合计萼片宽度X2 .190 -.122花瓣宽度X4 -.122 .581对数行列式总体秩对数行列式1 2 -6.4962 2 -6.1413 2 -5.189汇聚的组内 2 -5.583检验结果箱的M 52.832F 近似。
8.632df1 6df2 538562.769Sig. .000Wilks 的Lambda函数检验Wilks 的Lambda 卡方df Sig.1 到2 .038 477.868 4 .0002 .809 31.075 1 .000典型判别式函数系数函数1 2萼片宽度X2 -1.987 2.680花瓣宽度X4 5.477 .817(常量) -.494 -9.174非标准化系数组质心处的函数总体函数1 21 -5.958 .2152 1.265 -.6673 4.693 .452分类结果b,c总体预测组成员1 2 3 合计初始计数 1 50 0 0 502 0 49 1 503 04 46 50% 1 100.0 .0 .0 100.02 .0 98.0 2.0 100.03 .0 8.0 92.0 100.0 交叉验证a计数 1 50 0 0 502 0 48 2 503 04 46 50% 1 100.0 .0 .0 100.02 .0 96.0 4.0 100.03 .0 8.0 92.0 100.0。
一、实验目的及要求:1、目的用SPSS软件实现判别分析及其应用。
2、内容及要求用SPSS对实验数据利用Fisher判别法和贝叶斯判别法,建立判别函数并判定宿州、广安等13个地级市分别属于哪个管理水平类型。
二、仪器用具:三、实验方法与步骤:准备工作:把实验所用数据从Word文档复制到Excel,并进一步导入到SPSS 数据文件中,同时,由于只有当被解释变量是属性变量而解释变量是度量变量时,判别分析才适用,所以将城市管理的7个效率指数变量的变量类型改为“数值(N)”,度量标准改为“度量(S)”,以备接下来的分析。
四、实验结果与数据处理:表1 组均值的均等性的检验Wilks 的 Lambda F df1 df2 Sig.综合效率标准指数.582 23.022 2 64 .000 经济效率标准指数.406 46.903 2 64 .000 结构效率标准指数.954 1.560 2 64 .218 社会效率标准指数.796 8.225 2 64 .001 人员效率标准指数.342 61.645 2 64 .000 发展效率标准指数.308 71.850 2 64 .000 环境效率标准指数.913 3.054 2 64 .054表1是对各组均值是否相等的检验,由该表可以看出,在0.05的显著性水平上我们不能拒绝结构效率标准指数和环境效率标准指数在三组的均值相等的假设,即认为除了结构效率标准指数和环境效率标准指数外,其余五个标准指数在三组的均值是有显著差异的。
表2 对数行列式group 秩对数行列式1 6 -33.4102 6 -33.1773 6 -40.584汇聚的组内 6 -32.308 打印的行列式的秩和自然对数是组协方差矩阵的秩和自然对数。
表3 检验结果箱的 M 140.196F 近似。
2.498df1 42df2 1990.001Sig. .000 对相等总体协方差矩阵的零假设进行检验。
以上是对各组协方差矩阵是否相等的Box’M检验,表2反映协方差矩阵的秩和行列式的对数值。
由行列式的值可以看出,协方差矩阵不是病态矩阵。
表3是对各总体协方差阵是否相等的统计检验,由F值及其显著水平,在0.05的显著性水平下拒绝原假设,认为各总体协方差阵不相等。
1)Fisher判别法:图一图二表4 特征值函数特征值方差的 % 累积 % 正则相关性1 3.763a75.0 75.0 .8892 1.257a25.0 100.0 .746a. 分析中使用了前 2 个典型判别式函数。
表5 Wilks 的 Lambda函数检验Wilks 的 Lambda 卡方df Sig.1 到2 .093 146.042 12 .0002 .443 50.053 5 .000表4反映了判别函数的特征值、解释方差的比例和典型相关系数。
第一判别函数解释了75%的方差,第二判别函数解释了25%的方差,它们两个判别函数解释了全部方差。
表5是对两个判别函数的显著性检验,由Wilks’Lambda检验,认为两个判别函数在0.05的显著性水平上是显著的。
表6 标准化的典型判别式函数系数函数1 2综合效率标准指数-.228 -.578 经济效率标准指数.566 .404 结构效率标准指数.097 .472 社会效率标准指数.378 .233人员效率标准指数-.328 1.099 发展效率标准指数.621 .675表7 结构矩阵函数1 2发展效率标准指数.752*.305 经济效率标准指数.611*.222 综合效率标准指数.426*.170 社会效率标准指数.261*-.001 环境效率标准指数a.141*-.129 人员效率标准指数-.547 .797*结构效率标准指数.070 -.156*判别变量和标准化典型判别式函数之间的汇聚组间相关性按函数内相关性的绝对大小排序的变量。
*. 每个变量和任意判别式函数间最大的绝对相关性a. 该变量不在分析中使用。
表6为标准化的判别函数,表7为结构矩阵,即判别载荷。
由判别权重和判别载荷可以看出发展效率标准指数、经济效率标准指数对判别函数1的贡献较大,而人员效率标准指数对判别函数2的贡献较大。
表8 典型判别式函数系数函数1 2综合效率标准指数-5.216 -13.231 经济效率标准指数 5.168 3.688 结构效率标准指数.999 4.848 社会效率标准指数 4.877 3.011 人员效率标准指数-3.319 11.138 发展效率标准指数7.145 7.774 (常量) -1.363 -6.424 非标准化系数表9 组质心处的函数group 函数1 20 1 -.210 -.7302 3.964 1.2633 -2.725 1.905在组均值处评估的非标准化典型判别式函数表8为非标准化的判别函数,我们可以根据这个判别函数计算每个观测的判别Z 得分。
表9反映判别函数在各组的重心。
根据结果,判别函数在group=1这一组的重心为(-0.210,-0.730),在group=2这一组的重心为(3.964,1.263),在group=3这一组的重心为(-2.725,1.905)。
这样,我们就可以根据每个观测的判别Z得分将观测进行分类。
表11 分类结果b,cgroup 预测组成员合计1 2 3初始计数 1 46 0 0 462 0 10 0 103 2 0 9 11未分组的案例 6 3 3 12 % 1 100.0 .0 .0 100.02 .0 100.0 .0 100.03 18.2 .0 81.8 100.0未分组的案例50.0 25.0 25.0 100.0 交叉验证a计数 1 45 0 1 462 1 9 0 103 2 0 9 11% 1 97.8 .0 2.2 100.02 10.0 90.0 .0 100.03 18.2 .0 81.8 100.0a. 仅对分析中的案例进行交叉验证。
在交叉验证中,每个案例都是按照从该案例以外的所有其他案例派生的函数来分类的。
b. 已对初始分组案例中的 97.0% 个进行了正确分类。
c. 已对交叉验证分组案例中的 94.0% 个进行了正确分类。
表10为各组的先验概率,在分类选项中选择的是所有组的先验概率相等。
表11为分类矩阵表,这里交叉验证是采用“留一个在外”的原则,即每个城市是通过除了这个城市以外的其他城市推导出来的判别函数来分类的。
由该表可以看出,通过判别函数预测,有65个城市是分类正确的,其中,group=1组46个城市全部被判对,group=2组的10个城市也全部被判对,group=3组11个城市中有9个被判对,即有97%的原始城市被判对。
在交叉验证中,三组中分别有45、9、9个城市被判对,交叉验证有94%的城市被判对。
图三图三为分类结果图,从图中可以看到第2组与第3组可以很清晰地分开,与第1组也能分开,而第3组和第1组存在重合区域,即存在误判。
同时,根据对待判城市的判别可以看出:在13个待判城市中,宿州、广安、河地被判到了第3组,佛山、苏州、东营被判到了第2组,咸阳、盘锦、汉中、保定、宝鸡、衡阳被判到了第1组,而以纯由于只有环境效率标准指数的值,其他变量值确实,系统未对其进行判别。
2)贝叶斯判别法:图四图五贝叶斯判别法输出的结果与Fisher判别法很大程度上是一致的,这里不再列出。
表12 组的先验概率group先验用于分析的案例未加权的已加权的0 1 .687 46 46.0002 .149 10 10.0003 .164 11 11.000 合计 1.000 67 67.000表13 分类函数系数group1 2 3综合效率标准指数-89.225 -137.370 -110.980 经济效率标准指数18.318 47.236 15.041 结构效率标准指数112.414 126.246 122.679 社会效率标准指数61.509 87.864 57.179 人员效率标准指数77.419 85.768 115.125 发展效率标准指数57.663 102.980 60.184 (常量) -46.457 -74.840 -66.632 Fisher 的线性判别式函数表12为各族的先验概率,在分组选项中选择的是“根据组大小计算”。
表13展示了每组的分类函数,也称费歇线性判别函数,由表中的结果可以说明:group=1这一组的分类函数为:f=- 46.457-89.225综合效率标准指数+18.318经济效率标准指数1+112.414结构效率标准指数+61.509社会效率标准指数+77.419人员效率标准指数+57.663发展效率标准指数其他两组的分类函数同样可以写出,我们可以根据每个城市在各组的分类函数值然后将城市分类到较大的分类函数值中。
表14为贝叶斯判别的分类结果,其交叉验证有95.5%的城市被判对,这一概率比Fisher判别要高。
表14 分类结果b,cgroup 预测组成员合计1 2 3初始计数 1 46 0 0 462 0 10 0 103 2 0 9 11未分组的案例 6 3 3 12 % 1 100.0 .0 .0 100.02 .0 100.0 .0 100.03 18.2 .0 81.8 100.0未分组的案例50.0 25.0 25.0 100.0 交叉验证a计数 1 46 0 0 462 1 9 0 103 2 0 9 11% 1 100.0 .0 .0 100.02 10.0 90.0 .0 100.03 18.2 .0 81.8 100.0a. 仅对分析中的案例进行交叉验证。
在交叉验证中,每个案例都是按照从该案例以外的所有其他案例派生的函数来分类的。
b. 已对初始分组案例中的 97.0% 个进行了正确分类。
c. 已对交叉验证分组案例中的 95.5% 个进行了正确分类。
五、讨论与结论(1)由前面的分析我们知道,协方差矩阵并不相等,考虑采用分组协方差矩阵。
在分类中使用协方差矩阵“分组(P)”,其他选择同上,得到分类结果表如下。
分类结果agroup 预测组成员1 2 3合计初始计数 1 44 0 2 462 0 10 0 103 0 0 11 11未分组的案例 6 3 3 12 % 1 95.7 .0 4.3 100.02 .0 100.0 .0 100.03 .0 .0 100.0 100.0未分组的案例50.0 25.0 25.0 100.0a. 已对初始分组案例中的 97.0% 个进行了正确分类。
可以看出这个结果与采用组内协方差矩阵的预测效果没有明显的差别,而且分类结果图与图三也没有很大的差异,因此,可以采用组内协方差矩阵来进行判别。
(2)之前的分析是采用“一起输入自变量”的方法,由表1可知,在0.05的显著性水平上不能拒绝结构效率标准指数和环境效率标准指数在三组的均值相等的假设,考虑“使用步进式方法”,最终确定进入分析的变量有3个:经济效率标准指数、人员效率标准指数、发展效率标准指数,上表给出了最终的分类结果,可以看出,在原有数据的所有城市中,有95.5%的城市被判对,在交叉验证中有92.5%的城市被判对。