图论及其应用第一章答案(电子科大版)

电子科技大学研究生试题《图论及其应用》(参考答案)考试时间：120分钟一．填空题(每题3分，共18分)1．4个顶点的不同构的简单图共有__11___个；2．设无向图G 中有12条边，已知G 中3度顶点有6个，其余顶点的度数均小于3。

则G 中顶点数至少有__9___个；3．设n 阶无向图是由k(k ?2)棵树构成的森林，则图G 的边数m= _n-k____;4．下图G 是否是平面图？答__是___; 是否可1-因子分解？答__是_.5．下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。

图G二．单项选择(每题3分，共21分)1．下面给出的序列中，是某简单图的度序列的是( A )(A) (11123); (B) (233445); (C) (23445); (D) (1333).2．已知图G 如图所示，则它的同构图是（ D ）3． 下列图中，是欧拉图的是（ D ）4． 下列图中，不是哈密尔顿图的是（B ）5． 下列图中，是可平面图的图的是（B ）AC DA B CD6．下列图中，不是偶图的是（ B ）7．下列图中，存在完美匹配的图是（B ）三．作图(6分)1．画出一个有欧拉闭迹和哈密尔顿圈的图；2．画出一个有欧拉闭迹但没有哈密尔顿圈的图；3．画出一个没有欧拉闭迹但有哈密尔顿圈的图；解： 四．(10分)求下图的最小生成树，并求其最小生成树的权值之和。

解：由克鲁斯克尔算法的其一最小生成树如下图：权和为：20.五．(8分)求下图G 的色多项式P k (G).解：用公式(G P k -G 的色多项式：)3)(3)()(45-++=k k k G P k 。

六．(10分) 22，n 3个顶点的度数为3，…，n k 个顶点的度数为k ，而其余顶点的度数为1，求1度顶点的个数。

解：设该树有n 1个1度顶点，树的边数为m.一方面：2m=n 1+2n 2+…+kn k另一方面：m= n 1+n 2+…+n k -1 v v 13图G由上面两式可得：n 1=n 2+2n 3+…+(k -1)n k七．证明：(8分) 设G 是具有二分类(X,Y)的偶图，证明(1)G 不含奇圈；（2）若|X |≠|Y |，则G 是非哈密尔顿图。

1电子科技大学研究生试卷（考试时间： 至 ，共__2_小时）课程名称 图论及其应用 教师 学时 60 学分 教学方式 讲授 考核日期_2013__年_6__月__20__日 成绩 考核方式： （学生填写）一．填空题(每空2分，共20分)1． n 阶k 正则图G 的边数m =_____。

2．4个顶点的不同构单图的个数为________。

3．完全偶图,r s K (,2r s ≥且为偶数)，则在其欧拉环游中共含____条边。

4．高为h 的完全2元树至少有_______片树叶。

5. G 由3个连通分支124,,K K K 组成的平面图，则其共有_______个面。

6. 设图G 与5K 同胚，则至少从G 中删掉_______条边，才可能使其成为可平面图。

7. 设G 为偶图，其最小点覆盖数为α，则其最大匹配包含的边数为________。

8. 完全图6K 能分解为________个边不重合的一因子之并。

9. 奇圈的边色数为______。

10. 彼得森图的点色数为_______。

二．单项选择(每题3分，共15分) 1．下面说法错误的是( )学 号 姓 名 学 院…………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效……………………2(A) 图G 中的一个点独立集，在其补图中的点导出子图必为一个完全子图；(B) 若图G 连通，则其补图必连通； (C) 存在5阶的自补图； (D) 4阶图的补图全是可平面图. 2．下列说法错误的是（ ） (A) 非平凡树是偶图；(B) 超立方体图(n 方体,1n ≥)是偶图； (C) 存在完美匹配的圈是偶图； (D) 偶图至少包含一条边。

3.下面说法正确的是( )(A) 2连通图一定没有割点（假定可以有自环）； (B) 没有割点的图一定没有割边；(C) 如果3阶及其以上的图G 是块，则G 中无环，且任意两点均位于同一圈上；(D) 有环的图一定不是块。

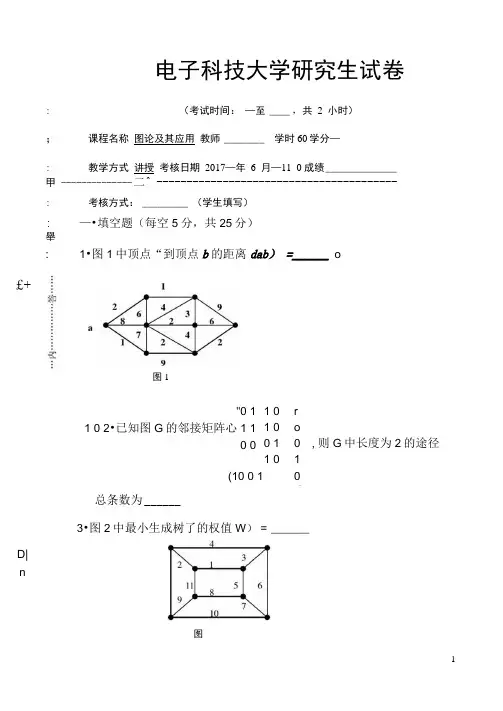
电子科技大学研究生试卷: （考试时间： —至 ____ ，共_2_小时）； 课程名称 图论及其应用 教师 ________ 学时60学分—: 教学方式 讲授 考核日期_2017—年_6_月—11_0 成绩 ______________甲 -------------- 二^ ---------------------------------------- : 考核方式： _________ （学生填写）: —•填空题（每空5分，共25分）舉: 1•图1中顶点“到顶点b 的距离dab ） = ______ o总条数为 ______ 3•图2中最小生成树了的权值W ） = ______£+"0 1 1 0 2•已知图G 的邻接矩阵心1 1 0 0 1 0 1 0 0 1 1 0 (10 0 1 ro0 1丿,则G 中长度为2的途径D|n£+图1图4•图3的最优欧拉环游的权值为5.树叶带权分别为1,245,6,8的最优二元树权值为W(T)=________ 。

二・单项选择(每题3分，共15分)1・关于图的度序列，下列说法正确的是()(A) 对任意一个非负整数序列来说，它都是某图的度序列;(B) 如果非负整数序列K归…心满足「为偶数则它一定是图序/-I列；(C) 若图G度弱于图H ,则图G的边数小于等于图H的边数；(D) .如果图G的顶点总度数大于或等于图H的顶点总度数，则图G度优于图H o2・关于图的割点与割边，下列说法正确的是()(A) 有割边的图一定有割点；(B) 有割点的图一定有割边；(C) 有割边的简单图一定有割点;(D) 割边不在图的任一圈中。

3•设k(G) , 2(G) , 5(G)分别表示图G的点连通度，边连通度和最小度。

下面说法错误的是()(A) 存在图G ,使得狀G)= 5(G) = 2(G)；(B) 存在图G ,使得k(G)<A(G)<3(G)；(C) 设G是n阶简单图，若J(G)> J ,则G连通,且A(G)=J(G);(D) 图G是£连通的，则G的连通度为44•关于哈密尔顿图，下列命题错误的是()(A) 彼得森图是非哈密尔顿图;(B) 若图G的闭包是哈密尔顿图，则其闭包一定是完全图；(C) 若图G的闭包是完全图，则图G是哈密尔顿图；(D) 设G是三阶以上简单图，若G中任意两个不邻接点“与I，,满足,则G是哈密尔顿图。

第一章：图论基本概念 1.定义平凡图/非平凡图 简单图/复合图 空图 n 阶图 连通图/非连通图完全图n K12n n n m K偶图,m n K 完全偶图,m n m K mn K 正则图图和补图，自补图 自补图判定方法 定点的度 d v 最小度 最大度 握手定理2d v m图的度序列与图序列，图序列判定方法（注意为简单图） 图的频序列 2.图运算删点/删边 图并/图交/图差/图对称差 图联 积图/合成图111122,u adjv u v u adjv 或 超立方体 3.连通性 途径 迹 路图G 不连通，其补图连通一个图是偶图当且仅当它不包含奇圈 4.最短路算法（b t A T ） 5.矩阵描述邻接矩阵及其性质，图的特征多项式 关联矩阵 6.极图？？L 补图 完全L 部图 完全L 几乎等部图 托兰定理第二章：树 1.定义树：连通的无圈图 森林 树的中心和树的形心？入<=sqrt(2m(n-1)/n)生成树 根树 出度 入度 树根 树叶 分支点 m 元根树 完全m 元根树 2.性质每棵非平凡树至少有两片树叶图G 是树当且仅当G 中任意两点都被唯一的路连接T 是(n,m)树，则m = n – 1 具有k 个分支的森林有n-k 条边每个n 阶连通图边数至少为n-1（树是连通图中边的下界） 每个连通图至少包含一棵生成树 3.计算 生成树计数 递推计数法： G G e G e关联矩阵计数法：去一点后，每个非奇异阵对应一棵生成树最小生成树（边赋权）避圈法 破圈法完全m 元树： 11m i t第三章：图的连通性1. 割边、割点和块（性质使用反证法） 割边： w G e w G边e 为割边当且仅当e 不在任何圈中割点： w G v w Gv 是无环连通图G 的一个顶点，v 是G 的割点当且仅当V(G-e)可以被划分为两个子集，v 在两个子集内点互连的路上 块：没有割点的连通子图 G 顶点数>=3，G 是块当且仅当G 无环且任意两顶点位于同一圈上v 是割点当且仅当v 至少属于G 的两个不同的块2. 连通度点割 k 顶点割 最小点割（最少用几个点把图割成两份） G 的连通度 G连通图没顶点割时连通度 1G n ，非连通图 0G边割 k 边割 最小边割（最少用几条边把图割成两份） G 的边连通度 G递推到无圈，自环不算圈性质： 任意图G 有 G G GG 是(n,m)连通图， 2m G nG 是(n,m)单图，若 2n G，则G 必定连通 G 是(n,m)单图，对应k n ，若 22n k G，则G 是k 连通G 是(n,m)单图，若 2n G，则 G G敏格尔定理： G 中分离不相邻x,y 的最小点数等于独立的x,y 路最大数目G 中分离x,y 的最小边数等于边不重x,y 路最大数目第四章 E 图与H 图 一、 E 图（走完所有边） 1. 定义，性质与判定E 图（欧拉环游）与E 迹，走完所有边回到出发点与不回到出发点E 图性质与判定：E 图 G 的顶点度数为偶数度 G 的边集合能划分为圈 E 迹性质与判定：E 迹 G 中只有两个顶点度为奇数 2. 求解路径算法 找欧拉环游：都是偶数度点：Fleury 算法（避割边行走）两奇数点欧拉环游：奇数点补充最短路后得到欧拉环游多奇数点欧拉环游：补充偶数度并不断交换 （中国邮路问题算法） 二、 H 图（走完所有点） 1. 定义与性质H 图（H 圈）与H 路：走完所有点回到出发点与不回到出发点 G 图是H 图 w G S S 2. H 图判定3n 的单图G ，如果 2nGG 是H 图3n 的单图G ，任意不相邻u,v 有 d u d v n G 是H 图图G 的闭包是H 图 G 是H 图 度序列判定法：123n d d d d ，3n ，若对任意的2nm，有m d m 或n m d n m ，则G 是H 图123n d d d d ，3n ，若对任意的2nm，有m d m 且n m d n m ，则G 是非H 图 2. 极大非哈密尔顿图定义：如果图G 的度大于等于其他非H 图，则称G 为极大非H 图（非H 图的度上限）,m n C 图： ,2m n m m n m C K K K,m n C 图是非H 图G 是非H 图 G 度弱于某个,m n C 图（证） N 阶单图G 度优于所有,m n C 图 G 为H 图 彼得森图是超H 图4. TSP 问题（边赋权近似最优H 圈求解）最优H 图下界：去点求最小生成树，选最小关联边12e e ， 11w T w e w e第五章 图的匹配与因子分解 1.边匹配定义： 匹配 饱和点/非饱和点 最大匹配/完美匹配 M 交错路/M 可扩路 贝尔热定理：G 的匹配M 是最大匹配，当且仅当G 不包含M 可扩路（反证） 2.偶图匹配Hall 定理（偶图匹配存在性定理，完美匹配）： N S S 推论：k 正则偶图G 存在完美匹配（证） 匹配算法： 匈牙利算法最优匹配算法3.点覆盖边匹配数等于点覆盖数时匹配为最大匹配覆盖为最小覆盖 哥尼定理：偶图中最大匹配边数等于最小覆盖点数（用） 4.托特定理一般图G 有完美匹配当且仅当 G S S推论：没有割边的3正则图存在完美匹配（充分条件）（证） 5.因子分解因子分解，n 度正则因子 一因子分解：2n K 可一因子分解具有H 圈的三正则图可一因子分解 若三正则图有割边，则它不能一因子分解 二因子分解： G 的一个H 圈肯定是一个二因子，但二因子不一定是H 圈（二因子可以不连通）21n K 可2因子分解2n K 可分解为一个1因子和n-1个2因子之和。

2019电⼦科技⼤学研究⽣试卷答案电⼦科技⼤学研究⽣试卷（考试时间：⾄，共 2 ⼩时）课程名称图论及应⽤教师学时 60 学分 3 教学⽅式堂上授课考核⽇期 2019 年 5 ⽉⽇成绩考核⽅式：（学⽣填写）⼀．填空题(每空3分，共15分) 1. 图G 的邻接矩阵为0111101111001100?? ? ? ? ? ???, 则G 的⽣成树的棵数为 8 . 2. 设1G 是11(,)n m 简单图,2G 是22(,)n m 简单图,则1G 和2G 的(Cartesian)积图12G G ?的边数()m G =1221n m n m +. 3. 图1中最⼩⽣成树T 的权值()W T = 23 .4. 图2中S 到T 的最短路的长度为 8 .5. 设G 是n 阶简单图,且不包含三⾓形,则其边数⼀定不超过24n . ⼆．单项选择题(每题3分，共15分) 学号姓名学院……………………密……………封……………线……………以……………内……………答……………题……………⽆……………效……………………座位号图1 图21. 关于彼得森(Petersen)图, 下⾯说法正确的是 ( B )A. 彼得森图是哈密尔顿图;B. 彼得森图是超哈密尔顿图;C. 彼得森图可1-因⼦分解;D. 彼得森图是可平⾯图.2. 下⾯说法正确的是 ( C )A. 有割点的三正则图⼀定没有完美匹配;B. 有割边的三正则图⼀定没有完美匹配;C. 存在哈密尔顿圈的三正则图必能1因⼦分解;D. 正则的哈密尔顿图必能2因⼦分解.3. 关于图的度序列, 下⾯说法正确的是 ( B )A. 任意两个有相同度序列的图都同构;B. 若图G 度弱于图H ，则图G 的边数⼩于等于图H 的边数;C. 若⾮负整数序列12(,,,)n d d d π=满⾜1ni i d =∑为偶数，则它⼀定是图序列;D. 如果图G 所有顶点的度和⼤于或等于图H 所有顶点的度和，则图G 度优于图H.4. 关于图的补图, 下⾯说法错误的是 ( A )A. 若图G 连通，则其补图必连通;B. 若图G 不连通，则其补图必连通;C. 图G 中的⼀个点独⽴集，在其补图中的点导出⼦图必为⼀个团;D. 存在5阶的⾃补图.5. 关于欧拉图, 下⾯说法正确的是 ( D )A. 每个欧拉图有唯⼀的欧拉环游;B. 每个顶点的度均为偶数的图是欧拉图;C. 欧拉图中⼀定没有割点;D. 欧拉图中⼀定没有割边.(三).(10分)若阶为25且边数为62的图G 的每个顶点的度只可能为3，4，5或6，且有两个度为4的顶点，11个度为6的顶点，求G 中5度顶点的个数。

)2214(题后两个算法不作要求题，除第图的基本概念<1.>若G 是简单图，证明：()()2V G E G ⎛⎫≤ ⎪⎝⎭。

证明：()()1()()()1v Gd v V G d v V G V G ∈≤-∴≤-∑（当且仅当G 是完全图时取等号） 又11()()()()122v G E G d v V G V G ∈=≤-∑ ()()2V G E G ⎛⎫∴≤ ⎪⎝⎭。

<2.>设G 是(,)p q 简单图，且12p q -⎛⎫>⎪⎝⎭。

求证G 为连通图。

证明：反证法，假设G 为非连通图。

设G 有两个连通分支1G 和2G ，且112212()1,()1,V G p V G p p p p =≥=≥+= 则1212()()22p p E G E G q ⎛⎫⎛⎫+=≤+⎪ ⎪⎝⎭⎝⎭而1211221(1)(1)(1)(2)222222p p p p p p p p p -⎛⎫⎛⎫⎛⎫----+-=+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222221212121222()2()222p p p p p p p p p p +-+-+-+++-==12(1)(1)0p p =--≤（因为121,1p p ≥≥），矛盾。

<3.>超图H 是有序二元组((),())V H E H ，其中()V H 是顶点非空有限集合，()E H 是()V H 的非空子集簇，且()()i i E E H E V H ∈=。

其中，()E H 中的元素i E 称为超图的边，没有相同边的超图称为简单超图。

证明：若H 是简单超图，则21υε≤-，其中,υε分别是H 的顶点数和边数。

证明：()V H υ=，有一条边的子集个数为1υ⎛⎫ ⎪⎝⎭，有i 条边的子集个数为,1,,.i n i υ⎛⎫= ⎪⎝⎭又02,211i i υυυυυυυ=⎛⎫⎛⎫⎛⎫=∴++=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑ 。

<4.>若G 是二部图，则2()()4V G E G ≤。

2005年研究生期末试题(120分钟)《图论及其应用》一、填空(15分，每空1分)1、已知图G有10条边，4个度数为3的顶点，其余顶点的度数均小于2,则G中至少有8个顶点.2、m条边的简单图G中所有不同的生成子图(包括G和空图)的个数为2"3、4个顶点的非同构的简单图有11个.4、图G的最小生成树各边权值之和为285、若W是图G中一条包含所有边的闭通道，则W在这样的闭通道中具有最短度的充要条件是："(1) 每一条边最多重复经过_4_次；(2) 在G的每一个圈上，重复经过的边的数目不超过圈的长度的一一半6 5阶度极大非哈密尔顿图族有_C5, _C；7、在图G2中，图的度序列为(44443322),频序列为(422),独立数为3,团数为4,点色数为4,边色数为4,直径为3.:、选择(15分)(1) 下列序列中，能成为某简单图的度序列的是(C)(2) 已知图G有13条边，2个5度顶点，4个3度顶点，其余顶点的的度数为2, 则图G有(A)个2度点。

（A ） 2 （ B ） 4 （C ） 8（3）图G 如（a ）所示，与G 同构的图是（C ）⑷下列图中为欧拉图的是（B ），为H 图的是（AB ）,为偶图的是（BC ）・5•下列图中可1 •因子分解的是（B ）四、正整数序列（dd 丄，dn ）是棵树的度序列的充分必要条件是 d.2（n1）i 1（10分）・ 证明：””结论显然n,,H设正整数序列（小,衣丄,山）满足 d.2 （n 1）,易知它是度序列。

设G 是这个度序列的图族中连通分支最少的一个图，知 m 二E （G ）nh假设G 不连通，则（G ） 2,且至少有一个分支G 含有圈C,否则，G 是森林,、设 和 分别是（n, m ）图G 的最大度与最小度，求证: 证明：n 2mvV(G)d (v) n2m n有m 二E （G ） 矛盾！从C 中任意取出一条边© mw 。

并在另一分支G2中任意 取出一条边©2U2V2,作图G G UlVl,U2V2U|V2,U2A则G 的度序列仍然为（did 丄，dn ）且（G ） （G ） h 这与G 的选取矛盾！所以G 是连通的，G 是树。

习题一1. 一个工厂为一结点；若两个工厂之间有业务联系，则此两点之间用边相联；这样就得到一个无向图。

若每点的度数为3，则总度数为27，与图的总度数总是偶数的性质矛盾。

若仅有四个点的度数为偶数，则其余五个点度数均为奇数，从而总度数为奇数，仍与图的总度数总是偶数的性质矛盾。

2.若存在孤立点，则m 不超过K n-1的边数, 故m <= (n-1)(n-2)/2, 与题设矛盾。

3.4. 用向量(a 1,a 2,a 3)表示三个量杯中水的量, 其中a i 为第i 杯中水的量, i = 1,2,3.以满足a 1+a 2+a 3 = 8 (a 1,a 2,a 3为非负整数)的所有向量作为各结点, 如果(a 1,a 2,a 3)中某杯的水倒满另一杯得到 ( a ’1, a ’2, a ’3 ) , 则由结点到结点画一条有向边。

这样可得一个有向图。

本题即为在此图中找一条由( 8, 0, 0 )到( 4, 4, 0 )的一条有向路，以下即是这样的一条：5. 可以。

7. 同构。

同构的双射如下：∑∑∑∑∑∑∑==+====-=++=-==---=--=ni i n i i n i n i n i ni i i n i i n i i i i a a n n a a a n n n a n a v v 1111121212/)1()1(2)1(])1[(。

，　所以 因为 ，＋ 的负度数，则为结点的正度数，为结点记－－－－－2 2 222 i i C a a ( 8, 0, 0 ) ( 5, 3, 0 ) ( 5, 0,3 ) ( 2, 3, 3 ) ( 2, 5, 1 )(7, 0, 1 ) ( 7, 1, 0 ) ( 4, 4, 0 )( 4, 1, 3 )8. 记e 1= (v 1,v 2), e 2= ( v 1,v 4), e 3= (v 3,v 1), e 4= (v 2,v 5), e 5= (v 6,v 3), e 6= (v 6,v 4), e 7= (v 5,v 3), e 8= (v 3,v 4), e 9 = (v 6,v 1), 则邻接矩阵为： 关联矩阵为：边列表为：A= (1,1,3,2,6,6,5,3,6), B= (2,4,1,5,3,4,3,4,1). 正向表为：A= (1,3,4,6,6,7,10), B= (2,4,5,1,4,3,3,4,1).⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------100110000001001000010100010011010100000001001100000111, 001101000100000000001001010000001010⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡。