2013-2014下学期安义中学高二课时练数学试卷
- 格式:doc
- 大小:56.00 KB
- 文档页数:1

试卷第1页,总2页安义中学2019—2020学年度下学期高二年级第一次周练数学(文)试卷一、单选题(每小题8分,共48分)1.若复数z 满足(23)z i i +=,则z 在复平面上对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.曲线f (x )=e x lnx 在x =1处的切线与坐标轴围成的三角形面积为( ) A .e4B .e2C .eD .2e3.若复数a 2iz 1i+=+是实数(i 为虚数单位),则实数a 的值是( )A .1B .2C .3D .44.若复数z 满足(1)2i z i +=,其中i 为虚数单位,则复数z 的虚部为( ) A .-1B .1C .i -D .i5.投掷一枚骰子,若事件A ={点数小于5},事件B ={点数大于2},则()|P B A =( )A .15B .14C .13D .126.曲线x y e =上的点到直线2y x =-的最短距离是( )A .2B .2C .322D .1二、填空题(每空8分,共16分)7.甲,乙,丙三人独立破译同一份密码.已知甲乙丙各自独立破译出密码的概率分别为12,13,14,且他们是否破译出密码互不影响,则至少有1人破译出密码的概率是______. 8.计算=+⋯+++202032202032i i i i ___________.三、解答题(请将答案写在反面答题卡上)9.(18分)已知函数()()2,ln f x x x g x x =-=.(Ⅰ)求函数()()y f x g x =-的极值;(Ⅱ)求函数[]⎥⎦⎤⎢⎣⎡⋅+=e e x g x x f y ,1)()(在的值域.10.(18分)某研究机构对高一学生的记忆力x 和判断力y 进行了统计分析,得出如下数据:x6 8 10 12y2 356(1)画出上表数据的散点图;(2)根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆybx a =+; (3)试根据(2)求出的线性回归方程,预测记忆力为11的同学的判断力.试卷第2页,总2页安义中学2019—2020学年度下学期高二年级第一次周练数学(文)答题卡班级: 姓名: 学号: 得分: 一、单选题(每小题8 分,共48分)题号 1 2 3 4 5 6 答案二、填空题(每空8分)7. 8. 三、解答题9.(18分)已知函数()()2,ln f x x x g x x =-=.(Ⅰ)求函数()()y f x g x =-的极值;(Ⅱ)求函数[]⎥⎦⎤⎢⎣⎡⋅+=e ex g x x f y ,1)()(在的值域.10.(18分)某研究机构对高一学生的记忆力x 和判断力y 进行了统计分析,得出如下数据:x6 8 10 12y2 356(1)画出上表数据的散点图;(2)根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆybx a =+;(3)试根据(2)求出的线性回归方程,预测记忆力为11的同学的判断力.参考答案1.D【解析】【分析】先求出复数z,再求复数z即得解.【详解】由题得(23)3223(23)(23)13i i i izi i i-+===++-,所以321313z i =-,所以z在复平面上对应的点为32) 1313(,-,故选D【点睛】本题主要考查复数的除法运算和共轭复数的求法,考查复数的几何意义,意在考查学生对这些知识的理解掌握水平和分析推理能力.2.B【解析】【分析】先对函数进行求导,求出在x=1处的导数值即为切线的斜率值,从而写出切线方程,然后求出切线方程与两坐标轴的交点可得三角形面积.【详解】∵y=e x ln x,∴f′(x)=e x(lnx+1x),∴f'(1)=e,f(1)=0,点(1,0)处的切线为:y=e(x﹣1)与坐标轴的交点为:(0,-e),(1,0),S=12×e×1=e2,故选:B.【点睛】本题主要考查导数的几何意义,即函数在某点处的导数值等于该点的切线的斜率,属基本知识的考查.3.B【解析】 【分析】由复数的除法运算可得解. 【详解】()()()()()()2i 1i 22i1i 1i 2a a a +-++-=+-是实数,所以2a = 故选B . 【点睛】本题主要考查了复数的运算,属于基础题. 4.A 【解析】 【分析】把已知等式变形, 利用复数的除法运算法则:分子、分母同乘以分母的共轭复数,化简复数z ,求出复数z ,从而可得结果.【详解】由()12i z i +=可知,()()()2i 1i 2i 22i1i 1i 1i 1i 2z -+====+++-, 故1i z =-,所以其虚部为1-,故选A. 【点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数、复数的模这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分. 5.D 【解析】 【分析】先由题意得到()P AB ,再由()()|()P AB P B A P A =,即可求出结果. 【详解】因为投掷一枚骰子,事件A ={点数小于5},事件B ={点数大于2}, 所以()4263P A ==,()2163P AB ==, 所以()()1|()2P AB P B A P A ==. 故选D 【点睛】本题主要考查条件概率,熟记公式即可,属于常考题型. 6.C 【解析】 【分析】先求与2y x =-平行且与xy e =相切的切线切点,再根据点到直线距离公式得结果.【详解】设与2y x =-平行的直线与xy e =相切,则切线斜率 1.k =,'x x y e y e =∴=,由'1x y e ==得0x =,当0x =时,01y e ==,即切点坐标为()0,1,则点()0,1到直线2y x =-的距离是曲线xy e =上的点到直线2y x =-的最短距离,点()0,1到直线的距离为d ==∴曲线x y e =上的点到直线:2l y x=-的距离的最小值为2选C.【点睛】本题考查导数几何意义与点到直线距离公式,考查基本分析求解能力,属基础题. 7.34【解析】 【分析】设A 表示至少有1人破译出密码,可得()1()P A P A =-,计算可得答案. 【详解】解:依题意,设A 表示至少有1人破译出密码,则A 的对立事件A 表示三人都没有破译密码, 则1113()1()11112344P A P A ⎛⎫⎛⎫⎛⎫=-=--⨯-⨯-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故填:34. 【点睛】本题主要考察对立事件的概率和独立事件的乘法公式,相对简单. 8.10081008i - 【解析】 【分析】利用复数单位的幂运算化简求解即可. 【详解】232016232016(234)(5678)2016i i i i i i i i +++⋯+=--++--++⋯+504(22)10081008i i =-=-.故答案为:10081008i -. 【点睛】本题考查复数的幂运算,考查计算能力. 9.(Ⅰ)极小值0;(Ⅱ)1,64⎡⎤-⎢⎥⎣⎦.【解析】试题分析:(Ⅰ)先求函数()()y f x g x =-的导函数,令导函数的值为零,可求得所有可能的极值点,导函数值在极值点两侧的正负,确定该点为极大(小)值点;(Ⅱ)由]2)([-=x xg f y 可得6)ln (5)ln (2+-=x x x x y ,利用换元法令x x x u ln )(=,可将函数6)ln (5)ln (2+-=x x x x y 转化为一元二次函数,从而求得其值域.试题解析:(Ⅰ)因为()()2ln y f x g x x x x =-=--,所以()()221112121x x x x y x x x x+---'=--==因为0x >,所以当01x <<时,0y '<;当1x >时,0y '>. 即函数()()y f x g x =-在()0,1上单调递减,在()1,+∞上单调递增, 故当1x =时,函数y 有极小值0,无极大值.(Ⅱ)()()()()()222ln 2ln 2ln 5ln 6y f xg x x x x x x x x x =-=---=-+⎡⎤⎣⎦ 令ln u x x =,当[]1,x e ∈时,ln 10u x '=+>,所以ln u x x =在[]1,e 上单调递增,所以0u e ≤≤,2()56y h u u u ==-+,()h u 图象的对称轴52u =.()h u 在5[0,]2上单减,在5(,]2e 上单增. min 51()24h u h ⎛⎫==- ⎪⎝⎭,又()()206,56h h e e e ==-+,则max ()6h u =.所以所求函数的值域为1,64⎡⎤-⎢⎥⎣⎦. 考点:函数的极值,复合函数的值域.10.(1)详见解析;(2)0723y x =-..;(3)5.4.【解析】 【分析】(1)根据表中数据画出散点图;(2)根据公式得到相应的参数值,进而求出方程;(3)将11x =代入方程求出结果. 【详解】(1)散点图如图:(2)因为416283105126158i ii x y==⨯+⨯+⨯+⨯=∑,68101223569,444x y ++++++====,4222221681012344ii x==+++=∑,所以215849414073444920b -⨯⨯===-⨯., 40.79 2.3a y bx =-=-⨯=-,故线性回归方程为0723y x =-... (3)由(2)中线性回归方程可知,当11x =时,07112354y =⨯-=...所以预测记忆力 为11的同学的判断力约为5.4 【点睛】本题考查回归分析,考查线性回归直线过样本中心点,在一组具有相关关系的变量的数据间,这样的直线可以画出许多条,而其中的一条能最好地反映x 与Y 之间的关系,这条直线过样本中心点.线性回归方程适用于具有相关关系的两个变量,对于具有确定关系的两个变量是不适用的, 线性回归方程得到的预测值是预测变量的估计值,不是准确值。

2014届高三第六次课时练数学试卷(文)一、选择题1、直线的倾斜角是().A . B. C. D.2、已知直线l过点(3,4)且与点A(-2,2),B(4,-2)等距离,则直线l的方程为( )A.2x+3y-18=0 B.2x-y-2=0C.3x-2y+18=0或x+2y+2=0 D.2x+3y-18=0或2x-y-2=03、若直线y=kx 与圆-4x+3=0的两个交点关于直线x+y+b=0对称,则()A.k=1,b=-2 B.k=1,b=2C.k=-1,b=2 D.k=-1,b=-24、已知数列{}的前项和为,且+=2(∈N*),则下列数列中一定是等比数列的是A.{} B.{-1} C.{-2} D.{+2}5、设、是关于的方程的两个不相等的实数根,那么过两点,的直线与圆的位置关系是()A. 相切B. 相离C. 相交D. 随的变化而变化6、下列四个正方体图形中,,为正方体的两个顶点,,,分别为其所在棱的中点,能得出平面的图形的序号是()①②③④A.①、② B.①、③C.②、③D.②、④二、填空题7、数列前n 项和=8、直线与互相垂直,则实数___;9、从直线上的点向圆引切线,则切线长的最小值为.10、圆上到直线x+y+1=0的距离为的点共有_______个.三、解答题11、如图边长为4的正方形ABCD 所在平面与正△PAD所在平面互相垂直,M、Q分别为PC、AD的中点①求四棱锥P -ABCD的体积②求证:PA ∥平面MBD③试问在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,指出点N的位置,并给予证明,若不存在请说明理由。
12、已知圆C的半径为2,圆心在轴正半轴上,直线与圆C相切(1)求圆C的方程(2)过点的直线与圆C交于不同的两点且为时求:的面积ACDQPB。
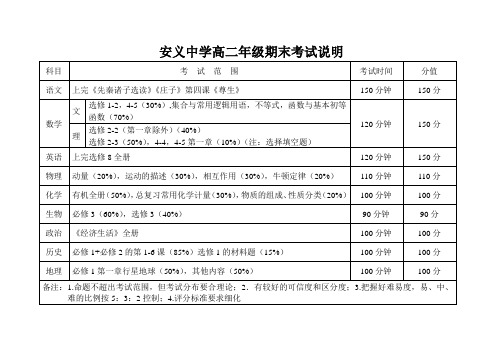
![安义二中2012—2013年第二学期第二次考试数学试卷(含答案)[1]](https://img.taocdn.com/s1/m/fb3eb4c90c22590102029d4d.png)
AB D OC 第4题 安义二中2012—2013年第二学期第二次考试数学试卷一、选择题(本大题共12小题,每小题3分,共计36分)在每小题所给出的四个选项中, 1.下列四个数中,在-2和1之间的数是 ( ) A. -3 B. -1 C. 2 D. 32. 下列说法正确的是 ( ) A .4的平方根是2 B .将点(-2,-3)向右平移5个单位长度到点 (-2,2) C.是无理数 D .点(-2,-3)关于x 轴的对称点是(-2,3)3.据有关部门统计,全国大约有1010万名考生参加了今年的高考,1010万这个数用科学记数法可表示为( )名.A .1.010×103B .1010×104C .1.010×106D .1.010×107 4.如图,在四边形ABCD 中,∠COD =100°,∠ADC 、∠DCB 的平分线相交于点O ,则(∠A +∠B )的和是( ).A.160° B .180° C .200° D .260°5..如图所示的几何体的左视图是( )6. 今年3月,某校举行“唱红歌”歌咏比赛,有19位同学参加选拔赛,所得分数互不相同,按成绩取前9名进入决赛,若知道某同学分数,要判断他能否进入决赛,只需知道19位同 学分数的( )A.中位数B. 平均数C. 极差D.方差7.如图,AC 是电杆AB 的一根拉线,测得BC =6米,∠ACB =52°,则拉线AC 的长为 ( )A .6sin 52︒米 B .6tan 52︒米C . 6·cos52°米D .6cos52︒米8.已知等腰三角形中有两个内角的度数之比为1∶4,则这个等腰三角形顶角的度数为( )A .20°B .120°C .20°或120°D .36°9.如图,在菱形ABCD 中,100B ∠=,O 是对角线AC 的中点,过点O 作MN ⊥AD 交AD 于点M ,交BC 于点N ,则下列结论错误的...是( ) A .40ACD ∠=B .OM ON =C .AM BN AB +=D .MN =21AC 10.下面三角形中,面积为无理数的是( )二.填空题(本大题共4小题,每小题3分,共计12分)不需写出解答过程,请把答案直接填写在答题卡相应位置上. 13.计算:922-a a -31-a = .14.如图,tan α= .15.如图,点E 、D 分别是正三角形ABC 、正四边形ABCM 、正五边形ABCMN 中以C 点为顶点的一边延长线和另一边反向延长线上的点,且BE =CD ,DB 的延长线交AE 于点F ,则第14题9第9题图1中∠AFB 的度数为 ;若将条件“正三角形、正四边形、正五边形”改为“正n 边形”,其他条件不变,则∠AFB 的度数为 .(用n 的代数式表示,其中,n ≥3,且n 为整数)图1E FB ADC图2AC DB F EM图3NAC DB F EM16.在Rt △ABC 中,∠BAC =90°,AB =AC =2.以AC 为一边,在△ABC 外部作等腰直角△ACD ,则线段BD 的长为 . 三.解答题(本大题共4小题,每题6分,共24分)17.解不等式组211, (1)1+21; (2)3x xx -+≤-⎧⎪⎨>-⎪⎩ ,并把它的解集在数轴上表示出来. 18.在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A (2,4),B (4,2).点C 是第一象限内的一个格点,由点C 与线段AB 组成一个以AB 为底,且腰长为无理数的等腰三角形. (1)画出△ABC ,点C 的坐标是 ,△ABC 的面积是 ;(2)将△ABC 绕点C 旋转180°得到△A 1B 1C ,连结AB 1、 BA 1,试判断四边形AB 1A 1B请说明理由;19. 在2012年元旦期间有甲、乙两个小型超市举行有奖促销活动,顾客每购货20元就有一回按下面规则转盘获奖机会,且两超市奖额等同.规则是甲、乙两超市各把一转盘分成4个、3个区域,并标上了数字(如图甲、乙),顾客一回转盘要转两次........,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).(1)利用树形图或列表法分别求出甲、乙两超市顾客一回转盘获奖的概率;(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.第18题图 第15题20.“你记得父母的生日吗?”这是我校在九年级学生中开展主题为“感恩”教育时设置的一个问题,有以下四个选项:A .父母生日都记得;B .只记得母亲生日;C .只记得父亲生日;D .父母生日都不记得.在随机调查了(1)班和(2)班各50名学生后,根据相关数据绘出如图所示的统计图.(1)补全频数分布直方图;(2)据此推算,九年级共900名学生中,“父母生日都不记得”的学生共多少名? (3)若两个班中“只记得母亲生日”的学生占22%,则(2)班“只记得母亲生日”的学生所占百分比是多少?四、(本大题共3小题,每题8分,共24分)21. 在平面直角坐标系中,点A 的坐标是(0,6),点B 在一次函数y =-x +m 的图象上,且AB =OB =5.求一次函数的解析式.22.某风景区的漂流项目:路线A------B----C ,水路长15千米,甲乘皮筏从A 处出发,AB 段漂流用1小时,BC 段的平均漂流速度比AB 段减少2.5千米/时;乙同时..从A 处骑摩托车走公路到C 处接应甲, AC 段公路长60千米, 摩托车的速度是AB 段的平均漂流速度的3倍,结果甲与乙同时到达C 处..求AB 段的平均漂流速度?23.如图,直线l 与⊙O 相交于A ,B 两点,AC 是⊙O 的直径,D 是⊙O 上一点,DE ⊥l 于点 E ,连结AD ,且AD 平分∠CAM . (1)求证:DE 是⊙O 的切线;(2)若DE =6,AE =23,求⊙O 的半径;(3)在第(2)小题的条件下,则图中阴影部分的面积为 .五、(本大题共2小题,每题12分,共24分)l第23题A B C D 93 20九年级(1)班九年级(2)班24.如图,抛物线y = ax 2+bx +c (a ≠0)与直线y =b kx +交于A (1,0)、C (0,3)两点,抛物线的顶点坐标为Q (2,-1).点P 是该抛物线上一动点,从点C 沿抛物线向点A 运动(点P 与A 不重合),过点P 作PD ∥y 轴,交直线AC 于点D . ⑴求该抛物线的解析式;⑵设P 点的横坐标为t ,PD 的长度为l ,求l 与t 之间的函数关系式,并求l 取最大值时,点P 的坐标. ⑶在问题⑵的结论下,若点E 在x 轴上,点F 在抛物线上,问是否存在以A 、P 、E 、F 为顶点的平行四边形?若存在,求点F 的坐标;若不存在,请说明理由.25如图,边长为2的等边△ABC ,射线AB 上有一点动P (P 不与点A 、点B 重合),以PC 为边作等边△PDC ,点D 与点A 在BC 同侧,E 为AC 中点,连接AD 、PE 、ED . (1)试探讨四边形ABCD 的形状,并说明理由。

2012~2013学年度下学期高二第二次月考数 学 试 卷(文)一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.集合M ={x |lg x >0},N ={x |x 2≤4},则M ∩N =( ) A .(1,2) B .[1,2) C .(1,2]D .[1,2]2.若sin θ·tan θ>0,则θ所在的的象限是( )A .二、四B .一、二C .一、四D .二、三3.函数y=│log 2x│的定义域为 ,值域为 ,则区间 的长度 b-a 的最小值为( )A 、3B 、C 、2D 、 4.若0.23121log 2,,log 33a b c -⎛⎫=== ⎪⎝⎭,则,,a b c 的大小关系为( )A.b a c >>B.a b c >>C.c a b >>D.a c b >> .5. 已知0<a <1,b <–1,函数f (x )=a x+b 的图象不经过:( )A.第一象限;B.第二象限;C.第三象限;D.第四象限 6.若A 是△AB C 的最小内角,则A A cos sin 3+能取到的一个值是( )A 、lB 、23C 、D 、 7. 如图所示,曲线是函数32()f x x bx cx d =+++的大致图象,则2212x x +等于( )A.89B.109 C.169D.548.设函数f(x)是定义在R 上的奇函数,若f(x)的最小正周期为3, 且f(1)>1,,则m 的取值范围是( )A 、m <B 、m < 且m ≠-1C 、-1< m <D 、m> 或m<-19.定义两种运算:a ○+ b= ,a ○×b= ,则函数f(x)= 为( )A 、奇函数B 、偶函数C 、奇函数或偶函数D 、既非奇函数又非偶函数10.设)(x f 是定义在R 上的周期函数,周期为4=T ,对R x ∈都有)()(x f x f =-,且当]0,2[-∈x 时,121)(-⎪⎭⎫⎝⎛=xx f ,若在区间]6,2(-内关于x 的方程)2(log )(+-x x f a =0)1(>a 恰有3个不同的实根,则a 的取值范围是( ) A.(1,2)B.),2(+∞C.()34,1D.()2,43二、填空题(本大题共5小题,每小题5分,共25分,把正确答案填入答题卡上) 11.已知角α的终边经过点P(-5,12),则2sin α+ cos α的值为 。

1.B(横hèng 诌zhōu 胖pán)2. B(A.和-合 C.法-砝 D.认-任输-疏)3. D(独树一帜:单独树立起一面旗帜,比喻自成一家。
A.指日可待:指日,可以指出日期,为期不远;待,期待。
为期不远,不久就可以实现,含有褒义,不能用在表示灾难很快来临。
B. 。
罪不容诛:罪恶极大,杀了也抵不了所犯的罪恶。
用在此处不合语境。
C.不赞一词:指文章写得完美,别人不能再添一词一语;也指一言不发)4. D.(A项,“谋财害命”后的逗号应改为问号;B项,句号应移到双引号里面;C项,应删去“等”和后面的句号)5. C (A.搭配不当,在“职业道德水平”前加“提高”;B.顺序不当,应为“获得国家相关部门的高度认可”;D.语序不当,第一处为定语的顺序不当,应为“一艘行驶在浩瀚的人生海洋里的背负着沉重使命的航船”,第二处为关联词语位置不当,应为“虽然没有得到的付出是令人遗憾的,但没有付出的得到更是令人悲哀的”)6.A解析B:寰huán 数shǔC:弭mǐ胖pán D:载zài 仆pú7.B (义——意;支——枝暗——岸;既——即韧——轫)8、C (A 截至:截止到某个时候;截止:到一定期限停止 B 咋舌:咬住舌头,形容吃惊、害怕,说不出话来 C 原封不动:指保持原来的样子,一点不加变动。
此处宜用“一成不变” D 陈词滥调:陈旧而不切合实际的话。
)9、C。
A句式杂糅,将“具有意义”与“起到作用”保留一个即可。
B关联词语位置不当,“虽然”应该放在“这个”之前。
D搭配不当,应改为打造……旅游带。
10.A(B方兴未艾:指事物正在发展,尚未达到止境。
这里可用“如火如荼”;C 特立独行:形容人的志行高洁,不同流俗。
这里可用“独树一帜”;D不刊之论:指正确的、不可修改的言论。
这里可用“奇谈怪论”)11. C(A层见迭出,当为叠B泻漏,当为泄D曲指可数,当为屈)12.B(冷落①不热闹②使受到冷淡的待遇③沉着而不感情用事,如头脑~。
高二第三次周练数学试卷(理)一、选择题(每题6分)1.等于则且)34()28)(27(20x x x ,x N x ---<∈Λ( ) A .827x A -B .xx A --2734C .734x A -D .834x A -2.从5名男医生,4名女医生中选3名医生组成一个医疗小分队,要求其中男、女医生都有,则不同的组队方案共有( ) A .70种 B .80种 C .100种 D .140种3.从6名短跑运动员中选4人参加4×100m 接力,如果其中甲不能跑第一棒,乙不能跑第四棒,则共有不同的参赛方法( )种。
A .210 B .252 C .260 D .2724.将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴世博会的四个不同场馆服务,则不同的分配方案有( )种。
A .1000 B .1080 C .1100 D .12005.函数1)(23++-=x x x x f 在点(1,2)处的切线与函数2)(x x g =围成的图形的面积等于( ) A .32B .34 C .1 D .26.已知函数f (x )的定义域为[-2,+∞),且f (4)=f (-2)=1,)()('x f x f 为的导函数,函数)('x f y =的图像如图所示。
则平面区域⎪⎩⎪⎨⎧<+≥≥1)2(00b a f b a 所围成的面积是( )A .2B .4C .5D .6二、填空题(每题6分)7.计算=++++521420464544A C C C C Λ 。
8.3人坐在一排八个座位上,若每人的左右两边都要有空位,则不同坐法的种数为 种。
9.现有10个保送上大学的名额,分配给7所学校,每校至少分1个名额,问名额分配的方法共有 种。
10.四名男生三名女生排成一排,若三名女生中有两名站在一起,但三名女生不能全排在一起,则不同的排法数有 。
三、解答题(每大题20分) 11.(1)按下列要求分配6本不同的书,各有多少种不同的分配方式? ①平均分成三份,每份2本;②分成三份,1份4本,另外两份每份1本;③甲、乙、丙三人中,一人得4本,另外两人每人得1本。
2014~2015学年度下学期高二期中考试数 学 试 卷(理)命题人: 王仪汉一、选择题(本大题共12小题,每小题5分,共60分) 1、若i 为虚数单位,m ,n R ,且=n+i 则mn=( ) A .-2 B .1C .2D .32、已知)1(2)(2f x x x f '+=,则)0(f '等于( ) A .2B .0C .-2D .-43.抛物线x x y -=2与x 轴围成的图形面积为 ( ) A .81B .1C .61 D .21 4、有一串彩旗,▼代表蓝色,▽代表黄色。
两种彩旗排成一行如下所示:▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼… 那么在前200个彩旗中有( )个黄旗。
A 、111B 、89C 、133D 、67 5. 如右图所示,使电路接通,开关不同的开闭方式有( )A. 11种B. 20种C. 21种D. 12种6、曲线ln(21)y x =-上的点到直线230x y -+=的最短距离是 ( )A .35B .25C .5D .07.若9922109)51(x a x a x a a x Λ+++=-,那么||||||||9210a a a a ++++Λ的值是( ) A.1B.94C. 95D. 968.用反证法证明命题“三角形的内角中至少有一个不大于︒60”时,反设正确的是( ) A 假设三内角都不大于︒60 B 假设三内角都大于︒60C 假设三内角至多有一个大于︒60D 假设三内角至多有两个大于︒60 9、已知函数d cx bx x x f +++=23)(在区间[-1,2]上是减函数,那么b +c ( )A .有最大值215 B .有最大值215-C .有最小值215D .有最小值215-10.奥运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案共有 ( )A. 48种B. 36种C. 18种D. 12种 11、已知在R 上可导的函数()f x 的图象如图所示,则不等式()()0f x f x ⋅'<的解集为( )。
2013-2014学年江西省南昌市高二(下)期中数学试卷(甲卷)(理科)高中期中试卷江西 2014年200一、选择题(本大题共10小题,每小题3分,共30分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的代号填在答卷的相应表格内)1. 已知向量→a=(1,1,0),→b=(−1,0,2),且k→a+→b与2→a−→b互相垂直,则k的值是( )A.1B.15C.35D.752. 以下说法正确是( )A.垂直于同一条直线的两条直线互相垂直B.平行于同一条直线的两条直线互相平行C.垂直于同一条直线的两个平面互相垂直D.平行于同一条直线的两个平面互相平行3. 若一个圆锥的轴截面是等边三角形,其面积为4√3,则这个圆锥的全面积是( )A.8πB.12√3πC.12πD.9π4. 设l,m,n均为直线,其中m,n在平面α内,则“l⊥α”是“l⊥m且l⊥n”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5. 若直线l//平面α,直线l的方向向量为→s,平面α的法向量为→n,则下列结论正确的是( )A.→s=(−1,0,2),→n=(1,0,−1)B.→s=(−1,0,1),→n=(1,2,−1)C.→s=(−1,1,1),→n=(1,2,−1)D.→s=(−1,1,1),→n=(−2, 2)6. 设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:①若m⊥α,n//α,则m⊥n②若α//β,β//γ,m⊥α,则m⊥γ③若m//α,n//α,则m//n④若α⊥γ,β⊥γ,则α//β其中正确命题的序号是( )A.①和②B.②和③C.③和④D.①和④7. 在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为( )A. B. C. D.8. 在棱长为a的正方体ABCD−A1B1C1D1中,M是AA1的中点,则点A到平面MBD的距离是( )A.√63aB.√36aC.√34aD.√66a9. 若{→a,→b,→c}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )A.a,→a+→b,→a−→bB.→b,→a+→b,→a−→bC.→c,→a+→b,→a−→bD.→a+→b,→a−→b,→a+2→b10. 过球面上三点A、B、C的截面和球心的距离是球半径的一半,且AB=6,BC=8,AC=10,则球的表面积是( )A.100πB.300πC.1003πD.4003π二、填空题(本大题共5小题,每小题4分,共20分,请将正确答案填空在答卷上)11. 两平行平面α,β分别经过坐标原点O和点A(2,1,1),且两平面的一个法向量→n=(−1,0,1),则两平面间的距离是________.12.一个水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45∘,AB=AD=1,DC⊥BC,则这个平面图形的面积为________.13. 菱形ABCD中,已知∠BAD=60∘,AB=10cm,PA垂直于ABCD所在平面且PA=5cm,则P到CD的距离为________.14. 如图,在正三棱柱ABC−A1B1C1中,侧棱长为√2,底面三角形的边长为2,则异面直线BC1与A1C所成的角是________.15. α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n②α⊥β③m⊥β④n⊥α以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________.三、解答题(本大题共5小题,共50分.解答应写出文字说明、证明过程或演算步骤)16. 如图,在四棱锥P−ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB、AD的夹角都等于60∘,M是PC的中点,设→AB=→a,→AD=→b,→AP=→c.(1)试用→a,→b,→c表示出向量→BM;(2)求BM的长.17. 如图直角梯形OABC中,∠COA=∠OAB=90∘,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O−xyz.(1)求→SC与→OB夹角的余弦值;(2)求OC与平面SBC夹角的正弦值;(3)求二面角S−BC−O.18. 如图,三棱柱ABC−A1B1C1中,侧棱垂直底面,∠ACB=90∘,AC=BC=12AA1,D是棱AA1的中点.(1)证明:BDC1⊥平面BDC;(2)平面BDC1分此棱柱为两部分,求这两部分的体积比.19. 如图,在三棱锥P−ABC中,AC=BC=2,∠ACB=90∘,AP=BP=AB,PC⊥AC.(1)求证:PC⊥AB;(2)求二面角B−AP−C的大小的余弦.20.如图组合体由直三棱柱ABC−A1B1C1与正三棱锥B−ACD组成,其中,AB⊥BC.它的正视图、俯视图、从左向右的侧视图的面积分别为2√2+1,2√2+1,1.(I)求直线CA1与平面ACD所成角的正弦;(II)在线段AC1上是否存在点P,使B1P⊥平面ACD.若存在,确定点P的位置;若不存在,说明理由.。
2014~2015学年度下学期高二第二次月考数 学 试 卷(理)命题人:熊玉明一、选择题:(本小题12题,每题5分,共60分)1.某班联欢会,原定的6个节目,已排出节目单,临时又增加了两个节目,插入原节目单中,则不同的排法数为( )A .42B .56C .60D .722.12件产品有5件次品,从中任取3件,至少有1件次品的不同取法( )A .180B .185C .190D .1953.若变量x 满足正态分布N (3,4),则D (3x +1)=( )A .9B .10C .36D .374.若一位学生把单词“error ”字母的拼写错了,则错误的种数( )A .20B .19C .10D .95.由905)1(xx +展开式中有理项有多少项( )A .17B .18C .19D .206.已知变量满足正态分布N (3,δ2)且P (x >4)=0.2则P (2≤x <4)A .0.4B .0.5C .0.6D .0.87.由曲线y =x 2,y =x 3围成的封闭图形面积为( )A . 31B .41C .121D .1278.已知:f (x )=f ′x x sin cos )4(+π,则f )4(π为( )A .1B .-1C .2D .-29.函数f (x )=(x -3)e x 的单调递增区间是( )A .(-∞,2)B .(0,3)C .(1,4)D .(2,+∞)10.设随机变量ξ服从正态分布N (μ,62)函数f (x )=x 2+2 x +ξ有零点的概率是21,则μ=( )A .3B .2C .1D .011.从1,2,3……16中任取3个数,则3个数能构成等差数列的不同取法有( )种A .112B .56C .28D .9012.4人参加4个不同的兴趣小组,分上、下午,每人只能参加一个小组且每个小组只能有1人,要求上午、下午每人都不同,有( )种A .324B .9C .216D .264二、填空题:(本小题共4小题,每题5分,共20分) 13.(x +2)10·(x 2+x -1)展开式中x 10系数是 。
高二第二次课时练数学试卷(理)
一、选择题 1.已知复数i
i
z -=12,则| z | = ( ) A .0
B .2
C .2
D .-2
2.已知复数i
i
a z ++=
1(其中i 是虚数单位)在复平面内对应的点z 落在第二象限,则a 的范围为( )
A .(-1,+∞)
B .(-1,1)
C .(-∞,-1)
D .(1,+∞)
3.已知i
i z -+=11,其中i 是虚数单位,则2013
32z z z z Λ+++的值为( ) A .1+i
B .1-i
C .i
D .-i
4.定义在R 上的函数f (x )满足f (1) = 0,且对任意x ∈R 都有2
1
)('<
x f ,则不等式2
1
)(22
+>x x f 的解集为( )
A .(1,2)
B .(0,1)
C .(1,+∞)
D .(-1,1)
5.已知二次函数1)(2
++=bx ax x f 的导函数x x f f x f 与)(,0)0('),('>轴恰有一个交点,则
)
0(')
1(f f 的最小值为( ) A .3
B .
2
5 C .2 D .
2
3 6.已知函数a a bx ax x 72
2
3
--++在x = 1处取到极大值10,则b
a
的值为( ) A .3
2-
B .-2
C .3
2
-
或-2 D .不存在
二、填空题
7.
i
-11
的共轭复数为 。
8.复数i i i 2)
1)(1(+-在复平面内对应的点到原点的距离为 。
9.函数x x y ln 2
12
-=单调减区间是 。
10.已知函数1)6()(2
3++++=x m mx x x f 既有极大值又有极小值,则实数m 的取值范围为 。
三、解答题
11.设l 的为曲线C :x
x
y ln =
在点(1,0)处的切线。
(1)求l 的方程;
(2)证明:除切点(1,0)之外,曲线C 在直线l 的下方。
12.已知函数.ln 2
)(2
x x x f -= (1)求f (x )的最值;
(2)证明:2 f (x )>e –x -x 恒成立。