【优教通,备课参考】2014年高中数学同步练习：第2章 算法初步 算法初步(北师大版必修3)]

北师大版高中数学必修3第二章《算法初步》全部教案第一课时 §2。

1.1 算法的基本思想一、教学目标：1．知识与技能：（1）通过对解决具体问题过程与步骤的分析，体会算法的思想，了解算法的含义；（2）能够用语言叙述算法；（3）会写出将自然数分解成素因数乘积的算法；（4）会写出求两个自然数的最大公因数的算法和两个自然数的最小公倍数的算法。

2．过程与方法：通过对物品价格的猜测，体会猜测者的基本思路，得到一个一般步骤，而这个步骤就是一个算法。

结合具体问题，模仿算法步骤，写出将自然数分解成素因数乘积的算法和求两个自然数的最大公因数的算法，从而体会算法的基本思想，了解算法的含义。

3．情感态度与价值观：通过本节的学习，使学生对算法的思想有一个初步的认识,体会算法的基本思想——程序化思想，在归纳概括中培养学生的逻辑思维能力，从而进一步体会算法与现实世界的密切关系。

二、教学重点与难点：重点：体会算法的思想，了解算法的含义； 难点：能够用语言来叙述算法。

三、学法与教法：学法：学生通过对具体问题的感受，主动思考，互相交流，共同讨论，总结概括，从而更好地完成本节课的教学目标。

教法：探究讨论法。

四、教学过程（一）、创设情景章头图体现了中国古代数学与现代计算机科学的联系，它们的基础都是“算法”。

算法作为一个名词，在中学教科书中并没有出现过，我们在基础教育阶段还没有接触算法概念。

但是我们却从小学就开始接触算法，熟悉许多问题的算法。

如，做四则运算要先乘除后加减，从里往外脱括弧，竖式笔算等都是算法，至于乘法口诀、珠算口诀更是算法的具体体现。

广义地说，算法就是做某一件事的步骤或程序。

菜谱是做菜肴的算法，洗衣机的使用说明书是操作洗衣机的算法，歌谱是一首歌曲的算法。

在数学中，主要研究计算机能实现的算法，即按照某种机械程序步骤一定可以得到结果的解决问题的程序。

(古代的计算工具：算筹与算盘. 20世纪最伟大的发明：计算机，计算机是强大的实现各种算法的工具。

第一章 算法初步1.1 算法与程序框图 1.1.1 算法的概念1.下面四种叙述能称为算法的是( ) A.在家里一般是妈妈做饭B.做米饭需要刷锅、淘米、添水、加热这些步骤C.在野外做饭叫野炊D.做饭必须要有米2.下列关于算法的描述正确的是( ) A.算法与求解一个问题的方法相同B.算法只能解决一个问题，不能重复使用C.算法过程要一步一步执行，每步执行的操作必须确切D.有的算法执行完后，可能无结果3.对“求1＋2＋3＋4＋5的和”，下列说法正确的是( ) A.只能设计一个算法 B.可以设计两种算法 C.不能设计算法D.设计的算法可以不包含输出 4.阅读下面的算法：第一步，输入两个实数a ，b .第二步，若a <b ，则交换a ，b 的值. 第三步，输出a .这个算法输出的是( )A.a ，b 中的较大数B.a ，b 中的较小数C.原来的a 的值D.原来的b 的值5.烧水泡茶需要洗刷茶具(5 min)、刷水壶(2 min)、烧水(8 min)、泡茶(2 min)等几个步骤，从下列选项中最好的一种算法是( )A.第一步，洗刷茶具.第二步，刷水壶.第三步，烧水.第四步，泡茶B.第一步，刷水壶.第二步，洗刷茶具.第三步，烧水.第四步，泡茶C.第一步，烧水.第二步，刷水壶.第三步，洗刷茶具.第四步，泡茶D.第一步，烧水.第二步，烧水的同时洗刷茶具和刷水壶.第三步，泡茶 6.写出解方程2x ＋3＝0的算法步骤：第一步，________________________________________________________________. 第二步，________________________________________________________________. 第三步，________________________________________________________________. 7.(教材改编)完成解不等式2x ＋2<4x －1的算法过程： 第一步，移项并合并同类项，得____________.第二步，在不等式的两边同时除以x 的系数，得____________.8.写出求解方程组⎩⎪⎨⎪⎧2x ＋y ＝7， ①4x ＋5y ＝11 ②的一个算法.9.已知直线l的倾斜角是α(α≠90°)，且直线l过点P(x0，y0)，请完成求直线l的方程的一个算法：第一步，设直线l的方程为y－y0＝k(x－x0).第二步，___________________________________________________________________.第三步，___________________________________________________________________.10.有5个小球，其中4个的重量相同，仅有一个较重，打算用天平(不用砝码)找出那个重的小球.下面设计了一种用最少的测量次数测出那个重的小球的算法：第一步，将5个小球分成A，B，C三组，每组分别有2,2,1个.第二步，将A，B两组的小球分别放在天平的两侧，若____________________，则________________，然后执行第三步；若______________________，则C组的小球为那个重的小球.第三步，将含那个重的小球的一组的两个小球分别放在天平的两侧，则较重的球为那个重的小球.(1)将上述算法补充完整；(2)若80个小球中含有1个较重的小球，请仿照上述算法设计一个算法，找出那个重的小球.1.1.2程序框图和顺序结构1.下列框图是判断框的是()2.下列是程序框图的一部分，表示恰当的是()A. B.C. D.3.在程序框图中，算法中间要处理数据或计算，可分别写在不同的()A.处理框内B.判断框内C.输入、输出框内D.终端框内4.下列关于程序框图的说法，正确的有()①程序框图只有一个入口，也只有一个出口；②程序框图中的每一部分都应有一条从入口到出口的路径通过它；③程序框图中的循环可以是无限的循环.A.①②③B.②③C.①③D.①②5.如图1-1-4，该算法的功能是计算长方体的()图1-1-4A.体积B.面对角线的长C.体对角线的长D.表面积6.如图1-1-5所示的框图的输出结果为()图1-1-5A.2,3,1B.2,3,2C.3,1,2D.3,2,17.已知三角形边长为a ，b ，c ，计算其面积公式为S ＝p (p －a )(p －b )(p －c ) ⎝⎛⎭⎫其中p ＝a ＋b ＋c 2.如图1-1-6所示的框图是表示求三角形面积的一个算法，但缺少了两个框图，缺少的是______________、____________.图1-1-68.已知小张的期末考语文成绩为102分，数学成绩为120分，英语成绩为116分，求他的总分和平均分的算法为：第一步，输入A ＝102，B ＝120，C ＝116. 第二步，计算A ＋B ＋C .第三步，计算A ＋B ＋C3.第四步，得出总分和平均分. 请用程序框图表示这个算法.9.如图1-1-7所示的程序框图的功能是求一个数的相反数，则 内应填____________.图1-1-710.已知直角三角形的两直角边长分别为a ，b ，设计一个求该三角形周长的算法，并画出相应的程序框图.11.一个人带三只狼和三只羚羊过河.只有一条船，可以同时载一个人和两只动物.没有人在的时候，如果狼的数量不少于羚羊的数量，狼就会吃掉羚羊.设计一个安全渡河的算法，并画出相应的程序框图.1.1.3条件结构和循环结构1.下列说法不正确的是()A.顺序结构是由若干个依次执行的处理步骤组成的，每一个算法都离不开顺序结构B.循环结构中一定包含条件结构C.循环结构中不一定包含条件结构D.循环结构中反复执行的步骤叫做循环体2.如果一个算法的程序框图中有◇，那么表示该算法中一定有()A.循环结构和条件结构B.条件结构C.循环结构D.无法确定3.图1-1-16是描述求一元二次方程ax2＋bx＋c＝0的根的过程的程序框图，则虚线框内是________结构.图1-1-164.(2014年广东茂名一模)某程序框图如图1-1-17，现输入如下四个函数，则可以输出的函数是( )图1-1-17A.f (x )＝x 2B.f (x )＝1xC.f (x )＝e xD.f (x )＝sin x 5.阅读图1-1-18，运行相应程序，则输出的i 值为( )A.3B.4C.5D.6图1-1-186.下面是求10的所有正约数的一个算法，请完成这个算法. 第一步，n ＝1.第二步，若n ≤10，则判断10n是否为整数，若是，则____________，若不是，则执行第三步；若n >10，则执行第四步.第三步，将n 用n ＋1代替，返回____________. 第四步，结束.7.(2013年广东)执行如图1-1-19所示的程序框图，若输入n 的值为4，则输出s 的值为________.图1-1-198.如图1-1-20，该程序框图所表示的算法的功能是()图1-1-20A.比较a，b，c三个数的大小B.求a，b，c三个数中的最大数C.求a，b，c三个数中的最小数D.求a，b，c三个数的和9.(高考改编)如果执行如图1-1-21所示的程序框图后，输出的S＝2550，那么判断框内应填()A.k<50?B.k≤50?C.k≤49?D.k<49?图1-1-2110.(创新题)阅读图1-1-22所示的程序框图，试说明它解决的是什么问题.图1-1-2211.(2012年全国)如果执行图1-1-23的程序框图，输入正整数N (N ≥2)和实数a 1，a 2，…，a N ，输出A ，B ，则( )图1-1-23A.A ＋B 为a 1＋a 2＋…＋a N 的和B.A ＋B 2为a 1，a 2，…，a N 的算术平均数C.A 和B 分别是a 1，a 2，…，a N 中最大的数和最小的数D.A 和B 分别是a 1，a 2，…，a N 中最小的数和最大的数1.2 基本算法语句1.2.1 输入语句、输出语句和赋值语句1．下列给出的赋值语句中不正确的是 A ．x ＝－x B ．x ＝x －3 C ．x ＝x 2＋1 D ．4＝x2．执行“PRINT 3＋2＝”，则输出的结果是( ) A ．3＋2＝3＋2 B ．3＋2＝5 C ．5＝3＋2 D ．53．下列说法不正确的是( ) A ．输入语句无计算功能 B ．输出语句有计算功能C ．赋值语句左边是变量，不能是表达式D ．一个输入语句只能给一个变量赋值 4．下列赋值能使y 的值为4的是( )A ．y －2＝6B ．2]D.y ＝2]5．在程序语言中，下列符号分别表示什么运算：*____________；/____________；∧______________；SQR( )_____________；ABS( )___________. 6．下面程序运行的结果是( )M ＝1M ＝M ＋1M ＝M ＋2PRINT M ENDA ．2B ．3C ．4D ．57．写出下列各语句描述的算法的输出结果． (1)______________；(2)________________．a ＝5b ＝3c ＝(a ＋b)/2d ＝c*cPRINT “d ＝”；d ENDa ＝1b ＝2c ＝a ＋bb ＝a+c －bPRINT “a ，b ，c ＝”；a ，b ，c END8．下列程序若输出的结果为3，则输入的x 值可能是________．INPUT “x ＝”；x y ＝x*x ＋2*xPRINT y END9．“x ＝3×5”，“x ＝x ＋1”是某一程序中的先后相邻的两个语句，那么下列说法正确的是( )①x ＝3×5的意思是x ＝3×5＝15，此式与算术中的式子是一样的； ②x ＝3×5的意思是将数值15赋给x ；③x ＝3×5可以写成3×5＝x ； ④x ＝x ＋1语句在执行时“＝”右边x 的值是15，执行后左边x 的值是16. A ．①③ B ．②④ C ．①④ D ．②③10．已知函数f (x )＝x 2＋3x ＋1，编写一个程序计算f (4)的值．11．给出下列程序，此程序的功能为()INPUT“实数”；x 1，y 1，x 2，y 2a ＝x 1－x 2 b ＝y 1－y 2m ＝a ∧2 n ＝b ∧2S ＝m ＋nPRINT SQR(S)ENDA ．求点到直线的距离B ．求两点之间的距离C ．求一个多项式的值D ．求输入值的平方根1.2.2 条件语句1.下列关于条件语句的说法正确的是( ) A.条件语句中必须有ELSE 和END IF B.条件语句中可以没有END IFC.条件语句中可以没有ELSE ，但是必须有END IFD.条件语句中可以没有END IF ，但是必须有ELSE2.如下表示的程序，当输入a ，b 的值分别为2,3时，最后输出的值是( )INPUT a ，b IF a>b THEN m ＝a ELSEm ＝b END IF PRINT m ENDA.2B.3C.2或3D.53.已知函数y ＝⎩⎪⎨⎪⎧x ，x ≥0，－x ，x <0，计算y 的值的程序是( )INPUT “x ＝”；x IF x ＝0 THEN y ＝xEND IF PRINT y END INPUT “x ＝”；x IF x>＝0 THEN y ＝xELSE y ＝－x END IF PRINT yENDA BINPUT “x ＝”；xIF x>＝0 THENx ＝yEND IFPRINT yENDINPUT “x ＝”；xIF x>＝0 THENy ＝xELSE y ＝－xPRINT yENDC D4.在设计求解一元一次方程ax ＋b ＝0(a ，b 为常数)的算法时，需要用条件语句判断________________________________________________________________________.5.写出下列程序的运行结果：若x ＝6，则P ＝________；若x ＝20，则P ＝________.6.函数“MOD”表示求余数，如3MOD2＝1(3除以2，余数为1)，将下列程序补充完整：7.为了使运行下面程序之后输出y ＝9，键盘输入应为( )INPUT “x ＝”；x IF x>＝0 THEN y ＝(x ＋1)*(x ＋1)ELSEy ＝(x －1)*(x －1)END IF PRINTy ENDA.x ＝－2B.x ＝－4C.x ＝－2或x ＝2D.x ＝－4或x ＝48.对于函数y ＝⎩⎪⎨⎪⎧x (0<x ≤10)，2x －11 (x >10)，请补全下面的算法程序(其中x >0).9.铁路部门托运行李的收费方法如下：y 是收费额(单位：元)，x 是行李重量(单位：kg).当0＜x ≤20时，按0.35元/kg 收费；当x ＞20时，20 kg 的部分按0.35元/kg ，超出20 kg 的部分，则按0.65元/kg 收费.请根据上述收费方法编写程序.10.已知在a，b，c三个实数中，有且只有一个正数，设计一个程序(用算法语句表示)，筛选出这个正数.1.2.3循环语句1.循环语句有WHILE和UNTIL语句两种，下面说法错误的是()A.WHILE语句和UNTIL语句之间可以相互转化B.当计算机遇到WHILE语句时，先判断条件真假，如果条件符合，就执行WHILE和WEND之间的循环体C.当计算机遇到UNTIL语句时，先执行一次DO和UNTIL之间的循环体，再对UNTIL 后的条件进行判断D.WHILE语句与UNTIL语句之间不可以相互转化2.下面程序执行后，输出的结果是()n＝5s＝0WHILE s<15s＝s＋nn＝n－1WENDPRINT nENDA.－1B.0C.1D.23.阅读下面程序，该程序是哪个和式的计算？()i＝1S＝0WHILE i<＝10S＝S＋ii＝i＋1WENDPRINT SENDA. B.1＋2＋3＋…＋11C.1＋2＋3＋…＋9D.1＋2＋3＋…＋104.以下给出的程序的功能是___________________________.i＝1S＝1WHILE S<＝5000S＝S*ii＝i＋1WENDi＝i－2PRINT iEND()5.下面是求30C.i>＝30D.i<＝306.把求n！的程序补充完整]：[注：n！＝1×2×…×(n－1)×n7.设计一个计算5×7×…×99的算法，并写出相应的算法程序.8.下面程序输出的n 值是____________.j ＝1 n ＝0WHILE j<＝11 j ＝j ＋1IF jMOD 4＝0 THENn ＝n ＋1END IF j ＝j ＋1WEND PRINT n END 9.读程序：甲 乙i ＝1S ＝0WHILE i<＝1000S ＝S ＋ii ＝i ＋1WENDPRINT SENDi ＝1000S ＝0DOS ＝S ＋i i ＝i －1LOOP UNTIL i<1PRINTSEND 对甲、乙程序和输出结果判断正确的是( )A.程序不同，结果不同B.程序不同，结果相同C.程序相同，结果不同D.程序相同，结果相同10.设计一个程序，求立方小于等于1000的所有正整数.1.3 算法案例1.整数108与84的最大公约数是( ) A.6 B.8 C.12 D.242.补全下面的求45和75的最大公约数的算法过程： 第1步，将45进行因数分解45＝32×5. 第2步，将75进行因数分解75＝3×52.第3步，写出45和75的最大公约数为________.3.用秦九韶算法求多项式f (x )＝7x 6＋6x 5＋3x 2＋2当x ＝4时的值，先算的是( ) A.4×4＝16 B.7×4＝28C.4×4×4＝64D.7×4＋6＝344.用秦九韶算法计算多项式x4＋x3＋x2＋x＋1的值时，其表达式应写成________________.5.用秦九韶算法计算多项式f(x)＝x7－5x5＋2x4＋4x3＋7x2＋9x＋2当x＝2时的值时，需要做乘法和加法运算的次数分别是()A.7,7B.7,6C.6,7D.6,66.将下面的八进制数化为十进制数.(1)24(8)；(2)1357(8).7.用辗转相除法求210与162的最大公约数，并用更相减损术检验.8.根据如图1-3-1所示的求公约数方法的程序框图，输入m＝2146，n＝1813，则输出的实数m的值为()图1-3-1A.36B.37C.38D.399.若六进制数13a 502(6)转化为十进制数后，等于12 710，求数字a的值(要求用两种方法解答).10.用秦九韶算法求多项式f(x)＝7x7＋6x6＋5x5＋4x4＋3x3＋2x2＋x当x＝3时的值.参考答案第一章 算法初步 1．1 算法与程序框图 1．1.1 算法的概念 【课后巩固提升】1．B 2.C 3.B 4.A 5.D6．移项，得2x ＝－3 系数化为1，得x ＝－32输出x ＝－327．－2x <－3 x >328．解：用加减消元法解这个方程组，其算法步骤是： 第一步，①×2－②，得－3y ＝3. ③ 第二步，解③，得y ＝－1.第三步，①×5－②，得6x ＝24. ④(或第三步，将y ＝－1代入①，得2x －1＝7. ④) 第四步，解④，得x ＝4.第五步，方程组的解为⎩⎪⎨⎪⎧x ＝4，y ＝－1.9．第二步，求k 值，k ＝tan α第三步，把k ＝tan α代入直线l 的方程得y －y 0＝tan α(x －x 0)10．解：(1)天平不平衡 那个重的小球在较重的一组中 天平平衡 (2)算法如下：第一步，将全部小球分成A ，B ，C 三组，使A ，B 两组的球一样多，且比C 组多一个球．第二步，将A ，B 两组的小球分别放在天平的两侧，若天平不平衡，则那个重的小球在较重的一组中，执行第三步；若天平平衡，则那个重的小球在C 组中；第三步，对含那个重的小球的一组，重复第一步、第二步的操作直至找出那个重的小球为止．这样至多测量4次就可找出那个重的小球．1．1.2 程序框图和顺序结构 【课后巩固提升】 1．D 2.A 3.A4．D 解析：程序框图有且仅有一个入口和一个出口，其中每一部分都应有一条从入口到出口的路径通过它．程序框图的循环必须在有限步骤内完成，无限的循环被称为死循环，在程序框图中是禁止出现的．5．C6．B 解析：本框图是一个赋值语句．先把y 的值2赋给x ，即x ＝2；然后再把z 的值3赋给y ，即y ＝3；最后把x 的值2赋给z ，即z ＝2.∴输出的x ，y ，z 的值分别为2,3,2.7. 8．解：如图D4.图D4 9．y＝－x10．解：算法步骤如下：第一步，输入实数a，b.第二步，计算a2＋b2，并将结果赋给c.第三步，计算l＝a＋b＋c.第四步，输出l.程序框图如图D5.图D5 11．解：算法步骤如下：第一步，人带两只狼过河．第二步，人自己返回．第三步，人带一只羚羊过河．第四步，人带两只狼返回．第五步，人带两只羚羊过河．第六步，人自己返回．第七步，人带两只狼过河．第八步，人自己返回．第九步，人带一只狼过河．程序框图如图D6.图D61．1.3条件结构和循环结构【课后巩固提升】1．C 2.B 3.条件 4.D5．B解析：列表依照循环执行过程可得出结果．6．输出n第二步7．7解析：根据题意，该算法的功能为第一步：i＝1，s＝1＋(1－1)＝1，i＝2；第二步：i＝2，s＝1＋(2－1)＝2，i＝3；第三步：i＝3，s＝2＋(3－1)＝4，i＝4；第四步：i＝4，s＝4＋(4－1)＝7，i＝5.5>4，此时退出程序，输出s＝7.8．B9．B解析：因为S＝2＋4＋6＋…＋100＝2550，故k＝50，故判断框内填“k≤50？”．10．解：本题为当型循环结构，先执行i≤n？，再循环．i＝1是奇数，执行循环体时，i均取奇数，M是所有奇数的3次幂之和，即计算13＋33＋53＋…＋n3的值．11．C1．2基本算法语句1．2.1输入语句、输出语句和赋值语句【课后巩固提升】1．D 2.B 3.D 4.D5．乘除乘方求算术平方根求绝对值6．C7．(1)16(2)1,2,38．1或－39.B10．解：程序如下：INPUT“x＝”；xx＝4y＝x∧2＋3*x＋1PRINT“f(4)＝”；yEND11．B1．2.2 条件语句【课后巩固提升】1．C 2.B 3.B 4.a 是否为05．2.1 10.5解析：求分段函数P ＝⎩⎪⎨⎪⎧ 0.35x (x ≤10)，3.5＋0.7(x －10) (x >10)的值． 6．m<>0 7.C8．y ＝x y ＝2*x -119．解：由题意，得y ＝⎩⎪⎨⎪⎧0.35x (0<x ≤20)，0.35×20＋0.65(x －20) (x >20)， 该函数是一个分段函数，需要对行李的重量作出判断，因此，这个过程可以用算法中的条件结构来实现．程序如下：10．解：程序框图如图D10，程序如下： INPUT a ，b ，cIF a>0 THENPRINT “正数”；aELSEIF b>0 THENPRINT “正数”；bELSEPRINT “正数”；cEND IFEND IFEND图D101．2.3 循环语句【课后巩固提升】1．D2．B 解析：试运行程序，n ＝5，s ＝0；s ＝5，n ＝4；s ＝9，n ＝3；s ＝12，n ＝2；s ＝14，n ＝1；s ＝15，n ＝0.输出n ＝0.3．D4．求使1×2×3×…×i ≤5000成立的最大正整数5．A6．INPUT WHILE WEND7．解：算法如下：第一步，令S ＝5，i ＝7.第二步，S ＝S ×i ，i ＝i ＋2.第三步，判断i>99是否成立，若成立，则执行下一步；否则，返回第二步．第四步，输出S，结束．程序如下：S＝5i＝7DOS＝S*ii＝i＋2LOOP UNTIL i>99PRINT SEND8．3解析：试运行程序，j＝1，n＝0；j＝2，j＝3；j＝4，n＝1，j＝5；j＝6，j＝7；j ＝8，n＝2，j＝9；j＝10，j＝11；j＝12，n＝3，j＝13，输出n＝3.9．B解析：甲、乙都是计算1＋2＋3＋…＋1000的值．10．解：程序如下：i＝0DOi＝i＋1m＝i*i*iLOOP UNTIL m>1000PRINT iEND1．3算法案例【课后巩固提升】1．C 2.153．D解析：因为f(x)＝a n x n＋a n－1x n－1＋…＋a1x＋a0＝(…((a n x＋a n－1)x＋a n－1)x＋…＋a1)x＋a0，所以用秦九韶算法求多项式f(x)＝7x6＋6x5＋3x2＋2当x＝4时的值，先算的是7×4＋6＝34.4．x(x(x(x＋1)＋1)＋1)＋15．A解析：此n次多项式的最高次项系数为1且含有系数为0的项，但仍需进行n 次乘法运算和n次加法运算．6．解：(1)24(8)＝2×8＋4＝20.(2)1357(8)＝1×83＋3×82＋5×8＋7＝751.7．解：210＝162×1＋48,162＝48×3＋18,48＝18×2＋12，18＝12×1＋6,12＝6×2＋0.所以210与162的最大公约数为6.检验：因为210与162都是偶数，可同时除以2，即取105与81的最大公约数后再乘2，105－81＝24,81－24＝57,57－24＝33，33－24＝9,24－9＝15,15－9＝6,9－6＝3,6－3＝3.所以210与162的最大公约数为3×2＝6.8．B解析：算法的功能是利用辗转相除法求2146与1813的最大公约数，2146＝1813＋333；1813＝5×333＋148；333＝2×148＋37；148＝4×37＋0，最大公约数是37.故选B.9．解：方法一：将六进制数转化为十进制数．13a 502(6)＝1×65＋3×64＋a×63＋5×62＋0×6＋2＝12 710(10)．即7776＋3888＋216a＋180＋0＋2＝12 710，216a＝864，a＝4.∴a的值为4.方法二：将十进制数12 710(10)化成六进制数．∴12 710(10)＝134 502(6)，故a＝4.10．解：原多项式可化为：f(x)＝((((((7x＋6)x＋5)x＋4)x＋3)x＋2)x＋1)x.v0＝7，v1＝7×3＋6＝27，v2＝27×3＋5＝86，v3＝86×3＋4＝262，v4＝262×3＋3＝789，v5＝789×3＋2＝2369，v6＝2369×3＋1＝7108，v7＝7108×3＋0＝21 324.所以当x＝3时，f(3)＝21 324.。

1a = 3b = a a b =+ b a b =- PRINT a ，bIF 10a < THEN 2y a =*else y a a =*第一章：算法初步[基础训练A 组] 一、选择题1．下面对算法描述正确的一项是：（ ）A ．算法只能用自然语言来描述B ．算法只能用图形方式来表示C ．同一问题可以有不同的算法D ．同一问题的算法不同，结果必然不同 2．用二分法求方程022=-x 的近似根的算法中要用哪种算法结构（ ）A ．顺序结构B ．条件结构C ．循环结构D ．以上都用 3．将两个数8,17a b ==交换,使17,8a b ==,下面语句正确一组是 ( )4．计算机执行下面的程序段后，输出的结果是（ ）A ．1,3B ．4,1C ．0,0D ．6,0 5．当3=a 时，下面的程序段输出的结果是（ ）A ．9B ．3C ．10D ．6二、填空题1．把求 2按从大到小进行排序时，经过第一趟排序后得到的新数列为 。

3．用“秦九韶算法”计算多项式12345)(2345+++++=x x x x x x f ，当x=2时的值的过程中，要经过 次乘法运算和 次加法运算。

4．以下属于基本算法语句的是 。

① INPUT 语句；②PRINT 语句；③IF-THEN 语句；④DO 语句；⑤END 语句； ⑥WHILE 语句；⑦END IF 语句。

5．将389化成四进位制数的末位是____________。

三、解答题1．把“五进制”数)5(1234转化为“十进制”数，再把它转化为“八进制”数。

2．用秦九韶算法求多项式x x x x x x x x f ++++++=234567234567)(当3=x 时的值。

3．编写一个程序，输入正方形的边长，输出它的对角线长和面积的值。

4．某市公用电话（市话）的收费标准为：3分钟之内（包括3分钟）收取0.30元；超过3分钟部分按0.10元/分钟加收费。

设计一个程序，根据通话时间计算话费。

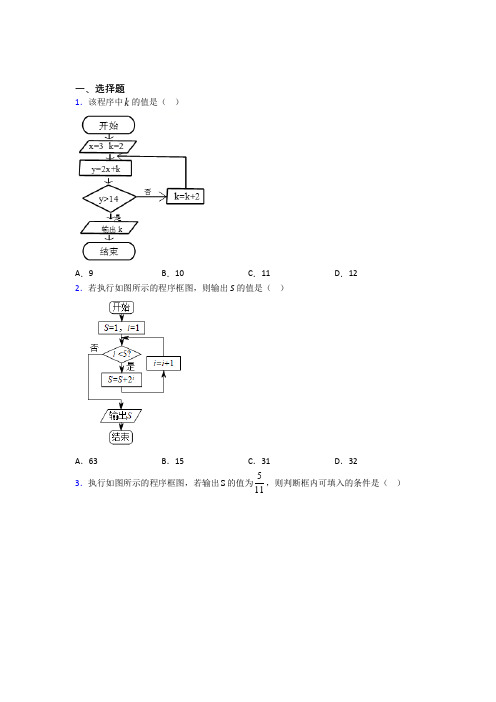
一、选择题1．该程序中k的值是（）A．9 B．10 C．11 D．12 2．若执行如图所示的程序框图，则输出S的值是（）A．63 B．15 C．31 D．323．执行如图所示的程序框图，若输出S的值为511，则判断框内可填入的条件是（）A ．4i ≤B ．5i ≤C ．5i <D ．6i ≤4．执行如图所示的程序框图，如果输入4n =，则输出的结果是（ ）A ．32B ．116C ．2512D ．137605．执行如图所示的程序框图，若输入x =9，则循环体执行的次数为（ ）A ．1次B ．2次C ．3次D ．4次6．明代数学家程大位（1533~1606年），有感于当时筹算方法的不便，用其毕生心血写出《算法统宗》，可谓集成计算的鼻祖．如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题．执行该程序框图，若输出的y 的值为2，则输入的x 的值为（ ）A ．74B ．5627C ．2D ．164817．若正整数N 除以正整数m 后的余数为r ，则记为(,)Mod N m r =，例如(10,4)2Mod =.如图所示的程序框图的算法源于我国古代数学名著《孙子算经》中的“中国剩余定理”，则执行该程序框图输出的i =（ ）A ．8B ．18C ．23D ．388．执行如下的程序框图，则输出的S 是（ ）A ．36B ．45C ．36-D ．45-9．对任意非零实数a 、b ，若a b ⊗的运算原理如图所示，则121log 43-⎛⎫⊗ ⎪⎝⎭的值为（ ）A ．13B ．1C ．43D ．210．如图给出的是计算1111246102+++⋅⋅⋅+的值的一个程序框图，其中判断框中应填入的是（ ）A ．102i >B ．102i ≤C ．100i >D ．100i ≤ 11．某程序框图如图所示，若运行该程序后输出S =（ ）A ．53B ．74C ．95D ．11612．执行如下图的程序框图，那么输出S 的值是( )A ．2B ．1C ．12D ．-1二、填空题13．已知某程序框图如图所示，则该程序运行后输出S 的值为__________．14．执行如图所示的程序框图，输出的S值为__________.15．执行如图所示的程序框图，输出S的值为___________.16．执行如图所示的程序框图，输出的S 值是__________．17．执行如图所示的算法框图，若输入的x 的值为2，则输出的n 的值为__________．18．某程序流程框图如图所示，现执行该程序，输入下列函数()2sin 3f x x π=， ()2cos 3f x x π=，()4tan 3f x x π=，则可以输出的函数是()f x =__________.19．程序如下：20．如图所示的程序框图，输出的结果是_________.三、解答题21．用二分法设计一个求方程230x -=在[]1,2上的近似根的算法.（近似根与精确解的差的绝对值不超过0.0005）22．如图所示，已知底角为45°的等腰梯形ABCD ，底边BC 长为7 cm ，腰长为22cm ，当一条垂直于底边BC (垂足为F )的直线l 从B 点开始由左至右移动(与梯形ABCD 有公共点)时，直线l 把梯形分成两部分，令BF ＝x (0≤x ≤7)，左边部分的面积为y ，求y 与x 之间的函数关系式，画出程序框图，并写出程序．23．读下列程序：（1）根据程序，画出对应的程序框图；（2）写出该程序表示的函数，并求出当输出的4y =时，输入的x 的值.24．画出解关于x 的不等式0ax b +<的程序框图，并用语句描述.25．给出30个数：1，2，4，7，，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，以此类推，要计算这30个数的和，现已给出了解决该问题的算法框图（如图所示）.（1）请在图中处理框内①处和判断框中的②处填上合适的语句，使之能完成该题算法功能；（2）根据算法框图写出算法语句.26．古希腊杰出的数学家丢番图的墓碑上有这样一首诗:这是一座古墓,里面安葬着丢番图.请你告诉我,丢番图的寿数几何?他的童年占去了一生的六分之一,接着十二分之一是少年时期,又过了七分之一的时光,他找到了自己的终身伴侣.五年之后,婚姻之神赐给他一个儿子,可是儿子不济,只活到父亲寿数的一半,就匆匆离去.这对父亲是一个沉重的打击,整整四年,为失去爱子而悲伤,终于告别了数学,离开了人世.试用循环结构,写出算法分析和算法程序.【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】本题只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可（注意避免计算错误）． 【详解】3,2,8,814x k y ===<，第一次循环，4,10,1014k y ==<； 第二次循环，6,12,1214k y ==<； 第三次循环，8,14,1414k y ===； 第四次循环，10,16,1614k y ==>， 退出循环，输出10k =， 故选：B. 【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.2．C解析：C 【分析】根据程序框图模拟程序计算即可求解. 【详解】模拟程序的运行，可得1S =，1i =； 满足条件5i <，执行循环体，3S =，2i =； 满足条件5i <，执行循环体，7=S ，3i =； 满足条件5i <，执行循环体，15S =，4i =； 满足条件5i <，执行循环体，31S =，5i =； 此时，不满足条件5i <，退出循环，输出S 的值为31. 故选：C 【点睛】本题主要考查了程序框图，循环结构，属于中档题.3．B解析：B 【分析】模拟运行程序1i =，满足条件，1013S =+⨯，2i =，满足条件，进入循环体，反复操作，直到输出511S =，核对满足的条件即可. 【详解】1i =，满足条件，1013S =+⨯； 2i =，满足条件，111335S =+⨯⨯； 3i =，满足条件，111133557S =++⨯⨯⨯； 4i =，满足条件，111113355779S =+++⨯⨯⨯⨯； 5i =，满足条件，11111115(1)1335577991121111S =++++=-=⨯⨯⨯⨯⨯； 6i =，不满足条件，输出511S =. 故选：B. 【点睛】本题考查了对程序框图的理解与应用，由程序运行结果，补充条件，数列求和的裂项相消法，属于中档题.4．B解析：B 【分析】根据题意，运行程序可实现111112341S n =++++⋯+-运算求值，从而得答案． 【详解】第一次执行程序，1,2S i ==， 第二次执行程序，11,32S i =+=， 第三次执行程序，111,423S i =++=， 因为44=，满足条件，跳出循环，输出结果116S =. 故选：B ． 【点睛】本题主要考查了程序框图，循环结构，条件分支结构，属于容易题．5．C解析：C 【分析】根据程序框图依次计算得到答案. 【详解】9,5x y ==，41y x -=>；115,3x y ==，413y x -=>； 1129,39x y ==，419y x -=<；结束. 故选：C . 【点睛】本题考查了程序框图的循环次数，意在考查学生的理解能力和计算能力.6．C解析：C 【分析】根据程序框图依次计算得到答案. 【详解】34y x =-，1i =；34916y y x =-=-，2i =；342752y y x =-=-，3i =；3481160y y x =-=-，4i =；34243484y y x =-=-，此时不满足3i ≤，跳出循环，输出结果为243484x -，由题意2434842y x =-=，得2x =． 故选:C 【点睛】本题考查了程序框图的计算，意在考查学生的理解能力和计算能力.7．C解析：C 【分析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量i 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案． 【详解】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出同时满足条件： ①被3除余2， ②被5除余3， ③被7除余2， 故输出的i 为23， 故选C ． 【点睛】本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于基础题．8．A解析：A 【分析】列出每一步算法循环，可得出输出结果S 的值. 【详解】18i =≤满足，执行第一次循环，()120111S =+-⨯=-，112i =+=； 28i =≤成立，执行第二次循环，()221123S =-+-⨯=，213i =+=；38i =≤成立，执行第三次循环，()323136S =+-⨯=-，314i =+=； 48i =≤成立，执行第四次循环，()4261410S =-+-⨯=，415i =+=； 58i =≤成立，执行第五次循环，()52101515S =+-⨯=-，516i =+=； 68i =≤成立，执行第六次循环，()62151621S =-+-⨯=，617i =+=； 78i =≤成立，执行第七次循环，()72211728S =+-⨯=-，718i =+=； 88i =≤成立，执行第八次循环，()82281836S =-+-⨯=，819i =+=；98i =≤不成立，跳出循环体，输出S 的值为36，故选A. 【点睛】本题考查算法与程序框图的计算，解题时要根据算法框图计算出算法的每一步，考查分析问题和计算能力，属于中等题.9．B解析：B 【解析】模拟执行程序框图可得程序的功能是计算并输出分段函数1,2,b a b aa b a a b b-⎧⎪⎪⊗=⎨+⎪>⎪⎩的值，∵121log 4233-⎛⎫=<= ⎪⎝⎭.∴12131log 4132--⎛⎫⊗== ⎪⎝⎭.本题选择B 选项.10．B解析：B 【解析】 【分析】根据题目所求表达式1111246102+++⋅⋅⋅+中最后一个数字1102，确定填写的语句.【详解】由于题目所求是1111246102+++⋅⋅⋅+，最后一个数字为1102，即当102i =时，判断是，继续循环，2104i i =+=，判断否，退出程序输出S 的值，由此可知应填102i ≤.故选B. 【点睛】本小题主要考查填写程序框图循环条件，属于基础题.11．D解析：D 【分析】通过分析可知程序框图的功能为计算211n S n +=+，根据最终输出时n 的值，可知最终赋值S 时5n =，代入可求得结果. 【详解】根据程序框图可知其功能为计算：()111111111211111112231223111n S n n n n n n +=+++⋅⋅⋅+=+-+-+⋅⋅⋅+-=+-=⨯⨯++++初始值为1n =，当6n =时，输出S 可知最终赋值S 时5n = 25111516S ⨯+∴==+ 本题正确选项：D 【点睛】本题考查根据程序框图的功能计算输出结果，关键是能够明确判断出最终赋值时n 的取值.12．A解析：A 【解析】 【分析】模拟程序的运行，依次写出每次循环得到的k 和S 值，根据题意即可得到结果. 【详解】程序运行如下，k=0, S ＝112-＝﹣1， k ＝1，S ＝()111--＝12；k ＝2，S ＝12112=-；k ＝3，S ＝11-2＝-1… 变量S 的值以3为周期循环变化，当k=2018时，s=2， K=2019时，结束循环，输出s 的值为2． 故选：A ． 【点睛】本题考查程序框图，是当型结构，即先判断后执行，满足条件执行循环，不满足条件，跳出循环，算法结束，解答的关键是算准周期，是基础题．二、填空题13．【分析】执行程序框图依次写出每次循环得到的Si 的值当i ＝2019时不满足条件退出循环输出S 的值为【详解】执行程序框图有S ＝2i ＝1满足条件执行循环Si ＝2满足条件执行循环Si ＝3满足条件执行循环Si解析：12-【分析】执行程序框图，依次写出每次循环得到的S ，i 的值，当i ＝2019时，不满足条件2018i ≤退出循环，输出S 的值为12-． 【详解】 执行程序框图，有 S ＝2，i ＝1满足条件2018i ≤ ，执行循环，S 3=-，i ＝2 满足条件2018i ≤ ，执行循环，S 12=-，i ＝3 满足条件2018i ≤ ，执行循环，S 13=，i ＝4 满足条件2018i ≤ ，执行循环， S ＝2，i ＝5 …观察规律可知，S 的取值以4为周期，由于2018＝504*4+2，故有： S 12=-, i ＝2019， 不满足条件2018i ≤退出循环，输出S 的值为12-， 故答案为12-． 【点睛】本题主要考查了程序框图和算法，其中判断S 的取值规律是解题的关键，属于基本知识的考查．14．37【解析】根据图得到：n=18S=19n=12S=31n=6S=37n=0判断得到n>0不成立此时退出循环输出结果37故答案为：37解析：37 【解析】根据图得到：n=18,S=19,n=12 S=31,n=6,S=37,n=0,判断得到n>0不成立，此时退出循环，输出结果37. 故答案为：37.15．48【解析】第1次运行成立第2次运行成立第3次运行成立第3次运行不成立故输出的值为48解析：48 【解析】第1次运行，1,2,122,4i S S i ===⨯=<成立 第2次运行，2,2,224,4i S S i ===⨯=<成立 第3次运行，3,4,3412,4i S S i ===⨯=<成立 第3次运行，4,12,41248,4i S S i ===⨯=<不成立， 故输出S 的值为4816．【解析】由框图可知其功能为因为每相邻6个值的为0所以=填解析：2【解析】由框图可知其功能为232017sin sinsin sin3333S ππππ=++++，因为每相邻6个值的为0，所以sin3S π= 17．2【解析】当x=2时x2﹣4x+3=﹣1＜0满足继续循环的条件故x=3n=1；当x=3时x2﹣4x+3=0满足继续循环的条件故x=4n=2；当x=4时x2﹣4x+3=3＞0不满足继续循环的条件故输出解析：2 【解析】当x=2时，x 2﹣4x+3=﹣1＜0，满足继续循环的条件，故x=3，n=1； 当x=3时，x 2﹣4x+3=0，满足继续循环的条件，故x=4，n=2； 当x=4时，x 2﹣4x+3=3＞0，不满足继续循环的条件， 故输出的n 值为2； 故答案为2．点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括顺序结构、条件结构、循环结构，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.18．【分析】根据得知函数的图象关于点对称由可得知函数的周期为于此可在题中三个函数中找出合乎条件的函数作出输出结果【详解】可知函数的图象关于点对称由得所以函数的周期为由三角函数的周期公式可知函数和的最小正解析：()2cos 3f x x π=. 【分析】根据()302f x f x ⎛⎫+--= ⎪⎝⎭得知函数()y f x =的图象关于点3,04⎛⎫- ⎪⎝⎭对称，由()f x + 302f x ⎛⎫+= ⎪⎝⎭可得知函数()y f x =的周期为3，于此可在题中三个函数中找出合乎条件的函数作出输出结果． 【详解】()302f x f x ⎛⎫+--= ⎪⎝⎭，可知函数()y f x =的图象关于点3,04⎛⎫- ⎪⎝⎭对称，由()302f x f x ⎛⎫++=⎪⎝⎭，得()3322f x f x f x ⎛⎫⎛⎫+=-=- ⎪ ⎪⎝⎭⎝⎭，所以函数()y f x =的周期为3.由三角函数的周期公式可知，函数()2sin3f x x π=和()2cos 3f x x π=的最小正周期为3，函数()4tan3f x x π=的最小正周期为34，不合乎要求； 对于函数()2sin 3f x x π=，323sin sin 04342f ππ⎡⎤⎛⎫⎛⎫-=⨯-=-≠ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦；对于函数()2cos3f x x π=，323cos cos 04342f ππ⎡⎤⎛⎫⎛⎫⎛⎫-=⨯-=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，合乎题意． 所以，函数()2cos3f x x π=的图象关于点3,04⎛⎫- ⎪⎝⎭对称， 故输出的函数为()2cos 3f x x π=，故答案为()2cos 3f x x π=． 【点睛】本题考查程序框图，考查三角函数的周期性和对称性，能根据抽象函数关系式得出函数的基本性质，是解本题的关键，属于中等题．19．24【解析】考点：程序框图专题：图表型分析：由程序中循环的条件为i≤4我们易得到最后一次循环时i=4又由循环变量i 的初值为2故我们从2开始逐步模拟循环的过程即可得到结论解答：解：模拟程序的运行结果：解析：24 【解析】 考点：程序框图． 专题：图表型．分析：由程序中循环的条件为i≤4，我们易得到最后一次循环时i=4，又由循环变量i 的初值为2，故我们从2开始逐步模拟循环的过程，即可得到结论． 解答：解：模拟程序的运行结果： i=2时，t=2，i=3时，t=6， i=4时，t=24， 故答案为24点评：本题考查的知识点是程序框图及程序代码，在写程序运行结果时，模拟程序的运行过程是解答此类问题最常用的方法，模拟时要分析循环变量的初值，步长和终值20．1【解析】试题分析：根据程序框图可知该程序执行的是所以输出的的值为1考点：本小题主要考查程序框图的执行和对数的运算点评：高考中程序框图的题目一般离不开循环结构要分清是当型循环还是直到型循环要搞清楚退解析：1 【解析】试题分析：根据程序框图可知，该程序执行的是34103410lg 2lg lg lglg(2)lg101239239b =++++=⋅⋅⋅⋅==，所以输出的的值为1. 考点：本小题主要考查程序框图的执行和对数的运算.点评：高考中程序框图的题目一般离不开循环结构，要分清是当型循环还是直到型循环，要搞清楚退出循环的条件，避免多执行或少执行一步.三、解答题21．见解析 【分析】计算(1)0,(2)0f f <>，设121,2x x ==，122x x m +=，判断()f m 的符号，根据零点存在定理得到算法. 【详解】第一步：令2()3f x x =-，(1)20,(2)10f f =-<=>，∴设121,2x x ==；第二步：令122x x m +=，判断()f m 是否为0，若是，则m 为所求；若不是，则继续判断()1()f x f m ⋅大于0还是小于0；第三步：若()1()0f x f m ⋅>，则令1x m =；否则，令2x m =；第四步：判断120.0005x x -≤是否成立？若是，则12,x x 之间的任意值均为满足条件的近似根；若不是，则返回第二步. 【点睛】本题考查了求方程近似根的算法，意在考查学生对于算法的理解和应用.22．221,02222,251(7)10,572x x y x x x x ⎧≤≤⎪⎪=-<≤⎨⎪⎪-+<<⎩，程序框图和程序见解析． 【分析】根据直线l 将梯形分割的左边部分的形状进行分类讨论，求出函数关系式，即可根据条件结构画出程序框图，并写出程序． 【详解】过点A ，D 分别作AG ⊥BC ，DH ⊥BC ，垂足分别是G ，H .∵四边形ABCD 是等腰梯形，底角是45°，AB ＝2cm ， ∴BG ＝AG ＝DH ＝HC ＝2 cm . 又BC ＝7cm ，∴AD ＝GH ＝3cm ，当02x ≤≤时，212y x =； 当25x <≤时，22y x =-；当57x <<时，21(7)102y x =-+， 所以221,02222,251(7)10,572x x y x x x x ⎧≤≤⎪⎪=-<≤⎨⎪⎪-+<<⎩ ． 程序框图如下：程序：INPUT “x ＝”；xIF x >＝0 AND x <＝2 THENy ＝0.5 *x ^2ELSEIF x <＝5 THENy ＝2*x -2ELSEy =-0.5*(x -7) ^2+10END IFEND IFPRINT yEND【点睛】本题主要考查分段函数解析式的求法、程序框图的画法以及程序语句的书写，意在考查学生分类讨论思想和算法语句的理解和书写．23．（1）程序框图见解析；（2）2,02,0x x y x x ⎧<=⎨≥⎩，2x =±. 【分析】（1）根据程序语句可知该程序是条件结构框图，并根据程序语句作出相应的程序框图； （2）根据程序语句得出当x 取不同范围内的值时，函数的解析式也不同，然后可根据程序框图结合x 的不同取值范围，得出函数的解析式，然后分0x <和0x ≥解方程4y =，从而可解出输入的x 的值.【详解】（1）对应的程序框图如图所示：（2）该程序表示的函数是2,02,0x x y x x ⎧<=⎨≥⎩. 当0x <时，由24y x ==得2x =-；当0x ≥时，由24y x ==得2x =.出当输出的4y =时，输入的x 的值是2x =±.【点睛】本题考查条件程序框图的应用，同时考查了根据程序框图计算输入值，解题时要对x的取值范围分段来讨论，考查分析问题和解决问题的能力，属于中等题.24．见解析【详解】解：流程图如下：程序如下：INPUT a，bIF a＝0 THENIF b＜0 THENPRINT“任意实数”ELSEPRINT“无解”ELSEIF a＞0 THENPRINT“x＜“；﹣b/aELSEPRINT“x＞“；﹣b/aENDIFENDIFENDIFEND点睛：解决算法问题的关键是读懂程序框图，明晰顺序结构、条件结构、循环结构的真正含义，本题巧妙而自然地将算法、不等式、交汇在一起，用条件结构来进行考查.这类问题可能出现的错误：①读不懂程序框图；②条件出错；③计算出错.25．(1) ①处应填；②处应填 (2)见解析【解析】分析：（1）由已知中程序的功能是给出个数，其规律是：第个数是；第个数是；第个数比第个数大，第个数比第大，，依次类推，要计算区间个数的和，可以根据循环此时，循环变量的初值、步长计算出循环变量的终值，得到①中的条件；再根据累加的变化规律，得到②中累加通项的表达式；（2）利用直到型循环结构，写出程序.详解：（1）因为是求30个数的和，故循环体应执行30次，其中是计数变量，因此判断框内的条件就是限制计数变量的，故应为，算法中的变量实质是表示参与求和的各个数，由于它也是变化的，且满足第个数比其前一个数大，第个数比其前一个数大，故应有，故①处应填；②处应填.（2）根据框图，写出算法如下：点睛：本题主要考查了直到型的循环结构的算法框图，解答中循环体的循环次数=（循环终值-初值）+步长+1，确定循环的次数，其中循环次数、终值、初值、步长中，能知道其中的三个可求解另一个，对于循环结构的程序框图，判断框内的内容容易出错，做题时要注意，同时注意循环点所在的位置.26．答案见解析【解析】试题分析：先设丢番图的寿数为x, x为正整数，列出方程，再用验证的方法找到方程的解，即得到丢番图的寿数.再根据算法写出算法程序.试题设丢番图的寿数为x,则x为正整数,根据题意可知16x+112x+17x+5+12x+4=x,我们可以从x=1,依次验证是不是方程的解.算法如下: S1x=1;S2判断16x+112x+17x+5+12x+4=x是否成立,如果成立,则输出x;否则,转至S3;S3x=x+1,转至S2.算法程序如下:x=1;while 16x+112x+17x+5+12x+4< >xx=x+1; wendx=x-1print xend点睛：本题的难点在于写出找丢番图的寿数的算法，这里只能采取验证的方法.。

一、选择题1．给出一个算法的程序框图如图所示，该程序框图的功能是（ ）A ．求出,,a b c 三数中的最小数B ．求出,,a b c 三数中的最大数C ．将,,a b c 从小到大排列D ．将,,a b c 从大到小排列2．程大位是明代著名数学家，他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行宇内，成为明清之际研习数学者必读的教材，而且传到朝鲜、日本及东南亚地区，对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是：“今有三角果一垛，底阔每面七个，问该若干？”如图是解决该问题的程序框图.执行该程序框图，求得该垛果子的总数S 为( )A ．84B ．56C ．35D ．283．执行如图所示的程序框图，输出S 的值为（ ）A．1-B．0 C．1 D．2 4．执行如图所示的程序框图，若输入10n=，则输出的结果是（）A．11114135717P⎛⎫=-+-++⎪⎝⎭B．11114135719P⎛⎫=-+-+-⎪⎝⎭C．11114135721P⎛⎫=-+-+⋯+⎪⎝⎭D．11114135721P⎛⎫=-+-+-⎪⎝⎭5．执行如图所示的程序框图，若输出的结果为126，则判断框内的条件可以为（）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤ 6．正整数N 除以正整数m 后的余数为n ,记为()N n MODm ≡,例如()2516MOD ≡.如图所示程序框图的算法源于“中国剩余定理”,若执行该程序框图,当输入49N =时,则输出结果是( )A ．58B ．61C ．66D ．767．执行如图所示的程序框图，则输出的k 的值为（ ）A ．3B ．4C ．5D ．68．执行如下图的程序框图，如果输入的N 的值是7，那么输出的p 的值是（ ）A ．3B ．15C ．105D ．945 9．读下面的程序：上面的程序在执行时如果输入6，那么输出的结果为()A．6 B．720 C．120 D．5040 10．执行如图所示的程序框图，则输出的n值是（）A．5B．7C．9D．1111．执行如图所示的程序框图，若输出的值为﹣1，则判断框①中可以填入的条件是（）A．n≥999B．n≤999C．n＜999 D．n＞999 12．若执行如图所示的程序框图，则输出S的值为( )A．10072015B．10082017C．10092019D．10102021二、填空题13．如图是一个算法流程图，若输入x的值为2，则输出y的值为_______. .14．执行如图所示的程序框图，输出的值为__________．15．如下图，程序框图中，若输入4,10m n ==，则输出a 的值是________.16．执行如图所示的算法框图，若输入的x 的值为2，则输出的n 的值为__________．17．如图是一个算法的流程图，则输出的a 的值是___________．18．101110（2）转化为十进制数是__________．19．程序如下：以上程序输出的结果是_________________20．如图所示的程序框图输出的值是 .三、解答题21．（1）用辗转相除法求840与1 764的最大公约数；（2）用更相减损术求440 与556的最大公约数.1,2上的近似根的算法.（近似根与精确解的差22．用二分法设计一个求方程230x-=在[]的绝对值不超过0.0005）23．某函数的解析式由如图所示的程序框图给出.（1）写出该函数的解析式；（2）执行该程序框图，若输出的结果为4，求输入的实数x 的值.24．图是求239111112222S =+++++的一个程序框图． (1)在程序框图的①处填上适当的语句；(2)写出相应的程序．25．分别标有1,2,3,4,5,6六个号码的小球,有一个最重,写出挑出最重球的算法,并画出程序框图.26．已知华氏温度与摄氏温度的转换公式是(华氏温度532)9-⨯=摄氏温度．编写一个程序，输入一个华氏温度，输出其相应的摄氏温度．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】对a 、b 、c 赋三个不等的值，并根据程序框图写出输出的结果，可得知该程序的功能．【详解】令2a =，3b =，1c =，则23>不成立，21>成立，则1a =，输出的a 的值为1， 因此，该程序的功能是求出a 、b 、c 三数中的最小数，故选A ．【点睛】本题考查程序框图的功能，解题的关键就是根据题意将每个步骤表示出来，考查分析问题的能力，属于中等题．2．A解析：A【分析】按照程序框图运行程序，直到满足7i ≥时输出结果即可.【详解】按照程序框图运行程序，输入0i =，0n =，0S =，则1i =，1n =，1S =，不满足7i ≥，循环；2i =，3n =，4S =，不满足7i ≥，循环；3i =，6n =，10S =，不满足7i ≥，循环；4i =，10n =，20S =，不满足7i ≥，循环；5i =，15n =，35S =，不满足7i ≥，循环；6i =，21n =，56S =，不满足7i ≥，循环；7i =，28n =，84S =，满足7i ≥，输出84S =.故选：A .【点睛】本题考查根据程序框图循环结构计算输出结果的问题，属于基础题.3．C解析：C【分析】由函数()πsin 2x f x =，可求周期为4，()(1)(2)(3)40+++=f f f f ，由题意可知()(1)(2)(2021)=2021(1)1=+++==S f f f f f【详解】 由函数()πsin 2x f x =的周期为2π4π2T ==， ()π1sin 12f ==，()2π2sin 02f ==， ()3π3sin 12f ==-，()4π4sin 02f ==，()(1)(2)(3)40+++=f f f f ()(1)(2)(2021)=2021(1)1∴=+++==S f f f f f .故选：C【点睛】 本题考查了程序框图求和，正弦型三角函数的周期等基本知识，考查了运算求解能力和逻辑推理能力，属于一般题目.4．B解析：B【分析】按照程序框图运行程序，寻找规律，直到i n >输出结果即可.【详解】按照程序框图运行程序，输入10n =，0S =，1i =，则1S =，2i =，不满足i n >，循环；113S =-，3i =，不满足i n >，循环；11135S =-+，4i =，不满足i n >，循环； 以此类推，1111135719S =-+--⋅⋅⋅-，11=i ，满足i n >，则4P S =， 11114135719P ⎛⎫∴=-+--⋅⋅⋅- ⎪⎝⎭. 故选：B .【点睛】本题考查根据程序框图循环结构计算输出结果的问题，属于常考题型.5．B解析：B【分析】根据框图，模拟程序运行即可求解.【详解】根据框图，执行程序，12,2S n ==；1222,3S n =+=；⋯12222,1i S n i =++⋯+=+，令12222126i S =++⋯+=，解得6i =，即7n =时结束程序，所以6n ≤，故选 ：B【点睛】本题主要考查了程序框图，循环结构，条件分支结构，等比数列求和，属于中档题.genju 6．B解析：B【分析】该程序框图的作用是求被3和5除后的余数为1的数，根据所给的选项，得出结论.【详解】模拟程序的运行，可得49N =，50N =，不满足条件()13N MOD ≡，51N =；不满足条件()13N MOD ≡，52N =；满足条件()13N MOD ≡，不满足条件()15N MOD ≡，53N =；不满足条件()13N MOD ≡，54N =；不满足条件()13N MOD ≡，55N =； 满足条件()13N MOD ≡，不满足条件()15N MOD ≡，56N =；不满足条件()13N MOD ≡，57N =；不满足条件()13N MOD ≡，58N =； 满足条件()13N MOD ≡，不满足条件()15N MOD ≡，59N =；不满足条件()13N MOD ≡，60N =；不满足条件()13N MOD ≡，61N =； 满足条件()13N MOD ≡，满足条件()15N MOD ≡，输出61N =.故选：B.【点睛】本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于基础题.7．C解析：C【分析】根据框图模拟程序运算即可.【详解】第一次执行程序，2111S =⨯-=，25S >-，继续循环，第二次执行程序，2k =，2121S =⨯-=-，25S >-，继续循环，第三次执行程序，3k =，2(1)35S =⨯--=-，25S >-，继续循环，第四次执行程序，4k =，2(5)414S =⨯--=-，25S >-，继续循环，第五次执行程序，5k =，2(14)532S =⨯--=-，25S <-，跳出循环，输出5k =，结束.故选C.【点睛】本题主要考查了程序框图，涉及循环结构，解题关键注意何时跳出循环，属于中档题. 8．C解析：C【分析】由已知中的程序框图，得到该程序的功能是利用循环结构计算并输出变量p 的值，模拟程序的运行过程，分析循环中各变量的变化情况，可得答案．【详解】模拟程序的运行，可得：7,1,1N k p ===，满足条件7k <，执行循环体，3,3k p ==；满足条件7k <，执行循环体，5,15k p ==；满足条件7k <，执行循环体，7,105k p ==；此时，不满足条件7k <，推出循环，输出p 的值为105，故选C ．【点睛】本题主要考查了程序框图的应用问题，解答中应模拟程序框图的运行过程，逐次计算是解答的关键，着重考查了推理与运算能力，属于基础题．9．B解析：B【解析】【分析】执行程序，逐次计算，根据判断条件终止循环，即可求解输出的结果，得到答案.【详解】由题意，执行程序，可得：第1次循环：满足判断条件，1,2S i ==；第2次循环：满足判断条件，2,3S i ==；第3次循环：满足判断条件，6,4S i ==；第4次循环：满足判断条件，24,5S i ==；第5次循环：满足判断条件，120,6S i ==；第6次循环：满足判断条件，720,7S i ==；不满足判断条件，终止循环，输出720S =，故选B.【点睛】本题主要考查了循环结构的程序框图的计算输出，其中解答中正确理解循环结构的程序框图的计算功能，逐次计算是解答的关键，着重考查了推理与运算能力，属于基础题. 10．C解析：C【分析】根据程序框图列出算法循环的每一步，结合判断条件得出输出的n 的值.【详解】执行如图所示的程序框图如下：409S =≥不成立，11S 133==⨯，123n =+=； 1439S =≥不成立，1123355S =+=⨯，325n =+=； 2459S =≥不成立，2135577S =+=⨯，527n =+=； 3479S =≥不成立，3147799S =+=⨯，729n =+=. 4499S =≥成立，跳出循环体，输出n 的值为9，故选C. 【点睛】本题考查利用程序框图计算输出结果，对于这类问题，通常利用框图列出算法的每一步，考查计算能力，属于中等题.11．C解析：C【分析】分析循环结构中求和式子的特点，可到最终结果：2lg(1)S n =-+，当1S =-时计算n 的值，此时再确定判断框的内容.【详解】由图可得：2lg1lg 2lg 2lg3...lg lg(1)S n n =+-+-++-+，则2lg(1)1S n =-+=-，所以999n =，因为此时需退出循环，所以填写：999n <. 故选C.【点睛】lg lg lg(1)1n n n n =-++，通过将除法变为减法，达到简便运算的目的. 12．C解析：C【解析】【分析】首先确定流程图的功能为计数111113355720172019S =++++⨯⨯⨯⨯的值，然后利用裂项求和的方法即可求得最终结果.【详解】 由题意结合流程图可知流程图输出结果为111113355720172019S =++++⨯⨯⨯⨯， 11(2)111(2)2(2)22n n n n n n n n +-⎛⎫=⨯=- ⎪+++⎝⎭， 111113355720172019S ∴=++++⨯⨯⨯⨯ 11111111123355720172019⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦1110091220192019⎛⎫=-= ⎪⎝⎭. 本题选择C 选项.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．二、填空题13．5【分析】直接模拟程序即可得结论【详解】输入的值为2不满足所以故答案是：5【点睛】该题考查的是有关程序框图的问题涉及到的知识点有程序框图的输出结果的求解属于简单题目解析：5【分析】直接模拟程序即可得结论.【详解】输入x 的值为2，不满足1x ≤，所以3325y x =+=+=，故答案是：5.【点睛】该题考查的是有关程序框图的问题，涉及到的知识点有程序框图的输出结果的求解，属于简单题目.14．【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件即可得到输出的的值【详解】输入第一次循环；第二次循环；第三次循环；第四次循环；第五次循环；第六次循环退出循环输出故答案为解析：42【分析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的S 的值．【详解】输入0,2,1S a i ===，第一次循环，2,4,2S a i ===；第二次循环，6,6,3S a i ===；第三次循环，12,8,4S a i ===；第四次循环，20,10,5S a i ===；第五次循环，30,12,6S a i ===；第六次循环，42,14,7S a i ===，退出循环，输出42S =，故答案为42.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.15．20【解析】模拟执行程序可得：不满足条件整除以不满足条件整除以不满足条件整除以不满足条件整除以满足条件整除以退出循环输出的值为点睛：本题主要考查的程序框图的知识点解题的关键是要读懂程序框图模拟执行程 解析：20【解析】模拟执行程序，可得：4,10m n ==，1i =，4a =不满足条件n 整除以a2i =，8a =不满足条件n 整除以a3i =，12a =不满足条件n 整除以a4i =，16a =不满足条件n 整除以a5i =，20a =满足条件n 整除以a ，退出循环，输出a 的值为20点睛：本题主要考查的程序框图的知识点．解题的关键是要读懂程序框图．模拟执行程序，依次写出每次循环得到的i ，a 的值，当20a =的时候，满足条件n 整除以a ，退出循环，即可得到输出a 的值为20．16．2【解析】当x=2时x2﹣4x+3=﹣1＜0满足继续循环的条件故x=3n=1；当x=3时x2﹣4x+3=0满足继续循环的条件故x=4n=2；当x=4时x2﹣4x+3=3＞0不满足继续循环的条件故输出解析：2【解析】当x=2时，x 2﹣4x+3=﹣1＜0，满足继续循环的条件，故x=3，n=1；当x=3时，x 2﹣4x+3=0，满足继续循环的条件，故x=4，n=2；当x=4时，x 2﹣4x+3=3＞0，不满足继续循环的条件，故输出的n 值为2；故答案为2．点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括顺序结构、条件结构、循环结构，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项. 17．9【解析】:试题分析：由题意可得a 是在不断变大的b 是在不断变小当程序运行两次时a=9b=5a>b 跳出程序输出a=9;考点：算法的流程图的计算 解析：9【解析】:试题分析：由题意可得，a 是在不断变大的，b 是在不断变小，当程序运行两次时，a=9,b=5，a>b,跳出程序，输出a="9;"考点：算法的流程图的计算18．46【解析】试题分析：考点：进位制间的关系解析：46【解析】试题分析：2345(2)101110121212021246=⨯+⨯+⨯+⨯+⨯=．考点：进位制间的关系． 19．24【解析】考点：程序框图专题：图表型分析：由程序中循环的条件为i≤4我们易得到最后一次循环时i=4又由循环变量i 的初值为2故我们从2开始逐步模拟循环的过程即可得到结论解答：解：模拟程序的运行结果：解析：24【解析】考点：程序框图．专题：图表型．分析：由程序中循环的条件为i≤4，我们易得到最后一次循环时i=4，又由循环变量i 的初值为2，故我们从2开始逐步模拟循环的过程，即可得到结论．解答：解：模拟程序的运行结果：i=2时，t=2，i=3时，t=6，i=4时，t=24，故答案为24点评：本题考查的知识点是程序框图及程序代码，在写程序运行结果时，模拟程序的运行过程是解答此类问题最常用的方法，模拟时要分析循环变量的初值，步长和终值 20．144【分析】直接利用循环结构计算循环各个变量的数值当满足判断框的条件推出循环输出结果【详解】判断前第1次判断循环；第2次判断循环第3次判断循环；第4次判断循环；第5次判断循环；第6次判断循环；第7 解析：144【分析】直接利用循环结构,计算循环各个变量的数值,当10k =满足判断框的条件,推出循环,输出结果.【详解】判断前,2c =,第1次判断循环,1,2,2,3a b k c ====；第2次判断循环,2,3,3,5a b k c ====第3次判断循环,3,5,4,8a b k c ====；第4次判断循环,5,8,5,13a b k c ====；第5次判断循环,8,13,6,21a b k c ====；第6次判断循环,13,21,7,34a b k c ====；第7次判断循环,21,34,8,55a b k c ====；第8次判断循环,34,55,9,89a b k c ====；第9次判断循环,55,89,10,144a b k c ====；第10次判断不满足判断框条件,退出循环,输出144c =，故答案为144.【点睛】本题考查循环结构的应用,注意每一步循环的变量的数值,计算准确是解题的关键.三、解答题21．（1）84；（2）4.【分析】（1）根据辗转相除法，求余数，直至余数为零，（2）根据更相减损术，求减数，直至减数为零.【详解】（1）用辗转相除法求840与1 764 的最大公约数.1 764 = 840×2 + 84 840 = 84×10 +0所以840与1 764 的最大公约数是84.(2)用更相减损术求440 与556的最大公约数.556－440 = 116 440－116 = 324324－116 = 208 208－116 = 92116－92 = 24 92－24 = 6868－24 = 44 44－24 = 2024－20 = 4 20－4 = 1616－4 = 12 12－4 = 88－4 = 4所以440 与556的最大公约数4.【点睛】本题考查辗转相除法与更相减损术,考查基本求解能力.22．见解析【分析】计算(1)0,(2)0f f <>，设121,2x x ==，122x x m +=，判断()f m 的符号，根据零点存在定理得到算法.【详解】第一步：令2()3f x x =-，(1)20,(2)10f f =-<=>，∴设121,2x x ==； 第二步：令122x x m +=，判断()f m 是否为0，若是，则m 为所求；若不是，则继续判断()1()f x f m ⋅大于0还是小于0；第三步：若()1()0f x f m ⋅>，则令1x m =；否则，令2x m =； 第四步：判断120.0005x x -≤是否成立？若是，则12,x x 之间的任意值均为满足条件的近似根；若不是，则返回第二步.【点睛】本题考查了求方程近似根的算法，意在考查学生对于算法的理解和应用.23．(1) 22,0log ,042,4x x x y x x x ⎧<⎪=<≤⎨⎪>⎩当0x =时，y 无解.(2) 2x =-.【分析】(1)根据框图得到函数解析式；（2）结合第一问得到的函数表达式，分情况得到x 值即可.【详解】（1）函数解析式为22,0log ,042,4x x x y x x x ⎧<⎪=<≤⎨⎪>⎩，当0x =时，y 无解.（2）当0x <时，24x =，2x =-或2（舍）.当04x ≤≤时，2log 4x =，解得16x =（舍）.当4x >时，24x =，解得2x =（舍）所以2x =-【点睛】这个题目考查了程序框图的应用，以及分段函数的应用；解决分段函数求值问题的策略：(1)在求分段函数的值f (x 0)时，一定要首先判断x 0属于定义域的哪个子集，然后再代入相应的关系式；(2)分段函数是指自变量在不同的取值范围内，其对应法则也不同的函数，分段函数是一个函数，而不是多个函数；分段函数的定义域是各段定义域的并集，值域是各段值域的并集，故解分段函数时要分段解决；(3)求f (f (f (a )))的值时，一般要遵循由里向外逐层计算的原则.24．（1）2T T =；（2）见解析 【解析】【分析】⑴要计算239111112222S =+++++的一个程序框图的值需要用直到型循环结构，利用被累加数列的通项公式求解即可⑵根据框图写出对应得程序语句，即可得解【详解】(1)的意图为表示各累加项，即数列的通项公式，故为2T T =(2)程序如下：【点睛】本题主要考查了程序框图的补全，结合题意运用数列的通项公式求出结果，然后再给出程序，需要熟练掌握各知识点。

【步步高】2014届高三数学一轮 13.1 算法初步2导学案理北师大版2014高考会这样考 1.考查算法框图的应用，重点考查算法框图的功能及算法框图的补充；2.和函数、数列、统计等知识相综合，考查算法思想和基本的运算能力、逻辑思维能力．复习备考要这样做 1.准确理解算法的基本概念、理解算法框图的含义和作用是解题的关键，所以复习时要立足双基，抓好基础，对算法语句的复习不需过难，仅需理解几种基本的算法语句；2.复习算法的重点应放在读懂算法框图上，尤其要重视循环结构的算法框图，弄清当型与直到型循环结构的区别，以及进入、退出循环的条件、循环的次数．1．算法通常是指按照一定规则解决某一类问题的明确和有限的步骤．2．算法框图又称程序框图，是一种用程序框、流程线及文字说明来表示算法的图形．通常算法框图由程序框和流程线组成，一个或几个程序框的组合表示算法中的一个步骤；流程线带方向箭头，按照算法步骤的执行顺序将程序框连接起来．3．三种基本逻辑结构(1)顺序结构是由若干个依次执行的步骤组成的，这是任何一个算法都离不开的基本结构．其结构形式为(2)选择结构是指算法的流程根据给定的条件是否成立而选择执行不同的流向的结构形式．其结构形式为(3)循环结构是指从某处开始，按照一定条件反复执行的处理步骤称为循环体，其结构形式为(4)算法的五个特征：概括性、逻辑性、有穷性、不惟一性、普遍性．4．基本算法语句任何一种程序设计语言中都包含五种基本的算法语句，它们分别是：输入语句、输出语句、赋值语句、条件语句、循环语句．5．赋值语句(1)一般形式：变量＝表达式(2)作用：将表达式所代表的值赋给变量．6．条件语句(1)If—Then—Else语句的一般格式为：其结构如图：(2)If—Then语句的一般格式是：其结构如图：7．循环语句(1)For语句的一般格式：其结构如图：(2)Do Loop语句的一般格式：其结构如图：[难点正本疑点清源]1．在数学中，现代意义上“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成的．2．顺序结构、循环结构和选择结构的关系顺序结构是每个算法结构都含有的，而对于循环结构有重复性，选择结构具有选择性没有重复性，并且循环结构中必定包含一个选择结构，用于确定何时终止循环体．循环结构和选择结构都含有顺序结构．3．关于赋值语句，有以下几点需要注意：(1)赋值号左边只能是变量名字，而不是表达式，例如3＝m是错误的．(2)赋值号左右不能对换，赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量，例如Y＝x，表示用x的值替代变量Y的原先的取值，不能改写为x＝Y.因为后者表示用Y的值替代变量x的值．(3)在一个赋值语句中只能给一个变量赋值，不能出现多个“＝”．4．两种循环语句的区别 (1)For 语句For 语句是循环体得以运行的外部“环境”，控制着循环的开始与结束，决定着循环运行的次数． (2)Do Loop 语句Do Loop 语句一般用于不知道循环次数的循环结构，要根据其他形式的终止条件停止循环，在这种情况下才采用．1．如图，是求实数x 的绝对值的算法算法框图，则判断框①中可填________．答案 x >0(或x ≥0)解析 由于|x |＝⎩⎪⎨⎪⎧x ， x ≥0，－x ，x <0或|x |＝⎩⎪⎨⎪⎧x ，x >0，－x ，x ≤0，故根据所给的算法框图，易知可填“x >0？”或“x ≥0？”． 2．(2012·福建)阅读如图所示的算法框图，运行相应的程序，输出的s 值等于________． 答案 －3解析 第一次循环：s ＝1，k ＝1<4，s ＝2×1－1＝1，k ＝1＋1＝2； 第二次循环：k ＝2<4，s ＝2×1－2＝0，k ＝2＋1＝3； 第三次循环：k ＝3<4，s ＝2×0－3＝－3，k ＝3＋1＝4； 当k ＝4时，k <4不成立，循环结束，此时s ＝－3.3．关于算法框图的图形符号的理解，正确的有( )①任何一个算法框图都必须有起止框；②输入框只能在开始框之后，输出框只能放在结束框之前；③判断框是唯一具有超过一个退出点的图形符号；④对于一个算法框图来说，判断框内的条件是唯一的．A．1个B．2个C．3个 D．4个答案 B解析任何一个程序都有开始和结束，因而必须有起止框；输入和输出可以放在算法中任何需要输入、输出的位置；判断框内的条件不是唯一的，如a>b，亦可写为a≤b.故只有①③对．4．(2011·课标全国)执行如图所示的算法框图，如果输入的N是6，那么输出的p是( )A．120 B．720 C．1 440 D．5 040答案 B解析当输入的N是6时，由于k＝1，p＝1，因此p＝p·k＝1.此时k＝1，满足k<6，故k＝k＋1＝2.当k＝2时，p＝1×2，此时满足k<6，故k＝k＋1＝3.当k＝3时，p＝1×2×3，此时满足k<6，故k＝k＋1＝4.当k＝4时，p＝1×2×3×4，此时满足k<6，故k＝k＋1＝5.当k＝5时，p＝1×2×3×4×5，此时满足k<6，故k＝k＋1＝6.当k＝6时，p＝1×2×3×4×5×6＝720，此时k<6不再成立，因此输出p＝720.5．(2012·辽宁)执行如图所示的算法框图，则输出的S值是( )A ．－1B.23C.32D ．4答案 D解析 因为S ＝4，i ＝1<9，所以S ＝－1，i ＝2<9；S ＝23，i ＝3<9；S ＝32，i ＝4<9；S ＝4，i ＝5<9； S ＝－1，i ＝6<9；S ＝23，i ＝7<9；S ＝32，i ＝8<9；S ＝4，i ＝9<9不成立，输出S ＝4.题型一 算法的设计例1 已知函数y ＝⎩⎪⎨⎪⎧－2，x >0，0，x ＝0，2，x <0，写出求该函数函数值的算法及算法框图．思维启迪：可以利用算法的选择结构，严格遵循算法的概念设计算法． 解 算法如下： 第一步，输入x .第二步，如果x >0，则y ＝－2；如果x ＝0，则y ＝0；如果x <0，则y ＝2. 第三步，输出函数值y . 相应的算法框图如图所示．探究提高给出一个问题，设计算法应注意：(1)认真分析问题，联系解决此问题的一般数学方法；(2)综合考虑此类问题中可能涉及的各种情况；(3)将解决问题的过程划分为若干个步骤；(4)用简练的语言将各个步骤表示出来．的值．设计出解决该问题的一个算法，并画出算法框图．解算法如下：第一步，令x＝3.第二步，把x＝3代入y1＝x2－2x－3.第三步，令x＝－5.第四步，把x＝－5代入y2＝x2－2x－3.第五步，令x＝5.第六步，把x＝5代入y3＝x2－2x－3.第七步，把y1，y2，y3的值代入y＝y1＋y2＋y3.第八步，输出y1，y2，y3，y的值．该算法对应的算法框图如图所示：题型二 算法的基本逻辑结构例2 设计算法求11×2＋12×3＋13×4＋…＋12 011×2 012的值，并画出算法框图．思维启迪：(1)这是一个累加求和问题，共2 011项相加； (2)设计一个计数变量，一个累加变量，用循环结构实现这一算法． 解 算法如下：第一步，令S ＝0，i ＝1；第二步，若i ≤2 011成立，则执行第三步； 否则，输出S ，结束算法；第三步，S ＝S ＋1i i ＋；第四步，i ＝i ＋1，返回第二步． 算法框图：方法一 方法二探究提高 利用循环结构表示算法，第一要确定循环变量和初始条件；第二要确定算法中反复执行的部分，即循环变量；第三要确定循环的终止条件．(2012·湖南)如果执行如图所示的算法框图，输入x＝－1，n＝3，则输出的数S＝________.答案－4解析当n＝3时，i＝3－1＝2，满足i≥0，故S＝6×(－1)＋2＋1＝－3.执行i＝i－1后i的值为1，满足i≥0，故S＝(－3)×(－1)＋1＋1＝5.再执行i＝i－1后i的值为0，满足i≥0，故S＝5×(－1)＋0＋1＝－4.继续执行i＝i－1后i的值为－1，不满足i≥0，故输出S＝－4.题型三算法框图的识别及应用例3 如图是求x1，x2，…，x10的乘积S的算法框图，图中空白框中应填入的内容为( ) A．S＝S*(n＋1)B．S＝S*x n＋1C．S＝S*nD．S＝S*x n思维启迪：根据已知条件，结合算法框图求解；可以模拟程序运行的过程，一步一步明确程序运行结果，确定应填入的内容．答案 D解析由题意可知，输出的是10个数的乘积，故循环体应为S＝S*x n，所以选D.探究提高识别算法框图和完善算法框图是高考的重点和热点．解决这类问题：第一，要明确算法框图中的顺序结构、选择结构和循环结构；第二，要识别运行算法框图，理解框图解决的实际问题；第三，按照题目的要求完成解答．对框图的考查常与函数和数列等相结合，进一步强化框图问题的实际背景．如图是统计该6名队员在最近三场比赛中投进的三分球总数的算法框图，则图中判断框应填________，输出的s＝________.答案i<7(i≤6)a1＋a2＋…＋a6解析由题意可知，算法框图是要统计6名队员投进的三分球的总数，由算法框图的循环逻辑知识可知，判断框应填i<7或i≤6，输出的结果就是6名队员投进的三分球的总数，而6名队员投进的三分球数分别为a1，a2，a3，a4，a5，a6，故输出的s＝a1＋a2＋…＋a6.题型四基本算法语句例4 如图所示，在边长为4的正方形ABCD的边上有一点P，沿着折线BCDA 由点B(起点)向点A(终点)运动．设点P运动的路程为x，△APB的面积为y，求y与x之间的函数关系式．并画出算法框图，并写出算法语句．思维启迪：写出函数表达式→分析解析式特征→选择用条件语句．解 由题意可得y ＝⎩⎪⎨⎪⎧2x x x －x x.算法框图如图所示：算法语句：探究提高 实际问题的编程设计一般是先对问题进行认真分析，设计出合理的算法，然后将算法用算法框图表示出来，最后根据框图利用算法语句写出程序．设计求满足条件1＋23＋33＋…＋n 3>106的最小自然数的算法语句，并画出算法框图．解 算法框图如图所示： 算法语句如下：高考中的算法问题典例：(5分)(2012·安徽)如图所示，算法框图(算法流程图)的输出结果是( )A．3 B．4 C．5 D．8考点分析本题属于算法和数列的交汇性问题，主要考查算法框图的功能和基本运算．解题策略本题可以直接按照算法框图的流程逐步进行计算，也可以从算法框图的功能出发，分析x的值的规律来解决问题．解析方法一当x＝1，y＝1时，满足x≤4，则x＝2，y＝2；当x＝2，y＝2时，满足x≤4，则x＝2×2＝4，y＝2＋1＝3；当x＝4，y＝3时，满足x≤4，则x＝2×4＝8，y＝3＋1＝4；当x＝8，y＝4时，不满足x≤4，则输出y＝4.方法二由算法框图，可知x的值构成一个首项为1，公比为2的等比数列，其通项公式为a n＝2n－1，而y的值构成一个首项为1，公差为1的等差数列，其通项公式为b n＝n.显然该算法框图就是求解使得a n>4时b n的值．由a n>4，即2n－1>4，解得n>3，故n的最小值为4，所以输出的值为y＝b4＝4.答案 B解后反思算法框图的填充和功能是算法问题在高考中的主要考查形式，和函数、数列的结合是算法问题的常见载体，解决问题的关键是搞清算法的实质，模拟运行算法的结果.方法与技巧1．在设计一个算法的过程中要牢记它的五个特征：概括性、逻辑性、有穷性、不唯一性、普遍性．2．在画算法框图时首先要进行结构的选择．若所要解决的问题不需要分情况讨论，只用顺序结构就能解决；若所要解决的问题要分若干种情况讨论时，就必须引入选择结构；若所要解决的问题要进行许多重复的步骤，且这些步骤之间又有相同的规律时，就必须引入变量，应用循环结构．3．算法框图的选择结构和循环结构分别对应算法语句的条件语句和循环语句，两种语句的阅读理解是复习重点．失误与防范1．注意起止框与处理框、判断框与循环框的不同．2．注意选择结构与循环结构的联系．3．要弄清楚三种基本逻辑结构的构成方式及功能，以免使用时造成混乱或错误．4．循环语句主要解决遇到需要反复执行的任务，用循环语句来编写程序．A组专项基础训练(时间：35分钟，满分：57分)一、选择题(每小题5分，共20分)1．算法共有三种逻辑结构，即顺序结构、选择结构、循环结构，下列说法正确的是( ) A．一个算法只能含有一种逻辑结构B．一个算法最多可以包含两种逻辑结构C．一个算法必须含有上述三种逻辑结构D．一个算法可以含有上述三种逻辑结构中的任一种答案 D解析在一个算法中，可出现顺序结构、选择结构、循环结构三种结构中的任一种．2．已知一个算法：(1)m＝a.(2)如果b<m，则m＝b，输出m；否则执行第3步．(3)如果c<m，则m＝c，输出m.如果a＝3，b＝6，c＝2，那么执行这个算法的结果是( )A．3 B．6 C．2 D．m答案 C解析当a＝3，b＝6，c＝2时，依据算法设计，执行后，m＝a＝3<b＝6，c＝2<a＝3 ＝m，∴c＝2＝m，即输出m的值为2，故选C.3．(2012·天津)阅读如图所示的算法框图，运行相应的程序，当输入x的值为－25时，输出x的值为( )A．－1 B．1 C．3 D．9答案 C解析当x＝－25时，|x|>1，所以x＝25－1＝4>1，x＝4－1＝1>1不成立，所以输出x＝2×1＋1＝3.4．(2012·北京)执行如图所示的算法框图，输出的S值为( )A．2 B．4 C．8 D．16答案 C解析当k＝0时，满足k<3，因此S＝1×20＝1；当k＝1时，满足k<3，因此S＝1×21＝2；当k＝2时，满足k<3，因此S＝2×22＝8；当k＝3时，不满足k<3，因此输出S＝8.二、填空题(每小题5分，共15分)5．某算法的算法框图如图所示，则输出量y与输入实数x满足的关系式是________．答案 y ＝⎩⎪⎨⎪⎧2x，x ≤1x －2，x >1解析 由题意知，算法框图表达的是一个分段函数y ＝⎩⎪⎨⎪⎧2x，x ≤1x －2，x >1.6．如图是求12＋22＋32＋…＋1002的值的算法框图，则正整数n ＝________.答案 100解析 第一次判断执行后，i ＝2，s ＝12；第二次判断执行后，i ＝3，s ＝12＋22，而题目要求计算12＋22＋…＋1002，故n ＝100.7．(2012·广东)执行如图所示的算法框图，若输入n 的值为8，则输出s 的值为________．答案 8解析 当i ＝2，k ＝1时，s ＝1×(1×2)＝2；当i ＝4，k ＝2时，s ＝12×(2×4)＝4；当i ＝6，k ＝3时，s ＝13×(4×6)＝8；当i＝8时，i<n不成立，输出s＝8.三、解答题(共22分)8．(10分)任意给定3个正实数，设计一个算法，判断以这3个正实数为三条边边长的三角形是否存在，并画出这个算法的算法框图．解算法如下：第一步，输入3个正实数a，b，c.第二步，判断a＋b>c，b＋c>a，c＋a>b是否同时成立．若是，则存在这样的三角形；否则，不存在这样的三角形．算法框图：9．(12分)某工种按工时计算工资，每月总工资＝每月劳动时间(小时)×每小时工资，从总工资中扣除10%作公积金，剩余的为应发工资，当输入劳动时间和每小时工资数时，试编写一个算法输出应发工资，并写出程序，画出算法框图．解算法如下：第一步，输入每月劳动时间t和每小时工资a；第二步，求每月总工资y＝每月劳动时间t×每小时工资a；第三步，求应发工资z＝每月总工资y×(1－10%)；第四步，输出应发工资z.算法框图如图：程序：B 组 专项能力提升 (时间：25分钟，满分：43分)一、选择题(每小题5分，共15分)1．(2011·天津)阅读下边的算法框图，运行相应的程序，则输出的i 的值为( )A ．3B ．4C ．5D ．6答案 B解析 i ＝1时，a ＝2；i ＝2时，a ＝5；i ＝3时，a ＝16；当i ＝4时，a ＝65>50.即条件a >50成立，所以输出的i 的值为4.2．(2012·课标全国)如果执行如图所示的算法框图，输入正整数N (N ≥2)和实数a 1，a 2，…，a N ，输出A ，B ，则 ( )A ．A ＋B 为a 1，a 2，…，a N 的和B.A ＋B 2为a 1，a 2，…，a N 的算术平均数C ．A 和B 分别是a 1，a 2，…，a N 中最大的数和最小的数D ．A 和B 分别是a 1，a 2，…，a N 中最小的数和最大的数 答案 C解析 由于x ＝a k ，且x >A 时，将x 值赋给A ，因此最后输出的A 值是a 1，a 2，…，a N 中最大的数；由于x ＝a k ，且x <B 时，将x 值赋给B ，因此最后输出的B 值是a 1，a 2，…，a N 中最小的数．3．如图，若依次输入的x 分别为56π、π6，相应输出的y 分别为y 1、y 2，则y 1、y 2的大小关系是( )A ．y 1＝y 2B ．y 1>y 2C ．y 1<y 2D ．无法确定答案 C解析 由算法框图可知，当输入的x 为5π6时，sin 5π6>cos 5π6成立，所以输出的y 1＝sin 5π6＝12；当输入的x 为π6时，sin π6>cos π6不成立，所以输出的y 2＝cos π6＝32，所以y 1<y 2.二、填空题(每小题5分，共15分)4．(2012·浙江)若某算法框图如图所示，则该程序运行后输出的T 的值是________．答案1120解析 由算法框图可知，当T ＝1，i ＝1时，T ＝Ti ＝1，i ＝2，不满足i >5； T ＝T i ＝12，i ＝3，不满足i >5； T ＝T i ＝16，i ＝4，不满足i >5； T ＝T i ＝124，i ＝5，不满足i >5； T ＝T i ＝1120，i ＝6，满足i >5. 输出T ＝1120.5．(2011·安徽)如图所示，算法框图(流程图)的输出结果是________．答案 15解析 由T ＝T ＋k 可知T 是一个累加变量，原题实质为求1＋2＋3＋...＋k 的和，其和为k k ＋2.令k k ＋2≤105，得k ≤14.故当k ＝15时，T ＝1＋2＋3＋ (15)120>105，此时输出k ＝15.6．执行如图所示的算法框图，输出的A 为________．答案 2 047解析本题计算的是递推数列a0＝1，a n＋1＝2a n＋1 (n＝0,1,2，…)的第11项，{a n＋1}是首项为2，公比为2的等比数列，故a10＋1＝211，故a10＝2 047.三、解答题7．(13分)给出以下10个数：5,9,80,43,95,73,28,17,60,36.要求把大于40的数找出来并输出．试画出该问题的算法程序框图．解算法框图如下：。

一、选择题1．执行如图所示的程序框图输出的结果是（）A．8B．6C．5D．32．该程序中k的值是（）A．9 B．10 C．11 D．12 3．阅读算法框图，如果输出的函数值在区间[]1,8上，则输入的实数x的取值范围是（）A ．[)0,2B ．[]2,7C ．[]2,4 D ．[]0,74．执行如下图的程序框图，输出S 的值是（ ）A ．2B ．1C ．12 D ．-15．执行如图所示的程序框图，则输出的S =（ ）A ．1-B ．2-C ．2D ．126．执行如图所示的程序框图，输出S 的值为（ ）A ．1-B ．0C ．1D ．27．执行如图所示的程序框图，若输出的结果为126，则判断框内的条件可以为（ ）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤8．某程序框图如图所示，则该程序运行后输出的值是（ ）A ．3B ．3C 3D 3 9．如图所给的程序运行结果为41S =，那么判断框中应填入的关于k 的条件是( )A ．7k ≥？B ．6k ≥？C ．5k ≥？D ．6k >？ 10．执行如下图的程序框图，如果输入的N 的值是7，那么输出的p 的值是（ ）A ．3B ．15C ．105D ．945 11．若如图所示的程序框图的输出结果为二进制数(2)10101化为十进制数(注：01234(2)101011202120212=⨯+⨯+⨯+⨯+⨯)，那么处理框①内可填入（ ）A ．2S S i =+B ．S S i =+C ．21S S i =+-D ．2S S i =+ 12．《数书九章》是我国宋代数学家秦九韶的著作，其中给出了求多项式的值的秦九韶算法，如图所示的程序框图给出了一个利用秦九韶算法求某多项式值的实例，若输入的13x =，输出的12181=y 则判断框“”中应填入的是（ ）A ．2?k ≤B ．3?k ≤C ．4?k ≤D ．5?≤k二、填空题13．按下列程序框图运算：规定：程序运行到“判断结果是否大于244”为1次运算.若运算进行3次才停止，则x 的取值范围是__________．14．若下面程序中输入的n 值为2017，则输出的值为__________.15．执行如图所示的程序框图若输人x 的值为3，则输出y 的值为______．16．执行如图所示的程序框图，输入l=2，m=3，n=5，则输出的y 的值____17．更相减损术是出自《九章算术》的一种算法.如图所示的程序框图是根据更相减损术写出的，若输入91a =，39b =，则输出的值为______．18．如下图，程序框图中，若输入4,10m n ==，则输出a 的值是________.19．如图所示的程序框图，输出S 的结果是__________．20．某程序框图如图所示，该程序运行后输出的S 为____________.三、解答题21．如图所示的程序框图，根据该图和下列各小题的条件回答下面的几个小题．(1)该程序框图解决的是一个什么问题？(2)当输入的x的值为0和4时，输出的值相等，问当输入的x的值为3时，输出的值为多大？(3)在(2)的条件下要想使输出的值最大，输入的x的值应为多大？22．某函数的解析式由如图所示的程序框图给出.（1）写出该函数的解析式；（2）执行该程序框图，若输出的结果为4，求输入的实数x的值.23．某城市规定，在法定工作时间内每小时的工资是8元，在法定工作时间外每小时的加班工资为16元，某人在一周内工作60小时，其中加班20小时．编写程序，计算这个人这一周所得的工资.24．图C1-6所示的程序框图表示了一个什么样的算法？试用当型循环写出它的算法并画出相应的程序框图．25．写出一个算法，求底面边长为42，侧棱长为5的正四棱锥的体积．26．由键盘输入三个整数a,b,c,输出其中最大的数,画出其算法的程序框图,并写出程序.【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】根据程序框图循环结构运算，依次代入求解即可．【详解】根据程序框图和循环结构算法原理，计算过程如下：1,1,x y z x y ===+第一次循环2,1,2z x y ===第二次循环3,2,3z x y ===第三次循环5,3,5z x y ===第四次循环8z =，退出循环输一次8z =.所以选A【点睛】本题考查了程序框图的基本结构和运算，主要是掌握循环结构在何时退出循环结构，属于基础题．2．B解析：B【分析】本题只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可（注意避免计算错误）．【详解】3,2,8,814x k y ===<，第一次循环，4,10,1014k y ==<；第二次循环，6,12,1214k y ==<；第三次循环，8,14,1414k y ===；第四次循环，10,16,1614k y ==>，退出循环，输出10k =，故选：B.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.3．D解析：D 【详解】 解答： 根据题意，得 当x ∈(−2,2)时,f (x )=2x ， 1⩽2x ⩽8，∴0⩽x ⩽3；故02x ≤< 当x ∉(−2,2)时,f (x )=x +1， ∴1⩽x +1⩽8， ∴0⩽x ⩽7，∴x 的取值范围是[2,7]. 故选：D点睛：本题考查的实质问题是分段函数，当给出函数值求自变量的值时，先假设所求的值在分段函数定义区间的各段上，然后求出相应自变量的值，切记要代入检验，看所求的自变量的值是否满足相应段自变量的取值范围．4．C解析：C 【分析】模拟程序的运行，依次写出每次循环得到的k 和S 值，根据题意即可得到结果. 【详解】程序运行如下，k =1，S ＝112-＝﹣1， k ＝2，S ＝()111--＝12；k ＝3，S ＝12112=-；k ＝4，S ＝11-2＝﹣1… 变量S 的值以3为周期循环变化，当k =2015时，12S =， k =2016时，结束循环，输出S 的值为12． 故选：C ． 【点睛】本题考查程序框图，是当型结构，即先判断后执行，满足条件执行循环，不满足条件，跳出循环，算法结束，解答的关键是算准周期，属于中档题．5．D解析：D 【分析】列举出前四次循环，可知，该算法循环是以3为周期的周期循环，利用周期性可得出输出的S 的值. 【详解】第一次循环，02020k =≤成立，1112S ==--，011k =+=； 第二次循环，12020k =≤成立，()11112S ==--，112k =+=；第三次循环，22020k =≤成立，12112S ==-，213k =+=；第四次循环，32020k =≤成立，1112S ==--，314k =+=； 由上可知，该算法循环是周期循环，且周期为3，依次类推，执行最后一次循环，20202020k =≤成立，且202036731=⨯+，此时12S =， 202012021k =+=，20212020k =≤不成立，跳出循环体，输出S 的值为12. 故选：D. 【点睛】本题考查利用程序框图计算输出结果，推导出循环的周期性是解题的关键，考查计算能力，属于中等题.6．C解析：C 【分析】 由函数()πsin2xf x =，可求周期为4，()(1)(2)(3)40+++=f f f f ，由题意可知()(1)(2)(2021)=2021(1)1=+++==S f f f f f【详解】由函数()πsin 2x f x =的周期为2π4π2T ==， ()π1sin 12f ==，()2π2sin 02f ==，()3π3sin12f ==-，()4π4sin 02f ==，()(1)(2)(3)40+++=f f f f()(1)(2)(2021)=2021(1)1∴=+++==S f f f f f .故选：C 【点睛】本题考查了程序框图求和，正弦型三角函数的周期等基本知识，考查了运算求解能力和逻辑推理能力，属于一般题目.7．B解析：B 【分析】根据框图，模拟程序运行即可求解. 【详解】根据框图，执行程序，12,2S n ==；1222,3S n =+=；⋯12222,1i S n i =++⋯+=+，令12222126i S =++⋯+=， 解得6i =，即7n =时结束程序， 所以6n ≤， 故选 ：B 【点睛】本题主要考查了程序框图，循环结构，条件分支结构，等比数列求和，属于中档题.genju8．D解析：D 【分析】 该框图的功能是计算:234562017sinsin sin sin sin sin sin3333333πππππππ+++++++,再根据正弦函数的周期性以及特殊角的三角函数值计算可得答案. 【详解】该框图的功能是计算:234562017sinsinsin sin sin sin sin3333333πππππππ+++++++.因为7132017sinsinsin sin 33332ππππ=====28142012sinsin sin sin3333ππππ=====,39152013sinsin sin sin03333ππππ=====,410162014sin sin sin sin 3333ππππ=====,511172015sinsin sin sin3333ππππ===== 612182016sinsin sin sin 03333ππππ=====, 所以234562017sin sinsin sin sin sin sin3333333πππππππ+++++++3373363360336(336(3360=+⨯+⨯+⨯+⨯=故选:D 【点睛】本题考查了程序框图的循环结构,考查了三角函数的周期性以及特殊角的三角函数值,理解程序框图的功能是解题关键,属于基础题.9．B解析：B 【分析】程序运行结果为41S =,执行程序,当6k =时,判断条件成立,当5k =时,判断条件不成立,输出41S =,即可选出答案. 【详解】根据程序框图,运行如下: 初始10,1k S ==,判断条件成立,得到11011S =+=,1019k =-=; 判断条件成立,得到11920S =+=,918k =-=; 判断条件成立,得到20828S =+=,817k =-=; 判断条件成立,得到28735S =+=,716k =-=; 判断条件成立,得到35641S =+=,615k =-=; 判断条件不成立,输出41S =,退出循环,即6k ≥符合题意. 故选:B. 【点睛】本题考查了程序框图的识别与判断,弄清进入循环体和跳出循环体的条件是解决本题的关键,考查了学生的推理能力,属于基础题.10．C解析：C 【分析】由已知中的程序框图，得到该程序的功能是利用循环结构计算并输出变量p 的值，模拟程序的运行过程，分析循环中各变量的变化情况，可得答案． 【详解】模拟程序的运行，可得：7,1,1N k p ===， 满足条件7k <，执行循环体，3,3k p ==； 满足条件7k <，执行循环体，5,15k p ==； 满足条件7k <，执行循环体，7,105k p ==； 此时，不满足条件7k <，推出循环，输出p 的值为105， 故选C ． 【点睛】本题主要考查了程序框图的应用问题，解答中应模拟程序框图的运行过程，逐次计算是解答的关键，着重考查了推理与运算能力，属于基础题．11．D解析：D 【解析】 【分析】由二进制数化为十进制数，得出(2)1010121=，得到运行程序框输出的结果，验证答案，即可求解. 【详解】由题意，二进制数()210101化为十进制数43210(2)10101120212021221=⨯+⨯+⨯+⨯+⨯=，即运行程序框输出的结果为21，经验证可得，处理框内可填入2S S i =+，故选D. 【点睛】本题主要考查了二进制与十进制的转化，以及循环结构的程序框图的计算与输出，着重考查了推理与运算能力，属于基础题.12．C解析：C 【解析】 【分析】模拟程序的运行过程，即可得出输出y 的值时判断框中应填入的是什么． 【详解】模拟程序的运行过程如下， 输入114,1,11333x k y ===⨯+=， 41132,1339k y ==⨯+=，131403,19327k y ==⨯+=， 4011214,127381k y ==⨯+=， 此时不满足循环条件，输出12181=y ； 则判断框中应填入的是4?k ≤．故选：C ． 【点睛】本题考查了算法与程序框图的应用问题，理解框图的功能是解题的关键，是基础题．二、填空题13．【分析】根据题意得到不等式和计算得到答案【详解】根据题意知：且故故答案为：【点睛】本题考查了程序框图没有考虑完整情况是容易发生的错误 解析：(]10,28【分析】根据题意得到不等式()3322244x --≤和()333222244x --->⎡⎤⎣⎦，计算得到答案. 【详解】根据题意知：()332224428x x --≤∴≤且()33322224410x x --->∴>⎡⎤⎣⎦ 故(]10,28x ∈ 故答案为：(]10,28 【点睛】本题考查了程序框图，没有考虑完整情况是容易发生的错误.14．【分析】根据程序框图的算法功能可知该程序是计算的值再根据裂项相消法即可求出【详解】根据程序框图的算法功能可知该程序是计算的值所以故答案为：【点睛】本题主要考查程序框图的算法功能的理解以及数列求和属于解析：20172018【分析】根据程序框图的算法功能可知，该程序是计算111112233420172018++++⨯⨯⨯⨯的值，再根据裂项相消法即可求出． 【详解】根据程序框图的算法功能可知，该程序是计算111112233420172018++++⨯⨯⨯⨯的值．所以111112233420172018++++⨯⨯⨯⨯111111112017122334201720182018⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． 故答案为：20172018． 【点睛】本题主要考查程序框图的算法功能的理解以及数列求和，属于基础题．常见的数列求和方法有：公式法，裂项相消法，分组求和法，倒序相加求和法，并项求和法，错位相减法等，根据数列的特征选择对应的方法是解题的关键．15．63【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量y 的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】解：模拟程序的运行可得x=3y=7不满足条件|x-y|解析：63 【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量y 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案． 【详解】解：模拟程序的运行，可得 x=3 y=7不满足条件|x-y|＞31，执行循环体，x=7，y=15 不满足条件|x-y|＞31，执行循环体，x=15，y=31 不满足条件|x-y|＞31，执行循环体，x=31，y=63 此时，满足条件|x-y|＞31，退出循环，输出y 的值为63． 故答案为63． 【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．16．68【解析】试题分析：第一次循环：；第二次循环：；第三次循环：；结束循环输出考点：循环结构流程图【名师点睛】算法与流程图的考查侧重于对流程图循环结构的考查先明晰算法及流程图的相关概念包括选择结构循环解析：68 【解析】试题分析：第一次循环：702213155278y =⨯+⨯+⨯=；第二次循环：278105173y =-=；第三次循环：173********y =-=<；结束循环，输出68.y =考点：循环结构流程图【名师点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.17．【解析】输入执行程序框图第一次；第二次；第三次；第四次满足输出条件输出的的值为故答案为 解析：13【解析】输入91,39a b ==，执行程序框图，第一次52,39a b ==；第二次13,39a b ==；第三次13,26a b ==；第四次13,13,a b a b ===，满足输出条件，输出的a 的值为13，故答案为13.18．20【解析】模拟执行程序可得：不满足条件整除以不满足条件整除以不满足条件整除以不满足条件整除以满足条件整除以退出循环输出的值为点睛：本题主要考查的程序框图的知识点解题的关键是要读懂程序框图模拟执行程解析：20 【解析】模拟执行程序，可得：4,10m n ==，1i =，4a =不满足条件n 整除以a2i =，8a =不满足条件n 整除以a 3i =，12a =不满足条件n 整除以a 4i =，16a =不满足条件n 整除以a5i =，20a =满足条件n 整除以a ，退出循环，输出a 的值为20点睛：本题主要考查的程序框图的知识点．解题的关键是要读懂程序框图．模拟执行程序，依次写出每次循环得到的i ，a 的值，当20a =的时候，满足条件n 整除以a ，退出循环，即可得到输出a 的值为20．19．【解析】阅读流程图可得该流程图计算的数值为： 解析：【解析】阅读流程图可得，该流程图计算的数值为：13sin 0sin 1sin 52626262S ππππππ⎛⎫⎛⎫⎛⎫=⨯++⨯+++⨯+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 20．【分析】列出前几次循环找出该算法循环的周期性然后利用周期性求出输出结果的值【详解】成立执行第一次循环；成立执行第二次循环；成立执行第三次循环；成立执行第四次循环；成立执行第五次循环由上可知该算法循环解析：13. 【分析】列出前几次循环，找出该算法循环的周期性，然后利用周期性求出输出结果S 的值. 【详解】12011i =≤成立，执行第一次循环，12312S +==--，112i =+=； 22011i =≤成立，执行第二次循环，()()131132S +-==---，213i =+=；32011i =≤成立，执行第三次循环，11121312S ⎛⎫+- ⎪⎝⎭==⎛⎫-- ⎪⎝⎭，314i =+=； 42011i =≤成立，执行第四次循环，1132113S +==-，415i =+=；52011i =≤成立，执行第五次循环，12312S +==--，516i =+=. 由上可知，该算法循环是以4次为一个循环周期，执行完最后一次循环，2012i =，201255024=⨯+，因此，输出的结果S 的值为13，故答案为13. 【点睛】本题考查算法的周期性，解题时要结合算法程序框图得出算法循环的周期性，考查推理能力与计算能力，属于中等题.三、解答题21．（1）求二次函数f (x )＝－x 2＋mx 的函数值（2）输入的x 的值为3时，输出的f (x )的值为3（3）2 【分析】（1）模拟执行程序框图即可确定程序框图的功能是求2()f x x mx =-+的函数值． （2）由已知可得：(0)f f =（4），从而有1640m -+=，即可解得m ，即可求f （3）的值．（3）由已知可得2()(2)4f x x =--+，从而当2x =时，()4max f x =，即可得解． 【详解】解：（1）该程序框图解决的是求二次函教2()f x x mx =-+的函数值的问题； （2）当输入的x 的值为0和4时，输出的值相等，即()()04f f =， 因为(0)0f =， ()4164f m =-+， 所以1640m -+=， 所以4m =，所以2()4f x x x =-+，则()233433f =-+⨯=，所以当输入的x 的值为3时，输出的()f x 值为3； （3）因为22()4(2)4f x x x x =-+=--+， 当2x =时，()4max f x =，所以要想使输出的值最大，输入的x 的值应为2； 【点睛】本题主要考查了二次函数的图象和性质，考查了程序框图和算法，属于基础题．22．(1) 22,0log ,042,4x x x y x x x ⎧<⎪=<≤⎨⎪>⎩当0x =时，y 无解.(2) 2x =-.【分析】(1)根据框图得到函数解析式；（2）结合第一问得到的函数表达式，分情况得到x 值即可. 【详解】（1）函数解析式为22,0log ,042,4x x x y x x x ⎧<⎪=<≤⎨⎪>⎩， 当0x =时，y 无解.（2）当0x <时，24x =，2x =-或2（舍）. 当04x ≤≤时，2log 4x =，解得16x =（舍）. 当4x >时，24x =，解得2x =（舍） 所以2x =- 【点睛】这个题目考查了程序框图的应用，以及分段函数的应用；解决分段函数求值问题的策略：(1)在求分段函数的值f (x 0)时，一定要首先判断x 0属于定义域的哪个子集，然后再代入相应的关系式；(2)分段函数是指自变量在不同的取值范围内，其对应法则也不同的函数，分段函数是一个函数，而不是多个函数；分段函数的定义域是各段定义域的并集，值域是各段值域的并集，故解分段函数时要分段解决；(3)求f (f (f (a )))的值时，一般要遵循由里向外逐层计算的原则. 23．见解析； 【解析】试题分析: 先利用INPUT 语句输入法定工作时间以及加班工作时间，再分别赋值法定工作时间工资,加班工作时间工资以及总工资，最后输出一周所得的工资. 试题 程序如下：点睛：24．见解析【解析】【分析】根据图中的流程图表示的算法可知这是一个计算10个数的平均数的算法，根据当型循环结构的特点，先判断I 是否小于等于10，再执行运算，由此写出当型循环的算法并画出流程图【详解】这是一个计算10个数的平均数的算法．当型循环的算法如下：第一步，0S =.第二步，1I =.第三步，如果I 小于等于10，执行第四步；否则，转第七步第四步，输入G .第五步，.S S G =+第六步，1I I =+，返回第三步． 第七步，10S A =. 第八步，输出A .程序框图如图．【点睛】本题是一道关于设计流程图的题目，解答本题的关键是理解流程图的功能，属于中档题。

一、选择题1．如图是计算11113519++++的值的一个程序框图，其中判断框内应填的是（ ）A ．10iB ．10i ≤C ．10i >D ．10i <2．执行如图所示的程序框图，如果输入n=3，输出的S=（ ）A ．67B ．37C ．89D ．493．若执行如图所示的程序框图，则输出S 的值是（ ）A．63 B．15 C．31 D．32 4．执行如图所示的程序框图，若输入10n=，则输出的结果是（）A．11114135717P⎛⎫=-+-++⎪⎝⎭B．11114135719P⎛⎫=-+-+-⎪⎝⎭C．11114135721P⎛⎫=-+-+⋯+⎪⎝⎭D．11114135721P⎛⎫=-+-+-⎪⎝⎭5．已知函数1()(1)g xx x=+，程序框图如图所示，若输出的结果1011S=，则判断框中可以填入的关于n的判断条件是（）A ． 10?n ≤B ．10?n >C ． 11?n ≤D ． 11?n >6．程大位是明代著名数学家，他的《新编直指算法统宗》是中国历史上一部影响巨大的著作．卷八中第33问：“今有三角果一垛，底阔每面七个．问该若干？”如图是解决该问题的程序框图．执行该程序框图，求得该垛果子的总数S 为（ ）A ．28B ．56C ．84D ．1207．执行如图所示的程序框图，则输出的k的值为（）A．3 B．4 C．5 D．6 8．下列赋值语句正确的是 ()A．S＝S＋i2B．A＝－AC．x＝2x＋1 D．P＝9．执行如图的程序框图，则输出x的值是 ()A．2018B．2019C．12D．210．执行如图所示的程序框图，若输出的结果为63，则判断框中应填入的条件为（）A．4i≤B．5i≤C．6i≤D．7i≤11．执行如图所示的程序框图，若输出的结果为48，则输入k的值可以为A．6B．10C．8D．4) 12．执行如图所示程序框图，当输入的x为2019时，输出的y(A．28B．10C．4D．2二、填空题13．按下列程序框图运算：规定：程序运行到“判断结果是否大于244”为1次运算.若运算进行3次才停止，则x 的取值范围是__________．14．执行如图所示的程序框图若输人x 的值为3，则输出y 的值为______．15．执行如图所示的程序框图，若输入的255a =，68b =，则输出的a 是__________．16．下图程序运行结果是________．17．将二进制数110 101（2）转为七进制数，结果为________． 18．右图程序框图的运行结果是____________________19．已知实数]9[1x ，，执行如图所示的流程图，则输出的x 不小于55的概率为________．20．一个算法的程序框图如图所示，则该算法运行后输出的结果为________.三、解答题21．已知函数1,00,03,0x x y x x x +>⎧⎪==⎨⎪--<⎩，设计一个算法，输入自变量x 的值，输出对应的函数值．（1）请写出算法步骤； （2）画出算法框图．22．如图是解决某个问题而绘制的程序框图，仔细分析各框内的内容及图框之间的关系，回答下面的问题：(1).图框①中2x ＝的含义是什么？ (2).图框②中1y ax b ＝＋的含义是什么？ (3).图框④中2y ax b ＝＋的含义是什么？ (4).该程序框图解决的是怎样的问题？(5).当最终输出的结果是13y ＝，22y ＝-时，求()y f x ＝的解析式．23．编写一个程序，要求输入两个正数a 和b 的值，输出a b 和b a 的值，并画出程序框图. 24．已知某算法的程序框图如图所示,若将输出的(x ,y )值依次记为(x 1,y 1),(x 2,y 2),…,(x n ,y n ),… (1)若程序运行中输出的一个数组是(9,t ),求t 的值. (2)程序结束时,共输出(x ,y )的组数为多少? (3)写出程序框图的程序语句.25．写出计算102+202+…+1 0002的算法程序,并画出相应的程序框图.26．画出求的程序框图．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】分析式子11113519++++的特征，可以得到程序框图的功能是求11113519S=++++的值，观察循环量i的特征，得到结果.【详解】由于程序框图的功能是求11113519S=++++的值，分母n的初值为1，终值为19，步长为2，故程序共执行10次，故循环变量i的值不大于10时，应不满足条件，继续执行循环，大于10时，应满足条件，退出循环，故判断框内应填的是i＞10，故选：C.【点睛】思路点睛：该题考查的是有关程序框图的问题，解题思路如下：（1）观察式子的特征，得到程序框图的功能；（2）由式子的项数，得到循环量i的特征，得到结果.2．B解析：B【详解】试题分析：由题意得，输出的为数列的前三项和，而，∴，故选B.考点：1程序框图；2.裂项相消法求数列的和.【名师点睛】本题主要考查了数列求和背景下的程序框图问题，属于容易题，解题过程中首先要弄清程序框图所表达的含义，解决循环结构的程序框图问题关键是列出每次循环后的变量取值情况，循环次数较多时，需总结规律，若循环次数较少可以全部列出.3．C解析：C 【分析】根据程序框图模拟程序计算即可求解. 【详解】模拟程序的运行，可得1S =，1i =； 满足条件5i <，执行循环体，3S =，2i =； 满足条件5i <，执行循环体，7=S ，3i =； 满足条件5i <，执行循环体，15S =，4i =； 满足条件5i <，执行循环体，31S =，5i =； 此时，不满足条件5i <，退出循环，输出S 的值为31. 故选：C 【点睛】本题主要考查了程序框图，循环结构，属于中档题.4．B解析：B 【分析】按照程序框图运行程序，寻找规律，直到i n >输出结果即可. 【详解】按照程序框图运行程序，输入10n =，0S =，1i =，则1S =，2i =，不满足i n >，循环；113S =-，3i =，不满足i n >，循环；11135S =-+，4i =，不满足i n >，循环；以此类推，1111135719S =-+--⋅⋅⋅-，11=i ，满足i n >，则4P S =， 11114135719P ⎛⎫∴=-+--⋅⋅⋅- ⎪⎝⎭.故选：B . 【点睛】本题考查根据程序框图循环结构计算输出结果的问题，属于常考题型.5．A解析：A 【分析】按照程序框图执行几次，找出此框图的算法功能，再根据已知条件1011S =进一步判断框内条件即可.【详解】按照程序框图依次执行： 110,1,01122S n S ===+=-⨯ 1111112,11+12232233n S ==-+=--=-⨯ 以此类推，可得111S n =-+ . 若1011S =，可得10n =，若要输出1011S =，则判断框内应填10n ≤？. 故选：A.【点睛】本题主要考查根据程序框图的输出结果判断程序框图中的选择条件，考查逻辑推理能力. 6．C解析：C【分析】由已知中的程序可知：该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序运行过程，分析循环中各变量值的变化情况，即可求解.【详解】模拟程序的运行，可得：0,0,0i n S ===执行循环体，1,1,1i n S ===；不满足判断条件7i ≥，执行循环体，2,3,4i n S ===；不满足判断条件7i ≥，执行循环体，3,6,10i n S ===；不满足判断条件7i ≥，执行循环体，4,10,20i n S ===；不满足判断条件7i ≥，执行循环体，5,15,35i n S ===；不满足判断条件7i ≥，执行循环体，6,21,56i n S ===；不满足判断条件7i ≥，执行循环体，7,28,84i n S ===；满足判断条件7i ≥，退出循环，输出S 的值为84.故选C.【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中模拟程序运行的过程，通过逐次计算和找出计算的规律是解答的关键，着重考查了推理与计算能力，属于基础题.7．C解析：C【分析】根据框图模拟程序运算即可.【详解】第一次执行程序，2111S =⨯-=，25S >-，继续循环，第二次执行程序，2k =，2121S =⨯-=-，25S >-，继续循环，第三次执行程序，3k =，2(1)35S =⨯--=-，25S >-，继续循环，第四次执行程序，4k =，2(5)414S =⨯--=-，25S >-，继续循环，第五次执行程序，5k =，2(14)532S =⨯--=-，25S <-，跳出循环，输出5k =，结束.故选C.【点睛】本题主要考查了程序框图，涉及循环结构，解题关键注意何时跳出循环，属于中档题. 8．B解析：B【解析】在程序语句中乘方要用“^”表示，所以A 项不正确；乘号“*”不能省略，所以C 项不正确；DSQR(x)表示，所以D 项不正确；B 选项是将变量A 的相反数赋给变量A ，则B 项正确．选B.9．D解析：D【分析】模拟执行程序框图，依次写出每次循环得到的x ，y 的值，当2019y = 时，不满足条件退出循环，输出x 的值即可得解．【详解】解：模拟执行程序框图，可得2,0x y ==.满足条件2019y <，执行循环体，1,1x y =-=；满足条件2019y <，执行循环体，1,22x y == ； 满足条件2019y <，执行循环体，2,3x y ==； 满足条件2019y <，执行循环体，1,4x y =-= ；…观察规律可知，x 的取值周期为3，由于20196733⨯＝，可得：满足条件2019y <，执行循环体，当2,2019x y == ,不满足条件2019y <，退出循环，输出x 的值为2．故选D ．【点睛】本题主要考查了循环结构的程序框图，依次写出每次循环得到的x ，y 的值，根据循环的周期，得到跳出循环时x 的值是解题的关键．10．B解析：B【解析】【分析】模拟执行程序框图，依次写出每次循环得到的,i S 的值，当输出的63S =时，退出循环，对应的条件为5i ≤，从而得到结果.【详解】当=11S i =，时，不满足输出条件，故进行循环，执行循环体；当1123,2S i =+==，不满足输出条件，故进行循环，执行循环体；当2327,3S i =+==，不满足输出条件，故进行循环，执行循环体；当37215,4S i =+==，不满足输出条件，故进行循环，执行循环体；当415231,5S i =+==，不满足输出条件，故进行循环，执行循环体；当313263,6S i =+==，满足输出条件，故判断框中应填入的条件为5i ≤， 故选B.【点睛】该题考查的是有关程序框图的问题，根据题意写出判断框中需要填入的条件，属于简单题目. 11．C解析：C【分析】执行如图所示的程序框图，逐次循环，计算其运算的结果，根据选项即可得到答案.【详解】由题意可知，执行如图所示的程序框图，可知：第一循环：134,2146n S =+==⨯+=；第二循环：437,26719n S =+==⨯+=；第三循环：7310,2191048n S =+==⨯+=，要使的输出的结果为48，根据选项可知8k，故选C. 【点睛】本题主要考查了循环结构的计算与输出问题，其中解答中正确理解循环结构的程序框图的计算功能，逐次准确计算是解答的关键，着重考查了运算与求解能力，属于基础题. 12．C解析：C【分析】x 的变化遵循以2-为公差递减的等差数列的变化规律，到0x <时结束，得到1x =-，然后代入解析式，输出结果.【详解】0x ≥时，每次赋值均为2x - x 可看作是以2019为首项，2-为公差的等差数列{}n x()()20191220212n x n n ⇒=+-⨯-=-当0x <时输出，所以0n x <，即202120n -< 20212n ⇒> 即：10100x >，10110x < 10112021210111x ⇒=-⨯=-1314y ∴=+=本题正确选项：C【点睛】本题结合等差数列考查程序框图问题，关键是找到程序框图所遵循的规律.二、填空题13．【分析】根据题意得到不等式和计算得到答案【详解】根据题意知：且故故答案为：【点睛】本题考查了程序框图没有考虑完整情况是容易发生的错误 解析：(]10,28【分析】根据题意得到不等式()3322244x --≤和()333222244x --->⎡⎤⎣⎦，计算得到答案.【详解】根据题意知：()332224428x x --≤∴≤且()33322224410x x --->∴>⎡⎤⎣⎦ 故(]10,28x ∈故答案为：(]10,28【点睛】本题考查了程序框图，没有考虑完整情况是容易发生的错误.14．63【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量y 的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】解：模拟程序的运行可得x=3y=7不满足条件|x-y|解析：63【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量y 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】解：模拟程序的运行，可得x=3y=7不满足条件|x-y|＞31，执行循环体，x=7，y=15不满足条件|x-y|＞31，执行循环体，x=15，y=31不满足条件|x-y|＞31，执行循环体，x=31，y=63此时，满足条件|x-y|＞31，退出循环，输出y 的值为63．故答案为63．【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．15．17【解析】分析：模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件即可得到输出的的值详解：模拟程序的运行可得执行循环体不满足条件执行循环体；不满足条件执行循环体；不满足条件退出 解析：17【解析】分析：模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的a 的值.详解：模拟程序的运行，可得255,68a b ==，执行循环体51,68,51r a b ===，不满足条件0r =，执行循环体17,51,17r a b ===；不满足条件0r =，执行循环体0,17,0r a b ===；不满足条件0r =，退出循环，输出a 的值为17，故答案为17.点睛：本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.16．34【解析】由题设循环体要执行四次图知第一次循环结束后第二次循环结束后第三次循环结束后第四次循环结束后故答案为34解析：34【解析】由题设循环体要执行四次，图知第一次循环结束后2a a b =+=，3b a b =+=， 第二次循环结束后5a a b =+=，8b a b =+=，第三次循环结束后13a a b =+=，21b a b =+=，第四次循环结束后34a a b =+=，55b a b =+=，故答案为 34. 17．【解析】试题分析：把十进制的化为七进制则所以结果为考点：进位制解析：7104（）【解析】试题分析：245(2)110101112121253=+⨯+⨯+⨯=，把十进制的53化为七进制，则53774÷=，7710÷=，1701÷=，所以结果为(7)104．考点：进位制．18．120【解析】输出s=120解析：120【解析】6,16,530,4120,34a s s a s a s a ==→==→==→==<．输出s=12019．【解析】设实数x ∈19经过第一次循环得到x=2x+1n=2经过第二循环得到x=2(2x+1)+1n=3经过第三次循环得到x=22(2x+1)+1+1n=4此时输出x 输出的值为8x+7令8x+7⩾55 解析：38【解析】设实数x ∈[1,9]，经过第一次循环得到x =2x +1，n =2，经过第二循环得到x =2(2x +1)+1，n =3，经过第三次循环得到x =2[2(2x +1)+1]+1，n =4此时输出x ，输出的值为8x +7，令8x +7⩾55，得x ⩾6， 由几何概型得到输出的x 不小于55的概率为963918P -==-. 故答案为38. 20．1320【分析】由题意结合所给的流程图执行程序确定其输出值即可【详解】程序运行如下：首先初始化数据：第一次循环满足执行；第二次循环满足执行；第三次循环不满足跳出循环输出故答案为【点睛】识别运行程序框 解析：1320【分析】由题意结合所给的流程图执行程序，确定其输出值即可.【详解】程序运行如下：首先初始化数据：12,1i S ==，第一次循环，满足10i ≥，执行12,111S S i i i =⨯==-=；第二次循环，满足10i ≥，执行132,110S S i i i =⨯==-=；第三次循环，不满足10i ≥，跳出循环，输出1320S =.故答案为1320．【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．三、解答题21．（1）详见解析；（2）详见解析【分析】（1）根据分段函数求值时的运算步骤，先判断自变量所在的范围，然后带入对应的解析式中求解，即可写出算法；（2）根据算法即可画出算法框图．【详解】解：（1）算法如下：第一步，输入自变量x 的值．第二步，判断0x >是否成立，若成立，计算1y x =+，否则，执行下一步． 第三步，判断0x =是否成立，若成立，令0y =，否则，计算3y x =--.第四步，输出y .（2）算法框图如下图所示．【点睛】本题主要考查利用条件结构设计算法求分段函数的值，以及绘制算法框图，属于中档题． 22．见解析【分析】（1）根据赋值语句的意义可得结果；（2）当2x =时计算ax b +的值，并把这个值赋给1y ；（3）当3x ＝－时，计算ax b +的值，并把这个值赋给2y ；（4）该程序框图解决的是求函数()f x ax b =+的函数值的问题；（5）列出关于,a b 的一元一次方程组求解即可.【详解】(1)图框①中2x ＝表示把2赋值给变量x .(2)图框②中1y ax b ＝＋的含义是：该图框在执行①的前提下，即当2x ＝时，计算ax b ＋的值，并把这个值赋给1y .(3)图框④中，2y ax b ＝＋的含义是：该图框在执行③的前提下，即当3x ＝－时，计算ax b ＋的值，并把这个值赋给2y .(4)该程序框图解决的是求函数y ax b =+的函数值的问题，其中输入的是自变量x 的值，输出的是对应x 的函数值．(5)13y =，即2+=3a b .⑤22y =-，即3+2a b -=-.⑥由⑤⑥，得1a ＝，1b ＝，所以()1f x x =+.【点睛】本题主要考查了对顺序结构程序框图的理解，属于基础题．23．见解析；【解析】试题分析: 先利用INPUT 语句输入两个正数a 和b 的值，再分别赋值a b 和b a 的值，最后输出a b 和b a 的值试题程序和程序框图分别如下：24．(1)-4；(2)1009；(3)答案见解析.【解析】试题分析：(1)利用所给的程序框图运行程序可得当x=9时,y=-4,则t 的值为-4.(2)结合程序的算法和循环结构的特点可知共输出(x ,y )的组数为1009；(3)将所给的程序框图翻译为算法语句，利用循环语句设计相应的程序即可，注意循环语句应设计为DO 语句的形式.试题(1)由程序框图知,当x=1时,y=0;当x=3时,y=-2;当x=9时,y=-4,所以t=-4.(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 017时,输出最后一对,共输出(x ,y )的组数为20182=1 009. (3)程序框图的程序语句如下:x =1y =0n =1DOPRINT (x ,y )n =n +2x =3*xy =y -2LOOP UNTIL n >2 017END点睛：程序框图的条件结构和循环结构分别对应算法语句的条件语句和循环语句，两种语句的阅读理解是复习重点．输入、输出和赋值语句是任何一个算法必不可少的语句，一个语句可以输出多个表达式．在赋值语句中，一定要注意其格式的要求，如“＝”的右侧必须是表达式，左侧必须是变量；一个语句只能给一个变量赋值；变量的值始终等于最近一次赋给它的值，先前的值将被替换.25．见解析【解析】试题分析：确定循环体为：S=S+i^2，i=i+10，再确定初始值和结束的条件即可试题程序如下:S=0;i=10;while i<=1000S=S+i^2;i=i+10;endprint(%io(2),S);程序框图如图所示:26．见解析【解析】试题分析：根据已知的函数解析式的规律，可利用循环结构得算法及流程图，用计数器i 来控制循环次数，限制条件为7i >，15x x=+求解析式. 试题由题意，所求程序框图如下：。

一、选择题1．该程序中k的值是（）A．9 B．10 C．11 D．122．执行如图所示的程序框图，输出的S值为（）A．511 B．512 C．1022 D．10243．运行如图所示的程序框图，若输出S的值为129，则判断框内可填入的条件是（）A ．4?k <B ．5?k <C ．6?k <D ．7?k < 4．如图所示的程序框图输出的结果是（ ）A ．34B ．55C ．78D ．895．在如图算法框图中，若6a =，程序运行的结果S 为二项式5(2)x +的展开式中3x 的系数的3倍，那么判断框中应填入的关于k 的判断条件是（ ）A ．3k <B ．3k >C ．4k <D ．4k > 6．某程序框图如图所示，其中21()g n n n =+，若输出的20192020S =，则判断框内可以填入的条件为（ ）A ．2020?n <B ．2020?nC ．2020?n >D ．2020?n 7．某程序框图如图所示，则该程序运行后输出的值是（ ）A ．3-B ．32-C ．3D ．328．如图是一个程序框图，则输出k 的值为（ ）A ．6B ．7C ．8D ．99．被称为宋元数学四大家的南宋数学家秦九韶在《数书九章》一书中记载了求解三角形面积的公式，如图是利用该公式设计的程序框图，则输出的k 的值为（ ）A ．4B ．5C ．6D ．710．对任意非零实数a 、b ，若a b ⊗的运算原理如图所示，则121log 43-⎛⎫⊗ ⎪⎝⎭的值为（ ）A．13B．1 C．43D．211．执行如图所示的程序框图，若输出的值为﹣1，则判断框①中可以填入的条件是（）A．n≥999B．n≤999C．n＜999 D．n＞999 12．执行如图的程序框图，则输出x的值是 ()A．2018B．2019C．12D．2二、填空题13．执行下面的程序框图，若输入的a，b，k分别为1，2，3，则输出的M=_____14．某程序框图如图所示，若输入的4t=，则输出的k=______．15．执行如图程序框图，输出的结果为______.16．如图所示的伪代码，最后输出的S值为__________．17．执行如图的程序框图，则输出的S __________．18．根据如图所示的算法流程图，可知输出的结果S为______．19．如图所示的程序框图，输出的结果是_________.20．阅读如图所示的程序框图，该程序输出的结果是__________.三、解答题21．某班共有学生50人，在一次数学测试中，要搜索出测试中及格(60分及以上)的成绩，试设计一个算法，并画出程序框图．22．图C1-6所示的程序框图表示了一个什么样的算法？试用当型循环写出它的算法并画出相应的程序框图．23．函数y=x 1,x 0,0,x 0,x 1,x 0,-+>⎧⎪=⎨⎪+<⎩ 试写出给定自变量x,求函数值y 的算法.24．写出一个算法，求底面边长为42，侧棱长为5的正四棱锥的体积．25．画出解关于x 的不等式0ax b +<的程序框图，并用语句描述.26．给出30个数:1,2,4,7,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),请在图中判断框内①处和执行框中的②处填上合适的语句,使之能完成该题算法功能.【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】本题只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可（注意避免计算错误）．【详解】3,2,8,814x k y ===<，第一次循环，4,10,1014k y ==<；第二次循环，6,12,1214k y ==<；第三次循环，8,14,1414k y ===；第四次循环，10,16,1614k y ==>，退出循环，输出10k =，故选：B.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.2．C解析：C【分析】直接根据程序框图计算得到答案.【详解】 根据程序框图知：92391012222 (2222102212)S -=++++==-=-. 故选：C.【点睛】 本题考查了程序框图，意在考查学生的计算能力和理解能力，确定程序框图表示的意义是解题的关键.3．C解析：C【分析】最常用的方法是列举法，即依次执行循环体中的每一步，直到循环终止，但在执行循环体时要明确循环终止的条件是什么，什么时候要终止执行循环体．【详解】0S =，1k =；110121S -=+⨯=，2k =；211225S -=+⨯=，3k =；3153217S -=+⨯=，4k =；41174249S -=+⨯=，5k =；514952129S -=+⨯=，6k =，此时输出S ，即判断框内可填入的条件是“6?k <”.故选：C ．【点睛】本题考查循环结构程序框图.解决程序框图填充问题的思路(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、执行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．4．B解析：B【分析】通过不断的循环赋值，得到临界值，即可得解.【详解】1,1,21,2,32,3,53,5,85,8,138,13,2113,21,3421,34,55x y z x y z x y z x y z x y z x y z x y z x y z ======================== 不满足50z ≤，输出即可，故选：B.【点睛】本题考查了程序框图循环结构求输出结果，考查了计算能力，属于中当题.5．C解析：C【分析】根据二项式（2+x ）5展开式的通项公式，求出x 3的系数，模拟程序的运行，可得判断框内的条件．【详解】∵二项式5(2)x +展开式的通项公式是5152r r r r T C x -+=⋅⋅,令3r =，3233152T C x +∴=⋅⋅，332356(4)21408x x C x∴⨯⋅⋅=， ∴程序运行的结果S 为120，模拟程序的运行，由题意可得k=6，S=1不满足判断框内的条件，执行循环体，S=6，k=5不满足判断框内的条件，执行循环体，S=30，k=4不满足判断框内的条件，执行循环体，S=120，k=3此时，应该满足判断框内的条件，退出循环，输出S 的值为120．故判断框中应填入的关于k 的判断条件是k ＜4？故选：C【点睛】本题考查了二项式展开式的通项公式的应用问题，考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，属于中档题．6．A解析：A【分析】因为()()2111111g n n n n n n n ===-+++，此程序框图是对函数()g n 求和，利用裂项相消法求和，可知201912020n S n ==+，可知2019满足条件进入循环，2020不满足条件没有进入循环，根据选项得到正确结果.【详解】 由2221111111112019(1111222231112020n S n n n n n n ⎫⎛⎫⎛⎫=++⋯+=-+-+⋯+-=-==⎪ ⎪ ⎪++++++⎭⎝⎭⎝⎭，解得2019n =，可得n 的值为2019时.满足判断框内的条件，当n 的值为2020时，不满足判断框内的条件，退出循环，输出S 的值，故判断框内可以填人的条件为“2020n <？”.故选A.【点睛】本题考查根据循环框图的输出结果填写判断框的内容，关键是分析出满足输出结果时的n 值，再根据选项判断结果.7．D解析：D【分析】该框图的功能是计算:234562017sin sin sin sin sin sin sin 3333333πππππππ+++++++,再根据正弦函数的周期性以及特殊角的三角函数值计算可得答案.【详解】 该框图的功能是计算:234562017sin sin sin sin sin sin sin 3333333πππππππ+++++++.因为7132017sin sin sin sin3333ππππ=====28142012sin sin sin sin 3333ππππ=====, 39152013sin sin sin sin 03333ππππ=====,410162014sinsin sin sin 33332ππππ=====-,511172015sin sin sin sin33332ππππ=====-, 612182016sinsin sin sin 03333ππππ=====, 所以234562017sin sin sin sin sin sin sin 3333333πππππππ+++++++3373363360336(336(3360=+⨯+⨯+⨯+⨯= 故选:D【点睛】 本题考查了程序框图的循环结构,考查了三角函数的周期性以及特殊角的三角函数值,理解程序框图的功能是解题关键,属于基础题.8．B解析：B 【分析】根据程序框图，模拟计算过程即可求解.【详解】程序框图的执行过程如下：1S =，10k =；1011S =，9k =； 911S =，8k ；811S =，7k =， 循环结束.故选B.【点睛】 本题主要考查了程序框图，算法结构，属于中档题.9．B解析：B【分析】模拟程序运行，依次计算可得所求结果【详解】当4a =，3b =，2c =时，12S =<，2k =； 当5a =，4b =，3c =时，612S =<，3k =；当6a =，5b =，4c =时，27124S =<，4k =； 当7a =，6b =，5c =时，12S =>，5k =；故选B【点睛】本题考查程序运算的结果，考查运算能力，需注意1k k =+所在位置10．B解析：B【解析】 模拟执行程序框图可得程序的功能是计算并输出分段函数1,2,b a b a a b a a b b-⎧⎪⎪⊗=⎨+⎪>⎪⎩的值， ∵121log 4233-⎛⎫=<= ⎪⎝⎭.∴12131log 4132--⎛⎫⊗== ⎪⎝⎭. 本题选择B 选项. 11．C解析：C【分析】分析循环结构中求和式子的特点，可到最终结果：2lg(1)S n =-+，当1S =-时计算n 的值，此时再确定判断框的内容.【详解】由图可得：2lg1lg 2lg 2lg3...lg lg(1)S n n =+-+-++-+，则2lg(1)1S n =-+=-，所以999n =，因为此时需退出循环，所以填写：999n <.故选C.【点睛】lg lg lg(1)1n n n n =-++，通过将除法变为减法，达到简便运算的目的. 12．D解析：D【分析】模拟执行程序框图，依次写出每次循环得到的x ，y 的值，当2019y = 时，不满足条件退出循环，输出x 的值即可得解．【详解】解：模拟执行程序框图，可得2,0x y ==.满足条件2019y <，执行循环体，1,1x y =-=；满足条件2019y <，执行循环体，1,22x y == ； 满足条件2019y <，执行循环体，2,3x y ==； 满足条件2019y <，执行循环体，1,4x y =-= ；…观察规律可知，x 的取值周期为3，由于20196733⨯＝，可得：满足条件2019y <，执行循环体，当2,2019x y == ,不满足条件2019y <，退出循环，输出x 的值为2．故选D ．【点睛】本题主要考查了循环结构的程序框图，依次写出每次循环得到的x ，y 的值，根据循环的周期，得到跳出循环时x 的值是解题的关键．二、填空题13．12【分析】由题意可知从开始判断框条件成立执行第一次循环得到一组新的的值再从开始判断框条件成立执行第一次循环得到一组新的的值当时判断条件框不成立输出此时的值即可得出答案【详解】当时执行程序框图得；当 解析：12【分析】由题意可知，从1n =开始，判断框条件成立，执行第一次循环，得到一组新的,,M a b 的值，再从2n =开始，判断框条件成立，执行第一次循环，得到一组新的,,M a b 的值，当3n =时，判断条件框不成立，输出此时M 的值，即可得出答案．【详解】当1n =时，执行程序框图得，1225,2,5M a b =+⨯===；当2n =时，执行程序框图得，22512,5,12M a b =+⨯===；当3n =时，不满足判断条件框，直接输出 12M =．故答案为12．【点睛】本题主要考查了根据程序框图写出执行结果的问题，对于这类题目，首先要弄清框图的结构和执行过程，本题为循环结构的程序框图．14．【分析】根据题意执行循环结构的程序框图逐次计算即可得到答案【详解】由题意执行程序框图：可得；第一循环不满足条件；第二次循环不满足条件；第三次循环不满足条件；第四次循环不满足条件；第五次循环不满足条件 解析：【分析】根据题意，执行循环结构的程序框图，逐次计算，即可得到答案．【详解】由题意执行程序框图：可得0S =， 8k =；第一循环，不满足条件，8S =，7k =；第二次循环，不满足条件，1S =，6k =；第三次循环，不满足条件，5S =，5k =；第四次循环，不满足条件0S =，4k =；第五次循环，不满足条件4S =，3k =，第六次循环，满足条件，输出3k =．【点睛】本题主要考查了循环结构的程序框图的计算输出问题，其中解答中根据给定的程序框图，逐次循环，逐次计算，注意把握判定条件是解答的关键，着重考查了推理与运算能力，属于基础题．15．【分析】n=2018时输出S 利用三角函数的周期性即可得出【详解】n=2018时输出SS=又的周期为12由图象易知：∴S==故答案为：【点睛】本题的实质是累加满足条件的数据可利用循环语句来实现数值的累 解析：12. 【分析】n=2018时，输出S ．利用三角函数的周期性即可得出．【详解】n=2018时，输出S ． S=232017 6666sin sin sin sin ππππ++++ 又y sin 6x π=的周期为12，由图象易知：2312 06666sin sinsin sin ππππ++++=，∴S=23122017 168?66666sin sin sin sin sin πππππ⎛⎫++++⨯+ ⎪⎝⎭=12 故答案为：12． 【点睛】 本题的实质是累加满足条件的数据，可利用循环语句来实现数值的累加（乘）常分以下步骤：（1）观察S 的表达式分析，确定循环的初值、终值、步长；（2）观察每次累加的值的通项公式；（3）在循环前给累加器和循环变量赋初值，累加器的初值为0，累乘器的初值为1，环变量的初值同累加（乘）第一项的相关初值；（4）在循环体中要先计算累加（乘）值，如果累加（乘）值比较简单可以省略此步，累加（乘），给循环变量加步长；（5）输出累加（乘）值．16．21【解析】分析：先根据伪代码执行循环直到I<8不成立结束循环输出S 详解：执行循环得结束循环输出点睛：算法与流程图的考查侧重于对流程图循环结构的考查先明晰算法及流程图的相关概念包括选择结构循环结构伪解析：21【解析】分析：先根据伪代码执行循环，直到I<8不成立，结束循环输出S.详解：执行循环得3,23+3=95,25+3=137,27+3=179,29+3=21;8I S I S I S I S I ==⨯==⨯==⨯==⨯>；；；结束循环，输出21S =.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.17．88【解析】运行该程序即答案为88解析：88【解析】运行该程序，2,2;3,7;4,18;5,41;6,88;k S k S k S k S k S ==========即答案为88.18．【解析】执行循环为点睛：算法与流程图的考查侧重于对流程图循环结构的考查先明晰算法及流程图的相关概念包括选择结构循环结构伪代码其次要重视循环起点条件循环次数循环终止条件更要通过循环规律明确流程图研究的解析：34【解析】执行循环为1111111131122334223344 S=++=-+-+-=⨯⨯⨯点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.19．1【解析】试题分析：根据程序框图可知该程序执行的是所以输出的的值为1考点：本小题主要考查程序框图的执行和对数的运算点评：高考中程序框图的题目一般离不开循环结构要分清是当型循环还是直到型循环要搞清楚退解析：1【解析】试题分析：根据程序框图可知，该程序执行的是34103410lg2lg lg lg lg(2)lg101239239b=++++=⋅⋅⋅⋅==，所以输出的的值为1.考点：本小题主要考查程序框图的执行和对数的运算.点评：高考中程序框图的题目一般离不开循环结构，要分清是当型循环还是直到型循环，要搞清楚退出循环的条件，避免多执行或少执行一步.20．120【分析】由题意首先确定程序的功能然后计算其输出结果即可【详解】由题意可得题中流程图的功能为计算的值据此计算可得输出的结果为故答案为120【点睛】识别运行程序框图和完善程序框图的思路：(1)要明解析：120【分析】由题意首先确定程序的功能，然后计算其输出结果即可.【详解】由题意可得，题中流程图的功能为计算12345S=⨯⨯⨯⨯的值，据此计算可得输出的结果为120S=.故答案为120．【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．三、解答题21．见解析．【解析】试题分析：由题意，从成绩中搜索出大于等于60的成绩，由此可得选择结构的判断框的条件，再依据搜索数据的个数确定循环的条件，得到算法，即可画出相应框图试题算法如下：第一步：i ＝1.第二步，输入x .第三步，若x ≥60则输出．第四步，i ＝i ＋1.第五步，判断i >50，是，结束；否则执行第二步．程序框图如图所示：22．见解析【解析】【分析】根据图中的流程图表示的算法可知这是一个计算10个数的平均数的算法，根据当型循环结构的特点，先判断I 是否小于等于10，再执行运算，由此写出当型循环的算法并画出流程图【详解】这是一个计算10个数的平均数的算法．当型循环的算法如下：第一步，0S =.第二步，1I =.第三步，如果I 小于等于10，执行第四步；否则，转第七步第四步，输入G .第五步，.S S G =+第六步，1I I =+，返回第三步． 第七步，10S A =. 第八步，输出A .程序框图如图．【点睛】本题是一道关于设计流程图的题目，解答本题的关键是理解流程图的功能，属于中档题。