探索三角形相似的条件同步练习4

2022-2023学年北师大版九年级数学上册《4.4探索三角形相似的条件》同步达标测试题（附答案）一．选择题（共12小题，满分48分）1．图形中，每个小网格均为正方形网格，带阴影部分的三角形中与如图△A1B1C1相似的是（）A．B．C．D．2．如图，在△ABC中，D，E两点分别在BC，AC上，且AD平分∠BAC，若∠ABE＝∠C，BE与AD相交于点F，则图中与△ABD相似的是（）A．△ABC B．△ABF C．△BFD D．△AEF3．如图，在△ABC中，点D、E分别在AB、AC边上，DE与BC不平行，那么下列条件中，不能判断△ADE∽△ACB的是（）A．∠ADE＝∠C B．∠AED＝∠B C．＝D．＝4．已知△ABC三边长是，，2，与△ABC相似的三角形三边长可能是（）A．1，，B．1，，C．1，，D．1，，5．如图，D是△ABC边AB上一点，添加一个条件后，仍然不能使△ACD∽△ABC的是（）A．∠ACB＝∠ADC B．∠ACD＝∠ABC C．D．6．已知Rt△ABC中，∠C＝90°，∠A≠∠B，点P是边AC上一点（不与A、C重合），过P点的一条直线与△ABC的边相交，所构成的三角形与原三角形相似，这样的直线有（）条．A．1B．2C．3D．47．如图，△ABC中，点D、E分别在AB、AC边上，则下列条件中，不一定能使△AED∽△ABC的是（）A．∠2＝∠B B．∠1＝∠C C．D．8．如图：点D在△ABC的边AB上，连接CD，下列条件：①∠ACD＝∠B；②∠ADC＝∠ACB；③AC2＝AD•AB；④AB•CD＝AC•BC．其中能判定△ACD∽△ABC的共有（）A．1个B．2个C．3个D．4个9．如图，在△ABC中，点D、E分别在边AB、AC上，则在下列四个条件中：①∠AED＝∠B；②DE∥BC；③；④AD•BC＝DE•AC，能满足△ADE∽△ACB的条件有（）A．1个B．2个C．3个D．4个10．如图，在△ABC中，AB＝AC＝8，BC＝6，点P从点B出发以1个单位/s的速度向点A运动，同时点Q从点C出发以2个单位/s的速度向点B运动．当以B，P，Q为顶点的三角形与△ABC相似时，运动时间为（）A．s B．s C．s或s D．以上均不对11．如图，在△ABC中，点D、E分别在边AB、AC上，则在下列五个条件中：①∠AED＝∠B；②DE∥BC；③＝；④AD•BC＝DE•AC；⑤∠ADE＝∠C，能满足△ADE∽△ACB的条件有（）A．1个B．2个C．3个D．4个12．如图，正方形ABCD中，F为AB上一点，E是BC延长线上一点，且AF＝EC，连接EF，DE，DF，M是FE中点，连接MC，设FE与DC相交于点N．则4个结论：①DN ＝DG；②△BFG∽△EDG∽△BDE；③CM垂直BD；④若MC＝，则BF＝2；正确的结论有（）个A．4B．3C．2D．1二．填空题（共4小题，满分20分）13．如图，∠B＝∠D，请你添加一个条件，使得△ABC∽△ADE，这个条件可以是．14．如图，在边长为4的正方形ABCD中，点E、F分别是BC、CD的中点，DE、AF交于点G，AF的中点为H，连接BG、DH．给出下列结论：①AF⊥DE；②DG＝；③HD∥BG；④△ABG∽△DHF．其中正确的结论有．（请填上所有正确结论的序号）15．如图，在△ABC中，AB≠AC．D、E分别为边AB、AC上的点．AC＝3AD，AB＝3AE，点F为BC边上一点，添加一个条件：，可以使得△FDB与△ADE 相似．（只需写出一个）16．如图，在△ABC中，P为AB上一点，在下列四个条件中：①∠ACP＝∠B；②∠APC ＝∠ACB；③AC2＝AP•AB；④AB•CP＝AP•CB，能满足△APC与△ACB相似的条件是（只填序号）．三．解答题（共8小题，满分52分）17．已知：如图，点C，D在线段AB上，△PCD是等边三角形，且AC＝1，CD＝2，DB ＝4．求证：△ACP∽△PDB．18．如图，已知∠1＝∠2，∠AED＝∠C，求证：△ABC∽△ADE．19．如图，AB•AE＝AD•AC，且∠1＝∠2，求证：△ABC∽△ADE．20．如图，点E是四边形ABCD的对角线BD上一点，且∠BAC＝∠BDC＝∠DAE．求证：△ABE∽△ACD．21．如图，在△ABC中，BD平分∠ABC，交AC于点D，点E是AB上一点，连接DE，BD2＝BC•BE．证明：△BCD∽△BDE．22．如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q从点B开始沿BC向C点以4cm/s的速度移动．如果P，Q分别从A，B同时出发，经过几秒钟△PBQ与△ABC相似？23．如图，已知AD•AC＝AB•AE．求证：△ADE∽△ABC．24．如图，在△ABC中，AB＝AC＝1，BC＝，在AC边上截取AD＝BC，连接BD．（1）通过计算，判断AD2与AC•CD的大小关系；（2）求∠ABD的度数．参考答案一．选择题（共12小题，满分48分）1．解：因为△A1B1C1中有一个角是135°，选项中，有135°角的三角形只有B，且满足两边成比例夹角相等，故选：B．2．解：在△ABE与△ACB中，∠ABE＝∠C，∠BAE＝∠CAB，∴△ABE∽△ACB，∴∠AEB＝∠ABC，∵AD平分∠BAC，∴∠BAD＝∠EAF，∴△ABD∽△AEF．故选：D．3．解：∵∠DAE＝∠CAB，∴当∠ADE＝∠C时，△ADE∽△ACB；当∠AED＝∠B时，△ADE∽△ACB；当＝时，△ADE∽△ACB．故选：C．4．解：∵△ABC三边长是，，2，∴△ABC三边长的比为：2：＝1：：，∴△ABC相似的三角形三边长可能是1，，，故选：A．5．解：A、当∠ACB＝∠ADC时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；B、当∠ACD＝∠ABC时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；C、当＝时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；D、当＝时，无法得出△ACD∽△ABC，故此选项符合题意；故选：D．6．解：如图，过点P作AB的平行线，或作BC的平行线，或作AB的垂线，或作∠CPD＝∠B，共4条直线，故选：D．7．解：∠A＝∠A，A、若添加∠2＝∠B，可利用两角法判定△AED∽△ABC，故本选项错误；B、若添加∠1＝∠C，可利用两角法判定△AED∽△ABC，故本选项错误；C、若添加＝，可利用两边及其夹角法判定△AED∽△ABC，故本选项错误；D、若添加＝，不能判定△AED∽△ABC，故本选项正确；故选：D．8．解：①∠A＝∠A，∠ACD＝∠B，∴△ACD∽△ABC，②∵∠A＝∠A，∠ADC＝∠ACB，∴△ACD∽△ABC，③∵AC2＝AD•AB，∴，∵∠A＝∠A，∴△ACD∽△ABC，④条件不符合，不能判定△ACD∽△ABC，故选：C．9．解：①∠B＝∠AED，∠A＝∠A，则可判断△ADE∽△ACB，故①符合题意；②DE∥BC，则△ADE∽△ABC，故②不符合题意，③，且夹角∠A＝∠A，能确定△ADE∽△ACB，故③符合题意；④由AD•BC＝DE•AC可得＝，此时不确定∠ADE＝∠ACB，故不能确定△ADE∽△ACB，故④不符合题意，故选：B．10．解：设运动时间为t秒．BP＝t，CQ＝2t，BQ＝BC﹣CQ＝6﹣2t，当△BAC∽△BPQ，＝，即＝，解得t＝；当△BCA∽△BPQ，＝，即＝，解得t＝，综上所述，当以B，P，Q为顶点的三角形与△ABC相似时，运动时间为s或s，故选：C．11．解：①∠B＝∠AED，∠A＝∠A，则可判断△ADE∽△ACB，故①符合题意；②DE∥BC，则△ADE∽△ABC，故②不符合题意，③，且夹角∠A＝∠A，能确定△ADE∽△ACB，故③符合题意；④由AD•BC＝DE•AC可得，此时不确定∠ADE＝∠ACB，故不能确定△ADE∽△ACB；故④不符合题意，⑤∠ADE＝∠C，∠A＝∠A，则可判断△ADE∽△ACB，故⑤符合题意；故选：C．12．解：正方形ABCD中，AD＝CD，在△ADF和△CDE中，，∴△ADF≌△CDE（SAS），∴∠ADF＝∠CDE，DE＝DF，∴∠EDF＝∠FDC+∠CDE＝∠FDC+∠ADF＝∠ADC＝90°，∴∠DEF＝45°，∵∠DGN＝45°+∠FDG，∠DNG＝45°+∠CDE，∠FDG≠∠CDE，而∠FDG与∠CDE不一定相等，∴∠DGN与∠DNG不一定相等，故判断出①错误；∵△DEF是等腰直角三角形，∵∠ABD＝∠DEF＝45°，∠BGF＝∠EGD（对顶角相等），∴△BFG∽△EDG，∵∠DBE＝∠DEF＝45°，∠BDE＝∠EDG，∴△EDG∽△BDE，∴△BFG∽△EDG∽△BDE，故②正确；连接BM、DM．∵△AFD≌△CED，∴∠FDA＝∠EDC，DF＝DE，∴∠FDE＝∠ADC＝90°，∵M是EF的中点，∴MD＝EF，∵BM＝EF，∴MD＝MB，在△DCM与△BCM中，，∴△DCM≌△BCM（SSS），∴∠BCM＝∠DCM，∴CM在正方形ABCD的角平分线AC上，∴MC垂直平分BD；故③正确；过点M作MH⊥BC于H，则∠MCH＝45°，∵MC＝，∴MH＝＝1，∵M是EF的中点，BF⊥BC，MH⊥BC，∴MH是△BEF的中位线，∴BF＝2MH＝2，故④正确；综上所述，正确的结论有②③④．故选：B．二．填空题（共4小题，满分20分）13．解：∵∠B＝∠D，∴添加∠C＝∠E或∠BAC＝∠DAE或∠BAD＝∠CAE或＝，可证△ABC∽△ADE．故答案为：∠C＝∠E或∠BAC＝∠DAE或∠BAD＝∠CAE或＝．14．解：∵四边形ABCD为正方形，∴∠ADC＝∠BCD＝90°，AD＝CD，∵E和F分别为BC和CD中点，∴DF＝EC＝2，∴△ADF≌△DCE（SAS），∴∠AFD＝∠DEC，∠F AD＝∠EDC，∵∠EDC+∠DEC＝90°，∴∠EDC+∠AFD＝90°，∴∠DGF＝90°，即DE⊥AF，故①正确；∵AD＝4，DF＝CD＝2，∴AF＝，∴DG＝AD×DF÷AF＝，故②错误；∵H为AF中点，∴HD＝HF＝AF＝，∴∠HDF＝∠HFD，∵AB∥DC，∴∠HDF＝∠HFD＝∠BAG，∵AG＝＝，AB＝4，∴，∴△ABG∽△DHF，故④正确；∴∠ABG＝∠DHF，而AB≠AG，则∠ABG和∠AGB不相等，故∠AGB≠∠DHF，故HD与BG不平行，故③错误；故答案为：①④．15．解：DF∥AC，或∠BFD＝∠A．理由：∵∠A＝∠A，＝＝，∴△ADE∽△ACB，∴①当DF∥AC时，△BDF∽△BAC，∴△BDF∽△EAD．②当∠BFD＝∠A时，∵∠B＝∠AED，∴△FBD∽△AED．故答案为DF∥AC，或∠BFD＝∠A．16．解：前三项正确，因为他们分别符合有两组角对应相等的两个三角形相似；两组对应边的比相等且相应的夹角相等的两个三角形相似．故相似的条件是①，②，③．三．解答题（共8小题，满分52分）17．证明：∵△PCD是等边三角形，∴∠PCD＝∠PDC＝60°，PC＝CD＝PD＝2，∴∠PCA＝∠PDB＝120°，∵AC＝1，BD＝4，∴，＝，∴＝，∴△ACP∽△PDB．18．证明：∵∠1＝∠2，∴∠1+∠BAE＝∠2+∠BAE，即∠DAE＝∠BAC，∵∠AED＝∠C，∴△ABC∽△ADE．19．证明：如图，∵AB•AE＝AD•AC，∴＝．又∵∠1＝∠2，∴∠2+∠BAE＝∠1+∠BAE，即∠BAC＝∠DAE，∴△ABC∽△ADE．20．解：∵∠BAC＝∠BDC，∠AOB＝∠DOC，∴∠ABE＝∠ACD又∵∠BAC＝∠DAE∴∠BAC+∠EAC＝∠DAE+∠EAC∴∠DAC＝∠EAB∴△ABE∽△ACD．21．证明：∵BD平分∠ABC，∴∠DBE＝∠CBD．∵BD2＝BC•BE，∴，∴△BCD∽△BDE．22．解：设在开始运动后第x秒，△BPQ与△BAC相似，由题意得：AP＝2xcm，PB＝（8﹣2x）cm，BQ＝4x，分两种情况考虑：当∠BPQ＝∠C，∠B＝∠B时，△PBQ∽△CBA，∴，即解得：x＝0.8，当x＝0.8秒时，△BPQ与△BAC相似；当∠BPQ＝∠A，∠B＝∠B时，△BPQ∽△BAC，∴，即，解得：x＝2，当x＝2秒时，△BPQ与△BAC相似．综上，当x＝0.8秒或2秒时，△BPQ与△BAC相似．23．证明：∵AD•AC＝AE•AB，∴＝在△ABC与△ADE中∵＝，∠A＝∠A，∴△ABC∽△ADE．24．解：（1）∵AD＝BC，BC＝，∴AD＝，DC＝1﹣＝．∴AD2＝＝，AC•CD＝1×＝．∴AD2＝AC•CD．（2）∵AD＝BC，AD2＝AC•CD，∴BC2＝AC•CD，即．又∵∠C＝∠C，∴△BCD∽△ACB．∴，∠DBC＝∠A．∴DB＝CB＝AD．∴∠A＝∠ABD，∠C＝∠BDC．设∠A＝x，则∠ABD＝x，∠DBC＝x，∠C＝2x．∵∠A+∠ABC+∠C＝180°，∴x+2x+2x＝180°．解得：x＝36°．∴∠ABD＝36°．。

2022-2023学年北师大版九年级上册数学4 探索三角形相似的条件同步练习一、单选题(共15题，共计45分)1、如图，在△ABC中，点D在AB上，下列条件能使△BCD和△ABC相似的是（）A.∠ACD=∠BB.∠ADC=∠ACBC.AC 2=AD•ABD.BC2=BD•BA2、如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A.∠ABP=∠CB.∠APB=∠ABCC.D.3、已知Rt△ABC中，∠C=90°，∠A≠∠B，点P是边AC上一点（不与A、C重合），过P点的一条直线与△ABC的边相交，所构成的三角形与原三角形相似，这样的直线有（）条．A.1B.2C.3D.44、如图，点D是△ABC的边AB上的一点，过点D作BC的平行线交AC于点E，连接BE，过点D作BE的平行线交AC于点F，则下列结论错误的是（）A. B. C. D.5、如图，在矩形ABCD中，E在AD上，，交CD于F，连结BF，则图中与△ABE 一定相似的三角形是（）A.△EFBB.△DEFC.△CFBD.△EFB与△DEF6、如图，AC是矩形ABCD的对角线，E是边BC延长线上一点，AE与CD相交于F，则图中的相似三角形共有（）A.2对B.3对C.4对D. 5对7、如果一个三角形能够分成两个与原三角形都相似的三角形，我们把这样的三角形称为孪生三角形，那么孪生三角形是（）A.不存在B.等腰三角形C.直角三角形D.等腰三角形或直角三角形8、如图，在正方形ABCD中，E是CD的中点，点F在BC上，且FC= BC．图中相似三角形共有（）A.1对B.2对C.3对D.4对9、下列各组中两个图形不一定相似的是（）A.有一个角是35°的两个等腰三角形B.两个等腰直角三角形C.有一个角是120°的两个等腰三角形D.两个等边三角形10、如图，在△ABC中，点D、E分别在边AB、AC上，下列条件中不能判断△ABC∽△AED的是（）A.∠AED=∠BB.∠ADE=∠CC. =D. =11、如图，已知DE//BC，那么下列结论正确的是（）A. B. C. D.12、如图，AB是⊙O的直径，OD垂直弦AC于点E，且交⊙O于点D，过点D作⊙O的切线与BA的延长线相交于点F，下列结论不一定正确的是（）A.∠CDB=∠BFDB.△BAC∽△OFDC.DF∥ACD.OD=BC13、如图，在△ABC中，∠A=78º，AB=4，AC=6，将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不一定相似的是（）A. B. C. D.14、如图，E为矩形ABCD的CD边延长线上一点，BE交AD于G ， AF⊥BE于F ，图中相似三角形的对数是（）A.5B.7C.8D.1015、下列说法中，错误的是A.所有的等边三角形都相似B.和同一图形相似的两图形相似C.所有的等腰直角三角形都相似D.所有的矩形都相似二、填空题(共10题，共计30分)16、如图，点P是△ABC中AB边上的一点，过P作直线（不与AB重合）截△ABC，使截得的三角形与原三角形相似，满足条件的直线最多有________条．17、如图，在△ABC中，∠C=90°，BC=16cm，AC=12cm，点P从点B出发，沿BC以2cm/s的速度向点C移动，点Q从点C出发，以1cm/s的速度向点A移动，若点P、Q分别从点B、C同时出发，设运动时间为t s，当t=________时，△CPQ与△CBA相似．18、如图，在△ABC与△ADE中，，要使△ABC与△ADE相似，还需要添加一个条件，这个条件可以是________ 。

【提升版】北师大版数学九年级上册 4.4探索三角形相似的条件同步练习一、选择题1．（2019九上·东源期中）如图所示，小正方形的边长均为1，则下列选项中阴影部分的三角形与△ABC相似的是（ ）A．B．C．D．2．（2024九上·铜仁期末）“黔绣”的技师擅长在叶脉上飞针走绣，巧妙地将传统刺绣图案与树叶天然纹理完美结合，创作出神奇的“叶脉苗绣”作品．实际上，很多叶片本身都蕴含着黄金分割的比例，在大自然中呈现出优美的样子．如图，点P大致是AB的黄金分割点(AP>PB)，如果AP的长为4cm，那么AB的长约为（ ）A．(25+2)cm B．(25−2)cm C．(25+1)cm D．(25−1)cm 3．（2024九上·兰州期中）在学习画线段AB的黄金分割点时，小明过点B作AB的垂线BC，取AB 的中点M，以点B为圆心，BM为半径画弧交射线BC于点D，连接AD，再以点D为圆心，DB为半径画弧，前后所画的两弧分别与AD交于E，F两点，最后，以A为圆心，“■■”的长度为半径画弧交AB于点H，点H即为AB的其中一个黄金分割点，这里的“■■”指的是线段（ ）A．AF B．DF C．AE D．DE4．（2023九上·平山月考）如图，在△ABC中，∠ABC为锐角，BC=8cm，AB=4cm，要在边BC上找一点D，使△DBA∽△ABC，需添加一个条件，下列方案不正确的是（ ）A．∠BAD=∠C B．CD=6cm C．AD平分∠BAC D．∠ADB=∠BAC 5．（2024九上·杭州月考）如图，在△ABC纸片中，∠A＝72°，∠B＝38°．将△ABC纸片沿某直线剪开，下列四种方式中剪下的阴影三角形与△ABC相似的是（ ）A．①②B．②④C．③④D．①③6．（2024九上·岳阳期末）如图，已知∠DAB=∠CAE，那么添加一个条件后，依然无法判定ΔABC∽ΔADE（ ）A．∠AED=∠C B．∠D=∠B C．ABAD =ACAED．ADAB=DEBC7．（2023九上·石家庄期中）两千多年前，古希腊数学家欧多克索斯发现了黄金分割，即：如图，点P是线段AB上一点（AP＞BP），若满足BPAP =APAB，则称点P是AB的黄金分割点，世界上最有名的建筑物中几乎都包含“黄金分割”，若图中AB＝8，则BP的长度是（ ）A．12−45B．4+45C．45−4D．2 8．下列条件中，能使△ABC和△DEF相似的条件是（ ）．A．AB=c，AC=b，BC=a，DE=a，EF=b，DF=cB．AB=1，AC=1.5，BC=2，DE=12，EF=8，DF=1C．AB=3，AC=4，BC=6，DE=12，EF=8，DF=6D．AB=2，AC=3，BC=5，DE=6，EF=3，DF=3二、填空题9．（2024九上·织金期末）如图，乐器上的一根弦AB=100cm，两个端点A，B固定在乐器板面上，支撑点C是靠近点B的黄金分割点，支撑点D是靠近点A的黄金分割点，C，D之间的距离为 cm．10．（2024九上·兰州期中）在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．有一张矩形纸片ABCD如图所示，点N在边AD上，现将矩形折叠，折痕为BN，点A对应的点记为点M，若点M恰好落在边DC上，则图中与△NDM一定相似的三角形是 ．11．（2023九上·瑶海月考）五角星是我们常见的图形，如图点C，D分别是线段AB的黄金分割点，AB=20cm，则EC+CD= cm．12．（2023九上·宁远期中）如图，在正方形网格上，若使△ABC∽△PBD，则点P应在 ．13．如图，在△ABC中，AB=8 cm，BC=16 cm．点P从点A出发，沿AB边向点B以2cm/s的速度运动，点Q从点B出发，沿BC边向点C以4 cm/s的速度运动．如果P，Q分别从A，B同时出发，那么运动时间为 时，△PBQ与△ABC相似．三、解答题14．（2023九上·萧山月考）如图，矩形ABCD中，BC<2AB，点M是BC的中点，连接AM．将△ABM沿着AM折叠后得△APM，延长AP交CD于E，连接ME．（1）求证：ME平分∠PMC；（2）求证：△EMC∽△MAB.15．如图，AD⊥AB，BC⊥AB，垂足分别为A，B，且AD=2，BC=6，AB=7．P是线段AB上的一个动点．问：是否存在一点P，使以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似？若存在，求出PA的长；若不存在，请说明理由．16．（2023九上·佛山期中）如图，在4×7的正方形方格纸中（每个小方格的边长均为1）有线段AC 和EF，点A，C，E，F均在方格的格点上．（1）在方格纸中画出一个以AC为对角线的菱形ABCD，点D在直线AC的下方，且点B，D都在方格的格点上；（2）在方格纸中画出以EF为边的正方形EFGH，且点G，H在方格的格点上；（3）连接BD交AC于点O，连线得△OCE和△CHD，请证明△CHD∽△OCE．17．（2019九上·昌平期中）如图，在Rt△ABC中，∠C=90°，AC=8m，BC=6m，点P由C点出发以2m/s的速度向终点A匀速移动，同时点Q由点B出发以1m/s的速度向终点C匀速移动，当一个点到达终点时另一个点也随之停止移动．（1）经过几秒△PCQ的面积为△ACB的面积的13？（2）经过几秒，△PCQ与△ACB相似？18．（2022九上·哈尔滨月考）在四边形ABCD中，AC为对角线，AC=AB=BC，BE⊥AC于点E，CD=BE=3，AD=1．（1）如图1，求证：∠ADC=90°；（2）如图2，延长BE，交AD边的延长线于点F，交CD边于点G，连接CF，DE，在不添加任何字母和辅助线的条件下，请直接写出图中与△ABF相似，但不全等的三角形．19．（2020九上·江阴期中）如图（1）如图1，Rt△ABC中，∠B=90°，AB=2BC，现以C为圆心、CB长为半径画弧交边AC于D，再以A为圆心、AD为半径画弧交边AB于E.求证：AEAB =5−12.（这个比值5−12叫做AE与AB的黄金比.）（2）如果一等腰三角形的底边与腰的比等于黄金比，那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰，用直尺和圆规，作一个黄金三角形ABC.（注：直尺没有刻度！作图不要求写作法，但要求保留作图痕迹，并对作图中涉及到的点用字母进行标注）20．（2021九上·常山期中）【问题提出】已知有两个Rt△ABC和Rt△A'B′C'，其中∠C＝∠C′＝90°，∠A ＝60°，∠A′＝45°．（1）如图1，作线段CD，C′D′，分别交AB于点D，交A'B′于点D′，使得∠BCD＝45°，∠B'C′D'＝30°，问△BCD与△B'C′D'，△ACD与△A′C′D′是否相似？并选择其中相似的一对三角形，说明理由．（2）如图2，作线段AD，B'D′，分别交BC于点D，交A'C'于点D，若△ACD与△B′C′D′、△ABD与△A′B'D'均相似，求∠CAD，∠C'B'D′的度数．（3）【拓展思考】已知任意两个不相似的直角三角形，能否分别作一条直线对其进行分割，使其中一个三角形所分割得到的两个三角形与另一个三角形所分割得到的两个三角形分别对应相似？如果可以，请直接画出一种分割示意图；如果不能，请说明理由．答案解析部分1．【答案】A【知识点】勾股定理；相似三角形的判定【解析】【解答】解：∵∠ACB=90°+45°=135°，AC=2，CB=12+12=2，又∵B、C、D三选项中最大角都小于135°，∴B、C、D都不对，又∵选项A中最大角是135°，且夹边之比=2∶1=2∶2。

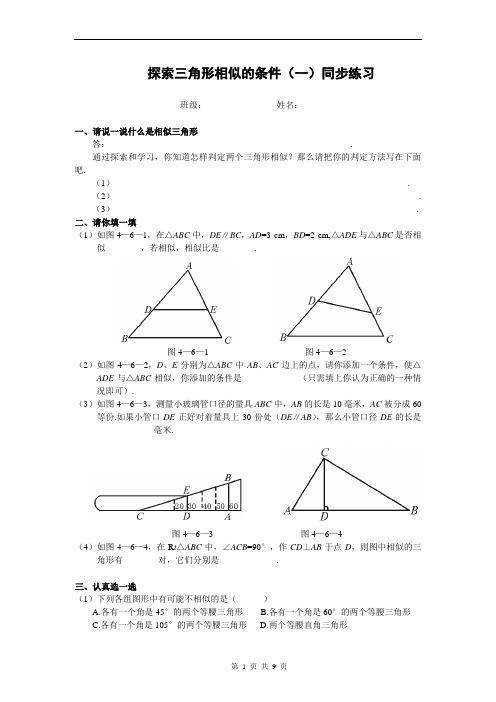
探索三角形相似的条件（一）同步练习班级：_______ 姓名：_______一、请说一说什么是相似三角形答：_______________________________________________________.通过探索和学习，你知道怎样判定两个三角形相似？那么请把你的判定方法写在下面吧.（1）___________________________________________________________________.（2）______________________________________________________________________.（3）_____________________________________________________________________.二、请你填一填（1）如图4—6—1，在△ABC中，DE∥BC，AD=3 cm，BD=2 cm,△ADE与△ABC是否相似________，若相似，相似比是________.图4—6—1 图4—6—2（2）如图4—6—2，D、E分别为△ABC中AB、AC边上的点，请你添加一个条件，使△ADE与△ABC相似，你添加的条件是_____________（只需填上你认为正确的一种情况即可）.（3）如图4—6—3，测量小玻璃管口径的量具ABC中，AB的长是10毫米，AC被分成60等份.如果小管口DE正好对着量具上30份处（DE∥AB），那么小管口径DE的长是_____________毫米.图4—6—3 图4—6—4（4）如图4—6—4，在R t△ABC中，∠ACB=90°，作CD⊥AB于点D，则图中相似的三角形有________对，它们分别是_____________.三、认真选一选（1）下列各组图形中有可能不相似的是（）A.各有一个角是45°的两个等腰三角形B.各有一个角是60°的两个等腰三角形C.各有一个角是105°的两个等腰三角形D.两个等腰直角三角形（2）△ABC 和△A ′B ′C ′符合下列条件，其中使△ABC 和△A ′B ′C ′不相似的是（ ）A.∠A =∠A ′=45° ∠B =26° ∠B ′=109°B.AB =1 AC =1.5 BC =2 A ′B ′=4 A ′C ′=2 B ′C ′=3C.∠A =∠B ′ AB =2 AC =2.4 A ′B ′=3.6 B ′C ′=3D.AB =3 AC =5 BC =7 A ′B ′=3 A ′C ′=5 B ′C ′=7（3）如图4—6—5，AB ∥CD ，AD 与BC 相交于点O ，那么在下列比例式中，正确的是（ ）A.ADOACD AB = B.BC OB OD OA = C.OCOBCD AB = D.ODOBAD BC =图4—6—5 图4—6—6（4）如图4—6—6，D 为△ABC 的边AB 上一点，且∠ABC =∠ACD ，AD =3 cm, AB =4 cm ，则AC 的长为（ ）A.2 cmB.3 cmC.12 cmD.23 cm四、用数学眼光看世界如图4—6—7，长梯AB 斜靠在墙壁上，梯脚B 距墙80 cm ，梯上点D 距墙70 cm ，量得BD 长55 cm ，求梯子的长.图4—6—7参考答案一、答：对应角相等、对应边成比例的两个三角形是相似三角形判定两个三角形相似的方法详见课本，略. 二、（1）相似 3∶5 （2）∠C =∠ADE （或∠B =∠AED 等）（3）5 （4）三 △ACD ∽△ABC △BCD ∽△BAC △ACD ∽△CBD 三、（1）A （2）D （3）C （4）D 四、解：设梯子的长AB 为x cm （如图）由Rt △ADE ∽Rt △ABC 得：ABADBC DE = ∴xx 558070-= 解得：x =440答：梯子的长是440 cm.探索三角形相似的条件（二）同步练习班级：_______ 姓名：_______一、请你填一填（1）如图4—6—8，在△ABC 中，AC 是BC 、DC 的比例中项，则△ABC ∽________,理由是________.图4—6—8 图4—6—9（2）如图4—6—9，D 、E 、F 分别是△ABC 各边的中点，则△DEF ∽________,理由是________. （3）如图4—6—10，∠BAD =∠CAE ，∠B =∠D ，AB =2AD ，若BC =3 cm,则DE =________cm.图4—6—10 图4—6—11（4）如图4—6—11，正方形ABCD 的边长为2，AE =EB ，MN =1，线段MN 的两端分别在CB 、CD 上滑动，那么当CM =________时，△ADE 与△MN C 相似. 二、认真选一选（1）如图4—6—12，下列条件不能判定△ABC 与△ADE 相似的是（ ）A.ABACAD AE = B.∠B =∠ADE C.BCDEAC AE = D.∠C =∠AED图4—6—12 图4—6—13（2）在□ABCD 中，E 在BC 边上，AE 交BD 于F ，若BE ∶EC =4∶5，则BF ∶FD 等于（ ）A.4∶5B.5∶4C.5∶9D.4∶9（3）如图4—6—13，在Rt △ABC 中，∠ACB =90°，CD ⊥AB 于点D ，CD =2，BD =1，则AD 的长是（ ）A.1B.2C.2D.4三、开动脑筋哟如图4—6—14，在四边形ABCD 中，AC 、BD 相交于点O ，∠ABD =∠ACD ，试找出图中的相似三角形，并加以证明.图4—6—14四、用数学眼光看世界如图4—6—15，为了估算河的宽度，我们可以在河对岸选定一点A ，再在河的这一边选定点B 和点C ，使得AB ⊥BC ，然后选定点E ，使EC ⊥BC ，确定BC 与AE 的交点D ，若测得BD =180米，DC =60米，EC =50米，你能知道小河的宽是多少吗？图4—6—15参考答案一、（1）△DAC 这两个三角形的两边对应成比例且夹角相等，这两个三角形相似（2）△ABC 这两个三角形的三边对应成比例，这两个三角形相似（3）1.5 （4）552或55二、（1）C （2）D （3）D三、（1）△AOB ∽△DOC （2）△AOD ∽△BOC证明：（1）∵∠ABD =∠ACD ，∠AOB =∠DOC （对顶角相等） ∴△AOB ∽△DOC（2）由（1）知△AOB ∽△DOC∴OC OBOD OA =， ∴OCODOB OA = 又∵∠AOD =∠BOC ∴△AOD ∽△BOC四、解：∵由已知得∠ABD =∠DCE =90°,∠ADB =∠CDE∴△ABD ∽△ECD ∴DCBDEC AB = 将EC =50，BD =180，DC =60代入上式得：6018050=AB ，∴AB =150 即：小河的宽是150米.探索三角形相似的条件一、选择题:1.下列命题错误的是( )A.两角对应相等的两个三角形相似;B.两边对应成比例的两个三角形相似C.两边对应成比例且夹角相等的两个三角形相似;D.三边对应成比例的两个三角形相似 2.下面关于直角三角形的相似叙述错误的是( )A.有一锐角对应相等的两个直角三角形相似;B.两直角边对应成比例的两个直角三角形相似C.直角边与斜边对应成比例的两个直角三角形相似;D.两个等腰直角三角形相似 3.使△ABC 和△ABC 不相似的条件是( ) A.∠A=∠A ′=65°,∠B=45°,∠C ′=70°B.AB=1,BC=1.2,AC=1.5,A ′B ′=6,B ′C ′=4,A ′C ′=4.8C.∠A=∠A ′,AB=4,BC=2,A ′B ′=6,B ′C ′=3D.AB=3,BC=4,AC=5,A ′B ′=6,B ′C ′=8,A ′C ′=10 4.有一个角等于40°的两个等腰三角形( )A.全等B.相似C.既不相似也不全等D.无法确定 5.如图1,∠AED=∠B,一定可得 ( )A.AD:AC=AE:ABB.DE:BC=AD:DBC.DE:BC=AE:ACD.AD:AB=AE:ACEDCBACB APEDCBADBA(1) (2) (3) (4) 6.如图2,P 是AB 上一点,补充下列条件①∠ACP=∠B; ②∠APC=∠ACB;③AP ACAC AB=;④AP PCAC BC=,其中一定能使△ACP ∽△ABC 的是( ) A.①②③ B.①②④ C.②③④ D.①②③④ 二、填空题:1.如图3,在Rt △ABC 中,AC ⊥BC,DE ⊥AB,则________∽________.2.P 是Rt △ABC 斜边BC 上异于B 、C 的一点,过点P 作直线截△ABC,使截得的三角形与△ABC 相似,满足这样条件的直线共有________条.3.如图4,在△ABC 中,点D 在AB 上,请再添一个适当的条件,使△ADC ∽△ACB,•那么要添加的条件是_________.4.如图,在△ABC 中,AB=AC,∠A=36°,BD 是∠ABC 的平分线,则_______•和______________相似.5.一个直角三角形的两条直角边长分别为8cm 和12cm,另一个直角三角形的两条直角边长分别是6cm 和9cm,这两个直角三角形______相似三角形(填是或不是),理由是_____________.6.一个三角形的三边长分别为8、9、12,另一个三角形的三边长分别为12、272、18,•那么这两个三角形的关系是________,理由是_______. 三、计算题1.如图,根据图形中提供的数据,你能得到三角形相似吗?为什么?31.521EDCB A2.如图,∠A=52°,AB=2.5,AC=5.5,△DEF 中,∠E=52°,DE=7,EF=3,•△ABC•与△EDF 是否相似?为什么?52︒5.52.5C B A52︒37D EF3.如图,在□ABCD 中,E 为BA 延长线上一点,EC 交AD 于F,找出图中相似的三角形,并进行证DCBA明.DFE CBA四、将两块完全相同的等腰直角三角板摆放成如图的样子,试问△ABE ∽△DAE 成立吗?D FECBA G五、已知:如图,D 、E 分别是△ABC 两边AB 、AC 上的点,∠A=60°,∠C=70•°,•∠AED=50°. 试问:AD ·AB=AE ·AC 成立吗?DECA六、如图,△ABC 中,D 为BC 上一点,且∠CAD=∠B,AD=8,AB=10,AC=9,求:DC 的长.•D CB A七、如图,在Rt △ABC 中,∠C=90°,CD ⊥AB.(1)找出图中相似的三角形;(2)设计一种分法,把Rt △ABC 分割成四个小直角三角形,使每个小直角三角形与Rt △ABC 相似.DC BA答案:一、1.B 2.C 3.C 4.D 5.A 6.A二、1.△BDE;△BAC 2.33.∠ADC=∠ACB或其他的4.△ABC;△BDC5.是;两边对应成比例且夹角相等的两个三角形相似6.相似,对应边成比例的两个三角形相似三、1.能:因为11123ADAB==+,1.511.533AEAC==+所以AD AE AB AC=,又因为∠A=∠A所以△ADE∽△ABC2.不相似,因为对应边不成比例3.△EAF∽△EBC;△EAF∽△CDF;△EBC∽△CDF因为 ABCD中,AD∥BC,AB∥CD,所以∠EAF=∠B,∠EFA=∠ECB;∠EAF=∠D,∠E=∠FCD;∠B=∠D, 所以△EAF∽△EBC,•△EAF∽△CDF,△EBC∽△CDF四、成立,△ABC和△AFG都是等腰直角三角形∠B=∠DAE=45°∠ADE=∠B+∠BAD⇒∠ADE=∠DAE+∠BAD=∠BAE⇒△ABE∽△DAE五、成立, ∠A=60°,∠C=70°∴∠B=50°,∠AED=50°,∴∠B=∠AED，∠A=∠A⇒△ADE∽△ACB⇒AD AEAC AB=⇒AD·AB=AE·AC六、∠CAD=∠B,∠C=∠C⇒△ACD∽△BCA⇒CD ADAC AB= ,即8910CD=∴CD=7.2七、(1)△ADC∽△ACB;△ADC∽△CDB;△CDB∽△ACB(2)过点D作DE⊥AC,DF⊥CB即可.。

2021年北师大版九年级数学上册同步练习《4.4探索三角形相似的条件》学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，小正方形边长均为1，则下列图形中三角形(阴影部分)与△ABC相似的是A．B．C．D．2．如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，且∠DCE＝∠B．那么下列各判断中，错误的是（）A．△ADE∽△ABC B．△ADE∽△ACDC．△DEC∽△CDB D．△ADE∽△DCB3．在Rt△ACB中，∠C=90°，AC=BC，一直角三角板的直角顶角O在AB边的中点上，这块三角板绕O点旋转，两条直角边始终与AC、BC边分别相交于E、F，连接EF，则在运动过程中，△OEF与△ABC的关系是（）A．一定相似B．当E是AC中点时相似C．不一定相似D．无法判断4．下列各组条件中，一定能推得△ABC与△DEF相似的是（）A．∠A=∠E且∠D=∠F B．∠A=∠B且∠D=∠FC．∠A=∠E且AB EFAC ED=D．∠A=∠E且AB DFBC ED=5．如图，在△ABC与△ADE中，∠BAC=∠D，要使△ABC与△ADE相似，还需满足下列条件中的( )A ．AC AB AD AE = B ．AC BC AD DE = C ．AC AB AD DE = D ．AC BC AD AE = 6．如图，每个小正方形的边长均为1，则下列图形中的三角形（阴影部分）与111A B C ∆相似的是（ ）A ．B ．C ．D ．7．如图，下列条件使△ACD ∽△ABC 成立的是（ ）A ．AC AB CD BC = B ．CD BC AD AC = C ．AC 2＝AD·AB D ．CD 2＝AD·BD 8．如图，正方形ABCD 的边长为2，BE =CE ，MN =1，线段MN 的两端点在CD 、AD 上滑动，当DM 为 时，△ABE 与以D 、M 、N 为顶点的三角形相似.A B C D 9．如图所示，在▱ABCD 中，BE 交AC ，CD 于G ，F ，交AD 的延长线于E ，则图中的相似三角形有（ ）A ．3对B ．4对C ．5对D ．6对10．如图，∠A=∠B=90°，AB=7，AD=2，BC=3，在边AB 上取点P ，使得△PAD 与△PBC 相似，则这样的P 点共有（ ）A ．1个B ．2个C ．3个D ．4个11．如图，△ABC 中，∠A=78°，AB=4，AC=6．将△ABC 沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（ ）A ．B ．C ．D ．12．（2016江苏省盐城市）如图，点F 在平行四边形ABCD 的边AB 上，射线CF 交DA 的延长线于点E ，在不添加辅助线的情况下，与△AEF 相似的三角形有（ ）A ．0个B ．1个C ．2个D ．3个二、填空题 13．如图，在ABC 中，90BAC ∠=，30B ∠=，AD BC ⊥，AE 平分BAD ∠，则ABC ∽________，BAD ACD ∽（写出一个三角形即可）．14．如图，已知点B、E、C、F在同一条直线上，∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是______．（只需写一个条件，不添加辅助线和字母）15．如图所示，已知点E在AC上，若点D在AB上，则满足条件__（只填一个条件），使△ADE与原△ABC相似．16．如图，在△ABC中，AB=9，AC=6，BC=12，点M在AB边上，且AM=3，过点M 作直线MN与AC边交于点N，使截得的三角形与原三角形相似，则MN=______．17．如图，矩形ABCD中，AD=2，AB=5，P为CD边上的动点，当△ADP与△BCP相似时，DP=__．18．过△ABC（AB＞AC）的边AC边上一定点M作直线与AB相交，使得到的新三角形与△ABC相似，这样的直线共有__条．三、解答题19．如图，在△ABC中，∠BAC=90°，M是BC的中点，过点A作AM的垂线，交CB 的延长线于点D．求证：△DBA∽△DAC．20．如图，点C是线段AB上一点，△ACD和△BCE都是等边三角形，连结AE，BD，设AE交CD于点F．（1）求证：△ACE≌△DCB；（2）求证：△ADF∽△BAD．21．如图，△ABC中，∠C=90°，AC=3，BC=4，点D是AB的中点，点E在DC的延长线上，且CE=13CD，过点B作BF∥DE交AE的延长线于点F，交AC的延长线于点G．（1）求证：AB=BG；（2）若点P是直线BG上的一点，试确定点P的位置，使△BCP与△BCD相似．22．如图，在△ABC中，AB=AC=1，BC=√5−12，在AC边上截取AD=BC，连接BD．（1）通过计算，判断AD2与AC•CD的大小关系；（2）求∠ABD的度数．23．如图所示，在正方形ABCD中，E，F分别是边AD，CD上的点，AE＝ED，DF=14 DC，连结EF并延长交BC的延长线于点G，连结BE．（1）求证：△ABE∽△DEF．（2）若正方形的边长为4，求BG的长．参考答案1．B【分析】根据网格的特点求出三角形的三边，再根据相似三角形的判定定理即可求解.【详解】已知给出的三角形的各边AB、CB、AC2、只有选项B的各边为1、B．【点晴】此题主要考查相似三角形的判定，解题的关键是熟知相似三角形的判定定理.2．D【分析】由相似三角形的判定方法得出A、B、C正确，D不正确；即可得出结论．【详解】∵DE∥BC，∴△ADE∽△ABC，∠BCD=∠CDE，∠ADE=∠B，∠AED=∠ACB，∵∠DCE=∠B，∴∠ADE=∠DCE，又∵∠A=∠A，∴△ADE∽△ACD；∵∠BCD=∠CDE，∠DCE=∠B，∴△DEC∽△CDB；∵∠B=∠ADE，但是∠BCD<∠AED，且∠BCD≠∠A，∴△ADE与△DCB不相似；正确的判断是A、B、C，错误的判断是D；故选D．【点睛】考查了相似三角形的判定方法；熟练掌握相似三角形的判定方法，由两角相等得出三角形相似是解决问题的关键．3．A【分析】略【详解】连结OC ，∵∠C=90°，AC=BC ，∴∠B=45°，∵点O 为AB 的中点，∴OC=OB ，∠ACO=∠BCO=45°，∵∠EOC+∠COF=∠COF+∠BOF=90°，∴∠EOC=∠BOF ，在△COE 和△BOF 中，{OCE BOC OBEOC FOB∠=∠=∠=∠ ∴△COE ≌△BOF （ASA ），∴OE=OF ，∴△OEF 是等腰直角三角形，∴∠OEF=∠OFE=∠A=∠B=45°，∴△OEF ∽△△CAB ．故选A ．【点睛】略4．C【解析】试题解析：A 、∠D 和∠F 不是两个三角形的对应角，故不能判定两三角形相似，故此选项错误；B 、∠A=∠B ，∠D=∠F 不是两个三角形的对应角，故不能判定两三角形相似，故此选项错误；C 、由AB EF AC ED＝可以根据两组对应边的比相等且夹角对应相等的两个三角形相似可以判断出△ABC 与△DEF 相似，故此选项正确； D 、∠A=∠E 且AB DF BC ED ＝不能判定两三角形相似，因为相等的两个角不是夹角，故此选项错误.故选C ．点睛：三角形相似的判定方法：（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；（2）三边法：三组对应边的比相等的两个三角形相似；（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；（4）两角法：有两组角对应相等的两个三角形相似．5．C【解析】试题解析：∵∠BAC=∠D ，AC AB AD DE＝， ∴△ABC ∽△ADE ．故选C ．6．B【解析】【分析】根据相似三角形的判定方法一一判断即可．【详解】解：因为111A B C 中有一个角是135°，选项中，有135°角的三角形只有B ，且满足两边成比例夹角相等，故选：B ．【点睛】本题考查相似三角形的性质，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．7．C【解析】试题分析：本题主要考查的就是三角形相似的判定，本题根据有一个角相等，且对应角的两边对应成比例，则两个三角形相似可以得出答案.根据题意可得∠A为公共角，则要使三角形相似则必须满足ACAB=ADAC.点晴：本题主要考查的就是三角形相似的判定定理，在有一个角相等的情况下，必须是角的两边对应成比例，如果不是角的两边对应成比例，则这两个三角形不相似；相似还可以利用有两个角对应相等的两个三角形全等.8．C【解析】∵四边形ABCD是正方形，∴AB=BC，∵BE=CE，∴AB=2BE，又∵△ABE与以D. M、N为顶点的三角形相似，∴①DM与AB是对应边时，DM=2DN∴DM2+DN2=MN2=1∴DM2+14DM2=1，解得DM= ；②DM与BE是对应边时,DM=12 DN，∴DM2+DN2=MN2=1，即DM2+4DM2=1，解得DM=5.∴DM△ABE与以D. M、N为顶点的三角形相似．故选C.点睛：本题考查了相似三角形的性质、正方形的性质以及勾股定理的应用，掌握相似三角形的对应边的比相等时解题的关键，注意分情况讨论思想与属性结合思想在本题中的应用.9．C【分析】根据相似三角形的判定来找出共有多少对相似的三角形【详解】解：∵AD∥BC，∴△AGE∽△CGB，△DFE∽△CFB，∵AB∥CD，∴△ABG∽△CFG，△ABE∽△CFB，△EDF∽△EAB．∴共有5对，故选C．【点睛】本题考查的是相似三角形的判定，熟练掌握相似三角形的判定定理是解题关键．10．C【详解】设AP=x，则BP=7-x，然后根据对应关系，分情况为：①当△ADP∽△BCP时，可得AD APBC BP=，即237xx=-，解得x=145，这时有一个P点；②当△ADP∽△BPC时，可得AD APBP BC=，即273xx=-，解得x=1或x=6，因此这样的点有两个；因此符合条件的P点共有3个.故选C【点睛】此题主要考查了相似三角形的性质，解题时，先根据相似三角形的性质，和相似三角形的对应关系，列出相应的比例式，求解即可.11．C【解析】试题解析：A、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；B、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；C、两三角形的对应边不成比例，故两三角形不相似，故本选项正确；D、两三角形对应边成比例且夹角相等，故两三角形相似，故本选项错误．故选C ．12．C【解析】试题分析：∵四边形ABCD 是平行四边形，∴AD ∥BC ，AB ∥DC ，∴△AEF ∽△CBF ，△AEF ∽△DEC ，∴与△AEF 相似的三角形有2个．故选C ．考点：相似三角形的判定；平行四边形的性质．13．△DBA．【解析】试题解析：△ABC ∽DBA ，理由是：∵AD ⊥BC ，∠BAC=90°， ∴∠ADB=∠BAC ，∵∠B=∠B ，∴△ABC ∽△DBA.14．∠B=∠DEC（不唯一）【解析】试题解析：答案不唯一，如.B DEC ∠=∠可添加.B DEC ∠=∠B DEC AD ∠=∠∠=∠，，.ABC DEF ∴∽故答案为.B DEC ∠=∠点睛：两角分别相等的两个三角形相似.15．∠B=∠AED．【解析】试题解析：已知点E 在AC 上，若点D 在AB 上，则满足条件∠B=∠AED （只填一个条件），使△ADE 与原△ABC 相似.16．4或6【分析】分别利用，当MN ∥BC 时，以及当∠ANM ＝∠B 时，分别得出相似三角形，再利用相似三角形的性质得出答案．【详解】如图1，当MN∥BC时，则△AMN∽△ABC，故AM AN MN AB AC BC==，则3912MN =，解得：MN＝4，如图2所示：当∠ANM＝∠B时，又∵∠A＝∠A，∴△ANM∽△ABC，∴AM MN AC BC=，即3612MN =，解得：MN＝6，故答案为：4或6．【点睛】此题主要考查了相似三角形判定，正确利用分类讨论得出是解题关键．17．1或4或2.5．【分析】需要分类讨论：△APD∽△PBC和△PAD∽△PBC，根据该相似三角形的对应边成比例求得DP的长度．【详解】设DP=x，则CP=5-x，本题需要分两种情况情况进行讨论，①、当△PAD∽△PBC时，AD BC=DP CP∴225xx=-，解得：x=2.5；②、当△APD∽△PBC时，ADCP=DPBC，即25x-=2x，解得：x=1或x=4，综上所述DP=1或4或2.5【点晴】本题主要考查的就是三角形相似的问题和动点问题，首先将各线段用含x的代数式进行表示，然后看是否有相同的角，根据对应角的两边对应成比例将线段写成比例式的形式，然后分别进行计算得出答案．在解答这种问题的时候千万不能出现漏解的现象，每种情况都要考虑到位.18．2【解析】试题解析：如图所示：过M作MN∥BC交AB于N，△ANM∽△ABC；过M作∠AMD=∠B，交AB于D，△AMD∽△ABC；因此符合条件的直线共有2条.19．证明见解析.【解析】证明：∵∠BAC=90°，点M是BC的中点，∴AM=CM，∴∠C=∠CAM，∵DA⊥AM，∴∠DAM=90°，∴∠DAB=∠CAM，∴∠DAB=∠C，∵∠D=∠D，∴△DBA∽△DAC．20．（1）证明见解析；（2）证明见解析.【分析】有两组边对应相等，并且它们所夹的角也相等，那么这两个三角形全等；有两组角分别相等，且其中一组角所对的边对应相等，那么这两个三角形全等；全等三角形的对应边相等，对应角相等．（1）根据全等三角形的判定定理SAS证得结论；（2）利用（1）中全等三角形的对应角相等，平行线的判定与性质以及两角法证得结论．【详解】解：（1）∵△ACD和△BCE都是等边三角形，∴AC=CD，CE=CB，∠ACD=∠BCE=60°∴∠ACE=∠DCB=120°．∴△ACE≌△DCB（SAS）；（2）∵△ACE≌△DCB，∴∠CAE=∠CDB．∵∠ADC=∠CAD=∠ACD=∠CBE=60°，∴DC∥BE，∴∠CDB=∠DBE，∴∠CAE=∠DBE，∴∠DAF=∠DBA．∴△ADF∽△BAD．21．（1）证明见解析；（2）当PB=2.5或325时，△BCP与△BCD相似．【解析】试题分析：（1）利用平行分线段成比例定理得出AD AC AEBD CG EF==，进而得出△ABC≌△GBC（SAS），即可得出答案；（2）分别利用第一种情况：若∠CDB=∠CPB，第二种情况：若∠PCB=∠CDB，进而求出相似三角形即可得出答案．试题解析：（1）证明：∵BF∥DE，∴AD AC AE BD CG EF==，∵AD=BD，∴AC=CG，AE=EF，在△ABC和△GBC中：AC CG ACB GCB BC BC =⎧⎪∠=∠⎨⎪=⎩，∴△ABC ≌△GBC （SAS ），∴AB=BG ；（2）当BP 长为52或325时，△BCP 与△BCD 相似； ∵AC=3，BC=4，∴AB=5，∴CD=2.5，∴∠DCB=∠DBC ，∵DE ∥BF ，∴∠DCB=∠CBP ，∴∠DBC=∠CBP ，第一种情况：若∠CDB=∠CPB ，如图1：在△BCP 与△BCD 中CDB CPB DBC PBC BC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCP ≌△BCD （AAS ），∴BP=CD=2.5；第二种情况：若∠PCB=∠CDB ，过C 点作CH ⊥BG 于H 点．如图2：∵∠CBD=∠CBP ，∴△BPC ∽△BCD ，∵CH ⊥BG ，∴∠ACB=∠CHB=90°，∠ABC=∠CBH ， ∴△ABC ∽△CBH ， ∴AB BC CB BH， ∴BH=165，BP=325． 综上所述：当PB=2.5或325时，△BCP 与△BCD 相似． 22．（1）AD 2=AC•CD ．（2）36°． 【解析】试题分析：（1）通过计算得到AD 2=3−√52，再计算AC·CD ，比较即可得到结论；（2）由AD 2=AC ⋅CD ，得到BC 2=AC ⋅CD ，即BC AC =CD BC ，从而得到△ABC ∽△BDC ，故有AB BD=AC BC ，从而得到BD=BC=AD ，故∠A=∠ABD ，∠ABC=∠C=∠BDC ． 设∠A=∠ABD=x ，则∠BDC=2x ，∠ABC=∠C=∠BDC=2x ，由三角形内角和等于180°，解得：x=36°，从而得到结论． 试题解析：（1）∵AD=BC=，∴AD 2=(√5−12)2=3−√52． ∵AC=1，∴CD=1−√5−12=3−√52，∴AD 2=AC ⋅CD ；（2）∵AD 2=AC ⋅CD ，∴BC 2=AC ⋅CD ，即BC AC =CD BC ，又∵∠C=∠C ，∴△ABC ∽△BDC ，∴AB BD =ACBC ，又∵AB=AC ，∴BD=BC=AD ，∴∠A=∠ABD ，∠ABC=∠C=∠BDC ． 设∠A=∠ABD=x ，则∠BDC=∠A+∠ABD=2x ，∴∠ABC=∠C=∠BDC=2x ，∴∠A+∠ABC+∠C=x+2x+2x=180°，解得：x=36°，∴∠ABD=36°．考点：相似三角形的判定与性质．23．（1）见解析；（2）BG=BC+CG=10．【分析】（1）利用正方形的性质，可得∠A=∠D，根据已知可得AE：AB=DF：DE，根据有两边对应成比例且夹角相等三角形相似，可得△ABE∽△DEF；（2）根据相似三角形的预备定理得到△EDF∽△GCF，再根据相似的性质即可求得CG的长，那么BG的长也就不难得到.【详解】（1）证明：∵ABCD为正方形，∴AD=AB=DC=BC，∠A=∠D=90 °.∵AE=ED，∴AE：AB=1：2.∵DF=14 DC，∴DF：DE=1：2，∴AE：AB=DF：DE，∴△ABE∽△DEF；（2）解：∵ABCD为正方形，∴ED∥BG，∴△EDF∽△GCF，∴ED：CG=DF：CF.又∵DF=14DC，正方形的边长为4，∴ED=2，CG=6，∴BG=BC+CG=10.【点睛】本题考查了正方形的性质，相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解答本题的关键.。

4．6探索三角形相似的条件⑵一、目标导航两角对应相等(非平行)的两个三角形相似方法及应用．二、根底过关1．△ABC中，∠BAC=900，AD⊥BC于D，图中共有对相似三角形．2．Rt△ABC中，∠ACB=900，CD⊥AB于D，AD=4，BD=2，那么CD=_______，AC=________．3．△ABC中，DE∥BC交AB于D，AC于E，AB=12，AD-DB=4，BC=9，那么DE=________．4．△ABC中AB=AC=10，∠A=36°，BD是角平分线交AC于D，那么DC________．5．△ABC中P是AB上一点，且∠ACP=∠B，AC=4，AB=6，那么PB=________．6．如图，矩形ABCD中，AB=2，BC=3，E是AD的中点，那么点C到BE的距离CF=．C EFD B第1题图6题三、能力提升7．以下图形中不一定相似的是()A．各有一个角等于45°的两个等腰三角形A．AD2=BD·DCB．CD2=CF·CA C．DE2=AE·EB D．AD2=AF·AC11．梯形ABCD中，AD∥BC，∠A=90°，AC⊥BD，AD=1，BC=4，那么两条对角线AC∶BD为()A．4∶1B．2∶1C．3:1D．2:212．如图，在等边△ABC中，P是BC上一点，D为AC上一点，A 且∠APD=60°，BP=1，CD=2，那么△ABC的边长为()3A．3B．4C．5D．6D13．如图，等边△ABC，点D、E分别在BC、AC上，且BD=CE，B PC题AD与BE相交于点F．A12⑴试说明△ABD≌△BCE．；⑵△AEF与△ABE相似吗?说说你的理由；E⑶BD2=AD·DF吗?请说明理由．FBDC14．如图，在梯形 ABCD中，AD∥BC，∠B=∠ACDA D⑴请再写出图中另外一对相等的角；⑵假设AC=6，BC=9，试求梯形ABCD的中位线的长度．B CB．各有一个角等于60°的两个等腰三角形C．两个等腰直角三角形 D ．各有一个角等于105°的两个等腰三角形8．△ABC中，D，E分别是AB，AC上一点，假设∠AED=∠B，那么以下各式中，成立的是( )A．AD∶AB=AE∶AC B ．AD∶BD=AE∶CEC．AD·AB=AE·AC D ．AD·BD=AE·CE9．在Rt△ABC中，∠C=90°，CD⊥AB于D，且BC∶AC=2∶3，那么BD∶AD=()A．2:3B ．4:9C．2:5 D ．2: 310．在△ABC中，AD⊥BC于D，DE⊥AB于E，DF⊥AC于F，那么以下式子中错误的选项是()15．如图，AD是Rt△ABC斜边上的高，DE⊥DF，且 DE和E，F．求证:AF BE．AD BDB16．如图，在△ABC中，AB=AC，D为△ABC外一点，连结AD交BC于E，假设∠C=∠D，AE=6，DE=2．求AC的长．17．如图，四边形ABCD是菱形，AF⊥BC交BD于E，DF分别交AB，AC于AE FCDCDEA B交BC于F．求证:AD2=1DE·DB．2A DBEF C22．如图，△ABC中，∠ACB=900，AC=BC，点E，F在AB上，∠ECF=45°．18．如图，P是等边三角形△ABC的一边BC上任意一点，连结平分线交AB，AC于M，N两点．求证:BP·PC=BM·CN．AP，AP的垂直AMNB CP⑴求证:△ACF∽△BEC；⑵设△ABC的面积为S，求证:AF·BE=2S．AEF19．如图，O是△ABC的内角平分线的交点，过O作DE⊥AO交AB，AC于D，E．求证:BD·CE=OD·OE．ADEOB C20．:如图，△ABC中，AD是∠BAC的平分线，AD的垂直平分线交AD于E，交BC的延长线于F．求证：⑴FD2=FB·FC；⑵AB2:AC2=BF:CF．AEBDC四、聚沙成塔21．如图，在等腰梯形ABCD中，AD∥BC，AD=3㎝，BC=7㎝，∠B=60°，P下底BC上一点〔不与B、C重合〕，连结AP，过P点作PE交DC于使得∠APE=∠B．⑴求证：△ABP∽△PCE；⑵求等腰梯形的腰AB的长；⑶底边BC上是否存在一点P，使得DE∶EC=5∶3?如果存在，求出BP的长，如果不存在，请说明理由．A DE45C B23．，梯形ABCD中，AD∥BC，AD<BC，且AD=5，AB=DC=2．⑴P为AD上一点，满足∠BPC=∠A，求证:△ABP∽△DPC；⑵如果点P在AD边上移动〔P与点A、D不重合〕，且满足∠BPE=∠A，PE交直线BC于点E，同时交直线DC于点Q，那么，当点Q在线段DC的延长线上时，设AP=x，CQ=y，求y关于x的函数解析式，并写出函数的自变量取值范围．A P DB CPA DB CEQ24．如图，在△ABC中，∠BAC=90°D为BC的中点，AE⊥AD，AE交CB的延长线于点E．⑴求证:△EAB∽△ECA；⑵△ABE和△ADC是否一定相似?如果相似，加以说明，如果不相似，那么增加一个怎样的条件，△ABE和△ADC一定相似．AE B D4．6探索三角形相似的条件⑵ 1．三；2．22，26；3．6；4；15－55；5．10；6．；7．A ；8．C ；9．B ；310．A ；11．B ；12．A ；13．⑴略．⑵相似，由⑴得∠AFE=∠BAC=600，∠AEF 公共．⑶由△BDF∽△ABD 得:DF BD，即BD 2=AD·DF．BDAD14．⑴∠BAC=∠D 或∠CAD=∠ACB．⑵由△ABC∽△ACD 得ADAC，解得:AD=4，ACBC所以中位线的长=．15．证:△ADF∽△BDE 即可． 16．AC=43．17．提示:连结AC 交BD 于O ．18．连结PM ，PN ．证: △BPM∽△CPN 即可． 19．证△BOD∽△EOC 即可．20．⑴连结 AF ．证; △ACF∽△BAF 可得AF 2=FB·FC，即 FD 2=FB·FC．⑵由⑴相 似可得:ABAF AB BFAB 2BF．AC，AC，即AC 2CFCFAF21．⑴略．⑵作AF//CD 交BC 与F ．可求得AB=4．⑶存在．设 BP=x ，由⑴可得x 3 48 ，解得x 1=1，x 2=6．所以BP 的长为1cm 或6cm ．47 x22．⑴由∠AFC=∠BCE=∠BCF+450，∠A=∠B=450可证得相似．⑵由⑴得 AF·BE=AC·BC =2S ．23．⑴略．⑵△ABP∽△DPQ，AB PD，x y2，得y=－1x2+5x－AP DQ25x222．(1＜x＜4)．24．⑴略．⑵不相似．增加的条件为: ∠C=300或∠ABC=600．。

北师大版九年级数学上册同步练习《4.4 探索三角形相似的条件》（无答案）1 / 6 《4.4 探索三角形相似的条件》一、选择题1. 下列两个三角形不一定相似的是A. 两个等边三角形B. 两个全等三角形C. 两个等腰直角三角形D. 有一个 角的两个等腰三角形2. 如图，要使 ∽ 只需添加的条件是A.B.C.D.3. 如图， 中，D 、E 分别在AB 、AC 上，单独添加下列条件可使 ∽ ，其中错误的是A.B.C.D.4. 如图1，在三角形纸片ABC 中， ， ， 将 沿图示中的虚线剪开，剪下的阴影三角形与原三角形相似的有A. B.C. D.第2页，共6页5. 如图， 网格中有一个 ，图中与 相似的三角形的个数有A. 1个B. 2个C. 3个D. 4个6. 下列条件不能判定 与 相似的是A.B. ，C. ，D. ，7. 如图， ，则图中相似三角形的对数为A. 4对B. 3对C. 2对D. 1对8. 如图，点P 在 的边AC 上，要判断 ∽ ，添加一个条件，不正确的是A.B.C.D.9. 如图，已知 ， ，则图中共有相似三角形的对数为A. 2B. 4北师大版九年级数学上册同步练习《4.4 探索三角形相似的条件》（无答案）3 / 6C. 6D. 810. 在等腰 和等腰 中， 与 是顶角，下列判断不正确的是A. 时，两三角形相似B. 时，两三角形相似C. 时，两三角形相似D. 时，两三角形相似11. 在 中，点D 、E 分别在边AB 、AC 上，联结DE ，那么下列条件中不能判断和 相似的是A. B.C. AE ： ：ACD. AE ： ：BC二、解答题12. 如图，在 中， ， 是BC 的中点，过点A 作AM 的垂线，交CB 的延长线于点 求证：∽ ．13.14.第4页，共6页15. 如图，在 中， ， 分别是 ， 上的点， ， 的平分线AF 交DE 于点G ，交BC 于点F ．试写出图中所有的相似三角形，并说明理由若 ，求 的值．16. 如图，在 和 中， ，．写出图中两对相似三角形 不得添加字母和线 ；请分别说明两对三角形相似的理由．17.18.北师大版九年级数学上册同步练习《4.4 探索三角形相似的条件》（无答案） 5 / 619.20.21. 已知：如图 ，求证： ∽ ．22.23.24.25.26.27.28. 如图在 中， ， ， ，点Q 从B 出发，沿BC 方向以 的速度移动，点P 从C出发，沿CA 方向以 的速度移动 若Q 、P 分别同时从B 、C 出发，试探究经过多少秒后，以点C 、P 、Q 为顶点的三角形与 相似？29.30.31.32.第6页，共6页。

4.4 探索三角形相似的条件课时4 黄金分割题型1 黄金分割的定义1、已知P为线段AB的黄金分割点，且AP<PB，则（）A.AP2=AB∙PBB.AP2=AB∙PBC.PB2=AP∙ABD.AP2+ BP2=AB22、如果C是线段AB的黄金分割点，并且AC>CB，AB=1，那么AC的长度为（）A.23 B.12C.√5−12D.3−√523、已知点C是线段AB的黄金分割点，且AB=6cm，则BC的长为（ ）A.(3√5−3)cmB.(9−3√5)cmC.(3√5−3)cm或(9−3√5)cmD. (9−3√5)cm或(6√5−6)cm4、宽与长的比是√5−12（约0.618）的矩形叫黄金矩形，矩形的长与宽分别为a和b，下列数据能构成黄金矩形的是（ ）A.a=4，b=√5+2B.a=4，b=√5−2C.a=2，b=√5+1D.a=2，b=√5−15、定义：如图1,点C在线段AB上,若满足AC2=BC⋅AB,则称点C为线段AB的黄金分割点。

如图2,在△ABC中,AB=AC=1,∠A=36°，BD平分∠ABC交AC于点D.(1)求证：点D是线段AC的黄金分割点；(2)求出线段AD的长。

题型2 黄金分割的应用6、主持人主持节目时,站在舞台的黄金分割点处最自然得体。

如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她要到达最理想的位置至少走（ ）A.(18−6√5)米B.(6√5−6)米C. (6√5+6)米D. (18−6√5)米或(6√5−6)米7、某种乐器的弦AB长为120cm,点A、B固定在乐器面板上,弦AB之间有一个支撑点C,且点C是AB的黄金分割点(AC>BC),则AC的长为( )A.(120−30√5)cmB.(160−60√5)cmC.(60√5−120)cmD.(60√5−60)cm8、宽与长的比是√5−1（约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调2和匀称的美感。

《探索三角形全等的条件》同步测试一、选择题1. 如图，已知AB=AD，那么添加下列一个条件后，能用SAS判定△ABC≌△ADC的是（）A．CB=CD B．∠BAC=∠DAC C．∠BCA=∠DCA D．∠B=∠D=90°2.如图，AB=AC，添加下列条件，能用SAS判断△ABE≌△ACD的是（）A．∠B=∠C B．∠AEB=∠ADC C．AE=AD D．BE=DC3. 如图，已知E，F是AC上的两点，AE=CF，DF=BE，∠AFD=∠CEB，则下列不成立的是（）A．∠A=∠C B．AD=CB C．BC=DF D．DF∥BE4.如图，在△ABD中，AC⊥BD，点C是BD的中点，则下列结论错误的是（）A.AB=ADB.AB=BDC. ∠B=∠DD.AC平分∠BAD5.如图，FE=BC，DE=AB，∠B=∠E=40°，∠F=70°，则∠A=（）A ．40°B ．50°C ．60°D ．70°6.在下列条件中，不能说明△ABC ≌△A ’B ’C ，，的是( )A.∠A ＝∠A ’，∠C ＝∠C ’，AC ＝A ’C ’ B .∠A ＝∠A ’，AB ＝A ’B ’，BC ＝B ’C ’ C.∠B ＝∠B ’，∠C ＝∠C ’，AB ＝A ’B ’ D .AB ＝A ’B ’， BC ＝B ’ C ’AC ＝A ’C ’ 7.在下列说法中，正确的有（ ）个．①三角对应相等的两个三角形全等；②三边对应相等的两个三角形全等；③两角，一边对应相等的两个三角形全等；④两边，一角对应相等的两个三角形全等.A.1B.2C.3D.4 8.下列说法正确的是（ ）A.两个周长相等的长方形全等B.两个周长相等的三角形全等 C .两个面积相等的长方形全等 D .两个周长相等的圆全等 9. 使两个直角三角形全等的条件是（ ） A . 一锐角对应相等 B . 两锐角对应相等 C . 一条边对应相等 D . 两条边对应相等10.如图，D E ，分别为ABC △的AC ，BC 边的中点，将此三角形沿DE 折叠，使点C 落在AB 边上的点P 处．若48CDE ∠=°，则APD ∠等于（ ）A ．42°B ．48°C ．52°D ．58°11. 如图，△ABC ≌△CDA ,且AD ＝CB ，下列结论错误的是（ ） A.∠B ＝∠D B.∠CAB ＝∠ACD C.BC ＝CD D.AC ＝CAD12.已知:如图,AC =CD ,∠B =∠E =90°, AC ⊥CD ,则不正确的结论是 ( )A.∠A与∠D互为余角B.∠A=∠2C.△ABC≌△CEDD.∠1=∠213. 如图，AC＝AD，BC＝BD，则有（）A．AB垂直平分CD B．CD垂直平分ABC．AB与CD互相垂直平分D．CD平分∠ACBA BCD14.如图，已知AB∥CD，AB=CD,AE=FD,则图中的全等三角形有（）A.1对B.2对C.3对D.4对15.已知：如图，点A，E，F，D在同一条直线上，AE＝DF，AB=CD，BF⊥AD，CE⊥AD，垂足分别为F，E，则△ABF≌△DCE的依据是（）A. SSSB. SASC. ASAD. HL二、填空题16．如图，MN与PQ相交于点O，MO=OP，QO=ON，∠M=65°，∠Q=30°，则∠P= ，∠N= .17．如图，已知AB＝AC=12 cm，AE=AF=7 cm，CE=10 cm，△ABF的周长是.18．如图，已知BC=EC，∠BCE=∠ACD，要使能用SAS说明△ABC≌△DEC，则应添加的一个条件为______．(答案不唯一，只需填一个)A BC DEF第15题图FEA19．如图, 已知：AB=AC , D是BC边的中点, 则∠1＋∠C=_____度．20．如图所示的方格中，连接AB，AC，则∠1+∠2＝____ ____度．三、解答题21．（2014•常州）已知：如图，点C为AB中点，CD=BE，CD∥BE．求证：△ACD≌△CBE．22．（2014•吉林）如图，△ABC和△DAE中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD，CE，求证：△ABD≌△AEC．23．已知：如图，AD是△ABC的高，E是AD上一点，BE的延长线交AC于点F，BE=AC，DE=DC，BE和AC垂直吗？说明理由．24．如图，已知AB=AC，E，D分别是AB，AC的中点，且AF•⊥BD交BD的延长线于F，AG⊥CE交CE的延长线于G，试判断AF和AG的关系是否相等，并说明理由．FEA25． 如图所示，AD 是∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，且BD =CD ，那么BE 与CF 相等吗？为什么？第24题图D CFEB AGDFACEB第25题图答案与解析一、选择题1. 答案：B解析：∵AB=AD（已知），AC=AC（公共边）∴只需要BAC=∠DAC∴△ABE≌△ACD故选B.分析：本题考察了全等三角形的判定方法中的SAS，较为简单.2. 答案：C解析：∵AB=AC（已知），∠A=∠A（公共角）∴只需要AE=AD∴△ABE≌△ACD故选C.分析：本题考察了全等三角形的判定方法中的SAS，较为简单.3. 答案：C解析：∵AE＝CF（已知），∴AE+EF＝EF+CF∴AF＝EC∵∠AFD=∠CEB∴△AFD≌△CEB（SAS）∴∠A=∠CAD=CBBC=DA∵∠AFD=∠CEB∴DF∥BE故选C.分析：本题综合考察了三角形的多个知识点，考察学生灵活运用所学知识处理问题的能力，是一道综合性很强的题目.4.答案：B解析：∵AC⊥BD，点C是BD的中点∴AB=AD（线段中垂线的性质）∴∠B=∠D（等边对等角）∴∠BAC=∠DAC（等腰三角形三线合一）∴AC平分∠BAD选B .分析：本题综合考察了三角形的多个知识点，考察学生灵活运用所学知识处理问题的能力，是一道综合性很强的题目.5. 答案：D解析：∵∠E=40°，∠F=70°∴∠D =70°∵FE=BCDE=AB∠B=∠E=40°∴△ABC≌△DEF（SAS）∴∠A=∠D =70°选D .分析：本题综合考察了三角形全等的判定，全等三角形的性质和三角形的内角和，考察学生灵活运用所学知识处理问题的能力，是一道综合性很强的题目.6. 答案：B解析：对于B，如果∠A＝∠A’＝90°，全等，但题目中没告诉是否为90°，故不一定全等.故选B .分析：本题综合考察了三角形全等的判定，考察学生灵活运用所学知识处理问题的能力，是一道综合性很强的题目.7. 答案：B解析：对于①，只能得到相似；对于②，运用SSS可以得到全等；对于③可以运用ASA 或AAS判定全等；对于④，当SAS时全等，但当SSA时不一定全等.故选B .分析：本题综合考察了三角形全等的判定，考察学生灵活运用所学知识处理问题的能力，是一道综合性很强的题目.8. 答案：D解析：对于两个图形，只有知道两个圆的半径相等，则这两个圆就全等，其余选项，皆不能得到全等，故选D .分析：本题综合考察了全等图形的判定，结合了上一节内容，考察学生灵活处理问题的能力.9. 答案：D解析：对于两个直角三角形，已经知道有一组角对应相等了，因此，运用HL定理可以判定两个直角三角形全等，选D .分析：本题综合考察了全等三角形的判定中的HL定理，内容简单.10.答案：B解析： 由翻折得△PDE ≌△CDE ∴∠PDE ＝∠CDE ＝48°∵D E ，分别为ABC △的AC ，BC 边的中点， ∴D E ∥AB∴∠APD ＝∠PDE ＝48° ∴选B.分析：本题综合考察了全等三角形的性质，三角形的中位线定理和平行线的性质，考察知识点较多，是一道不错的题目.11.答案：C解析： ∵△ABC ≌△CDA ,且AD ＝CB ∴∠B ＝∠D ∠CAB ＝∠ACD AC ＝CA ∴选C.分析：本题综合考察了全等三角形的性质，考察知识点较多，是一道不错的题目. 12.答案：D 解析： ∵AC ⊥CD∴∠ACD =90° ∵∠1+∠2+∠ACD ＝180° ∴∠1+∠2=90° ∴选D.分析：本题综合考察了三角形全等的判定和全等三角形的性质，根据不同的视角，可以考察不同的知识点，是一道不错的题目.13. 答案：A 解析： ∵AC ＝AD BC ＝BD （已知） AB ＝AB∴△ABC ≌Rt △ABD （SSS ） ∴∠CAB =∠DAB ∠CBA =∠DBA ∴选A.分析：本题综合考察了三角形全等的判定和全等三角形的性质，是一道综合性很好的题目.14.答案：C解析：由原题所给条件，可以得到有以下三对三角形全等（1）△ABE≌△DCF（2）△ABF≌△DCE（3）△FBE≌△ECF故有3对，选C.分析：本题综合考察了三角形全等的多种判定方法，是一道综合性很好的题目.15. 答案：D解析：∵AE＝DF（已知），∴AE+EF＝EF+DF∴AF＝ED∵AB=CD，BF⊥AD，CE⊥AD∴Rt△ABF≌Rt△DCE（HL）分析：本题考查了全等三角形的判定方法中的HL判定定理.二、填空题16．答案：65°| 30°解析：∵MO=OP，QO=ON（已知），∠MO Q=∠PO N（对项角相等）∴△MOQ≌△PON（SAS）∴∠P=∠M=65°，∠N=∠Q=30°分析：本题考查了全等三角形的判定和全等三角形的性质，是一道综合性较好的题目. 17．答案：29cm解析：∵AB=AC，AE=AF=7（已知），∠A=∠A（公共角）∴△ABC≌△ACE（SAS）∴BF=CE=10 cm，∴△ABF的周长＝AB+BF+FA＝12+7+10＝29(cm)分析：本题考查了全等三角形的判定和三角形周长的计算，是一道较好的题目. 18．答案：AC=CD解析：∵∠BCE=∠ACD（已知），∴∠BCE +∠ACE =∠ACE +∠ACD ∴∠BCA =∠ECD ∵BC =EC ，AC =CD ∴△ABC ≌△DEC （SAS ）分析：本题考查了全等三角形的判定和角的计算，是一道较好的题目. 19． 答案：90．解析：∵AB =AC , D 是BC 边的中点（已知）， ∴∠B ＝∠C ， AD ⊥BC ∴∠1＋∠B ＝90° ∴∠1+∠C ＝90度分析：本题考查了等腰三角形的性质和角的计算，是一道较好的题目. 20． 答案：90．解析：∵由题知小方格边长相等（已知），∴AC 与AB 所在的两个直角三角形全等 ∵AC 是其所在直角三角形的斜边 ∴两个锐角互余 ∴易得∠1+∠2＝90度分析：本题考查了全等三角形的判定方法SAS ，以及数形结合，是一道较好的题目.三、解答题21． 答案：答案见解析解析：∵C 是AB 的中点（已知）， ∴AC =CB （线段中点的定义）． ∵CD ∥BE （已知），∴∠ACD =∠B （两直线平行，同位角相等）． 在△ACD 和△CBE 中，⎪⎩⎪⎨⎧=∠=∠=.,BE CD CBE ACD CB AC ∴△ACD ≌△CBE （SAS ）．分析：本题考查了线段中点的性质以及全等三角形的判定方法，综合性比较强. 22． 答案：答案见解析 解析：∵∠BAC =∠DAE ， ∴∠BAC -BAE =∠DAE -∠BAE ， 即∠BAD =∠CAE ，在△ABD 和△AEC 中，⎪⎩⎪⎨⎧=∠=∠=.,AE AB EAC BAD AC AD∴△ABD ≌△AEC （SAS ）．分析：本题考查了角的和差计算以及全等三角形的判定方法，是一道综合性比较强的题目.需要在审题时细心研究，不急不躁.23． 答案：BE ⊥AC .解析：在Rt △BDE 和 Rt △ACD 中， ⎩⎨⎧==DC DE AC BE ∴Rt △BDE ≌ Rt △ACD (HL )．∴∠BDE =∠CAD .∵AD 是△ABC 的高，∴∠CAD +∠C =90°.∴∠BDE +∠C =90°.∴∠BFD =90°.∴BE ⊥AC .分析：本题考查了余角的性质，垂直的判定以及全等三角形的判定方法，是一道综合性比较强的题目.需要在审题时细心研究，不急不躁.24． 答案：AF =AG.解析：∵AB =AC ，E ，D 分别是AB ，AC 的中点，∴ AD =AE . ∴在△ABD 和△ACE 中，⎪⎩⎪⎨⎧=∠=∠=.,,AE AD CAE BAD AC AB∴△ABD ≌△ACE (SAS )．∴∠ABD ≌∠ACE .在△ABF 和△ACG 中，⎪⎩⎪⎨⎧=∠=∠∠=∠.,,AC AB ACG ABF G F∴△ABF ≌△ACG (AAS )．∴AF =AG .分析：本题考查了线段中点的性质应用以及多种全等三角形的判定方法，是一道综合性比较强的题目.需要在审题时细心研究，不急不躁.25．答案：BE =CF解析：∵AD 是∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ， ∴ DE =DF .∴在Rt △BDE 和Rt △CDF 中，⎩⎨⎧==.,DF DE CD BD ∴Rt △BDE ≌Rt △CDF （HL ）.∴BE =CF .分析：本题考查了角平线的性质和全等三角形的判定方法。

九年级数学下册同步练习6.4探索三角形相似的条件（三边成比例的两个三角形相似）一、选择题1.下面给出4个结论：①所有的等腰三角形都相似；②所有的直角三角形都相似；③所有的等边三角形都相似；④所有的矩形都相似，其中正确的有A．1个B．2个C．3个D．4个,2，2，△A'B'C'的两边长分别为1，5，要使△ABC∽△A'B'C'，则△A'B'C' 2.△ABC的三边长分别为10的第三边长为（）3.如图，小正方形的边长均为1，则图中的三角形（阴影部分）与△ABC相似的是（）A B C D4.若一个三角形的三边长分别是5cm.6cm.8cm，另一个三角形三边的长分别是24cm.15cm.18cm，则这两个三角形（）A．全等B．相似C．不相似D．不一定相似5.下面给出4个结论：①所有的等腰三角形都相似；②所有的直角三角形都相似；③所有的等边三角形都相似；④所有的矩形都相似，其中正确的有（）A．1个B．2个C．3个D．4个6.如图，∠AOD＝90°，OA＝OB＝BC＝CD，下列结论正确的是（）A．△OAB∽△OCA B．△OAB∽△ODAC．△BAC∽△BDA D．△AOC∽△DOA第6题第7题7.如图，若A.B.C.P.Q.甲.乙.丙.丁都是方格纸中的格点，为使△ABC∽△PQR，则点R应是甲.乙.丙.丁四点A．甲B．乙C．丙D．丁二、填空题8.在△ABC中，AB：BC：CA＝2：3：4，在△A'B'C'中，A'B'＝1，C'A'＝2，当B'C'＝＿＿＿＿＿时，△ABC∽△A'B'C'9.在△ABC中，BA＝6，AC＝8，在△A'B'C'中，A'B'＝4，A'C'＝3，若BC：B'C'＝＿＿＿＿＿，则△ABC∽△＿＿＿＿＿＿＿＿10.已知：在△ABC中，AB＝4，BC＝5，CA＝6（1）如果DE＝10，那么当EF＝＿＿＿，FD＝＿＿＿＿时，△DEF∽△ABC；（2）如果DE＝10，那么当EF＝＿＿＿，FD＝＿＿＿＿时，△FDE∽△ABC.11.如图，在△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于点D．给出下列结论：①∠AFC=∠C；②DF=CF；③△ADE∽△FDB；④∠BFD=∠CAF，其中正确的结论是＿＿＿＿＿＿(写出所有正确结论的序号)．第11题第12题12.如图，正方形网格的每一个小正方形的边长都是1，则∠A1E2A2+∠A4E2C4+∠A4E5C4=＿＿＿＿＿．13.在等腰△ABC中，顶角∠A=36°，底角平分线BD交AC于点D，得点D是线段AC的黄金分割点．若AC=10 cm．则AD≈＿＿＿＿＿cm．三、解答题14.在△ABC和△A’B’C’中，AB＝12，BC＝15，AC＝24，A’B’＝25，B’C’＝40，C’A’＝20.求证：△ABC 和△A’B’C’相似.15.如图，已知O为△ABC内一点，D，E，F分别是OA，OB，OC的中点．（1）求证：△DEF∽△ABC．（2）图中还有哪几对相似三角形？16.如图，在△ABC 和△ADE 中，AE AC DE BC AD AB ==，试说明△ABD ∽△ACE.17.如图，在大小为4×4的正方形方格中，△ABC 的顶点A.B.C 在单位正方的顶点上，请在图中画出一个△A 1B 1C 1，使△A 1B 1C 1∽△ABC （相似比不为1），且点A 1，B 1，C 1都在单位正方形的顶点上.18.如图，已知格点△ABC ，请在图中分别画出与△ABC 相似的格点△A 1B 1C 1和格点△A 2B 2C 2，并使△A 1B 1C 1与△ABC 的相似比等于2，而A 2B 2C 2与△ABC 的相似比等于5.19.已知：如图在△ABC 中，AD 为边BC 上的高，E.F 分别为边AB.AC 上的中点，△DEF 与△ABC 相似吗？说明你的理由.20.如图，在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC交BD的延长线于点M．(1)请判断的值及∠AMB的度数，并说明理由；(2)若∠OBD=15°，AM=4，求AB的长。