高中数学选修2-1《圆锥曲线与方程》知识点讲义上课讲义

2．1.1 曲线与方程曲线的方程与方程的曲线在直角坐标系中，如果某曲线C (看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f (x ，y )＝0的实数解建立了如下的关系：(1)曲线上点的坐标都是□01这个方程的解； (2)以□02这个方程的解为坐标的点都是曲线上的点． 那么，这个方程叫做□03曲线的方程，这条曲线叫做□04方程的曲线．1．判一判(正确的打“√”，错误的打“×”)(1)若以方程f (x ，y )＝0的解为坐标的点都在曲线C 上，则方程f (x ，y )＝0即为曲线C 的方程．( )(2)若曲线C 上的点满足方程F (x ，y )＝0，则坐标不满足方程F (x ，y )＝0的点不在曲线C 上．( )(3)方程x ＋y －2＝0是以A (2,0)，B (0,2)为端点的线段的方程．( ) 答案 (1)× (2)√ (3)×2．做一做(请把正确的答案写在横线上)(1)写出曲线xy ＋4x －3y ＝0与坐标轴的交点的坐标________． (2)直线C 1：x ＋y ＝0与直线C 2：x －y ＋2＝0的交点坐标为________．(3)(教材改编P 37T 2)点A ⎝ ⎛⎭⎪⎫m3，m 在方程x 2＋(y ＋1)2＝5表示的曲线上，则m ＝________.(4)x 2＋y 2＝1(x >0)表示的曲线是________．答案 (1)(0,0) (2)(－1,1) (3)－3或65 (4)以(0,0)为圆心，1为半径的圆在y 轴右侧的部分探究1 曲线与方程的概念例1 分析下列曲线上的点与相应方程的关系：(1)过点A (2,0)平行于y 轴的直线与方程|x |＝2之间的关系； (2)与两坐标轴的距离的积等于5的点与方程xy ＝5之间的关系； (3)第二、四象限两轴夹角平分线上的点与方程x ＋y ＝0之间的关系．[解] (1)过点A (2,0)平行于y 轴的直线上的点的坐标都是方程|x |＝2的解；但以方程|x|＝2的解为坐标的点不一定都在过点A(2,0)且平行于y轴的直线上．因此，|x|＝2不是过点A(2,0)平行于y轴的直线的方程．(2)与两坐标轴的距离的积等于5的点的坐标不一定满足方程xy＝5；但以方程xy＝5的解为坐标的点与两坐标轴的距离之积一定等于5.因此，与两坐标轴的距离的积等于5的点的轨迹方程不是xy＝5.(3)第二、四象限两轴夹角平分线上的点的坐标都满足x＋y＝0；反之，以方程x＋y＝0的解为坐标的点都在第二、四象限两轴夹角的平分线上．因此，第二、四象限两轴夹角平分线上的点的轨迹方程是x＋y＝0.拓展提升判断方程是否是曲线的方程的两个关键点一是检验点的坐标是否适合方程；二是检验以方程的解为坐标的点是否在曲线上．【跟踪训练1】设方程f(x，y)＝0的解集非空，如果命题“坐标满足方程f(x，y)＝0的点都在曲线C上”是不正确的，则下列命题正确的是( )A．坐标满足方程f(x，y)＝0的点都不在曲线C上B．曲线C上的点的坐标都不满足方程f(x，y)＝0C．坐标满足方程f(x，y)＝0的点有些在曲线C上，有些不在曲线C上D．一定有不在曲线C上的点，其坐标满足方程f(x，y)＝0答案 D解析命题“坐标满足方程f(x，y)＝0的点都在曲线C上”是不正确的，即“坐标满足方程f(x，y)＝0的点不都在曲线C上”是正确的，“不都在”包括“都不在”和“有的在，有的不在”两种情况，故A，C错误，而B显然错误，选D.探究2 点与曲线的位置关系例2 已知方程x2＋(y－1)2＝10.(1)判断P(1，－2)，Q(2，3)是否在此方程表示的曲线上；(2)若曲线y2＝xy＋2x＋k通过点(a，－a)，a∈R，求k的取值范围．[解] (1)∵12＋(－2－1)2＝10，(2)2＋(3－1)2＝6≠10，∴P(1，－2)在方程x2＋(y－1)2＝10表示的曲线上，Q(2，3)不在此曲线上．(2)因为曲线y2＝xy＋2x＋k过点(a，－a)，所以a2＝－a2＋2a＋k.所以k ＝2a 2－2a ＝2⎝ ⎛⎭⎪⎫a －122－12，所以k ≥－12，所以k 的取值范围是⎣⎢⎡⎭⎪⎫－12，＋∞. 拓展提升点与曲线位置关系问题的求解方法判断点与曲线的位置关系要从曲线与方程的定义入手．(1)要判断点是否在方程表示的曲线上，只需检验点的坐标是否满足方程即可； (2)若所给点在已知曲线上，则点的坐标适合已知曲线的方程，将所给点的坐标代入曲线的方程，可求点或方程中的参数．【跟踪训练2】 已知0≤α<2π，若点P (cos α，sin α)在曲线(x －2)2＋y 2＝3上，求α.解 ∵点P (cos α，sin α)在曲线(x －2)2＋y 2＝3上， ∴(cos α－2)2＋sin 2α＝3， ∴cos 2α－4cos α＋4＋sin 2α＝3， ∴cos α＝12.又∵0≤α<2π，∴α＝π3或5π3.探究3 由方程研究曲线的类型和性质例3 方程(x ＋y －2)x 2＋y 2－9＝0表示的曲线是( ) A ．一条直线和一个圆 B ．一条直线和半个圆 C ．两条射线和一个圆 D ．一条线段和半个圆[解析] 由题意方程(x ＋y －2)x 2＋y 2－9＝0可化为x 2＋y 2－9＝0或x ＋y －2＝0(x 2＋y 2－9≥0)，∴方程(x ＋y －2) x 2＋y 2－9＝0表示的曲线是两条射线和一个圆．故选C. [答案] C 拓展提升判断方程表示曲线的方法判断方程表示什么曲线，常需对方程进行变形，如配方、因式分解或利用符号法则、基本常识转化为熟悉的形式，然后根据化简后的特点判断．特别注意，方程变形前后应保持等价，否则，变形后的方程表示的曲线不是原方程表示的曲线．另外，当方程中含有绝对值时，常采用分类讨论的思想．【跟踪训练3】 方程4x 2－y 2＋6x －3y ＝0表示的图形是( ) A ．直线2x －y ＝0 B ．直线2x ＋y ＋3＝0C ．直线2x －y ＝0或直线2x ＋y ＋3＝0D ．直线2x ＋y ＝0和直线2x －y ＋3＝0 答案 C解析 ∵4x 2－y 2＋6x －3y ＝(2x ＋y )(2x －y )＋3(2x －y )＝(2x －y )(2x ＋y ＋3)＝0， ∴原方程表示直线2x －y ＝0或直线2x ＋y ＋3＝0. 探究4 两曲线的交点问题例4 已知直线y ＝mx ＋3m 和曲线y ＝4－x 2有两个不同的交点，则实数m 的取值范围是( )A.⎣⎢⎡⎭⎪⎫0，255B.⎣⎢⎡⎦⎥⎤－255，0 C.⎝ ⎛⎭⎪⎫－255，255D.⎣⎢⎡⎭⎪⎫0，147 [解析] 直线y ＝m (x ＋3)过定点(－3,0)，曲线y ＝4－x 2即x 2＋y 2＝4(y ≥0)表示半圆，设直线y ＝mx ＋3m 与半圆x 2＋y 2＝4(y ≥0)相切时的倾斜角为α，sin α＝23，又α∈⎝⎛⎭⎪⎫0，π2，所以cos α＝1－⎝ ⎛⎭⎪⎫232＝53，所以切线斜率m ＝tan α＝2353＝255.由图可知，为使直线y ＝mx ＋3m 和曲线y ＝4－x 2有两个不同的交点，m 的取值范围是⎣⎢⎡⎭⎪⎫0，255.[答案] A[条件探究] 如果直线方程改为“y ＝x ＋3m ”，其他条件不变，应该怎样解答？ 解 直线y ＝x ＋3m 与直线y ＝x 平行，且在y 轴上的截距为3m ，当3m ＝2，即m ＝23时，直线y ＝x ＋3m 与半圆y ＝4－x 2恰有两个不同的交点，当3m ＝22，即m ＝223时，直线y ＝x ＋3m 与半圆y ＝4－x 2相切．由图可知，为使直线y ＝x ＋3m 与曲线y ＝4－x 2有两个不同的交点，m 的取值范围是⎣⎢⎡⎭⎪⎫23，223. 拓展提升求曲线交点的三个步骤(1)联立：联立方程组把两条曲线的方程联立，构成方程组； (2)求解：求解联立的方程组；(3)得交点：根据方程组的解确定交点，解的个数决定两曲线交点的个数．【跟踪训练4】 已知直线l ：x ＋y ＝a 及曲线C ：x 2＋y 2－4x －4＝0，则实数a 取何值时分别有一个交点，两个交点，无交点．解 联立方程组⎩⎪⎨⎪⎧x ＋y ＝a ，x 2＋y 2－4x －4＝0，消去y ，得2x 2－(2a ＋4)x ＋a 2－4＝0， 则Δ＝(2a ＋4)2－8(a 2－4)＝－4a 2＋16a ＋48， 当Δ＝0，即a 2－4a －12＝0，得a ＝6或a ＝－2， 此时有两相等实根；当Δ>0，即a 2－4a －12<0，得－2<a <6， 此时有两不相等实根；当Δ<0即a 2－4a －12>0得a <－2或a >6， 此时无根．综上所述，当a ＝－2或a ＝6时有一个交点； 当－2<a <6时有两个交点； 当a <－2或a >6时无交点．1.判断曲线与方程关系的思路曲线与方程建立了对应，即把点和坐标的对应过渡到曲线和方程的对应，因此判断曲线与方程的关系时，需同时判断以方程的解为坐标的点是否都在曲线上，曲线上点的坐标是否都是方程的解.2.点与曲线位置关系问题的求解方法(1)判断点是否在某个方程表示的曲线上，就是检验该点的坐标是不是方程的解，是否适合方程．若适合方程，就说明点在曲线上；若不适合，就说明点不在曲线上.(2)已知点在某曲线上，可将点的坐标代入曲线的方程，从而可研究有关参数的值或范围问题.3.研究两曲线交点问题的方法关于曲线的交点问题，通常表现为两种类型：一是判定两曲线是否存在交点；二是求解交点及和交点有关的问题．在解决这些问题时，除要用到方程(组)的方法及相关知识外，有时还需综合应用各种曲线自身所具有的某些几何性质.1．下列选项中方程与其表示的曲线正确的是( )答案 C解析 对于A ，x 2＋y 2＝1表示一个整圆；对于B ，x 2－y 2＝(x ＋y )(x －y )＝0表示两条相交直线；对于D ，由lg x ＋lg y ＝0知x >0，y >0.2．已知直线l ：x ＋y －4＝0及曲线C ：(x －3)2＋(y －2)2＝2，则点M (2,2)( ) A ．在直线l 上，但不在曲线C 上 B ．在直线l 上，也在曲线C 上 C ．不在直线l 上，也不在曲线C 上 D ．不在直线l 上，但在曲线C 上 答案 A解析 将点M (2,2)的坐标代入方程验证知M ∈l ，M ∉C . 3．方程(x 2－4)2＋(y 2－4)2＝0表示的图形是( ) A ．两个点 B ．四个点 C ．两条直线 D ．四条直线答案 B解析 由已知⎩⎪⎨⎪⎧ x 2－4＝0，y 2－4＝0，所以⎩⎪⎨⎪⎧x ＝±2，y ＝±2，即⎩⎪⎨⎪⎧x ＝2，y ＝2或⎩⎪⎨⎪⎧x ＝2，y ＝－2或⎩⎪⎨⎪⎧x ＝－2，y ＝2或⎩⎪⎨⎪⎧x ＝－2，y ＝－2.4．方程(x －1)2＋y －2＝0表示的是________． 答案 点(1,2)解析 由(x －1)2＋y －2＝0，知(x －1)2＝0且y －2＝0即x ＝1，且y ＝2，所以(x －1)2＋y －2＝0表示的是点(1,2)．5．证明：到两坐标轴距离相等的点的轨迹方程是y ＝±x . 证明 (1)如图所示，设M(x0，y0)是轨迹上任一点，因为点M到x轴的距离为|y0|，到y轴的距离为|x0|，所以|x0|＝|y0|，即y0＝±x0，所以轨迹上任一点的坐标都是方程y＝±x的解．(2)设点M1的坐标为(x1，y1)，且是方程y＝±x的解，则y1＝±x1，即|x1|＝|y1|，而|x1|，|y1|分别是点M1到y轴，x轴的距离，因此点M1到两坐标轴的距离相等，即点M1是曲线上的点．由(1)(2)可知，y＝±x是到两坐标轴距离相等的点的轨迹方程．。

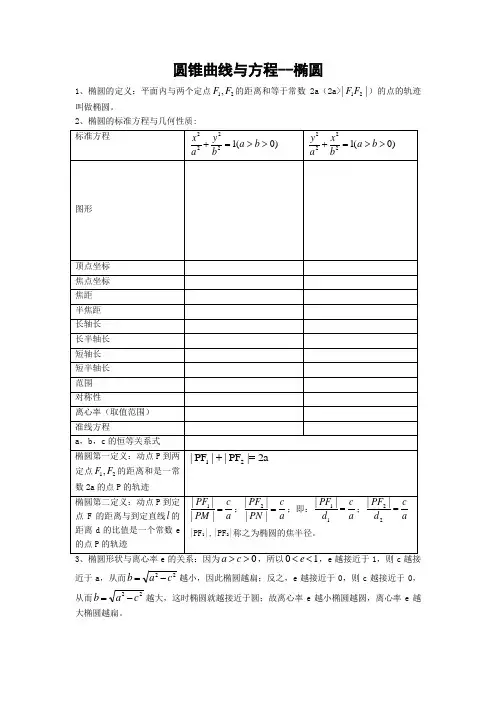
圆锥曲线与方程--椭圆1、椭圆的定义：平面内与两个定点21,F F 的距离和等于常数2a （2a>||21F F ）的点的轨迹叫做椭圆。

2、椭圆的标准方程与几何性质:近于a ，从而22c a b -=越小，因此椭圆越扁；反之，e 越接近于0，则c 越接近于0，从而22c a b -=越大，这时椭圆就越接近于圆；故离心率e 越小椭圆越圆，离心率e 越大椭圆越扁。

4、弦长公式（一）：;12222⎪⎩⎪⎨⎧=++=b ya x m kx y 由)0(02≠=++a c bx ax y 得：消去⎪⎪⎩⎪⎪⎨⎧=-=+;;2121a c x x a b x x 由韦达定理知：，则，，，弦端点设)()(2211y x B y x A[]212212221222122212212214)()1())(1()()()()(x x x x k x x k x x k x x y y x x AB -++=-+=-+-=-+-=∴5、弦长公式（二）：;12222⎪⎩⎪⎨⎧=++=b yax mkx y 由)0'(0'''2≠=++a c y b y a x 得：消去⎪⎪⎩⎪⎪⎨⎧=-=+;;''21''21a c y y a b y y 由韦达定理知：[]212212221222122122212214)()11())(11()()(1)()(y y y y k y y ky y y y k y y x x AB -++=-+=-+-=-+-=直线和椭圆相交，求其弦长，通常利用根与系数的关系，设出交点坐标，但是不求出，从而求出弦长。

这种方法称为设而不求，这个公式叫做弦长公式。

1、双曲线的定义：平面内与两个定点21,F F 的距离的差的绝对值等于常数2a （2a<||21F F ）的点的轨迹叫做双曲线。

2、双曲线的标准方程与几何性质:1122222-=-=-==e ac a a c a b k ；所以e 越大，则渐近线的斜率的绝对值就越大，这时双曲线的形状就从扁狭逐渐变得开阔。

数学·选修2－1(人教A版)
圆锥曲线与方程
本章知识概述
课程导航
在探究圆锥曲线几何特征的基础上，建立它们的方程，通过方程研究它们的简单性质，并用坐标法解决一些与圆锥曲线有关的简单几何问题和实际问题，进一步感受数形结合的基本思想．
学习内容
1．圆锥曲线．
(1)了解圆锥曲线的实际背景，了解圆锥曲线在刻画现实世界和解决实际问题中的作用；
(2)掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质；
(3)了解双曲线的定义、几何图形和标准方程，知道它的简单几何性质；
(4)了解圆锥曲线的简单应用；
(5)理解数形结合的思想．
2．曲线与方程．
了解方程的曲线与曲线的方程的对应关系．
网络构建。