最新中考主观试题(十)“意义”型题目专项练习

【初中道德与法治】中考主观题答题模板，各大题型！1、初中政治主观题类型“是什么”型题目只需熟悉课本的知识点，按照题目答题就可以。

“认识”型简答题这类题目的设问方式通常是“如何认识”、“如何看待”、“谈谈你的看法”、“分析这一现象”等等。

这类题目的解题方法通常按照“是什么”、“为什么”、“怎么办”的思路去解答，即“对与错”、“重要性、必要性”、“具体措施”等。

“启示”型题目这类题目的设问方式是：这个事给我们有什么启示？回答时，要注意提炼材料中的观点，结合所学的知识点来分析，从中归纳出材料反映的道理。

“评析”型题目这类题目一般是“运用所学知识对这一观点进行评析”。

回答这类题目时，首页要判断是对还是错，或者是不全面，然后根据相应的依据如法律法规和教材的理论等，再联系材料中的观点进行分析。

“漫画”型题目漫画类的题目，要找准漫画与知识点的链接点，首先要看标题，看标题能否给出指引性的知识点或者观点；然后看文字，看看漫画中有哪些文字，通常漫画里的文字都是“意味深长”的；最后看画面，漫画夸张之处通常是其弦外之音，真正的寓意也就在这里。

“图表”型题目“图表”类型的，首先要看标题，标题比较直观的说明了图表的内容；然后要将图片数据做三个对比，“横向比”、“纵向比”和“综合比”，将三个对比的数据归纳整理，通常就会得出想要说明的问题；最后要看看图表下面的注释，看看有没有特别的注释。

“体现型”题目这类题目通常会问“体现了什么？、怎么体现”等等。

回答的时候，应该写上教材的知识点，再加上材料的关键词来体现这一知识点。

所以解题的思路就是：定知识点、联系知识点、梳理答题。

“反映”型题目这类题目通常会问“反映了某一问题发生了哪些变化”、“反映了什么现象或什么问题？”、“说明了什么？”等。

回答的时候要对题目材料所给的信息全面把握，将感性的材料理性化。

“为什么”型题目这类题目的设问方式是：为什么说……、为什么要……。

回答这类为什么题目的时候，最重要的是说明你为什么要这样说、这样做的依据，有时也要回答不这样做的危害等等。

2020中考道德与法治意义类题目总结句式：“有利于……”“促进了……”“给……带来积极影响”从问题本身或者材料中的的关键词（限定词）分析举例：国家依法打击珍稀偷猎野生动物的违法犯罪行为有什么意义？关键词（1）珍稀野生动物（2）违法犯罪行为逐个分析：（1）珍稀野生动物：动物也有生命——有利于保护珍稀野生动物的生命——进而有利于保护生物多样性，实现人与大自然的和谐相处。

从整体上分析，落脚到公民角度：有利于增强公民的生态环保意识。

（2）违法犯罪行为看到“法”首先想到依法治国、法治和法律，进而总结答案（1））有利于实行依法治国基本方略，建设社会主语法治国家。

法治是社会主义核心价值观的基本内容进而得出（2）有利于弘扬法治精神，践行社会主义核心价值观。

打击违法发罪行为就是制裁违法犯罪，就有利于维护公民合法权益，由此想到法律的作用（3）有利于制裁违法犯罪，维护公民的合法权益。

从整体上分析，落脚到公民角度：有利于增强公民的法律意识和生态环保意识。

(二)考虑对哪一方面有意义（相对固定答案）对个人的意义,对国家、集体、社会和民族的意义。

个人：一般包括维护个人利益,使思想觉悟得以提升,行动得以规范,提高生活、工作和学习的效率、质量,增强（）意识等。

国家：侧重政治：国家统一和安全；侧重经济：繁荣富强；对外：考虑综合国力，国际地位和国际影响力。

社会：从五位一体角度包括社会、经济、政治、文化、社会、生态社会本身：社会主义核心价值观全面小康社会主义现代化和谐社会社会公平正义经济：经济实力、综合国力，物质文明政治：政治文明，民主政治建设文化：精神文明、先进文化生态：生物多样性，人与大自然和谐相处，可持续发展战略，科学发展观，保护环境和合理利用资源的基本国策，生态文明，美丽中国民族：民族振兴，中华民族伟大复兴，民族团结集体：集体荣誉和利益具体答案整理：个人：（1）有利于维护个人利益，使思想觉悟得以提升,行动得以规范,提高生活、工作和学习的效率、质量。

专题31 中考热点新定义问题专项训练（原卷版）专题诠释：新定义题型是近几年来中考的热点问题。

它常集合数形结合思想，类比思想，转化思想，分类讨论思想，方程思想，函数思想于一体。

常以压轴题身份出现。

本专题精选新定义问题共20条，欢迎使用。

一．选择题1．（2021•河北模拟）对于实数x，y，我们定义符号max{x，y}的意义：当x≥y时，max{x，y}＝x，当x＜y时，max{x，y}＝y．例如max{﹣1，﹣2}＝﹣1，max{3，π}＝π，则关于x的函数y＝max{3x，x+2}的图象为（）A．B．C．D．二．填空题2．（2021•深圳模拟）用“●”“□”定义新运算：对于数a，b，都有a●b＝a和a□b＝b．例如3●2＝3，3□2＝2，则（2020□2021）●（2021□2020）＝．3．（2021•碑林区校级模拟）（正多边形的每个内角都相等）如图，在正八边形ABCDEFGH中，对角线BF 的延长线与边DE的延长线交于点M，则∠M的大小为．4．（2019•福田区三模）对于m，n（n≥m）我们定义运算A n m＝n（n﹣1）（n﹣2）（n﹣3）…（n﹣（m﹣1）），A73＝7×6×5＝210，请你计算A42＝．6．（2022秋•魏县期中）若x是不等于1的实数，我们把11−x 称为x的差倒数，如2的差倒数是11−2=−1，﹣1的差倒数为11−(−1)=12，现已知x1=13，x2是x1的差倒数，x3是x2的差倒数，x4是x3的差倒数，…，依此类推，则x2022的值为．三．解答题7．（2021秋•汉阳区期中）对任意一个四位数n，如果千位与十位上的数字之和为9，百位与个位上的数字之和也为9，则称n为“极数”．（1）请任意写出两个“极数”，；（2）猜想任意一个“极数”是否是99的倍数，请说明理由；（3）如果一个正整数a是另一个正整数b的平方，则称正整数a是完全平方数．若四位数m为“极数”，记D（m）=m33，则满足D（m）是完全平方数的所有m的值是．8．（2022秋•胶州市期末）《道德经》中的“道生一，一生二，二生三，三生万物”道出了自然数的特征．在数的学习过程中，我们会对其中一些具有某种特性的数进行研究，如学习自然数时，我们研究了奇数、偶数、质数、合数等．现在我们来研究另一种特殊的自然数——“纯数”．定义：对于自然数n，在计算n+（n+1）+（n+2）时，各数位都不产生进位，则称这个自然数n为“纯数”．例如：32是“纯数”，因为计算32+33+34时，各数位都不产生进位；23不是“纯数”，因为计算23+24+25时，个位产生了进位．（1）判断2022是否是“纯数”？请说明理由；（2）请直接写出2023到2050之间的“纯数”；（3）不大于100的“纯数”的个数为．9．（2021•任城区二模）如果一个三角形有一条边上的高等于这条边的一半，那么我们把这个三角形叫做“半高三角形”．这条高称为“半高”．如图1，对于△ABC，BC边上的高AD等于BC的一半，△ABC就是“半高三角形”．此时，称△ABC是“BC边半高三角形”，AD是“BC边半高”；如图2，对于△EFG，EF边上的高GH等于EF的一半，△EFG就是半高三角形，此时，称△EFG是EF边半高三角形，GH 是“EF边半高”．（1）在Rt△ABC中，∠ACB＝90°，AB＝10cm，若ABC是“BC边半高三角形”，则AC＝cm；（2）若一个三角形既是等腰三角形又是半高三角形，且“半高”长为2cm，则该等腰三角形底边长的所有可能值为．（3）如图3，平面直角坐标系内，直线y＝x+2与抛物线y＝x2交于R，S两点，点P是抛物线y＝x2上的一个动点，点Q是坐标系内一点，且使得△RSQ为“RS边半高三角形”．当点P介于点R与点S之间，且PQ取得最小值时，求点P的坐标．10．（2022春•梁平区期末）在平面直角坐标系中，对于任意两点A（a，b），B（c，d），若点T（x，y）满足x=a+c3，y=b+d3那么称点T是点A，B的融合点．例如：A＝（﹣1，8），B＝（4，﹣2），当点T（x，y）满足x=−1+43=1，y=8+(−2)3=2时，则点T（1，2）是点A，B的融合点．（1）已知点A（﹣1，5），B（7，7），C（2，4），请说明其中一个点是另外两个点的融合点．（2）如图，点D（3，0），点E（t，2t+3）是直线l：y＝2x+3上任意一点，点T（x，y）是点D，E的融合点．①试确定y与x的关系式．②若直线ET交x轴于点H，当∠TDH为直角时，求直线ET的解析式．11．（2019•浙江）如图，在平面直角坐标系中，正方形OABC的边长为4，边OA，OC分别在x轴，y轴的正半轴上，把正方形OABC的内部及边上，横、纵坐标均为整数的点称为好点．点P为抛物线y＝﹣（x ﹣m）2+m+2的顶点．（1）当m＝0时，求该抛物线下方（包括边界）的好点个数．（2）当m＝3时，求该抛物线上的好点坐标．（3）若点P在正方形OABC内部，该抛物线下方（包括边界）恰好存在8个好点，求m的取值范围．12．（2022•亭湖区校级三模）定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB 是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连接DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝4BE，QB＝6，求邻余线AB的长．13．（2021•南丰县模拟）如果一个四边形的对角线把四边形分成两个三角形，一个是等边三角形，另一个是该对角线所对的角为60°的三角形，我们把这条对角线叫做这个四边形的理想对角线，这个四边形称为理想四边形．（1）如图1，在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD⊥AB，E为BC中点，连接DE．求证：四边形ADEC为理想四边形；（2）如图2，△ABD是等边三角形，若BD为理想对角线，为使四边形ABCD为理想四边形，小明同学给出了他的设计图（见设计后的图），其中圆心角∠BOD＝120°；请你解释他这样设计的合理性．（3）在（2）的条件下，①若△BCD为直角三角形，BC＝3，求AC的长度；②如图3，若CD＝x，BC＝y，AC＝z，请直接写出x，y，z之间的数量关系．14．（2020•朝阳区一模）在平面直角坐标系xOy中，点A（t，0），B（t+2，0），C（n，1），若射线OC上存在点P，使得△ABP是以AB为腰的等腰三角形，就称点P为线段AB关于射线OC的等腰点．（1）如图，t＝0，①若n＝0，则线段AB关于射线OC的等腰点的坐标是；②若n＜0，且线段AB关于射线OC的等腰点的纵坐标小于1，求n的取值范围；（2）若n=√33，且射线OC上只存在一个线段AB关于射线OC的等腰点，则t的取值范围是．15．（2022•房山区模拟）对于平面直角坐标系xOy中的图形W1和图形W2，给出如下定义：在图形W1上存在两点A，B（点A，B可以重合），在图形W2上存在两点M，N（点M，N可以重合）使得AM＝2BN，则称图形W1和图形W2满足限距关系．（1）如图1，点C（√3，0），D（0，﹣1），E（0，1），点P在线段CE上运动（点P可以与点C，E重合），连接OP，DP．①线段OP的最小值为，最大值为；线段DP的取值范围是；②在点O，点D中，点与线段DE满足限距关系；（2）在（1）的条件下，如图2，⊙O的半径为1，线段FG与x轴、y轴正半轴分别交于点F，G，且FG∥EC，若线段FG与⊙O满足限距关系，求点F横坐标的取值范围；（3）⊙O的半径为r（r＞0），点H，K是⊙O上的两个点，分别以H，K为圆心，2为半径作圆得到⊙H 和⊙K，若对于任意点H，K，⊙H和⊙K都满足限距关系，直接写出r的取值范围．16．（2022•西城区校级模拟）点P （x 1，y 1），Q （x 2，y 2）是平面直角坐标系中不同的两个点，且x 1≠x 2．若存在一个正数k ，使点P ，Q 的坐标满足|y 1﹣y 2|＝k |x 1﹣x 2|，则称P ，Q 为一对“限斜点”，k 叫做点P ，Q 的“限斜系数”，记作k （P ，Q ）．由定义可知，k （P ，Q ）＝k （Q ，P ）．例：若P （1，0），Q （3，12），有|0−12|=14|1﹣3|，所以点P ，Q 为一对“限斜点”，且“限斜系数”为14． 已知点A （1，0），B （2，0），C （2，﹣2），D （2，12）． （1）在点A ，B ，C ，D 中，找出一对“限斜点”： ，它们的“限斜系数”为 ；（2）若存在点E ，使得点E ，A 是一对“限斜点”，点E ，B 也是一对“限斜点”，且它们的“限斜系数”均为1．求点E 的坐标；（3）⊙O 半径为3，点M 为⊙O 上一点，满足MT ＝1的所有点T ，都与点C 是一对“限斜点”，且都满足k （T ，C ）≥1，直接写出点M 的横坐标x M 的取值范围．17．（2020•密云区一模）对于平面直角坐标系xOy 中的任意一点P ，给出如下定义：经过点P 且平行于两坐标轴夹角平分线的直线，叫做点P 的“特征线”．例如：点M （1，3）的特征线是y ＝x +2和y ＝﹣x +4；（1）若点D 的其中一条特征线是y ＝x +1，则在D 1（2，2）、D 2（﹣1，0）、D 3（﹣3，4）三个点中，可能是点D 的点有 ；（2）已知点P （﹣1，2）的平行于第二、四象限夹角平分线的特征线与x 轴相交于点A ，直线y ＝kx +b （k ≠0）经过点P ，且与x 轴交于点B ．若使△BP A 的面积不小于6，求k 的取值范围；（3）已知点C （2，0），T （t ，0），且⊙T 的半径为1．当⊙T 与点C 的特征线存在交点时，直接写出t 的取值范围．18．（2022秋•西城区校级期中）已知函数y＝x2+bx+c（x≥2）的图象过点A（2，1），B（5，4）．（1）直接写出y＝x2+bx+c（x≥2）的解析式；（2）如图，请补全分段函数y={−x2+2x+1(x＜2)x2+bx+c(x≥2)的图象（不要求列表）．并回答以下问题：①写出此分段函数的一条性质：；②若此分段函数的图象与直线y＝m有三个公共点，请结合函数图象直接写出实数m的取值范围；（3）横、纵坐标都是整数的点叫做整点，记（2）中函数的图象与直线y=12x−1围成的封闭区域（不含边界）为“W区域”，请直接写出区域内所有整点的坐标．20．（2021春•丰台区校级月考）在平面直角坐标系xOy中，过⊙T（半径为r）外一点P引它的一条切线，切点为Q，若0＜PQ≤2r，则称点P为⊙T的伴随点．（1）当⊙O的半径为1时，①在点A（﹣3，0），B（﹣1，√3），C（2，﹣1）中，⊙O的伴随点是；②点D在直线y＝﹣x+3上，且点D是⊙O的伴随点，求点D的横坐标d的取值范围；（2）⊙M的圆心为M（m，0），半径为3，直线y＝2x+3与x轴，y轴分别交于点E，F．若线段EF上的所有点都是⊙M的伴随点，直接写出m的取值范围．19．（2020•丰台区校级开学）已知：点P为图形M上任意一点，点Q为图形N上任意一点，若点P与点Q 之间的距离PQ始终满足PQ＞0，则称图形M与图形N相离．（1）已知点A（1，2）、B（0，﹣5）、C（2，﹣1）、D（3，4）．①与直线y＝3x﹣5相离的点是；②若直线y＝3x+b与△ABC相离，求b的取值范围；（2）设直线y＝x+3、直线y＝﹣x+3及直线y＝﹣3围成的图形为W，正方形T的对角线长为2，两条对角线分别平行于坐标轴，该正方形对角线的交点坐标为（t，0），直接写出正方形T与图形W相离的t 的取值范围．。

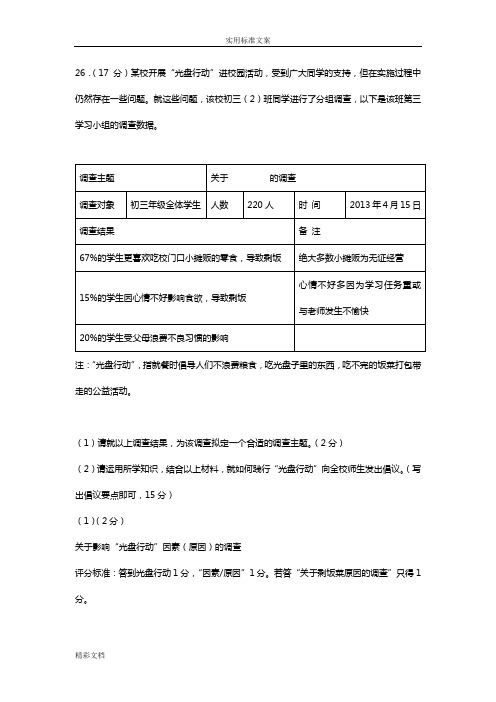
26．（17分）某校开展“光盘行动”进校园活动，受到广大同学的支持，但在实施过程中仍然存在一些问题。

就这些问题，该校初三（2）班同学进行了分组调查，以下是该班第三学习小组的调查数据。

注：“光盘行动”，指就餐时倡导人们不浪费粮食，吃光盘子里的东西，吃不完的饭菜打包带走的公益活动。

（1）请就以上调查结果，为该调查拟定一个合适的调查主题。

（2分）（2）请运用所学知识，结合以上材料，就如何践行“光盘行动”向全校师生发出倡议。

（写出倡议要点即可，15分）（1）（2分）关于影响“光盘行动”因素（原因）的调查评分标准：答到光盘行动1分，“因素/原因”1分。

若答“关于剩饭菜原因的调查”只得1分。

（2）（15分）①针对67%的学生更喜欢吃校门口小摊贩的零食，导致剩饭，我们要学会拒绝不良诱惑，增强自我保护意识，自觉履行同违法犯罪行为作斗争的义务（增强正义感）。

（4分）②针对15%的同学因心情不好影响食欲，导致剩饭，我们要学会正确调控情绪，不因不良情绪而影响进餐。

针对心情不好多为学习任务重或与老师同学发生不愉快的现象，我们应学会正确面对学习压力、正确与老师交往。

（4分）③针对20%的学生受父母浪费不良习惯的影响而导致剩饭，我们要做到正确对待父母的关爱和教育。

（2分）④针对很多同学倒掉饭菜的现象，我们要发扬艰苦创业精神，支持可持续发展战略。

（3分）⑤我们要积极投身精神文明建设，增强社会责任感，践行“光盘行动”。

（2分）评分标准：材料1分、观点1分，观点不正确材料不得分。

正义感同违法犯罪行为作斗争替换。

27.【换位思考让生活更美好】材料一：只是为了让一个素不相识的患癌老人不带着遗憾离开人世，80后南京女子靳冰便主动说自己是老人非常想念的遗弃之女，并六年如一日恪守孝顺义务。

材料二：在白下区租房的小陈同学常常要接待贸然进屋的房东，让他感觉很尴尬。

而房东认为房子是她的，她有权这么做。

小陈劝说无效，愤然退租。

材料三：晓芸数学薄弱，妈妈让她参加周末辅导班，她坚决不愿意，和妈妈大吵一顿。

初升高中考试题库及答案初升高中考是学生教育生涯中的一个重要阶段，它不仅关系到学生能否进入理想的高中，也是对学生初中阶段学习成果的一次全面检验。

以下是一份模拟的初升高中考试题库及答案，供学生和教师参考。

语文试题一、选择题（每题2分，共20分）1. 下列词语中，没有错别字的一项是：A. 锲而不舍B. 涣然冰释C. 恣意妄为D. 一愁莫展答案：C2. 下列句子中，没有语病的一项是：A. 他因为努力学习，所以成绩优异。

B. 通过这次活动，使我们受益匪浅。

C. 他不仅对历史感兴趣，而且对地理也颇有研究。

D. 我们不能因为一点小挫折就放弃追求。

答案：D二、填空题（每空1分，共10分）1. “海内存知己，天涯若比邻”是唐代诗人王勃的名句，出自他的《送杜少府之任蜀州》。

2. 《红楼梦》中，贾宝玉的通灵宝玉上刻有“莫失莫忘，仙寿恒昌”的字样。

三、阅读理解（共30分）阅读下文，回答问题。

（文章略）1. 文章的中心思想是什么？请简要概括。

（5分）2. 作者通过哪些细节描写来表现主人公的性格特点？（10分）3. 请分析文章中的象征手法及其作用。

（15分）四、作文（共40分）题目：《我的梦想》要求：1. 字数不少于800字。

2. 可以结合自身经历，表达对未来的憧憬和规划。

数学试题一、选择题（每题3分，共15分）1. 下列哪个数是最小的正整数？A. 0B. 1C. 2D. 3答案：B2. 如果一个角的度数是30°，那么它的余角是：A. 30°B. 45°C. 60°D. 90°答案：C二、填空题（每空2分，共20分）1. 圆的周长公式是C = 2πr，其中r是半径。

2. 一个直角三角形的两条直角边分别是3和4，斜边的长度是5，这是根据勾股定理得出的。

三、解答题（共65分）1. 解一元二次方程 x^2 - 5x + 6 = 0。

（10分）2. 证明：如果一个三角形的两边之和大于第三边，那么这个三角形是存在的。

东枣庄中考意义模拟题及答案在中考的复习备考过程中，模拟试题的积累是十分重要的，我们平时就要充分利用好，才能真正有效提高成绩。

以下是给你带来的最新模拟试题，希望能帮到你哈。

第I 卷第一局部听力第一节听下面五段对话。

每段对话后有一个题，从题中所给的A、A、C三个选项中选出最正确答案，并标在试卷的相应位置。

听完每段对话后，你将有5秒钟的时间来答复有关小题和阅读下一小题。

每段对话读两遍。

1. What’s John’s schoolbag?A. On his sofa.B. Under his table.C. In the bedroom.2. This dialogue is mainly about the of Laura’s cousin.A. lookB. hairC. build3. Why does Anna refuse to go to the party? Because .A. she needs to buy drinksB. there is something wrong with herC. she is not asked to buy food4. What was the woman doing at the time of snow yesterday?A. Learning from Mr. Zhang.B. Giving a lesson to Mr. Zhang.C. Listening to the sound of snow.5. What does the man want Susan to do?A. Turn off the lights.B. Save waterC. Save the environment第二节听下面一段对话，答复第6~10五个小题。

现在你有20秒钟时间阅读这五个小题，该对话读两遍。

6. Why does the man think this is Rita’s basketball? Because she .A. bought a baseball yesterdayB. sometimes plays basketballC. loves baseball most7. What does Bob’s little brother like?A. Toy truckB. Toy spaceshipC. Toy plane8. What did Anna leave?A. A bookB. A bagC. A dictionary9. What does Grace usually like doing?A. Making a toy spaceship.B. Playing basketballC. Playing tennis10. Who left a necklace?A. KathyB. LindaC. A boy第三节听下面一段短文，答复第11~15五个小题。

专题5 新定义问题中考题型训练1．（2022•娄底）若10x＝N，则称x是以10为底N的对数．记作：x＝lgN．例如：102＝100，则2＝lg100；100＝1，则0＝lg1．对数运算满足：当M＞0，N＞0时，lgM+lgN＝lg（MN）．例如：lg3+lg5＝lg15，则（lg5）2+lg5×lg2+lg2的值为（）A．5B．2C．1D．02．（2022•重庆）在多项式x﹣y﹣z﹣m﹣n中任意加括号，加括号后仍只有减法运算，然后按给出的运算顺序重新运算，称此为“加算操作”．例如：（x﹣y）﹣（z﹣m﹣n）＝x﹣y﹣z+m+n，x﹣y﹣（z﹣m）﹣n ＝x﹣y﹣z+m﹣n，…．下列说法：①至少存在一种“加算操作”，使其运算结果与原多项式相等；②不存在任何“加算操作”，使其运算结果与原多项式之和为0；③所有可能的“加算操作”共有8种不同运算结果．其中正确的个数是（）A．0B．1C．2D．33．（2022•常德）我们发现：＝3，＝3，＝3，…，＝3，一般地，对于正整数a，b，如果满足＝a时，称（a，b）为一组完美方根数对．如上面（3，6）是一组完美方根数对，则下面4个结论：①（4，12）是完美方根数对；②（9，91）是完美方根数对；③若（a，380）是完美方根数对，则a＝20；④若（x，y）是完美方根数对，则点P（x，y）在抛物线y＝x2﹣x上，其中正确的结论有（）A．1个B．2个C．3个D．4个4．（2022•南通）定义：函数图象上到两坐标轴的距离都不大于n（n≥0）的点叫做这个函数图象的“n阶方点”．例如，点（，）是函数y＝x图象的“阶方点”；点（2，1）是函数y＝图象的“2阶方点”．（1）在①（﹣2，﹣）；②（﹣1，﹣1）；③（1，1）三点中，是反比例函数y＝图象的“1阶方点”的有（填序号）；（2）若y关于x的一次函数y＝ax﹣3a+1图象的“2阶方点”有且只有一个，求a的值；（3）若y关于x的二次函数y＝﹣（x﹣n）2﹣2n+1图象的“n阶方点”一定存在，请直接写出n的取值范围．5．（2022•安顺）在平面直角坐标系中，如果点P的横坐标和纵坐标相等，则称点P为和谐点．例如：点（1，1），（，），（﹣，﹣），……都是和谐点．（1）判断函数y＝2x+1的图象上是否存在和谐点，若存在，求出其和谐点的坐标；（2）若二次函数y＝ax2+6x+c（a≠0）的图象上有且只有一个和谐点（，）．①求a，c的值；②若1≤x≤m时，函数y＝ax2+6x+c+（a≠0）的最小值为﹣1，最大值为3，求实数m的取值范围．6．（2022•遵义）新定义：我们把抛物线y＝ax2+bx+c（其中ab≠0）与抛物线y＝bx2+ax+c称为“关联抛物线”．例如：抛物线y＝2x2+3x+1的“关联抛物线”为：y＝3x2+2x+1．已知抛物线C1：y＝4ax2+ax+4a﹣3（a≠0）的“关联抛物线”为C2．（1）写出C2的解析式（用含a的式子表示）及顶点坐标；（2）若a＞0，过x轴上一点P，作x轴的垂线分别交抛物线C1，C2于点M，N．①当MN＝6a时，求点P的坐标；②当a﹣4≤x≤a﹣2时，C2的最大值与最小值的差为2a，求a的值．7．（2022•重庆）对于一个各数位上的数字均不为0的三位自然数N，若N能被它的各数位上的数字之和m 整除，则称N是m的“和倍数”．例如：∵247÷（2+4+7）＝247÷13＝19，∴247是13的“和倍数”．又如：∵214÷（2+1+4）＝214÷7＝30……4，∴214不是“和倍数”．（1）判断357，441是否是“和倍数”？说明理由；（2）三位数A是12的“和倍数”，a，b，c分别是数A其中一个数位上的数字，且a＞b＞c．在a，b，c中任选两个组成两位数，其中最大的两位数记为F（A），最小的两位数记为G（A），若为整数，求出满足条件的所有数A．8．（2022•长沙）若关于x的函数y，当t﹣≤x≤t+时，函数y的最大值为M，最小值为N，令函数h＝，我们不妨把函数h称之为函数y的“共同体函数”．（1）①若函数y＝4044x，当t＝1时，求函数y的“共同体函数”h的值；②若函数y＝kx+b（k≠0，k，b为常数），求函数y的“共同体函数”h的解析式；（2）若函数y＝（x≥1），求函数y的“共同体函数”h的最大值；（3）若函数y＝﹣x2+4x+k，是否存在实数k，使得函数y的最大值等于函数y的“共同体函数“h的最小值．若存在，求出k的值；若不存在，请说明理由．9．（2022•湘西州）定义：由两条与x轴有着相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”，如图①，抛物线C1：y＝x2+2x﹣3与抛物线C2：y＝ax2+2ax+c组成一个开口向上的“月牙线”，抛物线C1和抛物线C2与x轴有着相同的交点A（﹣3，0）、B（点B在点A右侧），与y轴的交点分别为G、H（0，﹣1）．（1）求抛物线C2的解析式和点G的坐标．（2）点M是x轴下方抛物线C1上的点，过点M作MN⊥x轴于点N，交抛物线C2于点D，求线段MN 与线段DM的长度的比值．（3）如图②，点E是点H关于抛物线对称轴的对称点，连接EG，在x轴上是否存在点F，使得△EFG 是以EG为腰的等腰三角形？若存在，请求出点F的坐标；若不存在，请说明理由．10．（2022•德州）教材呈现以下是人教版八年级上册数学教材第53页的部分内容．如图，四边形ABCD中，AD＝CD，AB＝CB．我们把这种两组邻边分别相等的四边形叫做“筝形”．概念理解（1）根据上面教材的内容，请写出“筝形”的一条性质：；（2）如图1，在△ABC中，AD⊥BC，垂足为D，△EAB与△DAB关于AB所在的直线对称，△F AC与△DAC关于AC所在的直线对称，延长EB，FC相交于点G．请写出图中的“筝形”：；（写出一个即可）应用拓展（3）如图2，在（2）的条件下，连接EF，分别交AB，AC于点M，H，连接BH．①求证：∠BAC＝∠FEG；②求证：∠AHB＝90°．1．（2023•叙州区校级模拟）新定义：[a，b，c]为二次函数y＝ax2+bx+c（a≠0，a，b，c为实数）的“图象数”，如：y＝x2﹣2x+3的“图象数”为[1，﹣2，3]，若“图象数”是[m，2m+4，2m+4]的二次函数的图象与x轴只有一个交点，则m的值为（）A．﹣2B．C．﹣2或2D．22．（2023•苏州模拟）定义：如果三角形的一个内角是另一个内角的2倍，那么称这个三角形为“倍角三角形”．若△ABC是“倍角三角形”，∠A＝90°，BC＝4，则△ABC的面积为．3．（2022•西湖区一模）已知y1，y2均为关于x的函数，当x＝a时，函数值分别为A1，A2，若对于实数a，当0＜a＜1时，都有﹣1＜A1﹣A2＜1，则称y1，y2为亲函数，则以下函数y1和y2是亲函数的是（）A．y1＝x2+1，y2＝B．y1＝x2+1，y2＝2x﹣1C．y1＝x2﹣1，y2＝D．y1＝x2﹣1，y2＝2x﹣14．（2022•平桂区一模）在数的学习过程中，我们总会对其中一些具有某种特性的数充满好奇，如学习自然数时，我们发现一种特殊的自然数——“好数”．定义：对于三位自然数n，各位数字都不为0，且百位数字与十位数字之和恰好能被个位数字整除，则称这个自然数n为“好数”．例如：426是“好数”，因为4，2，6都不为0，且4+2＝6，6能被6整除；643不是“好数”，因为6+4＝10，10不能被3整除．则百位数字比十位数字大5的所有“好数”的个数是（）A．8B．7C．6D．55．（2022•威县校级模拟）如图，在平面直角坐标系中，矩形OABC的顶点坐标分别为A（8，0），C（0，6）．把横，纵坐标均为偶数的点称为偶点．（1）矩形OABC（不包含边界）内的偶点的个数为．（2）若双曲线L：y＝上（x＞0）将矩形OABC（不包含边界）内的偶点平均分布在其两侧，则k的整数值有个．6．（2022•宁波模拟）在平面直角坐标系xOy中，对于点P（a，b），若点P′的坐标为（ka+b，a+）（其中k为常数且k≠0），则称点P′为点P的“k关联点”．已知点A在反比例函数y＝的图象上运动，且点A是点B的“关联点”，当线段OB最短时，点B的坐标为．7．（2022•天府新区模拟）给定一个矩形，如果存在另一个矩形，它的周长和面积分别是已知矩形的周长和面积的2倍，则我们称这个矩形是给定矩形的“加倍矩形”，当已知矩形的长和宽分别为3和1时，其“加倍矩形”的对角线长为．8．（2022•武侯区校级模拟）对于给定△ABC内（包含边界）的点P，若点P到△ABC其中两边的距离相等，我们称点P为△ABC的“等距点”，这段距离的最大值称为△ABC的“特征距离”．如图，在平面直角坐标系xOy中，已知点A（6，0），动点M（m，3），连接OM，AM．则△OAM的“特征距离”的最大值为．9．（2022•金牛区模拟）射线AB绕点A逆时针旋转a°，射线BA绕点B顺时针旋转b°，0°＜a＜90°，0°＜b＜90°，旋转后的两条射线交点为C，如果将逆时针方向旋转记为“+”，顺时针方向旋转记为“﹣”，则称（a，﹣b）为点C关于线段AB的“双角坐标”，如图1，已知△ABC，点C关于线段AB的“双角坐标”为（50，﹣60），点C关于线段BA的“双角坐标”为（﹣60，50）．如图2，直线AB：y＝x+交x轴、y轴于点A、B，若点D关于线段AB的“双角坐标”为（﹣m，n），y轴上一点E关于线段AB 的“双角坐标”为（﹣n，m），AE与BD交点为F，若△ADE与△ADF相似，则点F在该平面直角坐标系内的坐标是．10．（2022•长沙县校级三模）约定：若三角形一边上的中线将三角形分得的两个小三角形中有一个三角形与原三角形相似，我们则称原三角形为关于该边的“优美三角形”．例如：如图1，在△ABC中，AD为边BC上的中线，△ABD与△ABC相似，那么称△ABC为关于边BC的“优美三角形”．（1）如图2，在△ABC中，BC＝AB，求证：△ABC为关于边BC的“优美三角形”；（2）如图3，已知△ABC为关于边BC的“优美三角形”，点D是△ABC边BC的中点，以BD为直径的⊙O恰好经过点A．①求证：直线CA与⊙O相切；②若⊙O的直径为2，求线段AB的长；（3）已知三角形ABC为关于边BC的“优美三角形”，BC＝4，∠B＝30°，求△ABC的面积．11．（2023•定远县校级一模）定义：我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．（1）如图1，△ABC的三个顶点均在正方形网格中的格点上，若四边形ABCD是以AC为“相似对角线”的四边形，请只用无刻度的直尺，就可以在网格中画出点D，请你在图1中找出满足条件的点D，保留画图痕迹（找出2个即可）（2）①如图2，在四边形ABCD中，∠DAB＝90°，∠DCB＝135°，对角线AC平分∠DAB．请问AC 是四边形ABCD的“相似对角线”吗？请说明理由；②若AC＝，求AD•AB的值．（3）如图3，在（2）的条件下，若∠D＝∠ACB＝90°时，将△ADC以A为位似中心，位似比为：缩小得到△AEF，连接CE、BF，在△AEF绕点A旋转的过程中，当CE所在的直线垂直于AF时，请你直接写出BF的长．12．（2022•开福区校级一模）我们不妨定义：有两边之比为1：的三角形叫敬“勤业三角形”．（1）下列各三角形中，一定是“勤业三角形”的是；（填序号）①等边三角形；②等腰直角三角形；③含30°角的直角三角形；④含120°角的等腰三角形．（2）如图1，△ABC是⊙O的内接三角形，AC为直径，D为AB上一点，且BD＝2AD，作DE⊥OA，交线段OA于点F，交⊙O于点E，连接BE交AC于点G．试判断△AED和△ABE是否是“勤业三角形”？如果是，请给出证明，并求出的值；如果不是，请说明理由；（3）如图2，在（2）的条件下，当AF：FG＝2：3时，求∠BED的余弦值．。

初中语文阅读理解句子含义题主观题中考1. 引言在初中语文教学中，阅读理解是一个重要的环节，而句子含义题和主观题是其中的重要考察形式之一。

对于学生来说，这两种题型在中考中往往有一定的难度，需要在平时的学习中加以重点训练和掌握。

本文将从这两种题型的特点、考察内容、解题技巧等方面进行探讨，以期帮助学生在中考中取得更好的成绩。

2. 句子含义题2.1 特点句子含义题是通过对课文中抽取的一句话进行理解和分析来考察学生的阅读能力和语文表达能力的题型。

这种题型一般要求学生理解句子的具体含义，并根据上下文和语境来进行推断和解释。

2.2 考察内容句子含义题主要考察学生的文字理解能力、语言表达能力和逻辑推理能力，要求学生能够准确把握句子的含义，理解作者的意图，正确表达自己的理解，并且要能够举一反三，将句子的含义与课文内容进行联系，对整个文章进行全面的理解和分析。

2.3 解题技巧在解答句子含义题时，学生可以针对句子的词语、语气、语境等方面进行分析，通过逐字逐句的理解和推断，找出句子的核心含义，再根据上下文来进行推断和解释。

学生还可以将句子与课文内容进行对比，发现其中的联系和共通之处，以帮助自己更好地理解和解答。

3. 主观题3.1 特点主观题一般是对课文内容进行分析和理解，要求学生能够通过自己的思考和感悟对问题进行深入的分析和回答。

这种题型考察学生的文学鉴赏能力、逻辑思维能力和表达能力。

3.2 考察内容主观题主要考察学生对课文内容的深入理解和分析能力，要求学生能够就作者的用词、结构、情节等方面进行分析，提出自己的见解和看法，并能够用恰当的语言表达出来。

3.3 解题技巧在解答主观题时，学生可以从作者的用词、情节、人物形象等方面进行分析，根据自己的理解和感悟进行回答。

学生还可以适当地引用课文中的一些具体例子来支撑自己的观点，使得回答更加具体和有说服力。

4. 总结在中考中，句子含义题和主观题是语文阅读理解的重要考察形式，对学生的阅读能力、文字理解能力和表达能力都有一定的要求。

专项训练3 意义（作用、危害）类从近几年中考试题来看，非选择题多以社会重大热点为背景材料，考查形式灵活多样，作答时需从材料中提取和凝练要点，把材料语言转化为答题语言，并结合教材语言、时政语言组织答案。

试题综合探究性强，强调基础性但不是对单一、简单知识点的再现，侧重考查学生对基础知识的深入理解和综合运用。

作答时需要分析材料并结合教材知识归纳、整合，得出答案。

分析近几年中考试题可知，非选择题的设问类型呈现方式灵活多变，总结出以下几大重要设问类型：（一）说明（体现、反映）类；（二）意义（作用、危害）类；（三）原因（理由、必要性、依据）类；（四）认识（启示、警示、理解、看法）类；（五）评析（辨析）类；（六）做法（建议、践行）类；（七）开放性设问（倡议书、宣传标语、活动方案）类。

一、基本步骤和思路：“审、联、构、组”四字诀二、各步骤基本方法1．“审”——审题：先审设问，再带着对设问的理解去审材料。

这是事半功倍的做法，一定要带着问题去审材料，做到“有的放矢”。

【审设问】（1）审设问的类别：是什么；为什么；怎么做；综合型。

（2）审设问的类型：根据不同设问类型的解题方法和答题模式组织答案。

（详见下面“分类讲解”版块）（3）审设问的主语：主语的主体一般可分为国家、社会、集体、个人四种，不同的主语限定了答题的角度。

（4）审设问的限定条件：限定条件提示我们要在一定的范围内或按一定的方向答题。

例如，“分别说明了……”“共同说明了……”“联系材料……”“结合实际……”“举例说明……”“联系身边所见所闻……”“结合∕运用……的知识”“假如……”等。

【审材料】（1）学会“画题”：在材料中找出关键的词语、句子、数据等，把它们画出来。

图表题要注意画标题、数据及图表的表注内容，漫画题要注意画标题和画漫画里的文字。

（2）学会“归纳中心意思”：根据材料联系所学知识，概括出材料的中心意思，可以在材料旁边作简要文字说明。

有些材料比较复杂，可以根据题目要求（注意设问的答案是否分多个小点或角度），把材料划分层次进行分析解答。