知识总结：亥姆霍兹线圈的磁场分布特点

实验5－11 圆线圈和亥姆霍兹线圈的磁场本实验要求学生掌握弱磁场测量原理及如何用集成霍耳传感器测量磁场的方法；把测量磁感应强度值和理论值进行比较，并证明磁场迭加原理；学习亥姆霍兹线圈产生均匀磁场的特性。

实验原理1．圆线圈根据毕奥－萨伐尔定律，载流线圈在轴线（通过圆心并与线圈平面垂直的直线）上某点的磁感应强度为 ()I x R R B 2322202+=μ （1）式中I 为通过线圈的电流强度，R 为线圈平均半径，x 为圆心到该点的距离，μ0为真空磁导率。

而圆心处的磁感应强度B 0为I R B 200μ= （2）轴线外的磁场分布计算公式较复杂，这里简略。

2．亥姆霍兹线圈亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，每一线圈N 匝。

两线圈内的电流方向一致，大小相同。

线圈之间距离d 正好等于圆形线圈的半径R 。

这种线圈的特点是能在其公共轴线中点附近产生较广的均匀磁场区，故在生产和科研中有较大的实用价值，也常用于弱磁场的计量标准。

设z 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，则亥姆霍兹线圈轴线上任一点的磁感应强度为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++='--23222322202221z R R z R R NIR B μ （3）而在亥姆霍兹线圈轴线上中心O 处磁感应强度B 0为230058R NI B μ=' （4）实验仪器实验装置如图1所示，它由圆线圈和亥姆霍兹线圈实验平台（包括两个圆线圈、固定夹、不锈钢直尺等）、高灵敏度毫特计和数字式直流稳流电源等组成。

1．实验平台两个圆线圈各500匝，圆线圈的平均半径R =10.00cm 。

实验平台的台面应在两个对称圆线圈轴线上，台面上有相间1.00cm 的均匀刻线。

2．高灵敏度毫特计它采用两个参数相同的95A 型集成霍耳传感器（关于霍耳传感器请阅实验5－10），配对组成探测器，经信号放大后，用三位半数字电压表测量探测器输出信号。

实验五 磁场的描绘实验目的1．掌握感应法测量磁场的原理。

2．研究载流圆线圈轴向磁场的分布。

3．描绘亥姆霍兹线圈的磁场均匀区。

实验仪器磁场描绘仪，磁场描绘仪信号源，晶体管毫伏表，探测线圈等。

实验原理1．圆电流轴线上的磁场分布设一圆电流如图4－12－1所示。

根据毕奥—萨伐尔定律，它在轴线上某点P 的磁感应强度为2320])(1[-+=R xB B x （4－12－1）或320])(1[-+=RxB B x （4－12－2） 式中RI B 200μ=，是圆电流中心（x ＝0处）的磁感应强度，也是圆电流轴线上磁场的最大值。

当I 、R 为确定值时，B 0为一常数。

2．亥姆霍兹线圈的磁场分布亥姆霍兹线圈是由线圈匝数N 、半径R 、电流大小及方向均相同的两圆线圈组成（图4－12－2）。

两圆线圈平面彼此平行且共轴，二者中心间距离等于它们的半径R 。

若取两线圈中心连线的中点0为坐标原点，则此两线圈的中心O A 及O B 分别对应于坐标值2R 及2R -。

由于线圈中的电流方向相同，因而它们在轴线上任一点P 处所产生磁场同向。

按照（4－12－1）式，它们在P 点产生的磁感应强度分别为232220])2([2x RR NIR B A-+=μ和 232220])2([2x RR NIR B B++=μ故P 点的合磁场B (x )为B (x )＝B A ＋B B （4－12－3） 在x ＝0处（即两线圈中点处）)58()0(230R NIB μ= （4－12－4） 计算表明，当)10(R x <时，B (x)和B (0)间相对差别约万分之一，因此亥姆霍兹线圈能产生比较均匀的磁场。

在生产和科研中，若所需磁场不太强时，常用这种方法来产生较均匀的磁场。

3．测量磁场的方法磁感应强度是一个矢量，因此磁场的测量不仅要测量磁场的大小且要测出它的方向。

测定磁场的方法很多，本实验采用感应法测量磁感应强度的大小和方向。

感应法是利用通过一个探测线圈（如图4－12－3）中磁通量变化所感应的电动势大小来测量磁场。

亥姆霍兹线圈的磁场分布亥姆霍兹线圈是一种制造小范围区域均匀磁场的器件。

由于亥姆霍兹线圈具有开敞性质，很容易地可以将其它仪器置入或移出，也可以直接做视觉观察，所以，是物理实验常使用的器件。

因德国物理学者赫尔曼·冯·亥姆霍兹而命名。

【预习提示】1. 实验中如何保证霍尔传感器中心的高度位于亥姆霍兹线圈的轴线上？2. 实验中如何消除外磁场对测量结果的影响？【实验目的】1. 了解载流线圈轴线上磁场的分布，验证毕奥—莎伐尔定律，并证明磁场叠加原理。

2. 了解亥姆霍兹线圈内的磁场大小和方向分布规律。

【实验原理】1. 载流圆线圈轴线上的磁场对载流圆线圈周围磁场的研究是认识一般载流回路产生磁场的基础。

载流线圈通以直流电流，它的周围将产生一个不随时间变化的稳恒磁场。

按照毕奥—莎伐尔定律，圆电流周围任意一点的磁感应强度为 ⎰⨯=Lr r l Id B 304πμ 可以得到载流圆线圈轴线上的各点的磁感应强度B 的大小为2/32220)(2x R I R N B +=μ 式中I 为流经线圈的电流，R 线圈的平均半径，x 为该点到圆心的距离,μ0为真空磁导率，N 为线圈的匝数，磁感应强度的方向沿着轴线.满足右手螺旋定则．圆心O 处的磁感应强度大小为 RNI B 200μ=2. 亥姆霍兹线圈轴线上的磁感应强度 亥姆霍兹线圈是一对大小、形状完全相同、彼此平行放置的同轴线圈、它们之间的距离正好等于它们的半径，当两线圈中通以相同方向、相同大小的电流时，在其公共轴线中点附近产生一个较广的均匀磁场区。

它的这个特点在生产、科研中有较大的实用价值。

根据磁场叠加原理，亥姆霍兹线圈轴线上某点的磁感应强度值为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=--2/3222/322202221'x R R x R R R NI B μ 其中N 为每个线圈匝数。

而在亥姆霍兹线圈的中心O 处磁感应强度为2/30058⋅=R NIB μ 要特别指出的是，磁场叠加原理不仅适用于亥姆霍兹线圈，对于任何电流回路系统产生的磁场都适用。

圆形亥姆霍兹线圈磁场介绍圆形亥姆霍兹线圈磁场是物理学中一个重要的概念和实践应用，它在电磁学、实验物理学以及医学成像等领域中都有广泛的应用。

本文将对圆形亥姆霍兹线圈磁场进行全面、详细、完整且深入的探讨，包括其原理、性质、应用等方面的内容。

原理圆形亥姆霍兹线圈由两个同半径的圆形线圈组成，两个线圈的中心点重合且处于同一平面上。

圆形亥姆霍兹线圈的磁场主要由电流在线圈内部产生的磁场叠加得到。

磁场方向圆形亥姆霍兹线圈磁场的方向与电流的方向以及线圈的几何结构有关。

当电流通过线圈时，线圈内产生的磁场的方向垂直于线圈的平面，并形成一个向外的磁场。

两个同向电流通过的圆形线圈的磁场方向相同，可以将这两个线圈的磁场叠加，从而得到一个相对均匀的磁场。

磁场强度圆形亥姆霍兹线圈的磁场强度与电流、线圈的半径以及线圈的匝数有关。

根据比奥萨伐尔定律，磁场强度与电流成正比，与线圈的半径和匝数成正比，可以用以下公式表示：$ B = $其中，B为磁场强度，μ0为真空中的磁导率，I为通过线圈的电流，N为线圈的匝数，R为线圈的半径。

磁场分布圆形亥姆霍兹线圈中心的磁场比较均匀，随着离开中心点的距离增加，磁场的均匀性逐渐降低。

当距离线圈中心较近时，磁场的变化较小；而当距离线圈较远时，磁场的变化较大。

性质圆形亥姆霍兹线圈的磁场具有以下几个性质：1.磁场均匀性：圆形亥姆霍兹线圈在中心区域的磁场比较均匀，适用于一些需要均匀磁场的实验和应用。

2.可控性：通过调节电流、线圈半径以及匝数等参数，可以控制圆形亥姆霍兹线圈的磁场强度和分布。

3.空间方向性：圆形亥姆霍兹线圈的磁场主要在水平方向上产生，可以方便地应用于一些需要在水平方向上施加磁场的实验和设备中。

应用圆形亥姆霍兹线圈由于其磁场均匀性和可控性的特点，在许多领域中都有重要的应用。

磁场实验圆形亥姆霍兹线圈常常用于一些磁场实验和研究中，如磁场力实验、磁场梯度实验等。

其均匀且可调的磁场特性使得这些实验能够得到准确的、可重复的结果。

大学物理实验报告实验3-9 集成霍尔传感器测量圆线圈和亥姆霍兹线圈的磁场一、 实验名称：集成霍尔传感器测量圆线圈和亥姆霍兹线圈的磁场二、 实验目的：1、掌握霍尔效应原理测量磁场；2、测量单匝载流原线圈和亥姆霍兹线圈轴线上的磁场分布。

三、 实验器材：1、亥姆霍兹线圈磁场测定仪，包括圆线圈和亥姆霍兹线圈平台（包括两个圆线圈、固定夹、不锈钢直尺等）、高灵敏度毫特计和数字式直流稳压电源。

四、 实验原理：1、圆线圈的磁场：根据毕奥-萨伐尔定律，载流线圈在轴线（通过圆心并与线圈平面垂直的直线）上某点的磁感应强度为：NI x R R o 2/3222)(2B +=μ式中I 为通过线圈的电流强度，R 为线圈平均半径，x 为圆心到该点的距离，N 为线A m T o ⋅⨯=-7104πμ ，为真空磁导率。

因此，圆心处的磁感应强度为NI RB O2μ=轴线外的磁场分布计算公式较复杂。

2、亥姆霍兹线圈的磁场亥姆霍兹线圈如图3-9-1所示，是一对彼此平行且连通的共轴圆形线圈，两线圈内的电流方向一致，大小相同，线圈之间的距离d 正好等于圆形线圈的半径R 。

设z 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，根据毕奥-萨伐尔定律及磁场叠加原理可以从理论上计算出亥姆霍兹线圈周线上任意一点的磁感应强度为}])2([])2({[21B 232223222---++++⋅⋅⋅='z RR z R R R I N o μ 而在亥姆霍兹线圈上中心O 处的磁感应强度B 为RIN B o ⋅⋅='μ2358当线圈通有某一电流时，两线圈磁场合成如图：从图3-9-2可以看出，两线圈之间轴线上磁感应强度在相当大的范围内是均匀的。

五、 实验步骤：1、载流圈和骇姆霍兹线圈轴线上各点磁感应强度的测量亥姆霍兹线圈磁场测定仪:图3-9-3 亥姆霍兹线圈磁场测定仪器示意图1.毫特斯拉计2.电流表3.直流电流源4.电流调节旋钮5.调零旋钮6.传感器插头7.固定架 8.霍尔传感器 9.大理石 10.线圈 A 、B 、C 、D 为接线柱（1）按课本图3-9-3接线，直流稳流电源中数字电流表已串接在电源的一个输出端，测量电流A 100m I =时，单线圈a 轴线上各点磁感应强度a B ，每个1.00cm 测一个数据。

亥姆霍兹实验报告结论亥姆霍兹实验是一种经典的物理实验，它主要用于验证电流所产生的磁场的存在与性质。

在实验中，通过调整电流大小、线圈的半径以及测量磁场强度，可以得到一系列数据，并通过分析这些数据以得出结论。

亥姆霍兹实验首先得出了磁场的线性特性。

实验结果表明，当电流通过线圈时，线圈中产生的磁场的强度与电流成正比。

这一结论符合安培定律，即通过一段导线所产生的磁场强度与导线中的电流成正比。

其次，亥姆霍兹实验还验证了磁场的方向特性。

通过调整线圈的方向和形状，可以得到不同方向的磁场。

实验结果表明，线圈所产生的磁场是以线圈轴线为中心的，方向符合右手定则。

这意味着通过线圈的电流的方向决定了线圈所产生磁场的方向。

此外，亥姆霍兹实验还通过测量不同位置的磁场强度，得出了磁场的分布特性。

实验结果表明，两个相同的线圈并列放置时，两个线圈之间的磁场强度分布均匀。

这是因为两个线圈的磁场叠加形成的结果。

最后，亥姆霍兹实验还说明了磁场的强度与线圈的参数之间的关系。

通过调整线圈的半径和电流的大小，可以得到不同强度的磁场。

实验结果显示，磁场强度与线圈的半径的平方和电流的乘积成正比。

这一结果表明，磁场的强度可以通过控制线圈的参数来调节。

总结起来，亥姆霍兹实验验证了电流产生磁场的存在与性质。

通过分析实验数据，得出了磁场的线性特性、方向特性、分布特性以及强度与线圈参数之间的关系。

这些结论不仅仅在理论上验证了电磁学的基本原理，而且在实际应用中也具有重要意义，例如在电磁感应、电磁波传播等方面有广泛的应用。

因此，亥姆霍兹实验对于物理学的发展和应用具有重要的意义。

大学物理实验报告实验3-9 集成霍尔传感器测量圆线圈和亥姆霍兹线圈的磁场一、 实验名称：集成霍尔传感器测量圆线圈和亥姆霍兹线圈的磁场二、 实验目的：1、掌握霍尔效应原理测量磁场；2、测量单匝载流原线圈和亥姆霍兹线圈轴线上的磁场分布。

三、 实验器材：1、亥姆霍兹线圈磁场测定仪，包括圆线圈和亥姆霍兹线圈平台〔包括两个圆线圈、固定夹、不锈钢直尺等〕、高灵敏度毫特计和数字式直流稳压电源。

四、 实验原理：1、圆线圈的磁场：根据毕奥-萨伐尔定律，载流线圈在轴线〔通过圆心并与线圈平面垂直的直线〕上某点的磁感应强度为：NI x R R o 2/3222)(2B +=μ式中I 为通过线圈的电流强度，R 为线圈平均半径，x 为圆心到该点的距离，N 为线圈的匝数，A m T o ⋅⨯=-7104πμ ，为真空磁导率。

因此，圆心处的磁感应强度为NI RB O2μ=轴线外的磁场分布计算公式较复杂。

2、亥姆霍兹线圈的磁场亥姆霍兹线圈如图3-9-1所示，是一对彼此平行且连通的共轴圆形线圈，两线圈内的电流方向一致，大小相同，线圈之间的距离d 正好等于圆形线圈的半径R 。

设z 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，根据毕奥-萨伐尔定律及磁场叠加原理可以从理论上计算出亥姆霍兹线圈周线上任意一点的磁感应强度为}])2([])2({[21B 232223222---++++⋅⋅⋅='z RR z R R R I N o μ 而在亥姆霍兹线圈上中心O 处的磁感应强度B 为RIN B o ⋅⋅='μ2358当线圈通有某一电流时，两线圈磁场合成如图：从图3-9-2可以看出，两线圈之间轴线上磁感应强度在相当大的范围内是均匀的。

五、 实验步骤：1、载流圈和骇姆霍兹线圈轴线上各点磁感应强度的测量亥姆霍兹线圈磁场测定仪:图3-9-3 亥姆霍兹线圈磁场测定仪器示意图1.7.固定架 8.霍尔传感器 9.大理石 10.线圈 A 、B 、C 、D 为接线柱〔1〕按课本图3-9-3接线，直流稳流电源中数字电流表已串接在电源的一个输出端，测量电流A 100m I =时，单线圈a 轴线上各点磁感应强度a B ，每个1.00cm 测一个数据。

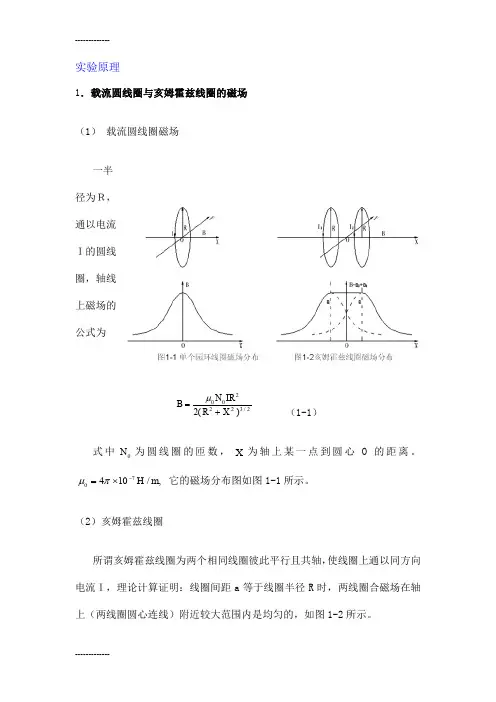
实验原理1．载流圆线圈与亥姆霍兹线圈的磁场（1） 载流圆线圈磁场一半径为Ｒ，通以电流Ｉ的圆线圈，轴线上磁场的公式为（1-1）式中为圆线圈的匝数，为轴上某一点到圆心O 的距离。

它的磁场分布图如图1-1所示。

（2）亥姆霍兹线圈所谓亥姆霍兹线圈为两个相同线圈彼此平行且共轴，使线圈上通以同方向电流Ｉ，理论计算证明：线圈间距a 等于线圈半径R 时，两线圈合磁场在轴上（两线圈圆心连线）附近较大范围内是均匀的，如图1-2所示。

23222002/)X R (IR N B +=μ0N X ,/10470m H -⨯=πμ2．霍尔效应法测磁场（1）霍尔效应法测量原理将通有电流I 的导体置于磁场中，则在垂直于电流I 和磁场B 方向上将产生一个附加电位差，这一现象是霍尔于1879电位差称为霍尔电压。

如图3-1所示N 型半导体，若在MN 两端加上电压U ，则有电流I 沿X 轴方向流动（有速度为V 运动的电子），此时在Z 轴方向加以强度为B 的磁场后，运动着的电子受洛伦兹力F B 的作用而偏移、聚集在S 平面；同时随着电子的向S 平面（下平面）偏移和聚集，在P 平面（上平面）出现等量的正电荷，结果在上下平面之间形成一个电场（此电场称之为霍尔电场）。

这个电场反过来阻止电子继续向下偏移。

当电子受到的洛伦兹力和霍尔电场的反作用力这二种达到平衡时，就不能向下偏移。

此时在上下平面（S 、P 平面）间形成一个稳定的电压（霍尔电压）。

（2）霍尔系数、霍尔灵敏度、霍尔电压设材料的长度为l ，宽为b ，厚为d ，载流子浓度为n ，载流子速度v ，则H U H E HU与通过材料的电流I有如下关系：I=nevbd霍尔电压 U H=IB/ned=R H IB/d=K H IB式中霍尔系数R H=1/ne，单位为m3/c；霍尔灵敏度K H=R H/d，单位为mV/mA 由此可见，使I为常数时，有U H= K H IB =k0B，通过测量霍尔电压U H，就可计算出未知磁场强度B。

亥姆霍兹线圈磁感应强度空间分布及其均匀性分析蒋悦090602117 网络一班摘要：根据亥姆霍兹线圈磁感应强度分布表达式，用 MATLA即矩阵实验室（Matrix Laboratory）软件对其进行数值计算，对亥姆霍兹线圈磁感应强度空间分布图象及匀强特性进行了分析。

重点讨论YOZ 平面的磁感应强度匀强特性、匀强磁场区域的三维图象、磁感应强度均匀性要求与准匀强磁场区域关系以及亥姆霍兹线圈半径R对匀强磁场区空间分布的影响。

关键词：亥姆霍兹线圈，MATLAB软件，磁感应强度空间分布，匀强特性Abstract: Based on the functions of magnetic field intensity ofHelmholtz loop , using the MATLAB did numerical analysis to study the distribution of magnetic field intensity of Helmholtz loop. The paper mainly studied the area of equivalent magnetizing filed, discussed the characteristics of the equivalent magnetization, drew the 3D picture and analyzed the approximately equivalent magnetizing field to the correspondence request. Studying the impact of changing radius of the Helmholtz loop to distribution of the equivalent magnetizing filed.Key words: Helmholtz loop、 MATLAB、 Distribution of the magnetic field intensity、Characteristic of the equivalent magnetizing filed引言如果有一对相同的载流圆线圈彼此平行且共轴，通以同方向电流，当线圈间距等于线圈半径时，两个载流线圈的总磁场在轴的中点附近的较大范围内是均匀的。

实验四十三亥姆霍兹线圈的磁场测量资料讲解
本实验旨在通过测量亥姆霍兹线圈的磁场，研究亥姆霍兹线圈的工作原理和磁场分布
规律。

亥姆霍兹线圈由两个相等的同向螺线管组成，它们刚好射线方向的中心轴上，并能
通过电源供电。

当两个螺线管通以相等的电流时，它们合成的磁场沿轴心方向，大小均匀，且磁感应强度与轴心距的平方成正比。

实验采用的仪器设备有亥姆霍兹线圈、直流电源、数字万用表、磁场探头等。

在进行
实验前，首先需要将亥姆霍兹线圈的内外半径、匝数等参数测量并记录好；同时将磁场探
头垂直于轴心放置，并用数字万用表检查并记录好其灵敏度。

实验步骤如下：
1.按照实验要求，调节电源电压和电流并用数字万用表确认电流大小。

2.将磁场探头沿轴心线移动测量磁感应强度，每次移动固定距离并记录数据。

3.移动磁场探头到亥姆霍兹线圈轴心上方一定距离处，测量此处的磁感应强度。

4.分别测量单个螺线管通电时的磁感应强度，并与两个螺线管通电时的磁感应强度进
行比较。

在进行实验测量时，需要注意以下几点：
1.在每组测量数据前，需要将电源电压和电流调至零并等待一段时间，确保仪器处于
稳态。

2.在移动磁场探头时，应该保持探头位置和朝向的一致性，并确保探头的垂直方向与
轴心平行。

3.每组数据的测量应该重复多次，并求取平均值以提高测量精度。

本实验测量到的结果可为今后深入研究电磁现象和应用提供基础数据和理论依据，对
于提高学生的实验能力和科学素养也具有一定的指导意义。

一、实验目的1. 了解电磁感应法测磁场的原理；2. 掌握用探测线圈测量载流线圈的磁场的方法；3. 验证矢量叠加原理；4. 了解亥姆霍兹线圈磁场的特点。

二、实验原理1. 电磁感应法测磁场：当导线中通有变化电流时，其周围空间必然产生变化磁场。

处在变化磁场中的闭合回路，由于通过它的磁通量发生变化，回路中将有感应电动势产生。

通过测量此感应电动势的大小就可以计算出磁场的量值。

2. 毕奥-萨伐尔定律：载流线圈在轴线（通过圆心并与线圈平面垂直的直线）上某点的磁感应强度为：\[ B = \frac{\mu_0 I}{2\pi r} \]式中，\( B \) 为磁感应强度，\( \mu_0 \) 为真空磁导率，\( I \) 为通过线圈的电流强度，\( r \) 为圆心到该点的距离。

3. 亥姆霍兹线圈磁场：亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，两线圈内电流方向一致，大小相似，线圈之间距离 \( d \) 恰好等于圆形线圈半径\( R \)。

亥姆霍兹线圈中心处的磁感应强度为零，轴线附近基本是一个匀强磁场。

三、实验仪器1. 圆线圈和亥姆霍兹线圈实验平台，台面上有等距离 1.0 cm 间隔的网格线；2. 高灵敏度三位半数字式毫特斯拉计；3. 三位半数字式电流表；4. 直流稳流电源；5. 霍尔传感器探头（2只配对的 95A 型集成霍尔传感器）。

四、实验步骤1. 将亥姆霍兹线圈放置在实验平台上，调整线圈位置，使其中心与网格线对齐。

2. 连接实验仪器，包括毫特斯拉计、电流表、直流稳流电源和霍尔传感器探头。

3. 设置直流稳流电源，调节电流，使线圈中的电流强度满足实验要求。

4. 将霍尔传感器探头置于亥姆霍兹线圈中心位置，调整探头角度，使探头平面与线圈轴线平行。

5. 读取毫特斯拉计的示数，记录该点的磁感应强度。

6. 移动霍尔传感器探头，按照网格线间隔，测量亥姆霍兹线圈中心附近各点的磁感应强度。

7. 改变线圈中的电流强度，重复步骤 5 和 6，记录不同电流强度下的磁感应强度数据。

第1篇一、实验目的1. 观察亥姆霍兹线圈中间磁场的均匀性。

2. 验证磁场叠加原理。

3. 了解一种得到均匀磁场的实验室方法。

二、实验原理亥姆霍兹线圈是由两个相同的线圈同轴放置，其中心间距等于线圈的半径。

当两个线圈通以同向电流时，磁场叠加增强，并在一定区域形成近似均匀的磁场；通以反向电流时，则叠加使磁场减弱，以至出现磁场为零的区域。

本实验中，通过霍尔元件测量磁场。

霍尔元件通以恒定电流时，它在磁场中会感应出霍尔电压，霍尔电压的高低与霍尔元件所在处的磁感应强度成正比。

因此，可以通过测量霍尔电压来间接测量磁感应强度。

三、实验仪器1. 亥姆霍兹线圈演示仪2. 霍尔元件3. 稳压电源4. 数码显示屏5. 导轨四、实验步骤1. 打开数码显示屏后面板的开关，先对LED显示屏调零。

2. 打开稳压电源（已调好），同方向闭合两电键（使两线圈通以相同方向电流），转动小手柄，使位于线圈轴线上的霍尔元件由导轨的一端缓慢移向另一端，观察两同向载流圆线圈磁场合成后的分布。

记录显示屏示数。

3. 改变其中一个线圈的电流方向，重复步骤2的操作，观察两反向载流圆线圈磁场合成后的分布。

记录显示屏示数。

4. 将霍尔元件移至线圈中心区域，观察磁场分布，记录显示屏示数。

5. 重复步骤2-4，分别改变电流大小，观察磁场分布变化。

五、实验结果与分析1. 实验结果（1）当两个线圈通以同向电流时，磁场叠加增强，显示屏示数逐渐增大，中间一段基本不变，最后又由大变小。

（2）当两个线圈通以反向电流时，磁场叠加减弱，显示屏示数由小变大，由大变小，又由小变大，由大变小。

（3）将霍尔元件移至线圈中心区域，显示屏示数在中间区域基本不变，两端逐渐减小。

2. 结果分析（1）实验结果验证了磁场叠加原理。

当两个线圈通以同向电流时，磁场叠加增强；通以反向电流时，磁场叠加减弱。

（2）实验结果表明，亥姆霍兹线圈中间区域磁场近似均匀，两端磁场逐渐减小。

（3）实验结果与理论分析基本一致，证明了亥姆霍兹线圈在中间区域能够形成近似均匀的磁场。